PhysBook:Электронный учебник физики — PhysBook

Содержание

• 1 Учебники
• 2 Механика
  • 2.1 Кинематика
  • 2.2 Динамика
  • 2.3 Законы сохранения
  • 2.4 Статика
  • 2.5 Механические колебания и волны
• 3 Термодинамика и МКТ
  • 3.1 МКТ
  • 3. 2 Термодинамика
• 4 Электродинамика
  • 4.1 Электростатика
  • 4.2 Электрический ток
  • 4.3 Магнетизм
  • 4.4 Электромагнитные колебания и волны
• 5 Оптика. СТО
  • 5.1 Геометрическая оптика
  • 5.2 Волновая оптика
  • 5. 3 Фотометрия
  • 5.4 Квантовая оптика
  • 5.5 Излучение и спектры
  • 5.6 СТО
• 6 Атомная и ядерная
  • 6.1 Атомная физика. Квантовая теория
  • 6.2 Ядерная физика
• 7 Общие темы
• 8 Новые страницы

Здесь размещена информация по школьной физике:

1. материалы из учебников, лекций, рефератов, журналов;
2. разработки уроков, тем;
3. flash-анимации, фотографии, рисунки различных физических процессов;
4. ссылки на другие сайты

и многое другое.

Каждый зарегистрированный пользователь сайта имеет возможность выкладывать свои материалы (см. справку), обсуждать уже созданные.

Учебники

Формулы по физике – 7 класс – 8 класс – 9 класс – 10 класс – 11 класс –

Механика

Кинематика

Основные понятия кинематики – Прямолинейное движение – Криволинейное движение – Движение в пространстве

Динамика

Законы Ньютона – Силы в механике – Движение под действием нескольких сил

Законы сохранения

Закон сохранения импульса – Закон сохранения энергии

Статика

Статика твердых тел – Динамика твердых тел – Гидростатика – Гидродинамика

Механические колебания и волны

Механические колебания – Механические волны

---

Термодинамика и МКТ

МКТ

Основы МКТ – Газовые законы – МКТ идеального газа

Термодинамика

Первый закон термодинамики – Второй закон термодинамики – Жидкость-газ – Поверхностное натяжение – Твердые тела – Тепловое расширение

---

Электродинамика

Электростатика

Электрическое поле и его параметры – Электроемкость

Электрический ток

Постоянный электрический ток – Электрический ток в металлах – Электрический ток в жидкостях – Электрический ток в газах – Электрический ток в вакууме – Электрический ток в полупроводниках

Магнетизм

Магнитное поле – Электромагнитная индукция

Электромагнитные колебания и волны

Электромагнитные колебания – Производство и передача электроэнергии – Электромагнитные волны

---

Оптика.

СТО

Геометрическая оптика

Прямолинейное распространение света. Отражение света – Преломление света – Линзы

Волновая оптика

Свет как электромагнитная волна – Интерференция света – Дифракция света

Фотометрия

Фотометрия

Квантовая оптика

Квантовая оптика

Излучение и спектры

Излучение и спектры

СТО

СТО

---

Атомная и ядерная

Атомная физика. Квантовая теория

Строение атома – Квантовая теория – Излучение атома

Ядерная физика

Атомное ядро – Радиоактивность – Ядерные реакции – Элементарные частицы

---

Общие темы

Измерения – Методы решения – Развитие науки- Статья- Как писать введение в реферате- Подготовка к ЕГЭ — Репетитор по физике

Новые страницы

Запрос не дал результатов.

Действие магнитного поля на движущийся заряд. Сила Лоренца.

Урок 4. Действие магнитного поля на движущийся заряд. Сила Лоренца.

Цель урока:  изучить новое физическое явление – действие магнитного поля на движущийся заряд, вывести формулу и ввести мнемоническое правило для определения модуля и направления силы Лоренца, показать возможность применения знаний для расчёта периода обращения частицы в магнитном поле, познакомить учащихся с практическим применением действия силы Лоренца в ускорителях.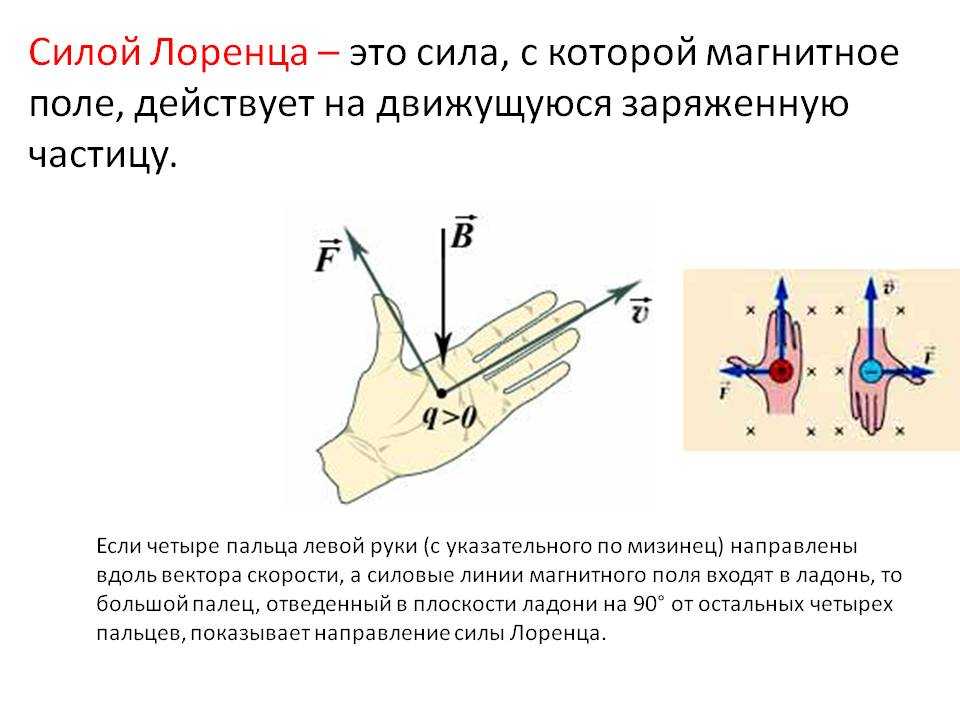

Задачи:

Образовательные: изучить поведение движущихся электрических зарядов в магнитном поле;

вывести формулу и правило для определения модуля и направления силы Лоренца.

Развивающие: развитие практических навыков рассчитывать силу Лоренца, определять ее направление.

Воспитательные: привитие наблюдательности, внимания.

Тип урока: комбинированный урок

План:

1) Организационный момент. Актуализация знаний.

2) Изучение нового материала.

3) Закрепление изученного. Итог урока.

Ход урока:

1)Организационный момент.

Объявление темы и цели урока.

Вопросы для повторения:

1. Почему магнитные силы, действующие на проводники катушки прибора, не зависят от угла поворота катушки?

2. Что удерживает рамку от вращения в магнитном поле?

3. Чем амперметр отличается от вольтметра?

4. Укажите направление вектора магнитной индукции, электрического тока и силы Ампера на схеме громкоговорителя (см. рис. 1.22).

2)Изучение нового материала

Электрический ток — это упорядоченно движущиеся заряженные частицы. Поэтому действие магнитного поля на проводник с током есть результат действия поля на движущиеся заряженные частицы внутри проводника. Найдем силу, действующую на одну частицу.

Силу, действующую на движущуюся заряженную частицу со стороны магнитного поля, называют силой Лоренца в честь великого голландского физика X. Лоренца (1853— 1928) — основателя электронной теории строения вещества. Силу Лоренца можно найти с помощью закона Ампера.

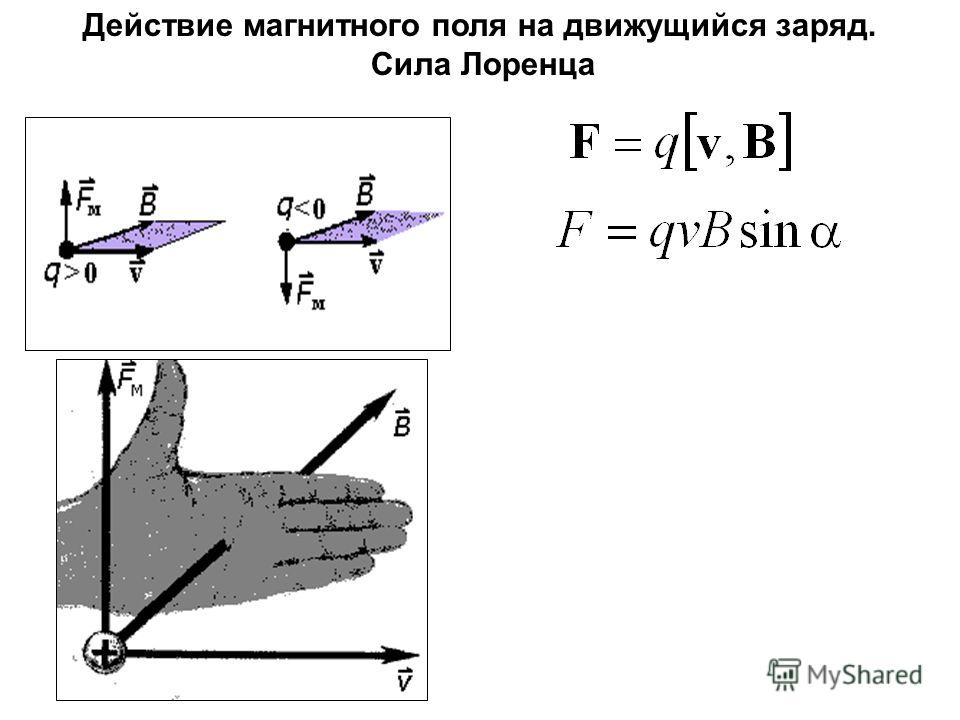
Модуль силы Лоренца

Модуль силы Лоренца равен отношению модуля силы F, действующей на участок проводника длиной Δl, к числу N заряженных частиц, упорядоченно движущихся в этом участке проводника:

Рассмотрим отрезок тонкого прямого проводника с током (рис.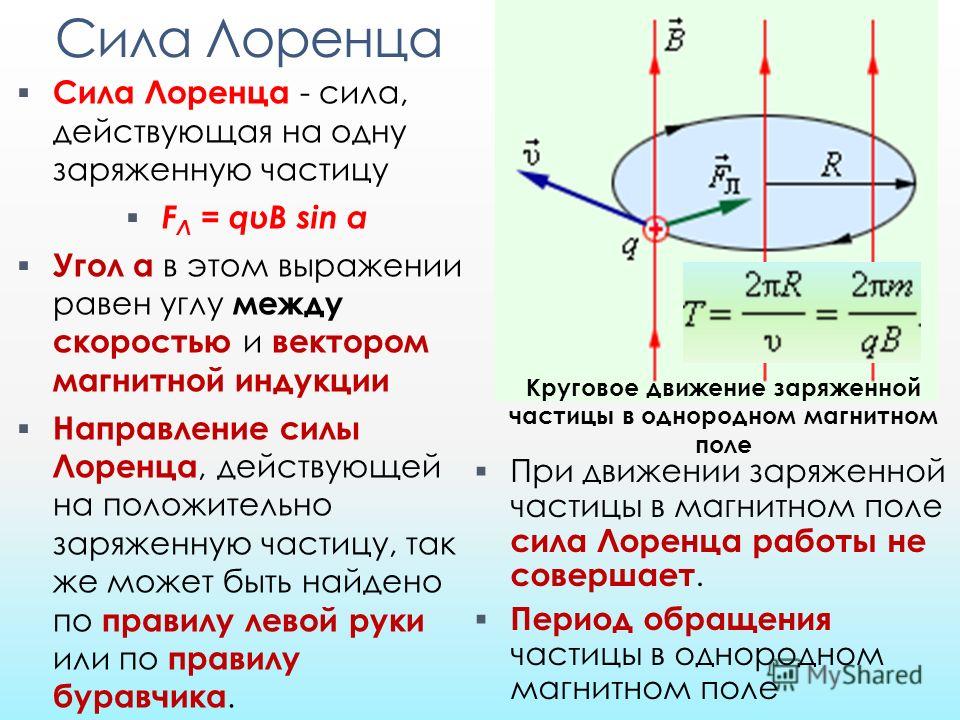 1.23). Пусть длина отрезка δl и площадь поперечного сечения проводника S настолько малы, что вектор индукции магнитного поля   можно считать одинаковым в пределах этого отрезка проводника. Сила тока I в проводнике связана с зарядом частиц q, концентрацией заряженных частиц (числом зарядов в единице объема) и скоростью их упорядоченного движения υ следующей формулой:

I = qnυS.                     (1.4)

Модуль силы, действующей со стороны магнитного поля на выбранный элемент тока, равен:

F = |I| BΔl sin α.

Подставляя в эту формулу выражение (1.4) для силы тока, получаем:

F = |q| nυS&ΔlB sin α = υ|q| NB sin α,

где N = nSΔl — число заряженных частиц в рассматриваемом объеме. Следовательно, на каждый движущийся заряд со стороны магнитного поля действует сила Лоренца, равная:

где α — угол между вектором скорости и вектором магнитной индукции.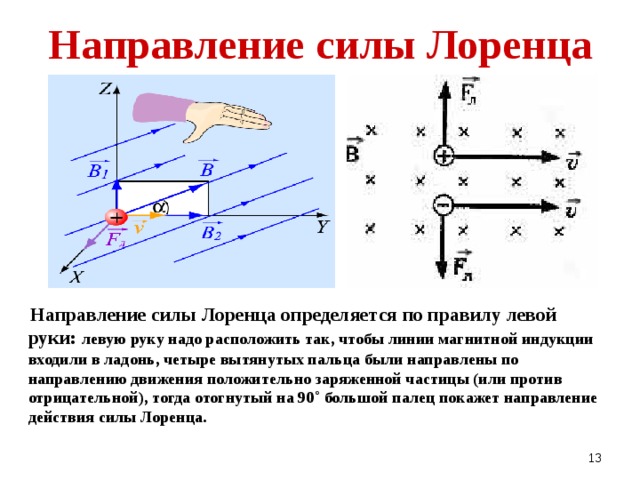

Сила Лоренца перпендикулярна векторам   и  . Ее направление определяется с помощью того же правила левой руки, что и направление силы Ампера: если левую руку расположить так, чтобы составляющая магнитной индукции  , перпендикулярная скорости заряда, входила в ладонь, а четыре вытянутых пальца были направлены по движению положительного заряда (против движения отрицательного), то отогнутый на 90° большой палец укажет направление действующей на заряд силы Лоренца F_л (рис. 1.24).

Электрическое поле действует на заряд q с силой F_эл = q . Следовательно, если есть и электрическое поле, и магнитное поле, то суммарная сила  , действующая на заряд, равна:

 = _ал + _л

Так как сила Лоренца перпендикулярна скорости частицы, то она не совершает работы. Согласно теореме о кинетической энергии (см. учебник физики для 10 класса) это означает, что сила Лоренца не меняет кинетическую энергию частицы и, следовательно, модуль ее скорости. Под действием силы Лоренца меняется лишь направление скорости частицы.

Движение заряженной частицы в однородном магнитном поле. Рассмотрим движение частицы с зарядом q в однородном магнитном поле  , направленном перпендикулярно к начальной скорости частицы   (рис. 1.25).

Сила Лоренца зависит от модулей векторов скорости частицы и индукции магнитного поля. Так как магнитное поле не меняет модуль скорости движущейся частицы, то остается неизменным и модуль силы Лоренца. Эта сила перпендикулярна скорости и, следовательно, определяет центростремительное ускорение частицы. Неизменность по модулю центростремительного ускорения частицы, движущейся с постоянной по модулю скоростью, означает, что частица равномерно движется по окружности радиусом r. Определим этот радиус.

Согласно второму закону Ньютона (см. рис. 1.25)

Время, за которое частица делает полный оборот (период обращения), равно:

Использование действия магнитного поля на движущийся заряд

Действие магнитного поля на движущийся заряд широко используют в современной технике. Достаточно упомянуть телевизионные трубки (кинескопы), в которых летящие к экрану электроны отклоняются с помощью магнитного поля, создаваемого особыми катушками.

Сила Лоренца используется в ускорителе заряженных частиц (циклотрон) для получения частиц с большими энергиями. Циклотрон состоит из двух полых полуцилиндров (дуантов) 3, находящихся в однородном магнитном поле (рис. 1.26). Между дуантами создается переменное электрическое поле. Согласно формуле (1.6) при увеличении скорости частицы 1 радиус окружности (траектории 2), по которой движется частица, увеличивается. Период обращения частицы не зависит от скорости (см. формулу (1.7)), и, следовательно, через полпериода, вследствие изменения направления электрического поля, частица снова оказывается в ускоряющем ее поле и т. д. На последнем витке частица вылетает из циклотрона.

На действии магнитного поля основано также и устройство приборов, позволяющих разделять заряженные частицы по их удельным зарядам, т. е. по отношению заряда частицы к ее массе, и по полученным результатам точно определять массы частиц. Такие приборы получили название масс-спектрографов.

На рисунке 1.27 изображена принципиальная схема простейшего масс-спектрографа. Вакуумная камера прибора помещена в магнитное поле (вектор индукции   перпендикулярен рисунку). Ускоренные электрическим полем заряженные частицы (электроны или ионы), описав дугу, попадают на фотопластинку, где оставляют след, позволяющий с высокой точностью измерить радиус траектории r. По этому радиусу определяется удельный заряд иона. Зная заряд иона, легко вычислить его массу.

На движущуюся заряженную частицу со стороны магнитного поля действует сила Лоренца. Эта сила перпендикулярна скорости и не совершает работы.

3) Закрепление изученного. Итог урока.

Домашнее задание.  §6 вопросы

1. Чему равен модуль силы Лоренца?

2. Как движется заряженная частица в однородном магнитном поле, если начальная скорость частицы перпендикулярна линиям магнитной индукции?

3. Как определить направление силы Лоренца?

Движение заряженных частиц в магнитном поле. Формула и типы

Мы читали о взаимодействии электрического поля и магнитного поля и о движении заряженных частиц в присутствии как электрического, так и магнитного полей, а также вывели соотношение сила, действующая на заряженную частицу, в данном случае определяется силой Лоренца. Мы также читали о магнитной силе, действующей на проводящий стержень с током, помещенный в магнитное поле. Но что происходит, когда заряженная частица движется в присутствии магнитного поля? Как определить траекторию такой частицы? В этом разделе мы узнаем об этом подробно.

Говорят, что сила, действующая на частицу, совершает работу, если составляющая силы направлена ​​в направлении движения частицы. В рассматриваемом случае, когда имеется заряженная частица с зарядом q, движущаяся в однородном магнитном поле величиной В, магнитная сила действует перпендикулярно скорости частицы. Здесь мы говорим, что магнитная сила не совершает никакой работы над частицей, и, следовательно, нельзя увидеть никакого изменения скорости частицы.

Математически, когда скорость частицы v перпендикулярна направлению магнитного поля, мы можем написать,

\(\begin{array}{l} F = q ( v \times B ) \end{array} \)

Здесь магнитная сила направлена ​​к центру кругового движения объекта и действует как центростремительная сила. Таким образом, если v и B перпендикулярны друг другу, частица описывает окружность. В других случаях, когда компонента скорости присутствует вдоль направления магнитного поля В, то ее величина остается неизменной на протяжении всего движения, так как на нее не ощущается влияние магнитного поля. Кроме того, движение из-за перпендикулярной составляющей скорости носит круговой характер, как обсуждалось выше. Результирующее движение из-за двух компонентов представляет собой спиральное движение, как показано на изображении ниже. 9{ 2 } }{ r } = q v B \end{массив} \)

или

\(\begin{array}{l} r = \frac{m v }{q B} \end{array} \)

Здесь r дает радиус окружности, описываемой частицей.

Кроме того, если мы запишем угловую частоту частицы как ω, то мы можем написать

\(\begin{array}{l} v = \omega r \end{array} \)

Итак,

\(\begin{array}{l} \omega = 2 \pi v = \frac{qB}{m} \end{array} \)

Здесь v — частота вращения частицы. Время одного оборота можно определить как

\(\begin{array}{l} T = \frac{ 2 \pi }{\omega } = \frac{ 1 }{v } \end{array} \)

Расстояние, пройденное частицей вдоль направления магнитного поля за один оборот, определяется ее шагом.

\(\begin{array}{l} p = v _ {p} T = \frac{ 2 \pi m v _ {p} }{q B} \end{array} \)

Где v _p — скорость, параллельная магнитному полю.

Лекция о движущихся зарядах и магнетизме на хинди

Чтобы узнать больше о движении заряженных частиц в магнитном поле, нажмите на видео ниже

Часто задаваемые вопросы – Часто задаваемые вопросы

Что такое магнитная сила?

Магнитная сила между двумя движущимися зарядами может быть описана как эффект, оказываемый на каждый заряд магнитным полем, создаваемым другим.

Определение плотности магнитного потока.

Плотность магнитного потока — это величина магнитного потока в области, взятой перпендикулярно направлению магнитного потока. Он обозначается символом B и измеряется в единицах Тесла.

Определение напряженности магнитного поля.

Интенсивность магнитного поля или напряженность магнитного поля — это отношение MMF, необходимого для создания определенной плотности потока (B) в определенном материале на единицу длины этого материала.

Существуют ли в космосе магнитные поля?

Да, в космосе есть магнитные поля. Спиральные рукава Млечного Пути, судя по исследованиям большого числа пульсаров и поляризации их радиосигналов, обладают очень крупномасштабным организованным магнитным полем. Обнаружено, что межзвездные пылевые облака обладают магнитными полями. Когда эти облака разрушаются, поля усиливаются.

Что такое сила Лоренца?

Сила Лоренца определяется как комбинация магнитной и электрической сил, действующих на точечный заряд из-за электромагнитных полей. Он используется в электромагнетизме и также известен как электромагнитная сила. В 1895 году Хендрик Лоренц вывел современную формулу силы Лоренца.

Посмотрите видео и узнайте о силе, действующей на движущийся заряд в магнитном поле

Следите за новостями BYJU’S и влюбитесь в обучение!

электромагнетизм — Как можно определить силу Лоренца для зарядов в состоянии покоя, а также для зарядов в движении?

спросил 2 года 8 месяцев назад

Изменено 2 года, 8 месяцев назад

Просмотрено 260 раз

$\begingroup$

Мы знаем, что электрическое поле или электрическая сила действует на заряды в состоянии покоя, а магнитная сила действует на заряды в движении. Но когда мы объединяем эти два, мы получаем то, что мы называем 9.

0110 Сила Лоренца. Итак, я хочу знать, как эти две силы могут действовать на один и тот же заряд. Либо должно быть так, что на заряд действует Э.Ф (если в покое), либо М.Ф (если в движении). Итак, почему мы объединяем эти две силы Лоренца. Какая потребность?

• электромагнетизм
• специальная теория относительности
• силы
• заряд
• инерциальные системы отсчета

$\endgroup$

2

$\begingroup$

В

не должно быть «следует»

Либо должно быть так, что на заряд действует Э.Ф (если он покоится), либо М.Ф (если он движется).

А именно, как упоминалось в комментариях, любая электрически заряженная частица испытывает силу электрического поля $\vec{E}$, равную $$\vec{F} = q \vec{E}$$

независимо от того, движется он или нет.