Кодирование звуковой информации

Двоичное кодирование звуковой информации

Временная дискретизация звука.

Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой.

Чем больше амплитуда сигнала, тем он громче для человека, чем больше частота сигнала, тем выше тон.

Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц).

 

В процессе кодирования непрерывного (аналогового) звукового сигнала производится его временная дискретизация.

Непрерывная звуковая волна разбивается на отдельные маленькие временные участки.

Для каждого участка устанавливается определенная величина амплитуды.

Непрерывная зависимость амплитуды сигнала от времени A (

t ) заменяется на дискретную последовательность уровней громкости.

На графике это выглядит как замена гладкой кривой на последовательность «ступенек»

Каждой «ступеньке» присваивается значение уровня гром к ости звука, его код (1, 2, 3 и так далее).

Уровни громкости звука — набор возможных состояний.

Чем большее количество уровней громкости будет выделено в процессе кодирования, тем большее количество информации несет значение каждого уровня и тем более качественным будет звучание.

Современные звуковые карты обеспечивают 16-битную глубину кодирования звука. Количество различных уровней сигнала (состояний при данном кодировании) можно рассчитать по формуле:

N = 2 I = 2 16 = 65536,

где I — глубина звука.

Таким образом, современные звуковые карты могут обеспечить кодирование 65536 уровней сигнала.

Частота дискретизации

При двоичном кодировании непрерывного звукового сигнала он заменяется последовательностью дискретных уровней сигнала.

Качество кодирования зависит от количества измерений уровня сигнала в единицу времени, то есть

частоты дискретизации.

Чем большее количество измерений производится за 1 секунду (чем больше частота дискретизации), тем точнее процедура двоичного кодирования.

Количество измерений в секунду может лежать в диапазоне от 8000 до 48 000, то есть частота дискретизации аналогового звукового сигнала может принимать значения от 8 до 48 кГц.

При частоте 8 кГц качество дискретизированного звукового сигнала соответствует качеству радиотрансляции .

При частоте 48 кГц — качеству звучания аудио-

CD .

Также возможны моно- (1 канал), и стерео- (2 канала) режимы.

Импульсно-кодовая модуляция (англ. Pulse Code Modulation , PCM ) заключается в том, что звуковая информация хранится в виде значений амплитуды, взятых в определенные моменты времени (т.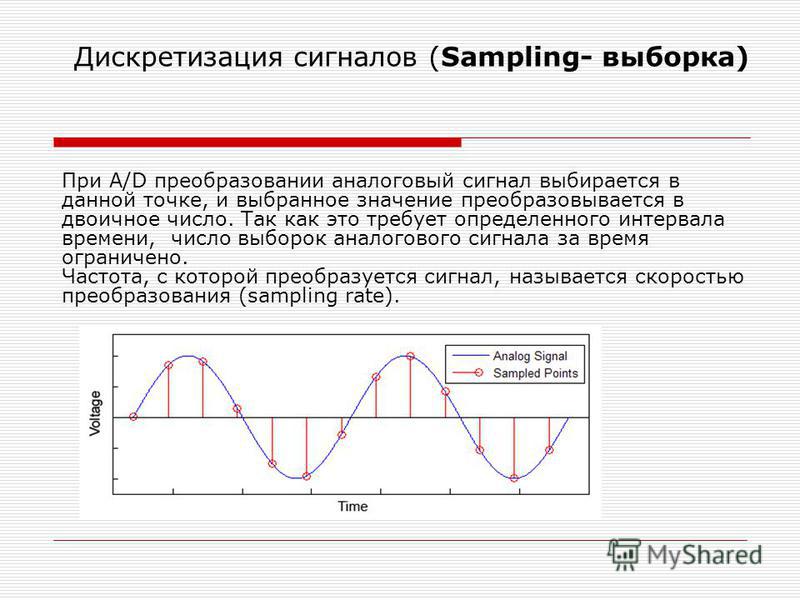 е. измерения проводятся «импульсами»).

При записи звука в компьютер амплитуда измеряется через равные интервалы времени с некоторой достаточно большой частотой.

При воспроизведении звука компьютер использует сохраненные значения для того, чтобы восстановить непрерывную форму выходного сигнала.

Исходный сигнал Хранимая информация Воспроизводимый сигнал

Процесс получения цифровой формы звука называют оцифровкой.

Устройство, выполняющее оцифровку звука, называется аналого-цифровым преобразователем (АЦП). Устройство, выполняющее обратное преобразование, из цифровой формы в аналоговую, называется цифро-аналоговым преобразователем (ЦАП).

В современных компьютерах основная обработка звука выполняется звуковыми картами .

Помимо АЦП и ЦАП звуковые карты содержат

сигнальный процессор — специализированный микрокомпьютер для обработки оцифрованного звука, выполняющий значительную часть рутинных расчетов при обработке звуков (смешение звуков, наложение спецэффектов, расчет формы выходного сигнала и т. п.; центральный процессор не тратит время на выполнение этих работ).

Можно оценить информационный объем стереоаудиофайла длительностью звучания 1 секунда при высоком качестве звука (16 битов, 48 кГц).

Для этого количество битов, приходящихся на одну выборку, необходимо умножить на количество выборок в 1 секунду и умножить на 2 (стерео – два канала):

16 бит • 48 000 • 2 = 1 536 000 бит =

=192 000 байт = 187,5 Кбайт.

З А Д А Ч И

1. Оцените информационный объем моноаудиофайла длительностью звучания 1 мин, если «глубина» кодирования и частота дискретизации звукового сигнала равны соответственно:

а) 16 бит и 8 кГц;

б) 16 бит и 24 кГц.

2. Определите качество звука (качество радиотрансляции, среднее качество, качество аудио- CD ), если известно, что объем моноаудиофайла длительностью звучания в 10 сек.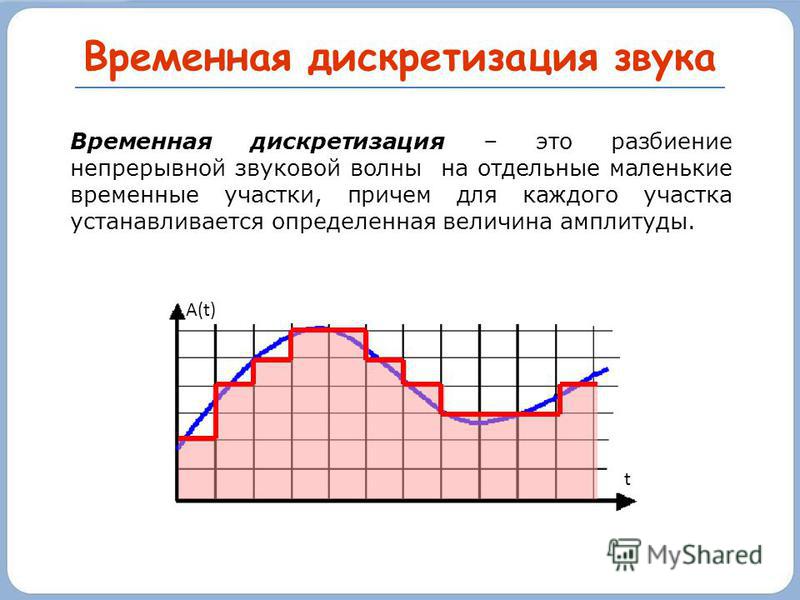

равен:

а) 940 Кбайт;

б) 157 Кбайт.

3. Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен:

а) 700 Кбайт;

б) 6300 Кбайт.

 

4. Аналоговый звуковой сигнал был дискретизирован сначала с использованием 256 уровней интенсивности сигнала (качество звучания радиотрансляции), а затем с использованием 65536 уровней интенсивности сигнала (качество звучания аудио- CD ). Во сколько раз различаются информационные объемы оцифрованного звука?

Звук – волна с непрерывно изменяющейся амплитудой и частотой. чем больше амплитуда, тем он громче для человека, чем больше частота, тем выше тон.

Звуковые сигналы в окружающем нас мире необычайно разнообразны. Сложные непрерывные сигналы можно с достаточной точностью представлять в виде суммы некоторого числа простейших синусоидальных колебаний.

Причем каждое слагаемое, то есть каждая синусоида, может быть точно задана некоторым набором числовых параметров – амплитуды, фазы и частоты, которые можно рассматривать как код звука в некоторый момент времени.

В процессе кодирования звукового сигнала производится его временная дискретизация – непрерывная волна разбивается на отдельные маленькие временные участки и для каждого такого участка устанавливается определенная величина амплитуды.

Таким образом непрерывная зависимость амплитуды сигнала от времени заменяется на дискретную последовательность уровней громкости.

Каждому уровню громкости присваивается его код. Чем большее количество уровней громкости будет выделено в процессе кодирования, тем большее количество информации будет нести значение каждого уровня и тем более качественным будет звучание.

Качество двоичного кодирования звука определяется глубиной кодирования и частотой дискретизации.

Частота дискретизации– количество измерений уровня сигнала в единицу времени.

Количество уровней громкости определяет глубину кодирования. Современные звуковые карты обеспечивают 16-битную глубину кодирования звука. При этом количество уровней громкости равно N = 216 = 65536.

Представление видеоинформации

В последнее время компьютер все чаще используется для работы с видеоинформацией. Простейшей такой работой является просмотр кинофильмов и видеоклипов. Следует четко представлять, что обработка видеоинформации требует очень высокого быстродействия компьютерной системы.

Что представляет собой фильм с точки зрения информатики? Прежде всего, это сочетание звуковой и графической информации. Кроме того, для создания на экране эффекта движения используется дискретная по своей сути технология быстрой смены статических картинок. Исследования показали, что если за одну секунду сменяется более 10-12 кадров, то человеческий глаз воспринимает изменения на них как непрерывные.

Казалось бы, если проблемы кодирования статической графики и звука решены, то сохранить видеоизображение уже не составит труда. Но это только на первый взгляд, поскольку, как показывает разобранный выше пример, при использовании традиционных методов сохранения информации электронная версия фильма получится слишком большой. Достаточно очевидное усовершенствование состоит в том, чтобы первый кадр запомнить целиком (в литературе его принято называть ключевым), а в следующих сохранять лишь отличия от начального кадра (разностные кадры).

Существует множество различных форматов представления видеоданных.

В среде Windows, например, уже более 10 лет (начиная с версии 3.1) применяется формат Video for Windows, базирующийся на универсальных файлах с расширением AVI (Audio Video Interleave – чередование аудио и видео).

Более универсальным является мультимедийный формат Quick Time, первоначально возникший на компьютерах Apple.

Практикум №3

Тема: Дискретное представление текстовой, графической, звуковой информации и видеоинформации.

Ход работы:

Задание №1.Используя таблицу символов, записать последовательность десятичных числовых кодов в кодировке Windows для своих ФИО, названия улицы, по которой проживаете. Таблица символов отображается в редакторе MS Word с помощью команды: вкладка ВставкаСимволДругие символы

В поле Шрифт выбираете Times New Roman, в поле из выбираете кириллица. Например, для буквы «А» (русской заглавной) код знака– 192.

Выполнение задания №1

Л

И

П

А

Т

О

В

А

Л

Е

К

С

Е

Й

А

Л

Е

К

С

А

Н

Д

Р

О

В

И

Ч

Ф	А	В	О	Р	С	К	О	Г	О

Задание №2. Используя стандартную программу БЛОКНОТ, определить, какая фраза в кодировке Windows задана последовательностью числовых кодов и продолжить код. Запустить БЛОКНОТ. С помощью дополнительной цифровой клавиатуры при нажатой клавише ALT ввести код, отпустить клавишу ALT.В документе появиться соответствующий символ.

Выполнение задания №2

я

у

ч

у

с

ь

в

б

и

к

п

о

с

п

е

ц

и

а

л

ь

н

о

с

т

и

Э	Л	Е	К	Т	Р	И	К

Задание №3. Заполнить пропуски числами:

Кбайт

=3072

байт

=24576

бит

Кбайт

=5120

байт

=40960

бит

Кбайт

=7168

байт

=57344

бит

Задание № 4

Статьи к прочтению:

• Абсолютное позиционирование
• Ацп последовательного приближения

Свойства звука:высота, длительность, громкость, тембр. Теория музыки, Урок 3.

Похожие статьи:

• Двоичное кодирование звука

  Лабораторная работа №5 Тема: Дискретное (цифровое) представление текстовой, графической, звуковой информации и видеоинформации Цель работы:научиться…

• Формулы шеннона для непрерывного и дискретного каналов

  Формулы Шеннона представляют собой математические записи теорем кодирования Шеннона для дискретных и непрерывных сообщений, передаваемых по каналам с…

Квантование и шум квантования — DSPIllustrations.

com

Квантизатор — это блок обработки сигналов, который преобразует непрерывную амплитуду в дискретную амплитуду. Выход квантователя является дискретным, то есть он может выводить только $Q$ различных значений. На практике квантователь представляет собой аналого-цифровой преобразователь, поскольку он отображает непрерывную входную амплитуду в цифровое представление этого значения. Формально квантованный выходной сигнал $Q[x]$ некоторого входного значения $x$ равен

$$Q[x] = \arg \min_{l\in\mathcal{S}} |l-x|.$$

Здесь множество $\mathcal{S}$ содержит все возможные выходные значения квантователя, которые мы называем уровней квантования

. Что это значит? Это означает, что для данного входа $x$ квантователь возвращает уровень квантования $l$, который ближе всего к входному значению. Следовательно, квантователь полностью определяется своим набором уровней квантования $\mathcal{S}$.

Предположим, что квантователь должен уметь квантовать значения между входными амплитудами $-U$ и $+U$, т.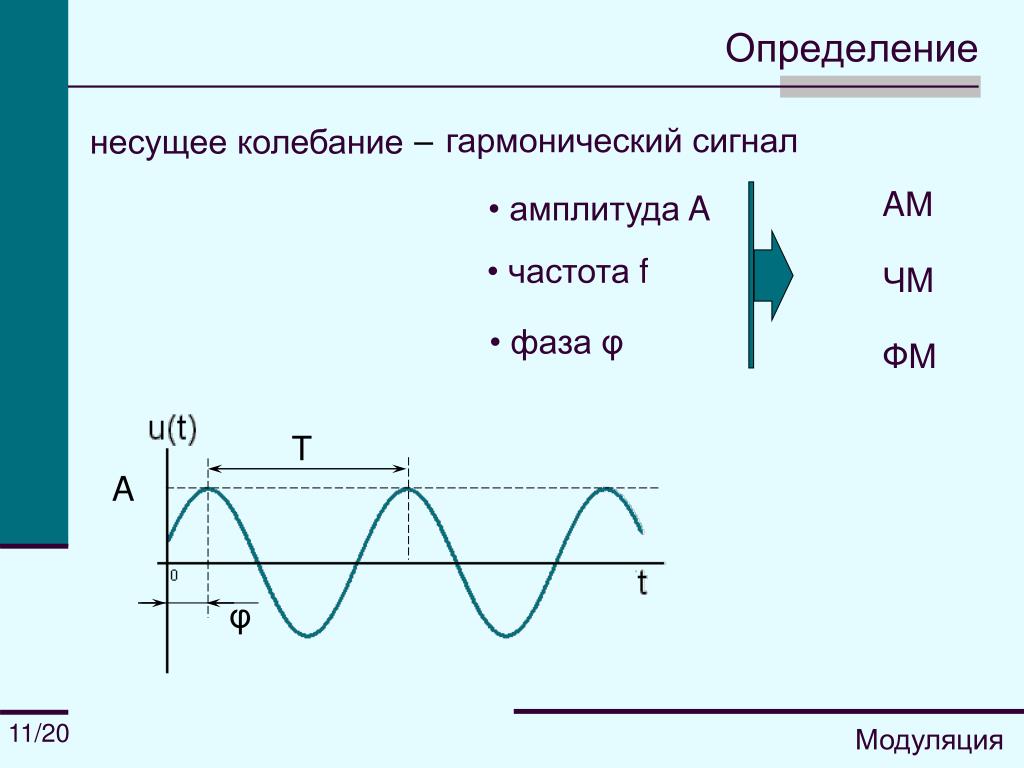 q$ различных уровней квантования в $\mathcal{S}$. Тогда логичным решением будет сделать расстояние $\Delta_s$ между уровнями квантования постоянным, равным

$$\Delta_s = \frac{2U}{q}.$$

Обычно используются два разных квантователя:

со средним подъемом и со средним шагом . Они отличаются настройкой своих уровней: для среднего протектора у нас есть $0\in\mathcal{S}$, тогда как для среднего роста квантизатор у нас есть $0\neq\mathcal{S}$, т.е. квантователь среднего шага имеет уровень для нулевого выходного значения. Уровни квантования для обоих квантователей определяются

$$\begin{выравнивание} \mathcal{S} &= \{-U+\frac{\Delta_s}{2}+\Delta_s\cdot(0,1,2,\dots, q-1)\}&\text{для средней высоты} \\ \mathcal{S} &= \{-U+\Delta_s\cdot(0,1,2,\dots, q-1)\}&\text{ для середины протектора} \end{выравнивание}$$ 9b=q$ — четное число, квантизатор среднего шага ни в коем случае не может быть симметричным.

Далее мы сосредоточимся на квантизаторе среднего роста.

Операция квантования вносит ошибку, поскольку бесконечное количество различных входных амплитуд отображается на конечный набор дискретных уровней квантования. Ошибка между входом и выходом квантователя называется Шум квантования $n_q(t)$. При обозначении $s(t)$ входного сигнала и $s_q(t)$ выходного сигнала квантователя выполняется следующее соотношение:

$$\begin{выравнивание} s_q(t)&=Q[s(t)]&&\text{Операция квантования}\\ n_q(t)&=s(t)-s_q(t)&&\text{Выражение шума квантования}\\ s_q(t)&=s(t)-n_q(t) \end{align}.$$

Глядя на последнее уравнение, шум квантования действительно можно понимать как шум поверх сигнала с непрерывной амплитудой, отсюда и его название. Давайте создадим синусоидальную волну и пропустим ее через квантователь, и посмотрим на квантованный сигнал и шум квантования.

Сначала определим функцию удобства calcLevels , который вычисляет уровни квантования для данного количества битов b.

Теперь давайте сгенерируем синусоидальный сигнал и покажем результирующий шум квантования.

Как видите, с увеличением количества битов квантования ошибка квантования практически исчезает. Однако важной мерой является отношение сигнал/шум квантования (SNR), и мы собираемся его измерить. При достаточно большом количестве битов шум квантования примерно равномерно распределяется в пределах $\pm\frac{\Delta_s}{2}$. В литературе, например. Proakis: Digital Signal Processing, было показано, что SNR квантования для синусоидального сигнала с полным возбуждением (т.е. амплитуда синуса равна диапазону квантования) может быть определена как

$$SNR\приблизительно (1,76 + 6,02b)дБ,$$

, где $b$ — количество битов для квантования.

Напишем функцию для измерения этого шума квантования. Здесь мы напрямую конвертируем SNR в шкалу дБ.

Теперь мы можем построить график зависимости шума квантования от количества битов и сравнить его с теоретической кривой $1,76+6,02b$.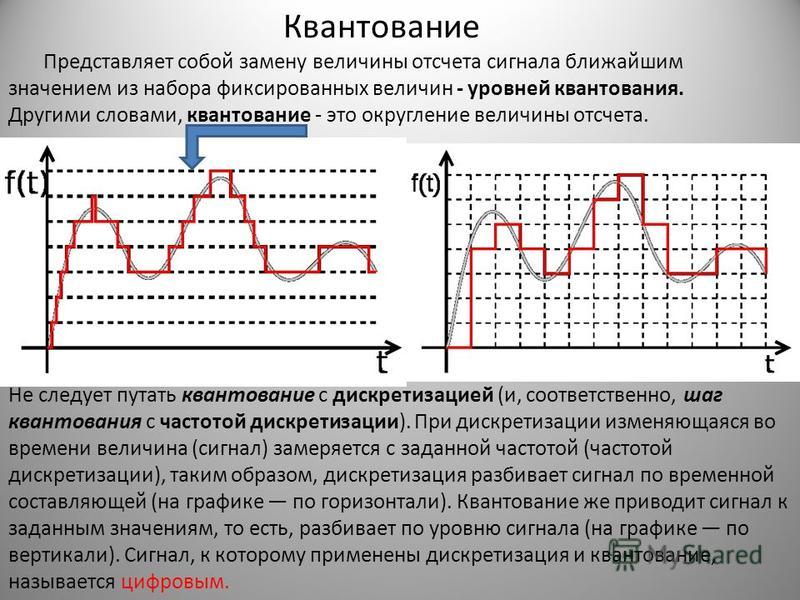

Как видим, приближение выполняется очень хорошо. Давайте теперь посмотрим, что происходит, когда мы уменьшаем амплитуду синуса:

Как мы видим, отношение SNR квантования ухудшается при уменьшении амплитуды синуса. Это разумно, так как шум квантования зависит только от количества битов квантования $b$ и, следовательно, не зависит от амплитуды сигнала и, следовательно, от мощности шума квантования. С другой стороны, мощность сигнала уменьшается при уменьшении амплитуды. Следовательно, мы видим деградацию SNR. Однако важным замечанием является то, что улучшение отношения сигнал-шум для каждого дополнительного бита остается на уровне $6$дБ, независимо от амплитуды сигнала.

Давайте теперь измерим SNR квантования для сигнала, который представляет собой просто гауссов шум:

Что здесь происходит? Отношение сигнал-шум квантования довольно низкое, несмотря на 14-битное разрешение? Глядя на исходный и квантованный сигнал, можно обнаружить проблему: квантизатор просто перегружен: входной сигнал выше, чем может вывести квантователь.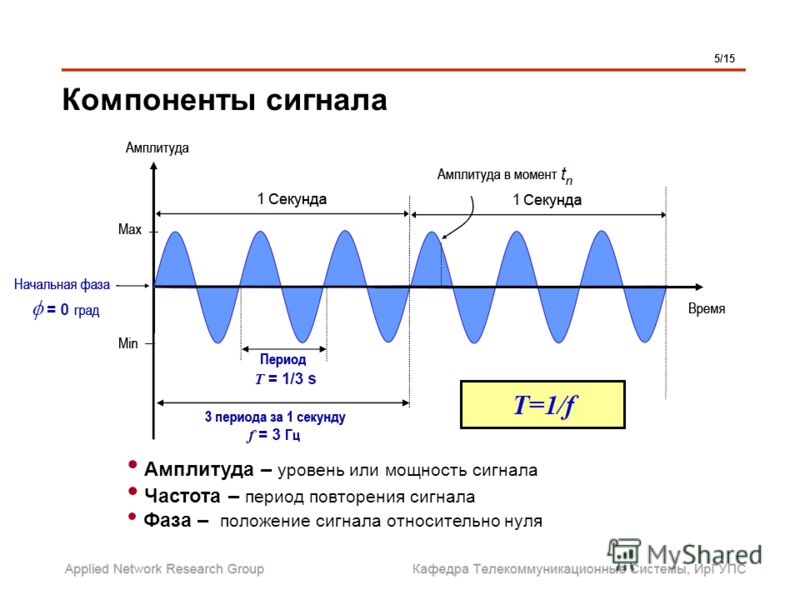 Таким образом, он никогда не сможет достичь хорошего квантования. Давайте со временем уменьшим амплитуду шума и посмотрим, поможет ли это:

Теперь мы видим, что отношение сигнал-шум квантования увеличивается на 6 дБ для каждого бита. Но, глядя на сигналы, мы видим еще одну важную вещь: хотя квантизатор мог бы выводить значения между $\pm 1$, большинство его значений сосредоточены в пределах $\pm 0,1$. Это связано с характером гауссовского шумового сигнала, который в основном концентрируется вокруг $s(t)=0$. Следовательно, для улучшения SNR имеет смысл увеличить разрешение на более низких уровнях квантования за счет более грубой дискретизации на более высоких амплитудах. Этот метод известен как нелинейные квантователи, но здесь он не рассматривается.

Страница не найдена

Не найдена, ошибка 404>

Страница, которую вы ищете, больше не существует. Возможно, вы сможете вернуться на домашнюю страницу сайта и посмотреть, сможете ли вы найти то, что ищете.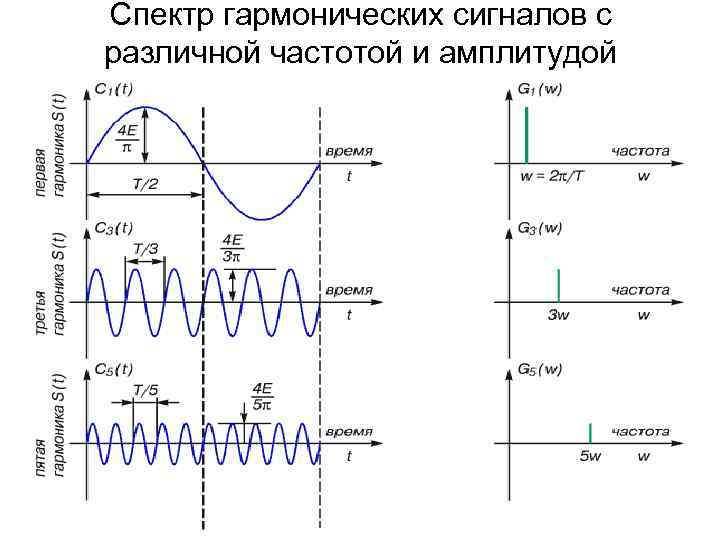 Или вы можете попытаться найти его с помощью информации ниже.

Страницы:

• Возможности публикации
• Дом
• О
• Исследования
  • Киберфизические системы
  • Мультимедийные и сенсорные сети
  • Умная сеть
  • Динамические системы
  • Цифровая криминалистика
  • Безопасность физического уровня
  • Безопасность мультимедиа
  • Восстановление слепого изображения
  • Слияние изображений
• Публикации
  • Журналы
  • Конференции
• Курсы
  • ECE 1518: Семинар по идентификации, конфиденциальности и безопасности (киберфизическая безопасность интеллектуальной сети)
  • ECE 286: Вероятность и статистика
  • ECE 455: цифровая обработка сигналов
  • ECE 316: Системы связи
  • ECE 362: цифровая обработка сигналов
  • Сигналы и системы
  • Цифровая обработка сигналов в реальном времени
  • Системы дискретного времени
  • Кибер-физическая безопасность интеллектуальной сети
• Награды
• Ресурсы
• Контакт
• *НОВИНКА* Вакансии для аспирантов
• Быстрые ссылки
• Блог

Категории:

• награда
• новости
• публикация
• ресурс
  • карьера
  • курсов
  • исследование

Авторы:

• admin (57)

Ежемесячно:

• Апрель 2021
• январь 2020 г.
• декабрь 2019 г.
• август 2019 г.
• май 2019 г.
• январь 2019 г.
• Апрель 2018 г.
• январь 2018 г.
• Декабрь 2017 г.
• ноябрь 2017 г.
• сентябрь 2017 г.
• август 2017 г.
• июнь 2017 г.
• май 2017 г.
• Февраль 2017 г.
• ноябрь 2016 г.
• октябрь 2016 г.
• июль 2016 г.
• июнь 2016 г.
• май 2016 г.
• март 2016 г.
• Январь 2016 г.
• ноябрь 2015 г.
• Октябрь 2015 г.
• июль 2015 г.
• июнь 2015 г.
• апрель 2015 г.
• март 2015 г.
• декабрь 2014 г.
• ноябрь 2014 г.
• октябрь 2014 г.
• май 2014 г.
• Январь 2014 г.
• ноябрь 2013 г.
• октябрь 2013 г.
• июнь 2012 г.
• май 2012 г.
• декабрь 2011 г.
• ноябрь 2011 г.
• апрель 2010 г.
• апрель 2009 г.
• март 2009 г.
• июнь 2004 г.

Последние сообщения:

• Текущие сообщения новостей
• CFP: Международная конференция по автономным системам 2020
• Возможности для написания дипломной работы по психиатрической информатике
• Специальный выпуск IET по интеллектуальным сетям, посвященный конфиденциальности и безопасности в интеллектуальных сетях
• Мастерская будущих дигилидеров
• Статья в журнале IEEE Signal Processing об адаптивной интеллектуальной сети
• 2019 Вакансии в Исследовательской группе Кундура
• Симпозиум GlobalSIP по обработке информации, обучению и оптимизации для интеллектуальных энергетических инфраструктур
• Несколько вакансий в Исследовательской группе Кундура
• Как инженеры разрабатывают изменения
• Национальный день памяти и борьбы с насилием в отношении женщин
• Джин Кочиш получает награду Microgrid Blockchain за лучшую бумагу
• Бумага, представленная Smart Cybersecurity Network
• Elevate AI на фестивале Elevate в Торонто
• Джин Вэй получает награду НАСА за раннюю карьеру
• Пиратайини Шрикантха в выпускных классах, чтобы посмотреть!
• CFP: J-STSP: обработка сигналов и информации для критически важных инфраструктур
• Будут ли кибератаки усиливаться?
• Jin Wei получает награду IEEE PES GM 2016 за лучшую бумагу
• Зимняя школа IEEE SPS по киберфизическим системам
• Хаммад и Шриканта получают стипендию C.