Звук – волна с непрерывно изменяющейся амплитудой и частотой. чем больше амплитуда, тем он громче для человека, чем больше частота, тем выше тон.
Звуковые сигналы в окружающем нас мире необычайно разнообразны. Сложные непрерывные сигналы можно с достаточной точностью представлять в виде суммы некоторого числа простейших синусоидальных колебаний.
Причем каждое слагаемое, то есть каждая синусоида, может быть точно задана некоторым набором числовых параметров – амплитуды, фазы и частоты, которые можно рассматривать как код звука в некоторый момент времени.
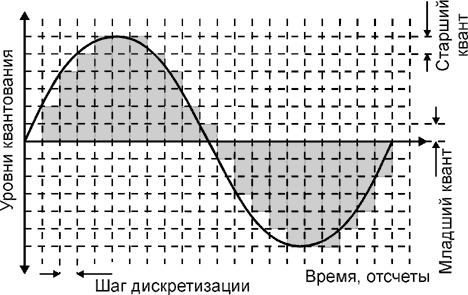
В процессе кодирования звукового сигнала производится его временная дискретизация – непрерывная волна разбивается на отдельные маленькие временные участки и для каждого такого участка устанавливается определенная величина амплитуды.
Таким образом непрерывная зависимость амплитуды сигнала от времени заменяется на дискретную последовательность уровней громкости.
Каждому уровню громкости присваивается его код. Чем большее количество уровней громкости будет выделено в процессе кодирования, тем большее количество информации будет нести значение каждого уровня и тем более качественным будет звучание.
Чем большее количество уровней громкости будет выделено в процессе кодирования, тем большее количество информации будет нести значение каждого уровня и тем более качественным будет звучание.
Качество двоичного кодирования звука определяется глубиной кодирования и частотой дискретизации.
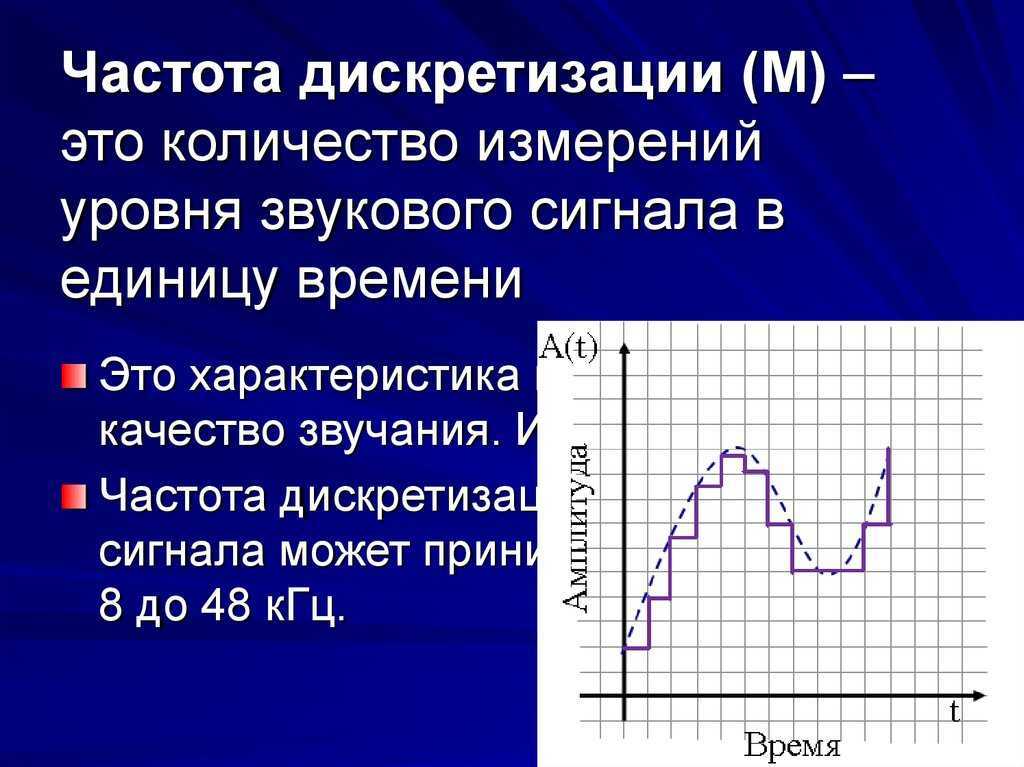
Частота дискретизации– количество измерений уровня сигнала в единицу времени.
Количество уровней громкости определяет глубину кодирования. Современные звуковые карты обеспечивают 16-битную глубину кодирования звука. При этом количество уровней громкости равно N = 216 = 65536.
Представление видеоинформации
В последнее время компьютер все чаще используется для работы с видеоинформацией. Простейшей такой работой является просмотр кинофильмов и видеоклипов. Следует четко представлять, что обработка видеоинформации требует очень высокого быстродействия компьютерной системы.
Что представляет собой фильм с точки зрения информатики? Прежде всего, это сочетание звуковой и графической информации. Кроме того, для создания на экране эффекта движения используется дискретная по своей сути технология быстрой смены статических картинок. Исследования показали, что если за одну секунду сменяется более 10-12 кадров, то человеческий глаз воспринимает изменения на них как непрерывные.
Кроме того, для создания на экране эффекта движения используется дискретная по своей сути технология быстрой смены статических картинок. Исследования показали, что если за одну секунду сменяется более 10-12 кадров, то человеческий глаз воспринимает изменения на них как непрерывные.
Казалось бы, если проблемы кодирования статической графики и звука решены, то сохранить видеоизображение уже не составит труда. Но это только на первый взгляд, поскольку, как показывает разобранный выше пример, при использовании традиционных методов сохранения информации электронная версия фильма получится слишком большой. Достаточно очевидное усовершенствование состоит в том, чтобы первый кадр запомнить целиком (в литературе его принято называть ключевым), а в следующих сохранять лишь отличия от начального кадра (разностные кадры).
Существует множество различных форматов представления видеоданных.
В среде Windows, например, уже более 10 лет (начиная с версии 3.1) применяется формат Video for Windows, базирующийся на универсальных файлах с расширением AVI (Audio Video Interleave – чередование аудио и видео).
Более универсальным является мультимедийный формат Quick Time, первоначально возникший на компьютерах Apple.
Практикум №3
Тема: Дискретное представление текстовой, графической, звуковой информации и видеоинформации.
Ход работы:
Задание №1.Используя таблицу символов, записать последовательность десятичных числовых кодов в кодировке Windows для своих ФИО, названия улицы, по которой проживаете. Таблица символов отображается в редакторе MS Word с помощью команды: вкладка ВставкаСимволДругие символы
В поле Шрифт выбираете Times New Roman, в поле из выбираете кириллица. Например, для буквы «А» (русской заглавной) код знака– 192.
Выполнение задания №1
| Л | И | П | А | Т | О | В | ||||||
| А | Л | Е | К | С | Е | Й | ||||||
| А | Л | Е | К | С | А | Н | Д | Р | О | В | И | Ч |
| Ф | А | В | О | Р | С | К | О | Г | О |
Задание №2. Используя стандартную программу БЛОКНОТ, определить, какая фраза в кодировке Windows задана последовательностью числовых кодов и продолжить код. Запустить БЛОКНОТ. С помощью дополнительной цифровой клавиатуры при нажатой клавише ALT ввести код, отпустить клавишу ALT.В документе появиться соответствующий символ.
Используя стандартную программу БЛОКНОТ, определить, какая фраза в кодировке Windows задана последовательностью числовых кодов и продолжить код. Запустить БЛОКНОТ. С помощью дополнительной цифровой клавиатуры при нажатой клавише ALT ввести код, отпустить клавишу ALT.В документе появиться соответствующий символ.
Выполнение задания №2
| я | у | ч | у | с | ь | в | б | и | к | п | о | ||||
| с | п | е | ц | и | а | л | ь | н | о | с | т | и |
| Э | Л | Е | К | Т | Р | И | К |
Задание №3. Заполнить пропуски числами:
Заполнить пропуски числами:
| Кбайт | =3072 | байт | =24576 | бит |
| Кбайт | =5120 | байт | =40960 | бит |
| Кбайт | =7168 | байт | =57344 | бит |
Задание № 4
Статьи к прочтению:
- Абсолютное позиционирование
- Ацп последовательного приближения
Свойства звука:высота, длительность, громкость, тембр. Теория музыки, Урок 3.
Похожие статьи:
Двоичное кодирование звука
Лабораторная работа №5 Тема: Дискретное (цифровое) представление текстовой, графической, звуковой информации и видеоинформации Цель работы:научиться…
Формулы шеннона для непрерывного и дискретного каналов
Формулы Шеннона представляют собой математические записи теорем кодирования Шеннона для дискретных и непрерывных сообщений, передаваемых по каналам с…
Кодирование звуковой информации
Двоичное кодирование звуковой информации
Временная дискретизация звука.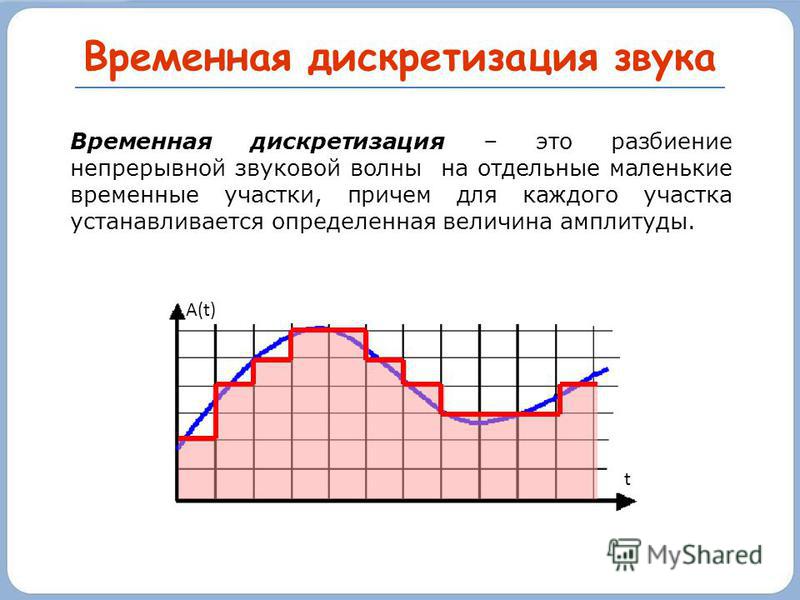
Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой.
Чем больше амплитуда сигнала, тем он громче для человека, чем больше частота сигнала, тем выше тон.
Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц).
В процессе кодирования непрерывного (аналогового) звукового сигнала производится его временная дискретизация.
Непрерывная звуковая волна разбивается на отдельные маленькие временные участки.
Для каждого участка устанавливается определенная величина амплитуды.
Непрерывная зависимость амплитуды сигнала от времени
На графике это выглядит как замена гладкой кривой на последовательность «ступенек»
Каждой «ступеньке» присваивается значение уровня гром к ости звука, его код (1, 2, 3 и так далее).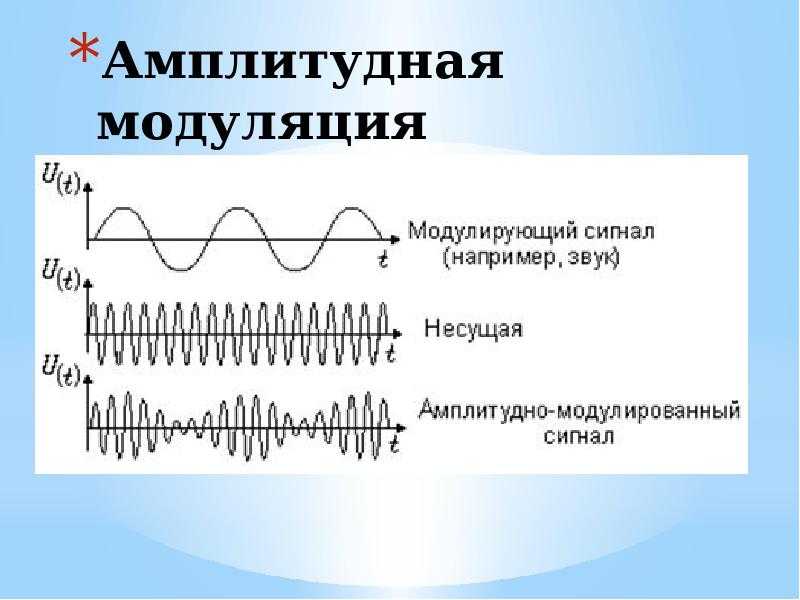
Уровни громкости звука — набор возможных состояний.
Чем большее количество уровней громкости будет выделено в процессе кодирования, тем большее количество информации несет значение каждого уровня и тем более качественным будет звучание.
Современные звуковые карты обеспечивают 16-битную глубину кодирования звука. Количество различных уровней сигнала (состояний при данном кодировании) можно рассчитать по формуле:
N = 2 I = 2 16 = 65536,
где I — глубина звука.
Таким образом, современные звуковые карты могут обеспечить кодирование 65536 уровней сигнала.
Частота дискретизации
При двоичном кодировании непрерывного звукового сигнала он заменяется последовательностью дискретных уровней сигнала.
Качество кодирования зависит от количества измерений уровня сигнала в единицу времени, то есть частоты дискретизации.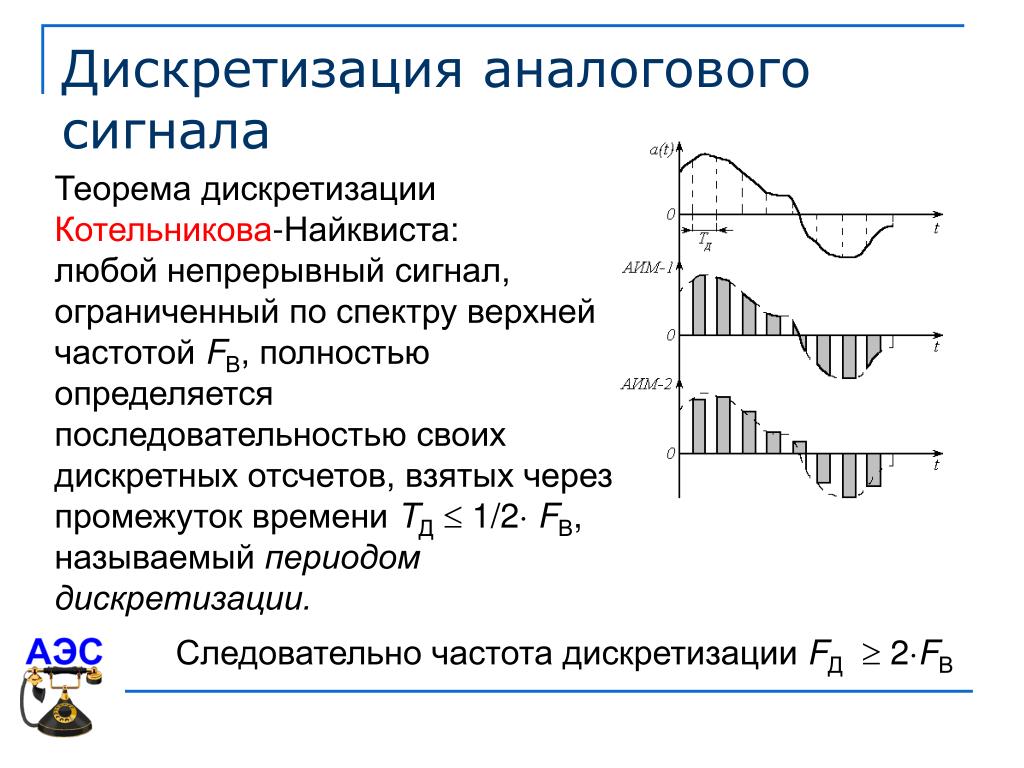
Чем большее количество измерений производится за 1 секунду (чем больше частота дискретизации), тем точнее процедура двоичного кодирования.
Количество измерений в секунду может лежать в диапазоне от 8000 до 48 000, то есть частота дискретизации аналогового звукового сигнала может принимать значения от 8 до 48 кГц.
При частоте 8 кГц качество дискретизированного звукового сигнала соответствует
При частоте 48 кГц — качеству звучания аудио- CD .
Также возможны моно- (1 канал), и стерео- (2 канала) режимы.
Импульсно-кодовая модуляция (англ. Pulse Code Modulation , PCM ) заключается в том, что звуковая информация хранится в виде значений амплитуды, взятых в определенные моменты времени (т. е. измерения проводятся «импульсами»).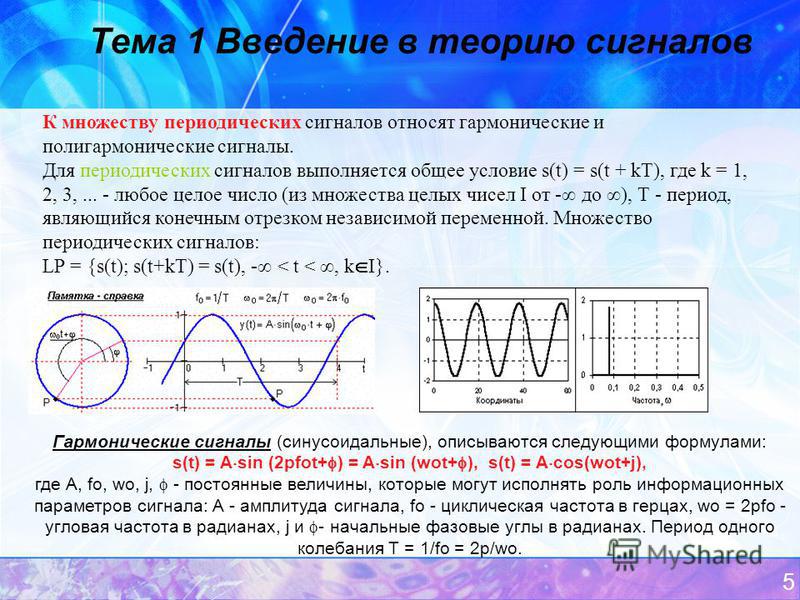
При записи звука в компьютер амплитуда измеряется через равные интервалы времени с некоторой достаточно большой частотой.
При воспроизведении звука компьютер использует сохраненные значения для того, чтобы восстановить непрерывную форму выходного сигнала.
Исходный сигнал Хранимая информация Воспроизводимый сигнал
Процесс получения цифровой формы звука называют оцифровкой.
Устройство, выполняющее оцифровку звука, называется аналого-цифровым преобразователем (АЦП). Устройство, выполняющее обратное преобразование, из цифровой формы в аналоговую, называется цифро-аналоговым преобразователем (ЦАП).
В современных компьютерах основная обработка звука выполняется
Помимо АЦП и ЦАП звуковые карты содержат сигнальный процессор — специализированный микрокомпьютер для обработки оцифрованного звука, выполняющий значительную часть рутинных расчетов при обработке звуков (смешение звуков, наложение спецэффектов, расчет формы выходного сигнала и т. п.; центральный процессор не тратит время на выполнение этих работ).
п.; центральный процессор не тратит время на выполнение этих работ).
Можно оценить информационный объем стереоаудиофайла длительностью звучания 1 секунда при высоком качестве звука (16 битов, 48 кГц).
Для этого количество битов, приходящихся на одну выборку, необходимо умножить на количество выборок в 1 секунду и умножить на 2 (стерео – два канала):
16 бит • 48 000 • 2 = 1 536 000 бит =
=192 000 байт = 187,5 Кбайт.
З А Д А Ч И
1. Оцените информационный объем моноаудиофайла длительностью звучания 1 мин, если «глубина» кодирования и частота дискретизации звукового сигнала равны соответственно:
а) 16 бит и 8 кГц;
б) 16 бит и 24 кГц.
2. Определите качество звука (качество радиотрансляции, среднее качество, качество аудио-
 равен:
равен:а) 940 Кбайт;
б) 157 Кбайт.
3. Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен:
а) 700 Кбайт;
б) 6300 Кбайт.
4. Аналоговый звуковой сигнал был дискретизирован сначала с использованием 256 уровней интенсивности сигнала (качество звучания радиотрансляции), а затем с использованием 65536 уровней интенсивности сигнала (качество звучания аудио-
Звук. Двоичное кодирование звуковой информаци
Статья отнесена к разделу: Преподавание физики, Преподавание информатики
Цели урока:
1)ознакомление учащихся со звуковой информацией, способами кодирования звуковой информации в компьютере
2)развитие логического мышления, умения анализировать и обобщать;
3)воспитание эстетического вкуса.
Тип учебного занятия: Урок изучения и первичного закрепления новых знаний и способов деятельности.
Оборудование: ПК, мультимедийный проектор, презентация, карточки – задания.
Ход урока
1. Организационный этап.
Учитель: Здравствуйте, ребята! Садитесь. Сегодня у нас с вами последний урок по теме “Двоичное кодирование информации”.
Какие виды информации мы с вами изучили?
Ученики: числовую, текстовую, графическую.
Учитель: Как вы думаете, о каком виде информации речь пойдет на этом уроке?
Ученики: Звуковой.
Учитель: Молодцы. Конечно, речь пойдет о звуковой информации.
Давайте поставим цели нашей с вами работы сегодня. (ребята предлагают цели урока).
Вопросы: 1 Что такое информация?
2 Что значит закодировать информацию?
3 Наименьшая единица информации.

4 Чему равно количество информации, уменьшающее неопределенность знаний в 4 раза?
5 Какие системы счисления вы знаете?
6 Назовите основания известных вам систем счисления.
7 Что называют мощностью алфавита?
8 Какое количество информации несет один символ алфавита мощность которого 256 символа? По какой формуле вы рассчитали?
9 Что надо сделать, чтобы закодировать графическую информацию?
11 Из каких символов состоит машинный (компьютерный) алфавит?
12 Что такое “информационный вес символа”?
13 Какое количество информации содержится в одном разряде восьмеричного числа?
14 Сколько вопросов и какие надо задать, чтобы угадать число, загаданное в интервале от 12 до 44?
Учитель.
Молодцы!
Для проведения урока необходимы консультанты. Учитель назначает экспертов для урока из числа учеников класса.
А теперь посмотрим, как вы усвоили предыдущие темы, для этого на рабочем столе компьютера вам предложен тест.
Консультанты выполняют тест на листах, а затем проверят вашу работу и запишут оценки.
3. Актуализация субъективного опыта учащихся.
Учитель. Итак, тема нашего урока Звук. Кодирование звука.
Вы знаете, что знание физики необходимо при изучении такой науки, как информатика. И сегодня мы почерпнем сведения из физики.
4. Этап усвоения новых знаний и способов деятельности (12 мин)
С начала 9О-х годов персональные компьютеры получили возможность работать со звуковой информацией. Каждый компьютер, имеющий звуковую плату, микрофон и колонки, может записывать, сохранять и воспроизводить звуковую информацию. С помощью специальных программных средств (редакторов звукозаписей) открываются широкие возможности по созданию, редактированию и прослушиванию звуковых файлов. Создаются программы распознавания речи и, в результате, появляется возможность управления компьютером при помощи голоса.
А что же такое звук?
Упругие волны в воздухе с частотой от 16 до 20000 Гц вызывают у человека звуковые ощущения.
 Волны с частотой меньше 16 Гц называют инфразвуковыми, а с частотой больше 20000 Гц — ультразвуковыми.
Волны с частотой меньше 16 Гц называют инфразвуковыми, а с частотой больше 20000 Гц — ультразвуковыми.Скорость распространения звука зависит от упругих свойств среды, ее плотности и температуры. Скорость звука не зависит от частоты.
По принятой классификации звук подразделяют на музыкальные звуки (тоны) и шумы.
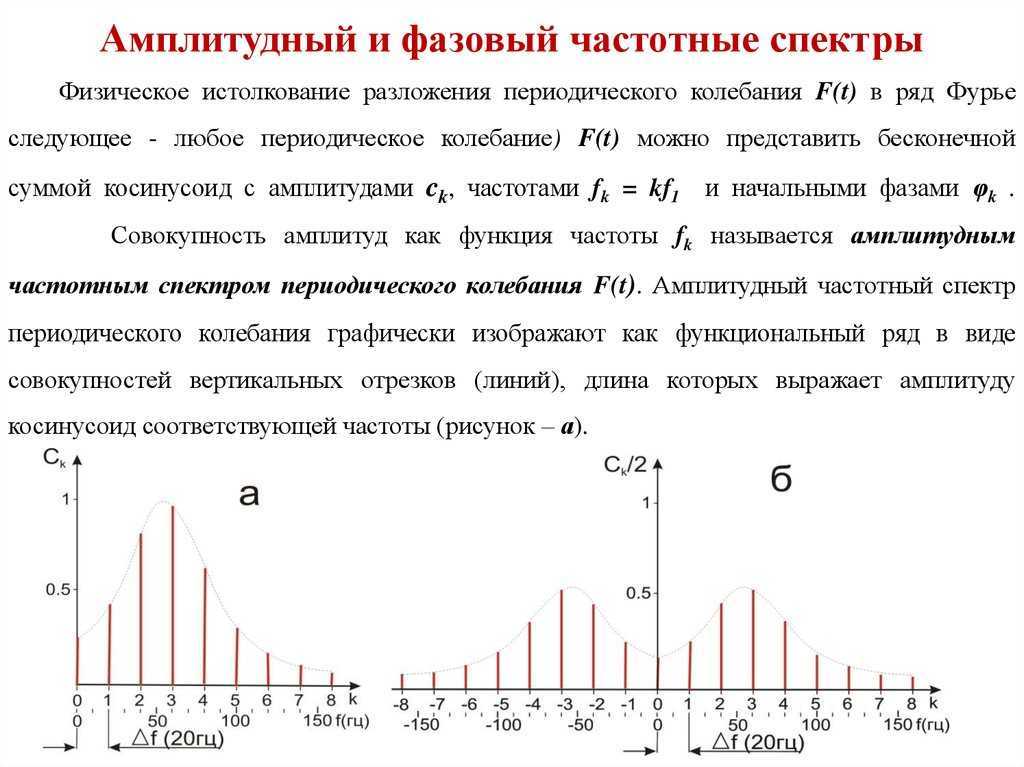
Музыкальный звук это сложное колебание. Любое сложное колебание можно разложить на ряд гармонических колебаний, частоты которых в целое число раз больше частоты основного тона. Акустическим спектром называется разложение сложного звука на гармонические колебания с учетом их амплитуды и частоты. Акустический спектр музыкального звука является линейчатым. Шумы вызываются апериодическими колебаниями. Их спектр сплошной. Физически высоту тона определяет частота. Чем она больше, тем выше тон. Тембр зависит от формы сложного колебания и его гармонического спектра.
Громкость есть функция двух переменных: силы звука и чувствительности уха. Сила звука это интенсивность, измеряемая в Вт/м2.
Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче для человека, чем больше частота сигнала, тем выше тон.
Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц).
Непрерывная звуковая волна разбивается на отдельные маленькие временные участки, причем для каждого такого участка устанавливается определенная величина амплитуды.
Таким образом, непрерывная зависимость амплитуды сигнала от времени А(t) заменяется на дискретную последовательность уровней громкости. На графике это выглядит как замена гладкой кривой на последовательность “ступенек”.
Каждой “ступеньке” присваивается значение уровня громкости звука, его код (1, 2, 3 и т.д.). Уровни громкости звука можно рассматривать как набор возможных состояний, соответственно, чем большее количество уровней громкости будет выделено в процессе кодирования, тем большее количество информации будет нести значение каждого уровня и тем более качественным будет звучание.
Современные звуковые карты обеспечивают 16-битную глубину кодирование звука. Количество различных уровней сигнала или состояний при данном кодировании можно рассчитать по формуле:
N=2I =216=65536
Таким образом, современные звуковые карты могут обеспечить кодирование 65536 уровней сигнала. Каждому значению амплитуды звукового сигнала присваивается 16-битный код.
При двоичном кодировании непрерывного звукового сигнала он заменяется последовательностью дискретных уровней сигнала. Качество кодирования зависит от количества измерений уровня сигнала в единицу времени, т.е. частоты дискретизации. Чем большее количество измерений производится за 1 секунду (чем больше частота дискретизации), тем точнее процедура двоичного кодирования.
Качество звукового сигнала определяется “глубиной” и частотой дискретизации.
Количество изменений в секунду может лежать в диапазоне от 8000 до 48000, т.е. частота дискретизации аналогово звукового сигнала может принимать значения от 8 до 48 кГц.

Можно оценить информационный объем стереоаудиофайла длительностью 1 секунда при высоком качестве звука 16 бит, 48 кГц. Для этого количество бит на одну выборку необходимо умножить на количество выборок в 1 с и умножить на 2.
16 бит*48000 Гц*2=1536000 бит=192000 байт=187,5 кбайт.
Записать:
Качество двоичного кодирования звука определяется глубиной кодирования и частотой дискретизации Глубина кодирования – количество бит, отводимых для кодирования уровня громкости (амплитуды) звукового сигнала Частота дискретизации — количество измерений уровня сигнала в единицу времени.
А теперь наши консультанты покажут, как записывается аудиофайл на компьютере (работа консультантов).
5. Этап обобщения и первичного закрепления полученных знаний
Ответьте на вопросы:
Волны какой частоты вызывают у человека звуковые ощущения?
От чего зависит громкость звука?
От чего зависит высота тона?
Что значит закодировать звуковую информацию?
От чего зависит качество кодирования звуковой информации?
6.
 Этап контроля и самоконтроля.
Этап контроля и самоконтроля.Учитель.
А теперь поработаем в группах. Разделитесь на 3 группы. (ребята пересаживаются). Для самостоятельного решения я вам предложу 2 задачи и одну практическую работу.
Класс делится на группы по 4 человека. Каждая группа получает задание.
1 группа
1. Оцените информационный объем моноаудиофайла длительностью звучания 20 с, если «глубина» кодирования и частота дискретизации звукового сигнала равны соответственно 8 бит и 8 кГц;
2. Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен 700 Кбайт;
3. Запишите звуковой моноаудиофайл длительностью 20 с, с «глубиной» кодирования 8 бит и частотой дискретизации 8 кГц. 2 группа
1. Определите качество звука (качество радиотрансляции, среднее качество, качество аудио-CD) если известно, что объем стериоаудиофайла длительностью звучания в 10 сек. Равен 940 Кбайт;
2.
 Оцените информационный объем стериоаудиофайла длительностью звучания 30 с, если «глубина» кодирования и частота дискретизации звукового сигнала равны соответственно 8 бит и 8 кГц;
Оцените информационный объем стериоаудиофайла длительностью звучания 30 с, если «глубина» кодирования и частота дискретизации звукового сигнала равны соответственно 8 бит и 8 кГц;3. Запишите звуковой файл длительностью 30с с «глубиной» кодирования 8бит и частотой дискретизации 8 кГц.
3 группа
1. Аналоговый звуковой сигнал был дискретизирован сначала с использованием 256 уровней интенсивности сигнала (качество звучания радиотрансляции), а затем с использованием 65536 уровней интенсивности сигнала (качество звучания аудио-CD). Во сколько раз различаются информационные объемы оцифрованного звука?
2. Оцените информационный объем моноаудиофайла длительностью звучания 1 мин. если «глубина» кодирования и частота дискретизации звукового сигнала равны соответственно:
16 бит и 48 кГц.
3. Запишите звуковой моноаудиофайл длительностью 1 минута с «глубиной» кодирования 16 бит и частотой дискретизации 48 кГц.
После выполнения задания учитель проверяет решение задач.
 Практическую часть самостоятельной работы прослушивает весь класс.
Практическую часть самостоятельной работы прослушивает весь класс.7. Информация о домашнем задании, инструктаж по его выполнению.
НА ГЛАВНУЮ
Кодирование звуковой информации — Кодирование информации
Кодирование и обработка звуковой информации Звуковая информация. Звук представляет собой распространяющуюся в воздухе, воде или другой среде волну с непрерывно меняющейся интенсивностью и частотой. Человек воспринимает звуковые волны (колебания воздуха) с помощью слуха в форме звука различных громкости и тона. Чем больше интенсивность звуковой волны, тем громче звук, чем больше частота волны, тем выше тон звука (Рис. 1).
Человеческое
ухо воспринимает звук с частотой от 20 колебаний в секунду (низкий звук) до 20
000 колебаний в секунду (высокий звук). Человек может воспринимать звук в огромном диапазоне интенсивностей, в котором максимальная интенсивность больше минимальной в 1014 раз (в сто тысяч миллиардов раз). Для измерения громкости звука применяется специальная единица «децибел» (дб) (табл. 5.1). Уменьшение или увеличение громкости звука на 10 дб соответствует уменьшению или увеличению интенсивности звука в 10 раз.
Таблица 1. Временная дискретизация звука. Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть преобразован в цифровую дискретную форму с помощью временной дискретизации. Непрерывная звуковая волна разбивается на отдельные маленькие временные участки, для каждого такого участка устанавливается определенная величина интенсивности звука. Таким образом, непрерывная зависимость громкости звука от времени A(t) заменяется на дискретную последовательность уровней громкости. На графике это выглядит как замена гладкой кривой на последовательность «ступенек» (Рис. 2). Рис. 2. Временная дискретизация звука. Частота дискретизации. Для
записи аналогового звука и преобразования в цифровую форму используется
микрофон, подключенный к звуковой плате. Качество полученного цифрового звука
зависит от количества измерений уровня громкости звука в единицу времени, т. е. частоты дискретизации. Чем большее
количество измерений производится за I секунду (чем больше частота
дискретизации), тем точнее «лесенка» цифрового
звукового сигнала повторяет кривую диалогового сигнала. Частота дискретизации звука — это количество измерений громкости звука за одну секунду. Частота дискретизации звука может лежать в диапазоне от 8000 до 48 000 измерений громкости звука за одну секунду. Глубина кодирования звука. Каждой «ступеньке» присваивается определенное значение уровня громкости звука. Уровни громкости звука можно рассматривать как набор возможных состояний N, для кодирования которых необходимо определенное количество информации I, которое называется глубиной кодирования звука. Глубина кодирования звука — это количество информации, которое необходимо для кодирования дискретных уровней громкости цифрового звука. Если известна глубина кодирования, то количество уровней громкости цифрового звука можно рассчитать по формуле N = 2I. Пусть глубина кодирования звука составляет 16 битов, тогда количество уровней громкости звука равно: N = 2I = 216 = 65 536. В
процессе кодирования каждому уровню громкости звука присваивается свой
16-битовый двоичный код, наименьшему уровню звука будет соответствовать код
0000000000000000, а наибольшему — 1111111111111111. Качество оцифрованного звука. Чем больше частота и глубина дискретизации звука, тем более качественным будет звучание оцифрованного звука. Самое низкое качество оцифрованного звука, соответствующее качеству телефонной связи, получается при частоте дискретизации 8000 раз в секунду, глубине дискретизации 8 битов и записи одной звуковой дорожки (режим «моно»). Самое высокое качество оцифрованного звука, соответствующее качеству аудио-CD, достигается при частоте дискретизации 48 000 раз в секунду, глубине дискретизации 16 битов и записи двух звуковых дорожек (режим «стерео»). Необходимо помнить, что чем выше качество цифрового звука, тем больше информационный объем звукового файла. Можно оценить информационный объем цифрового стереозвукового файла длительностью звучания 1 секунда при среднем качестве звука (16 битов, 24 000 измерений в секунду). Для этого глубину кодирования необходимо умножить на количество измерений в 1 секунду и умножить на 2 (стереозвук): 16
бит * 24 000 * 2 = 768 000 бит = 96 000 байт = 93,75 Кбайт. Звуковые редакторы. Звуковые редакторы позволяют не только записывать и воспроизводить звук, но и редактировать его. Оцифрованный звук представляется в звуковых редакторах в наглядной форме, поэтому операции копирования, перемещения и удаления частей звуковой дорожки можно легко осуществлять с помощью мыши. Кроме того, можно накладывать звуковые дорожки друг на друга (микшировать звуки) и применять различные акустические эффекты (эхо, воспроизведение в обратном направлении и др.). Звуковые редакторы позволяют изменять качество цифрового звука и объем звукового файла путем изменения частоты дискретизации и глубины кодирования. Оцифрованный звук можно сохранять без сжатия в звуковых файлах в универсальном формате WAV или в формате со сжатием МР3. При
сохранении звука в форматах со сжатием отбрасываются «избыточные» для
человеческого восприятия звуковые частоты с малой интенсивностью, совпадающие
по времени со звуковыми частотами с большой интенсивностью. Применение такого
формата позволяет сжимать звуковые файлы в десятки раз, однако приводит к
необратимой потере информации (файлы не могут быть восстановлены в
первоначальном виде).
Под обработкой звука следует понимать различные преобразования звуковой информации с целью изменения каких-то характеристик звучания. К обработке звука относятся способы создания различных звуковых эффектов, фильтрация, а также методы очистки звука от нежелательных шумов, изменения тембра и т.д. Все это огромное множество преобразований сводится, в конечном счете, к следующим основным типам: 1. Амплитудные преобразования. Выполняются над амплитудой сигнала и приводят к ее усилению/ослаблению или изменению по какому-либо закону на определенных участках сигнала. 2. Частотные преобразования. Выполняются над частотными составляющими звука: сигнал представляется в виде спектра частот через определенные промежутки времени, производится обработка необходимых частотных составляющих, например, фильтрация, и обратное «сворачивание» сигнала из спектра в волну. 3. Фазовые преобразования. Сдвиг фазы сигнала тем или иным способом; например, такие
преобразования стерео сигнала, позволяют реализовать эффект вращения или
«объёмности» звука. 4. Временные преобразования. Реализуются путем наложения, растягивания/сжатия сигналов; позволяют создать, например, эффекты эха или хора, а также повлиять на пространственные характеристики звука. Практическую обработку сигналов можно
разделить на два типа: обработка «на лету» и пост-обработка. Обработка «на лету»
подразумевает мгновенное преобразование сигнала (то есть с возможностью
осуществлять вывод обработанного сигнала почти одновременно с его вводом).
Простой пример – гитарные «примочки» или реверберация во время живого исполнения
на сцене. Такая обработка происходит мгновенно, то есть, скажем, исполнитель
поет в микрофон, а эффект-процессор преобразует его голос и слушатель слышит уже
обработанный вариант голоса. Пост-обработка – это обработка уже записанного
сигнала. Скорость такой обработки может быть сильно ниже скорости
воспроизведения. Такая обработка преследует те же цели, то есть придание звуку
определенного характера, либо изменение характеристик, однако применяется на
стадии мастеринга или подготовки звука к
тиражированию, когда не требуется спешка, а важнее качество и скрупулезная
проработка всех нюансов звучания. Аналоговый и дискретный способы представления звука Информация, в том числе графическая и звуковая, может быть представлена в аналоговой или дискретной форме. При аналоговом представлении физическая величина принимает бесконечное множество значений, причем ее значения изменяются непрерывно. При дискретном представлении физическая величина принимает конечное множество значений, причем ее величина изменяется скачкообразно. Рис. 3. Аналоговое и дискретное кодирование. Примером аналогового хранения звуковой информации является виниловая
пластинка (звуковая дорожка изменяет свою форму непрерывно), а дискретного — аудиокомпакт-диск
(звуковая дорожка которого содержит участки с различной отражающей
способностью). Восприятие звука человеком Звуковые волны улавливаются слуховым органом и вызывают в нем раздражение, которое передается по нервной системе в головной мозг, создавая ощущение звука. Колебания барабанной перепонки в свою очередь передаются во внутреннее ухо и раздражают слуховой нерв. Так образом человек воспринимает звук. В аналоговой форме звук представляет собой волну, которая характеризуется:
Герц (Гц или Hz) — единица измерения частоты колебаний. 1 Гц= 1/с Человеческое ухо может воспринимать звук с частотой от 20 колебаний в секунду
(20 Герц, низкий звук) до 20 000 колебаний в секунду (20 КГц, высокий звук). Рис.
Кодирование звуковой информации Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц).
Качество кодирования звуковой информации зависит от: 1)частотой дискретизации, т.е. количества измерений уровня сигнала в единицу времени. Чем большее количество измерений производится за 1 секунду (чем больше частота дискретизации), тем точнее процедура двоичного кодирования. 2)глубиной кодирования, т.е. количества уровней сигнала. Современные звуковые карты обеспечивают 16-битную глубину кодирования звука. Количество различных уровней сигнала (состояний при данном кодировании) можно рассчитать по формуле: N = 2i = 216 = 65536, где i — глубина звука. Таким образом, современные звуковые карты могут обеспечить кодирование 65536 уровней сигнала. Каждому значению амплитуды звукового сигнала присваивается 16-битный код. Количество
измерений в секунду может лежать в диапазоне от 8000 до 48 000, то есть частота
дискретизации аналогового звукового сигнала может принимать значения от 8 до 48
кГц. РСМ. РСМ расшифровывается как pulse code modulation, что и является в переводе как импульсно-кодовая. Файлы именно с таким расширением встречаются довольно редко. Но РСМ является основополагающей для всех звуковых файлов.
WAV. Самое простое хранилище дискретных данных. Один из типов файлов семейства RIFF. Помимо обычных дискретных значений, битности, количества каналов и значений уровней громкости, в wav может быть указано еще множество параметров, о которых Вы, скорее всего, и не подозревали — это: метки позиций для синхронизации, общее количество дискретных значений, порядок воспроизведения различных частей звукового файла, а также есть место для того, чтобы Вы смогли разместить там текстовую информацию.
RIFF.
IFF. Эта технология хранения данных проистекает от Amiga-систем. Interchange File Format. Почти то же, что и RIFF, только имеются некоторые нюансы. Начнем с того, что система Amiga — одна из первых, в которой стали задумываться о программно-сэмплернойэмуляции музыкальных инструментов. В результате, в данном файле звук делится на две части: то, что должно звучать вначале и элемент того, что идет за началом. В результате, звучит начало один раз, за тем повторяется второй кусок столько раз, сколько Вам нужно и нота может звучать бесконечно долго.
MOD. Файл хранит в себе короткий образец звука, который потом можно использовать в качестве шаблона для инструмента.
AIF или AIFF. Audio Interchange File Format. Данный формат распространен в системах Apple Macintosh и Silicon Graphics.
MID. Файл, хранящий в себе сообщения MIDI-системе, установленной на Вашем компьютере или в устройстве.
МР3. Самый скандальный формат за последнее время. Многие для объяснения параметров сжатия, которые в нем применяют, сравнивают его с jpeg для изображений. Там очень много наворотов в вычислениях, чего и не перечислишь, но коэффициент сжатия в 10-12 раз сказали о себе сами. Специалисты говорят о контурности звука как о самом большом недостатке данного формата. Действительно, если сравнивать музыку с изображением, то смысл остался, а мелкие нюансы ушли. Качество МР3 до сих пор вызывает много споров, но для «обычных немузыкальных» людей потери не ощутимы явно.
VQF. Хорошая
альтернатива МР3, разве что менее распространенная. Есть и свои недостатки.
Закодировать файл в VQF — процесс гораздо более долгий. К тому же, очень мало
бесплатных программ, позволяющих работать с данным форматом файлов, что,
собственно, и сказалось на его распространении.
RA. Real Audio или потоковая передача аудиоданных. Довольно распространенная система передачи звука в реальном времени через Интернет. Скорость передачи порядка 1 Кб в секунду. Полученный звук обладает следующими параметрами: 8 или 16 бит и 8 или 11 кГц. |
Информатика — Кодирование звуковой информации.
Аналоговый и дискретный способы представления звука
Информация, в том числе графическая и звуковая, может быть представлена в аналоговой или дискретной форме.
При аналоговом представлении физическая величина принимает бесконечное множество значений, причем ее значения изменяются непрерывно. При дискретном представлении физическая величина принимает конечное множество значений, причем ее величина изменяется скачкообразно. | Аналоговое и дискретное кодирование |
Примером аналогового хранения звуковой информации является виниловая пластинка (звуковая дорожка изменяет свою форму непрерывно), а дискретного — аудиокомпакт-диск (звуковая дорожка которого содержит участки с различной отражающей способностью).
Восприятие звука человеком
Звуковые волны улавливаются слуховым органом и вызывают в нем раздражение, которое передается по нервной системе в головной мозг, создавая ощущение звука.
Колебания барабанной перепонки в свою очередь передаются во внутреннее ухо и раздражают слуховой нерв. Так образом человек воспринимает звук.
В аналоговой форме звук представляет собой волну, которая характеризуется:
|
Герц (Гц или Hz) — единица измерения частоты колебаний. 1 Гц= 1/с
Человеческое ухо может воспринимать звук с частотой от 20 колебаний в секунду (20 Герц, низкий звук) до 20 000 колебаний в секунду (20 КГц, высокий звук).
— аналоговый — непрерывный — звук
| Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче для человека, чем больше частота сигнала, тем выше тон. |
Кодирование звуковой информации
Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц).
| В процессе кодирования непрерывного звукового сигнала производится его временная дискретизация. Непрерывная звуковая волна разбивается на отдельные маленькие временные участки, причем для каждого такого участка устанавливается определенная величина амплитуды. Т.о. при двоичном кодировании непрерывного звукового сигнала он заменяется последовательностью дискретных уровней сигнала. |
Рис. Временная дискретизация звука | Таким образом, непрерывная зависимость амплитуды сигнала от времени А(t) заменяется на дискретную последовательность уровней громкости.
На графике это выглядит как замена гладкой кривой на последовательность «ступенек»:
|
|
Каждой «ступеньке» присваивается значение уровня громкости звука, его код (1, 2, 3 и так далее).
Уровни громкости звука можно рассматривать как набор возможных состояний, соответственно, чем большее количество уровней громкости будет выделено в процессе кодирования, тем большее количество информации будет нести значение каждого уровня и тем более качественным будет звучание.
Преобразование аналоговой формы представления звука в дискретную происходит в процессе аналогово-цифрового преобразования (АЦП).
Преобразование дискретной формы представления звука в аналоговую происходит в процессе цифро-аналогового преобразования (ЦАП) |
Качество кодирования звуковой информации зависит от:
1) частотой дискретизации, т.е. количества измерений уровня сигнала в единицу времени. Чем большее количество измерений производится за 1 секунду (чем больше частота дискретизации), тем точнее процедура двоичного кодирования.
2) глубиной кодирования, т.е. количества уровней сигнала. |
Современные звуковые карты обеспечивают 16-битную глубину кодирования звука. Количество различных уровней сигнала (состояний при данном кодировании) можно рассчитать по формуле: N = 2i = 216 = 65536, где i — глубина звука.
Количество различных уровней сигнала (состояний при данном кодировании) можно рассчитать по формуле: N = 2i = 216 = 65536, где i — глубина звука.
Таким образом, современные звуковые карты могут обеспечить кодирование 65536 уровней сигнала. Каждому значению амплитуды звукового сигнала присваивается 16-битный код.
Количество измерений в секунду может лежать в диапазоне от 8000 до 48 000, то есть частота дискретизации аналогового звукового сигнала может принимать значения от 8 до 48 кГц. При частоте 8 кГц качество дискретизированного звукового сигнала соответствует качеству радиотрансляции, а при частоте 48 кГц — качеству звучания аудио-СD. Следует также учитывать, что возможны как моно-, так и стерео-режимы.
ЗАДАЧА 1.
Можно оценить информационный объем стереоаудиофайла длительностью звучания 1 секунда при высоком качестве звука (16 битов, 48 кГц). Для этого количество битов, приходящихся на одну выборку, необходимо умножить на количество выборок в 1 секунду и умножить на 2 (стерео):
Решение: 16 бит • 48 000 • 2 = 1 536 000 бит = 192 000 байт = 187,5 Кбайт.
ЗАДАЧА 2.
Оценить информационный объем цифрового стерео звукового файла длительностью звучания 1 минута при среднем качестве звука (16 битов, 24 кГц).
Решение: 16 бит × 24 000 × 2 × 60 = 46 080 000 бит = 5 760 000 байт = 5 625 Кбайт ≈ 5,5 Мбайт
Стандартное приложение Звукозапись играет роль цифрового магнитофона и позволяет записывать звук, то есть дискретизировать звуковые сигналы, и сохранять их в звуковых файлах в формате WАV. Эта программа позволяет редактировать звуковые файлы, микшировать их (накладывать друг на друга), а также воспроизводить.
Качество двоичного кодирования изображения или звука определяется частотой дискретизации и глубиной кодирования. |
Домашнее задание — решить задачи:
1. Определить количество уровней сигнала 24-битной звуковой карты .
Определить количество уровней сигнала 24-битной звуковой карты .
2.Уместиться ли песня на дискету размером 1,44 Мбайта, если она имеет следующие параметры: стерео длительностью звучания 3 минуты при качестве звука — 16 битов, 16 кГц.
Презентация — Кодирование звуковой информации
Поделиться
1,849
просмотров
Презентации / Информатика / Кодирование звуковой информации
Скачать презентацию Понравилось | 0
Текст этой презентации
Слайд 1
Кодирование звуковой информации
Слайд 2
У всех источников звука имеются колеблющиеся части, которые приводят в колебательное движение частицы окружающей среды (воздуха) → распространяющаяся звуковая волна вызывает колебательное движение барабанной перепонки уха человека, которое воспринимается мозгом как звук → не все источники колебаний являются источниками звука → звук – механические колебания в частотном диапазоне от 16 Гц до 22000 Гц
Слайд 3
Упругие волны в воздухе с частотой от 16 до 20000 Гц вызывают у человека звуковые ощущения. Волны с частотой меньше 16 Гц называют инфразвуковыми, а с частотой больше 20 000 Гц — ультразвуковыми.
Волны с частотой меньше 16 Гц называют инфразвуковыми, а с частотой больше 20 000 Гц — ультразвуковыми.
Слайд 4
Частота
Источники звука
Источники колебаний
Слайд 5
Чтобы измерять громкость звука применяют специальную единицу «децибел» (дБ)
Характерный звук Громкость, измеренная в децибелах
Нижний предел чувствительности человеческого уха 0
Шорох листьев 10
Разговор 60
Гудок автомобиля 90
Реактивный двигатель 120
Болевой порог 140
Слайд 6
Звук представляет собой звуковую волну с непрерывно меняющейся амплитудой и частотой. Чем больше амплитуда сигнала, тем он громче для человека, чем больше частота сигнала, тем выше тон.
Слайд 7
Звуки различной громкости
Слайд 8
Звуки различной высоты
Слайд 9
Для того чтобы компьютер мог обрабатывать звук, непрерывный звуковой сигнал должен быть превращен в последовательность электрических импульсов (двоичных нулей и единиц).
Слайд 10
Схема преобразования звуковой волны в двоичный код
Слайд 11
Схема воспроизведения звука, сохранённого в памяти ЭВМ
Звуковая волна
Звуковая плата (аудиоадаптер)
Память ЭВМ
Динамик
Слайд 12
Непрерывная звуковая волна разбивается на отдельные маленькие временные участки, причем для каждого такого участка устанавливается определенная величина амплитуды.
Таким образом, непрерывная зависимость амплитуды сигнала от времени А(t) заменяется на дискретную последовательность уровней громкости. На графике это выглядит как замена гладкой кривой на последовательность “ступенек”.
Слайд 13
Процесс преобразования непрерывного аналогового сигнала в дискретный (прерывистый) называется временной дискретизацей.
Слайд 14
Временная дискретизация
Т
2Т
Время
Громкость
Слайд 15
Временная дискретизация
Громкость
Время
Слайд 16
Временная дискретизация
Т
Время
Громкость
Слайд 17
Временная дискретизация
Т
Время
Громкость
Слайд 18
Временная дискретизация
Т
Время
Громкость
Слайд 19
Количество измерений уровня звукового сигнала за 1 секунду называют частотой дискретизации.
Слайд 20
Зависимость качества звука от частоты дискретизации
Слайд 21
Т
N →∞
Количество уровней громкости при дискретизации по времени
Время
Громкость
Слайд 22
N →∞
Изменение качества звука при дискретизации по уровню
Т
N = 4
Время
Громкость
Слайд 23
N = 4
N = 8
Изменение качества звука при дискретизации по уровню
Т
Время
Громкость
Слайд 24
Количество информации, которое необходимо для кодирования дискретных уровней громкости цифрового звука называют глубиной кодирования звука.
Слайд 25
Зависимость качества звука от глубины кодирования
Слайд 26
Соответствие звуков различных характеристик некоторым источникам звука
8 кГц
44,1 кГц
Радиотрансляция
AudioCD
192 кГц
DVD-Audio
8 бит
16 бит
24 бит
Слайд 27
Расчёт объёма звукового файла
I=k·ν·i·t
Где I – размер (объём) звукового файла k – количество дорожек в записи (k=1 – моно, k=2 – стерео) ν – частота дискретизации (в Герцах) i – глубина кодирования (в битах) t – время звучания (в секундах)
Слайд 28
Оценка объёма звукового файла
Ю. Антонов «Белый теплоход», время звучания 3 мин 18 сек, качество аудио-CD диска, стерео
Антонов «Белый теплоход», время звучания 3 мин 18 сек, качество аудио-CD диска, стерео
Дано:
ν = 44,1 кГц
I = 16 бит
t = 3 мин 18 с
k = 2
Найти:
V
Решение:
44,1 кГц = 44100 Гц
3 мин 18 с = 198 с
V = k ν I t = 2·44100 Гц·16 бит·198 с = = 279417600 бит = 34927200 байт ≈ ≈ 34108,6 Кб ≈ 33,3 Мб Ответ: V = 33,3 Мб
Слайд 29
Изменение качества при сжатии звуковых файлов
Спектрограмма несжатого звука (формат WAV)
Спектрограмма сжатого звука (формат mp3, битрейт 128 кбит/с)
Спектрограмма сжатого звука (формат WMA, битрейт 128 кбит/с)
Слайд 30
Звук «живой» и оцифрованный
Слайд 31
Задачи
1. Оцените информационный объем моноаудиофайла длительностью звучания 20 с, если «глубина» кодирования и частота дискретизации звукового сигнала равны соответственно 8 бит и 8 кГц.
Слайд 32
Задачи
2. Рассчитайте время звучания моноаудиофайла, если при 16-битном кодировании и частоте дискретизации 32 кГц его объем равен 700 Кбайт.
Похожие презентации
Кодирование и обработка звуковой информации Кодирование информации Кодирование графической информации Мышь – устройство ввода информации Поиск информации в Интернете
MSP Учебник 2: Регулируемый осциллятор
Откройте учебник.
Сигнал, который вы хотите прослушать — сигнал, который вы отправляете на ЦАП~ — должен иметь амплитуду в диапазоне от -1,0 до +1,0. Любые значения, превышающие эти границы, будут обрезаны dac~ (т.е. резко ограничены до 1 или -1). Это вызовет (в большинстве случаев довольно неприятное) искажение звука. Некоторые объекты, такие как цикл~, по умолчанию выводят значения в том же диапазоне.
Выход цикла~ по умолчанию имеет амплитуду 1
Для управления уровнем сигнала вы просто умножаете каждый семпл на коэффициент масштабирования. Например, чтобы уменьшить вдвое амплитуду сигнала, вы просто умножаете ее на 0,5. (Хотя математически это эквивалентно делению амплитуды сигнала на 2, умножение является более эффективной вычислительной процедурой, чем деление.
Например, чтобы уменьшить вдвое амплитуду сигнала, вы просто умножаете ее на 0,5. (Хотя математически это эквивалентно делению амплитуды сигнала на 2, умножение является более эффективной вычислительной процедурой, чем деление.
Амплитуда, скорректированная путем умножения
Если мы хотим непрерывно изменять амплитуду сигнала во времени , мы можем подавать изменяющийся сигнал на правый вход *~.Постоянно изменяя значение на правом входе *~, мы можем усиливать или ослаблять звук, создавать эффект крещендо или диминуэндо и т. д.
Однако внезапное резкое изменение амплитуды вызовет разрыв сигнала, который будет слышен как шумный щелчок.
Мгновенное изменение амплитуды вызывает шумовое искажение сигнала
По этой причине обычно лучше изменять амплитуду, используя сигнал, который изменяется постепенно с каждым отсчетом, скажем, по прямой линии в течение нескольких миллисекунд.
Если вместо мгновенного изменения амплитуды (которое может вызвать неприемлемое искажение сигнала) мы подаем на правый вход *~ сигнал, изменяющийся от 1,0 до 0,5 в течение 5 миллисекунд, мы интерполируем между начальная амплитуда и целевая амплитуда для каждого образца, создавая плавное изменение амплитуды.
Линейное изменение амплитуды в течение 5 миллисекунд с использованием линии~
Объект линия~ функционирует аналогично объекту линии Макс. На левом входе он получает целевое значение и время (в мс) для достижения этого целевого значения. line~ вычисляет правильное промежуточное значение для каждой выборки, чтобы изменить его по прямой линии от текущего значения до целевого значения.
Техническая деталь: Любое изменение общей амплитуды сигнала вносит некоторое искажение во время изменения амплитуды. (Форма волны фактически изменяется в течение этого времени по сравнению с исходным сигналом.) Является ли это искажение неприемлемым, зависит от того, насколько внезапным является изменение, насколько велико изменение амплитуды и насколько сложен исходный сигнал. Небольшое количество таких искажений, внесенных в уже сложный сигнал, может остаться незамеченным слушателем. И наоборот, даже незначительное искажение очень чистого исходного сигнала добавит к тону частичные искажения, тем самым изменив его тембр.
В предыдущем примере амплитуда синусоидального тона уменьшилась вдвое (6 дБ) за 5 миллисекунд. Хотя при падении амплитуды можно обнаружить небольшое изменение тембра, сдвиг не настолько резкий, чтобы его можно было услышать как щелчок. Если, с другой стороны, амплитуда синусоиды увеличивается в восемь раз (18 дБ) за 5 мс, изменение достаточно резкое, чтобы его можно было услышать как ударную атаку.
Восьмикратное (18 дБ) усиление за 5 мс создает ударный эффект
Пример патча использует эту комбинацию *~ и line~ для создания регулируемого усилителя для масштабирования амплитуды генератора. Объект упаковки добавляет время перехода к целевому значению амплитуды, поэтому каждое изменение амплитуды будет занимать 100 миллисекунд. Также было включено числовое поле для изменения частоты генератора.
Генератор с регулируемой частотой и амплитудой
Обратите внимание, что сигнальная сеть уже имеет значения по умолчанию, прежде чем в нее будет отправлено какое-либо сообщение Max. Объект цикла~ имеет указанную частоту 1000 Гц, а объект линии~ имеет начальное значение по умолчанию 0. Даже если бы *~ имел введенный аргумент для инициализации своего правого входа, его правый операнд все равно был бы равен 0, потому что line~ постоянно предоставляет ему это значение.
Объект цикла~ имеет указанную частоту 1000 Гц, а объект линии~ имеет начальное значение по умолчанию 0. Даже если бы *~ имел введенный аргумент для инициализации своего правого входа, его правый операнд все равно был бы равен 0, потому что line~ постоянно предоставляет ему это значение.
• Используйте числовое поле Amplitude , чтобы установить желаемый уровень громкости, затем щелкните переключатель с пометкой Audio On/Off , чтобы включить звук. Используйте объекты числового поля, чтобы изменить частоту и амплитуду тона. Нажмите на переключатель еще раз, чтобы выключить звук.
Сочетание строки~ и *~ также помогает избежать щелчков, которые могут возникать при включении и выключении звука. Сообщения «вкл» и «выкл» 1 и 0 от переключателя используются для плавного увеличения громкости до желаемой амплитуды или до 0, так же как сообщение запуска или остановки отправляется на dac~. Таким образом, звук плавно появляется и исчезает, а не включается мгновенно.
Сообщения о включении и выключении звука появляются или исчезают перед запуском или остановкой ЦАП
Непосредственно перед выключением звука объекту пакета отправляется переключатель 0 from, чтобы начать 100-мс затухание громкости генератора. Также введена задержка в 100 мс перед отправкой стоп-сообщения на dac~, чтобы произошло затухание. Непосредственно перед включением звука запускается желаемое значение амплитуды, начиная постепенное увеличение громкости; однако в действительности нарастание не начинается до тех пор, пока не будет запущен dac~ — в данном случае сразу после этого. (В реальной программе окна сообщений запуска и остановки могут быть скрыты от просмотра или инкапсулированы в подпатч, чтобы пользователь не мог щелкнуть их напрямую.)
Умножение каждой выборки аудиосигнала на любое число, отличное от 1, изменяет его амплитуду; поэтому объект *~ фактически является усилителем. Внезапное резкое изменение амплитуды может вызвать щелчок, поэтому обычно рекомендуется более плавное затухание амплитуды — путем управления амплитудой другим сигналом.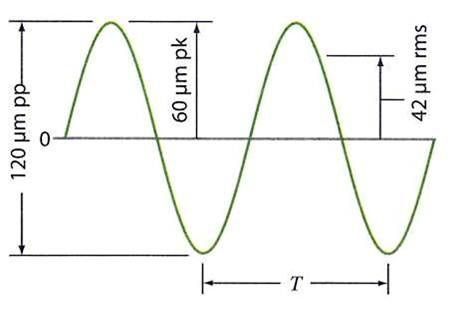 Генератор сигналов линейного сегмента line~ сравним с линией объекта Max и подходит для обеспечения линейно изменяющегося значения в сигнальной сети. Комбинация строки~ и *~ может использоваться для получения числа 9.0007 конверт для управления общей амплитудой сигнала.
Генератор сигналов линейного сегмента line~ сравним с линией объекта Max и подходит для обеспечения линейно изменяющегося значения в сигнальной сети. Комбинация строки~ и *~ может использоваться для получения числа 9.0007 конверт для управления общей амплитудой сигнала.
| Имя | Описание |
|---|---|
| цикл~ | Генератор поиска по таблице |
| дак~ | Аудиовыход и вкл/выкл |
| строка~ | Генератор линейных рамп |
Аналого-цифровое преобразование — GeeksforGeeks
Цифровой сигнал: Цифровой сигнал — это сигнал, представляющий данные в виде последовательности дискретных значений; в любой момент времени он может принимать только одно из конечного числа значений.
Аналоговый сигнал: Аналоговый сигнал — это любой непрерывный сигнал, для которого свойство сигнала, изменяющееся во времени, является представлением некоторой другой изменяющейся во времени величины, т. е. аналогично другому изменяющемуся во времени сигналу.
е. аналогично другому изменяющемуся во времени сигналу.
Для аналого-цифрового преобразования можно использовать следующие методы:
a. ИМПУЛЬСНО-КОДОВАЯ МОДУЛЯЦИЯ:
Наиболее распространенный метод преобразования аналогового сигнала в цифровые данные называется импульсно-кодовой модуляцией (ИКМ). Кодер PCM имеет следующие три процесса:
- Сэмплирование
- Квантование
- Кодирование
Фильтр нижних частот:
Фильтр нижних частот устраняет высокочастотные компоненты, присутствующие во входном аналоговом сигнале, чтобы гарантировать, что входной сигнал на сэмплер свободен от нежелательных частотных компонентов. .Это сделано для того, чтобы избежать искажения сигнала сообщения.
- Выборка – Первым шагом в PCM является выборка. Выборка — это процесс измерения амплитуды непрерывного сигнала в дискретные моменты времени с преобразованием непрерывного сигнала в дискретный.
 Существует три метода отбора проб:
Существует три метода отбора проб:(i) Идеальная выборка: В идеальной выборке, также известной как Мгновенная выборка импульсов аналогового сигнала. Это идеальный метод выборки, и его нелегко реализовать.
(ii) Естественная выборка: Естественная выборка — это практический метод выборки, при котором импульсы имеют конечную ширину, равную T. В результате получается последовательность выборок, сохраняющая форму аналогового сигнала.
(iii) Отбор проб с плоской поверхности: По сравнению с естественным отбором проб можно легко получить плоский верх. В этом методе семплирования верхняя часть сэмплов остается постоянной за счет использования схемы. Это наиболее распространенный метод выборки.
Теорема Найквиста:
Одним из важных соображений является частота дискретизации или частота. Согласно теореме Найквиста, частота дискретизации должна быть как минимум в 2 раза выше максимальной частоты, содержащейся в сигнале. Она также известна как минимальная частота дискретизации и определяется как:
Она также известна как минимальная частота дискретизации и определяется как:
Fs =2*fh - Квантование –
Результатом дискретизации является серия импульсов со значениями амплитуды между максимальной и минимальной амплитудами сигнала. Набор амплитуд может быть бесконечным с нецелыми значениями между двумя пределами.Следующие шаги квантования:
- Предположим, что сигнал имеет амплитуду между Vmax и Vmin
- Мы разделим его на L зон высотой d каждая, где
d= (Vmax-Vmin)/ L - Значение в верхней части каждого образца на графике показывает фактическую амплитуду.
- Значение нормализованной амплитудно-импульсной модуляции (ПАМ) рассчитывается по формуле амплитуда/d.
- После этого мы вычисляем квантованное значение, которое процесс выбирает из середины каждой зоны.
- Квантовая ошибка определяется разницей между квантованным значением и нормализованным значением PAM.
- Код квантования для каждого образца на основе уровней квантования в левой части графика.

- Кодирование –
Оцифровка аналогового сигнала осуществляется энкодером. После того, как каждая выборка квантуется и определяется количество битов в выборке, каждая выборка может быть преобразована в n-битный код. Кодирование также минимизирует используемую полосу пропускания.
б. ДЕЛЬТА МОДУЛЯЦИЯ :
Поскольку ИКМ является очень сложной техникой, были разработаны другие методы для уменьшения сложности ИКМ. Самый простой — дельта-модуляция. Дельта-модуляция находит изменение по сравнению с предыдущим значением.
Модулятор — Модулятор используется на стороне отправителя для создания потока битов из аналогового сигнала. Процесс регистрирует небольшое положительное изменение, называемое дельта. Если дельта положительна, процесс записывает 1, иначе процесс записывает 0. Модулятор создает второй сигнал, напоминающий лестницу. Затем входной сигнал сравнивается с этим постепенно создаваемым лестничным сигналом.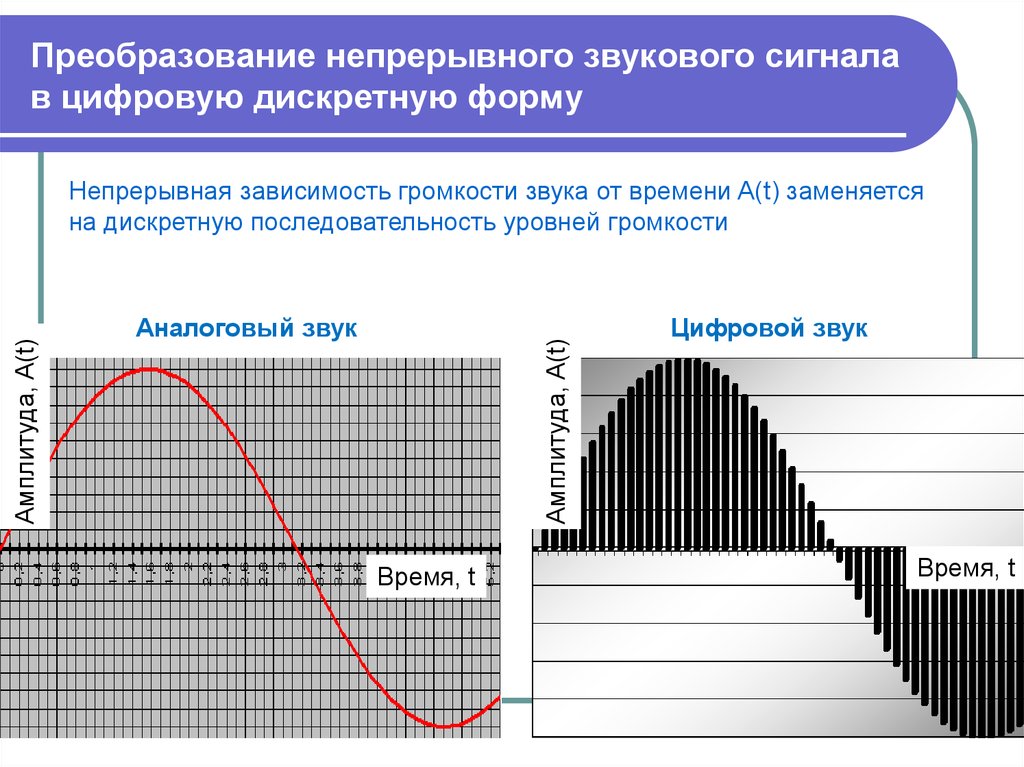
У нас есть следующие правила для вывода:
- Если входной аналоговый сигнал выше, чем последнее значение лестничного сигнала, увеличьте дельту на 1, а бит в цифровых данных равен 1.
- Если входной аналоговый сигнал ниже последнего значения лестничного сигнала, уменьшите дельту на 1, а бит в цифровых данных станет равным 0.
c. АДАПТИВНАЯ ДЕЛЬТА-МОДУЛЯЦИЯ:
Рабочие характеристики дельта-модулятора можно значительно улучшить, если сделать размер шага модулятора изменяющимся во времени. Больший размер шага необходим, когда сообщение имеет крутой наклон модулирующего сигнала, и меньший размер шага необходим, когда сообщение имеет небольшой наклон. Размер адаптируется в соответствии с уровнем входного сигнала. Этот метод известен как адаптивная дельта-модуляция (ADM).
Непрерывная цифровая обработка сигналов (DSP) с использованием реконфигурируемых устройств
Домашний
Агентство:
Министерство обороны
Филиал:
Армия
Программа | Фаза | Год:
СБИР | ОБА | 2020
Запрос:
DoD 2020. 1 SBIR Запрос
1 SBIR Запрос
Номер темы:
A20-080
ПРИМЕЧАНИЕ. Заявки и темы, перечисленные на этот сайт является копиями различных предложений агентства SBIR и не обязательно самые свежие и актуальные. По этой причине вам следует использовать ссылку агентства, указанную ниже, которая приведет вас непосредственно к соответствующий сервер агентства, где вы можете прочитать официальную версию этого ходатайства и скачать соответствующие формы и правила.
Официальная ссылка на это обращение: https://rt.cto.mil/rtl-small-business-resources/sbir-sttr/
Дата выпуска:
10 декабря 2019 г.
Дата открытия:
14 января 2020 г.
Срок подачи заявки :
12 февраля 2020 г.
Дата закрытия:
26 февраля 2020 г.
Описание:
ОБЛАСТЬ ТЕХНОЛОГИИ: Информационные системы,
ЦЕЛЬ: Современные ракетные системы требуют огромных объемов обработки сигналов и информации с использованием ограниченных ресурсов в экстремальных условиях. Мультиспектральные датчики, высокоскоростная связь и управление сверхзвуковым полетом требуют значительной вычислительной мощности, а ограничения по пространству и весу ограничивают доступную мощность и тепловыделение. Неясно, смогут ли обычные подходы цифровой обработки сигналов (DSP) обеспечить повышенную производительность, необходимую для ракетных систем следующего поколения. Чтобы удовлетворить эту потребность, желательны альтернативы традиционным, энергоемким подходам к цифровой обработке. Многообещающим новым подходом является цифровая обработка сигналов с непрерывным временем (CTDSP), которая обеспечивает аналогичную или улучшенную производительность при значительном снижении требований к мощности и рассеиванию тепла [1]. В частности, алгоритмы с непрерывным временем, которые могут быть реализованы на реконфигурируемом оборудовании, включая программируемые вентильные матрицы (FPGA), могут позволить гибко проектировать будущие ракетные системы. Поскольку снижение мощности этого метода зависит от приложения, точную выгоду для армейских систем в настоящее время невозможно определить количественно; однако сообщалось об экономии энергии в 3 раза [2]. Эти усилия направлены на то, чтобы повлиять на приоритеты модернизации сухопутных войск в области дальнего высокоточного огня и противовоздушной и противоракетной обороны.
В частности, алгоритмы с непрерывным временем, которые могут быть реализованы на реконфигурируемом оборудовании, включая программируемые вентильные матрицы (FPGA), могут позволить гибко проектировать будущие ракетные системы. Поскольку снижение мощности этого метода зависит от приложения, точную выгоду для армейских систем в настоящее время невозможно определить количественно; однако сообщалось об экономии энергии в 3 раза [2]. Эти усилия направлены на то, чтобы повлиять на приоритеты модернизации сухопутных войск в области дальнего высокоточного огня и противовоздушной и противоракетной обороны.
ОПИСАНИЕ: Непрерывная цифровая обработка сигналов (CTDSP) предлагает многообещающую альтернативу традиционной цифровой обработке сигналов (DSP) для систем, ограниченных по размеру, весу, мощности и стоимости [3]. Определяющим атрибутом является использование непрерывных цифровых состояний вместо выборок с дискретной тактовой частотой. Выходы затвора переключаются при изменении входных сигналов, в отличие от обычного DSP, где выходы затвора обновляются с фиксированной тактовой частотой. Таким образом, CTDSP можно описать как цифровую обработку без синхронизации. Основным потенциальным преимуществом CTDSP является снижение энергопотребления и тепловыделения за счет уменьшения количества переключений для малоактивных сигналов. По мере развития CTDSP стандартные модули и функции, лежащие в основе многих наиболее распространенных алгоритмов обработки сигналов, должны быть переработаны для работы с использованием нетактовой логики. Операции, включая линейные фильтры, смесители, корреляторы и даже простые математические функции, требуют нового подхода к проектированию. Были успешно продемонстрированы многие ключевые алгоритмы, в первую очередь фильтры с использованием FPGA [3] и специализированных интегральных схем (ASIC) [4]. Важно отметить, что развитию обычных цифровых систем в значительной степени способствовало широкое использование реконфигурируемых устройств, таких как ПЛИС. Включение реконфигурируемых устройств не только ускоряет начальную разработку, но также облегчает обслуживание и модернизацию полевых систем.
Таким образом, CTDSP можно описать как цифровую обработку без синхронизации. Основным потенциальным преимуществом CTDSP является снижение энергопотребления и тепловыделения за счет уменьшения количества переключений для малоактивных сигналов. По мере развития CTDSP стандартные модули и функции, лежащие в основе многих наиболее распространенных алгоритмов обработки сигналов, должны быть переработаны для работы с использованием нетактовой логики. Операции, включая линейные фильтры, смесители, корреляторы и даже простые математические функции, требуют нового подхода к проектированию. Были успешно продемонстрированы многие ключевые алгоритмы, в первую очередь фильтры с использованием FPGA [3] и специализированных интегральных схем (ASIC) [4]. Важно отметить, что развитию обычных цифровых систем в значительной степени способствовало широкое использование реконфигурируемых устройств, таких как ПЛИС. Включение реконфигурируемых устройств не только ускоряет начальную разработку, но также облегчает обслуживание и модернизацию полевых систем. Чтобы использовать последние достижения, крайне желательна разработка алгоритмов обработки цифровых сигналов с непрерывным временем, помимо сетей линейных фильтров, которые работают на реконфигурируемых цифровых устройствах. Эти алгоритмы могут использовать амплитудное квантование аналоговых входных сигналов, но обеспечивают непрерывную несинхронизированную обработку цифровых сигналов. Целевые алгоритмы позволят выполнять общие операции обработки сигналов, необходимые для связи, обнаружения и управления, которые типичны для современных ракетных систем. Проблемы включают непрерывную оцифровку входного аналогового сигнала, разработку алгоритма, оптимизацию ресурсов, эффекты амплитудного квантования, ограничения полосы пропускания и коррекцию ошибок или допуск. Предпочтительные проекты не зависят от поставщика и переносятся на реконфигурируемые устройства с минимальной настройкой, зависящей от устройства. Целью этого запроса является разработка набора алгоритмов CTDSP, позволяющих недорогим, маломощным, реконфигурируемым устройствам обработки сигналов поддерживать широкий спектр приложений.
Чтобы использовать последние достижения, крайне желательна разработка алгоритмов обработки цифровых сигналов с непрерывным временем, помимо сетей линейных фильтров, которые работают на реконфигурируемых цифровых устройствах. Эти алгоритмы могут использовать амплитудное квантование аналоговых входных сигналов, но обеспечивают непрерывную несинхронизированную обработку цифровых сигналов. Целевые алгоритмы позволят выполнять общие операции обработки сигналов, необходимые для связи, обнаружения и управления, которые типичны для современных ракетных систем. Проблемы включают непрерывную оцифровку входного аналогового сигнала, разработку алгоритма, оптимизацию ресурсов, эффекты амплитудного квантования, ограничения полосы пропускания и коррекцию ошибок или допуск. Предпочтительные проекты не зависят от поставщика и переносятся на реконфигурируемые устройства с минимальной настройкой, зависящей от устройства. Целью этого запроса является разработка набора алгоритмов CTDSP, позволяющих недорогим, маломощным, реконфигурируемым устройствам обработки сигналов поддерживать широкий спектр приложений. Таким образом, запрос не ограничивается конкретным приложением или спецификацией производительности.
Таким образом, запрос не ограничивается конкретным приложением или спецификацией производительности.
ЭТАП I. Проведите исследование конструкции, чтобы определить важные блоки обработки сигналов для реализации с использованием цифровых схем с непрерывным временем на реконфигурируемом устройстве. Эти важные блоки обработки должны, как минимум, реализовывать фильтры нижних частот, верхних частот, полосовые и режекторные фильтры, а также модуляцию. Моделирование и теоретический анализ позволят определить предпочтительный концептуальный дизайн для представления сигналов и модуляризации операций. Внимание будет уделено интерфейсу аналогового сигнала, требованиям к ресурсам, эффектам квантования и переносимости в реконфигурируемых архитектурах.
ЭТАП II: Завершить работу над оптимизированным набором инструментов непрерывной обработки сигналов, реализуемых на реконфигурируемых вентильных матрицах для поддержки различных требований к обработке сигналов, типичных для ракетных систем. Показатели производительности обеспечат улучшенную производительность по сравнению с традиционными подходами DSP с точки зрения размера, мощности, рассеивания тепла, стоимости и реконфигурируемости. Потенциальные военные и коммерческие приложения будут определены и нацелены на стадию III эксплуатации и коммерциализации.
Показатели производительности обеспечат улучшенную производительность по сравнению с традиционными подходами DSP с точки зрения размера, мощности, рассеивания тепла, стоимости и реконфигурируемости. Потенциальные военные и коммерческие приложения будут определены и нацелены на стадию III эксплуатации и коммерциализации.
ЭТАП III: Развитие цифровой обработки сигналов с непрерывным временем для удовлетворения требований к обработке сигналов с использованием реконфигурируемых массивов вентилей обеспечивает значительный прорыв в технологии обработки сигналов для поддержки связи, дистанционного зондирования и управления. Эти технологии предлагают потенциальные преимущества в широком спектре сетей связи и датчиков как для военных, так и для гражданских приложений.
ССЫЛКИ:
1: Ю. Цивидис, «Непрерывная цифровая обработка сигналов», Electronics Letters 39(21), 1551 (2003).
КЛЮЧЕВЫЕ СЛОВА: цифровая обработка сигналов (DSP), непрерывная цифровая обработка сигналов (CTDSP), программируемые вентильные матрицы (FPGA)
Квантование и шум квантования — DSPIllustrations.
 com
comКвантизатор — это блок обработки сигналов, который преобразует непрерывную амплитуду в дискретную амплитуду. Выход квантователя является дискретным, то есть он может выводить только $Q$ различных значений. На практике квантователь представляет собой аналого-цифровой преобразователь, поскольку он отображает непрерывную входную амплитуду в цифровое представление этого значения. Формально квантованный выход $Q[x]$ некоторого входного значения $x$ определяется как
$$Q[x] = \arg \min_{l\in\mathcal{S}} |l-x|.$$
Здесь множество $\mathcal{S}$ содержит все возможные выходные значения квантователя, которые мы называем уровней квантования . Что это значит? Это означает, что для данного входа $x$ квантователь возвращает уровень квантования $l$, который ближе всего к входному значению. Следовательно, квантователь полностью определяется своим набором уровней квантования $\mathcal{S}$.
Предположим, что квантователь должен уметь квантовать значения между входными амплитудами $-U$ и $+U$, т. q$ различных уровней квантования в $\mathcal{S}$. Тогда логичным решением будет сделать расстояние $\Delta_s$ между уровнями квантования постоянным, равным
q$ различных уровней квантования в $\mathcal{S}$. Тогда логичным решением будет сделать расстояние $\Delta_s$ между уровнями квантования постоянным, равным
$$\Delta_s = \frac{2U}{q}.$$
Обычно используются два разных квантователя: со средним подъемом и со средним шагом . Они различаются настройкой своих уровней: для среднего шага мы имеем $0\in\mathcal{S}$, тогда как для среднего шага квантизатора мы имеем $0\neq\mathcal{S}$, т.е. квантователь среднего шага имеет уровень для нулевого выходного значения. Уровни квантования для обоих квантователей определяются
$$\begin{выравнивание}
\mathcal{S} &= \{-U+\frac{\Delta_s}{2}+\Delta_s\cdot(0,1,2,\dots, q-1)\}&\text{для средней высоты} \\
\mathcal{S} &= \{-U+\Delta_s\cdot(0,1,2,\dots, q-1)\}&\text{ для середины протектора}
\end{выравнивание}$$
9b=q$ — четное число, квантизатор среднего шага ни в коем случае не может быть симметричным. Далее мы сосредоточимся на квантизаторе среднего роста.
Далее мы сосредоточимся на квантизаторе среднего роста.
Операция квантования вносит ошибку, поскольку бесконечное количество различных входных амплитуд отображается на конечный набор дискретных уровней квантования. Ошибка между входом и выходом квантователя называется Шум квантования $n_q(t)$. При обозначении $s(t)$ входного сигнала и $s_q(t)$ выходного сигнала квантователя выполняется следующее соотношение:
$$\begin{выравнивание} s_q(t)&=Q[s(t)]&&\text{Операция квантования}\\ n_q(t)&=s(t)-s_q(t)&&\text{Выражение шума квантования}\\ s_q(t)&=s(t)-n_q(t) \end{align}.$$
Глядя на последнее уравнение, шум квантования действительно можно понимать как шум поверх сигнала с непрерывной амплитудой, отсюда и его название. Давайте создадим синусоидальную волну и пропустим ее через квантователь, и посмотрим на квантованный сигнал и шум квантования.
Сначала определим функцию удобства calcLevels , который вычисляет уровни квантования для данного количества битов b.
Теперь давайте сгенерируем синусоидальный сигнал и покажем результирующий шум квантования.
Как видите, с увеличением количества битов квантования ошибка квантования практически исчезает. Однако важной мерой является отношение сигнал/шум квантования (SNR), и мы собираемся его измерить. При достаточно большом количестве битов шум квантования примерно равномерно распределяется в пределах $\pm\frac{\Delta_s}{2}$. В литературе, например. Proakis: Digital Signal Processing, было показано, что SNR квантования для синусоидального сигнала с полным возбуждением (т.е. амплитуда синуса равна диапазону квантования) может быть определена как
$$SNR\приблизительно (1,76 + 6,02b)дБ,$$
, где $b$ — количество битов для квантования.
Напишем функцию для измерения этого шума квантования. Здесь мы напрямую конвертируем SNR в шкалу дБ.
Теперь мы можем построить график зависимости шума квантования от количества битов и сравнить его с теоретической кривой $1,76+6,02b$.
Как видим, приближение выполняется очень хорошо. Давайте теперь посмотрим, что происходит, когда мы уменьшаем амплитуду синуса:
Как мы видим, отношение SNR квантования ухудшается при уменьшении амплитуды синуса. Это разумно, так как шум квантования зависит только от количества битов квантования $b$ и, следовательно, не зависит от амплитуды сигнала и, следовательно, от мощности шума квантования. С другой стороны, мощность сигнала уменьшается при уменьшении амплитуды. Следовательно, мы видим деградацию SNR. Однако важным замечанием является то, что улучшение отношения сигнал-шум для каждого дополнительного бита остается на уровне $6$дБ, независимо от амплитуды сигнала.
Давайте теперь измерим SNR квантования для сигнала, который представляет собой просто гауссов шум:
Что здесь происходит? Отношение сигнал-шум квантования довольно низкое, несмотря на 14-битное разрешение? Глядя на исходный и квантованный сигнал, можно обнаружить проблему: квантизатор просто перегружен: входной сигнал выше, чем может вывести квантователь. Таким образом, он никогда не сможет достичь хорошего квантования. Давайте со временем уменьшим амплитуду шума и посмотрим, поможет ли это:
Таким образом, он никогда не сможет достичь хорошего квантования. Давайте со временем уменьшим амплитуду шума и посмотрим, поможет ли это:
Теперь мы видим, что отношение сигнал-шум квантования увеличивается на 6 дБ для каждого бита. Но, глядя на сигналы, мы видим еще одну важную вещь: хотя квантизатор мог бы выводить значения между $\pm 1$, большинство его значений сосредоточены в пределах $\pm 0,1$. Это связано с характером гауссовского шумового сигнала, который в основном концентрируется вокруг $s(t)=0$. Следовательно, для улучшения SNR имеет смысл увеличить разрешение на более низких уровнях квантования за счет более грубой дискретизации на более высоких амплитудах. Этот метод известен как нелинейные квантователи, но здесь он не рассматривается.
5.1: Представление цифровых и аналоговых значений — выборка и квантование
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14853
- Харрисон Ньороге
- Африканский виртуальный университет
Этот раздел знакомит учащегося с сэмплированием и квантованием. Здесь сигналы представлены в виде горизонтальных и вертикальных значений (осей).
Здесь сигналы представлены в виде горизонтальных и вертикальных значений (осей).
Оцифровка аналогового сигнала включает две операции:
- Выборка и
- Квантование
Аналоговые сигналы состоят из непрерывных значений для обеих осей. Рассмотрим электрический сигнал, горизонтальная ось которого представляет время в секундах, а вертикальная ось представляет амплитуду в вольтах. Горизонтальная ось имеет диапазон значений от нуля до бесконечности со всеми возможными значениями между ними. Это делает горизонтальную ось непрерывной. Вертикальная ось также непрерывна, что позволяет амплитуде сигнала принимать любое значение от нуля до бесконечности. Каждому возможному значению времени соответствует значение амплитуды аналогового сигнала.
Аналоговый сигнал существует в течение непрерывного интервала времени и/или принимает непрерывный диапазон значений. Синусоидальный сигнал (также называемый в акустике чистым тоном) обладает обоими этими свойствами.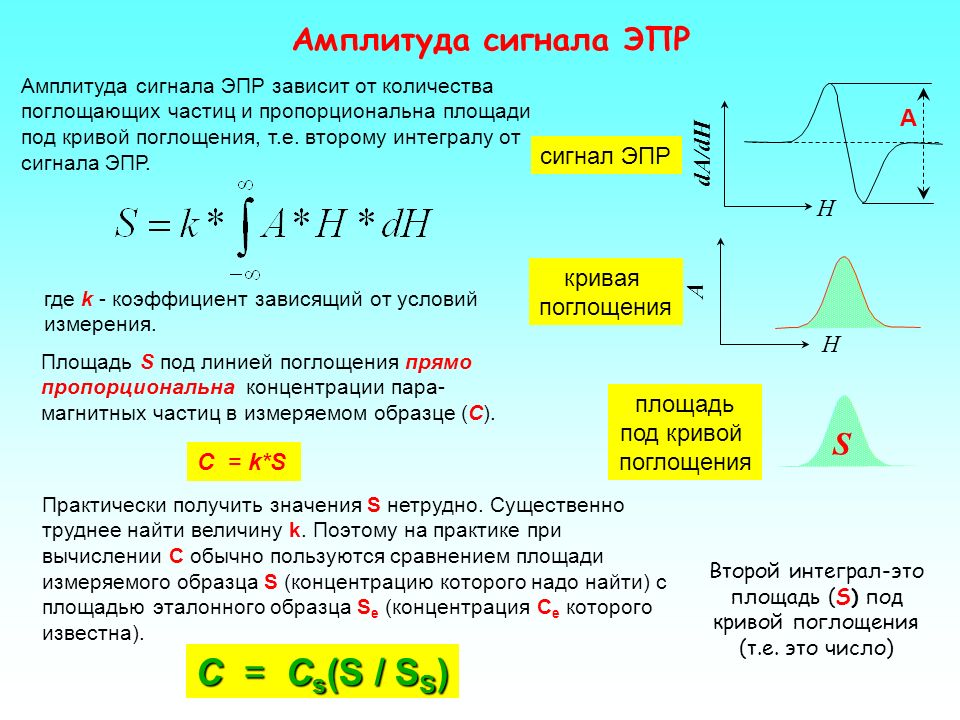
Рис. 1: Аналоговый сигнал. Этот сигнал \(v(t)=\cos (2\pi ft)\) может быть идеальной аналоговой записью чистого тона частотой \(f\) Гц. Если \(f=440\) Гц, то этим тоном является музыкальная нота \(A\) выше средней \(C\), на которую оркестры часто настраивают свои инструменты. Период \(T=1/f\) — это продолжительность одного полного колебания.
В действительности электрические записи страдают от шума, который неизбежно ухудшает качество сигнала. Чем больше запись переводится из одного аналогового формата в другой, тем больше она теряет точность оригинала.
Рис. 2: Зашумленный аналоговый сигнал. Шум ухудшает синусоидальный сигнал на рис. 1. Часто невозможно точно восстановить исходный сигнал из зашумленной версии.
С другой стороны, цифровые сигналы имеют дискретные значения как для горизонтальной, так и для вертикальной оси. Оси больше не являются непрерывными, как это было с аналоговым сигналом. В этом обсуждении время
Оси больше не являются непрерывными, как это было с аналоговым сигналом. В этом обсуждении время
будет использоваться как величина для горизонтальной оси, а вольты будут использоваться для вертикальной оси.
Цифровой сигнал представляет собой последовательность дискретных символов. Если эти символы нули и единицы, мы называем их битами. Таким образом, цифровой сигнал не является ни непрерывным во времени, ни непрерывным в своем диапазоне значений. И, следовательно, не может идеально представлять произвольные аналоговые сигналы. С другой стороны, цифровые сигналы устойчивы к шуму.
Рис. 3: Аналоговая передача цифрового сигнала. Рассмотрим цифровой сигнал 100110, преобразованный в аналоговый сигнал для радиопередачи. Принятый сигнал страдает от шума, но при достаточной битовой длительности Tb по-прежнему легко прочитать исходную последовательность 100110.
Цифровые сигналы могут храниться на цифровых носителях (таких как компакт-диски) и обрабатываться в цифровых системах (таких как интегральная схема в проигрывателе компакт-дисков). Эта цифровая технология позволяет осуществлять разнообразную цифровую обработку, недоступную аналоговым системам. Например, музыкальный сигнал, закодированный на компакт-диске, включает в себя дополнительные данные, используемые для цифровой коррекции ошибок. В случае, если компакт-диск поцарапан и часть цифрового сигнала повреждена, проигрыватель компакт-дисков все еще может восстановить недостающие биты точно из данных для исправления ошибок. Чтобы защитить целостность данных, несмотря на то, что они хранятся на поврежденном устройстве, обычно аналоговые сигналы преобразуются в цифровые с использованием шагов, называемых дискретизацией и квантованием.
Введение в сэмплирование Целью сэмплирования и квантования является необходимость хранения сигнала в цифровом формате. Чтобы преобразовать аналоговый сигнал в цифровой, аналоговый сигнал должен быть дискретизирован и проквантован. Выборка берет аналоговый сигнал и дискретизирует ось времени. После выборки ось времени состоит из дискретных моментов времени, а не из непрерывных значений во времени. Результирующий сигнал после дискретизации называется дискретным сигналом, дискретным сигналом или сигналом с дискретным временем. Результирующий сигнал после дискретизации не является цифровым сигналом. Хотя горизонтальная ось имеет дискретные значения, вертикальная ось не дискретизирована. Это означает, что для любого дискретного момента времени существует бесконечное число допустимых значений амплитуды сигнала. Чтобы сигнал был цифровым, обе оси должны быть дискретными.
Чтобы преобразовать аналоговый сигнал в цифровой, аналоговый сигнал должен быть дискретизирован и проквантован. Выборка берет аналоговый сигнал и дискретизирует ось времени. После выборки ось времени состоит из дискретных моментов времени, а не из непрерывных значений во времени. Результирующий сигнал после дискретизации называется дискретным сигналом, дискретным сигналом или сигналом с дискретным временем. Результирующий сигнал после дискретизации не является цифровым сигналом. Хотя горизонтальная ось имеет дискретные значения, вертикальная ось не дискретизирована. Это означает, что для любого дискретного момента времени существует бесконечное число допустимых значений амплитуды сигнала. Чтобы сигнал был цифровым, обе оси должны быть дискретными.
Сэмплирование — это процесс записи аналогового сигнала в регулярные дискретные моменты времени. Частота дискретизации fs — это количество выборок в секунду. Интервал времени между выборками
называется интервалом выборки \(T_s=1/fs\).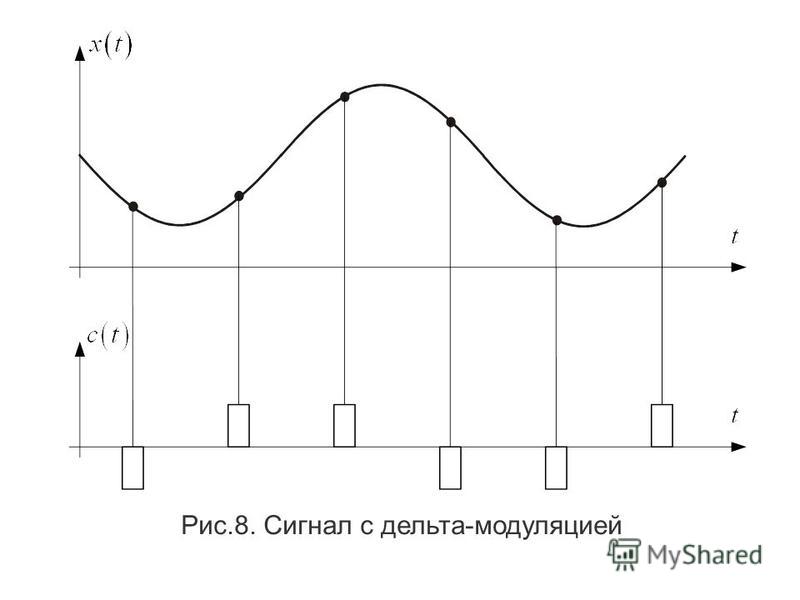
Рис. 4: Отбор проб. Сигнал \(v(t)=\cos (2\pi ft)\) на рис. 1 дискретизируется равномерно с 3 интервалами дискретизации в пределах каждого периода сигнала \(T\). Следовательно, интервал дискретизации \(T_s=T/3\) и частота дискретизации \(f_s=3f\). Другой способ увидеть, что \(f_s=3f\) — это заметить, что в каждом периоде сигнала \(T\) есть три выборки.
Чтобы выразить выборки аналогового сигнала \(v(t)\), мы используем обозначение \(v[n]\) (с квадратными скобками), где целые значения \(n\) индексируют выборки . Обычно выборка \(n = 0\) берется из точки времени \(t=0\) аналогового сигнала. Следовательно, выборка \(n=1\) должна исходить из момента времени \(t=T_s\), ровно через один интервал выборки; и так далее. Таким образом, последовательность выборок может быть записана как \(v[0] = v(0), v[1] = v[T_s], v[2] = v(2T_s)\),…
\ (v[n] = v(nT_s) \ \ \ \ \ \ \ \ \ \ \ \ \text{для целого числа} n . ……………….. ………………..1\)
……………….. ………………..1\)
В примере на рис. 4 \(v(t) = \cos (2 \pi ft)\) выбирается с интервалом дискретизации \(T_s = T/3\)
для получения следующих \(v [н]\).
\(\ begin {array} {rclcl} {v [n]} & = & {\ cos (2 \pi fn/T_s)} & \ \ \ \ \ \ \ & {\ text {путем замены} t = nT_s …………………………..2} \\ {} & = & {\cos (2 \ pi fn T/3)} & \ \ \ \ \ \ \ & {\ text {так как} T_s = T/3 ………………….. ……3} \\ {} & = & {\ cos (2 \pi n/3)} & \ \ \ \ \ \ \ & {\ text {так как} T = 1/f … ……………………..4} \end{массив}\)
Это выражение для \(v[n]\) дает примерные значения, изображенные на рис. 4, как показано ниже.
\(v[0] = \cos (0) = 1\)
\(v[1] = \cos (2\pi 3) = -0,5\)
\(v[2] = \ cos (4 \pi 3) = -0,5\)
\(v[3] = \cos (2\pi) = 1\)
Рис. 5: Образцы. Образцы на рис.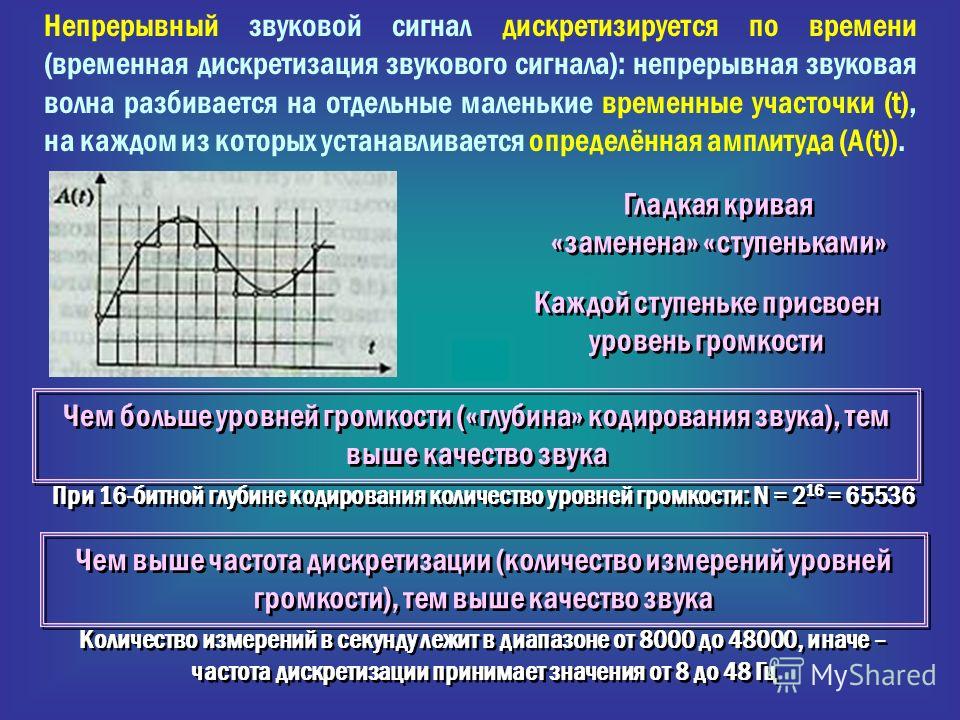 4 показаны как последовательность \(v[n]\), индексированная целыми значениями \(n\).
4 показаны как последовательность \(v[n]\), индексированная целыми значениями \(n\).
Поскольку дискретный сигнал имеет дискретные моменты времени, но по-прежнему имеет непрерывные значения амплитуды, амплитуда сигнала должна быть дискретизирована, чтобы сохранить его в цифровом формате. Значения амплитуды необходимо округлить до дискретных значений. Если вертикальная ось разделена на небольшие окна амплитуд, то каждое значение, лежащее в этом окне, будет округлено (или квантовано) до одного и того же значения.
Например, рассмотрим сигнал с размерами окна 0,5 вольт, начиная с -4 вольт и заканчивая +4 вольт. В дискретный момент времени любая амплитуда между 4,0 В и 3,5 В будет записана как 3,75 В. В этом примере центр каждого 0,5-вольтового окна (или области квантования) был выбран в качестве напряжения квантования для этой области.
В этом примере динамический диапазон сигнала составляет 8 вольт. Поскольку каждая область квантования составляет 0,5 вольта, в динамический диапазон включено 16 областей квантования. Важно, что в динамическом диапазоне имеется 16 областей квантования. Поскольку двоичное число будет представлять значение амплитуды, важно, чтобы количество областей квантования было степенью двойки. В этом примере потребуется 4 бита для представления каждого из 16 возможных значений амплитуды сигнала.
Важно, что в динамическом диапазоне имеется 16 областей квантования. Поскольку двоичное число будет представлять значение амплитуды, важно, чтобы количество областей квантования было степенью двойки. В этом примере потребуется 4 бита для представления каждого из 16 возможных значений амплитуды сигнала.
Последовательность выборок, подобная v[n] на рис. 5, не является цифровым сигналом, поскольку значения выборки потенциально могут принимать непрерывный диапазон значений. Чтобы завершить аналого-цифровое преобразование, каждое значение выборки отображается на дискретный уровень (представленный последовательностью битов) в процессе, называемом квантованием. В B-битном квантователе каждый уровень квантования представлен B битами, так что количество уровней равно 2B
Рис. 6: 3-битное квантование. На образцы \(v[n]\) с рис. 5 наложен 3-битный квантователь с 8 равномерно расположенными уровнями квантования. Квантизатор аппроксимирует каждое значение выборки в \(v[n]\) до ближайшего значения уровня (показанного слева), создавая квантованную последовательность \(vQ[n]\). В конечном счете, последовательность \(vQ[n]\) может быть записана как последовательность битов с использованием 3-битных представлений, показанных справа.
В конечном счете, последовательность \(vQ[n]\) может быть записана как последовательность битов с использованием 3-битных представлений, показанных справа.
Обратите внимание, что квантование вносит ошибку квантования между выборками и их квантованными версиями, определяемыми как \(e[n]=v[n]−vQ[n]\). Если образец находится между уровнями квантования, максимальная абсолютная ошибка квантования \(|e[n]|\) составляет половину интервала между этими уровнями. Для квантователя на рис. 6 максимальная ошибка между уровнями составляет 0,15, поскольку расстояние равно 0,3. Обратите внимание, однако, что если образец превышает самый высокий уровень или ниже самого низкого уровня более чем на 0,15, абсолютная ошибка квантования будет той разницей, которая больше 0,15.
В таблице ниже показан пример квантования на рис. 6 для \(n=0, 1, 2, 3\). 3-битные представления в последней строке могут быть окончательно объединены в цифровой сигнал 110001001110.
Таблица 1: Пример квантования.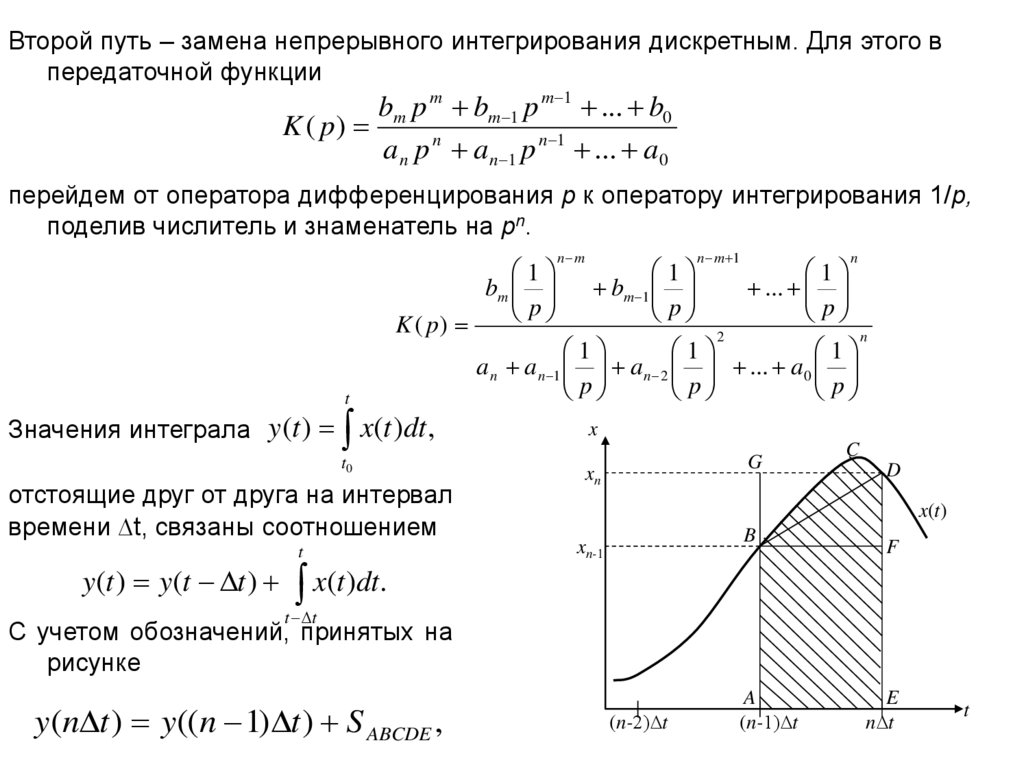
| Последовательность | \(n = 0\) | \(n = 1\) | \(n = 2\) | \(n = 3\) |
| Образцы \(v[n]\) | 1 | -0,5 | -0,5 | 1 |
| Квантованные выборки \(vQ[n]\) | 0,9 | -0,6 | -0,6 | 0,9 |
| 0,1 | 0,1 | 0,1 | 0,1 | |
| 3-битные представления | 110 | 1 | 1 | 110 |
В этом разделе учащиеся узнали, как аналоговые (непрерывные) данные могут быть оцифрованы
Оценка 1.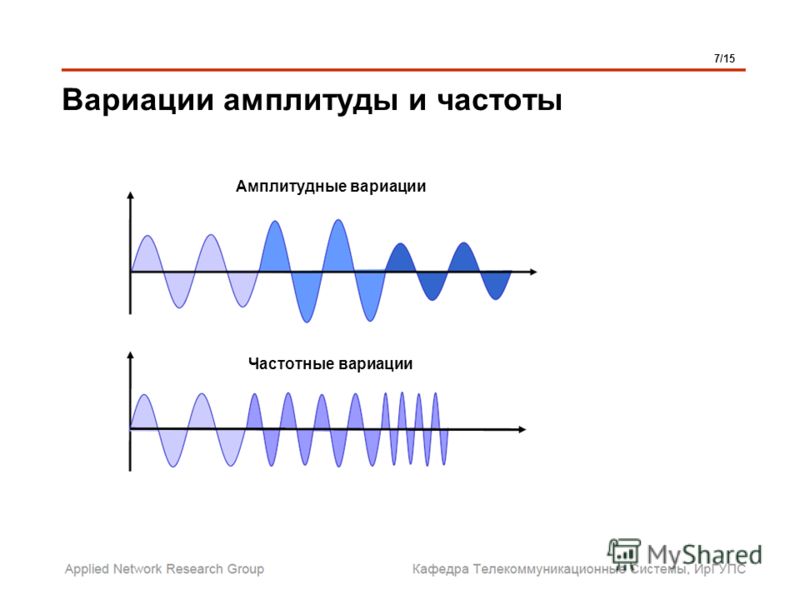 В чем разница между аналоговыми и цифровыми данными?
В чем разница между аналоговыми и цифровыми данными?
Аналоговые данные являются непрерывными, допуская бесконечное число возможных значений. Цифровые данные дискретны, что позволяет использовать конечный набор значений
2. Почему сложно сохранить аналоговые звуковые волны в цифровом формате?
Аналоговые данные — это непрерывные данные, преобразование непрерывных данных в дискретные значения может привести к некоторой потере точности
3. Различие между аналоговыми и цифровыми данными
Аналоговые относятся к цепям, в которых такие величины, как напряжение или ток, изменяются с постоянной скоростью. Например, когда вы поворачиваете ручку потенциометра, вы изменяете сопротивление с непрерывно меняющейся скоростью. Сопротивление потенциометра может быть любым значением между минимумом и максимумом, допустимым потенциометром. В цифровой электронике количества подсчитываются, а не измеряются. Существует важное различие между подсчетом и измерением. Когда вы что-то считаете, вы получаете точный результат. Когда вы что-то измеряете, вы получаете приблизительный результат.
Когда вы что-то измеряете, вы получаете приблизительный результат.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Харрисон Ньороге
- Лицензия
- СС BY-SA
- Теги
Представление сигналов во временной и частотной областях
Электрические сигналы имеют представление как во временной, так и в частотной областях.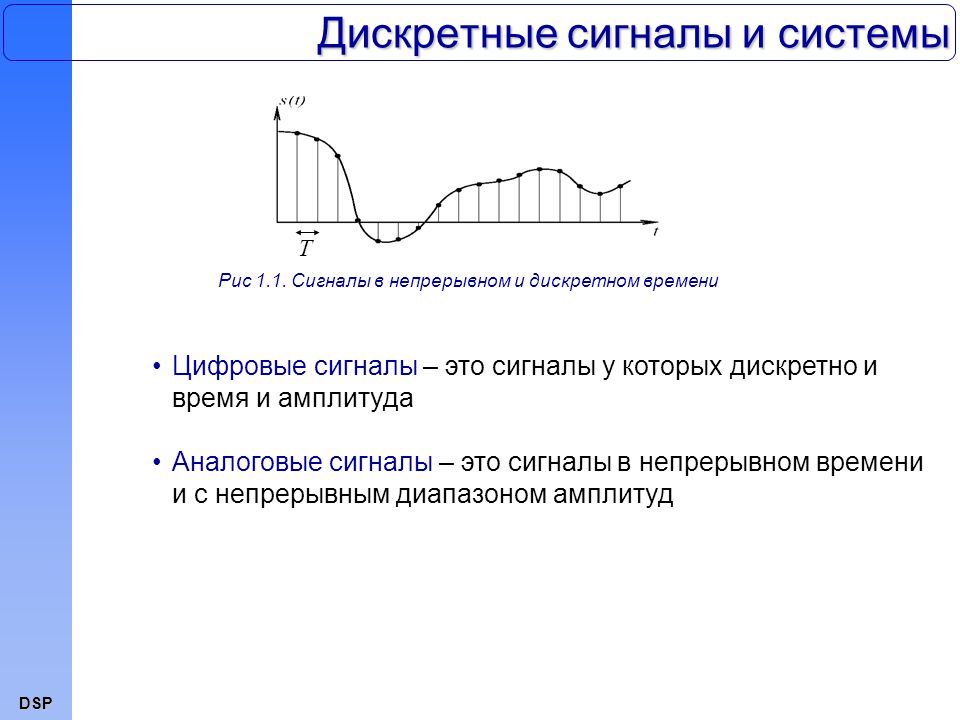 Во временной области напряжение или ток выражаются как функция времени, как показано на рисунке 1. Большинство людей относительно комфортно представляют сигналы во временной области. Сигналы, измеренные на осциллографе, отображаются во временной области, а цифровая информация часто передается в виде зависимости напряжения от времени.
Во временной области напряжение или ток выражаются как функция времени, как показано на рисунке 1. Большинство людей относительно комфортно представляют сигналы во временной области. Сигналы, измеренные на осциллографе, отображаются во временной области, а цифровая информация часто передается в виде зависимости напряжения от времени.
Рис. 1. Представление электрического сигнала во временной области.
Сигналы также могут быть представлены величиной и фазой в зависимости от частоты. Сигналы, которые периодически повторяются во времени, представлены спектром мощности, как показано на рисунке 2. Сигналы, которые ограничены во времени (т. е. не равны нулю только в течение конечного времени), представлены энергетическим спектром, как показано на рисунке 3.
Рис. 2. Спектр мощности периодического сигнала.
Рис. 3. Энергетический спектр ограниченного во времени (переходного) сигнала.
Представления в частотной области особенно полезны при анализе линейных систем.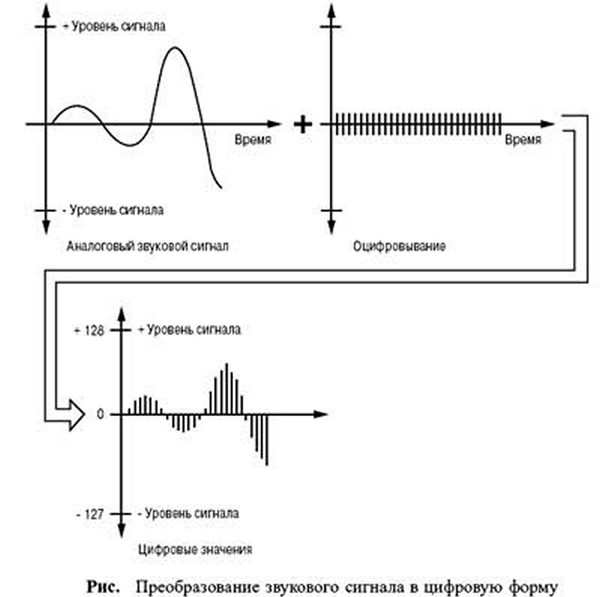 Инженеры по электромагнитной совместимости и целостности сигналов должны уметь работать с сигналами, представленными как во временной, так и в частотной областях. Источники сигналов и помехи часто определяются во временной области. Однако поведение системы и преобразования сигналов более удобны и интуитивно понятны при работе в частотной области.
Инженеры по электромагнитной совместимости и целостности сигналов должны уметь работать с сигналами, представленными как во временной, так и в частотной областях. Источники сигналов и помехи часто определяются во временной области. Однако поведение системы и преобразования сигналов более удобны и интуитивно понятны при работе в частотной области.
Линейные системы
Теория линейных систем играет ключевую роль в инженерном анализе электрических и механических систем. Инженеры моделируют множество вещей, включая поведение схемы, распространение сигнала, связь и излучение, как линейные преобразования. Поэтому важно точно определить, что мы подразумеваем под линейной системой, чтобы понять, как и когда использовать преимущества мощных инструментов анализа линейной системы, доступных нам.
На рис. 4 показана система с одним входом, x(t) и один выход, y(t)=H[x(t)] . Если вход x 1 (t) производит выход y 1 (t) , а ввод x 2 (t) производит выход y 2 0 7 2 7 , то система является линейной тогда и только тогда, когда являются константами. Другими словами, масштабирование ввода с помощью константы даст результат, масштабированный с помощью той же константы; и объединение (суммирование) двух входов даст выход, который представляет собой сумму выходов, произведенных отдельными входами.
Другими словами, масштабирование ввода с помощью константы даст результат, масштабированный с помощью той же константы; и объединение (суммирование) двух входов даст выход, который представляет собой сумму выходов, произведенных отдельными входами.
Рисунок 4: Линейная система.
Контрольный вопрос
Какое из следующих уравнений описывает связь между выходом y(t) и входом x(t) линейной системы?
- у=5х
- у(т)=0
- у=8х+3
- у=х 2
- у(т)=5т х(т)
- у=sin x
- y(t)=5 δ/δt [x(t)]
Из приведенных выше вариантов только a, b и g являются преобразованиями линейной системы. y=0 не очень интересная система, потому что ее выход всегда равен нулю, но она линейна. Простые производные и интегральные операторы являются линейными, поскольку они удовлетворяют условиям уравнения (1).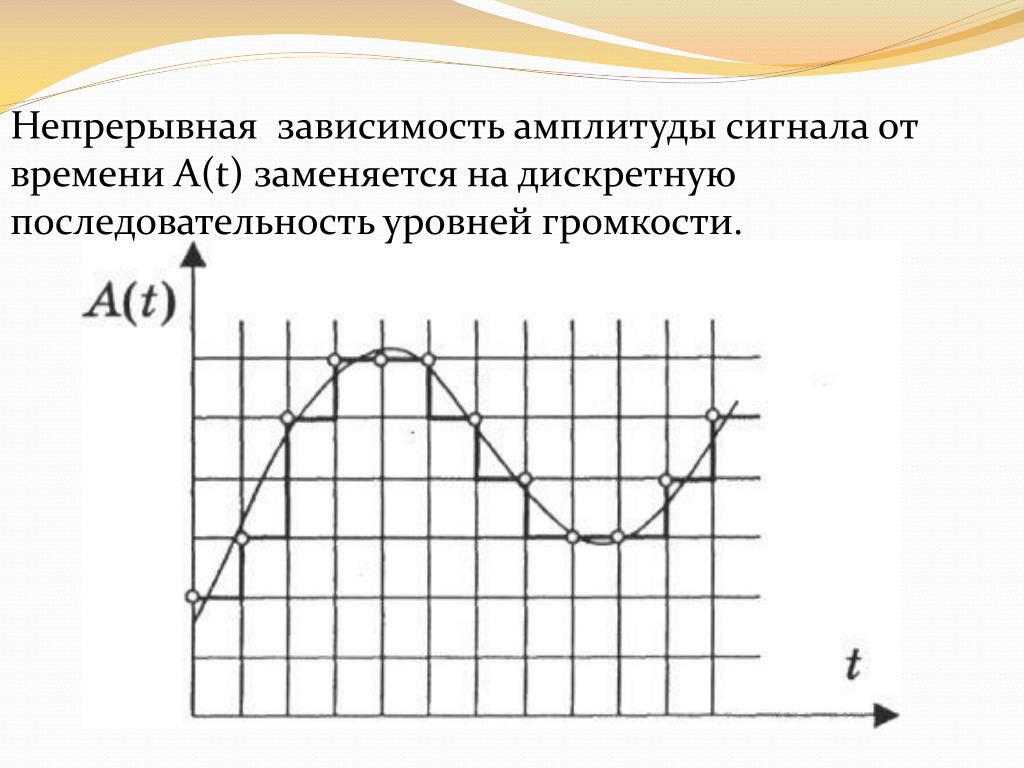 Остальные варианты не являются линейными операциями. Обратите внимание, что y=8x+3 — это уравнение прямой линии, но оно не описывает линейную систему, поскольку имеет ненулевой выход при отсутствии входных данных.
Остальные варианты не являются линейными операциями. Обратите внимание, что y=8x+3 — это уравнение прямой линии, но оно не описывает линейную систему, поскольку имеет ненулевой выход при отсутствии входных данных.
Анализ линейных систем в частотной области
Линейные системы обладают уникальным свойством, состоящим в том, что любой синусоидальный входной сигнал будет давать синусоидальный выходной сигнал с точно такой же частотой. Другими словами, если ввод имеет вид
x(t)=Aincos(ω0t+φin). (2)
, тогда вывод будет иметь вид
y(t)=Aoutcos(ω0t+φout). (3)
В общем случае амплитуда и фаза синусоидального сигнала могут изменяться, но частота должна быть постоянной. Это дает нам очень мощный инструмент для анализа линейных систем. Если мы представим входной сигнал как сумму его компонентов в частотной области, то мы можем выразить выход как простое масштабирование величин и сдвиг фаз этих компонентов.
Векторная запись
Для облегчения анализа откликов линейной системы на синусоидальные входные сигналы удобно представлять сигналы в сокращенной форме, известной как векторная запись. Рассмотрим ввод в форме
Рассмотрим ввод в форме
x(t)=Acos(ωt+φ). (4)
Это можно представить как
x(t)=Re{Aej(ωt+φ)}=A⋅Re{ejωtejφ}. (5)
, где Re{• } указывает действительную часть комплексной величины. Учитывая, что частота ω будет одинаковой во всей системе, нам не нужно специально записывать член e jωt , пока мы помним, что оно есть. То же самое относится к нотации Re{• } . Это позволяет нам выразить синусоидальный сигнал просто через его величину и фазу как
x=Aejϕ или A∠ϕ. (6)
Выражение в (6) представляет собой сигнал в (4), выраженный с помощью векторной записи. Обратите внимание, что мы должны знать частоту сигнала, чтобы перейти от векторной записи к представлению во временной области.
Вопрос викторины
Запишите следующие сигналы, используя векторную запись:
- x(t) = 5 cos(wt) вольт
- y(t)=5 sin(wt) ампер
- z(t) = 5t sin(wt) вольт
Первый сигнал, выраженный векторным представлением, представляет собой просто x = 5 вольт. Чтобы получить обозначение вектора для второго сигнала, мы признаем, что sin(ωt) = cos(ωt + π/2), поэтому y = 5e j(π/2) . Третий сигнал не является синусоидой и поэтому не может быть выражен с помощью векторной записи.
Чтобы получить обозначение вектора для второго сигнала, мы признаем, что sin(ωt) = cos(ωt + π/2), поэтому y = 5e j(π/2) . Третий сигнал не является синусоидой и поэтому не может быть выражен с помощью векторной записи.
Ряд Фурье
Конечно, многие из входных сигналов линейных систем, которые мы хотели бы проанализировать, не являются синусоидальными. В этом случае желательно представлять более произвольные формы сигнала в виде суммы синусоидальных частотных составляющих. Затем мы анализируем каждый компонент по отдельности и применяем концепцию суперпозиции для восстановления выходного сигнала.
Периодический сигнал может быть представлен как сумма его частотных составляющих путем вычисления его коэффициентов ряда Фурье. Периодический сигнал с периодом T можно записать,
x(t)=∑n=−∞∞cnejn2πf0t (7a)
где
cn=1T∫t0t0+Tx(t)e−jn2πf0tdt. (7b)
Если x(t) является сигналом в области реального времени, коэффициенты c n и c -n являются комплексно-сопряженными (т. е. ), и мы можем переписать уравнение (7) в виде
е. ), и мы можем переписать уравнение (7) в виде
x (t)=c0+∑n=1∞(cnejn2πf0t+cn∗e−jn2πf0t)=c0+∑n=1∞(|cn|ejn2πf0t+ϕn+|cn|e−(jn2πf0t+ϕn))=c0+∑n=1 ∞2|cn|cos(n2πf0t+ϕn). (8)
В этой форме мы видим, что коэффициенты ряда Фурье состоят из постоянной составляющей, c 0 , и частоты положительных гармоник, nω 0 (n = 1,2,3, …). Это односторонний ряд Фурье, и коэффициенты соответствуют амплитудам частотных гармоник, которые можно было бы измерить с помощью анализатора спектра.
Несколько периодических сигналов и их представления в частотной области показаны на рисунке 5. Представление периодического сигнала в частотной области представляет собой линейчатый спектр. Он может иметь ненулевые значения только при постоянном токе, основной частоте и гармониках основной частоты. Поскольку у периодических сигналов нет ни начала, ни конца, ненулевые периодические сигналы имеют бесконечную энергию, но обычно имеют конечную мощность. Суммарная мощность сигнала во временной области,
Ptotal=1T∫t0t0+Tx2(t) dt.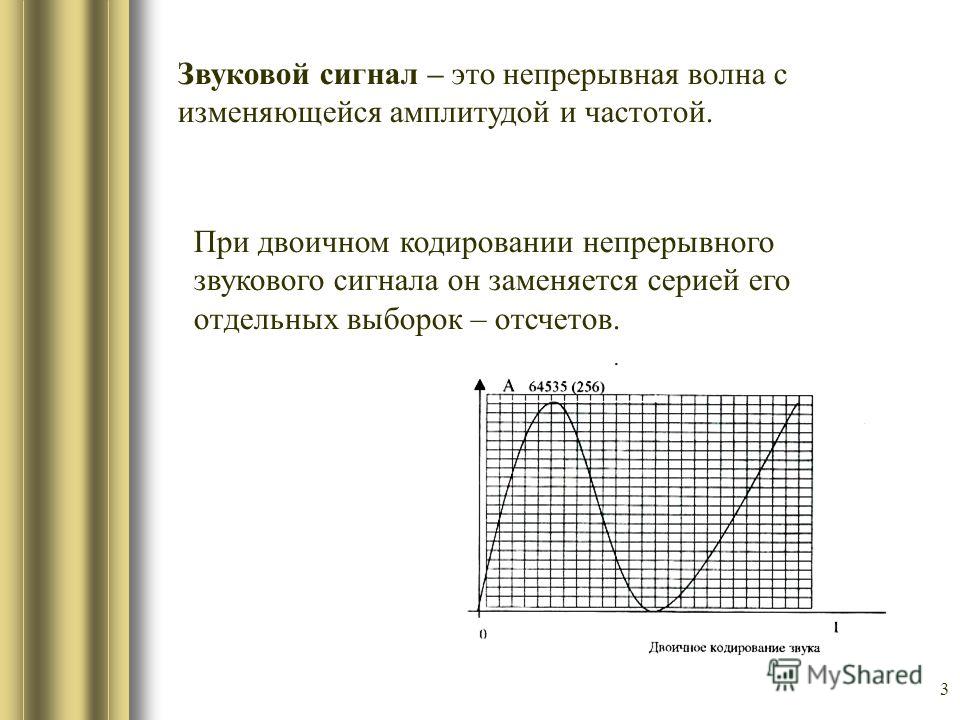 (9)
(9)
равно сумме мощностей в каждой компоненте частотной области,
Ptotal=∑n=−∞∞|cn|2. (10)
Рис. 5. Периодические сигналы во временной и частотной области.
Пример 1: Представление в частотной области последовательности импульсов
Определите представление в частотной области для последовательности импульсов, показанной на рис. 6.
Рис. 6: Последовательность импульсов.
Во временной области этот сигнал описывается следующей формулой:
x(t)={1 vnT Коэффициенты ряда Фурье затем рассчитываются с использованием уравнения (7b) как −jn2πt/T dt=AτT[sin(nπτT)(nπτT)]e−j(nπτT). (E2) Обратите внимание, что при τ→0 наш сигнал во временной области выглядит как последовательность импульсов, а амплитуды всех гармоник приближаются к одному и тому же значению. Когда τ→T/2, сигнал становится прямоугольным, а величина гармоники становится равной cn=A2|sin(nπ2)(nπ2)||e−j(nπ2)|={Anπn=±1,±3,±5⋯0n=±2,±4,±6⋯. В этом случае амплитуда четных гармоник равна нулю, а нечетные гармоники линейно уменьшаются с частотой (n). Переходные сигналы (т. е. сигналы, которые начинаются и заканчиваются в определенное время) также могут быть представлены в частотной области с помощью преобразования Фурье. Представление преобразования Фурье переходного сигнала, x(t), определяется как X(f)=∫−∞∞x(t) e−j2πftdt. (11) Обратное преобразование Фурье можно использовать для преобразования представления сигнала в частотной области обратно во временную область, x(t)=12π∫−∞∞X(f) ej2πftdf. (12) Некоторые переходные сигналы во временной области и их преобразование Фурье показаны на рисунке 7. Рисунок 7. Переходные сигналы во временной и частотной области. Обратите внимание, что переходные сигналы имеют нулевую среднюю мощность (при усреднении за все время), но они имеют конечную энергию. Полная энергия в переходном сигнале во временной области определяется выражением E=∫−∞∞x2(t) dt. Это должно равняться полной энергии в представлении сигнала в частотной области, E=∫−∞∞|X(f)|2 df. (14) Давайте рассмотрим представление периодической трапециевидной формы сигнала в частотной области, показанное на рис. в целом. Кроме того, сходство между трапециевидной формой волны и обычными формами цифровых сигналов будет полезно, когда мы будем исследовать проблемы с электромагнитной совместимостью или целостностью сигнала в цифровых системах. Рис. 8. Трапециевидный сигнал. Используя односторонний ряд Фурье, уравнения (7b) и (8), мы можем представить этот сигнал как сумму его частотных составляющих [1], x(t)=c0+∑n=1∞2 |cn|cos(n2πf0t+ϕn). (15) где 2|cn|=2AτT|sin(nπτT)(nπτT)||sin(nπtrT)(nπtrT)|. (16) Уравнение (16) можно вывести, заметив, что трапециевидную форму волны на рисунке 7 можно получить путем свертки последовательности импульсов на рисунке 9. Каждый член, 2| c n |, — амплитуда n-й гармоники. Если предположить, что t r < Рисунок 9: Представление трапециевидного сигнала в частотной области Форма волны, показанная на рисунке 10 ниже, измерена на осциллографе в лаборатории. Время нарастания и спада составляет 0,8 нс. а.) Что такое основная частота? b.) Рассчитайте амплитуды гармоник на частотах 50 МГц, 150 МГц, 250 МГц и 1,55 ГГц. Если время нарастания и спада увеличить до 1,6 нс, то на сколько дБ уменьшится гармоника на частотах 50, 150, 250 и 550 МГц? 9Рисунок 10. Трапециевидная форма волны для примера 2 Поэтому нас просят определить амплитуды гармоник 1-й -й, 3-й -й -й, 5-й -й -й и 11-й -й -й. Применяя уравнение (16) для n = 1,3,5 и 11, получаем амплитуды этих гармоник: 2|c1|=2(1 v)2|sin(1π(10)20)(1π(10) 20)||sin(1π(0,8)20)(1π(0,8)20)|=(1 v)(0,64)(1,00)=0,64 v2|c3|=2(1 v)2|sin(3π(10) )20)(3π(10)20)||sin(3π(0,8)20)(3π(0,8)20)|=(1 v)(0,21)(0,98)=0,21 v2|c5|=2(1 v)2|sin(5π(10)20)(5π(10)20)||sin(5π(0,8)20)(5π(0,8)20)|= (1 v)(0,13)(0,94)=0,12 v2|c11|=2(1 v)2|sin(11π(10)20)(11π(10)20)||sin(11π(0,8)20)( 11π(0,8)20)|=(1 v)(0,06)(0,71)=0,04 v Ни на одну из этих гармоник существенно не влияет время нарастания. 2|c1|=2(1 v)2|sin(1π(10)20)(1π(10)20)||sin( 1π(1,6)20)(1π(1,6)20)|=(1 v)(0,64)(0,99)=0,63 v2|c3|=2(1 v)2|sin(3π(10)20)(3π(10)20)||sin(3π(1,6)20)(3π(1,6)20)|= (1 v)(0,21)(0,91)=0,19 v2|c5|=2(1 v)2|sin(5π(10)20)(5π(10)20)||sin(5π(1,6)20)( 5π(1,6)20)|=(1 v)(0,13)(0,76)=0,10 v2|c11|=2(1 v)2|sin(11π(10)20)(11π(10)20)||sin (11π(1,6)20)(11π(1,6)20)|=(1 v)(0,06)(0,13)=0,008 v. Удвоение времени нарастания с 0,8 до 1,6 нс уменьшает первую гармонику всего на 20log(0,64,63) )=0,14 дБ. Третья гармоника уменьшается на 20 log (0,21,19) = 0,87 дБ. Пятая гармоника уменьшается на 20 log (0,12,10) = 1,6 дБ, а одиннадцатая гармоника уменьшается на 20 log (0,040,008) = 14 дБ. Обратите внимание, что изменение времени нарастания может оказать существенное влияние на амплитуду верхних гармоник без существенного изменения представления сигнала во временной области.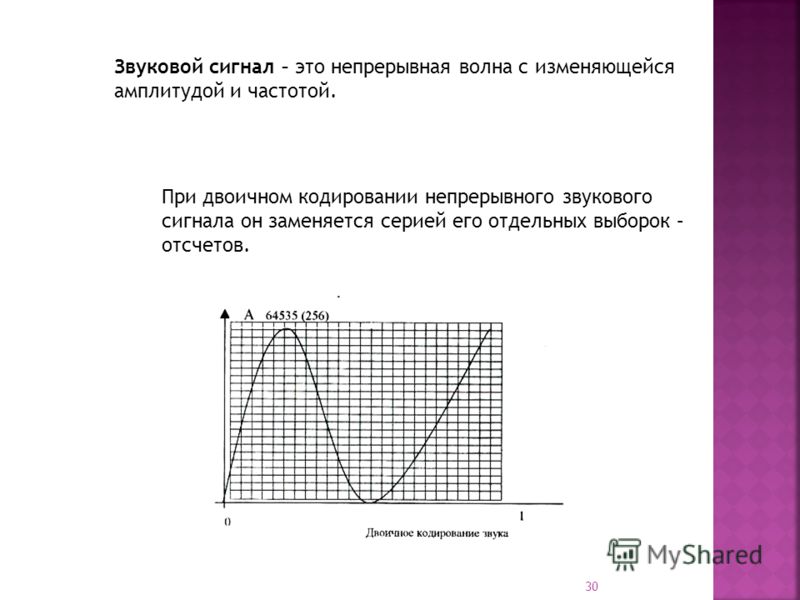 (E3)
(E3) Преобразование Фурье
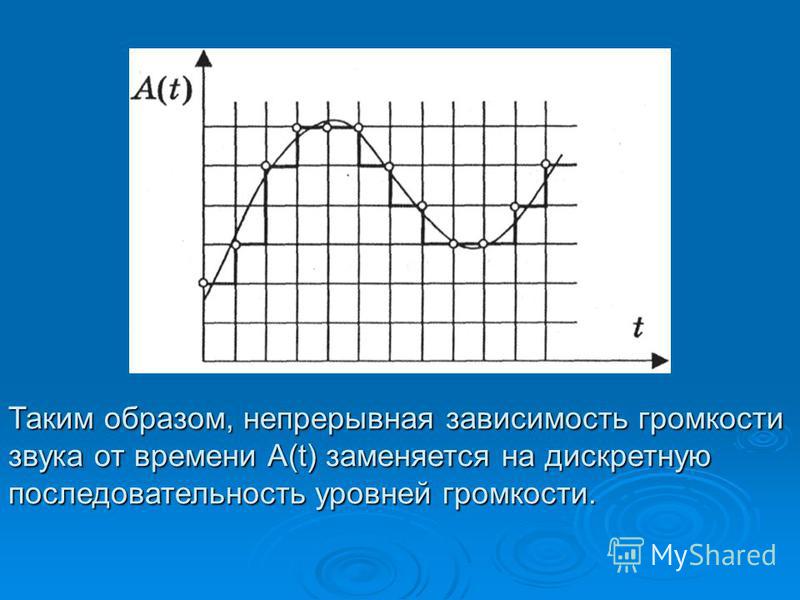 (13)
(13) Представление трапециевидного сигнала в частотной области
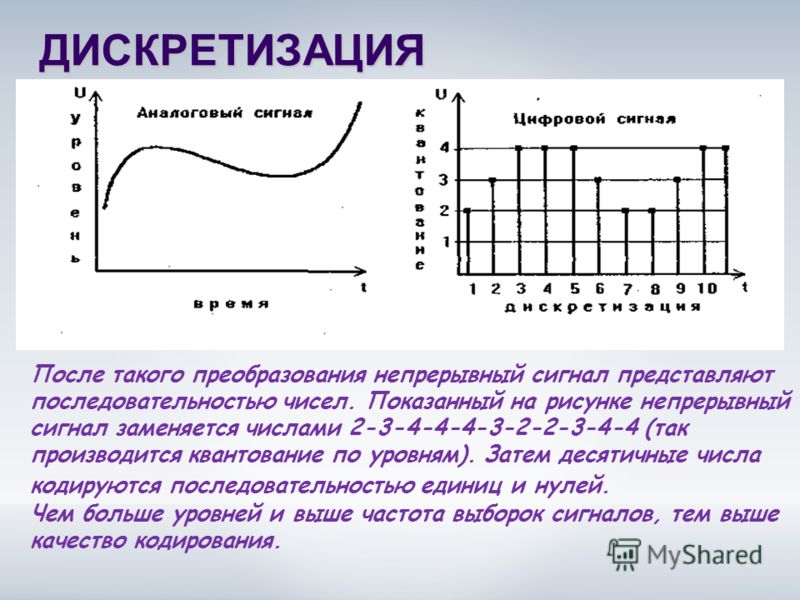 с другой последовательностью импульсов, импульсы которой имеют ширину t r и амплитуду A/t r . Свертка во временной области эквивалентна умножению в частотной области, поэтому мы можем просто перемножить два представления этих последовательностей импульсов в частотной области, чтобы получить уравнение (16).
с другой последовательностью импульсов, импульсы которой имеют ширину t r и амплитуду A/t r . Свертка во временной области эквивалентна умножению в частотной области, поэтому мы можем просто перемножить два представления этих последовательностей импульсов в частотной области, чтобы получить уравнение (16). Пример 2: Гармоники трапециевидного сигнала
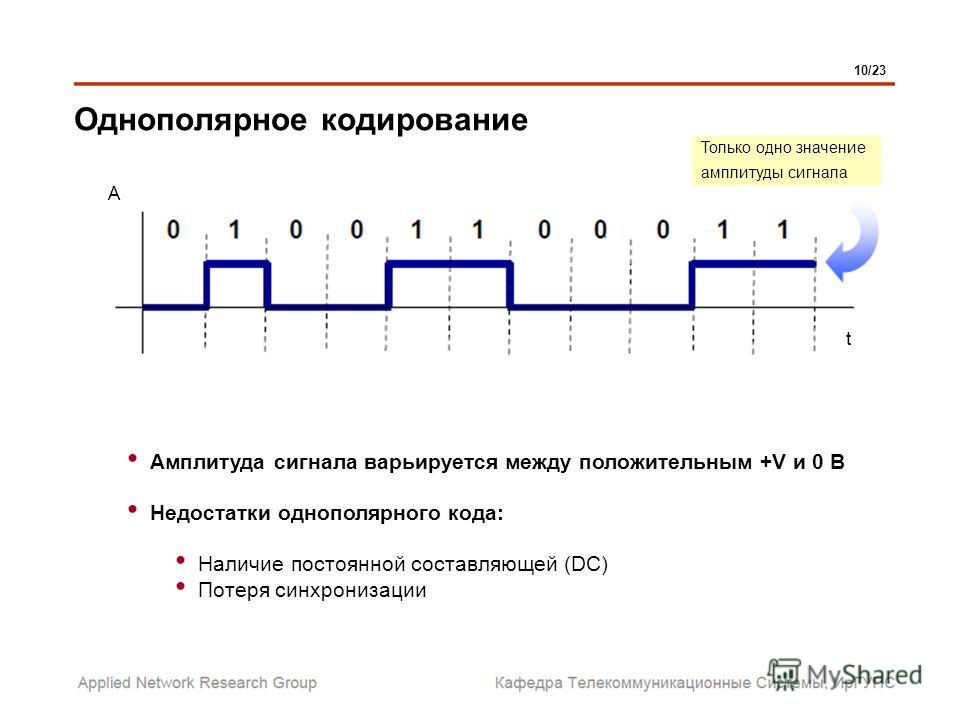 Они имеют практически ту же амплитуду, что и при нулевом времени нарастания. Однако увеличение времени нарастания до 1,6 нс существенно влияет на амплитуду верхних гармоник:
Они имеют практически ту же амплитуду, что и при нулевом времени нарастания. Однако увеличение времени нарастания до 1,6 нс существенно влияет на амплитуду верхних гармоник: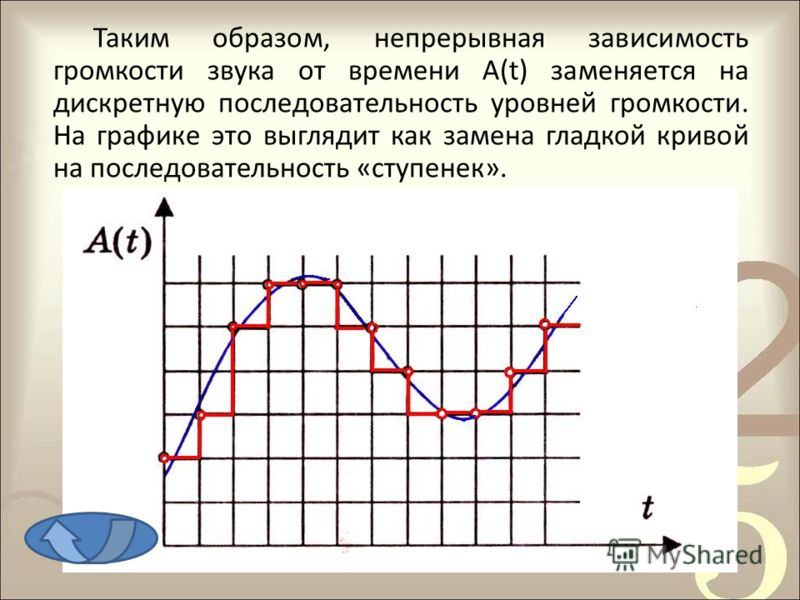


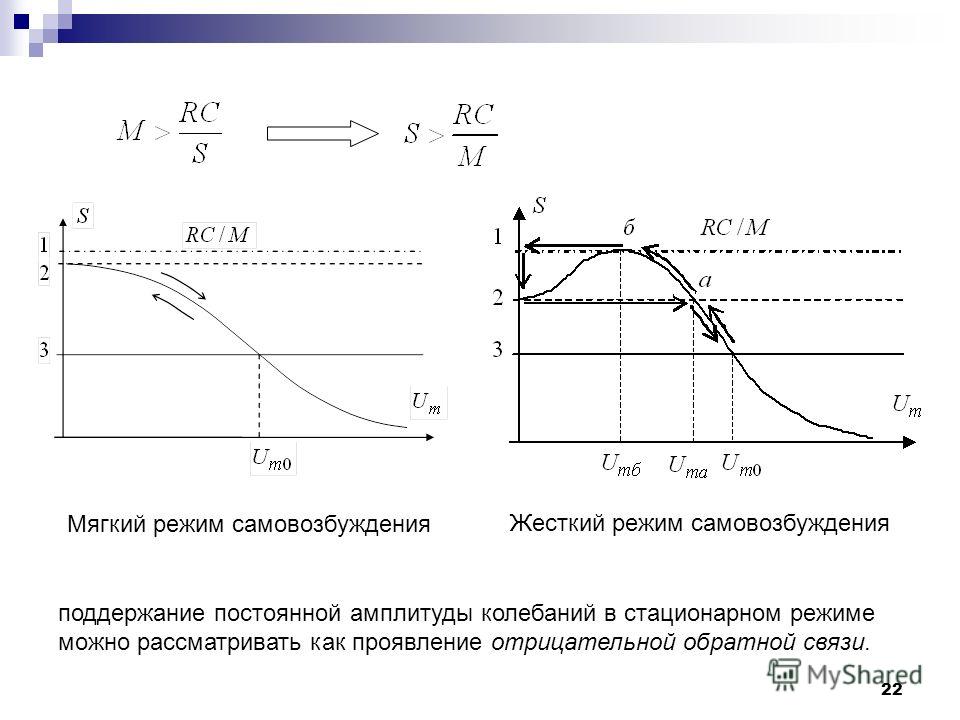
 Громкость звука.
Громкость звука.
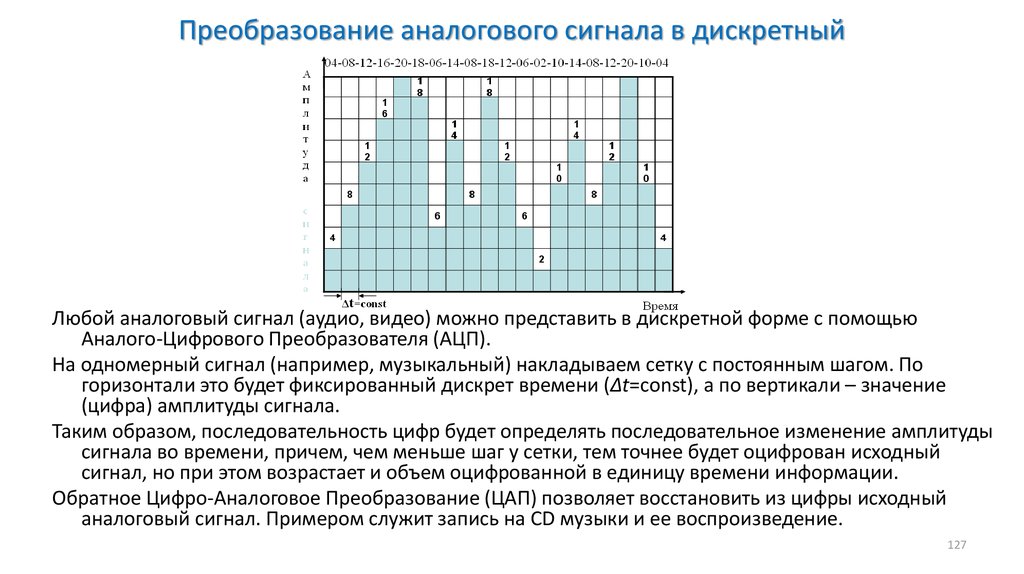



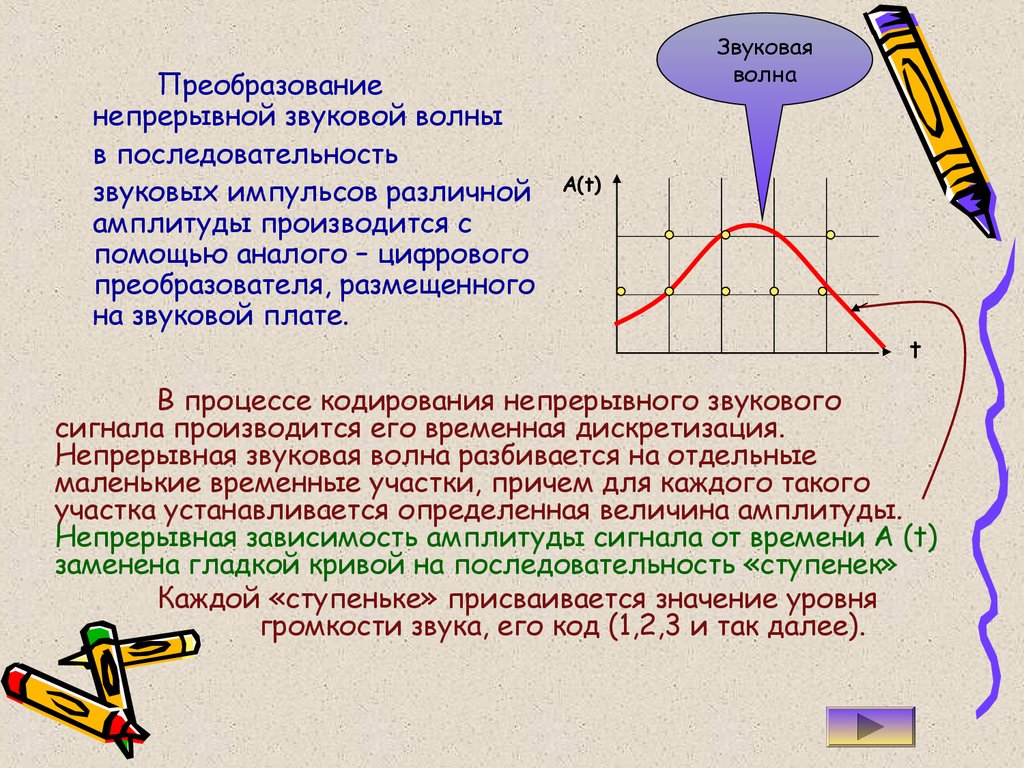 Существует множество различных операций над
звуком, которые вследствие недостаточной производительности сегодняшних
процессоров нельзя реализовать «на лету», поэтому такие преобразования проводят
лишь в пост-режиме.
Существует множество различных операций над
звуком, которые вследствие недостаточной производительности сегодняшних
процессоров нельзя реализовать «на лету», поэтому такие преобразования проводят
лишь в пост-режиме.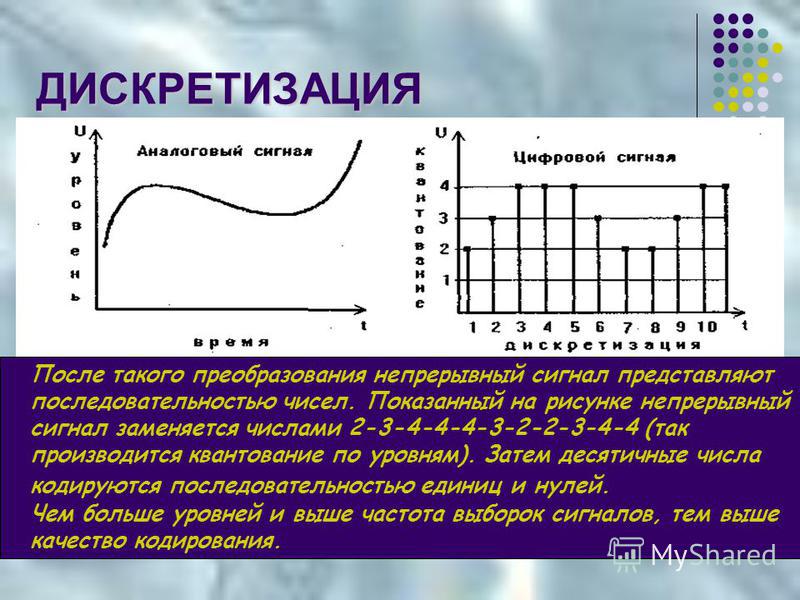
 4. Аналоговый непрерывный звук.
4. Аналоговый непрерывный звук.
 При частоте 8 кГц качество дискретизированного звукового сигнала соответствует
качеству радиотрансляции, а при частоте 48 кГц — качеству звучания аудио-СD. Следует также учитывать, что возможны
как моно-, так и стерео-режимы.
При частоте 8 кГц качество дискретизированного звукового сигнала соответствует
качеству радиотрансляции, а при частоте 48 кГц — качеству звучания аудио-СD. Следует также учитывать, что возможны
как моно-, так и стерео-режимы. Resource Interchange File Format. Уникальная система хранения любых
структурированных данных.
Resource Interchange File Format. Уникальная система хранения любых
структурированных данных. Заключает в себе сочетание
MOD и WAV.
Заключает в себе сочетание
MOD и WAV.
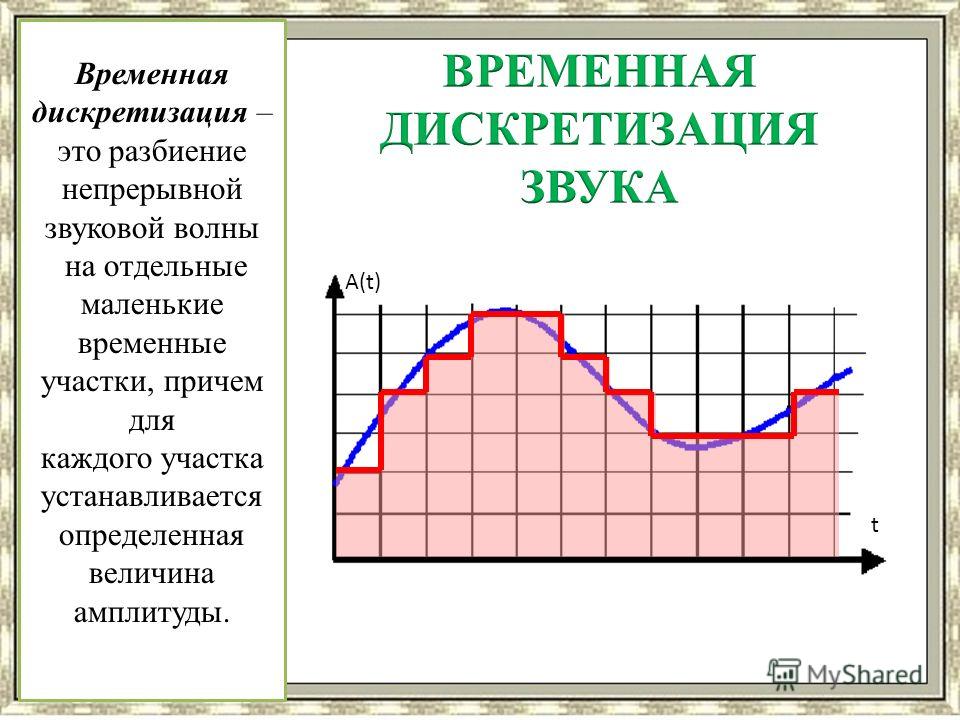
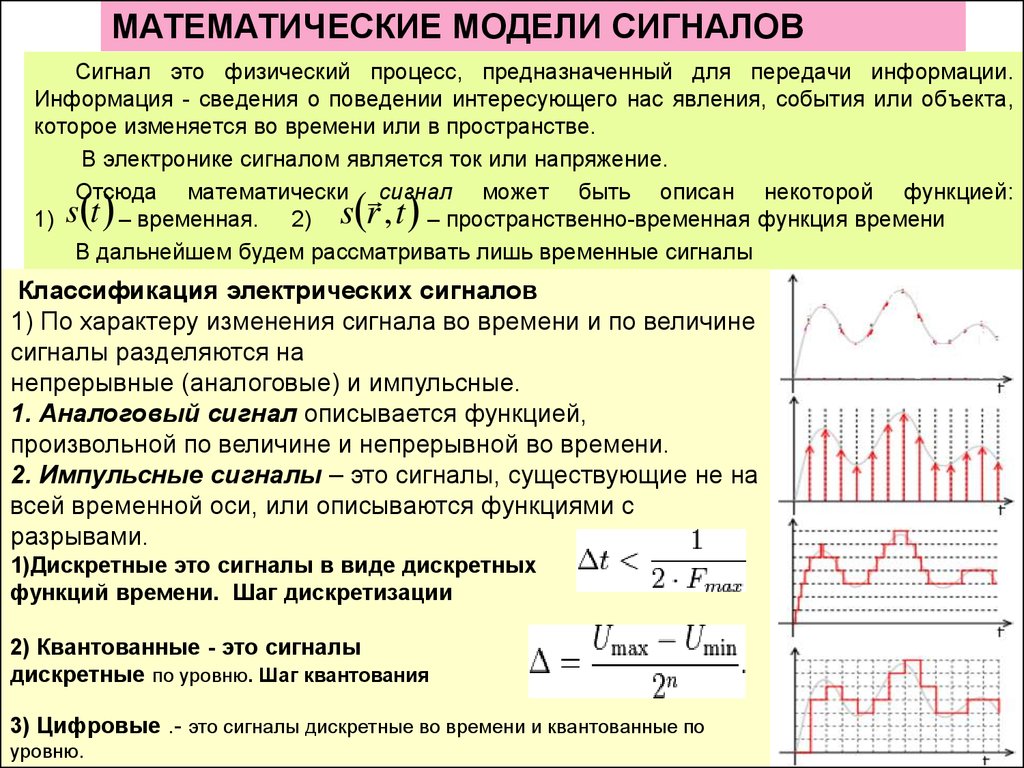 Существует три метода отбора проб:
Существует три метода отбора проб: Она также известна как минимальная частота дискретизации и определяется как:
Она также известна как минимальная частота дискретизации и определяется как: 