Преобразовать мВ в В (милливольт в вольт)
милливольт сколько вольт
Категории измерений:Активность катализатораБайт / Битвес ткани (текстиль)ВремяВыбросы CO2Громкость звукаДавлениеДинамическая вязкостьДлина / РасстояниеЁмкостьИмпульсИндуктивностьИнтенсивность светаКинематическая вязкостьКоличество веществаКулинария / РецептыМагнитный потокмагнитодвижущая силаМасса / ВесМассовый расходМолярная концентрацияМолярная массаМолярный объемМомент импульсаМомент силыМощностьМощностью эквивалентной дозыМузыкальный интервалНапряжённость магнитного поляНефтяной эквивалентОбъёмОбъёмный расход жидкостиОсвещенностьПлоский уголПлотностьПлотность магнитного потокаПлощадьПоверхностное натяжениеПоглощённая дозаПриставки СИпроизведение дозы на длинупроизведения дозы на площадьПроизводительность компьютера (флопс)Производительность компьютера (IPS)РадиоактивностьРазмер шрифта (CSS)Световая энергияСветовой потокСилаСистемы исчисленияСкоростьСкорость вращенияСкорость передачи данныхСкорость утечкиТекстильные измеренияТелесный уголТемператураТепловой потокТеплопроводностьУскорениеЧастей в .
Изначальное значение:
Изначальная единица измерения:абвольт [abV]вольт [В]Вт/Агигавольт [ГВ]Дж/Клкиловольт [кВ]мегавольт [МВ]микровольт [мкВ]милливольт [мВ]нановольт [нВ]пиковольт [пВ]планковское електрическое напряжениестатвольт [statV]теравольт [ТВ]
Требуемая единица измерения:абвольт [abV]вольт [В]Вт/Агигавольт [ГВ]Дж/Клкиловольт [кВ]мегавольт [МВ]микровольт [мкВ]милливольт [мВ]нановольт [нВ]пиковольт [пВ]планковское електрическое напряжениестатвольт [statV]теравольт [ТВ]
Числа в научной записи
Прямая ссылка на этот калькулятор:
https://www.preobrazovaniye-yedinits.info/preobrazovat+millivolt+v+volt.php
Сколько вольт в 1 милливольт?
1 милливольт [мВ] = 0,001 вольт [В] — Калькулятор измерений, который, среди прочего, может использоваться для преобразования милливольт в вольт. ), квадратный корень (√), скобки и π (число пи), уже поддерживаются на настоящий момент.
), квадратный корень (√), скобки и π (число пи), уже поддерживаются на настоящий момент.
С помощью этого калькулятора можно ввести значение для конвертации вместе с исходной единицей измерения, например, ‘636 милливольт’. При этом можно использовать либо полное название единицы измерения, либо ее аббревиатуруНапример, ‘милливольт’ или ‘мВ’. После ввода единицы измерения, которую требуется преобразовать, калькулятор определяет ее категорию, в данном случае ‘Электрическое напряжение’. После этого он преобразует введенное значение во все соответствующие единицы измерения, которые ему известны. В списке результатов вы, несомненно, найдете нужное вам преобразованное значение. Как вариант, преобразуемое значение можно ввести следующим образом: ’19 мВ в В‘ или ’74 мВ сколько В‘ или ’16 милливольт -> вольт‘ или ’66 мВ = В‘ или ‘4 милливольт в В‘ или ’74 мВ в вольт‘ или ’50 милливольт сколько вольт‘. В этом случае калькулятор также сразу поймет, в какую единицу измерения нужно преобразовать исходное значение. Независимо от того, какой из этих вариантов используется, исключается необходимость сложного поиска нужного значения в длинных списках выбора с бесчисленными категориями и бесчисленным количеством поддерживаемых единиц измерения. Все это за нас делает калькулятор, который справляется со своей задачей за доли секунды.
В списке результатов вы, несомненно, найдете нужное вам преобразованное значение. Как вариант, преобразуемое значение можно ввести следующим образом: ’19 мВ в В‘ или ’74 мВ сколько В‘ или ’16 милливольт -> вольт‘ или ’66 мВ = В‘ или ‘4 милливольт в В‘ или ’74 мВ в вольт‘ или ’50 милливольт сколько вольт‘. В этом случае калькулятор также сразу поймет, в какую единицу измерения нужно преобразовать исходное значение. Независимо от того, какой из этих вариантов используется, исключается необходимость сложного поиска нужного значения в длинных списках выбора с бесчисленными категориями и бесчисленным количеством поддерживаемых единиц измерения. Все это за нас делает калькулятор, который справляется со своей задачей за доли секунды.
Кроме того, калькулятор позволяет использовать математические формулы. В результате, во внимание принимаются не только числа, такие как ‘(13 * 63) мВ’. 3′. Объединенные таким образом единицы измерения, естественно, должны соответствовать друг другу и иметь смысл в заданной комбинации.
3′. Объединенные таким образом единицы измерения, естественно, должны соответствовать друг другу и иметь смысл в заданной комбинации.
Если поставить флажок рядом с опцией ‘Числа в научной записи’, то ответ будет представлен в виде экспоненциальной функции. Например, 6,444 521 546 293 1×1027. В этой форме представление числа разделяется на экспоненту, здесь 27, и фактическое число, здесь 6,444 521 546 293 1. В устройствах, которые обладают ограниченными возможностями отображения чисел (например, карманные калькуляторы), также используется способ записи чисел 6,444 521 546 293 1E+27. В частности, он упрощает просмотр очень больших и очень маленьких чисел. Если в этой ячейке не установлен флажок, то результат отображается с использованием обычного способа записи чисел. В приведенном выше примере он будет выглядеть следующим образом: 6 444 521 546 293 100 000 000 000 000. Независимо от представления результата, максимальная точность этого калькулятора равна 14 знакам после запятой. Такой точности должно хватить для большинства целей.
Изв. Вузов МВ и ССО, Физика — журнал
Индексирование: нет
Период активности журнала: не указан
- Другие названия журнала: Изв ВУЗов Физика, Изв ВУЗ Физика, Изв ВУЗов физика показать полностью…, Изв. ВУЗ, Физика, Изв. ВУЗов Физика
- Добавил в систему: Шалыгина (Чепурова) Елена Евгеньевна
Статьи, опубликованные в журнале
- 2014 Численное конструирование цилиндрических микромишеней на основе безударного сжатия
- Долголева Г.

- в журнале Изв. Вузов МВ и ССО, Физика, том 57, № 8/2, с. 115-122
- 2013 БАРС-1МП — программный комплекс для численных исследований внутрибаллистических процессов на многопроцессорных ЭВМ
- Семенов И.В., Меньшов И.С., Уткин П.С., Ахмедьянов И.Ф.
- в журнале Изв. Вузов МВ и ССО, Физика, том 56, № 6, с. 61-64
- 2013 Многомерное численное моделирование связанных задач внутренней и промежуточной баллистики
- Семенов И.

- в журнале Изв. Вузов МВ и ССО, Физика, том 56, № 6, с. 58-61
- 1998
- Силонов В.М., Энхтор Л.
- в журнале Изв. Вузов МВ и ССО, Физика, № 3, с. 71-77
- 1998
- 1996 Исследование ближнего порядка в сплаве магния с тербием
 М.,
Евлюхина Е.В.,
Рохлин Л.Л.
М.,
Евлюхина Е.В.,
Рохлин Л.Л.- в журнале Изв. Вузов МВ и ССО, Физика, № 7, с. 26-30
- 1989 магнитооптическое исследование областей обратной намагниченности в аморфном сплаве Сo70Fe5Si10B15
- Кринчик Г.С., Шалыгина Е.Е., Ахматова О.П., Пономарев Б.К., Жуков А.С.
- в журнале Изв. Вузов МВ и ССО, Физика, № 11, с.
 10-14
10-14
- 1984 Композиционный ближний порядок в аморфных сплавах
- Кацнельсон А.А., Кручинкина В.И., Попова И.И., Силонов В.М.
- в журнале Изв. Вузов МВ и ССО, Физика, № 6, с. 50-56
- 1984 Теоретическое и экспериментальное исследование атомного ближнего порядка в сплавах Ni-Ir
- Кацнельсон А.
 А.,
Тахир Аббас Силонов В.М
А.,
Тахир Аббас Силонов В.М - в журнале Изв. Вузов МВ и ССО, Физика, № 6, с. 29-32
- 1981 Расчет параметров ближнего порядка в сплавах Cu-Au
- Кацнельсон А.А., Силонов В.М.
- в журнале Изв. Вузов МВ и ССО, Физика, № 3, с. 113-114
- 1978
- Василев Г.
 П.,
Кацнельсон А.А.,
Силонов В.М.,
Аксенова О.В.
П.,
Кацнельсон А.А.,
Силонов В.М.,
Аксенова О.В. - в журнале Изв. Вузов МВ и ССО, Физика, № 4, с. 85-88
- 1978
- 1977 Ближний порядок в системах Nb-V,Ta-V и Nb-Ta
- Кацнельсон А.А., Силонов В.М., Хаваджа Ф.А.
- в журнале Изв. Вузов МВ и ССО, Физика, № 1, с. 11-16
Моментум
Спортивный диктор говорит: «Переходя к матчу всех звезд, команда «Чикаго Уайт Сокс» имеет импульс ».Заголовки гласят: «Чикаго Буллз набирает обороты ». Тренер накачивает своей команде в перерыве, говоря: «У вас есть импульс ; критически важно, чтобы вы использовали этот импульс и похоронили их в этой третьей четверти».
Импульс — широко используемый термин в спорте. Команда, у которой есть импульс, находится на ход и потребуется некоторое усилие, чтобы остановиться. Команда с большим импульсом на самом деле движется и будет трудно остановить . Импульс — это физический термин; это относится к количеству движения, которое имеет объект. Спортивная команда, которая на ходу , имеет импульс. Если объект находится в движении ( в движении ), то он имеет импульс.
Импульс можно определить как «массу в движении». Все объекты имеют массу; поэтому, если объект движется, то у него есть импульс — его масса движется. Величина импульса, которую имеет объект, зависит от двух переменных: насколько вещество движется и как быстро движется вещество . Импульс зависит от переменных массы и скорости. С точки зрения уравнения, импульс объекта равен массе объекта, умноженной на скорость объекта.
Импульс зависит от переменных массы и скорости. С точки зрения уравнения, импульс объекта равен массе объекта, умноженной на скорость объекта.
В физике количество импульса обозначается строчными буквами p . Таким образом, приведенное выше уравнение можно переписать как
, где м — это масса, а v — это скорость. Уравнение показывает, что импульс прямо пропорционален массе объекта и прямо пропорционален скорости объекта.
Единицами импульса будут единицы массы, умноженные на единицы скорости. Стандартной метрической единицей импульса является кг•м/с. В то время как кг•м/с является стандартной метрической единицей импульса, существует множество других единиц, которые являются приемлемыми (хотя и не общепринятыми) единицами импульса. Примеры включают кг•ми/ч, кг•км/ч и г•см/с. В каждом из этих примеров единица массы умножается на единицу скорости, чтобы получить единицу импульса. Это согласуется с уравнением для импульса.
Это согласуется с уравнением для импульса.
Импульс как векторная величина
Импульс является векторной величиной . Как обсуждалось в предыдущем разделе, векторная величина — это величина, которая полностью описывается как величиной, так и направлением. Чтобы полностью описать импульс 5-килограммового шара для боулинга, движущегося на запад со скоростью 2 м/с, вы должны включить информацию как о величине, так и о направлении шара для боулинга. недостаточно , чтобы сказать, что мяч имеет импульс 10 кг•м/с; импульс мяча равен не полностью описан, пока не будет дана информация о его направлении. Направление вектора импульса совпадает с направлением скорости мяча. В предыдущем разделе было сказано, что направление вектора скорости совпадает с направлением движения объекта. Если шар для боулинга движется на запад, то его импульс можно полностью описать, сказав, что он равен 10 кг•м/с в западном направлении. Как векторная величина, импульс объекта полностью описывается как величиной и направление .
Как векторная величина, импульс объекта полностью описывается как величиной и направление .
Уравнение импульса как руководство к размышлению
Из определения импульса становится очевидным, что объект имеет большой импульс, если велики его масса и скорость. Обе переменные одинаково важны для определения импульса объекта. Представьте, что грузовик Mack и роликовые коньки движутся по улице с одинаковой скоростью. Значительно большая масса грузовика Mack придает ему значительно больший импульс. Тем не менее, если бы грузовик Mack находился в состоянии покоя, то инерция наименее массивного роликового конька была бы наибольшей. Импульс любого покоящегося объекта равен 0. Покоящиеся объекты делают , а не имеют импульс — у них нет никакой «движущейся массы». Обе переменные — масса и скорость — важны при сравнении количества движения двух объектов.
Уравнение импульса может помочь нам подумать о том, как изменение одной из двух переменных может повлиять на импульс объекта. Рассмотрим физическую тележку массой 0,5 кг, нагруженную одним кирпичом массой 0,5 кг и движущуюся со скоростью 2,0 м/с. Полная масса загруженной тележки составляет 1,0 кг, а ее импульс равен 2,0 кг•м/с. Если вместо этого тележка была загружена тремя 0,5-килограммовыми кирпичами, то общая масса загруженная тележка будет иметь массу 2,0 кг, а ее импульс будет равен 4,0 кг·м/с. Удвоение массы приводит к удвоению импульса.
Рассмотрим физическую тележку массой 0,5 кг, нагруженную одним кирпичом массой 0,5 кг и движущуюся со скоростью 2,0 м/с. Полная масса загруженной тележки составляет 1,0 кг, а ее импульс равен 2,0 кг•м/с. Если вместо этого тележка была загружена тремя 0,5-килограммовыми кирпичами, то общая масса загруженная тележка будет иметь массу 2,0 кг, а ее импульс будет равен 4,0 кг·м/с. Удвоение массы приводит к удвоению импульса.
Аналогично, если бы тележка весом 2,0 кг имела скорость 8,0 м/с (вместо 2,0 м/с), то тележка имела бы импульс 16,0 кг•м/с (вместо 4,0 кг•м/с). ). учетверение скорости приводит к учетверению импульса. Эти два примера иллюстрируют, как уравнение p = m•v служит «руководством к мышлению» и , а не просто .0004 a « подключи и пей рецепт решения алгебраических задач.»
Выразите свое понимание концепции и математики импульса, ответив на следующие вопросы. Нажмите кнопку, чтобы просмотреть ответы.
Нажмите кнопку, чтобы просмотреть ответы.
1. Определить импульс а…
а. Полузащитник массой 60 кг движется на восток со скоростью 9 м/с.
б. Автомобиль массой 1000 кг движется на север со скоростью 20 м/с.
в. Первокурсник массой 40 кг движется на юг со скоростью 2 м/с.
2. Автомобиль обладает импульсом 20 000 единиц. Каким был бы новый импульс автомобиля, если бы…
а. его скорость удвоилась.
б. его скорость утроилась.
в. его масса была удвоена (за счет добавления большего количества пассажиров и большей нагрузки)
д. и его скорость удвоилась, и его масса удвоилась.
3. Полузащитник (m = 60 кг), тайт-энд (m = 90 кг) и лайнсмен (m = 120 кг) бегут по футбольному полю. Рассмотрим их модели бегущей строки ниже.
Сравните скорости этих трех игроков. Во сколько раз скорость полузащитника и тайт-энда больше скорости лайнмена?
Во сколько раз скорость полузащитника и тайт-энда больше скорости лайнмена?
У какого игрока самый большой импульс? Объяснять.
Следующий раздел:
Перейти к следующему уроку:
Импульс
Импульс — это то, насколько что-то хочет продолжать двигаться в том же направлении.
Этот грузовик будет трудно остановить …
… у него много импульса .
Быстрее? Больше импульса!
Тяжелее? Больше импульса!
Импульс равен массе, умноженной на скорость.
Символ p :
р = м v
Пример: Каков импульс автомобиля массой 1500 кг, движущегося по шоссе со скоростью
28 м/с (около 100 км/ч или 60 миль/ч)?p = m v
p = 1500 кг × 28 м/с
р = 42 000 кг м/с
Единица импульса:
- кг м/с (килограмм-метр в секунду), или
- Н·с (Ньютон-секунда)
Они одинаковые! 1 кг м/с = 1 Н·с
Здесь мы будем использовать оба.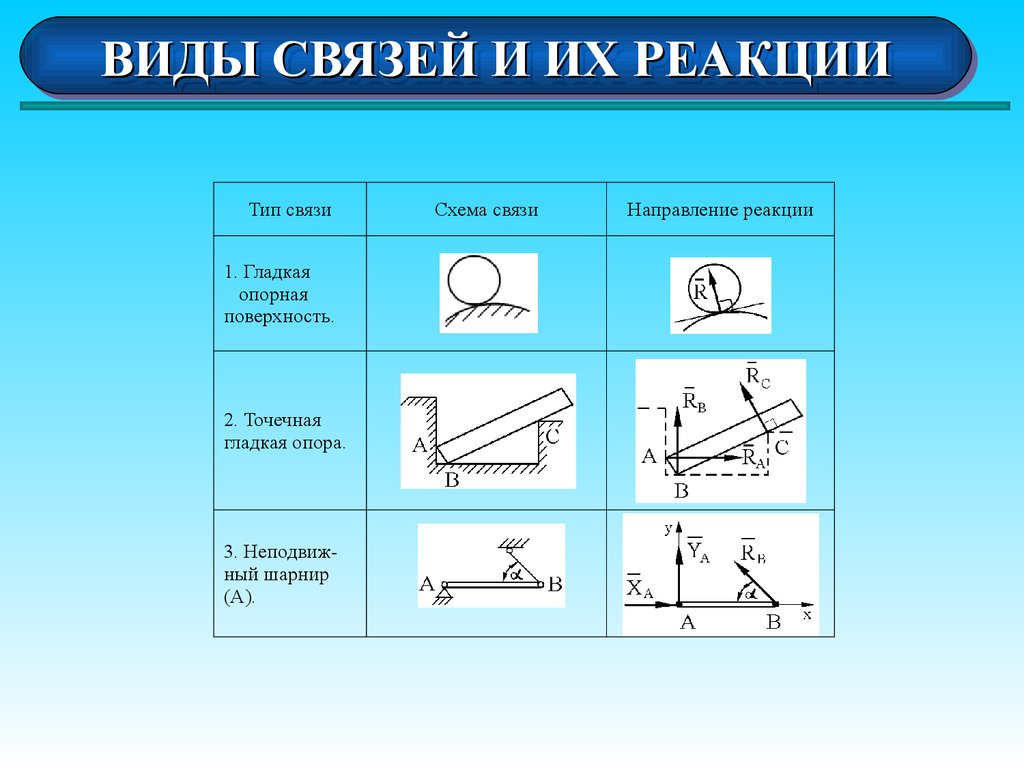
Другие примеры:
| Масса | Скорость | Импульс | |
|---|---|---|---|
| Пуля (9 мм) | 7,5 г 0,0075 кг | 1000 м/с | 0,0075 × 1000 = 7,5 кг м/с |
| Теннисный мяч | 57 г 0,057 кг | 50 м/с | 0,057 × 50 = 2,85 кг м/с |
| Футбольный мяч | 16 унций 0,45 кг | 100 км/ч 28 м/с | 0,45 × 28 = 12,6 кг м/с |
| Баскетбольный мяч | 22 унции 0,6 кг | 3 м/с | 0,6 × 3 = 1,8 кг м/с |
| Молоток | 400 г 0,4 кг | 7 м/с | 0,4 × 7 = 2,8 кг м/с |
| Бегун | 80 кг | 9 км/ч 2,5 м/с | 80 × 2,5 = 200 кг м/с |
| Автомобиль | 1500 кг | 100 км/ч 28 м/с | 1500 × 28 = 42 000 кг м/с |
Импульс имеет направление : точно такое же направление как и скорость.
Но во многих примерах здесь для простоты используется только скорость (скорость без направления).
Анимация
Играйте с импульсом в этой анимации.
Импульс
Импульс – это изменение импульса. Δ — это символ «изменения», поэтому:
Импульс Δp
Силу можно рассчитать по изменению импульса во времени (так называемая «скорость изменения импульса во времени»):
Ф = Δр Δt
Пример. Ваш вес 60 кг, и вы бежите со скоростью 3 м/с в стену.
Стена остановит вас через 0,05 с. Что такое сила?
Затем стена становится мягкой и останавливает вас через 0,2 с. Что такое сила?
Первый расчет импульса:
Δp = m v
Δp = 60 кг x 3 м/с
Δp = 180 кг м/с
Остановка через 0,05 с:
F = Δр Δt
Ф = 180 кг м/с 0,05 с = 3600 Н
Останов через 0,2 с:
F = Δр Δt
Ф = 180 кг м/с 0,2 с = 900 Н
Остановка с более низкой скоростью имеет гораздо меньшую силу!
- Вот почему прокладки так хорошо работают
- А также почему защитные шлемы спасают жизни
- А почему у автомобилей есть зоны деформации
В: Разве сила обычно не рассчитывается с использованием F = ma ?
А: Ну, F = Δр Δt это то же самое , только другая форма:
| Начните с: | Ф = ма | |
| Ускорение есть изменение скорости v во времени t : | Ф = м Δv Δt | |
| Изменить на: | Ф = Δмв Δt | |
| И Δmv есть изменение импульса: | Ф = Δр Δt |
Импульс Силы
Можем переставить:
Ф = Δр Δt
В:
Δp = F Δt
Таким образом, мы можем рассчитать Импульс (изменение импульса) по силе, приложенной в течение определенного периода времени.
Пример: Мяч ударяется с силой 300 Н. Высокоскоростные камеры показывают, что контакт длился 0,02 с. Какой был импульс?
Δp = F Δt
Δp = 300 Н × 0,02 с
Δp = 6 Н с
Импульс сохраняется
Сохранено : общее количество остается прежним (в закрытой системе).
Закрытая система : в которой ничего не перемещается внутрь или наружу и на нее не действует внешняя сила.
В нашей Вселенной:
- Масса сохраняется (может изменять форму, перемещаться, разрезаться или соединяться вместе, но общая масса остается неизменной с течением времени)
- Энергия сохраняется (она также может изменять форму, светиться, нагреваться и т. д.)
- И Импульс тоже сохраняется!
Примечание: на атомном уровне масса и энергия могут быть преобразованы через E=mc 2 , но ничего не потеряется.
Импульс — это вектор
Импульс — это вектор: он имеет размер И направление.
Иногда мы не указываем направление, но иногда это важно!
Одно измерение
Вопрос может иметь только одно измерение, и все, что нам нужно, это положительный или отрицательный импульс:
Два или более измерения
Вопросы могут быть в двух (или более) измерениях, например:
Пример: шар для бильярда отскакивает!
Ударяется о край со скоростью 8 м/с под углом 50° и отскакивает с той же скоростью и углом отражения.
Весит 0,16 кг. Каково изменение импульса?
Разобьем скорость на x и y части. До отскока:
- v x = 8 × cos(50°) … далее
- v y = 8 × sin(50°) …вверх
После отскока:
- v x = 8 × cos(50°) … далее
- v y = 8 × −sin(50°) …спуск
Скорость по оси x не изменится, но скорость по оси y изменится на:
Δv y = (8+8) × sin(50°)
= 16 × sin(50°)
И изменение по импульсу:
Δp = m Δv
Δp = 0,16 кг × 16 × sin(50°) м/с
Δp = 1,961.




 М.,
Евлюхина Е.В.,
Рохлин Л.Л.
М.,
Евлюхина Е.В.,
Рохлин Л.Л. 10-14
10-14 А.,
Тахир Аббас Силонов В.М
А.,
Тахир Аббас Силонов В.М П.,
Кацнельсон А.А.,
Силонов В.М.,
Аксенова О.В.
П.,
Кацнельсон А.А.,
Силонов В.М.,
Аксенова О.В.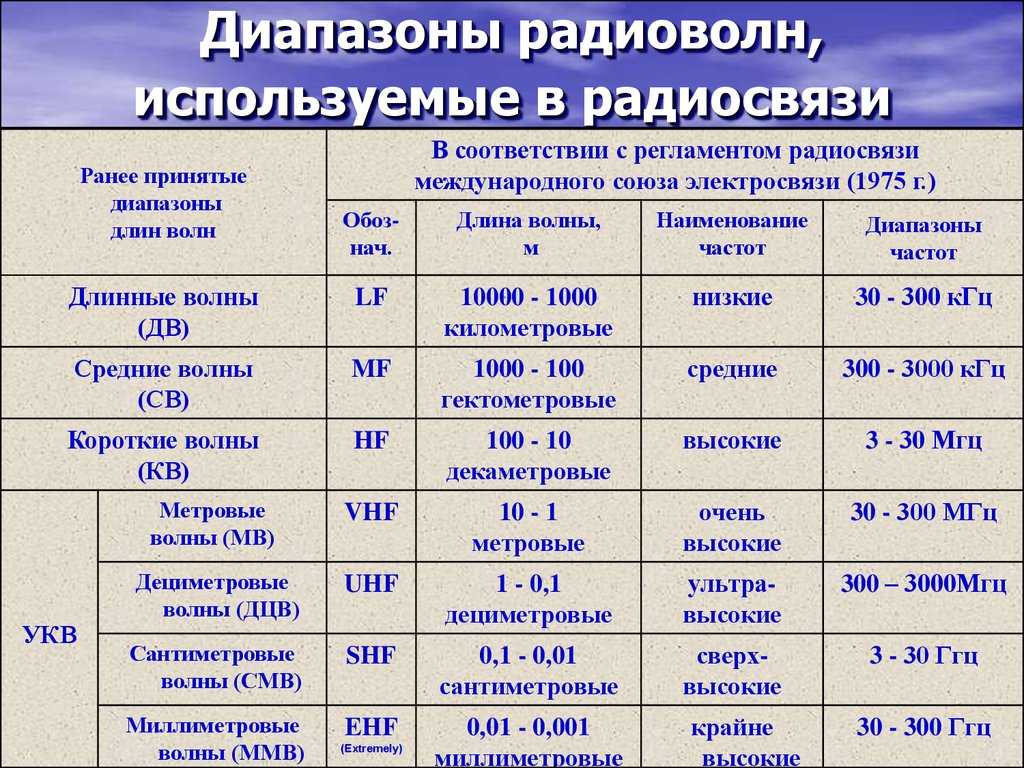 Заголовки гласят: «Чикаго Буллз набирает обороты ». Тренер накачивает своей команде в перерыве, говоря: «У вас есть импульс ; критически важно, чтобы вы использовали этот импульс и похоронили их в этой третьей четверти».
Заголовки гласят: «Чикаго Буллз набирает обороты ». Тренер накачивает своей команде в перерыве, говоря: «У вас есть импульс ; критически важно, чтобы вы использовали этот импульс и похоронили их в этой третьей четверти».