Мультиплексоры и демультиплексоры — Электротехника и основы электроники (Инженерия)
Лекция 16. Мультиплексоры и демультиплексоры
Мультиплексоры. Мультиплексором называют функциональный узел, который обеспечивает передачу цифровой информации, поступающей по нескольким входным линиям связи, на одну выходную линию. Выбор входной линии, информация с которой поступает на выход, осуществляется при помощи сигналов, поступающих на адресные входы.
Обобщенная схема мультиплексора приведена на рис. 16.1. Мультиплексор MUX (Multiplexer) в общем случае можно представить в виде коммутатора, управляемого входной логической схемой. Входные логические сигналы X, поступают на входы коммутатора и через коммутатор передаются на выход Y. Управление коммутатором осуществляется входной логической схемой. На вход логической схемы подаются адресные сигналы A,, (Adress). Мультиплексоры могут иметь дополнительный управляющий вход Е (Enable), который может выполнять стро-бирование выхода Y.
Кроме этого некоторые мультиплексоры могут иметь выход с тремя состояниями: два состояния 0 и 1 и третье состояние — отключенный выход (выходное сопротивление равно бесконечности). Перевод мультиплексора в третье состояние производится сигналом ОЕ (Output Enable).
Большинство мультиплексоров способно передавать сигналы информации X,
только в одном направлении — от входа на выход. Однако имеются мультиплексоры, которые могут передавать информационные сигналы в обоих направлениях. Такие мультиплексоры называются двунаправленными. Двунаправленные мультиплексоры способны передавать не только цифровые, но и аналоговые сигналы. В литературе такие мультиплексоры часто называют селекторами-мультиплексорами (Data Selector-Multiplexer).
Рис. 16 1. Обобщенная схема мультиплексора
Мультиплексоры со стробирующим входом Е выполняют функции передачи сигнялов х,—>-у только при поступлении сигнала строба Е. Мультиплексоры, имеющие три состояния выхода, можно каскадировать.
1), где п — число входов. Так, например, мультиплексор с функцией (1 —> 1) является одиночным ключом, а мультиплексор (4-*1) имеет четыре входа и один выход.
В зависимости от соотношения числа информационных входов п и числа адресных входов т мультиплексоры делятся на полные и неполные. Если выполняется условие п =2″ , то мультиплексор будет полным. Если это условие не выполняется, т. е. п<2″1 , то мультиплексор будет неполным. Наибольшее распространение получили мультиплексоры (2—1) с п=2 и т=, (4—1) с и =4 и т=2, (8—*!) с и=8 и т=3 и (16—*1) с и=16 и т=4. Для неполных мультиплексоров число входных линий может быть любым, но, разумеется, не больше 2″.
В качестве примера рассмотрим функционирование мультиплексора (4—» 1), состояние входов и выходов которого приведено в табл. 16.1. Используя таблицу состояний этого мультиплексора, получим выражение для его выходной функции
В общем виде выходная функция мультиплексора (и—*!) может быть представлена как
где К, называется мипитерм (К,=0 или 1) и равно логическому произведению сигналов на адресных линиях, соответствующих сигналу X,.
-Ao,
которое реализуется на двувходовых элементах И и ИЛИ, как показано на рис. 16.3 а.
Таблица 16.1
Состояние мультиплексора (4—1)
Аналогично реализуется че-тырехвходовой мультиплексор, однако для него потребуются четыре трехвходовых элемента И и один четьгрехвходовой элемент ИЛИ Схема такого мультиплексора, построенного по уравнению (16 1), приведена на рис 16.3 б Для получения прямых и инверсных адресных сигналов используются два дополнительных инвертора Поскольку для построения мультиплексоров с большим числом входов требуются элементы И и ИЛИ с числом входов больше четырех, то их проще выполнять путем каскадирования
Интегральные микросхемы мультиплексоров можно разделить на группы по следующим признакам
• по числу входов 2-, 4-, 8- и 16-входовые,
• по числу мультиплексоров в одном корпусе (числу разрядов),
• по наличию стробирующего входа Е,
Рис 16 2 Пирамидальное каскадирование мультиплексоров (4 -* 1) для реализации выходной функции (16—*1)
• по наличию выхода с тремя состояниями (наличию входа ОЕ),
• по способности передавать сигналы в двух направлениях.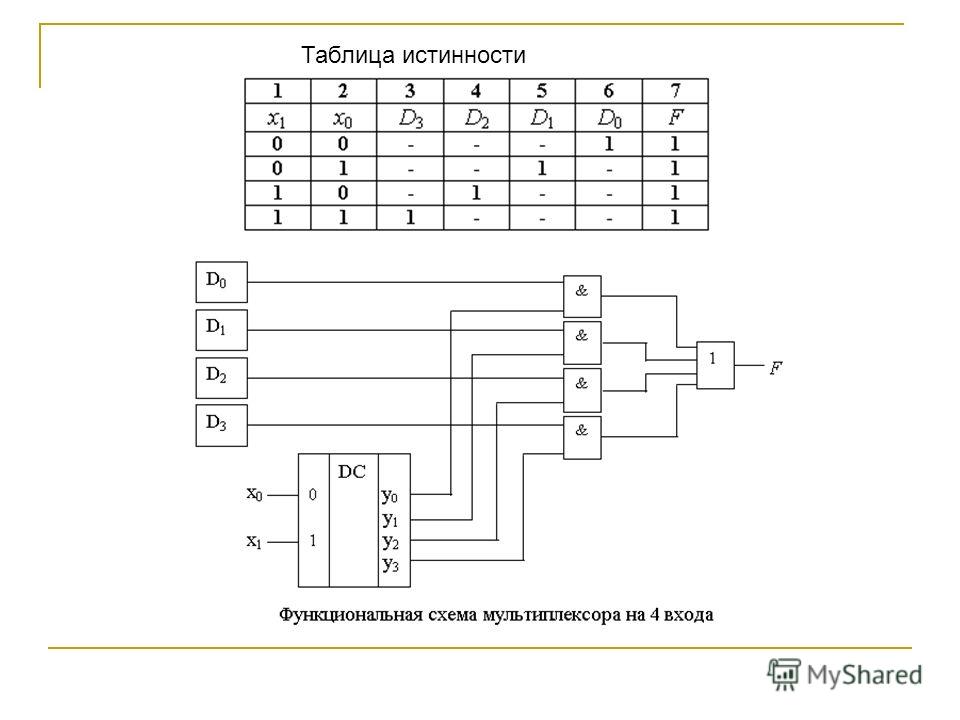
, Ац, А., и определяет, какой из восьми мультиплексоров DDI…DDS будет подключен к выходу Y. Вход стробирования Е можно использовать только у последнего мультиплексора DD9. Таким образом, на рис. 16.5 показана схема стробируемого мультиплексора с форматом (64-*1).
Помимо основного назначения коммутации входных сигналов мультиплексоры находят применение в сдвигающих устройствах, делителях частоты, триггер-ных устройствах и др.
Демультиплексоры. Демультиплексором (DMX) называют функциональный узел, который обеспечивает передачу цифровой информации, поступающей по одной линии, на несколько выходных линий. Выбор выходной линии осуществляется при помощи сигналов, поступающих на адресные входы. Таким образом, демультиплексор выполняет преобразование, обратное действию мультиплексора.
Обобщенная схема демультиплексора, приведенная на рис. 16.6, сходна со схемой мультиплексора. Входной сигнал х поступает на вход коммутатора и через него передается на выходы Yy.
4), состояния входа и выходов которого приведены в табл. 16.3 Используя данные этой таблицы, получим выражение для выходных сигналов демультиплексора
Рис 164 Каскадирование мультиплексоров с тремя состояниями выхода
Рис 165 Схема пирамидального мультиплексора (64—> 1) на мультиплексорах (8—*!)
Структура демультипдексора на элементах И, реализующая уравнения (16—-3), приведена на-puc.l6.76. Схема демультиплек-сора (1—-2), также выполненная на элементах И, приведена на рис. 16.7 я. Инверторы в этих схемах обеспечивают формирование необходимых сигналов управления. В каждой схеме И два входа задействованы для адресных сигналов Ад и А, а на третий вход подается входной сигнал X.
Рис. 16.6. Обобщенная схема демультиплексора
Как следует из уравнений
(16.3), реализация демультиплексора возможна также на элементах ИЛИ. Схема демультиплексора с четырьмя выходами на элементах ИЛИ, построенная по уравнениям (16.
3), приведена на рис. 16.8.
Интегральные микросхемы демультиплексоров, так же, как и схемы мультиплексоров, можно разделить на группы по следующим признакам:
• по числу выходов;
• по числу демультиплексоров в одном корпусе;
• по наличию стробирующего импульса Е,
• по способности передавать сигналы в двух направлениях. Поскольку функции демультиплексоров сходны с функциями дешифраторов, их условное обозначение сделано одинаковым, а именно ИД. Поэтому такие микросхемы часто называют дешифраторами-демультиплексорами. Так, например, дешифратор К155ИДЗ можно использовать в качестве демультиплексора с форматом (1-*16). При этом входы разрешения дешифрации используются в качестве основного входа демультиплексора X, а адресные входы и выходы используются по прямому назначению. В табл. 16.4 приведены некоторые схемы демультиплексоров и дешифраторов, которые можно использовать качестве демультиплексоров.
Мультиплексоры-демультиплексоры.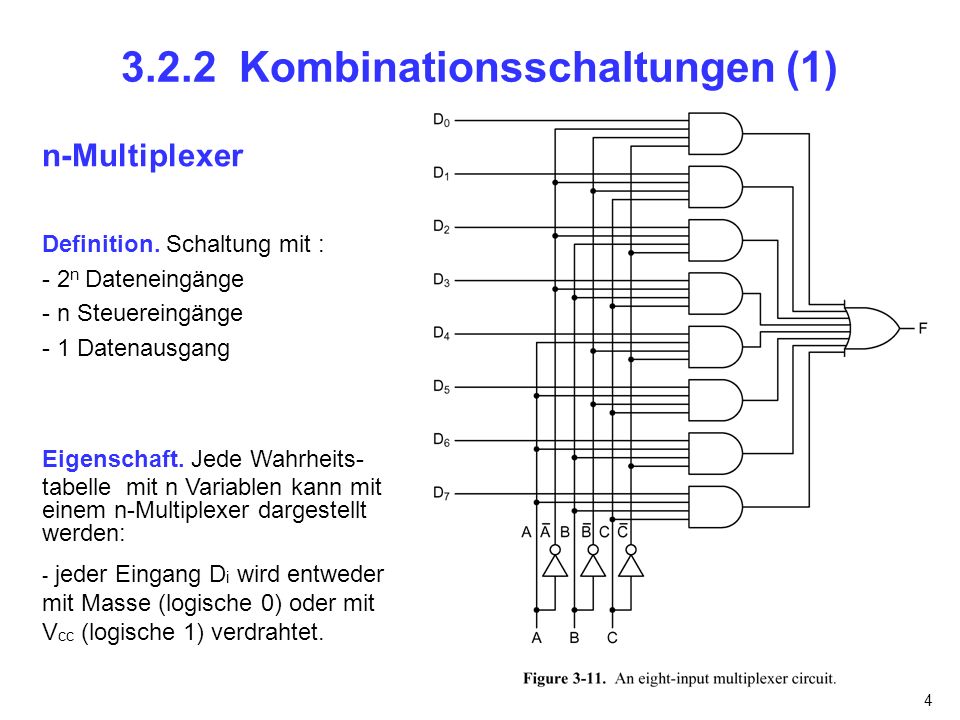
п), в котором двунаправленная стрелка указывает на двунаправленную передачу сигналов. В табл. 16.5 приведены сведения о некоторых ИМС мультиплексоров-демультиплексоров.
5.4.4 Мультиплексоры и демультиплексоры — Электронный учебно-методический комплекс по ТМ и О ЦВОСП
Именно правильная работа мультиплексоров и демультиплексоров обеспечивает высокую пропускную способности сети. В процессе тестирования необходимо проверить на соответствие заданным значениям целый ряд параметров мультиплексоров и демультиплексоров. Все измерения должны проводиться в стабильных условиях и в комбинации с другими компонентами, характеристики которых уже определены.
Тестирование
линии связи проводят на всех длинах волн, которые используются или могут быть
использованы в будущем. Тестирование демультиплексоров проводят при разных
уровнях мощности входногосигнала и допустимом относительном уровне ошибокBER на
выходе при подаче навход сигнала непосредственно от усилителяEDFA.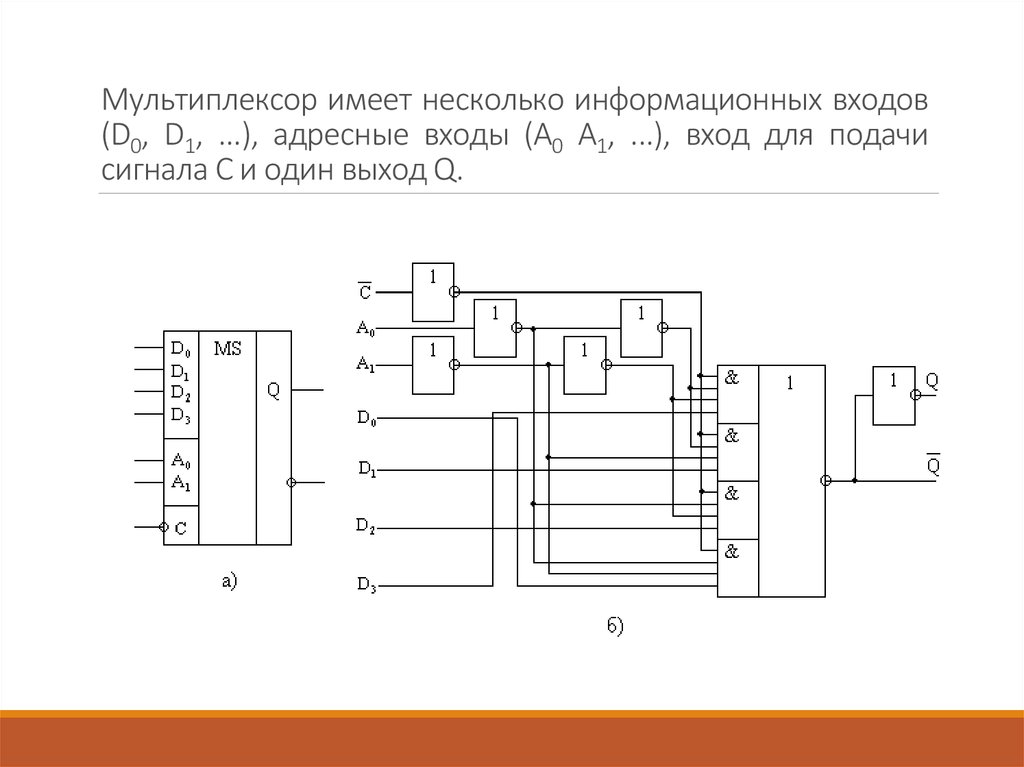
Эти измерения
выполняются наодном из концов линии связи с помощью тестераBER, рис.5.18. Эти
измерения выполняются на одном из концов линии связи с помощью тестера BER,
определяется как максимальный разброс между уровнем мощности различных каналов в
составном сигнале (для всех активных каналов). Эта величина измеряется
анализатором оптического спектра OSA.
Рисунок. 5.18. Неравномерность распределения мощности выходного сигнала мультиплексора
Неравномерность распределения мощности не должна превышать 3 дБ, чтобы не допустить существенного рассогласования характеристик сигналов в различных каналах. Соответствующий параметр для демультиплексора – мощность выходного сигнала в каждом канале. Эта величина измеряется калиброванным измерителем мощности и обычно составляет около –20 дБм, рис. 5.19.
Рисунок. 5.19. Измерение распределения мощности выходного сигнала между каналами с помощью измерителя мощности
Вносимые
потери тесно связаны с неравномерностью распределения мощности по каналам.
Величина потерь, вносимых мультиплексором в каждый канал, измеряется с помощью
перестраиваемого лазера (либо набора передатчиков с разными длинами волн) и
анализатора оптического спектра OSA, с помощью которого последовательно измеряют
входной и выходной сигнал для каждого канала, рис. 5.20. Можно также провести
такие измерения с помощью измерителя мощности, последовательно включая
передатчики с разными длинами волн.
Рисунок 5.20 Измерение вносимых потерь с помощью:
а) анализатора оптического спектра OSA для мультиплексора;
b) измерителя мощности для демультиплексора
Важными
характеристиками мультиплексоров и демультиплексоров являются центральная длина
волны и ширина полосы отдельных каналов. Кроме этого необходимо провести
измерение уровня перекрестных помех между каналами. Этиизмерения проводятся с
помощью анализаторов оптического спектра OSA имноговолнового измерителя (для
калибровки OSA), рис.
Рисунок 5.21. Измерение центральной длины волны канала с помощью:
а) источника ASE и анализатора оптического спектра OSA для демультиплексора;
б) анализатора оптического спектра OSA и имеющихся в системе передатчиков длямультиплексора
Направленность особенно существенна для мультиплексоров и ее также измеряют присдаче в эксплуатацию. Лазерный сигнал подают на один из входов мультиплексора иисследуют все остальные входы с помощью анализатора OSA, рис. 5.22.
Рисунок. 5.22 Измерение направленности мультиплексора с помощью анализатора оптического спектра OSA
Разница между мультиплексором и демультиплексором (с операционным рисунком и сравнительной диаграммой)
Основным фактором, отличающим мультиплексор от демультиплексора , является их способность принимать множественный вход и один вход соответственно.
Мультиплексор, также известный как MUX , работает с несколькими входами, но обеспечивает один выход. В отличие от демультиплексора, также известного как , DEMUX просто меняет операцию MUX и работает с одним входом, но передает данные на несколько выходов.
Здесь следует отметить, что мультиплексор действует как селектор данных, таким образом обеспечивая один выход из нескольких входов. Однако демультиплексор действует как распределитель данных и генерирует несколько выходов с одним входом.
Мы обсудим некоторые другие основные различия между MUX и DEMUX, но перед этим взглянем на содержание, которое будет обсуждаться в этой статье.
Содержание: Мультиплексор и демультиплексор
- Сравнительная таблица
- Определение
- Ключевые отличия
- Заключение
Сравнительная таблица
| Параметр | Мультиплексор | Демультиплексор |
|---|---|---|
| Определение | Мультиплексор представляет собой комбинационную схему, которая обеспечивает один выход, но принимает несколько входных данных. | Демультиплексор представляет собой комбинационную схему, которая принимает один вход, но этот вход может быть направлен через несколько выходов. |
| Символ | ||
| Количество вводов данных | Несколько | Одиночное |
| Количество выходных данных | Одиночный | Несколько |
| Метод преобразования | Выполняет параллельное последовательное преобразование. | Выполняет последовательное преобразование в параллельное. |
| Конфигурация устройства | Это устройство N к 1 и поэтому ведет себя как селектор данных. | Это устройство от 1 до N и поэтому ведет себя как распространитель данных. |
Определение мультиплексора
Это логическая схема, которая позволяет генерировать один выход, принимая несколько входных данных. Мультиплексор состоит из управляющего сигнала или входа выбора данных, который завершает вывод нескольких входов.
Таким образом, также известный как селектор данных.
Обозначается как схема «многие к одному» из-за возможности выбора одного выхода из нескольких входов.
На рисунке ниже показана схема мультиплексора, включая входные, выходные и управляющие сигналы.
Работает как многопозиционный переключатель с цифровым управлением управляющими сигналами. Здесь строки выбора определяют, какой вход будет переключен на выход из нескольких входов. Как видно на рисунке выше, n входных сигналов подаются на мультиплексор, содержащий m управляющих сигналов. Однако на выход передается только 1 источник данных.
Между строками ввода и выбора существует связь, которая заслуживает внимания и определяется как:
2 m = n
: m — линии выбора, n — входные линии
Можно иметь несколько конфигураций мультиплексора в зависимости от входных линий и подаваемого на него управляющего сигнала.
Давайте рассмотрим мультиплексор 4 к 1, который состоит из 4 входных сигналов и 2 управляющих сигналов, чтобы обеспечить один выход.
Здесь к MUX применяются 4 входных бита: D 0 , D 1 , D 2 , D 3 и управляющие сигналы a и b. Таким образом, любые входные данные могут быть переданы на выход при изменении уровня управляющего сигнала.
Таблица истинности для мультиплексора показана ниже. Давайте рассмотрим 4 отдельных случая, чтобы понять изменение выхода при управлении уровнем управляющих сигналов.
| Строки выбора данных | Выбран вход | Вход | Выход | |
|---|---|---|---|---|
| а | б | Д | Д | З |
| 0 | 0 | D 0 | 0 1 | 0 1 |
| 0 | 1 | D 1 | 0 1 | 0 1 |
| 1 | 0 | D | 0 1 | 0 1 |
| 1 | 1 | Д 3 | 0 1 | 0 1 |
Случай 1 : Учтите, что оба подаваемых управляющих сигнала a и b имеют низкий уровень, т.
е. 0. В таком состоянии из-за наличия входов вентиля НЕ I 1 и I 2 только вентиля И 1 высокий. Таким образом, если входной бит D 0 высокий, то выход высокий, а если вход D 0 низкий, то логический элемент И формирует свой выход как 0.
Таким образом, с уровнем управляющего сигнала 00 только A
Случай 2 : Когда управляющий сигнал a имеет низкий уровень, а сигнал b высокий, это приводит к включению логического элемента И 2, так как I 1 и I 2 из A 2 будут высокими. Таким образом, входной бит D 1 определяет вывод A 2 . Если D1 высокий, на выходе будет 1, иначе 0.
Случай 3 : Теперь рассмотрим, что уровень управляющего сигнала a высокий, а уровень b низкий. Это включает только логический элемент И 3 в качестве входов I 
Итак, подаваемый на вход бит D 2 даст нужный бит на выходе.
Случай 4 : Давайте теперь рассмотрим случай, когда уровень обоих подаваемых управляющих сигналов высок или равен 1. Тогда из-за этого только вентиль A 4 включается, а все остальные отключаются. В связи с этим на выходе будет результат примененного ввода D 3 .
Определение демультиплексора
Демультиплексор в основном работает в обратном порядке по сравнению с мультиплексором. Он переключает один вход на несколько выходов.
Здесь сигнал управления также играет важную роль, определяя выход, на который должен передаваться вход. Он также известен как распределитель данных, поскольку он позволяет распределять один вход между несколькими выходами.
Давайте посмотрим на показанную ниже конфигурацию DEMUX, которая имеет только один вход, но m управляющих и n выходных линий.
Двигаясь дальше, рассмотрим демультиплексор 1:4, состоящий из бита данных D, с двумя управляющими сигналами a и b.
Здесь Z 0 , Z 1 , Z 2 , Z 3 — это 4 выхода демультиплексора.
Как мы уже объясняли, для определенного значения управляющего сигнала включается только один логический элемент И, а все остальные отключаются.
The truth table for a 1:4 DEMUX is shown below
| a | b | D | Z 0 | Z 1 | Z 2 | З 3 |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 1 |
Схема демультиплексора также играет важную роль в системе связи, так как иногда требуется параллельный прием данных.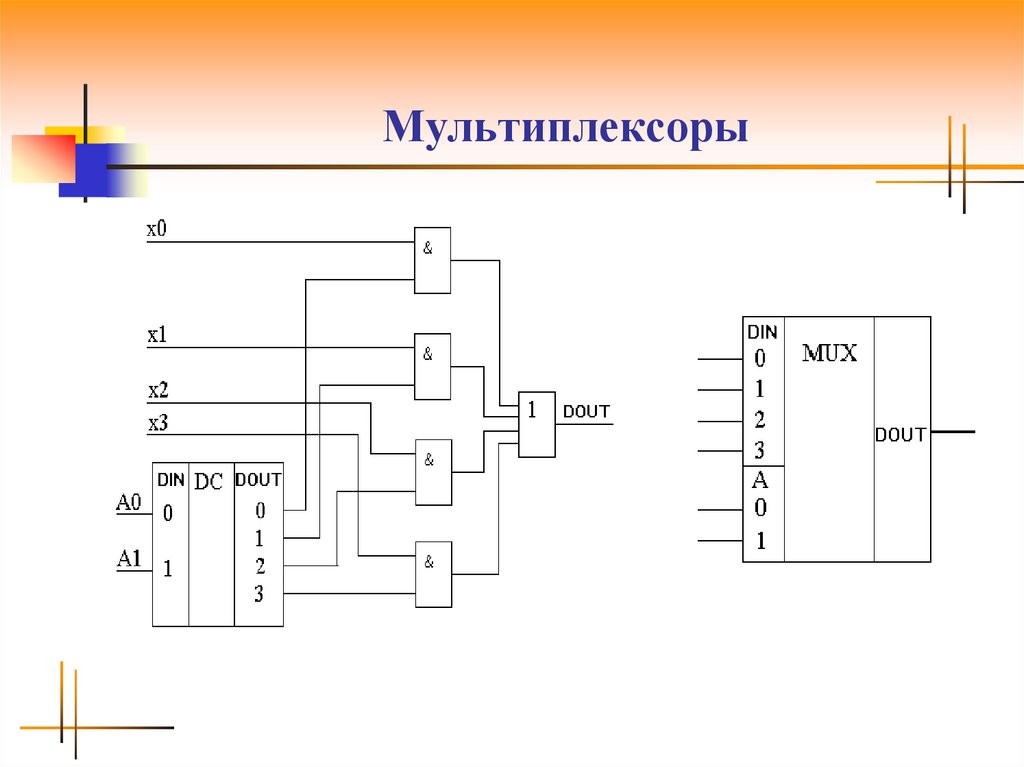
Таким образом, для таких приложений используются эти схемы.
Ключевые отличия Мультиплексор и демультиплексор
- И мультиплексоры, и демультиплексоры представляют собой комбинационные логические схемы , используемые в системе связи, но их работа полностью противоположна друг другу, поскольку одна работает с несколькими входами, а другая — с одним входом.
- Когда мы говорим о методе преобразования данных, то нетрудно понять, что MUX выполняет параллельное последовательное преобразование, поскольку требует нескольких входов. Однако DEMUX, наоборот, выполняет последовательное преобразование в параллельное, поскольку в его случае достигается несколько выходов.
- Мультиплексор с помощью сигналов управления выбирает конкретный вход, который должен быть передан на выходе. Напротив, демультиплексор использует управляющий сигнал и позволяет нам иметь несколько выходов.
- Другое ключевое различие между MUX и DEMUX заключается в том, что мультиплексор — это устройство N к 1, а демультиплексор — это устройство 1 к N.
Заключение
В системе связи требуются как мультиплексор, так и демультиплексор из-за ее двунаправленного характера, но их работа прямо противоположна друг другу. Наличие управляющих сигналов играет решающую роль в работе MUX и DEMUX.
Демультиплексор в цифровой электронике — Javatpoint
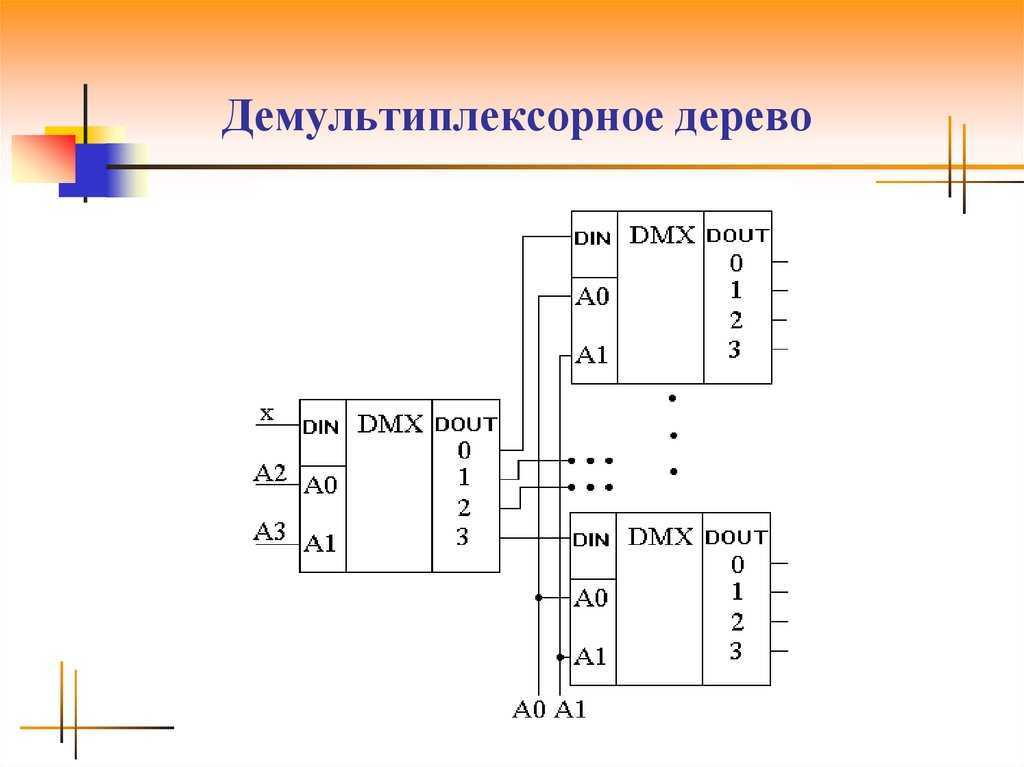
следующий → ← предыдущая Демультиплексор представляет собой комбинационную схему, которая имеет только 1 входную линию и 2 N выходных линий. Проще говоря, мультиплексор представляет собой комбинационную схему с одним входом и несколькими выходами. Информация поступает с отдельных входных линий и направляется на выходную линию. На основании значений линий выбора вход будет подключен к одному из этих выходов. Демультиплексор противоположен мультиплексору. В отличие от энкодера и декодера, имеется n строк выбора и 2 n выходы. Итак, всего 2 n возможных комбинаций входов. Демультиплексор также рассматривается как Демультиплексор . Существуют следующие типы демультиплексоров: Демультиплексор 1×2:В демультиплексоре 1 на 2 имеется только два выхода, т. е. Y 0 , и Y 1 , 1 линия выбора, т. е. S 0 , и один вход, т. е. A. На на основе выбранного значения вход будет подключен к одному из выходов. Блок-схема и таблица истинности 1 × 2 мультиплексора приведены ниже. Блок-схема:Таблица истинности:Логическое выражение терма Y следующее: Y 0 =S 0 ‘.A Логическая схема приведенных выше выражений приведена ниже: Демультиплексор 1×4: В демультиплексоре от 1 до 4 всего четыре выхода, т. е. Y 0 , Y 1 , Y 2 и Y 3 , 2 строки выбора, т. е. S 0 и S 1 , и один вход, т. е. A. На основе комбинации входов, присутствующих в строках выбора S 0 и S 1 вход должен быть подключен к одному из выходов. Блок-схема:Таблица истинности:Логическое выражение терма Y следующее: Д 0 =S 1 ‘ S 0 ‘ A Логическая схема приведенных выше выражений приведена ниже: Демультиплексор 1×8 В демультиплексоре от 1 до 8 всего восемь выходов, то есть Y 0 , Y 1 , Y 2 , Y 3 , Y 4 , Y 5 , Y 6 и Y 7 , 3 строки выбора, т. е. S 0 , S 1 и S 2 и одиночный ввод, т. е. A. На основе комбинации входов, которые присутствуют на линиях выбора S 0 , S 1 и S 2 , вход будет подключен к одному из этих выходов. Блок-схема:Таблица истинности:Логическое выражение терма Y следующее: Y 0 = S 0 ‘.S 1 ‘ .S 2 ‘.a Логическая схема приведенных выше выражений приведена ниже: Демультиплексор 1×8 с использованием демультиплексора 1×4 и 1×2Мы можем реализовать демультиплексор 1 × 8, используя демультиплексор более низкого порядка. Для реализации демультиплексора 1 × 8 нам потребуется два 1 × 4 демультиплексора и один 1 × 2 демультиплексора. Мультиплексор 1 × 4 имеет 2 линии выбора, 4 выхода и 1 вход. Демультиплексор 1 × 2 имеет только 1 линию выбора. Для получения 8 выходов данных нам потребуется два 1 × 4 демультиплексора. Демультиплексор 1×2 выдает два выхода. Итак, чтобы получить окончательный результат, мы должны передать выходы демультиплексора 1×2 как входы обоих демультиплексоров 1 × 4. Блок-схема 1 9Ниже приведен демультиплексор 0003 × 8 с использованием демультиплексора 1 × 4 и 1 × 2 . Демультиплексор 1 x 16В демультиплексоре 1×16 всего 16 выходов, т. е. Y 0 , Y 1 , …, Y 16 , 4 строки выбора, т. е. S 0 , S 5 1 , S 2 , S 3 и один вход, т. е. A. На основе комбинации входов, присутствующих на линиях выбора S 0 , S 1 и S 2 вход будет подключен к одному из этих выходов. Блок-схема и таблица истинности демультиплексора 1 × 16 приведены ниже. Блок-схема:Таблица истинности:Логическое выражение терма Y следующее: Y 0 = A.S 0 ‘.S 1 ‘ .S 2 ‘.S 3 ‘ Логическая схема приведенных выше выражений приведена ниже: Мы можем реализовать 1 × 16 демультиплексор с использованием демультиплексора более низкого порядка. Для реализации демультиплексора 1 × 16 нам потребуется два демультиплексора 1 × 8 и один демультиплексор 1 × 2 . Мультиплексор 1 × 8 имеет 3 линии выбора, 1 вход и 8 выходов. Демультиплексор 1 × 2 имеет только 1 линию выбора. |
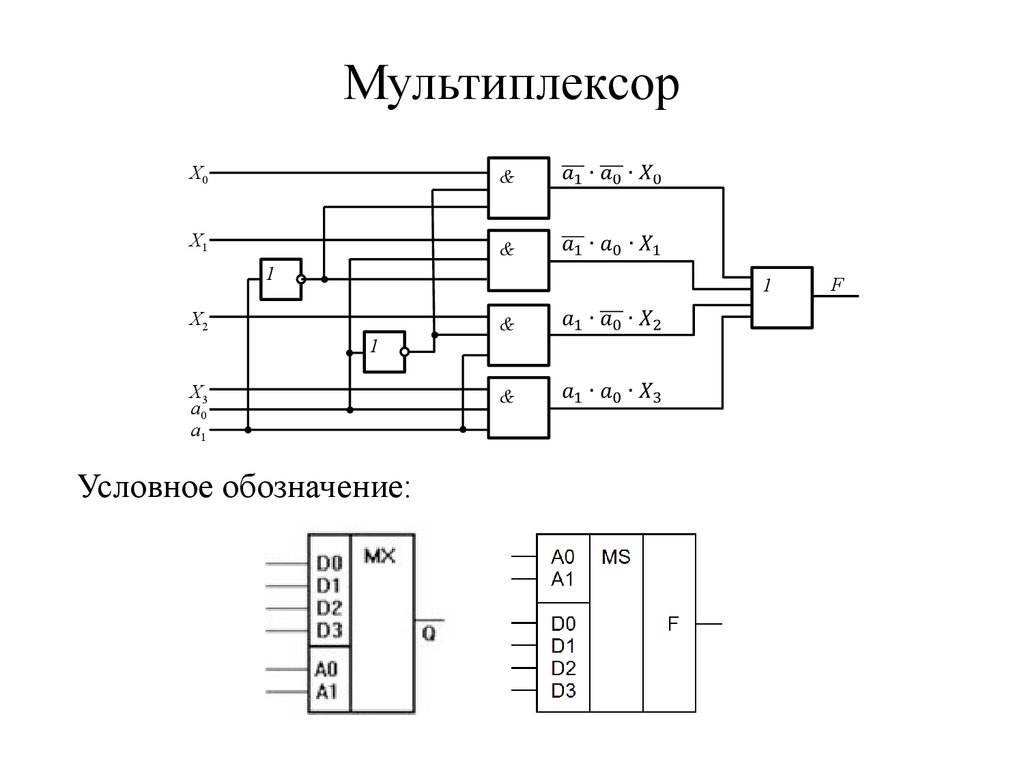
Блок-схема и таблица истинности мультиплексора 1 × 4 приведены ниже.
Блок-схема и таблица истинности демультиплексора 1 × 8 приведены ниже.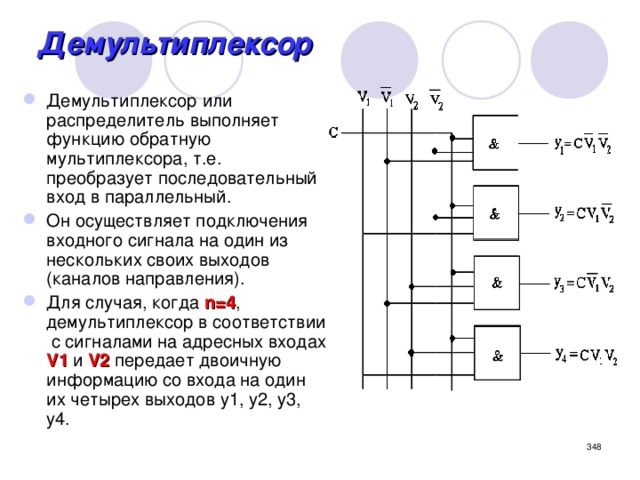
S 1 .S 2 A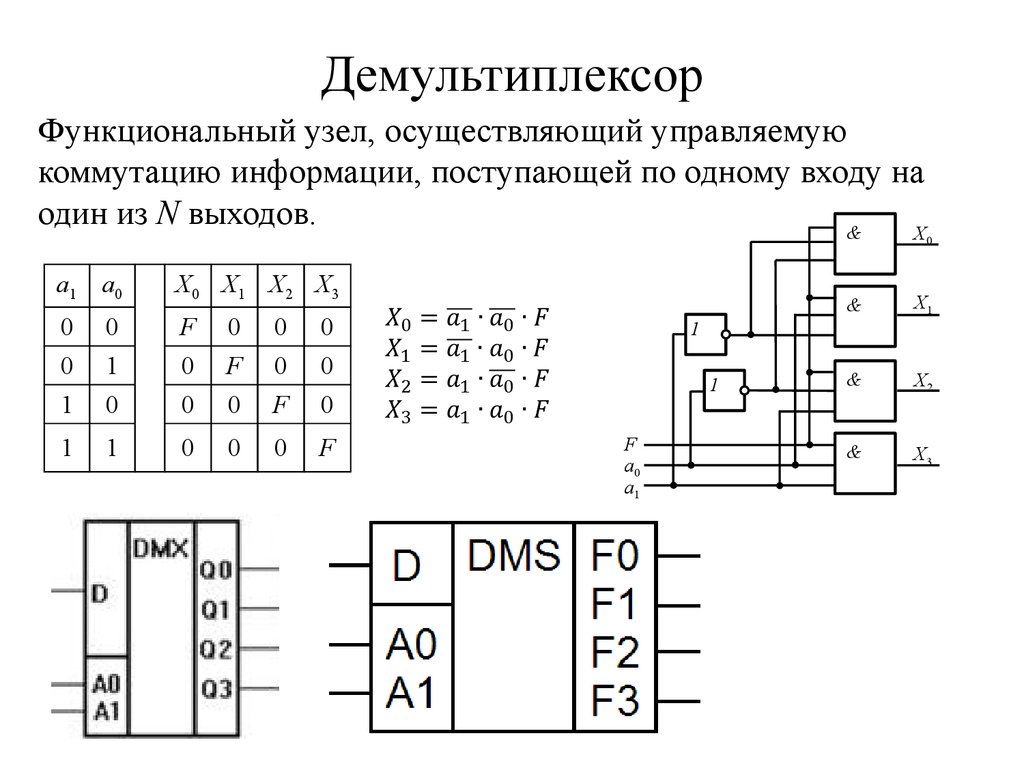 
.S 3 
S 0 291240125 .S 2 ‘.S 3 ‘ 
