3.2. Моменты инерции сечений

Моментами инерции сечений называются интегралы следующего вида:

– осевой момент инерции сечения относительно оси у;

– осевой момент инерции сечения относительно оси z;

– центробежный момент инерции сечения;

– полярный момент инерции сечения.

3.2.1. Свойства моментов инерции сечения

Размерность моментов инерции – [длина⁴], обычно [м⁴] или [см⁴].

Осевые и полярный моменты инерции всегда положительные. Центробежный момент инерции может быть положительным, отрицательным или равным нулю.

Оси, относительно которых центробежный момент инерции равен нулю, называются главными осями инерции сечения.

Оси симметрии всегда главные. Если из двух взаимно перпендикулярных осей хотя бы одна является осью симметрии, то обе оси главные.

Момент инерции составного сечения равен сумме моментов инерции элементов этого сечения.

Полярный момент инерции равен сумме осевых моментов инерции.

Докажем последнее свойство. В сечении с площадью А для элементарной площадки dA радиус-вектор ρ и координаты у и z (рис. 6) связаны по теореме Пифагора: ρ² = у² + z². Тогда

.

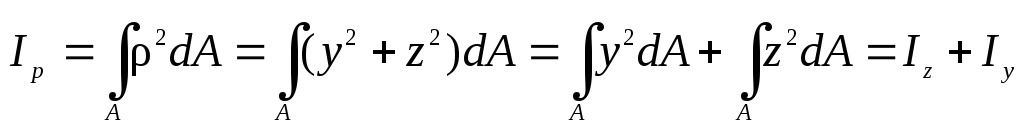
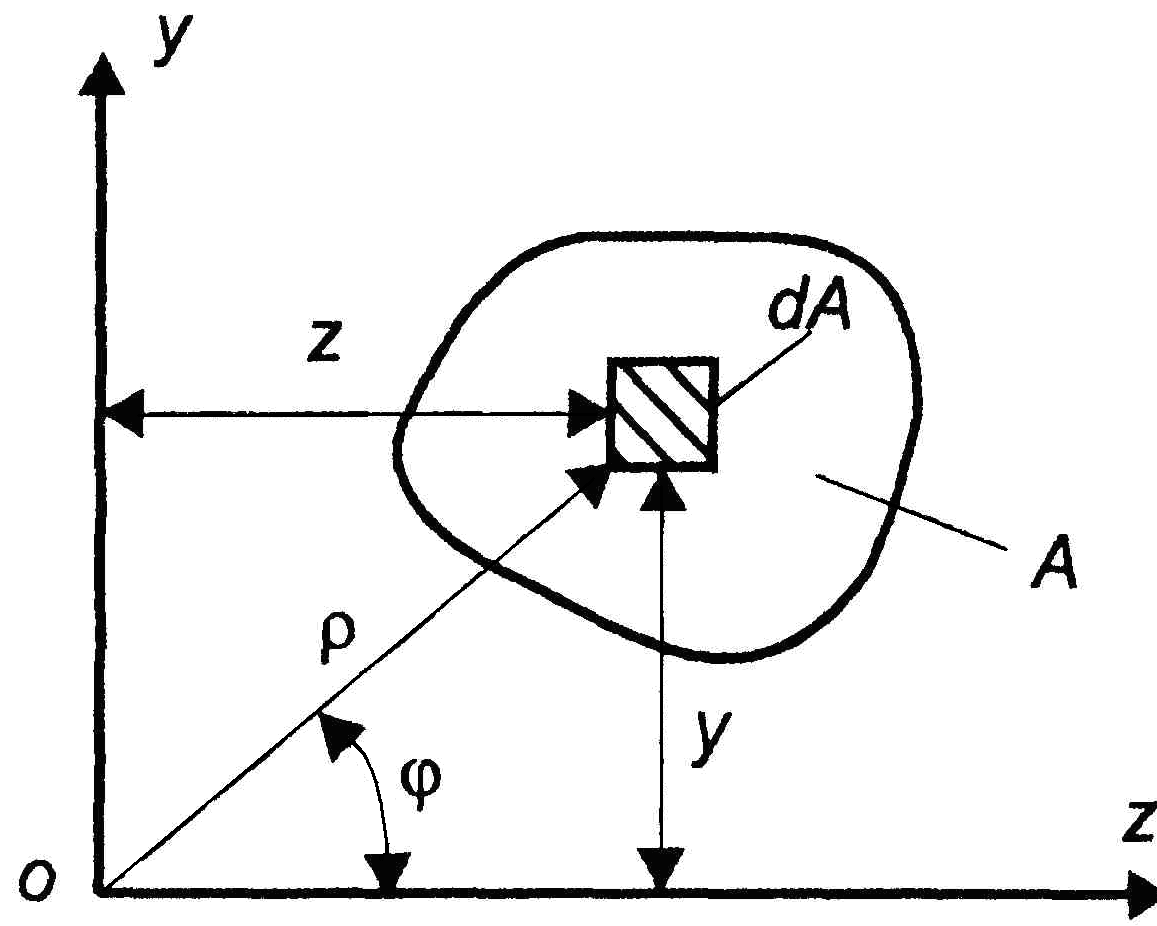
Рис. 6. Связь полярных и декартовых координат

элементарной площадки

3.2.2. Моменты инерции простейших фигур

В прямоугольном сечении (рис. 7) выберем элементарную площадку dA с координатами y и z и площадью dA = dydz.

Рис. 7. Прямоугольное сечение

Осевой момент инерции относительно оси у

.

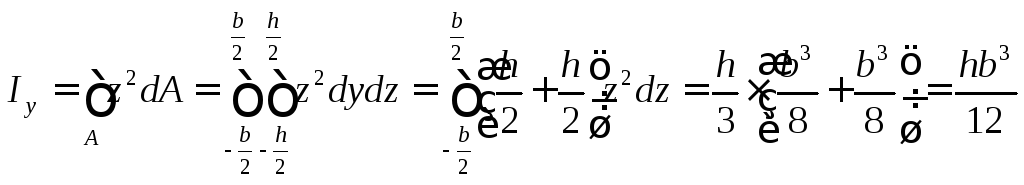
Аналогично получаем момент инерции относительно оси z:

.

Поскольку у и z – оси симметрии, то центробежный момент D_zy = 0.

Для круга диаметром d вычисления упрощаются, если учесть круговую симметрию и использовать полярные координаты. Возьмем в качестве элементарной площадки бесконечно тонкое кольцо с радиусом ρ и толщиной dρ (рис. 8). Его площадь dA = 2πρdρ. Тогда полярный момент инерции:

.

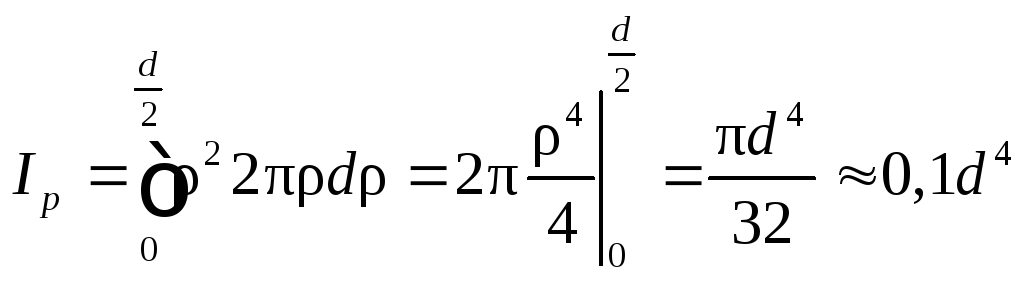
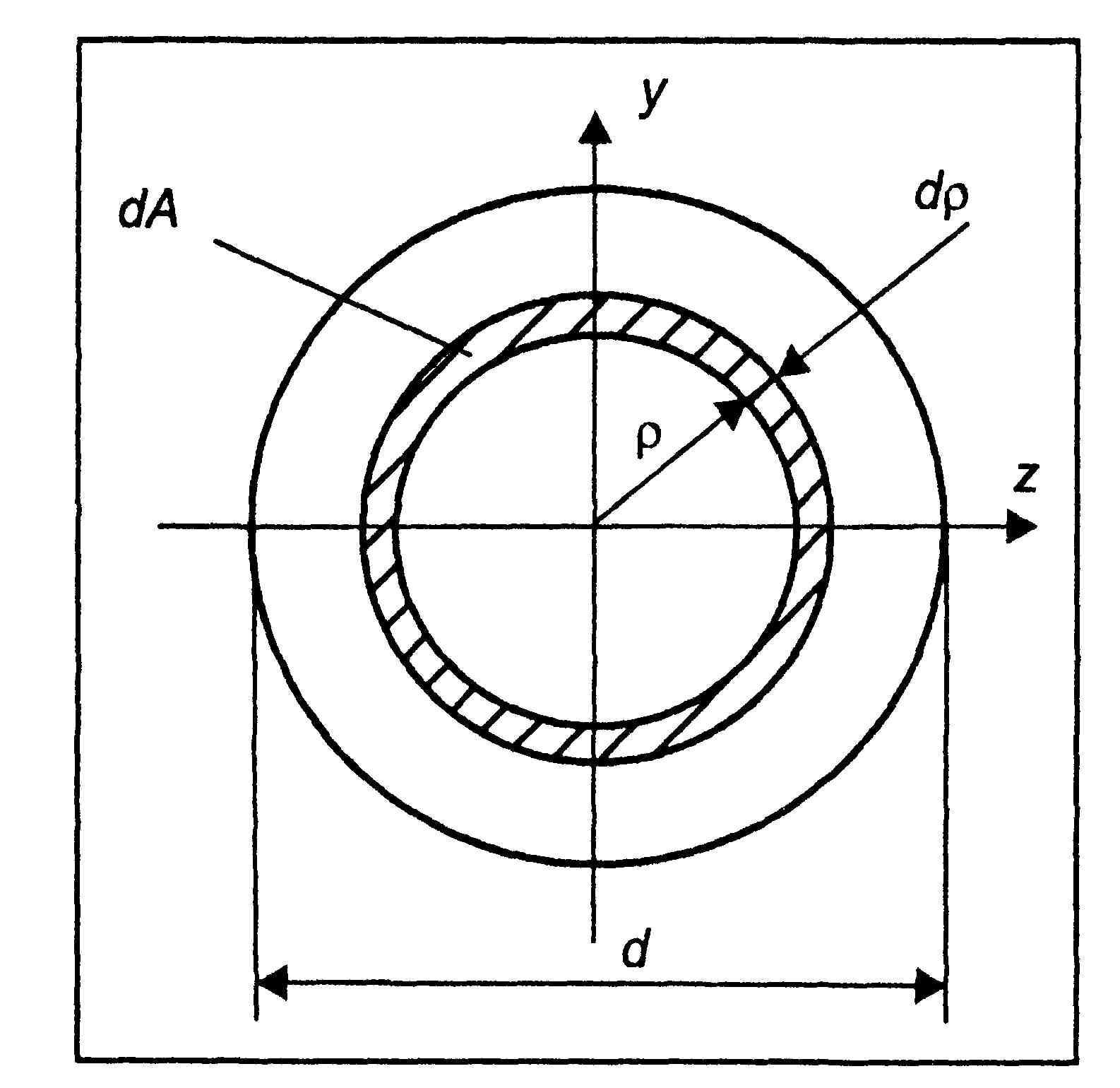
Рис. 8. Круглое сечение

Как показано выше, осевые моменты инерции относительно любой центральной оси одинаковы и равны

.

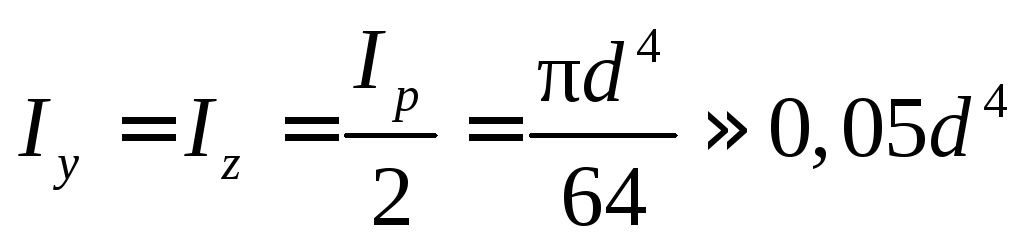Момент инерции кольца находим как разность моментов инерции двух кругов – наружного (с диаметром D) и внутреннего (с диаметром d):

,

,

где .

Момент инерции I_zтреугольникаопределим относительно оси, проходящей через центр тяжести (рис. 9). Очевидно, ширина элементарной полоски, находящейся на расстоянииуот осиz, равна

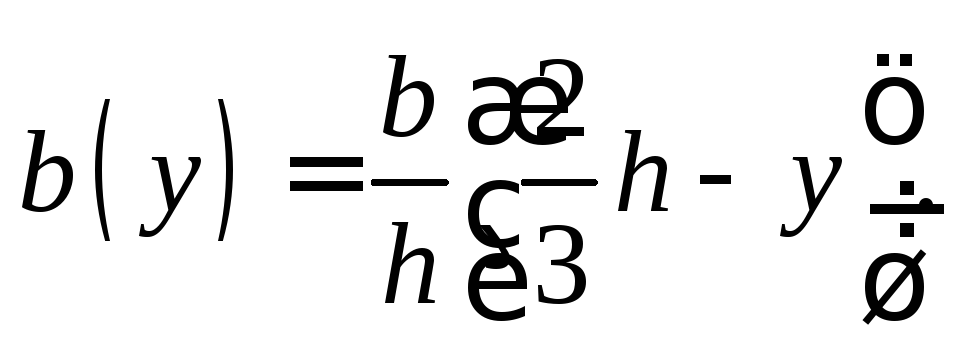
Следовательно,

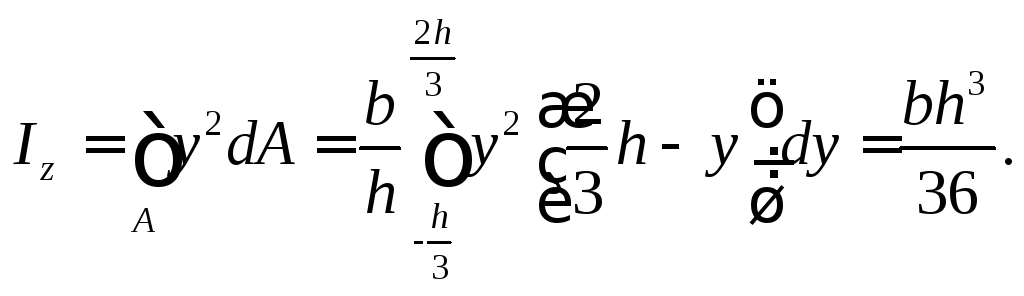
Рис. 9. Треугольное сечение

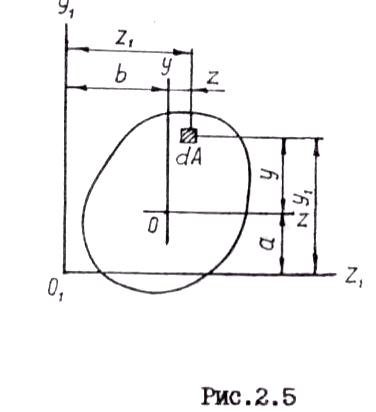
3.3. Зависимости между моментами инерции относительно параллельных осей

При известных величинах моментов инерции относительно осей

z и у определим моменты инерции относительно других осей z₁ и y₁, параллельных заданным. Пользуясь общей формулой для осевых моментов инерции, находим

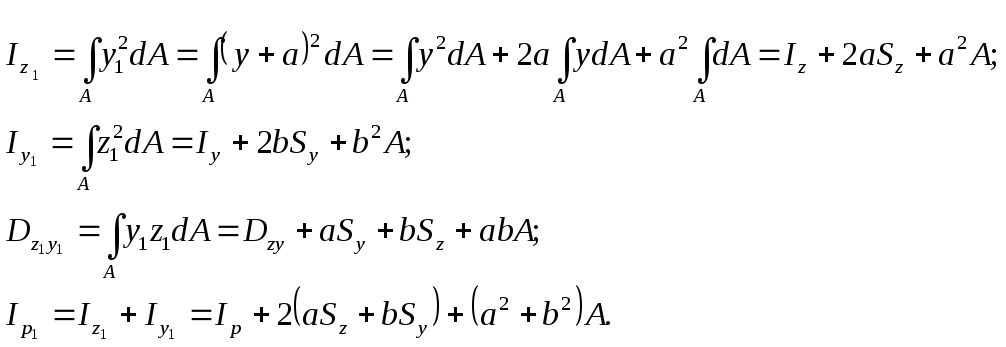
Если оси z и y центральные, то 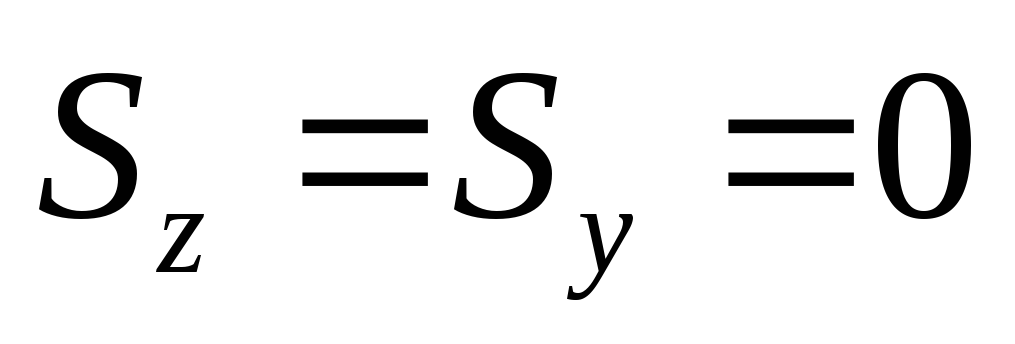, и

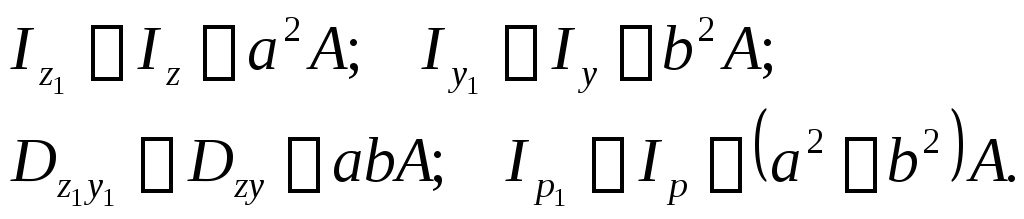
Из полученных формул видно, что моменты инерции относительно центральных осей (когда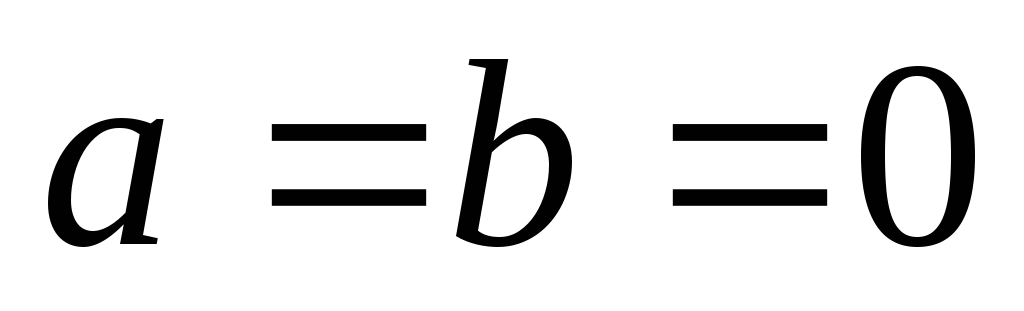

) имеют наименьшие значения по сравнению с моментами инерции относительно любых других параллельных осей.

3.4. Главные оси и главные моменты инерции

При повороте осей на угол α центробежный момент инерции становится равным

.

Определим положение главных главных осей инерции u, v относительно которых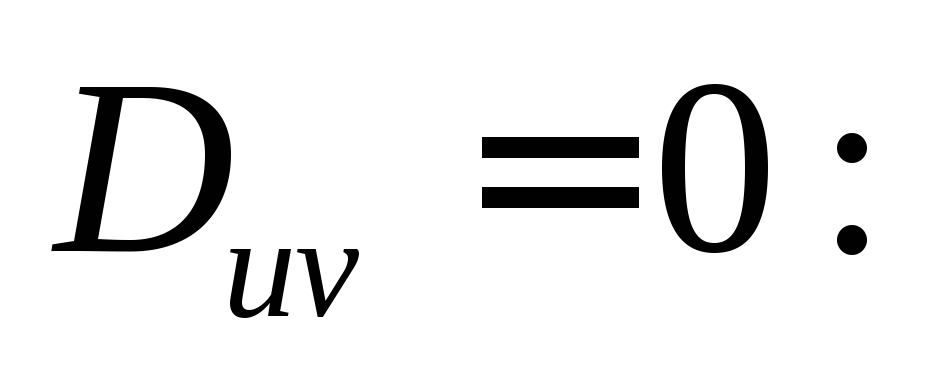

,

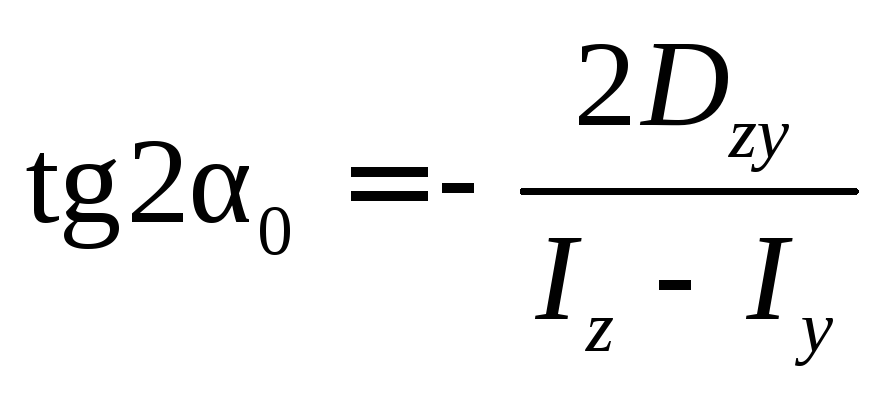
где α₀ – угол, на который надо развернуть оси y и z, чтобы они стали главными.

Поскольку формула дает два значения угла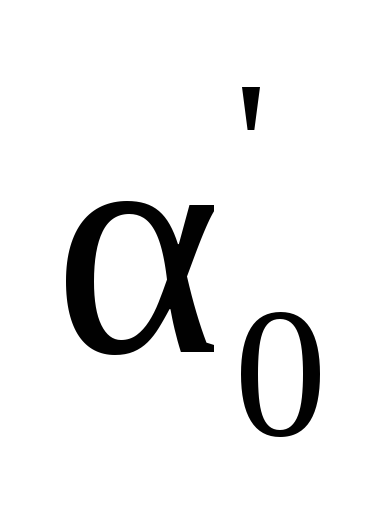и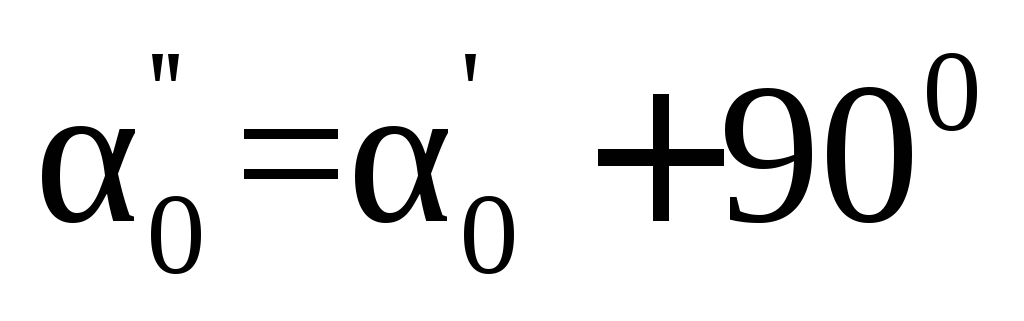, то существуют две взаимно перпендикулярные главные оси. Ось максимума всегда составляет меньший угол (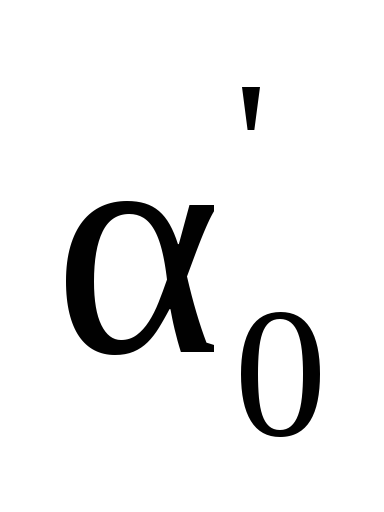) с той из осей (z или y), относительно которой осевой момент инерции имеет большее значение. Напомним, что положительные углы откладываются от оси

z против хода часовой стрелки.

Моменты инерции относительно главных осей называются главными моментами инерции. Можно показать, что они

.

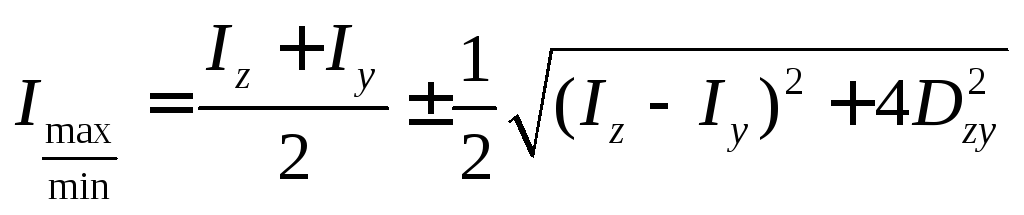Знак плюс перед вторым слагаемым относится к максимальному моменту инерции, знак минус – к минимальному.

Центробежный момент — инерция — Большая Энциклопедия Нефти и Газа, статья, страница 1

Центробежный момент — инерция

Cтраница 1

Центробежный момент инерции равен пулю.  [1]

Центробежные моменты инерции обычно вычисляются через главные центральные осевые моменты инерции.  [2]

Центробежный момент инерции может быть положительным, отрицательным и в частном случае равным нулю.  [3]

Центробежный момент инерции относительно этих осей равен нулю.  [4]

Центробежный момент инерции может быть положительным, отрицательным и равным нулю.  [5]

Центробежный момент инерции может быть положительным, отрицательным или равным нулю.  [7]

Центробежный момент инерции относительно осей х, у оказался, как видим, отрицательным.  [8]

Центробежный момент инерции может быть положительным, отрицательным и равным нулю.  [9]

Центробежный момент инерции имеет размерность см, но в отличие от осевого и полярного моментов инерции он может быть величиной положительной, отрицательной и равной нулю.  [10]

Центробежный момент инерции по отношению к осям, из которых хотя бы одна является осью симметрии, равен нулю.  [11]

Центробежный момент инерции определяется по осевым моментам инерции, найденным для осей х, у и оси.  [12]

Центробежный момент инерции достигает наибольшего по абсолютной величине значения для креста осей, повернутых на: 45 относительно главных осей. Это экстремальное значение равно полуразности главных моментов инерции. Осевые моменты инерции для этого креста осей равны между собой. Наоборот, если для случайного креста осей Ja Jv и Jav ф 0, то главные оси повернуты на: 45 относительно этого креста.  [13]

Центробежные моменты инерции

могут быть положительными, отрицательными или равным нулю.  [14]

Центробежный момент инерции / у1г1 0, так как ось ляется осью симметрии.  [15]

Страницы:      1    2    3    4

Центробежный момент инерции, теория и примеры

Центробежный момент инерции тела

Допустим, что имеется система координат с началом в точке O и осями OX; OY; OZ. По отношению к данным осям центробежными моментами инерции (произведениями инерции) называются величины , которые определяются равенствами:

   

где – массы материальных точек, на которые разбивают тело; – координаты соответствующих материальных точек.

Центробежный момент инерции обладает свойством симметрии, это следует из его определения:

   

Если тело можно считать сплошным (непрерывным), то определение центробежного момента инерции записывают как:

   

Центробежные моменты тела могут быть положительными и отрицательными, при определённом выборе осей OXYZ они могут обращаться в ноль.

Для центробежных моментов инерции существует аналог теоремы Штейнберга. Если рассмотреть две системы координат: и . Одна из этих систем имеет начало координат в центе масс тела (точка C), оси систем координат являются попарно параллельными (). Пусть в системе координат координатами центра масс тела являются (), тогда:

   

где – масса тела.

Главные оси инерции тела

Пусть однородное тело имеет ось симметрии. Построим координатные оси так, чтобы ось OZ была направлена вдоль оси симметрии тела. Тогда, как следствие симметрии каждой точке тела с массой и координатами соответствует точка, имеющая другой индекс, но такую же массу и координаты: . В результате получаем, что:

   

так как в данных суммах все слагаемые имеют свою равную по величине, но противоположную по знаку пару. Выражения (4) эквивалентны записи:

   

Мы получили, что осевая симметрия распределения масс по отношению к оси OZ характеризуется равенством нулю двух центробежных моментов инерции (5), которые содержат среди своих индексов наименование этой оси. В таком случае ось OZ называется главной осью инерции тела для точки О.

Главная ось инерции не всегда является осью симметрии тела. Если тело обладает плоскостью симметрии, то любая ось, которая перпендикулярна этой плоскости, является главной осью инерции для точки O, в которой ось пересекает рассматриваемую плоскость. Равенства (5) отображают условия того, что ось OZ является главной осью инерции тела для точки O (начала координат). Если выполняются условия:

   

то ось OY будет для точки O главной осью инерции.

В том случае, если выполняются равенства:

   

то все три координатные оси системы координат OXYZ являются главными осями инерции тела для начала координат.

Моменты инерции тела по отношению к главным осям инерции называются главными моментами инерции тела. Главные оси инерции, которые построены для центра масс тела, носят название главных центральных осей инерции тела.

Если тело обладает осью симметрии, то она является одной из главных центральных осей инерции тела, поскольку центр масс находится на этой оси. В том случае, если тело имеет плоскость симметрии, то ось, нормальная к этой плоскости и проходящая через центр масс тела является одной из главных центральных осей инерции тела.

Понятие главных осей инерции в динамике твердого тела имеет существенное значение. Если вдоль них направить оси координат OXYZ, то все центробежные моменты инерции становятся равными нулю, при этом значительно упрощаются формулы, которые следует применять при решении задач динамики. С понятием о главных осях инерции связано решение задач о динамическом уравнении тела находящегося во вращении и о центре удара.

Момент инерции тела ( и центробежный в том числе) в международной системем единиц измеряются в:

   

Центробежный момент инерции сечения

Центробежным моментом инерции сечения (плоской фигуры) относительно двух взаимно нормальных осей (OX и OY) называют величину, равную:

   

выражение (8) говорит о том, что центробежный момент инерции сечения относительно взаимно перпендикулярных осей есть сумма произведений элементарных площадок () на расстояния от них до рассматриваемых осей, по всей площади S.

Единицей измерения моментов инерции сечения в СИ является:

   

Центробежный момент инерции сложного сечения по отношению к любым двум взаимно нормальным осям равен сумме центробежных моментов инерции составляющих его частей относительно этих осей.

Примеры решения задач

хелп ми!!!!различия экваториального момента инерции от полярного момента инерции? 🙂

Момент инерции чего?? ? Старых носков забытых там или там? ? на полюсе, если считать эти носки за материальные точки, то и не крутятся. на экваторе крутятся по полной вокруг оси, которая сквозь полюса Хотя если перекрутить с с полюса их в космос вынесет кусочками разорвав во все стороны, а с экватора целиком (точнее то, что от них сквозь атмосферу не сгорит) (полюс (тут явно механический смысл) — обычно центр прохождения оси вращения сквозь поверхность данной тушки {r=0 => M=0} Экватор в разных науках разное — обычно самое дальнее от оси у центра масс — там уж по правилам именно той науки считать) термины в разных областях по разному определяются (ещё десятки несовместимых есть) — тут вообще непонятно о чём речь

ТЫ не знаешь чем экватор от полюсов отличается?

МОМЕНТ ИНЕРЦИИ — это величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Вы немного перепутали, бывают осевой и центробежный момент инерции. Осевой момент инерции равен сумме произведений масс Мi всех элементов тела на квадраты их расстояний hi от, например, оси z, относительно которой он вычисляется, т. е. Iz = М1*h2^2 +M2*h3^2 + .+Mn*hn^2 Центробежным моментом инерции относительно системы прямоугольных осей x, y, z называются величины Ix,y = Сумма (Mi*Xi*Yi) Ix,z = Сумма (Mi*Xi*Zi) Iy,z = Сумма (Mi*Yi*Zi) (или соответствующие объемные интегралы) . Они характеризуют динамическую неуравновешенность масс.

Экваториальный момент инерции-это момент инерции относительно оси, которая лежит в плоскости рассматриваемого тела. Полярный момент инерции-это момент инерции относительно точки, лежащей в плоскости рассматриваемого тела.

зависит ли момент инерции от времени?

нет только от воздействия силы

Сама по себе инерция зависит от массы и силы а не от времени. Чем больше масса, тем инерционный ход дольше.

Момент инерции зависит ТОЛЬКО от распределения МАССЫ относительно ОСИ вращения. Ни от каких сил и времён он НЕ зависит. Если распределение масс меняется со временем, то, ясен пень, и момент инерции — тоже.

Момент, ЕМНИП.. . -это сила, приложенная на — плечо… Инерция — явление сохранения скорости тела в случае, если внешние воздействия на него отсутствуют или взаимно скомпенсированы.