Физика Момент силы. Второе условие равновесия твёрдого тела

Материалы к уроку

Конспект урока

Одним из условий равновесия твердого тела является геометрическая сумма внешних сил, действующих на тело, которая должна быть равна нулю. Это условие является необходимым, но не является достаточным. Чтобы в этом убедиться проведем опыт. Приложим к дощечке, лежащей на плоской поверхности, в различных точках две силы равные по модулю, но направленные в противоположные стороны. Сумма этих двух сил равна нулю. Но дощечка не останется в равновесии, она будет поворачиваться. Первое условие равновесия твердого тела выполняется, но тело не находится в равновесии.
Другой пример, на руль автомобиля во время поворота действуют две силы, приложенные в двух разных точках. Эти силы одинаковые по модулю и противоположно направленные. Сумма этих двух сил так же равна нулю, а руль не находится в состоянии покоя. 
Почему же так происходит? Тело находится в равновесии, если сумма всех приложенных к каждому его элементу сил равна нулю. В наших примерах сумма внешних сил, приложенных к телу, равна нулю. Но если брать каждый отдельный элемент, сумма действующих на него сил может быть не равна нулю. Поэтому и дощечка, и руль в данных случаях не находятся в равновесии.

Для того чтобы выяснить, какое же еще условие должно выполняться, чтобы твердое тело находилось в равновесии, вспомним теорему об изменении кинетической энергии. Изменение кинетической энергии тела за некоторый промежуток времени равно работе, совершенной за то же время силой, действующей на тело.
Рассмотрим пример, при каком условии будет оставаться в равновесии стержень, шарнирно закрепленный на горизонтальной оси в точке 0.  Эта конструкция представляет собой обыкновенный рычаг.   Пусть к рычагу приложены две перпендикулярные стержню силы F1 и F2.

Предположим, что это силы натяжения веревок, к концам которых прикреплены грузы. Кроме этих двух сил,  на рычаг ещё действует направленная вертикально вверх сила реакции  опоры  со стороны оси рычага F3. При равновесии рычага сумма всех трех сил равна нулю.
Найдем работу, которую совершают внешние силы при повороте рычага на очень малый угол α. Точка приложения силы F1 пройдет путь равный BB1. А точка приложения силы F2 пройдёт путь равный CC1. Так как угол α невелик, можно считать линии BB1 и CC1 отрезками прямой.  Работа силы F1 положительна, потому что точка B перемещается в том же направлении, что и сила, а работа силы F2 отрицательна, так как точка приложения силы C движется в сторону противоположную направлению силы. Сила F3 работы не совершает, потому что точка 0 не перемещается.
Пройденные пути s1 и s2 можно выразить через угол поворота рычага α, измеренный в радианах. Тогда перемещение точки приложения силы F1 равно произведению угла α на длину отрезка BO. А перемещение точки приложения силы F2 равно произведению угла α на длину отрезка СO.
Подставим эти равенства в формулы работы сил F1 и F2. Получим, что работа силы F1 равна произведению модуля силы F1 на угол α и на длину отрезка ВО. Работа силы F2 равна произведению модуля силы F2 на угол α и на длину отрезка СО.
Радиусы ВО и СО дуг окружностей, описываемых точками приложения сил F1 и F2, являются перпендикулярами, опущенными из оси вращения на линии действия этих сил.
Кратчайшее расстояние от оси вращения до линии действия силы называют плечом силы.
Плечо силы обозначим буквой d. Плечо силы F1 равно d1. Плечо силы F2 равно d2. 
Тогда выражения для работы сил F1 и F2 примут следующий вид. Работа силы F1 равна произведению модуля силы F1 на угол α и на плечо силы F1. Работа силы F2 равна произведению модуля силы F2 на угол α и на плечо силы F2.
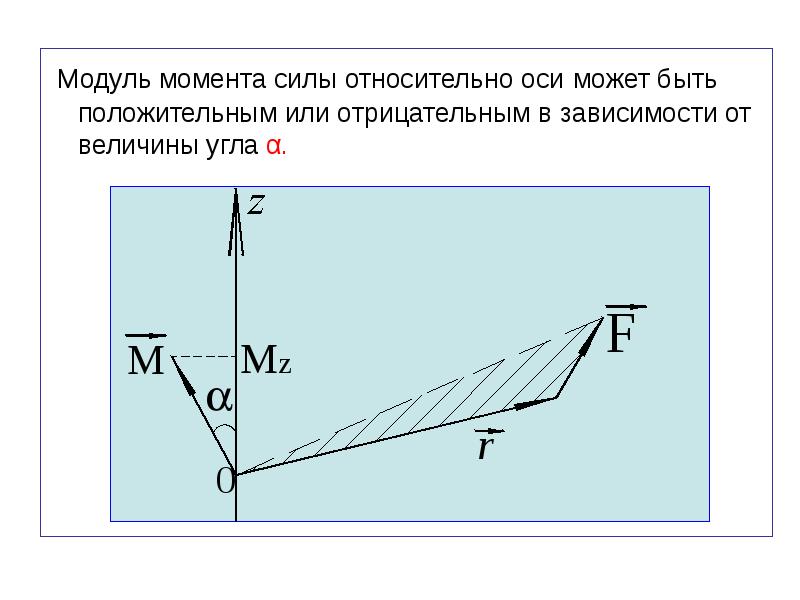
Полученные формулы показывают, что при заданном угле поворота тела работа каждой приложенной к этому телу силы равна произведению модуля силы на плечо взятому со знаком «+» или «-». Это произведение называют моментом силы.
Моментом силы относительно оси вращения тела называется произведение модуля силы на ее плечо. Момент силы может быть положительным или отрицательным.
Если сила, действующая на тело, направлена так, чтобы повернуть его против часовой стрелки, то момент силы считают положительным, если по часовой, то отрицательным. 
В нашем примере момент силы F1 равен произведению модуля силы F1 на плечо силы F1. Момент силы F2 равен произведению модуля силы F2 на плечо силы F2. Сила F1 стремится повернуть стержень против часовой стрелки, значит момент этой силы положительный. Сила F2 стремится повернуть стержень по часовой стрелке, значит момент этой силы отрицательный.
Следовательно, выражения для работы сил F1 и F2 можно записать в таком виде: работа силы F1 равна произведению момента силы F1 на угол α; работа силы F2 равна произведению момента силы F2 на угол α.
Полная работа внешних сил складывается из работы сил F1, F2 и F3.

Работа силы F3 равна нулю, потому что точка 0 не перемещается. Подставим в формулу вместо работы сил F1 и F2 произведения моментов сил на угол поворота. Получаем, что полная работа внешних сил равна произведению суммы моментов сил F1 и F2 на угол α.
Для того чтобы тело пришло в движение, нужно чтобы увеличилась его кинетическая энергия, а для этого внешние силы должны совершить работу. 
Согласно полученному уравнению, работа внешних сил может быть отлична от нуля только в том случае, если сумма моментов этих сил не равна нулю. Если же суммарный момент внешних сил, действующих на тело, равен нулю, то их работа равна нулю. Следовательно, кинетическая энергия тела не увеличивается, то есть остается равной нулю. Значит, тело не приходит в движение.
Это есть второе условие, необходимое для равновесия твердого тела.
При равновесии твердого тела сумма моментов всех внешних сил, действующих на него относительно любой оси, равна нулю. 
Если же на абсолютно твердое тело действует произвольное число сил, условия равновесия абсолютно твердого тела следующие:
‒    во-первых, геометрическая сумма внешних сил, действующих на тело, равна нулю,
‒    во-вторых, сумма моментов всех внешних сил, действующих на тело относительно любой оси, равна нулю.  
Эти условия являются необходимыми и достаточными для равновесия твердого тела. Если они выполняются, то тело остается в равновесии.
Если же тело не является абсолютно твердым, даже при соблюдении двух условий равновесия, это тело может и не оставаться в равновесии. 
Это происходит из-за того, что под воздействием приложенных к нему сил тело может деформироваться и тогда сумма всех сил, действующих на каждый его элемент, не будет равна нулю. Возьмем, например, резиновый шнур. Приложим к его концам две силы, равные по модулю и направленные вдоль шнура в противоположные стороны. Под действием этих сил шнур будет растягиваться, а, значит, выйдет из состояния равновесия, несмотря на то, что сумма внешних сил равна нулю и нулю равна сумма их моментов относительно оси, проходящей через любую точку шнура.

Остались вопросы по теме? Наши педагоги готовы помочь!

• Подготовим к ЕГЭ, ОГЭ и другим экзаменам

• Найдём слабые места по предмету и разберём ошибки

• Повысим успеваемость по школьным предметам

• Поможем подготовиться к поступлению в любой ВУЗ

Выбрать педагогаОставить заявку на подбор

9 ответов, которые вы должны знать

Может ли ускорение быть отрицательным? Чтобы ответить на этот вопрос, мы должны понять, что такое ускорение?

Мы знаем, что ускорение — это векторная величина, а векторная величина может быть положительной или отрицательной. Поэтому мы можем сказать, что ускорение объекта может быть как положительным, так и отрицательным.

Однако теперь возникает вопрос, в каких условиях ускорение объекта отрицательное, а когда положительное? Здесь мы собираемся обсудить те условия, в которых ускорение может быть отрицательным или положительным.

Ускорение: векторная величина

 Ускорение — это векторная величина; следовательно, он имеет как величину, так и направление. Представьте себе байкера, едущего на велосипеде, или человека, ведущего машину, тогда этот велосипед или автомобиль движется с непрерывно изменяющейся скоростью. Скорость изменения скорости автомобиля или мотоцикла в единицу времени называется ускорением. Когда объект меняет скорость, он начинает ускоряться, возможно, в направлении скорости или противоположном ей. Математически это выражается как,

A_птица — среднее ускорение

 Это уравнение дает величина ускорения. 

Направление ускорения

 Объект всегда ускоряется в направлении действующей на него чистой силы. Положительное или отрицательное ускорение объекта зависит от направления ускорения, а направление зависит от следующих двух факторов:

• ускорение или замедление объекта 
• + ve или -ve направление движения [здесь мы рассматриваем слева направо как + ve направление, а справа налево — как направление. Точно так же вверх — + ve, а вниз — — ve]

Представьте, что автомобиль движется по дороге, чтобы определить направление ускорения автомобиля, два вышеуказанных фактора составляют четыре комбинации для описания движения автомобиля.Автомобиль движется справа налево, ускорение отрицательное
Изображение предоставлено: https://pixabay.com/illustrations/christmas-tree-truck-santa-4636494/

• Автомобиль движется в положительном направлении и набирает скорость. 

В этом случае скорость и ускорение автомобиля идут в одном направлении. Сила, действующая на автомобиль, имеет положительное направление, а ускорение автомобиля положительное.

• Автомобиль движется в положительном направлении и замедляет ход. 

В этом случае скорость автомобиля находится в положительном направлении, а ускорение — в отрицательном направлении. Сила трения отвечает за замедление автомобиля, и она противоположна направлению скорости. В этом случае ускорение отрицательное.

• Автомобиль движется в обратном направлении и набирает скорость.

Автомобиль движется справа налево, т. Е. В направлении –ve. Автомобиль ускоряется в отрицательном направлении, поэтому ускорение также отрицательное. Ускорение в этом случае отрицательное.

• Автомобиль движется в обратном направлении и сбавляет скорость.

Здесь скорость автомобиля в направлении –ve. Автомобиль замедляется, а это означает, что на него действует сила в противоположном направлении. Следовательно, автомобиль ускоряется в положительном направлении.

Из приведенного выше обсуждения мы заключаем, что ускорение отрицательно в двух случаях.

когда объект движется в положительном направлении и замедляется 

когда объект движется в обратном направлении и набирает скорость

Может ли ускорение быть отрицательным при нулевой скорости?

Мы знаем, что ускорение — это скорость изменения скорости во времени. Это изменение может иметь форму ускорения или замедления.

Если ускорение отрицательное, это означает, что объект ускоряется в отрицательном направлении или замедляется в положительном направлении. когда объект замедляет движение, сила противодействует его движению, а направление ускорения совпадает с направлением силы, т. е. в обратном направлении. Через некоторое время тело приходит в состояние покоя, и его скорость становится равной нулю, но в этот момент оно все еще имеет отрицательное ускорение.

Чтобы лучше понять эту концепцию, вспомните движение маятника или движение мяча в вертикальном направлении, на определенной высоте мяч останавливается, и его скорость становится равной нулю. Но он по-прежнему имеет ускорение в направлении вниз, аналогично маятнику, в крайнем его положении. скорость становится равной нулю но он все еще имеет ускорение в направлении восстанавливающей силы. Следовательно, это доказывает, что ускорение может быть отрицательным, когда скорость становится равной нулю.

Некоторые примеры с отрицательным ускорением

Применение перерывов в движущемся автомобиле

Представьте, что автомобиль движется в + ve x-направлении с непрерывно изменяющимися скоростью и ускорением. После применения разрывов сила трения увеличивается против направления скорости, и скорость начинает уменьшаться. Когда скорость начинает уменьшаться, направление ускорения меняется с + ve x-direction на -ve x-direction; это происходит потому, что ускорение всегда в направлении силы. Следовательно, у движущегося автомобиля есть отрицательное ускорение, когда мы применяем тормоза для остановки движения.

Движение растянутой пружины 

растянутая пружина имеет восстанавливающую силу, противоположную направлению движения. Когда растянутая пружина отпускается, она выполняет SHM. Возвращающие силы всегда противодействуют движению пружины и уменьшают скорость.

 Пружина имеет как положительный, так и отрицательный тип ускорения. Когда пружина растягивается из своего среднего положения, она движется в + ve x-направлении, но замедляется из-за восстанавливающей силы. В этом случае его ускорение противоположно направлению движения, т.е. в направлении –ve x. Точно так же, когда пружина сжимается, ее ускорение составляет + ve x-направление, а движение — -ve x-направление от среднего положения.  Изображение предоставлено: AlvaroLopez12, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, через Wikimedia Commons

Бросок мяча вверх

Когда мы бросаем мяч вверх, он движется против силы тяжести. Достигнув некоторой высоты, он начинает падать на землю под действием силы тяжести. В первой половине движения гравитационная сила непрерывно противодействует движению шара, и его ускорение направлено вниз. Более того, согласно приведенному выше анализу, когда объект движется в положительном направлении (здесь — вверх) и замедляется, его ускорение отрицательное.

 Во второй половине движения мяч скорость становится равной нулю после достижения определенной высоты, и он начинает падать на землю под действием силы тяжести. Здесь и скорость, и ускорение имеют одно и то же направление, потому что мяч движется с ускорением вниз. Опять же из приведенного выше анализа, когда объект движется в обратном направлении и набирает скорость, его ускорение отрицательное. Таким образом, в обеих половинах движения ускорение мяча отрицательное.Изображение предоставлено: https://pixabay.com/photos/juggle-balls-sinai-in-the-air-4919335/

Круговое движение мяча, прикрепленного к веревке.

Когда шарик, привязанный к безмассовой нити, совершает круговое движение разные-разные силы воздействовать на это. Невесомая и нерастяжимая струна обеспечивает необходимую центростремительную силу. Все мы знаем, что центростремительная сила всегда действует по направлению к центру системы. Направление ускорения совпадает с центростремительная сила, т. е. всегда по направлению к центру системы по кругу. Направление линейной скорости постоянно меняется при круговом движении. Радиальное ускорение кругового движения всегда отрицательно.

 Радиальная составляющая ускорения при круговом движении равна,

         a_r = -rω²

a_r — радиальное ускорение

r – радиус окружности

ω – угловая скорость

             

Круговое движение мяча
Изображение предоставлено: AlvaroLopez12, CC BY-SA 4.0 https://creativecommons.org/licenses/by-sa/4.0, через Wikimedia Commons

Движение маятника

Движение маятника — это колебательное движение относительно его среднего положения, и чтобы понять природу ускорения маятника, давайте разберем его движение на четыре случая.

Дело 1— Маятник движется в + ve x-направлении от среднего положения к крайнему положению и замедляется

В этом случае восстанавливающая сила, создаваемая компонентом силы тяжести, пытается подтолкнуть маятник к среднему положению. Следовательно, скорость маятника уменьшается по мере его движения от среднего положения к крайнему. В этом случае ускорение маятника отрицательное, и его направление противоположно движению маятника.

Дело 2— Маятник перемещается из крайнего положения в среднее положение (т.е. справа налево) в направлении + x и ускоряется

В этом случае маятник ускоряется к среднему положению. Таким образом, движение и ускорение происходят в одном направлении, но ускорение идет справа налево, то есть в отрицательном направлении. Следовательно, ускорение маятника отрицательное.

Дело 3: Маятник перемещается из среднего положения в крайнее положение в направлении оси x и замедляется.

Этот случай почти аналогичен первому, только направление — по оси абсцисс. В этом случае ускорение противоположно движению и в положительном направлении. Следовательно, в этом случае ускорение равно + ve.  

Случай 4 — Маятник перемещается из крайнего положения в среднее (т. е. слева направо) и ускоряется.

Здесь маятник ускоряется за счет возвращающей силы по направлению к среднему положению. Обе скорости, как и ускорение, находятся в одном направлении. Направление ускорения находится в положительной оси x, поэтому ускорение считается положительным.движение маятника. Изображение предоставлено: Ruryk, CC BY-SA 3.0. https://creativecommons.org/licenses/by-sa/3.0, через Wikimedia Commons

Движение автомобиля по извилистой дороге

Автомобиль совершает круговое движение при движении по извилистой дороге. Необходимая центростремительная сила, необходимая для движения по криволинейной траектории, обеспечивается трением между шиной и дорогой. Ускорение направлено к центру системы, и оно отрицательное, потому что его направление справа налево, т.е. в направлении –ve x.

Движение автомобилей по кривой дороге
Изображение предоставлено: https://pixabay.com/photos/motorsport-race-car-car-racing-4525064/

Отрицательный импульс: что это значит?

Импульс — это понятие из физики, которое описывает величину движения объекта. Это векторная величина, то есть она имеет как величину, так и направление. Это означает, что он может быть как положительным, так и отрицательным, в зависимости от направления движения объекта.

Положительный импульс указывает на то, что объект движется вперед или вверх, а отрицательный импульс указывает на то, что объект движется назад или вниз. Величина импульса (скорость и масса объекта) будет определять, какая сила потребуется, чтобы изменить его направление или полностью остановить его.

Когда дело доходит до импульса, вам следует знать два важных уравнения: второй закон движения Ньютона и уравнение импульса. Второй закон Ньютона гласит, что сила равна массе, умноженной на ускорение, а уравнение импульса утверждает, что импульс равен массе, умноженной на скорость.

Уравнение количества движения показывает нам, как мы можем рассчитать количество движения объекта, умножив его массу на скорость. Поскольку скорость может быть как положительной, так и отрицательной, это означает, что импульс также может быть положительным или отрицательным — в зависимости от того, движется ли объект вперед или назад.

Итак, отвечая на наш первоначальный вопрос: да, импульс может быть отрицательным. Нам просто нужно посмотреть как на массу, так и на скорость объекта, чтобы определить, является ли его импульс положительным (движение вперед) или отрицательным (движение назад). Понимание этого понятия важно для понимания многих других понятий в физике, таких как импульс и сохранение импульса.

Может ли Импульс иметь негативное влияние?

Да, импульс может иметь отрицательное значение. Импульс является векторной величиной, то есть имеет как величину, так и направление. В физике знак величины (положительный или отрицательный) используется для указания ее направления. Следовательно, если направление импульса объекта противоположно положительному направлению, то его импульс будет считаться отрицательным.

Отрицательный импульс: что это значит?

Наличие отрицательного импульса означает, что объект движется в направлении, противоположном тому, которое было выбрано в качестве положительного направления. Обычно на это указывает отрицательный знак перед числовым значением импульса. Величина отрицательного импульса будет равна произведению массы объекта на его скорость, которая также будет отрицательной. Это означает, что хотя объект продолжает двигаться в том направлении, которое было выбрано в качестве отрицательного, он теряет скорость от одного момента к другому.

Идентификация положительных и отрицательных импульсов

Направление импульса можно определить, посмотрев на результирующую силу, действующую на объект. Если результирующая сила имеет положительное направление, то говорят, что импульс положительный. И наоборот, если результирующая сила имеет отрицательное направление, то импульс называется отрицательным. Импульс также можно рассчитать, используя изменение импульса объекта с течением времени. Если импульс объекта увеличивается в течение заданного промежутка времени, то это указывает на то, что к нему был приложен положительный импульс. Если импульс объекта уменьшается в течение заданного промежутка времени, то это указывает на то, что к нему был приложен отрицательный импульс.

Влияние отрицательного импульса на скорость

Да, отрицательный импульс означает замедление. Импульс является векторной величиной, то есть имеет величину (размер) и направление. Когда объект имеет отрицательный импульс, его скорость уменьшается, и он движется в направлении, противоположном его первоначальному движению. Это означает, что объект замедляется и теряет энергию.

Всегда ли общий импульс равен нулю?

Нет, полный импульс системы не всегда равен 0. Импульс является векторной величиной, то есть имеет как величину, так и направление. Следовательно, когда два объекта взаимодействуют, их импульсы могут компенсировать друг друга, если они имеют равные величины, но противоположные направления. Это означает, что общий импульс системы может быть равен 0, даже если отдельные импульсы не равны нулю. Например, два объекта, движущиеся навстречу друг другу в противоположных направлениях, будут иметь общий импульс, равный 0, даже если каждый из них имеет ненулевой импульс.

Положительный и отрицательный импульс

Положительный импульс — это результат действий, приносящих положительные результаты. Это может включать увеличение продаж, улучшение обслуживания клиентов или запуск новых продуктов или услуг. Эти действия помогают укрепить доверие и уверенность в компании и могут привести к расширению бизнеса и увеличению прибыли. В результате этого положительного импульса компании могут испытать рост общей выручки и доли рынка.

Отрицательный импульс, с другой стороны, является результатом действий, которые приводят к отрицательным результатам. Это может включать снижение уровня обслуживания клиентов, сокращение предложений продуктов или услуг или несвоевременное реагирование на жалобы клиентов. Подобные действия могут привести к снижению удовлетворенности клиентов и снижению продаж, что в конечном итоге может негативно сказаться на прибыли компании. Негативную динамику бывает трудно обратить вспять, поэтому компаниям важно в первую очередь предпринять активные шаги, чтобы избежать ее.

Может ли возникнуть отрицательный момент силы?

Да, момент силы может быть отрицательным. Момент силы — это произведение величины силы и ее перпендикулярного расстояния от точки отсчета. Если направление вращения, вызванное этой силой, против часовой стрелки вокруг этой контрольной точки, то момент считается отрицательным. Например, если к объекту приложена сила против часовой стрелки относительно его центра масс, то момент будет отрицательным.

Может ли объект иметь как отрицательный импульс, так и положительную кинетическую энергию?

Нет, объект не может иметь отрицательный импульс и положительную кинетическую энергию. Импульс — это векторная величина, которая является произведением массы объекта на его скорость. Поскольку масса и скорость всегда положительны, результирующий импульс также должен быть положительным. Между тем кинетическая энергия — это энергия, выделяющаяся в результате движения объекта, которая всегда является положительной величиной. Следовательно, объект не может одновременно иметь отрицательный импульс и положительную кинетическую энергию.

Почему изменение импульса всегда положительно?

Изменение импульса всегда положительно, поскольку импульс является векторной величиной, т. е. имеет как величину, так и направление. Следовательно, при расчете изменения импульса мы измеряем разницу в величине и направлении между двумя разными точками. Поскольку величина вектора никогда не может быть отрицательной, изменение импульса всегда будет положительным значением. Кроме того, поскольку знак импульса указывает его направление (положительный для движения вправо, отрицательный для движения влево), любое изменение направления приведет к увеличению или уменьшению величины и, следовательно, к положительному изменению импульса.

Могут ли отрицательные импульсы существовать в физике?

Да, в физике импульс может быть отрицательным. Импульс – это интеграл силы по времени. Это мера изменения импульса объекта во времени.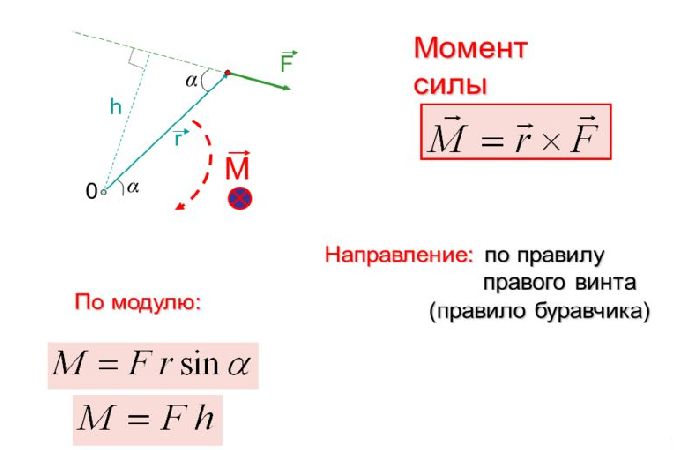 Когда сила действует на объект в течение короткого промежутка времени, это приводит к изменению количества движения, которое равно произведению силы на время, в течение которого она действовала. Если сила действует в направлении, противоположном направлению движения, то импульс будет отрицательным и произойдет уменьшение количества движения. Отрицательные импульсы обычно наблюдаются, когда объекты сталкиваются или взаимодействуют друг с другом, а также когда они взаимодействуют с поверхностями или средами, которые воздействуют на них силами, такими как силы трения и сопротивления.

Импульс и импульс — одно и то же?

Да, импульс и импульс одинаковы. Импульс — это векторная величина, которая определяется как произведение массы объекта на его скорость. Это мера сопротивления объекта остановке, обозначаемая символом «р». Импульс — это сила, приложенная к объекту в течение конечного периода времени, которая может быть использована для изменения его импульса. Таким образом, импульс и импульс представляют одно и то же физическое явление, но могут использоваться для описания разных его аспектов.

Важность импульса

Импульс — важное понятие классической механики, утверждающее, что общий импульс системы остается постоянным, если на него не действует внешняя сила. Это векторная величина, то есть она имеет как величину, так и направление. Импульс прямо пропорционален массе и скорости объекта: чем массивнее объект или чем быстрее он движется, тем больше его импульс. Вдобавок к этому импульс также меняется в зависимости от направления движения; если два тела имеют одинаковую массу и скорость, но движутся в противоположных направлениях, они будут иметь противоположные импульсы. Наконец, импульс сохраняется; если на объект не действуют никакие внешние силы, его импульс не может увеличиваться или уменьшаться с течением времени.

Могут ли массы иметь отрицательные значения?

Нет, масса не может быть отрицательной. Масса — это физическое свойство, описывающее количество материи, содержащейся в объекте, и может быть только положительным. Это означает, что количество материи в объекте не может быть меньше нуля — оно всегда должно быть больше нуля. Отсутствие отрицательной массы подтверждено многочисленными экспериментами и является фундаментальным свойством нашей Вселенной.

Отрицательная масса появляется в моделях теоретической физики и может существовать в других вселенных или альтернативных измерениях, но в нашей собственной вселенной она не наблюдалась. Теоретически отрицательная масса ведет себя иначе, чем обычная положительная масса; например, при толчке он будет двигаться от источника толчка, а не к нему, как можно было бы ожидать при обычной положительной массе.

В отличие от своего противоположного аналога, электрический заряд может принимать как положительные, так и отрицательные значения в зависимости от задействованной частицы. Положительно заряженные частицы имеют больше протонов в своем ядре, чем электронов, вращающихся вокруг них; отрицательно заряженные частицы имеют больше электронов, чем протонов.

Может ли существовать отрицательная скорость?

Нет, отрицательная скорость не имеет значения.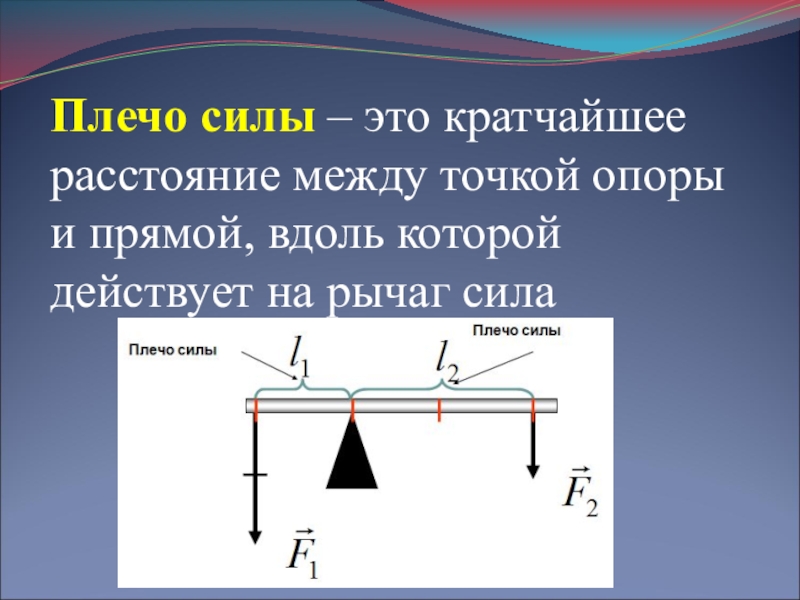 Скорость — это мера того, насколько быстро движется объект, и она не может быть отрицательной. Однако скорость может быть отрицательной — она измеряет скорость изменения положения объекта и учитывает направление. Если объект движется влево, то его скорость будет определена как отрицательная.

Влияние падения на скорость

Да, скорость отрицательна, когда объект падает. Это связано с тем, что ускорение силы тяжести представляет собой направленную вниз силу, которая действует на объекты и заставляет их ускоряться в направлении действия силы, которое в данном случае направлено вниз. Следовательно, поскольку ускорение имеет отрицательное направление, скорость падающего тела также будет отрицательной.

Заключение

В заключение, импульс может быть отрицательным, когда объект движется назад или вниз. Это связано с тем, что импульс является векторной величиной, а направление указывается знаком, положительным или отрицательным. Положительные числа означают, что объект движется вперед или вверх, а отрицательные числа означают, что объект движется назад или вниз. Импульс имеет как величину, так и направление, и это можно использовать для расчета импульса объекта в зависимости от его массы и скорости.

Формула определения Понятие единицы измерения » ExamLimiT

Если силы действуют на тело конечного размера, они могут вызвать эффект вращения. Этот эффект измеряется моментом силы. Это отличается от тенденции тела двигаться или перемещаться в направлении действия силы. Его единица Н-м.

Определение: Сила, приложенная к объекту, и перпендикулярное расстояние силы от его оси вращения – сочетание этих двух факторов вызывает вращательную тенденцию в объекте, называется моментом силы.

Предположим, что рукоятка (AB) типичного насоса установлена ​​над трубчатым колодцем [Рис. 1]. О — фиксированная точка опоры. Ручка обычно удерживается вверх и вниз за часть OA ручки. То есть ручка может вращаться (на поверхности страницы) вокруг неподвижной точки О. По-видимому, в этом случае ось вращения лежит в точке О и перпендикулярна странице книги.

Когда часть OA перемещается вниз, часть OB поднимается вверх, и вода поднимается через поршень, прикрепленный к точке B.

Момент силы Рисунок-1

Из нашего общего опыта мы знаем, что приложенная сила F не может повернуть ручку, когда она приложена к точке O. Сила F, приложенная немного в стороне от точки O, может вращать ручку, но трудно набрать воду. . Практически мы это чувствуем.

Так что не всегда можно сказать, что объект будет вращаться только при приложении к нему силы. Линия действия силы (ОА) фактически отвечает за вращение объекта только в том случае, если он находится немного в стороне от оси вращения (О). Приложенная сила не может вращать объект, когда линия действия силы проходит через центр вращения или ось вращения (О). Чем больше перпендикулярное расстояние действия силы от центра вращения (точка О), тем больше склонность тела к вращению, т. е. тем легче повернуть предмет.

Вертикальное расстояние линии действия приложенной силы от центра вращения называется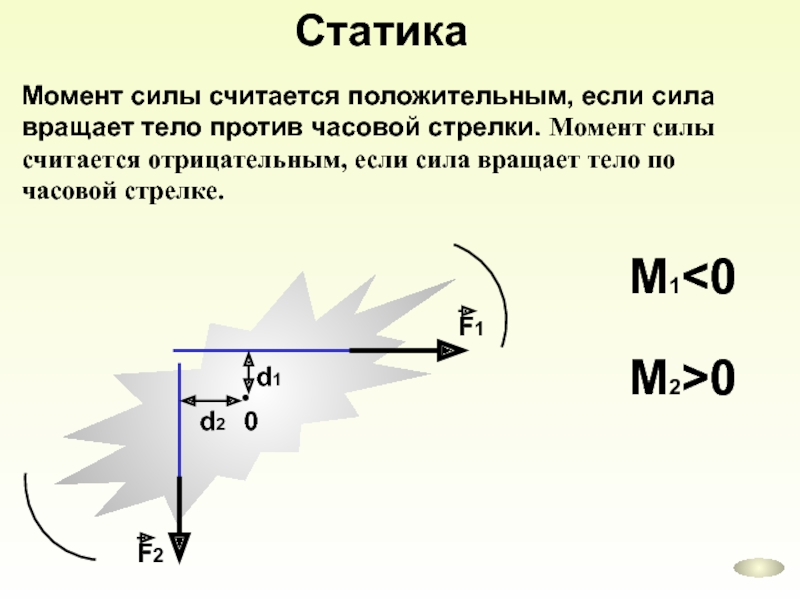

плечом этой силы . На данном рисунке длины плеч при различных действиях силы F равны 0, OL и OM. Получается, что тенденция вращения объекта зависит от двух факторов:

• (i) величины приложенной силы (F) и
• (ii) плечо приложенной силы (d).

Сочетание этих двух элементов приводит к вращению.

Произведение величины приложенной силы на перпендикулярное расстояние действия силы от точки вращения дает нам величину момента силы.

Это момент силы G = сила F × перпендикулярное расстояние (d).
или G = Fd

На данном рисунке моменты силы для различных действий силы F равны 0, F×OL и F×OM. Так как ОМ > ОЛ > О, то можно сказать, что при прохождении длины действия F через точку А величина момента силы больше относительно точки О.

Это означает, что ручка легче всего вращается, когда сила F приложена к точке A (самая дальняя точка). С другой стороны, когда сила F приложена к точке (O, ближайшая точка), момент силы равен нулю , и эта сила F не может вызвать никакого вращения .

Помните, наличие оси вращения неизбежно в случае вращения. Таким образом, сказать, что момент силы относится к точке, означает, что она подчинена оси вращения; Эта ось вращения перпендикулярна плоскости, на которой расположена точка и действует сила.

Пример : В случае распашных дверей дверь открывается так же легко, как ее отодвигают от петли, но дверь открывается не так легко, когда ее толкают где-то рядом с петлей — у всех нас есть этот опыт.

Момент силы также является осевым вектором , таким как угловое смещение, угловая скорость и угловое ускорение.

Единицы и размеры момента силы:

По определению, момент силы = величина силы × расстояние по перпендикуляру от оси вращения до точки приложения силы.
Итак, единица момента силы = единица силы × единица расстояния.

90 145 FPS единица момента силы

СГС единица момента силы	дина-см
СИ единица момента силы	Ньютон-метр
фунт-фут

Размер момента силы = размер силы × размер расстояния

Размерность момента силы = [MLT ⁻² ] × [L] = [ML ² T ⁻² ]

Мы знаем, что когда несколько сил действуют в одной плоскости, они называются копланарными силами . При приложении более чем одной силы вращение объекта ограничивается плоскостью этих сил. Предположим, что объект АВ относительно точки О может вращаться в некоторой плоскости (например, поверхности страницы) (рис. 2).

рисунок 2

При внимательном рассмотрении рисунка мы можем понять, что

1. Момент силы F ₁ = ноль.
2. Момент силы F ₂ направлен против часовой стрелки, потому что он может создать вращение против часовой стрелки. Поэтому для вращения против часовой стрелки момент ПОЛОЖИТЕЛЬНЫЙ.
3. Момент силы F ₃ направлен против часовой стрелки и создает вращение по часовой стрелке. Значит, при вращении по часовой стрелке момент силы ОТРИЦАТЕЛЬНЫЙ.

Таким образом, установлено, что момент силы может быть выражен простой алгебраической суммой, а величина этой суммы может быть положительной или отрицательной.

Алгебраическая сумма моментов силы:

Рассмотрим три копланарные силы F ₁ , F _2, и F ₃ , действующие на точки O, B и A объекта AB соответственно (рис. 2). ). Полная алгебраическая сумма или результирующий момент силы (G) равен –

G = F ₁ × 0 + F ₂ × OM + F ₃ × ON

1. Теперь, если G = 0, то вращения не происходит.
2. Если G = положительный, то вращение против часовой стрелки.
3. И, если G = Отрицательное, то вращение по часовой стрелке.

Момент силы: векторная формула

Продукты перекрестия вектора R и вектор силы F будут равны моменту вектор G вокруг точки O.

Момент силы является вектором. . Из приведенного выше рисунка можно представить момент направления. Направление следует правилу векторного векторного произведения или правилу правой руки . Векторная форма момента приведена ниже.

$$\overrightarrow{G} = \overrightarrow{r} \times \overrightarrow{F}$$

Упражнение 1: Найти момент силы F = 6i − 3j, приложенный в (4, 5) относительно точки (1, 2).

Здесь в этой задаче на точку B (4,5) действует сила F = 6i − 3j. Нам нужно найти момент этой силы относительно точки А (1,2).

Формула момента силы ( G ) определяется как –

$$\overrightarrow{G} = \overrightarrow{r} \times \overrightarrow{F}$$

Здесь,

$$\overrightarrow{r_{1}}= \шляпа{i} + 2\шляпа{j}$$

И,

$$\overrightarrow{r_{2}}= 4\ hat{i} + 5\hat{j}$$

Из треугольного закона сложения векторов мы можем легко найти вектор r .

$$\overrightarrow{r_{1}} + \overrightarrow{r} = \overrightarrow{r_{2}}$$

$$\overrightarrow{r}=\overrightarrow{r_{2}} – \overrightarrow {r_{1}}$$

$$\overrightarrow{r}= (4\шляпа{i} + 5\шляпа{j})-(\шляпа{i} + 2\шляпа{j}) \\ \\ \overrightarrow{r} =\: 3\шляпа{i} + 3\шляпа{j} \\ \\ \поэтому \overrightarrow{G} = \overrightarrow{r}\times \overrightarrow{F} \\ \\ = (3\шляпа{i} + 3\шляпа{j}) \times (6\шляпа{i} + 3\шляпа{j} ) \\ \\ = — 9\ шляпа {к} — 18 \ шляпа {к} \\ \\ \overrightarrow{G}= – 27\hat{k}$$

Следовательно, модуль момента силы равен − 27.