Когда момент силы считается отрицательным
Когда момент силы считают положительным (отрицательным)?
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
§ 77. Момент силы.
Итак, для равновесия тела, закрепленного на оси, существен не сам модуль силы, а произведение модуля силы на расстояние от оси до линии, вдоль которой действует сила (рис. 115; предполагается, что сила лежит в плоскости, перпендикулярной к оси вращения). Это произведение называется моментом силы относительно оси или просто моментом силы. Расстояние называется плечом силы. Обозначив момент силы буквой , получим
Расстояние называется плечом силы. Обозначив момент силы буквой , получим
Условимся считать момент силы положительным, если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным в противном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, силам и на рис. 116 нужно приписать положительный момент, а силе — отрицательный.
Рис. 115. Момент силы равен произведению ее модуля на плечо
Рис. 116. Моменты сил и положительны, момент силы отрицателен
Рис. 117. Момент силы равен произведению модуля составляющей силы на модуль радиус-вектора
Моменту силы можно дать еще и другое определение. Проведем из точки , лежащей на оси в той же плоскости, что и сила, в точку приложения силы направленный отрезок (рис. 117). Этот отрезок называется радиус-вектором точки приложения силы. Модуль вектора равен расстоянию от оси до точки приложения силы. Теперь построим составляющую силы , перпендикулярную к радиус-вектору . Обозначим эту составляющую через . Из рисунка видно, что , a . Перемножив оба выражения, получим, что .
Теперь построим составляющую силы , перпендикулярную к радиус-вектору . Обозначим эту составляющую через . Из рисунка видно, что , a . Перемножив оба выражения, получим, что .
Таким образом, момент силы можно представить в виде
где — модуль составляющей силы , перпендикулярной к радиус-вектору точки приложения силы, — модуль радиус-вектора. Отметим, что произведение численно равно площади параллелограмма, построенного на векторах и (рис. 117). На рис. 118 показаны силы, моменты которых относительно оси одинаковы. Из рис. 119 видно, что перенесение точки приложения силы вдоль ее направления не меняет ее момента. Если направление силы проходит через ось вращения, то плечо силы равно нулю; следовательно, равен нулю и момент силы. Мы видели, что в этом случае сила не вызывает вращения тела: сила, момент которой относительно данной оси равен нулю, не вызывает вращения вокруг этой оси.
Рис. 118. Силы и имеют одинаковые моменты относительно оси
Рис.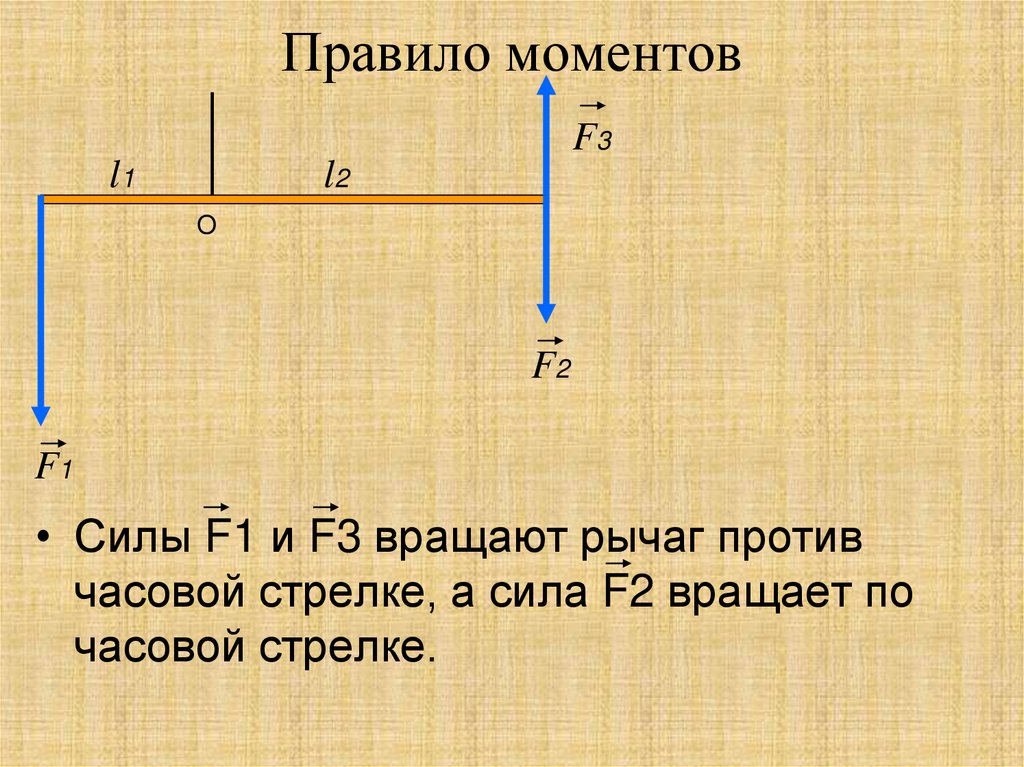 119. Равные силы с одинаковым плечом имеют равные моменты относительно оси
119. Равные силы с одинаковым плечом имеют равные моменты относительно оси
Пользуясь понятием момента силы, мы можем по-новому сформулировать условия равновесия тела, закрепленного на оси и находящегося под действием двух сил. В условии равновесия, выражаемом формулой (76.1), и есть не что иное, как плечи соответствующих сил. Следовательно, это условие состоит в равенстве абсолютных значений моментов обеих сил. Кроме того, чтобы не возникало вращение, направления моментов должны быть противоположными, т. е. моменты должны отличаться знаком. Таким образом, для равновесия тела, закрепленного на оси, алгебраическая сумма моментов действующих на него сил должна быть равна нулю.
Так как момент силы определяется произведением модуля силы на плечо, то единицу момента силы мы получим, взяв равную единице силу, плечо которой также равно единице. Следовательно, в СИ единицей момента силы является момент силы, равной одному ньютону и действующей на плече один метр. Она называется ньютон-метром (Н·м).
Если на тело, закрепленное на оси, действует много сил, то, как показывает опыт, условие равновесия остается тем же, что и для случая двух сил: для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю. Результирующим моментом нескольких моментов, действующих на тело (составляющих моментов), называют алгебраическую сумму составляющих моментов. Под действием результирующего момента тело будет вращаться вокруг оси так же, как оно вращалось бы при одновременном действии всех составляющих моментов. В частности, если результирующий момент равен нулю, то тело, закрепленное на оси, либо покоится, либо вращается равномерно.
Момент силы
Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают момент силы относительно центра (точки — полюса) и относительно оси.
Если имеется материальная точка О, к которой приложена сила , то момент силы относительно этой точки равен векторному произведению радиус-вектора , соединяющего точку О и точку приложения силы, на вектор силы :
Момент силы — аксиальный вектор[3]. Он направлен вдоль оси вращения.
Он направлен вдоль оси вращения.
Направление вектора момента силы определяется правилом буравчика, а величина его равна M (рис.4).
Модуль момента силы:
M =F• l =F •r •sin α,
где: M – момент силы (Ньютон •метр),
F – приложенная сила,
r – расстояние от центра вращения до места приложения силы,
l = r.sin α – плечо силы, т.е. длина перпендикуляра, опущенного из центра вращения на линию действия силы,
α — угол, между вектором силы F и вектором положения r.
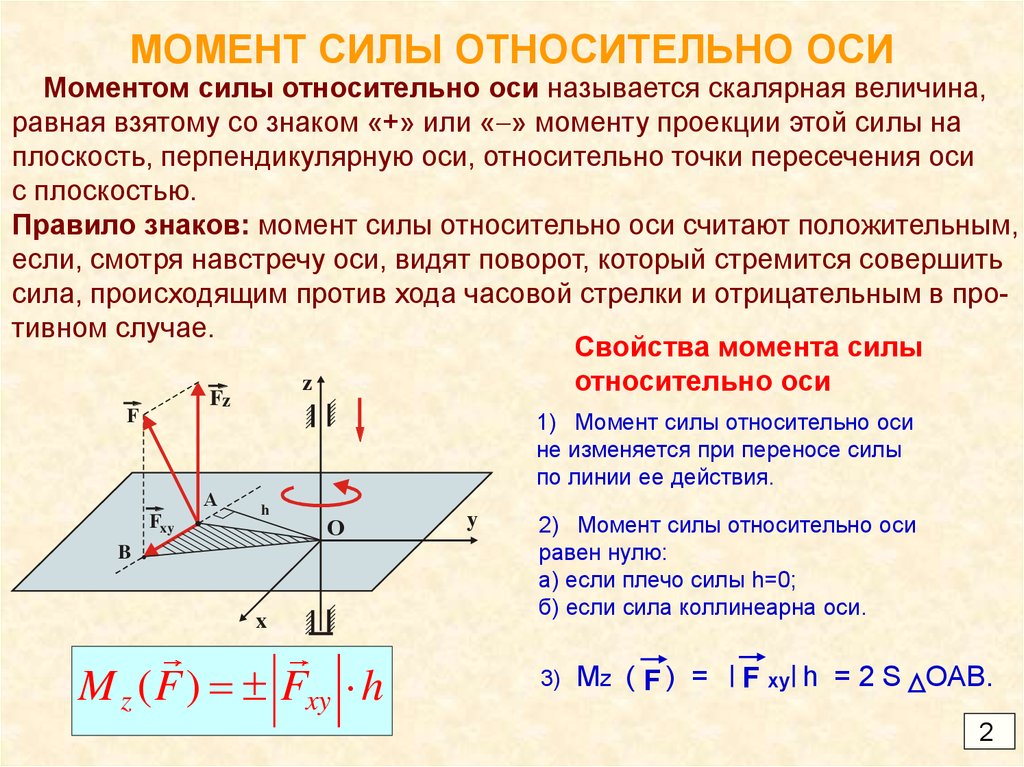
Момент силы относительно оси величина алгебраическая, равная проекции на эту ось вектора Ммомента силы относительно любой точки О оси.
Пользуясь понятием момента силы можно по-новому сформулировать условия равновесия тела, закрепленного на оси. Это условие называется правилом моментов:
если на тело, закрепленное на оси, действует много сил, то для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю:
Считают момент силы положительным, если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис.5, силам F1 и F2 следует приписать положительный момент, а силе F3— отрицательный.
Например, согласно рис.5, силам F1 и F2 следует приписать положительный момент, а силе F3— отрицательный.
Момент силы и правило моментов
теория по физике 🧲 статика
ОпределениеСтатика — раздел механики, изучающий условия равновесия тел.
Виды равновесия
Устойчивое равновесие | |
| Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (Ep min). | |
Неустойчивое равновесие | |
| Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (Ep max). | |
Безразличное равновесие | |
При выведении тела из положения безразличного равновесия дополнительных сил не возникает. | |
Момент силы
ОпределениеМомент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:
M = Fd
M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).
Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.
Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?
Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:
Следовательно:
M = Fd = mgd = 2∙10∙0,5 = 10 (Н∙м)
Момент силы может быть положительным и отрицательным.
Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:
M1 = F1
Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:
M2 = F2d2
Правило моментов
Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:
∑Mi=0
Иначе правило моментов можно сформулировать так:
Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.
∑Mпо час. стр.=∑Mпр. час. стр.
Условия равновесия тел
| Тело не участвует в поступательном движении: | ∑→Fi=0; →vo=0 |
| Тело не участвует во вращательном движении: | ∑Mi=0; ω0=0 |
| Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении) | ∑→Fi=0; →vo=0 и ∑→Fi=0; →vo=0 |
Простые механизмы
ОпределениеПростые механизмы — приспособления, служащие для преобразования силы.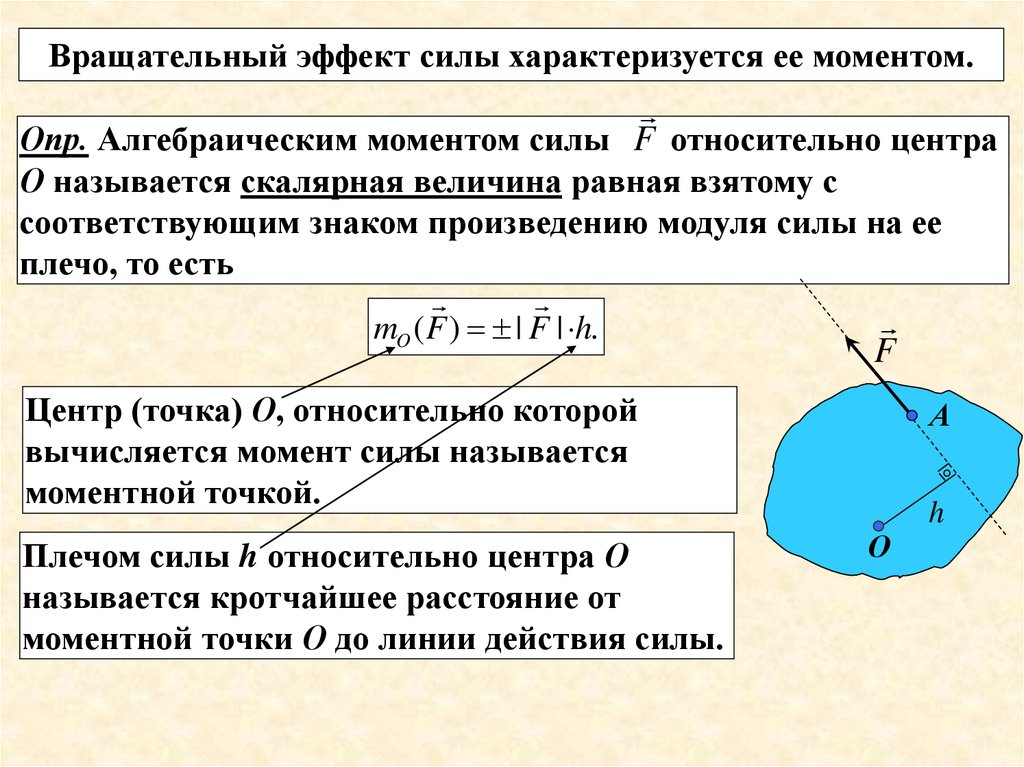 К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.
К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.
Наклонная плоскость | |
Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: mgsin.θ<mg | |
Рычаг | |
Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F1F2..=d2d1.. | |
Неподвижный блок | |
Изменяет направление действия силы. Модули и плечи сил при этом равны: F1 = F2 M1 = M2 | |
Подвижный блок | |
| Дает выигрыш в силе в 2 раза: d1 = R d2 = 2R F1 = 2F2 | |
Клин | |
Делит силу на две равные части, направление которых зависит от формы клина: →F=→F1+→F2 | |
При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.
Поэтому выигрыша в работе простые механизмы не дают.
Алгоритм решения
1.Записать исходные данные.
2.Записать правило моментов и выполнить решение в общем виде.
3.Подставить известные данные и вычислить искомую величину.
Решение
Известна лишь масса батона: m1 = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:
d1 = 0,3
d2 = 0,4
Запишем правило моментов:
F1 d1 = F2 d2
Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:
Поэтому:
m1gd1 = m2gd2
m1d1 = m2d2
Отсюда масса рыбы равна:
m2=m1d1d2..=0,8·0,30,4..=0,6 (кг)
.
Ответ: 0,6pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18706Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения Fтр относительно оси, проходящей через точку О3 перпендикулярно плоскости чертежа, равно…
Ответ:
а) 0
б) О2О3
в) О2В
г) О3В
Алгоритм решения
- Сформулировать определение плеча силы.
Решение
Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О3В.
Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О3В.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Алиса Никитина | Просмотров: 7.2k | Оценить:
Физика Момент силы. Второе условие равновесия твёрдого тела
Материалы к уроку
Конспект урока
Одним из условий равновесия твердого тела является геометрическая сумма внешних сил, действующих на тело, которая должна быть равна нулю. Это условие является необходимым, но не является достаточным. Чтобы в этом убедиться проведем опыт. Приложим к дощечке, лежащей на плоской поверхности, в различных точках две силы равные по модулю, но направленные в противоположные стороны. Сумма этих двух сил равна нулю. Но дощечка не останется в равновесии, она будет поворачиваться. Первое условие равновесия твердого тела выполняется, но тело не находится в равновесии.
Сумма этих двух сил равна нулю. Но дощечка не останется в равновесии, она будет поворачиваться. Первое условие равновесия твердого тела выполняется, но тело не находится в равновесии.
Другой пример, на руль автомобиля во время поворота действуют две силы, приложенные в двух разных точках. Эти силы одинаковые по модулю и противоположно направленные. Сумма этих двух сил так же равна нулю, а руль не находится в состоянии покоя.
Для того чтобы выяснить, какое же еще условие должно выполняться, чтобы твердое тело находилось в равновесии, вспомним теорему об изменении кинетической энергии. Изменение кинетической энергии тела за некоторый промежуток времени равно работе, совершенной за то же время силой, действующей на тело.
Рассмотрим пример, при каком условии будет оставаться в равновесии стержень, шарнирно закрепленный на горизонтальной оси в точке 0. Эта конструкция представляет собой обыкновенный рычаг. Пусть к рычагу приложены две перпендикулярные стержню силы F1 и F2. Предположим, что это силы натяжения веревок, к концам которых прикреплены грузы. Кроме этих двух сил, на рычаг ещё действует направленная вертикально вверх сила реакции опоры со стороны оси рычага F3. При равновесии рычага сумма всех трех сил равна нулю.
Найдем работу, которую совершают внешние силы при повороте рычага на очень малый угол α. Точка приложения силы F1 пройдет путь равный BB1. А точка приложения силы F2 пройдёт путь равный CC1. Так как угол α невелик, можно считать линии BB1 и CC1 отрезками прямой. Работа силы F1 положительна, потому что точка B перемещается в том же направлении, что и сила, а работа силы F2 отрицательна, так как точка приложения силы C движется в сторону противоположную направлению силы.
 Сила F3 работы не совершает, потому что точка 0 не перемещается.
Сила F3 работы не совершает, потому что точка 0 не перемещается.Пройденные пути s1 и s2 можно выразить через угол поворота рычага α, измеренный в радианах. Тогда перемещение точки приложения силы F1 равно произведению угла α на длину отрезка BO. А перемещение точки приложения силы F2 равно произведению угла α на длину отрезка СO.
Подставим эти равенства в формулы работы сил F1 и F2. Получим, что работа силы F1 равна произведению модуля силы F1 на угол α и на длину отрезка ВО. Работа силы F2 равна произведению модуля силы F2 на угол α и на длину отрезка СО.
Радиусы ВО и СО дуг окружностей, описываемых точками приложения сил F1 и F2, являются перпендикулярами, опущенными из оси вращения на линии действия этих сил.
Кратчайшее расстояние от оси вращения до линии действия силы называют плечом силы.
Плечо силы обозначим буквой d. Плечо силы F1 равно d1. Плечо силы F2 равно d2.
Тогда выражения для работы сил F1 и F2 примут следующий вид.
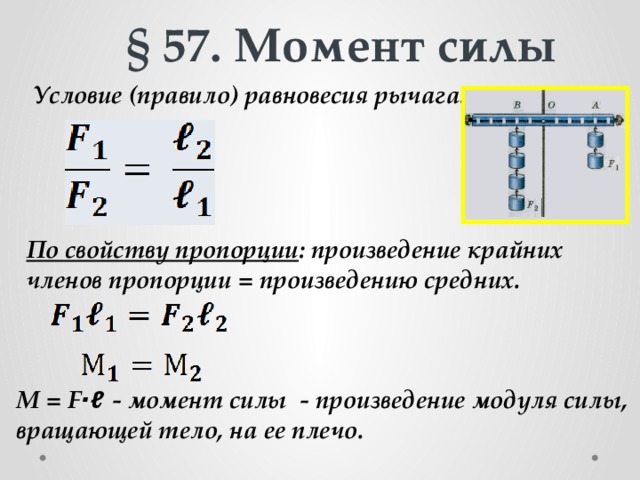 Работа силы F1 равна произведению модуля силы F1 на угол α и на плечо силы F1. Работа силы F2 равна произведению модуля силы F2 на угол α и на плечо силы F2.
Работа силы F1 равна произведению модуля силы F1 на угол α и на плечо силы F1. Работа силы F2 равна произведению модуля силы F2 на угол α и на плечо силы F2.Полученные формулы показывают, что при заданном угле поворота тела работа каждой приложенной к этому телу силы равна произведению модуля силы на плечо взятому со знаком «+» или «-». Это произведение называют моментом силы.
Моментом силы относительно оси вращения тела называется произведение модуля силы на ее плечо. Момент силы может быть положительным или отрицательным.
Если сила, действующая на тело, направлена так, чтобы повернуть его против часовой стрелки, то момент силы считают положительным, если по часовой, то отрицательным.
В нашем примере момент силы F1 равен произведению модуля силы F1 на плечо силы F1. Момент силы F2 равен произведению модуля силы F2 на плечо силы F2. Сила F1 стремится повернуть стержень против часовой стрелки, значит момент этой силы положительный. Сила F2 стремится повернуть стержень по часовой стрелке, значит момент этой силы отрицательный.

Следовательно, выражения для работы сил F1 и F2 можно записать в таком виде: работа силы F1 равна произведению момента силы F1 на угол α; работа силы F2 равна произведению момента силы F2 на угол α.
Полная работа внешних сил складывается из работы сил F1, F2 и F3. Работа силы F3 равна нулю, потому что точка 0 не перемещается. Подставим в формулу вместо работы сил F1 и F2 произведения моментов сил на угол поворота. Получаем, что полная работа внешних сил равна произведению суммы моментов сил F1 и F2 на угол α.
Для того чтобы тело пришло в движение, нужно чтобы увеличилась его кинетическая энергия, а для этого внешние силы должны совершить работу.
Согласно полученному уравнению, работа внешних сил может быть отлична от нуля только в том случае, если сумма моментов этих сил не равна нулю. Если же суммарный момент внешних сил, действующих на тело, равен нулю, то их работа равна нулю. Следовательно, кинетическая энергия тела не увеличивается, то есть остается равной нулю.
 Значит, тело не приходит в движение.
Значит, тело не приходит в движение.Это есть второе условие, необходимое для равновесия твердого тела.
При равновесии твердого тела сумма моментов всех внешних сил, действующих на него относительно любой оси, равна нулю.
Если же на абсолютно твердое тело действует произвольное число сил, условия равновесия абсолютно твердого тела следующие:
‒ во-первых, геометрическая сумма внешних сил, действующих на тело, равна нулю,
‒ во-вторых, сумма моментов всех внешних сил, действующих на тело относительно любой оси, равна нулю.
Эти условия являются необходимыми и достаточными для равновесия твердого тела. Если они выполняются, то тело остается в равновесии.
Если же тело не является абсолютно твердым, даже при соблюдении двух условий равновесия, это тело может и не оставаться в равновесии.
Это происходит из-за того, что под воздействием приложенных к нему сил тело может деформироваться и тогда сумма всех сил, действующих на каждый его элемент, не будет равна нулю.
 Возьмем, например, резиновый шнур. Приложим к его концам две силы, равные по модулю и направленные вдоль шнура в противоположные стороны. Под действием этих сил шнур будет растягиваться, а, значит, выйдет из состояния равновесия, несмотря на то, что сумма внешних сил равна нулю и нулю равна сумма их моментов относительно оси, проходящей через любую точку шнура.
Возьмем, например, резиновый шнур. Приложим к его концам две силы, равные по модулю и направленные вдоль шнура в противоположные стороны. Под действием этих сил шнур будет растягиваться, а, значит, выйдет из состояния равновесия, несмотря на то, что сумма внешних сил равна нулю и нулю равна сумма их моментов относительно оси, проходящей через любую точку шнура.Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитора
1.3: Моменты — Инженерные тексты LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 50570
- Jacob Moore & Contributors
- Pennsylvania State University Mont Alto via Mechanics Map
Момент (также иногда называемый крутящим моментом) определяется как «стремление силы вращать тело». Там, где силы вызывают линейные ускорения, моменты вызывают угловых ускорения . Таким образом, моменты можно рассматривать как скручивающие силы.
Там, где силы вызывают линейные ускорения, моменты вызывают угловых ускорения . Таким образом, моменты можно рассматривать как скручивающие силы.
Векторное представление момента:
Моменты, как и силы, могут быть представлены в виде векторов и иметь величину, направление и «точку приложения». Однако для некоторых моментов лучше назвать точку приложения осью вращения . Это будет точка или ось, относительно которой мы будем определять все моменты.
Величина:
Величина момента — это степень, в которой момент вызывает угловое ускорение тела, на которое он действует. Он представлен скаляром (одним числом). Величину момента можно представить как силу скручивающей силы, действующей на тело. Когда момент представлен в виде вектора, величина момента обычно указывается явно. хотя длина вектора момента также часто соответствует относительной величине момента.
Когда момент представлен в виде вектора, величина момента обычно указывается явно. хотя длина вектора момента также часто соответствует относительной величине момента.
Величина момента измеряется в единицах силы, умноженной на расстояние. Стандартными метрическими единицами величины момента являются ньютон-метры, а стандартными английскими единицами измерения момента являются футо-фунты.
\[ M = F * d \]
\[ \text{Метрика:} \,\, N * m \]
\[ \text{Английский:} \,\, lb * ft \]
Направление:
В двумерной задаче направление можно рассматривать как скалярную величину, соответствующую направлению вращения, которое вызовет момент. Момент, вызывающий вращение против часовой стрелки, является положительным моментом, а момент, вызывающий вращение по часовой стрелке, является отрицательным моментом.
Однако в трехмерной задаче тело может вращаться вокруг оси в любом направлении. Если это так, нам нужен вектор для представления направления момента. Направление вектора момента совпадет с осью вращения, которую вызовет этот момент, но чтобы определить, какое из двух направлений, которые мы можем использовать вдоль этой оси, мы используем правило правой руки. Чтобы использовать правило правой руки, выровняйте правую руку, как показано на рисунке \(\PageIndex{2}\), так, чтобы большой палец в данный момент был на одной линии с осью вращения, а согнутые пальцы указывали в направлении вращения для момент. Если вы сделаете это, ваш большой палец будет указывать в направлении вектора момента.
Направление вектора момента совпадет с осью вращения, которую вызовет этот момент, но чтобы определить, какое из двух направлений, которые мы можем использовать вдоль этой оси, мы используем правило правой руки. Чтобы использовать правило правой руки, выровняйте правую руку, как показано на рисунке \(\PageIndex{2}\), так, чтобы большой палец в данный момент был на одной линии с осью вращения, а согнутые пальцы указывали в направлении вращения для момент. Если вы сделаете это, ваш большой палец будет указывать в направлении вектора момента.
Если мы вернемся к двумерным задачам, то увидим, что все повороты происходят вокруг оси, указывающей прямо на страницу или за ее пределы (ось \(z\)). Используя правило правой руки, вращение против часовой стрелки представлено вектором в положительном направлении \(z\), а вращение по часовой стрелке представлено вектором в отрицательном направлении \(z\).
Используя правило правой руки, вращение против часовой стрелки представлено вектором в положительном направлении \(z\), а вращение по часовой стрелке представлено вектором в отрицательном направлении \(z\).
Ось вращения:
В задачах инженерной статики мы можем выбрать любую точку/ось в качестве оси вращения. Однако выбор этой точки повлияет на величину и направление результирующего момента, а момент действует только относительно этой точки.
Рисунок \(\PageIndex{3}\): Величина и направление момента зависят от выбранной оси вращения. Например, указанная выше единственная сила вызовет разные моменты относительно точки А и точки В, потому что она вызовет разные вращения в зависимости от точки, которую мы фиксируем на месте. Хотя мы можем взять момент относительно любой точки в задаче статики, если мы складываем вместе моменты от нескольких сил, все моменты должны быть взяты вокруг общей оси вращения . Моменты, снятые в разных точках, нельзя суммировать, чтобы найти «чистый момент».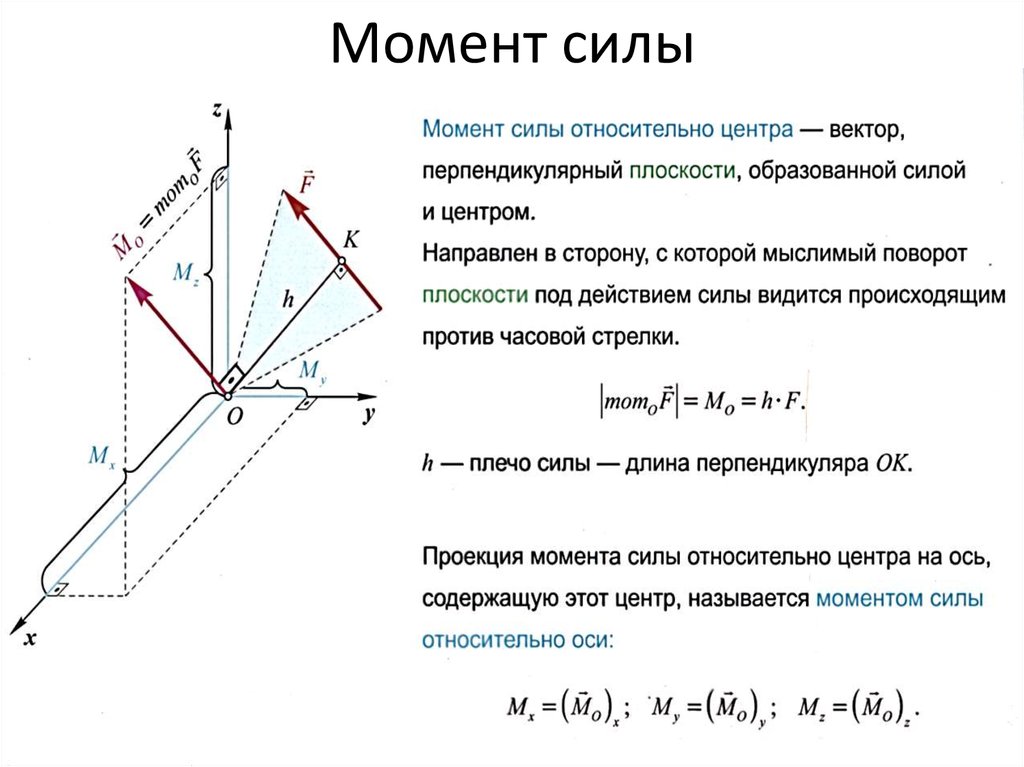
Кроме того, если мы перейдем к предмету динамики, когда тела движутся, мы захотим связать моменты с угловыми ускорениями. Чтобы это работало, нам нужно будет либо взять моменты относительно одной точки, которая не движется (например, петля на двери), либо нам нужно будет взять моменты относительно центра масс тела. Суммирование моментов относительно других осей вращения не приведет к правильным расчетам.
Расчет моментов:
Для расчета момента силы, действующей на тело, у нас будет два основных варианта: скалярные методы и векторные методы . Скалярные методы обычно быстрее для двумерных задач, когда тело может вращаться только по часовой стрелке или против часовой стрелки, тогда как векторные методы обычно быстрее для трехмерных задач, где ось вращения более сложная.
Видео \(\PageIndex{1}\): Видеолекция по этому разделу, прочитанная доктором Джейкобом Муром. Источник на YouTube: https://youtu.be/RyOwVvYEFHU.
Источник на YouTube: https://youtu.be/RyOwVvYEFHU.Эта страница под названием 1.3: Моменты публикуется в соответствии с лицензией CC BY-SA 4.0 и была создана, изменена и/или курирована Джейкобом Муром и участниками (Mechanics Map) с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Джейкоб Мур и авторы
- Лицензия
- CC BY-SA
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- угловое ускорение
- ось вращения
- момент
- источник@http://mechanicsmap.
 psu.edu
psu.edu - крутящий момент
В статике сумма сил равна нулю
Урок: В статике сумма сил равна нулю.
Термин статика относится к объекту или системе, находящейся в статическом равновесии. Объект или система неподвижны, потому что все силы равны нулю.
Второй закон Ньютона:
σf = σ (MA) = M 1 A 1 + M 2 A 2 + M 3 A 3 + • • • + M N A A A A A A A . Сумма сил равна произведению массы на ускорение. Второй закон говорит нам, что если объект или система неподвижны, ускорение равно нулю. Поэтому сумма векторных сил должна быть равна нулю.
Пример. Рассмотрим стол с четырьмя ножками и объект массой 200 кг, неподвижно покоящийся в центре стола:
Масса объекта = 200 кг
______________
| | Масса стола = 100 кг
| |
| | Какие силы действуют на
нижняя часть каждой ножки стола?
Сила, действующая вверх на ноги, определяется путем уравновешивания этих сил в уравнении, заданном законом Ньютона:
ΣF = ma = 0 = — (200 кг X 9,81 м/с 2 ) — (100 кг X 9,81 м/с 2 ) + (сила ноги X 4)
Гравитация действует вниз на 200-килограммовый объект и 100-килограммовый стол. Следовательно, мы можем заменить ускорение свободного падения (на Земле) g (9,81 м/с 2 ) вместо a.
Следовательно, мы можем заменить ускорение свободного падения (на Земле) g (9,81 м/с 2 ) вместо a.
Усилие опора = ((200 кг X 9,81 м/с 2 ) + (100 кг X 9,81 м/с 2 )) / 4
Единица кг•м/с 2 эквивалентна единице силы, называемой ньютоном (Н). Таким образом, при умножении килограммы сокращаются.
Сила нога = (1962 Н + 981 Н) / 4
Сила ноги = 735,75 Н
Это означает, что каждая ножка действует на пол с направленной вниз силой в 735,75 ньютонов, и одновременно пол воздействует на каждую ножку стола с той же силой вверх.
Обратите внимание, что очень важно соблюдать единое соглашение о знаках на протяжении всего анализа. Соглашение о знаках обычно выбирается в более сложных задачах, чтобы упростить общий объем алгебры, необходимый для анализа уравнений по осям x, y и z. Мы выбрали положительные значения для обозначения сил, направленных вверх, и отрицательные значения для обозначения сил, направленных вниз, но мы могли бы использовать и противоположные значения, если бы были последовательны.
Следствие для крутящего момента[править | править код]
Урок: В статике сумма крутящих моментов равна нулю.
Сумма всех вращательных сил или крутящих моментов, обозначаемая заглавной греческой буквой тау (T{\displaystyle \mathrm {T}}), также равна нулю. Обычно используемыми единицами измерения крутящего момента являются фут•фунты (ft•lb) и ньютон•метры (Н•м).
Второй закон Ньютона (применительно к крутящим моментам):
ΣT {\ displaystyle \ mathrm {T}} = Σ (ωI) = ω 1 I 1 + ω 2 I 2 + ω 3 I 3 + • • • + ω n I n
Сумма крутящих моментов равна инерционной массе (или моменту) вращения умножить на угловое ускорение (обозначается строчной греческой буквой омега, ω). Второй закон говорит нам, что если объект или система неподвижны, то угловое ускорение равно нулю. Поэтому сумма векторов моментов должна быть равна нулю.
Крутящий момент также можно рассчитать как силу, умноженную на расстояние:
ΣT {\ displaystyle \ mathrm {T}} = Σ (Fd) = F 1 d 1 + F 2 d 2 + F 3 d • + 9 3 n d n
Пример.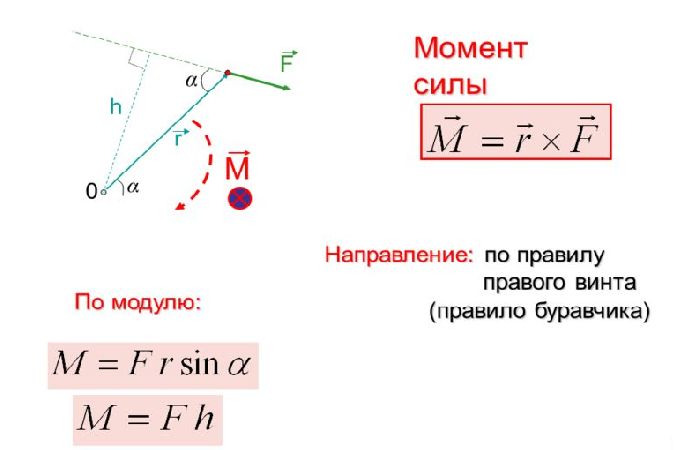 Рассмотрим невесомый рычаг с двумя прикрепленными грузами и одной невесомой опорой:
Рассмотрим невесомый рычаг с двумя прикрепленными грузами и одной невесомой опорой:
| + Вес объекта 1 = 10 фунтов | /| Расстояние от точки опоры = 10 футов | / | | Р/ | Расстояние поддержки Вт| E/|S w1 от точки опоры = 7 футов А| В/ |У л| E/ |P Вес объекта 2 = 80 фунтов л| л/| |P Расстояние от точки опоры = 4 фута | / w2 |О | / |R Какие силы действуют на |/ |T безмассовый рычаг ? ПОЛ
Сначала напишем уравнение статического крутящего момента для системы:
ΣT {\ displaystyle \ mathrm {T}} = Σ (Fd) = F 1 d 1 + F S d S + F 2 d 90 90 168 2 90
Силы 1 и 2 на самом деле являются весами двух объектов:
ΣT {\ displaystyle \ mathrm {T}} = Σ (Fd) = w 1 d 1 + F S d S + w 2 д 2 = 0
Замените известные значения:
ΣT {\ displaystyle \ mathrm {T}} = Σ (Fd) = (-10 фунтов) (10 футов) + F S (7 футов) + (-80 фунтов) (4 фута) = 0
Решите для F S :
ΣT {\ displaystyle \ mathrm {T}} = Σ (Fd) = (-100 ft•lb) + F S (7 футов) + (-320 ft•lb) = 0
F S (7 футов) = (420 фут•фунт)
F S = (420 ft•lb)/(7 ft) = 60 lb
Таким образом, сила в 60 фунтов действует на рычаг вверх от опоры, чтобы уравновесить крутящие моменты на рычаге. Так как общий вес на рычаге равен 90 фунтов и 60 из этих фунтов противодействуют опоре, остальные 30 фунтов должны воздействовать вверх на рычаг в точке опоры в нижнем, левом углу.
Так как общий вес на рычаге равен 90 фунтов и 60 из этих фунтов противодействуют опоре, остальные 30 фунтов должны воздействовать вверх на рычаг в точке опоры в нижнем, левом углу.
Обратите внимание, что нам не нужно было использовать точку опоры в качестве точки, от которой отсчитываются все расстояния, мы могли выбрать любую точку вдоль рычага. Однако, как и в случае с силами, необходимо использовать последовательное соглашение о знаках. В этом случае положительные значения могут использоваться для крутящих моментов по часовой стрелке (CW), измеренных с одной точки зрения, а отрицательные крутящие моменты могут использоваться для крутящих моментов против часовой стрелки (CCW), измеренных с той же точки обзора. Можно было бы использовать и противоположную систему, если бы мы были последовательны.
Также обратите внимание, что в приведенном ранее примере таблицы указано, что объект находится в центре стола. Если нет, то уравновешивание крутящих моментов (в двух направлениях) приведет к большей силе, поддерживаемой одними ножками стола, и меньшей — к другим.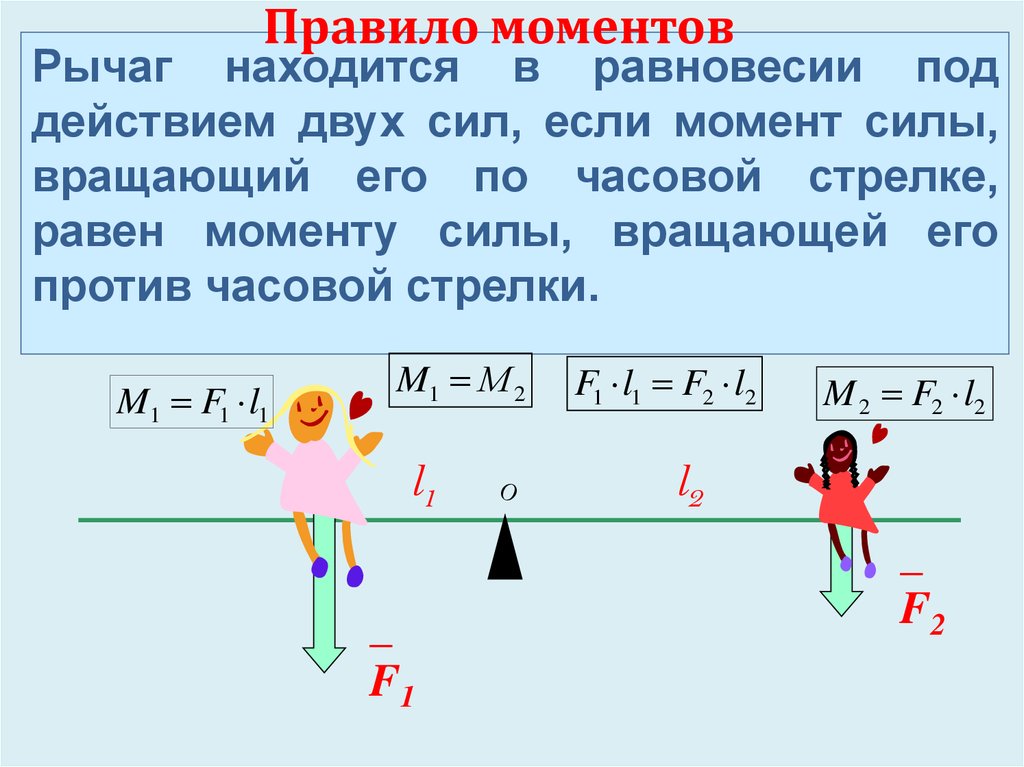 Например, если бы объект находился прямо над одной из ножек, то весь его вес поддерживался бы этой ногой в дополнение к одной четвертой веса стола. Тогда остальные ножки будут поддерживать только одну четвертую веса стола каждая.
Например, если бы объект находился прямо над одной из ножек, то весь его вес поддерживался бы этой ногой в дополнение к одной четвертой веса стола. Тогда остальные ножки будут поддерживать только одну четвертую веса стола каждая.
7.4 Мощность – University Physics Volume 1
7 Работа и кинетическая энергия
Цели обучения
К концу этого раздела вы сможете:
- Соотносить работу, выполненную в течение интервала времени, с передаваемой мощностью
- Найти мощность, затрачиваемую силой, действующей на движущееся тело
Понятие работы включает в себя силу и перемещение; теорема о работе-энергии связывает чистую работу, совершаемую над телом, с разницей его кинетической энергии, вычисленной между двумя точками на его траектории. Ни одна из этих величин или отношений не включает время в явном виде, однако мы знаем, что время, доступное для выполнения определенного объема работы, часто так же важно для нас, как и сам объем. На открывающем главу рисунке несколько спринтеров могли достичь одинаковой скорости на финише и, следовательно, выполнить одинаковый объем работы, но победитель гонки выполнил ее за наименьшее количество времени.
На открывающем главу рисунке несколько спринтеров могли достичь одинаковой скорости на финише и, следовательно, выполнить одинаковый объем работы, но победитель гонки выполнил ее за наименьшее количество времени.
Мы выражаем отношение между выполненной работой и интервалом времени, затрачиваемым на ее выполнение, вводя понятие мощности. Поскольку работа может меняться в зависимости от времени, мы сначала определим среднюю мощность как работу, выполненную за интервал времени, деленную на интервал
.[латекс] {P} _ {\ text {ave}} = \ frac {\ Delta W} {\ Delta t}. [/latex]
Затем мы можем определить мгновенную мощность (часто называемую просто мощностью ).
Мощность
Мощность определяется как скорость выполнения работы или предел средней мощности для интервалов времени, приближающихся к нулю,
[latex]P=\frac{dW}{dt}.[/latex]
Если мощность постоянна в течение временного интервала, средняя мощность для этого интервала равна мгновенной мощности, а работа, выполненная агентом, поставляющим мощность, равна [latex]W=P\Delta t[/latex]. Если мощность в течение интервала меняется со временем, то выполненная работа есть интеграл мощности по времени,
Если мощность в течение интервала меняется со временем, то выполненная работа есть интеграл мощности по времени,
[латекс]W=\int Pdt.[/латекс]
Теорема о работе-энергии описывает, как работа может быть преобразована в кинетическую энергию. Поскольку существуют и другие формы энергии, как мы обсудим в следующей главе, мы также можем определить мощность как скорость передачи энергии. Работа и энергия измеряются в джоулях, поэтому мощность измеряется в джоулях в секунду, которой в системе СИ присвоено название ватт, аббревиатура Вт: [латекс]1\,\текст{Дж/с}=1\, \text{W}[/латекс]. Другой распространенной единицей измерения мощности повседневных устройств является мощность в лошадиных силах: [latex]1\,\text{hp}=746\,\text{W}[/latex].
Пример
Мощность подтягивания
Военнослужащий массой 80 кг делает 10 подтягиваний за 10 с (рисунок). Какую среднюю мощность развивают мышцы тренирующегося при перемещении его тела? ( Подсказка: Сделайте разумные оценки для любых необходимых величин.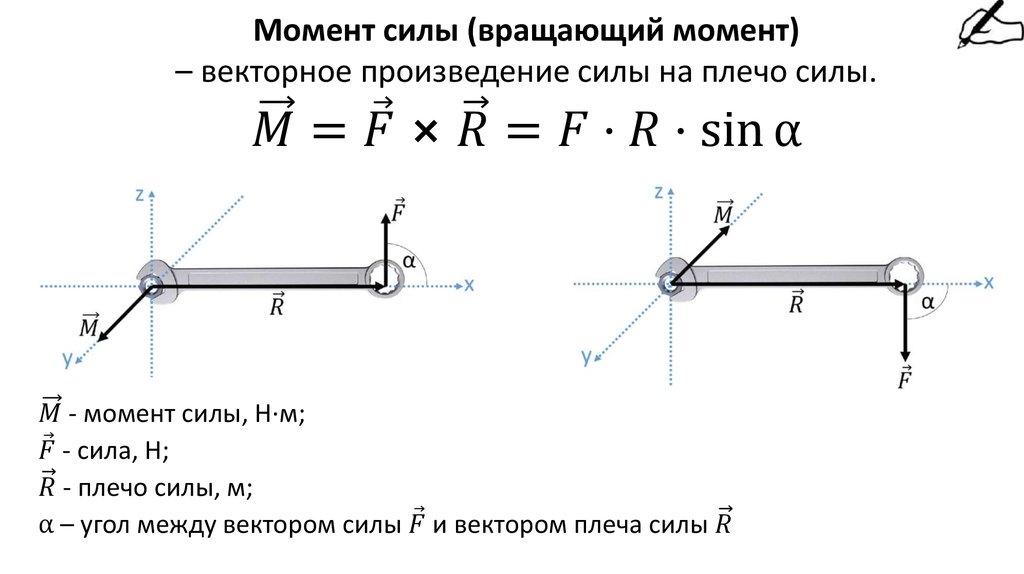 )
)
Стратегия
Работа, совершаемая против силы тяжести при движении вверх или вниз на расстояние [латекс]\Delta y[/latex], равна [latex]mg\Delta y[/latex] (если вы поднимаете и опускаете себя с постоянной скоростью , сила, которую вы прикладываете, компенсирует гравитацию на протяжении всего цикла подтягивания.) Таким образом, работа, выполняемая мышцами тренирующегося (движущими, но не ускоряющими свое тело) за полное повторение (вверх и вниз), составляет [латекс]2 мг\ Delta y.[/latex] Предположим, что [латекс]\Delta y=2\text{ft}\примерно 60\,\text{см}\text{.}[/latex] Также предположим, что длина ветвей составляет 10 % от массы тела и не входят в подвижную массу. При этих предположениях мы можем рассчитать работу, проделанную за 10 подтягиваний, и разделить на 10 с, чтобы получить среднюю мощность. 9{2})(0,6\,\text{m})}{10\,\text{s}}=850\,\text{W}\text{.}[/latex]
Значимость
Это типично для расхода энергии при напряженных упражнениях; в бытовых единицах это несколько больше одной лошадиной силы [латекс](1\,\text{hp}=746\,\text{W}). [/latex]
[/latex]
Проверьте свои знания
Оцените мощность, затрачиваемую тяжелоатлетом, поднимающим штангу массой 150 кг на 2 м за 3 с.
Показать раствор980 Вт
Сила, необходимая для перемещения тела, также может быть выражена через действующие на него силы. Если сила [латекс]\mathbf{\overset{\to }{F}}[/latex] действует на тело, которое смещается [латекс]d\mathbf{\overset{\to }{r}}[/latex ] за время dt , мощность затрачиваемая силой
[латекс] P = \ frac {dW} {dt} = \ frac {\ mathbf {\ overset {\ to {F}} \ cdot d \ mathbf {\ overset {\ to} {r}}} {dt } = \ mathbf {\ overset {\ to} {F}} \ cdot (\ frac {d \ mathbf {\ overset {\ to {r}}} {dt}) = \ mathbf {\ overset {\ to} {F}}\cdot\mathbf{\overset{\to}}{v}},[/латекс]
, где [латекс]\mathbf{\overset{\to }{v}}[/латекс] — скорость тела. Тот факт, что пределы, подразумеваемые производными, существуют для движения реального тела, оправдывает перестановку бесконечно малых величин.
Пример
Мощность автомобиля при движении вверх по склону
Сколько мощности должен затратить автомобильный двигатель, чтобы поднять автомобиль массой 1200 кг на подъем с уклоном 15% со скоростью 90 км/ч (рисунок)? Предположим, что 25% этой мощности рассеивается на преодоление сопротивления воздуха и трения.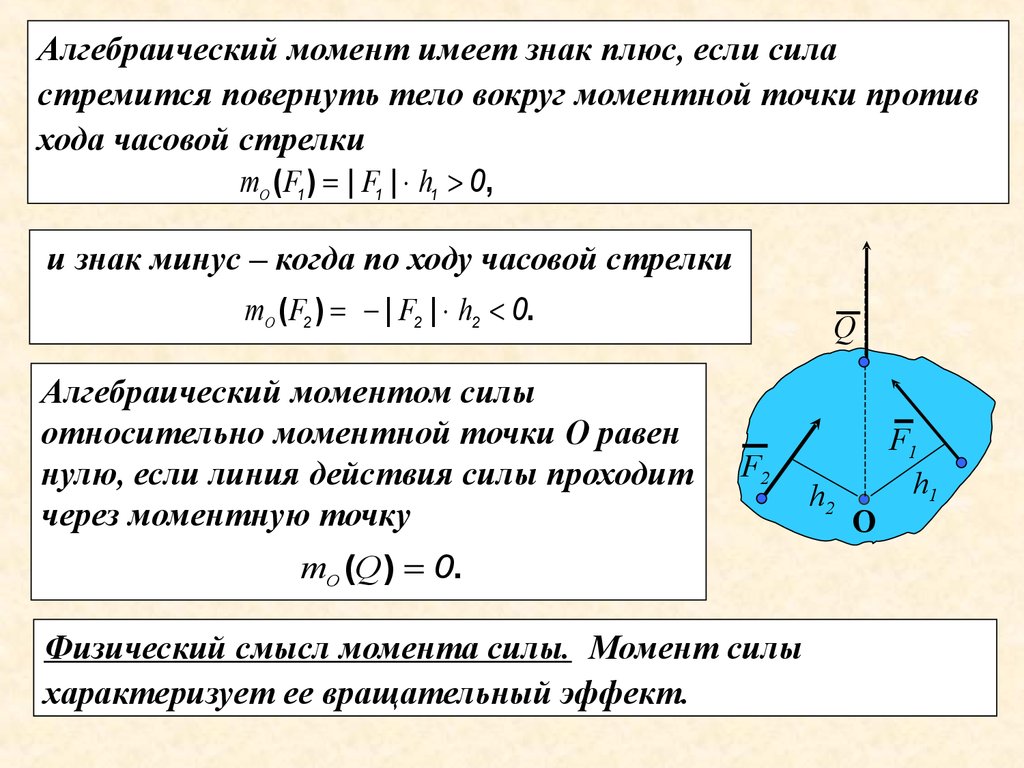
Стратегия
При постоянной скорости кинетическая энергия не изменяется, поэтому чистая работа, затраченная на перемещение автомобиля, равна нулю. Следовательно, мощность двигателя, необходимая для движения автомобиля, равна мощности, затрачиваемой на преодоление силы тяжести и сопротивления воздуха. По предположению, 75% мощности передается против силы тяжести, что равно ,\text{sin}\,\theta ,[/latex], где [latex]\theta[/latex] — угол наклона. Оценка 15% означает [латекс]\текст{тангенс}\,\тета = 0,15.[/латекс] Это рассуждение позволяет нам определить требуемую мощность. 9\circ)}{0,75}=58\,\text{кВт,}[/latex]
или около 78 л.с. (Вы должны указать шаги, используемые для преобразования единиц.)
Значимость
Это разумное количество энергии для двигателя автомобиля малого и среднего размера, чтобы обеспечить [латекс](1\,\text{hp}= 0,746\,\text{кВт}\text{).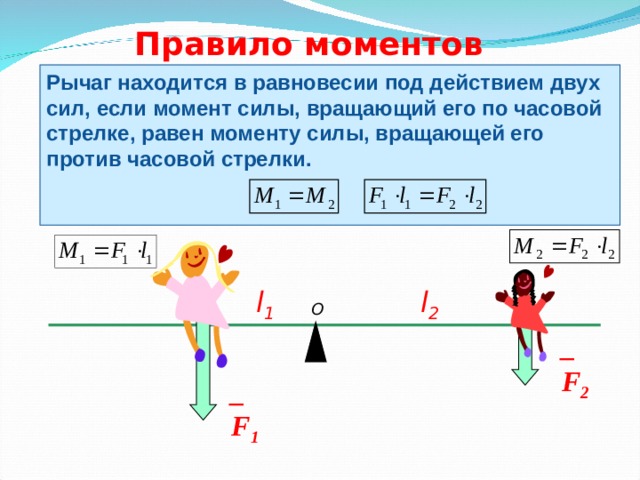 }[/latex] Обратите внимание, что это только мощность, затраченная на движение автомобиля. Большая часть мощности двигателя уходит куда-то еще, например, на отработанное тепло. Вот почему автомобилям нужны радиаторы. Любая оставшаяся мощность может быть использована для ускорения или для управления аксессуарами автомобиля.
}[/latex] Обратите внимание, что это только мощность, затраченная на движение автомобиля. Большая часть мощности двигателя уходит куда-то еще, например, на отработанное тепло. Вот почему автомобилям нужны радиаторы. Любая оставшаяся мощность может быть использована для ускорения или для управления аксессуарами автомобиля.
Резюме
- Мощность – это скорость выполнения работы; то есть производная работы по времени.
- В качестве альтернативы, работа, выполненная за интервал времени, является интегралом мощности, подаваемой за интервал времени.
- Мощность, передаваемая силой, действующей на движущуюся частицу, представляет собой скалярное произведение силы и скорости частицы.
Ключевые уравнения
Концептуальные вопросы
Мощность большинства электроприборов измеряется в ваттах. Зависит ли этот рейтинг от того, как долго прибор включен? (В выключенном состоянии это устройство с нулевой мощностью.) Объясните с точки зрения определения мощности.
Зависит ли этот рейтинг от того, как долго прибор включен? (В выключенном состоянии это устройство с нулевой мощностью.) Объясните с точки зрения определения мощности.
Приборы оцениваются по энергии, потребляемой за относительно небольшой интервал времени. Не имеет значения, как долго прибор включен, важна лишь скорость изменения энергии в единицу времени.
Объясните с точки зрения определения мощности, почему потребление энергии иногда указывается в киловатт-часах, а не в джоулях. Какова связь между этими двумя энергетическими единицами?
Искра статического электричества, которую можно получить от дверной ручки в холодный сухой день, может иметь мощность в несколько сотен ватт. Объясните, почему вы не ранены такой искрой.
Показать решениеИскра возникает в течение относительно короткого промежутка времени, поэтому вашему телу передается очень небольшое количество энергии.
Зависит ли работа, совершаемая при подъеме предмета, от скорости его подъема? Зависит ли затрачиваемая мощность от того, как быстро он поднимается?
Может ли мощность, затрачиваемая силой, быть отрицательной?
Показать решение Если сила антипараллельна или направлена в направлении, противоположном скорости, затрачиваемая мощность может быть отрицательной.
Как 50-ваттная лампочка может потреблять больше энергии, чем 1000-ваттная духовка?
Проблемы
Человек в хорошей физической форме может выдавать 100 Вт полезной мощности в течение нескольких часов подряд, возможно, крутя педали механизма, который приводит в действие электрогенератор. Пренебрегая любыми проблемами эффективности генератора и практическими соображениями, такими как время отдыха: (a) Сколько людей потребуется, чтобы запустить электрическую сушилку для белья мощностью 4,00 кВт? б) Сколько человек потребуется, чтобы заменить крупную электростанцию мощностью 800 МВт?
Показать раствора. 40; б. 8 миллионов
Какова стоимость эксплуатации электрических часов мощностью 3,00 Вт в течение года, если стоимость электроэнергии составляет 💲0,0900 за [латекс]\текст{кВт}\cdot \text{ч}[/латекс]?
Большой бытовой кондиционер может потреблять 15,0 кВт электроэнергии. Какова стоимость эксплуатации этого кондиционера 3,00 часа в день за 30,0 дня, если стоимость электроэнергии составляет 💲0,110 за [латекс]\текст{кВт}\cdot \text{ч}[/латекс]?
Показать решение💲149
(a) Каково среднее энергопотребление в ваттах устройства, потребляющего 5,00 [латекс]\текст{кВт}\cdot \текст{ч}[/латекс] энергии в день? б) Сколько джоулей энергии потребляет этот прибор в год? 9{6}\,\text{J}[/latex] полезной работы за 8 часов? б) За какое время при такой скорости этот человек поднимет 2000 кг кирпичей на высоту 1,50 м? (Работа, проделанная для подъема его тела, может быть опущена, поскольку здесь она не считается полезной. )
)
a. 208 Вт; б. 141 с
Драгстер массой 500 кг разгоняется из состояния покоя до конечной скорости 110 м/с на расстоянии 400 м (около четверти мили) и сталкивается со средней силой трения 1200 Н. Какова его средняя выходная мощность в ваттах и лошадиных силах, если это занимает 7,30 с?
(a) За какое время автомобиль массой 850 кг с полезной выходной мощностью 40,0 л.с. (1 л.с. равен 746 Вт) достигнет скорости 15,0 м/с без учета трения? б) Сколько времени займет это ускорение, если при этом автомобиль поднимется на холм высотой 3,00 м?
Показать раствора. 3,20 с; б. 4,04 с
а) Найдите полезную мощность двигателя лифта, который поднимает груз массой 2500 кг на высоту 35,0 м за 12,0 с, если он также увеличивает скорость из состояния покоя до 4,00 м/с. Обратите внимание, что общая масса уравновешенной системы составляет 10 000 кг, так что в высоту поднимается только 2 500 кг, но ускоряются полные 10 000 кг. (b) Сколько это стоит, если электричество стоит 💲0,09{5}\text{-kg}[/latex] самолет с двигателями мощностью 100 МВт, способный развивать скорость 250 м/с и высоту 12,0 км, если бы сопротивление воздуха было пренебрежимо малым? (b) Если это действительно занимает 900 с, какова мощность? в) Какова средняя сила сопротивления воздуха при этой мощности, если самолету потребуется 1200 с? ( Подсказка: Вы должны найти расстояние, которое самолет проходит за 1200 с при постоянном ускорении. \circ[/латекс] с той же скоростью. Предположим, что тормозящая сила трения в обоих случаях одинакова.
\circ[/латекс] с той же скоростью. Предположим, что тормозящая сила трения в обоих случаях одинакова.
1,7 кВт
Дополнительные задачи
Тележку тянут на расстояние D по плоской горизонтальной поверхности под действием постоянной силы F , действующей под углом [латекс]\тета[/латекс] к горизонтальному направлению. Другими силами, воздействующими на объект в это время, являются сила тяжести ([латекс]{F}_{w}[/латекс]), нормальные силы ([латекс]{F}_{N1}[/латекс]) и ([латекс ]{F}_{N2}[/latex]), и трения качения [латекс]{F}_{r1}[/латекс] и [латекс]{F}_{r2}[/латекс], как показано ниже. . Какую работу совершает каждая сила?
Рассмотрим частицу, на которую действует несколько сил, одна из которых, как известно, постоянна во времени: [латекс]{\mathbf{\overset{\to}{F}}}_{1}=(3\ ,\text{N})\mathbf{\hat{i}}+(4\,\text{N})\mathbf{\hat{j}}.[/latex] В результате частица движется по x -ось от [латекс]х=0[/латекс] до [латекс]х=5\,\текст{м}[/латекс] за некоторый интервал времени.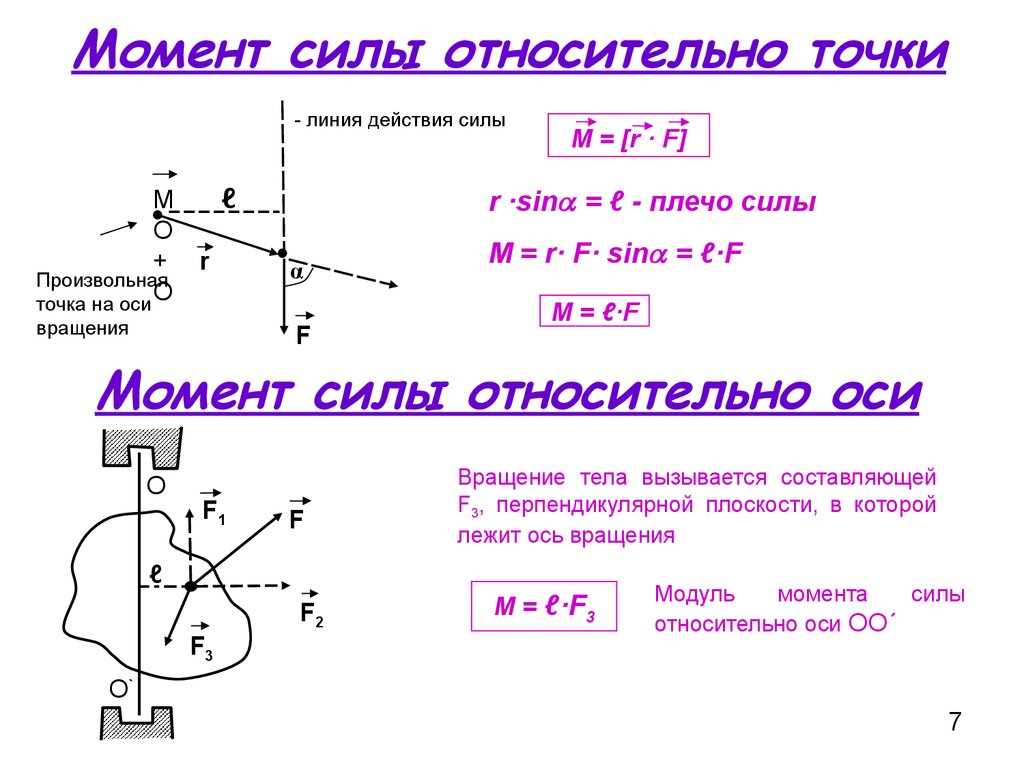 Какую работу выполняет [латекс]{\mathbf{\overset{\to}}{F}}}_{1}[/латекс]?
Какую работу выполняет [латекс]{\mathbf{\overset{\to}}{F}}}_{1}[/латекс]?
[латекс]15\,\текст{N}\cdot \текст{м}[/латекс]
Рассмотрим частицу, на которую действует несколько сил, одна из которых, как известно, постоянна во времени: [латекс]{\mathbf{\overset{\to}}{F}}}_{1}=(3\,\ text{N})\mathbf{\hat{i}}+(4\,\text{N})\mathbf{\hat{j}}.[/latex] В результате частица движется сначала по x -ось от [latex]x=0[/latex] до [latex]x=5\,\text{m}[/latex] и затем параллельно y -ось от [latex]y=0 [/latex] to [latex]y=6\,\text{m}\text{.}[/latex] Какую работу выполняет [latex]{\mathbf{\overset{\to} }{F}} }_{1}[/латекс]?
Рассмотрим частицу, на которую действует несколько сил, одна из которых, как известно, постоянна во времени: [латекс]{\mathbf{\overset{\to}}{F}}}_{1}=(3\,\ text{N})\mathbf{\hat{i}}+(4\,\text{N})\mathbf{\hat{j}}.[/latex] В результате частица движется по прямому пути от декартовой координаты (0 м, 0 м) до (5 м, 6 м). Какую работу выполняет [латекс]{\mathbf{\overset{\to}}{F}}}_{1}[/латекс]?
Показать решение[latex]39\,\text{N}\cdot \text{m}[/latex]
Рассмотрим частицу, на которую действует сила, зависящая от положения частицы.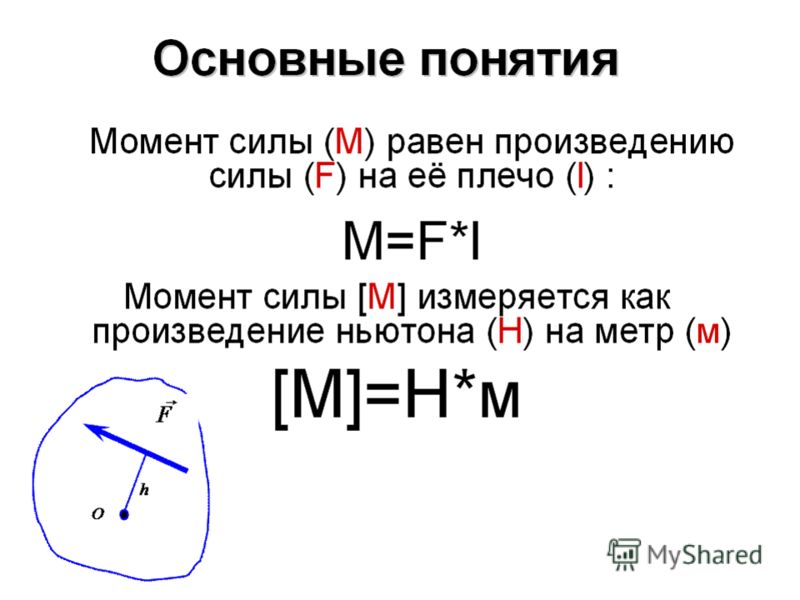 Эта сила определяется как [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {1} = (2y) \ mathbf {\ hat {i}} + (3x) \ mathbf {\ hat { j}}.[/latex] Найдите работу, совершаемую этой силой при перемещении частицы из начала координат в точку, расположенную на 5 метров вправо на 9\circ[/latex] над горизонталью на том же расстоянии?
Эта сила определяется как [латекс] {\ mathbf {\ overset {\ to} {F}}} _ {1} = (2y) \ mathbf {\ hat {i}} + (3x) \ mathbf {\ hat { j}}.[/latex] Найдите работу, совершаемую этой силой при перемещении частицы из начала координат в точку, расположенную на 5 метров вправо на 9\circ[/latex] над горизонталью на том же расстоянии?
а. [латекс]208\,\текст{N}\cdot \текст{м}[/латекс]; б. [латекс] 240\,\текст{N}\cdot \текст{м}[/латекс]
Ящик массой 200 кг необходимо перенести с площадки первого этажа в квартиру третьего этажа. Рабочие знают, что они могут либо сначала воспользоваться лифтом, а затем переместить его по третьему этажу в квартиру, либо сначала передвинуть ящик в другое место, отмеченное буквой C ниже, а затем подняться на лифте на третий этаж и сдвинуть его на третий. пол меньшее расстояние. Беда в том, что третий этаж очень неровный по сравнению с первым этажом. Учитывая, что коэффициент кинетического трения между ящиком и поверхностью пола равен 0,100, а между ящиком и поверхностью третьего этажа равен 0,300, найдите работу, которую затрачивают рабочие на каждом пути, показанном на рисунке 9. 0393 А до Е . Предположим, что силы, которую должны приложить рабочие, достаточно, чтобы сдвинуть ящик с постоянной скоростью (нулевое ускорение). Примечание: Работа лифта против силы тяжести не выполняется рабочими.
0393 А до Е . Предположим, что силы, которую должны приложить рабочие, достаточно, чтобы сдвинуть ящик с постоянной скоростью (нулевое ускорение). Примечание: Работа лифта против силы тяжести не выполняется рабочими.
Хоккейная шайба массой 0,17 кг брошена по шероховатому полу с разной шероховатостью в разных местах, что можно описать зависящим от положения коэффициентом кинетического трения. Для шайбы, движущейся по x -ось, коэффициент кинетического трения является следующей функцией x , где x выражено в метрах: [латекс]\mu (x)=0,1+0,05x.[/latex] Найдите выполненную работу кинетической силой трения хоккейной шайбы, когда она перемещается (a) из [латекс]x=0[/латекс] в [латекс]x=2\,\text{m}[/латекс] и (б) из [латекс]x=2\,\text{m}[/латекс] в [латекс]x=4\,\текст{м}[/латекс].
Показать раствора. [латекс]\текст{−}0,9\,\текст{N}\cdot \text{м}[/латекс]; б. [латекс]-0,83\,\текст{N}\cdot \текст{м}[/латекс]
Горизонтальная сила 20 Н требуется для того, чтобы ящик массой 5,0 кг двигался с постоянной скоростью вверх по наклонной поверхности без трения при изменении высоты по вертикали на 3,0 м. а) Какова работа силы тяжести при этом изменении высоты? б) Какую работу совершает нормальная сила? в) Какую работу совершает горизонтальная сила?
а) Какова работа силы тяжести при этом изменении высоты? б) Какую работу совершает нормальная сила? в) Какую работу совершает горизонтальная сила?
Коробка массой 7,0 кг скользит по горизонтальному полу без трения со скоростью 1,7 м/с и сталкивается с относительно невесомой пружиной, которая сжимается на 23 см, прежде чем коробка останавливается. а) Какой кинетической энергией обладает ящик до столкновения с пружиной? б) Вычислите работу, совершенную пружиной. в) Определите жесткость пружины.
Показать раствора. 10. Дж; б. 10. Дж; в. 380 Н/м
Вы едете на автомобиле по прямой дороге с коэффициентом трения между шинами и дорогой 0,55. Большой кусок обломков падает прямо перед вашим взором, и вы тут же нажимаете на тормоза, оставляя след длиной 30,5 м (100 футов) перед остановкой. Полицейский видит, что ваша машина остановилась на дороге, смотрит на след заноса и выписывает вам штраф за превышение скорости 13,4 м/с (30 миль/ч). Стоит ли оспаривать штраф за превышение скорости в суде?
По неровной поверхности пола толкают ящик. Если к ящику не приложено никакой силы, ящик замедлится и остановится. Если ящик массой 50 кг, движущийся со скоростью 8 м/с, останавливается через 10 с, с какой скоростью сила трения, действующая на ящик, отбирает энергию у ящика?
Если к ящику не приложено никакой силы, ящик замедлится и остановится. Если ящик массой 50 кг, движущийся со скоростью 8 м/с, останавливается через 10 с, с какой скоростью сила трения, действующая на ящик, отбирает энергию у ящика?
160 Дж/с
Предположим, что для поддержания скорости 8 м/с ящика массой 50 кг требуется горизонтальная сила 20 Н. а) Какова мощность этой силы? (b) Обратите внимание, что ускорение ящика равно нулю, несмотря на то, что сила 20 Н действует на ящик горизонтально. Что происходит с энергией, переданной ящику в результате работы этой силы в 20 Н? 9\circ[/latex] наклон горизонтальной силой [латекс]\mathbf{\overset{\to }{F}}.[/latex] Коэффициент кинетического трения между ящиком и наклоном равен [латекс]{\mu }_{k}=0,40.[/latex] Рассчитайте работу, совершаемую (а) приложенной силой, (б) силой трения, (в) силой тяжести и (г) результирующей силой.
Показать решение Если ящик поднимается: a. 3,46 кДж; б. −1,89 кДж; в. −1,57 кДж; д. 0; Если ящик опускается: a. −0,39 кДж; б. −1,18 кДж; в. 1,57 кДж; д. 0
0; Если ящик опускается: a. −0,39 кДж; б. −1,18 кДж; в. 1,57 кДж; д. 0
Поверхность предыдущей задачи изменена так, что коэффициент кинетического трения уменьшен. К ящику приложена такая же горизонтальная сила, и после того, как его толкнули на 8,0 м, его скорость составила 5,0 м/с. Какую работу теперь совершает сила трения? Предположим, что ящик находится в состоянии покоя.
Сила F ( x ) зависит от положения, как показано ниже. Найдите работу, совершаемую этой силой над частицей при ее перемещении из [латекс]x=1,0\,\text{m}[/latex] в [латекс]x=5,0\,\text{m}\text{.} [/latex]
Показать решение8,0 Дж
Найдите работу, совершаемую той же силой на рисунке, между теми же точками [латекс]A=(0,0)\,\text{и}\,B =(2\,\text{m},2\,\text{m})[/latex], по дуге окружности радиусом 2 м с центром в точке (0, 2 м). Оцените интеграл пути с помощью декартовых координат. ( Подсказка: Возможно, вам понадобится обратиться к таблице интегралов. )
)
Ответьте на предыдущую задачу, используя полярные координаты.
Показать раствор35,7 Дж
Найдите работу, совершаемую той же силой на рисунке, между теми же точками [латекс]A=(0,0)\,\text{и}\,B=(2\,\text{m},2\ ,\text{m})[/latex], по дуге окружности радиусом 2 м с центром в точке (2 м, 0). Оцените интеграл пути с помощью декартовых координат. ( Подсказка: Вам, вероятно, потребуется свериться с таблицей интегралов.) 9{3\text{/}2}.[/latex]
Предположим, что сопротивление воздуха, с которым сталкивается автомобиль, не зависит от его скорости. Когда автомобиль движется со скоростью 15 м/с, его двигатель передает на колеса мощность 20 л.с. а) Какая мощность передается на колеса, если автомобиль движется со скоростью 30 м/с? б) Сколько энергии затрачивает автомобиль, чтобы проехать 10 км со скоростью 15 м/с? При 30 м/с? Предположим, что двигатель имеет КПД 25%. в) Ответьте на те же вопросы, если сила сопротивления воздуха пропорциональна скорости автомобиля.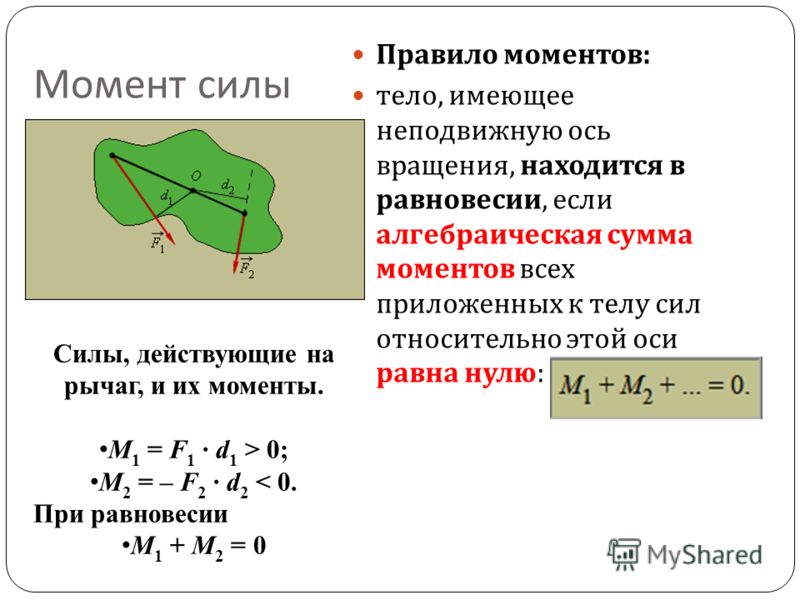


 psu.edu
psu.edu