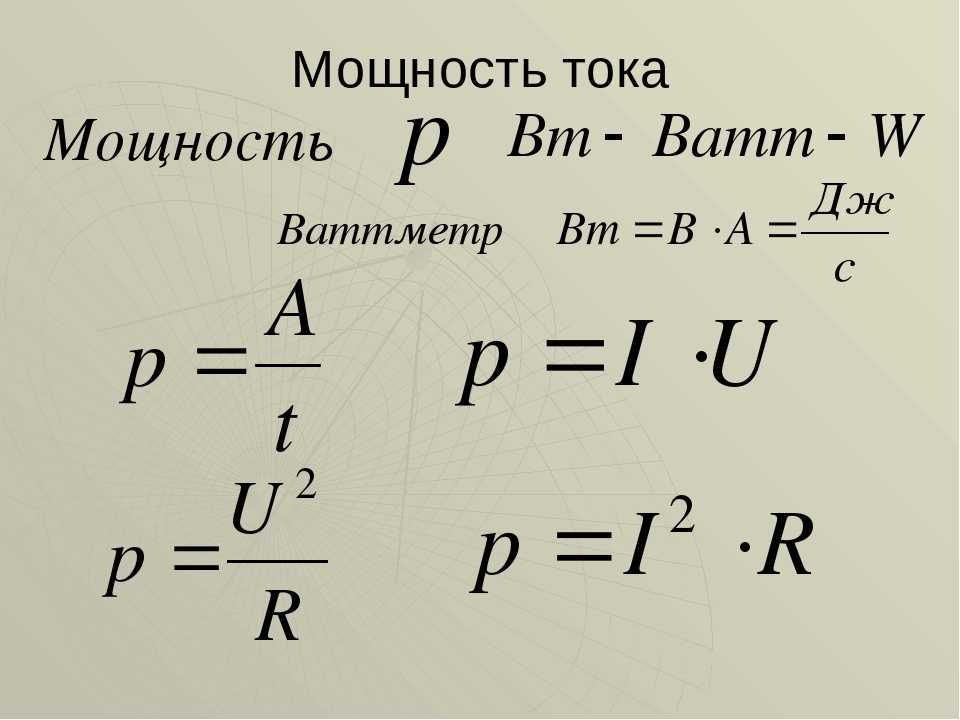
Мощность постоянного тока – кратко формула и работа в цепи
4.3
Средняя оценка: 4.3
Всего получено оценок: 279.
4.3
Средняя оценка: 4.3
Всего получено оценок: 279.
Работа электрического тока, как и любая работа, может совершаться с разной скоростью. Скорость совершения работы характеризуется такой величиной, как мощность. Кратко рассмотрим это понятие и порядок его определения.
Работа электрического тока
Электрический ток – это упорядоченное движение носителей заряда по проводнику. Такое движение возможно в результате совершения электрическим полем работы. Чему равна эта работа ?
Интуитивно понятно, что работа электрического поля тем больше, чем дольше и быстрее движутся носители заряда, и чем их больше. Действительно, носители движутся от точки с более высоким потенциалом $\varphi_1$ к точке с более низким потенциалом $\varphi_2$ (разность потенциалов в этом случае составляет $U=\varphi_1 – \varphi_2$).
Электрический потенциал точки равен работе поля по переносу единичного заряда из бесконечности в эту точку:Электрическое поле потенциально.
Следовательно, работа поля по переносу заряда из первой точки во вторую равна произведению разности потенциалов на величину перенесенного заряда:
$$A_{12} = (\varphi_1 – \varphi_2) q = Uq$$
Напомним, что при силе тока через проводник $I$ за время $Δt$ через поперечное сечение проводника проходит заряд $IΔt$.
Следовательно, работа электрического тока за время $Δt$ составит:
$$A_{12} = UIΔt$$
Вся эта работа совершается электрическим полем, переносящим заряды по проводнику. Согласно закону сохранения энергии, вся энергия поля при этом должна выделиться на рассматриваемом участке цепи. Выделение происходит в двух видах. Во-первых, носители заряда взаимодействуют с веществом проводника, и их энергия переходит во внутреннюю энергию проводника (в нагрев).
На этом принципе работают электродвигатели.
Рис. 1. Примеры потребителей электрического тока.Мощность электрического тока
Зная величину работы электрического тока, несложно получить значение мощности. Любая мощность равна отношению совершенной работы за время совершения:
$$P={A\over Δt}$$
Подставив в данную формулу выражение для работы, полученное выше, имеем:
$$P=IU$$
Полученное выражение – это универсальная формула мощности постоянного тока. Электрическая мощность равна произведению тока через электрическую цепь на напряжение на концах этой цепи. При этом предполагается, что внутри цепи нет дополнительных источников ЭДС, которые бы могли влиять на величину тока.
Рис. 2. Мощность электрического тока.Часто в задачах вместо тока через нагрузку или напряжения на ней известно сопротивление нагрузки $R$. В этом случае неизвестная величина вычисляется из закона Ома. Например, если известен ток, то мощность постоянного тока равна:
$$P={I^2R}$$
На практике чаще бывает случай, когда неизвестен ток.
2\over R}$$
Из последней формулы следует важный вывод. При уменьшении сопротивления нагрузки – ее мощность возрастает. То есть, если часть нагревательной спирали сгорит, а оставшиеся части будут соединены и подключены к тому же источнику напряжения, мощность спирали увеличится. В пределе, когда сопротивление нагрузки очень мало (выводы источника напряжения соединяются коротким проводником), а источник напряжения способен дать большую мощность – на нагрузке выделяется вся возможная мощность источника, как правило, в виде сильного нагрева. Такая ситуация называется коротким замыканием. Чтобы короткое замыкание не привело к пожару, в источнике напряжения должна быть защита, отключающая источник в случае короткого замыкания.
Рис. 3. Автоматы-предохранители.Что мы узнали?
Мощность электрического тока равна произведению тока через электрическую цепь на напряжение на концах этой цепи. При этом предполагается, что внутри цепи нет дополнительных источников ЭДС, которые бы могли влиять на величину тока.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.3
Средняя оценка: 4.3
Всего получено оценок: 279.
А какая ваша оценка?
Решение: При силе тока 2 А во внешней цепи выделяется мощность 24 Вт, а при силе тока 5 А
Условие задачи:
При силе тока 2 А во внешней цепи выделяется мощность 24 Вт, а при силе тока 5 А – мощность 30 Вт. Какая максимальная мощность может выделяться во внешней цепи?
Задача №7.4.53 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(I_1=2\) А, \(P_1=24\) Вт, \(I_2=5\) А, \(P_2=30\) Вт, \(P_{max}-?\)
Решение задачи:
Определим, при каких условиях мощность во внешней цепи будет максимальной. Мощность во внешней цепи \(P\) можно найти по формуле:
\[P = UI\;\;\;\;(1)\]
Здесь \(U\) – напряжение на внешней цепи, которое можно найти согласно закону Ома по формуле:
\[U = {\rm E} – Ir\;\;\;\;(2)\]
Подставим выражение (2) в формулу (1):
\[P = \left( {{\rm E} – Ir} \right)I\]
Рассмотрим функцию \(P\left( I \right)\), то есть зависимость мощности от силы тока:
\[P\left( I \right) = \left( {{\rm E} – Ir} \right)I\]
Раскроем скобки, тогда:
\[P\left( I \right) = {\rm E}I – {I^2}r\;\;\;\;(3)\]
Понятно, что графиком этой функции является парабола, обращенная ветвями вниз, при этом функция достигает максимума при силе тока \(I_{max}\), равной:
\[{I_{max }} = \frac{{\rm E}}{{2r}}\;\;\;\;(4)\]
Если подставить \(I_{max}\) в (3), то получим искомое значение максимальной мощности во внешней цепи \(P_{max}\):
\[{P_{max}} = {\rm E}{I_{max}} – I_{max}^2r\]
Учитывая (4), имеем:
\[{P_{max}} = \frac{{{{\rm E}^2}}}{{2r}} – \frac{{{{\rm E}^2}}}{{4r}}\]
\[{P_{max}} = \frac{{{{\rm E}^2}}}{{4r}}\;\;\;\;(5)\]
Получается нам нужно найти значения ЭДС \(\rm E\) и внутреннего сопротивления \(r\).
2}}}{{4 \cdot 2 \cdot 5 \cdot \left( {5 – 2} \right) \cdot \left( {24 \cdot 5 – 30 \cdot 2} \right)}} = 32\;Вт\]
Ответ: 32 Вт.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
7.4.52 Два чайника, каждый из которых потребляет при напряжении 200 В по 400 Вт, закипают
7.4.54 Элемент замыкают один раз сопротивлением 4 Ом, другой – резистором сопротивлением 9 Ом
7.4.55 Сила тока, протекающего в проводнике, сопротивление которого равно 15 Ом, меняется
Voltage — Если ватты это мощность, а амперы это ток, то что такое вольты
спросил
Изменено 8 лет, 11 месяцев назад
Просмотрено 1к раз
\$\начало группы\$
Я знаю, что мощность измеряется в ваттах, а ток измеряется в амперах, так что X означает напряжение?
- напряжение
- Вт
- сила тока
\$\конечная группа\$
6
\$\начало группы\$
- мощность измеряется в ваттах
- ток измеряется в амперах
- электрический потенциал измеряется в вольтах
\$\конечная группа\$
\$\начало группы\$
Напряжение – это разница в энергии между двумя точками электрического поля, выраженная на единицу заряда .
Вольт — это джоуль на кулон: \$V = J/C\$. Напряжение между двумя точками говорит нам, сколько энергии получит или потеряет каждый электрон, перемещаясь между этими двумя точками.
Разделение противоположных зарядов накапливает энергию. Если мы разделим заряды так, что между ними будет один вольт, это будет меньше энергии, чем если мы разделим те же самые заряды так, что между ними будет два вольта. И, конечно же, мы храним больше энергии, разделяя больше зарядов при том же напряжении.
Вот почему мощность связана как с током, так и с напряжением.
\$\конечная группа\$
4
\$\начало группы\$
\$1V=\dfrac{1J}{C}\$
\$1A=\dfrac{1C}{s}\$
\$\следовательно, P=IV=\dfrac{C}{s} \dfrac{J}{C}=\dfrac{J}{s}=W\$
Любая из различных формул для мощности может быть получена с использованием этих соотношений.
\$\конечная группа\$
\$\начало группы\$
В викторианских учебниках это прекрасно описано, и инженеры, более привыкшие к гидравлике или пару, знакомятся с электричеством…
- Мощность эквивалентна гидравлической мощности;
- Ток эквивалентен току;
- и Напряжение эквивалентно давлению.
На самом деле примерно до 1920-х годов в учебниках говорилось об «электрическом напряжении, измеряемом в вольтах».
Это действительно хорошая аналогия в том смысле, что концепции прекрасно переводятся и действительно помогают понять разницу между напряжением и током и принципом работы цепей.
\$\конечная группа\$
7
Напряжение – это разность электрической потенциальной энергии.
Думайте об этом как о гравитации, но для силы между электронами, а не для силы притяжения между двумя объектами с массой.
Google определяет его как
Единица СИ электродвижущей силы, разность потенциалов, будет нести ток в один ампер при сопротивлении в один ом.
\$\конечная группа\$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
Как переменный ток может питать что-либо?
Я чувствую, что вы неправильно понимаете, как энергия постоянного тока передается от источника к нагрузке, что мешает вам понять, как передается энергия переменного тока.
У многих людей в голове возникает картина, что источник энергии каким-то образом дает энергию электронам. Затем электроны текут по проводу, несущему эту энергию, а затем каким-то образом высвобождают энергию, когда электроны проходят через нагрузку. Могу поспорить, что ваше ментальное представление об электричестве примерно такое. И если это близко к тому, как вы смотрите на электричество, то вопрос о том, как источник энергии переменного тока передает энергию, вызывает недоумение. В конце концов, электроны не текут назад и вперед 50 или 60 раз в секунду от лампочки на вашей кухне до генератора на электростанции. Мы знаем, что электроны движутся намного, намного медленнее (они движутся порядка метра в час, в зависимости от ряда факторов, таких как сила тока, размер проводника и т.
Но это не так. Энергия не переносится от источника к нагрузке через электроны. Энергия даже не течет по проводам. Вместо этого электрическая энергия передается от источника электричества к электрической нагрузке через электромагнитное (ЭМ) поле в пространстве, окружающем источник, провода и нагрузку.
Посмотрите на рисунок ниже: цепь постоянного тока, состоящая из батареи, провода и резистора. Зеленые стрелки представляют собой магнитное поле, возникающее из-за протекания тока. Красные стрелки представляют электрическое поле из-за источника напряжения. Синие стрелки представляют собой плотность потока энергии или вектор Пойнтинга, который представляет собой векторное произведение электрического и магнитного полей. Вектор Пойнтинга можно рассматривать как скорость передачи энергии на единицу площади.
Обратите внимание, что поток энергии идет от батареи к резистору. Также обратите внимание, что энергия поступает в резистор не от провода, а через пространство, окружающее провода.
Если вы замените источник постоянного тока на источник переменного тока, вы сможете убедиться, глядя на электрические и магнитные поля, что вектор Пойнтинга по-прежнему указывает от источника к нагрузке, даже если ток меняет направление. . Поскольку вектор Пойнтинга представляет собой векторное произведение двух полей, его направление остается неизменным даже при изменении полей.
В комментариях были некоторые вопросы по поводу научной обоснованности того, что я сказал выше. То, как электромагнитная энергия распространяется по цепям, было известно уже давно… по крайней мере, с конца 1800-х годов. Вектор Пойнтинга, названный в честь Джона Генри Пойнтинга, который объяснил эту теорию в статье 1884 года под названием «О передаче энергии в электромагнитном поле» . Статья довольно читабельна и хорошо объясняет теорию.
Раньше течение считалось чем-то, движущимся по дирижера, причем внимание в основном обращено на дирижера, а энергия, появившаяся на каком-либо участке цепи, если рассматривать ее в все, должно было быть доставлено туда через кондуктора Текущий. Но существование индуцированных токов и электромагнитных действия на расстоянии от первичного контура, из которого они черпают их энергия привела нас под руководством Фарадея и Максвелла к смотреть на среду, окружающую дирижера, как на очень важную роль в развитии явлений. Если мы верим в непрерывности движения энергии, т. е. если мы считаем, что когда он исчезает в одном месте и появляется в другом, он должен прошли через промежуточное пространство, мы вынуждены заключить, что окружающая среда содержит по крайней мере часть энергии, и что он способен передавать его из точки в точку.
Далее он говорит:
Начиная с теории Максвелла, мы, естественно, приходим к рассмотрению проблемы: как энергия электрического тока переходит из точки в точку, то есть какими путями и по какому закону он перемещается от части цепи, где он впервые распознается как электрический и магнитный, к частям, где он превращается в тепло или другие формы?
Целью этой статьи является доказательство того, что существует общий закон для передача энергии, согласно которой он движется в любой точке перпендикулярно плоскости, содержащей силовые линии электрического поля и магнитная сила, и что количество, пересекающее единицу площади на секунда этой плоскости равна произведению интенсивностей две силы, умноженные на синус угла между ними, деленные на \$4\pi\$, а направление потока энергии такое, в котором правый винт будет двигаться, если его повернуть от положительного направление электродвигателя к положительному направлению магнитная напряженность.
Затем он показывает, как энергия проникает в провод и нагревает его:
Тогда кажется, что никакая энергия тока не движется по провода, но что он поступает из непроводящей среды, окружающей провод, который, как только он входит, начинает преобразовываться в тепла, количество пересекающих последовательные слои проволоки уменьшается пока не будет достигнут центр, где нет магнитного поля. сила, и поэтому никакая энергия не проходит, все это было преобразовано в тепло. Тогда можно сказать, что ток проводимости состоит из этого внутренний поток энергии с сопровождающими его магнитными и электродвижущими силы и превращение энергии в тепло в проводник.
Ричард Фейнман также говорит об этом в своих лекциях по физике. После объяснения этого явления Фейнман выводит, как зарядный конденсатор получает свою энергию, а затем говорит:
.Но это говорит нам о странной вещи: когда мы заряжаем конденсатор, энергия не поступает по проводам; он входит через края щели.
Затем Фейнман, как и Пойнтинг, объясняет, как энергия поступает в провод:
В качестве другого примера мы спрашиваем, что происходит с отрезком провода сопротивления. когда он несет ток. Так как провод имеет сопротивление, то электрическое поле вдоль него, приводящее в движение ток. Потому что есть падение потенциала вдоль провода, там тоже есть электрическое поле как раз вне проволоки, параллельно поверхности. Есть, кроме того, магнитное поле, которое огибает провод из-за электрический ток. E и B находятся под прямым углом; поэтому есть Вектор Пойнтинга направлен радиально внутрь, как показано на рисунке. Энергия течет по проводу со всех сторон. Это, конечно, равна энергии, теряемой в проводе в виде тепла. Итак, наш «сумасшедшая» теория говорит, что электроны получают свою энергию для выделять тепло из-за энергии, поступающей в провод от поле снаружи. Интуиция, казалось бы, подсказывает нам, что электроны получают их энергия от проталкивания по проводу, поэтому энергия должна быть течет вниз (или вверх) по проводу.
