Constant-Current — Электрический ток в физике

Электрическая энергия легко преобразуется в другие виды энергии — механическую, химическую, световую, внутреннюю энергию вещества, что широко применяется в промышленности и в быту.

Мерой изменения энергии электрического тока служит работа источника тока, создающего и поддерживающего электрическое поле в цепи.

Стационарное электрическое поле, перемещающее заряды по проводнику, совершает работу. Эту работу называют работой тока. Работа электрического тока на участке цепи, как следует из определения напряжения,

где q — электрический заряд, проходящий по участку цепи, а U — напряжение на участке.

Учитывая, что q = It, где I — сила тока в проводнике, а t — время прохождения электрического тока, для работы тока получим

Если R — сопротивление однородного участка цепи, то, используя закон Ома для участка цепи, можно получить формулу для расчета работы тока:

Если участок цепи не является однородным, то работу совершает не только стационарное электрическое поле, но и сторонние силы, и полная работа определяется по формуле

По вышеприведенным формулам можно рассчитать полную работу тока на данном участке цепи.

Если в цепи есть электродвигатель, то энергия электрического тока, во-первых, расходуется на совершение механической работы — полезная работа Ameh, во-вторых, затрачивается на нагревание обмоток электродвигателя и соединительных проводов — теряемая энергия. В этом случае коэффициент полезного действия можно рассчитать как

Говоря о коэффициенте полезного действия источника тока, под полезной работой подразумевают работу, совершаемую во внешней цепи постоянного тока:

Затраченная же работа источника тока равна работе сторонних сил:

где .

Тогда .

КПД источника , где U — напряжение во внешней цепи (напряжение на полюсах источника тока). Графическая зависимость η = f(R) при r = const приведена на рис. 1.

Рис. 1

Единица работы электрического тока в СИ — джоуль (Дж). 1 Дж представляет работу тока, эквивалентную механической работе в 1 Дж. 1 Дж = Кл·В = А·В·с.

Измеряют работу электрического тока счетчиками.

Скорость совершения работы тока на данном участке цепи характеризует мощность тока. Мощность тока определяют по формуле или P = IU.

Используя закон Ома для участка цепи, можно записать иначе формулу для мощности тока: . В этом случае речь идет о тепловой мощности.

Единица мощности тока — ватт: 1 Вт = Дж/с. Отсюда Дж = Вт·с.

Кроме того, применяют внесистемные единицы: киловатт-час или гектоватт-час: 1 кВт·ч = 3,6·106 Дж = 3,6 МДж; 1 гВт·ч = 3,6·105 Дж = 360 кДж.

Для измерения мощности тока существуют специальные приборы — ваттметры.

В электрической цепи при прохождении тока происходит ряд превращений энергии. Во внешнем участке цепи работу по перемещению заряда совершают силы стационарного электрического поля и энергия этого поля превращается в другие виды: механическую, тепловую, химическую, в энергию электромагнитного излучения.

Следовательно, полная работа тока на внешнем участке цепи

Если же на участке цепи под действием электрического поля не совершается механическая работа и не происходят химические превращения, то работа электрического тока приводит только к нагреванию проводника.

В этом случае количество выделившейся теплоты равно работе, совершаемой током.

Количество теплоты Q, выделяемой током I за время t на участке цепи сопротивлением R, равно .

Эта формула выражает закон Джоуля—Ленца, установленный опытным путем в XIX в. двумя учеными (английским — Дж. Джоулем и русским Э. X. Ленцем).

При прохождении электрического тока по проводнику количество теплоты, выделяющейся в проводнике, прямо пропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока.

На законе Джоуля Ленца основано действие многих электронагревательных приборов. Это утюги, электроплиты, электрочайники, кипятильники, паяльники, электрокамины и т.

д.

Основной частью любого электронагревательного прибора является нагревательный элемент (проводник с большим удельным сопротивлением наматывается на пластинку из жаростойкого материала: слюды, керамики).

Вышеприведенную формулу закона Джоуля—Ленца удобно применять при последовательном соединении резисторов, так как сила тока во всех участках последовательно соединенной цепи одинакова. Если последовательно соединены два резистора с сопротивлениями R1 и R2, то , откуда , т.е. количество теплоты, выделяемой током в участках последовательно соединенной цепи, пропорционально сопротивлениям этих участков.

Согласно закону Ома, для однородного участка цепи постоянного тока . Тогда .

Эту формулу удобно использовать при параллельном соединении резисторов, так как напряжение на каждой ветви такой цепи одинаково. Если параллельно соединены два резистора с сопротивлениями R1 и R2, то , откуда

т.е. количество теплоты, выделяемой током в ветвях параллельно соединенной цепи, обратно пропорционально сопротивлениям резисторов, включенных в эти ветви.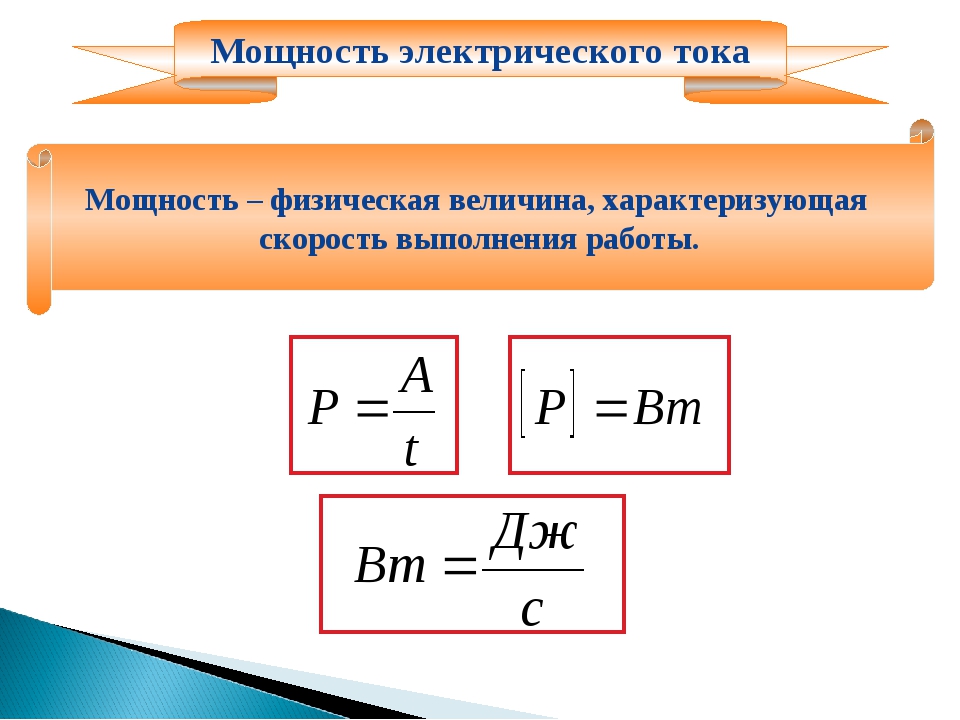

Работа и мощность тока

При протекании тока по однородному участку цепи электрическое поле совершает работу. За время Δt по цепи протекает заряд Δq = IΔt. Электрическое поле на выделенном участке совершает работу

ΔA = (φ1 – φ2)Δq = Δφ12IΔt = UIΔt,

где U = Δφ₁₂ – напряжение. Эту работу называют работой электрического тока. 

Если обе части формулы

RI = U,

выражающей закон Ома для однородного участка цепи с сопротивлением R, умножить на IΔt, то получится соотношение

RI2Δt = UIΔt = ΔA.

 

Это соотношение выражает закон сохранения энергии для однородного участка цепи.

Работа ΔA электрического тока I, протекающего по неподвижному проводнику с сопротивлением R, преобразуется в тепло ΔQ, выделяющееся на проводнике.

ΔQ = ΔA = RI 2Δt.

 

Закон преобразования работы тока в тепло был экспериментально установлен независимо друг от друга Дж. Джоулем и Э. Ленцем и носит название закона Джоуля–Ленца.

Мощность электрического тока равна отношению работы тока ΔA к интервалу времени Δt, за которое эта работа была совершена:

 

Работа электрического тока в СИ выражается в

джоулях (Дж), мощность – в ваттах (Вт).

Рассмотрим теперь полную цепь постоянного тока, состоящую из источника с электродвижущей силой и внутренним сопротивлением r и внешнего однородного участка с сопротивлением R. Закон Ома для полной цепи записывается в виде

(R + r)I = ε.

 

Умножив обе части этой формулы на Δq = IΔt, мы получим соотношение, выражающее закон сохранения энергии для полной цепи постоянного тока:

RI2Δt + rI2Δt =  IΔt = ΔAст.

 

Первый член в левой части ΔQ = RI²Δt – тепло, выделяющееся на внешнем участке цепи за время Δt, второй член ΔQ_ист = rI²Δt – тепло, выделяющееся внутри источника за то же время.

Выражение IΔt равно работе сторонних сил ΔA_ст, действующих внутри источника.

При протекании электрического тока по замкнутой цепи работа сторонних сил ΔA_ст

преобразуется в тепло, выделяющееся во внешней цепи (ΔQ) и внутри источника (ΔQ_ист).

ΔQ + ΔQист = ΔAст =  IΔt .

 

Следует обратить внимание, что в это соотношение не входит работа электрического поля. При протекании тока по замкнутой цепи электрическое поле работы не совершает; поэтому тепло производится одними только сторонними силами, действующими внутри источника. Роль электрического поля сводится к перераспределению тепла между различными участками цепи.

Внешняя цепь может представлять собой не только проводник с сопротивлением R, но и какое-либо устройство, потребляющее мощность, например, электродвигатель постоянного тока. В этом случае под R нужно понимать эквивалентное сопротивление нагрузки. Энергия, выделяемая во внешней цепи, может частично или полностью преобразовываться не только в тепло, на и в другие виды энергии, например, в механическую работу, совершаемую электродвигателем. Поэтому вопрос об использовании энергии источника тока имеет большое практическое значение.

Полная мощность источника, то есть работа, совершаемая сторонними силами за единицу времени, равна

Во внешней цепи выделяется мощность

Отношение равное

называется коэффициентом полезного действия источника.  

На рис. 1.4.13 графически представлены зависимости мощности источника P_ист , полезной мощности P, выделяемой во внешней цепи, и коэффициента полезного действия η от тока в цепи I для источника с ЭДС, равной , и внутренним сопротивлением r. Ток в цепи может изменяться в пределах от I = 0 (при ) до (при R = 0).

1

Рисунок 1.4.13 Зависимость мощности источника Pист, мощности во внешней цепи P и КПД источника η от силы тока.

Из приведенных графиков видно, что максимальная мощность во внешней цепи P_max , равная

достигается при R = r. При этом ток в цепи

а КПД источника равен 50 %. Максимальное значение КПД источника достигается при I → 0, то есть при R → ∞. В случае короткого замыкания полезная мощность P = 0 и вся мощность выделяется внутри источника, что может привести к его перегреву и разрушению. КПД источника при этом обращается в нуль

МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:

Рис. 2.

Соберите на экране цепь, показанную на рис. 2. Для этого сначала щелкните левой кнопкой мыши над кнопкой э.д.с. в нижней части экрана. Переместите маркер мыши на рабочую часть экрана, где расположены точки. Щелкните левой кнопкой мыши в рабочей части экрана, где будет расположен источник э.д.с.

Разместите далее последовательно с источником резистор, изображающий его внутреннее сопротивление (нажав предварительно кнопку в нижней части экрана) и амперметр (кнопка там же). Затем расположите аналогичным образом резисторы нагрузки и вольтметр , измеряющий напряжение на нагрузке.

Подключите соединительные провода. Для этого нажмите кнопку провода внизу экрана, после чего переместите маркер мыши в рабочую зону схемы. Щелкайте левой кнопкой мыши в местах рабочей зоны экрана, где должны находиться соединительные провода.

4. Установите значения параметров для каждого элемента. Для этого щелкните левой кнопкой мыши на кнопке со стрелкой . Затем щелкните на данном элементе. Подведите маркер мыши к движку появившегося регулятора, нажмите на левую кнопку мыши и, удерживая ее в нажатом состоянии, меняйте величину параметра и установите числовое значение, обозначенное в таблице 1 для вашей бригады.

Таблица 1. Исходные параметры электрической цепи

Номер бригады	1	2	3	4	5	6	7	8
Е, В	10,0	9,5	9,0	8,5	8,0	8,5	9,0	9,5
r, Ом	4,8	5,7	6,6	7,5	6,4	7,3	8,2	9,1

5.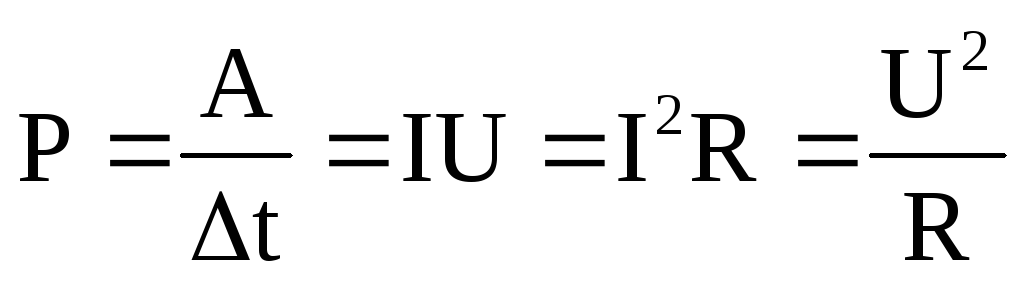 Установите сопротивление внешней цепи 2 Ом, нажмите кнопку «Счёт» и запишите показания электроизмерительных приборов в соответствующие строки таблицы 2.

6. Последовательно увеличивайте с помощью движка регулятора сопротивление внешней цепи на 0,5 Ом от 2 Ом до 20 Ом и, нажимая кнопку «Счёт», записывайте показания электроизмерительных приборов в таблицу 2.

7. Вычислите по формулам (2), (7), (8), (9) Р₁, Р₂, Р_полн и  для каждой пары показаний вольтметра и амперметра и запишите рассчитанные значения в табл.2.

8. Постройте на одном листе миллиметровой бумаге графики зависимости P₁ = f(R), P₂ = f(R), P_полн=f(R),  = f (R) и U = f(R).

9. Рассчитайте погрешности измерений и сделайте выводы по результатам проведённых опытов.

Таблица 2. Результаты измерений и расчётов

R, Ом	2,0	2,5	3,0	…			20
U, В
I, А
P1, Вт
P2, ВТ
Pполн, ВТ


Вопросы и задания для самоконтроля

1. Запишите закон Джоуля-Ленца в интегральной и дифференциальной формах.

2. Что такое ток короткого замыкания?

3. Что такое полная мощность?

4. Как вычисляется к.п.д. источника тока?

5. Докажите, что наибольшая полезная мощность выделяется при равенстве внешнего и внутреннего сопротивлений цепи.

6. Верно ли утверждение, что мощность, выделяемая во внутренней части цепи, постоянна для данного источника?

7. К зажимам батарейки карманного фонаря присоединили вольтметр, который показал 3,5 В.

8. Затем вольтметр отсоединили и на его место подключили лампу, на цоколе которой было написано: Р=30 Вт, U=3,5 В. Лампа не горела.

9. Объясните явление.

10.При поочерёдном замыкании аккумулятора на сопротивления R1 и R2 в них за одно и то же время выделилось равное количество тепла. Определите внутреннее сопротивление аккумулятора.

электрических цепей — Почему мы берем комплексный ток, почему не только действительную часть и аналогично силовую формулу, почему мы используем комплексно-сопряженное значение тока?

Комплексная экспонента используется потому, что при выводе этих формул из соответствующих дифференциальных уравнений обычным методом решения является «подстановка». Производная комплексной экспоненты пропорциональна самой себе, а это означает, что мы можем легко использовать замену, чтобы найти соответствующее соотношение дисперсии (поскольку константы пропорциональности сокращаются). Технически мы могли бы использовать обычные тригонометрические функции, однако с их производными гораздо сложнее получить какое-либо дисперсионное соотношение. Наконец, мы можем доказать, что re{} решения комплексного уравнения является решением некомплексного дифференциального уравнения.

Еще одна причина, по которой мы можем захотеть использовать комплексные числа для представления определенных величин, — компактность записи.

Возьмите закон Ома для частотно-зависимых электрических полей.

$$\vec{J} = re(\sigma \vec{E})$$

Здесь используется комплексное значение $\sigma$, что позволяет легко записать соответствующую величину плотности тока, и ТАКЖЕ аккуратно инкапсулирует соответствующую разность фаз между приложенным электрическим полем и плотностью тока.