HydroMuseum – Вольтампер
Выберите терминВакуумный насосВалВводы трансформаторовВентиляция генератораВероятность максимального расходаВероятность разрушенияВерховой клин (грань) плотиныВес сооруженийВетроводородные электростанцииВетровой нагонВетроэлектростанцияВетроэнергетическая установкаВечная мерзлотаВзаимная индукцияВибрации агрегатаВибрирование бетонаВизуальный контрольВинтовой насосВодное хозяйствоВодноэнергетическая установкаВодноэнергетические расчётыВодный транспортВодобойные устройства (гасители)Водовод турбин 2Водоводы турбинВодозаборВодомётный движительВодоотведениеВодоподпорное сооружениеВодоподъёмное колесоВодопользованиеВодопотреблениеВодоприёмникВодоприёмные устройстваВодопроводящее сооружениеВодопроницаемостьВодосбросное устройствоВодосбросные плотиныВодосливВодоснабжениеВодоспускВодохозяйственные расчетыВодохранилищеВодяное колесоВозбудительВозбуждение генератораВоздуходувкаВоздухосборники (ресиверы)Возобновляемые источники энергииВозобновляемые энергетические ресурсыВольтВольтамперВосполнимая энергия водотокаВосстанавливаемый элемент, узелВосстановление напряженияВосстановление работоспособностиВращающееся магнитное полеВращающий момент турбиныВращающийся векторВременная нагрузкаВременная неравномерность регулированияВременные ГТСВсасывающие патрубки линииВскрышные работыВторичная цепьВторостепенные ГТСВыклинивание водохранилищаВыключательВыключатель высоковольтныйВыключатель масляныйВыключатель нагрузкиВыключатель электромагнитный
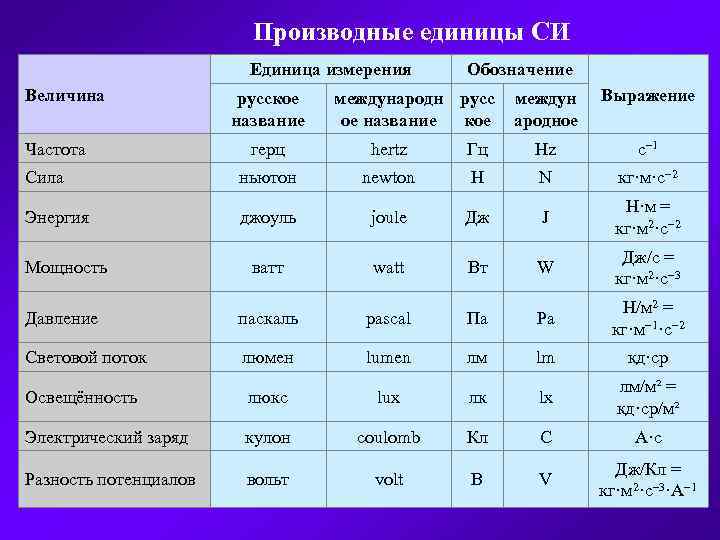
Вольтампер ─ произведение
среднеквадратических (эффективных) значений напряжения в вольтах или
киловольтах и силы тока в амперах.
Единица измерения полной мощности.
Вольтампер (обозначается В·А или V·A) — единица измерения электрической мощности в системе СИ, эквивалентная ватту (Вт). Используется в качестве единицы измерения величины полной мощности переменного тока.
Полная мощность переменного тока определяется как произведение действующего значения силы тока в цепи и действующего значения напряжения на её концах. Иногда полную мощность называют кажущейся, подчёркивая то обстоятельство, что эта мощность может не вся участвовать в совершении работы. Скорость совершения работы электрического тока равна активной мощности цепи и всегда не превышает полной мощности.
Полная
мощность и активная мощность — разные физические величины, имеющие размерность
мощности. Для того, чтобы на маркировках электроприборов или в технической
документации не требовалось лишний раз указывать, о какой мощности идёт речь, и
при этом не спутать эти физические величины, в качестве единицы измерения
полной мощности используют вольт-ампер вместо ватта.
Отношение активной мощности к полной мощности цепи называется коэффициентом мощности.
Нередко
единицу измерения вольт-ампер ошибочно отождествляют с физической величиной
полной мощности, в результате чего говорят о вольт-ампере и ватте как о
неэквивалентных единицах, хотя правильно было бы говорить о различии физических
величин. На самом деле, физическая величина и её размерность — разные понятия.
Две физические величины могут иметь одинаковую размерность (т. е. измеряться в
одних единицах или единицах, отличающихся только безразмерным сомножителем), но
иметь различный смысл. В эквивалентности вольт-ампера и ватта легко убедиться,
если вспомнить, что отношение активной и полной мощностей есть безразмерная
величина. Использование вольт-ампера для величины полной мощности является
соглашением, принятым по соображениям удобства и наглядности.
Операции с несколькими кубитами — Azure Quantum
- Статья
- Чтение занимает 13 мин
В этой статье изучаются правила создания многокубитных состояний из однокубитных состояний и операции с вентилями, которые должны присутствовать в множестве вентилей для создания универсального многокубитного квантового компьютера. Эти инструменты необходимы для изучения множеств вентилей, которые широко используются в коде Q#, и понимания того, как запутывание, интерференция и другие квантовые эффекты позволяют сделать квантовые вычисления более мощными, чем классические.
Истинная сила квантовых вычислений становится очевидной только по мере увеличения числа кубитов.
Однокубитные вентили имеют ряд необычных свойств, например возможность находиться одновременно в нескольких состояниях. Тем не менее, если все, что у вас было в квантовом компьютере, были однокубитными шлюзами, то калькулятор и, конечно, классический суперкомпьютер затмили бы его вычислительную мощность.
Мощь квантовых вычислений обуславливается тем, что размерность векторного пространства с векторами квантовых состояний растет экспоненциально с увеличением числа кубитов. Поэтому мы можем легко смоделировать работу одного кубита, но квантовые вычисления по пятидесяти кубитам уже упираются в пределы возможностей любого из существующих суперкомпьютеров. При увеличении объема вычислений на один кубит удваивается требуемый объем памяти для хранения состояний и почти удваивается длительность вычислений. Такой резкий рост вычислительной мощности легко объясняет, почему квантовый компьютер даже с относительно малым числом кубитов способен превзойти на некоторых типах вычислений не только самые мощные суперкомпьютеры из ныне существующих, но и любые теоретически возможные.
Если вам предоставляются два отдельных кубита, один в состоянии$\psi=\begin{bmatrix}\\\end{bmatrix}$\alpha\beta, а другой в состоянии $\phi=\begin{bmatrix}\\\delta\gamma\end{bmatrix}$, соответствующее двухкубитное состояние задается тензорным произведением (или произведением Кронекера векторов, которое определяется следующим образом.
$$\psi\otimes\phi=\begin{bmatrix}\alpha\\\beta\end{bmatrix}\otimes\begin{bmatrix}\gamma\\\delta\end{bmatrix}=\begin{bmatrix}\alpha\begin{bmatrix}\gamma\\\delta\end{bmatrix}\\\beta\begin{bmatrix}\gamma\\\delta\end{bmatrix}\end{bmatrix}=\begin{bmatrix}\alpha\gamma\\\alpha\delta\\\beta\gamma\\\beta\delta\end{bmatrix}. $$
Таким образом, для двух однокубитных состояний $\psi$ и $\phi$, каждое из которых имеет размерность 2, соответствующее им двухкубитное состояние $\psi\otimes\phi$ является уже 4-мерным. Вектор
$$\begin{bmatrix}\alpha_{{00}\\\alpha_{{01}\\\alpha_{{10}\\\alpha_{{11}\end{bmatrix}$$
представляет квантовое состояние двух кубитов, если $|\alpha_{00}|^2+|\alpha_{01}|^2+|\alpha_{{10}|^2+|\alpha_{11}|^2=1$.
n$. Как и с одиночными кубитами, вектор квантового состояния для нескольких кубитов содержит всю информацию, необходимую для описания поведения системы. Дополнительные сведения о векторах и тензорных произведениях см. в статье Векторы и матрицы в квантовых вычислениях.
Вычислительный базис для двухкубитных состояний формируется тензорным произведением однокубитных состояний. Например, у вас есть
\begin{align} 00 \equiv\begin{bmatrix}1 \\ 0 \end{bmatrix}\otimes\begin{bmatrix}1 \\ 0 \end{bmatrix}&=\begin{bmatrix}1 \\ 0\\ 0\\ 0 \end{bmatrix},\qquad 01 \equiv\begin{bmatrix}1 \\ 0 \end{bmatrix}\otimes\begin{bmatrix}0 \\ 1 \end{bmatrix}=\begin{bmatrix}0 \\ 1\\ 0\\ 0 \end{bmatrix},\\ 10 \equiv\begin{bmatrix}0 \\ 1 \end{bmatrix}\otimes\begin{bmatrix}1 \\ 0 \end{bmatrix}&=\begin{bmatrix}0 \\ 0\\ 1\\ 0 \end{bmatrix},\qquad 11 \equiv\begin{bmatrix}0 \\ 1 \end{bmatrix}\otimes\begin{bmatrix}0 \\ 1 \end{bmatrix}=\begin{bmatrix}0 \\ 0\\ 0\\ 1 \end{bmatrix}. \end{align}
Обратите внимание, что хотя вы всегда можете использовать тензорное произведение двух однокубитных состояний, чтобы сформировать двухкубитное состояние, не все двухкубитные квантовые состояния могут быть записаны как тензорное произведение двух однокубитных состояний.
Например, не существует таких состояний $\psi=\begin{bmatrix}\alpha\\\beta\end{bmatrix}$ и $\phi=\begin{bmatrix}\gamma\\\delta\end{bmatrix}$, чтобы их тензорное произведение соответствовало состоянию
$$\psi\otimes\phi=\begin{bmatrix} 1/\sqrt{{2}\\ 0 \\ 0 \\ 1/\sqrt{{2}\end{bmatrix}.$$
Такое двухкубитное состояние, которое невозможно выразить через тензорное произведение однокубитных состояний, называется &состоянием запутанности&, а два кубита в этом случае называются запутанными. Грубо говоря, информация, хранимая состоянием, не принадлежит ни одному из кубитов по отдельности, так как квантовое состояние нельзя рассматривать как тензорное произведение однокубитных состояний. Эта информация хранится нелокально, как набор корреляций между двумя состояниями. Такой нелокальный характер информации является основным отличием квантовых вычислений от классических и именно он применяется во многих квантовых протоколах, таких как квантовая телепортация и квантовая коррекция ошибок.
\dagger$.
Например, вентиль CNOT (контролируемое НЕ), который обычно применяется для операций с двумя кубитами, выражается следующей унитарной матрицей:
$$\operatorname{CNOT}=\begin{bmatrix} 1\ 0\ 0\ 0 \\ 0\ 1\ 0\ 0 \\ 0\ 0\ 0\ 1 \\ 0\ 0\ 1\ 0 \end{bmatrix}$$
Также мы можем создать двухкубитные вентили, применив однокубитные вентили к обоим кубитам. Например, при применении вентилей
$$\begin{bmatrix} a\ b\\ c\ d \end{bmatrix}$$
и
$$\begin{bmatrix} e\ f\\ g\ h \end{bmatrix}$$
к первому и второму кубитам, соответственно, это эквивалентно применению унитарного двухкубитного, заданного их тензорным произведением: $$\begin{bmatrix} a\ b\\ c\ d \end{bmatrix}\begin{bmatrix}\otimese\ f\\ g\ h \end{bmatrix}=\begin{bmatrix} ae\ af\ be\ bf \\ ag\ ah\ bg\ bh \\ ce\ cf\ de\ df \\ cg\ ch\ dg\ dh .\end{bmatrix}$$
Таким образом, можно сформировать двухкубитные ворота, взяв тензорное произведение некоторых известных однокубитных вентилей. Вот несколько примеров типичных двухкубитных вентилей: $H \otimes H$, $X \otimes\boldone$, $X \otimes Z$.
Еще раз обратим ваше внимание: тензорное произведение любого сочетания однокубитных вентилей определяет некоторый двухкубитный вентиль, но обратное утверждение неверно. Не каждый двухкубитный вентиль можно выразить как тензорное произведение сочетания однокубитных вентилей. Такие двухкубитные вентили называются запутывающими. Примером запутывающего вентиля является уже знакомый нам CNOT.
Интуитивные выводы, примененные к вентилю «управляемое НЕ», можно распространить и на любые другие вентили. Управляемый шлюз в целом — это шлюз, который выступает в качестве удостоверения (например, он не имеет никаких действий), если конкретный кубит не равен $1$. Вы обозначаете контролируемый унитарный объект, контролируемый в данном случае на кубите с меткой $x, с $\Lambdaпомощью _x(U)$$. В качестве примера возьмем $\Lambda_0(U) e_{1}\otimes{\psi}=e_{1}\otimes U{\psi}$ и $\Lambda_0(U) e_{{0}\otimes{\psi}=e_{{0}\otimes{\psi}$, где $e_0$ и $e_1$ являются векторами вычислительного базиса для одного кубита, соответствующими значениям $0$ и $1$.
Например, рассмотрим следующий контролируемый шлюз Z$$, чтобы выразить это как $$\Lambda_0(Z)\begin{bmatrix}=1&0 0&0&0\\0 1&&0 0&0\\0&0 0 1&&0 0\\0&0-1&&\end{bmatrix}= (\boldone\otimes H)\operatorname{CNOT}(\boldone\otimes H).
$$
Эффективное создание контролируемых унитарных преобразований — непростая задача. Простейшим подходом является реализация базы данных управляемых версий базовых вентилей с последующей заменой каждого базового вентиля в исходной унитарной операции на управляемый аналог. Но этот подход часто очень избыточен, и тщательный анализ часто позволяет получить аналогичный результат заменой всего нескольких вентилей на управляемые аналоги. По этой причине платформа предоставляет возможность выполнять либо наивный метод управления, либо позволить пользователю определить управляемую версию унитарного объекта, если известна оптимизированная версия, настроенная вручную.
Для управления вентилями можно применять информацию из классических вычислений.
Например, вентиль «НЕ», управляемый классической информацией, применяется не всегда, а только в том случае, когда некоторый классический (а не квантовый) бит имеет значение $1$. В некотором смысле управляемый классической информацией вентиль можно рассматривать как оператор ветвления в квантовом коде, после которого вентиль применяется только в одной ветви алгоритма.
Как и в случае с одним кубитом, множество двухкубитных вентилей считается универсальным, если любая матрица унитарных операций $4\times 4$ может быть с произвольной точностью приближенно выражена как произведение вентилей из этого множества. Например, универсальным является следующее множество вентилей: вентиль Адамара, T и CNOT. Принимая продукты этих вентилей, вы можете приблизить любую унитарную матрицу на двух кубитах.
Квантовая запутанность
Рассмотрим два кубита $A$ и $B$ в суперпозициях, чтобы состояние глобальной системы было равно
$$\ket{\psi}_{AB}=\frac1{\sqrt2}\ket{{00}\frac1{\sqrt2}\ket{{11}$$
В таком состоянии при измерении состояния обоих кубитов в стандартном режиме возможны только два результата: $|00\rangle$ и $|11\rangle$.
Обратите внимание, что каждый результат имеет одинаковую вероятность $\frac{1}{2}$. Вероятность получения $|01 и 10\rangle$\rangle$равна нулю.$| Если вы измеряете первый кубит и получаете, что он находится в $|состоянии 0\rangle$ , вы можете быть положительным, что второй кубит также находится в $|состоянии 0\rangle$ , даже не измеряя его. Результаты измерения коррелируют, а кубиты являются запутанными.
Примечание
В этих примерах используется два кубита, но квантовая запутанность не ограничивается двумя кубитами. Как правило, многокубитные системы имеют общую запутанность.
Запутанные кубиты коррелируются таким образом, что их нельзя описать независимо друг от друга. То есть, какая бы операция ни произошла с состоянием одного кубита в запутанной паре, также влияет на состояние другого кубита.
Практическую реализацию см. в руководстве по изучению квантовой запутанности с помощью Q# и Azure Quantum.
Запутанность в чистых состояниях
Чистые квантовые состояния — это такие состояния, которые характеризуются одним кет-вектором или волновой функцией и не могут быть записаны в виде статистического сочетания (или выпуклой комбинации) других квантовых состояний. На сфере Блоха чистые состояния представлены точкой на поверхности сферы, тогда как смешанные состояния представлены внутренней точкой.
Чистое состояние $\ket{\phi}{AB}$ запутано, если оно не может быть записано как сочетание состояний продукта подсистем, то есть $\ket{\phi}{AB}=\ket{a}_A\ket{\otimes b}_B.$
Например, рассмотрим состояние $$\ket{\psi}_{AB=\frac{}{1}{2} ({00}\ket{ + \ket{{10} +\ket{01} +)\ket{{11}$$
Сначала состояние $\ket{\psi}_{AB}$ не выглядит как состояние продукта, но если мы перезаписываем состояние как
$$\ket{\psi}_{AB}\frac{{2}}{1}{\sqrt{= (\ket{0}_A +{1}\ket{_A) \otimes\frac{1}{\sqrt{{2}} (\ket{{0}_B +\ket{{1}_B)=\ket{+}_A \ket{+_B}$$
состояние $\ket{\psi}_{AB}$ является состоянием продукта, поэтому оно не запутано.
{B}{j}\geq 0.$
Смешанное состояние $\rho$ запутано, если оно не является отделимым, то есть не может быть записано как выпуклое сочетание состояний продукта.
Совет
Отделяемое состояние содержит только классические корреляции.
Основные сведения о классических корреляциях
Классические корреляции обусловлены отсутствием знаний о состоянии системы. То есть, существует некоторая случайность, связанная с классической корреляцией, но она может быть устранена путем получения знаний.
Например, рассмотрим две коробки, каждая из которых содержит один шар. Мы знаем, что оба шара имеют одинаковый цвет, синий или красный. Если мы открываем одну коробку и узнаем, что шарик внутри синий, то мы знаем, что другой шар тоже синий. Поэтому они коррелируются. Тем не менее, неопределенность, которую мы имеем при открытии коробки, связана с нашим отсутствием знаний, это не является фундаментальным. Мяч был синий, прежде чем мы открыли коробку. Таким образом, это классическая корреляция, а не квантовая корреляция.
-})$$
Совет
- Если запутанное состояние $\rho$ чистое, оно содержит только квантовые корреляции.
- Если запутанное состояние $\rho$ является смешанным, оно содержит как классические, так и квантовые корреляции.
Системы с несколькими кубитами
Для создания многокубитных квантовых состояний на основе меньших систем применяется в точности тот же подход, который мы изучили в разделе о двухкубитных системах. Такие состояния получаются вычислением тензорных произведений состояний меньшей размерности. Для примера давайте выразим битовую строку $1011001$ на квантовом компьютере. Это можно закодировать как
$$ 1011001 \equiv\begin{bmatrix} 0 \\ 1 \end{bmatrix}\otimes\begin{bmatrix} 1 \\ 0 \end{bmatrix}\otimes\begin{bmatrix} 0 \\ 1 \end{bmatrix}\otimes\begin{bmatrix} 0 \\ 1 \end{bmatrix}\otimes\begin{bmatrix} 1 \\ 0 \end{bmatrix}\otimes\begin{bmatrix} 1 \\ 0 \end{bmatrix}\otimes\begin{bmatrix} 0 \\ 1 \end{bmatrix}. $$
Квантовые вентили работают точно так же.
Например, если вы хотите применить $шлюз X$ к первому кубиту, а затем выполнить CNOT между вторым и третьим кубитами, можно выразить это преобразование как
\begin{\begin{align}&(X \otimes\operatorname{CNOT}_{12}\otimes\boldone\otimes\boldone\otimes\boldone\otimes\boldone) \begin{bmatrix} 0 \\ 1 \end{bmatrix}\otimes\begin{bmatrix} 1 \\ 0 \end{bmatrix}\otimes\begin{bmatrix} 0 \\ 1 \end{bmatrix}\otimes\begin{bmatrix} 0 \\ 1 \end{bmatrix}\otimes\begin{bmatrix} 1 \\ 0 \end{bmatrix}\otimes\begin{bmatrix} 1 \\ 0 \end{bmatrix}\otimes\begin{bmatrix} 0 \\ 1 \end{bmatrix}\\&\qquad\qquad\equiv 0011001. \end{align}
Во многих системах для работы с кубитами часто требуется выделять и возвращать кубиты, выполняющие роль временного хранилища. Такой кубит называется вспомогательным. По умолчанию можно предположить, что состояние кубита инициализируется $для e_0$ при выделении. Кроме того, можно предположить, что он снова возвращается для $e_0$ перед освобождением. Это очень важное допущение, так как вспомогательные кубиты при освобождении могут становиться запутанными с другими регистрами кубитов, и тогда процесс освобождения повредит вспомогательный кубит.
И наконец, хотя для получения универсального метода квантовых вычислений для двухкубитных квантовых компьютеров нам пришлось добавить новые вентили в множество, при переходе к многокубитным вычислениям ничего добавлять уже не нужно. Вентили $H$, $T$ и CNOT создают универсальное множество вентилей для многокубитных вычислений, так как любое унитарное преобразование по нескольким кубитам можно разделить на последовательность поворотов двух кубитов. Затем вы можете использовать теорию, разработанную для двухкубитного варианта, и снова использовать ее здесь, когда у вас много кубитов.
Примечание
Хотя линейная алгебраическая нотация, которая использовалась до сих пор, безусловно, может использоваться для описания многокубитных состояний, она становится все более громоздкой по мере увеличения размера состояний. Результирующий вектор столбца для строки длиной 7 битов, имеет $128$ измерений, что значительно затрудняет его выражение с помощью описанной выше нотации.
Вместо этого используется
Измерения силы – Развитие организационной и управленческой мудрости – 2-е издание
Брэд С. Андерсон
Стивен Люкс разработал структуру, которая определила три измерения власти. [1]
- Первые два измерения рассматривают власть как относящуюся к конфликтующим интересам сторон.
- Третье измерение исследует, как те, у кого есть власть, могут избежать столкновения интересов, формируя желания и желания других.
Позднее другие ученые определили четвертое измерение, в котором власть рассматривалась как сеть отношений, обеспечивающая опору обществ.
Под властью понимается способность заставить кого-то делать то, что вы хотите. Здесь власть активна в прямых, наблюдаемых конфликтах. Наше внимание сосредоточено на поведении людей при принятии решений, когда интересы разных сторон противоречат друг другу.
В то время как первое измерение власти рассматривает способность одной стороны обеспечить согласие другой стороны в случае конфликта интересов, первое измерение рассматривает то, как обладающие властью подавляют конфликт.
То есть, группа обладает властью, если она может ограничить объем обсуждаемых тем, ограничивая тем самым принятие решений вопросами, которые они считают безопасными. Стороны могут добиться этого с помощью различных средств.
- Принуждение: Вы обеспечиваете подчинение других угрозами лишения. Например, работодатель может сказать: «Сделайте это, или я вас уволю».
- Влияние: Вы обеспечиваете согласие других, не прибегая к угрозам. Вместо этого вы убеждаете других подчиниться с помощью различных средств (например, приводя убедительные аргументы).
- Власть: другие подчиняются вам, потому что признают вашу власть (например, маленький ребенок может подчиняться своим родителям, потому что родители несут ответственность).
- Сила: вы обеспечиваете подчинение других, лишая их возможности несоблюдения (например, полиция может перекрыть дорогу, вынуждая вас искать другой путь домой).
- Манипуляция: вы обеспечиваете соблюдение других требований без их ведома (например, компания может скрывать данные о негативных побочных эффектах своих продуктов, чтобы вы их покупали).
Как при первом, так и при втором измерениях власти существуют конфликты интересов между сторонами. Первое измерение разрешает эти разногласия посредством открытого конфликта, второе — путем подавления способности или желания одной стороны участвовать в публичной битве.
Третье измерение рассматривает способность тех, кто обладает властью, вообще избегать конфликта.
Силой считается умение избегать конфликтов. Те, у кого есть власть, могут формировать восприятие людьми своей ситуации и влиять на то, как они думают и понимают мир. С помощью таких средств те, у кого есть власть, могут формировать предпочтения других до такой степени, что они подчиняются, потому что не способны представить себе альтернативу. Они считают согласие естественным.
Например, компания может продвигать идею о том, что признаком хорошего характера является готовность много работать.
Выходить за рамки служебного долга — это добродетель. Бизнес вознаграждает людей, обладающих этим достоинством, продвижением по службе и продвижением по службе.
Со временем работник, погруженный в эту среду, может прийти к выводу, что тяжелая работа — это добродетель. Когда компания просит этого работника поработать бесплатно сверхурочно в выходные дни, человек может сделать это добровольно. Они жертвуют своим временем на благо компании не по принуждению, а потому, что считают это добродетельным.
Компания сформировала убеждения и предпочтения работника до такой степени, что работник принимает интересы компании.
«Власть наиболее эффективна, когда она наименее заметна», Брэд С. Андерсон, Политехнический университет Квантлена, лицензия CC BY 4.0 / производная от оригинальной работы.
Другой ученый, Мишель Фуко, много писал о власти. Некоторые люди рассматривают его точку зрения как . Д-р Люкс, концептуализировавший первые три измерения, с этим не согласен.
Вот почему этот раздел называется « спорный » четвертое измерение. Однако работа Фуко оказала влияние, и люди классифицируют ее как четвертое измерение власти. Поэтому в данном учебнике он кратко представлен здесь.
Первые три измерения рассматривают власть как репрессию. Они исследуют, как интересы одной стороны могут превалировать над другой посредством:
- Конфликт
- Подавление конфликта или
- Настройка параметров.
Фуко, наоборот, считал власть продуктивной. С помощью силы цивилизации создают вещи.
Одной из наиболее важных вещей, создаваемых обществом, являются индивидуумы или то, что Фуко называл «субъектами». Общество создает субъектов, внушая людям роли и убеждения, передавая им культурные знания, наблюдая за поведением людей и обеспечивая соблюдение норм. Благодаря этим процессам мы создаем врачей, учителей, матерей, отцов и всех остальных субъектов, играющих определенную роль в жизни общества.
Фуко утверждал, что власть активна в «микропрактиках» или повседневной жизни.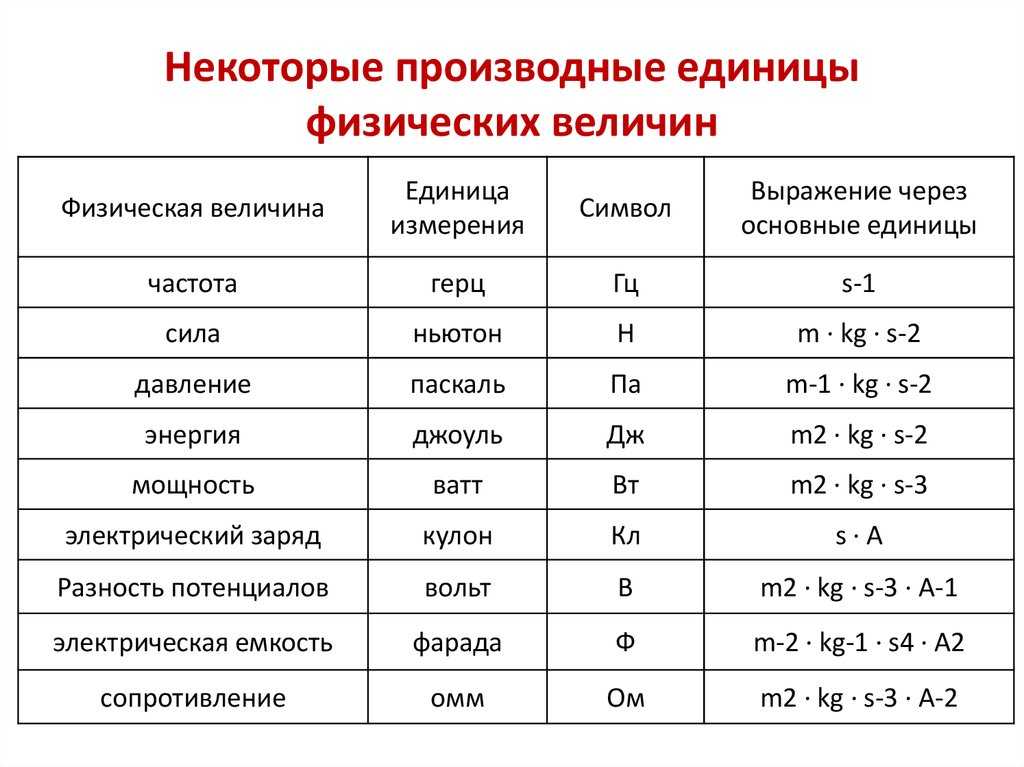
Когда вы обмениваете деньги на кофе, вы укрепляете властные структуры, с помощью которых наше общество создает экономику. Когда вы учитесь, чтобы хорошо сдать экзамен, вы укрепляете властные структуры, через которые наше общество передает знания. Общество — это богатая сеть властных отношений; наши повседневные действия служат созданию и воссозданию этих сетей. [2] [3]
- Ученые классифицируют силу по четырем измерениям.
- Одномерная власть: способность заставить людей делать то, что вы хотите, посредством открытого конфликта
- Двумерная сила: способность получать то, что вы хотите, путем подавления конфликта и ограничения масштабов дебатов
- Трехмерная сила: способность получать желаемое, влияя на предпочтения других
- Четырехмерная власть: плотная паутина сетей власти, посредством которой общества самоорганизуются
- Люкс, С. (2005). Сила: радикальный взгляд (2-е изд. ). Нью-Йорк: Пэлгрейв Макмиллан. ↵
- Фуко, М. (1977). Дисциплина и наказание: рождение тюрьмы. Торонто: Рэндом Хаус. ↵
- Фуко, М. (1978). История сексуальности — Том 1: Введение. Торонто, Канада: Рэндом Хаус. ↵
). Нью-Йорк: Пэлгрейв Макмиллан. ↵Единицы, преобразования и т. д.
Единицы, преобразования и т. д.Гидрология BC ENV 3025
Гидрологические величины
- основные измерения (например, скорость воды в потоке, масса воды в дождевание)
- производные количества (сброс в поток)
Единицы и размеры
- осадки имеют размерность длину [L] и единицу см или мм или дюйм
- многие величины имеют размерность, представляющую собой некоторую комбинацию этих фундаментальных размеры
- в уравнениях размеры с обеих сторон должны соответствовать
- Наиболее распространенная система единиц, используемая сегодня, — это СИ (Международная система д’Юнитес)
| Количество | Блок | |||
| Базовые блоки: | ||||
| длина | метр | |||
| масса | килограмм | |||
| температура | кельвин | |||
| время | секунда | |||
| Производные единицы: | ||||
| район | квадратный метр | |||
| объем | кубический метр | |||
| скорость | метр в секунду | |||
| ускорение | метр в секунду в квадрате | |||
| плотность | килограмм на кубический метр | |||
| сила | ньютон | |||
| давление | паскаль | |||
| напряжение | паскаль | |||
| энергия | джоуль | |||
| количество тепла | джоуль | |||
| работа | джоуль | |||
| сила | Вт | |||
| вязкость, динамическая | паскаль-секунда | |||
| вязкость, кинематическая | квадратный метр в секунду | |||
| удельная теплоемкость | джоуль на килограмм-кельвин |
