Работа и мощность силы — основные понятия и определения.

Работа, мощность, энергия



Работа постоянной силы на прямолинейном участке

Рассмотрим материальную точку М, к которой приложена сила F. Пусть точка переместилась из положения М₀ в положение М₁, пройдя путь s (рис. 1).

Чтобы установить количественную меру воздействия силы F на пути s, разложим эту силу на составляющие N и R, направленные соответственно перпендикулярно направлению перемещения и вдоль него. Так как составляющая N (перпендикулярная перемещению) не может двигать точку или сопротивляться ее перемещению в направлении s, то действие силы F на пути s можно определить произведением Rs.
Эта величина называется работой и обозначается W.
Следовательно,

W = Rs = Fs cos α,

т. е. работа силы равна произведению ее модуля на путь и на косинус угла между направлением вектора силы и направлением перемещения материальной точки.

Таким образом, работа является мерой действия силы, приложенной к материальной точке при некотором ее перемещении.

Работа является скалярной величиной.

Рассматривая работу силы, можно выделить три частных случая: сила направлена вдоль перемещения (α = 0˚), сила направлена в противоположном перемещению направлении (α = 180˚), и сила перпендикулярна перемещению (α = 90˚).
Исходя из величины косинуса угла α, можно сделать вывод, что в первом случае работа будет положительной, во втором – отрицательной, а в третьем случае (cos 90˚ = 0) работа силы равна нулю.
Так, например, при движении тела вниз работа силы тяжести будет положительной (вектор силы совпадает с перемещением), при подъеме тела вверх работа силы тяжести будет отрицательной, а при горизонтальном перемещении тела относительно поверхности Земли работа силы тяжести будет равна нулю.

Силы, совершающие положительную работу, называются движущимися силами, силы, а совершающие отрицательную работу – силами сопротивления.

Единицей работы принят джоуль (Дж):
1 Дж = сила×длина = ньютон×метр = 1 Нм.

Джоуль – это работа силы в один ньютон на пути в один метр.

***

Работа силы на криволинейном участке пути

На бесконечно малом участке ds криволинейный путь можно условно считать прямолинейным, а силу – постоянной.
Тогда элементарная работа dW силы на пути ds равна

dW = F ds cos (F,v).

Работа на конечном перемещении равна сумме элементарных работ:

W = ∫ F cos (F,v) ds.

На рисунке 2а изображен график зависимости между пройденным расстоянием и F cos (F,v). Площадь заштрихованной полоски, которую при бесконечно малом перемещении ds можно принять за прямоугольник, равна элементарной работе на пути ds:

dW = F cos (F,v) ds,

а работа силы F на конечном пути s графически выражается площадью фигуры ОАВС, ограниченной осью абсцисс, двумя ординатами и кривой АВ, которая называется кривой сил.

Если работа совпадает с направлением перемещения и возрастает от нуля пропорционально пути, то работа графически выражается площадью треугольника ОАВ (рис. 2 б), которая, как известно, может быть определена половиной произведения основания на высоту, т. е. половиной произведения силы на путь:

W = Fs/2.

***

Теорема о работе равнодействующей

Теорема: работа равнодействующей системы сил на каком-то участке пути равна алгебраической сумме работ составляющих сил на том же участке пути.

Пусть к материальной точке М приложена система сил (F₁, F₂, F₃,…F_n), равнодействующая которых равна F_Σ (рис. 3).

Система сил, приложенных к материальной точке, есть система сходящихся сил, следовательно,

F_Σ = F

1 + F₂ + F₃ + …. + F_n.

Спроецируем это векторное равенство на касательную к траектории, по которой движется материальная точка, тогда:

F_Σ cos γ = F₁ cos α₁ + F₂ cos α₂ + F₃ cos α₃ + …. + F_n cos α_n.

Умножим обе части равенства на бесконечно малое перемещение ds и проинтегрируем полученное равенство в пределах какого-то конечного перемещения s:

∫ F_Σ cos γ ds = ∫ F₁ cos α₁ ds + ∫ F₂ cos α₂ ds + ∫ F₃ cos α₃ ds + …. + ∫ F_n cos α_n

ds,

что соответствует равенству:

W_Σ = W₁ + W₂ + W₃ + … + W_n

или сокращенно:

W_Σ = ΣW_Fi

Теорема доказана.

***

Теорема о работе силы тяжести

Теорема: работа силы тяжести не зависит от вида траектории и равна произведению модуля силы на вертикальное перемещение точки ее приложения.

Пусть материальная точка М движется под действием силы тяжести G и за какой-то промежуток времени перемещается из положения М₁ в положение М₂, пройдя путь s (рис. 4).
На траектории точки М выделим бесконечно малый участок ds, который можно считать прямолинейным, и из его концов проведем прямые, параллельные осям координат, одна из которых вертикальна, а другая горизонтальна.

Из заштрихованного треугольника получим, что

dy = ds cos α.

Элементарная работа силы G на пути ds равна:

dW = F ds cos α.

Полная работа силы тяжести G на пути s равна

W = ∫ Gds cos α = ∫ Gdy = G ∫ dy = Gh.

Итак, работа силы тяжести равна произведению силы на вертикальное перемещение точки ее приложения:

W = Gh;

Теорема доказана.

***

Пример решения задачи по определению работы силы тяжести

Задача: Однородный прямоугольный массив АВСD массой m = 4080 кг имеет размеры, указанные на рис. 5.

Определить работу, которую необходимо выполнить для опрокидывания массива вокруг ребра D.

Решение.
Очевидно, что искомая работа будет равна работе сопротивления, совершаемой силой тяжести массива, при этом вертикальное перемещение центра тяжести массива при опрокидывании через ребро D является путем, который определяет величину работы силы тяжести.

Для начала определим силу тяжести массива: G = mg = 4080×9,81 = 40 000 Н = 40 кН.

Для определения вертикального перемещения h центра тяжести прямоугольного однородного массива (он находится в точке пересечения диагоналей прямоугольника), используем теорему Пифагора, исходя из которой:

КО₁ = ОD – КD = √(ОК² + КD²) – КD = √(3² +4²) — 4 = 1 м.

На основании теоремы о работе силы тяжести определим искомую работу, необходимую для опрокидывания массива:

W = G×КО₁ = 40 000×1 = 40 000 Дж = 40 кДж.

Задача решена.

***



Работа постоянной силы, приложенной к вращающемуся телу

Представим себе диск, вращающийся вокруг неподвижной оси под действием постоянной силы F (рис. 6), точка приложения которой перемещается вместе с диском. Разложим силу F на три взаимно-перпендикулярные составляющие: F

1 – окружная сила, F₂ – осевая сила, F₃ – радиальная сила.

При повороте диска на бесконечно малый угол dφ сила F совершит элементарную работу, которая на основании теоремы о работе равнодействующей будет равна сумме работ составляющих.

Очевидно, что работа составляющих F₂ и F₃ будет равна нулю, так как векторы этих сил перпендикулярны бесконечно малому перемещению ds точки приложения М, поэтому элементарная работа силы F равна работе ее составляющей F₁:

dW = F₁ds = F₁Rdφ.

При повороте диска на конечный угол φ работа силы F равна

W = ∫ F₁Rdφ = F₁R ∫ dφ = F₁Rφ,

где угол φ выражается в радианах.

Так как моменты составляющих F₂ и F₃ относительно оси z равны нулю, то на основании теоремы Вариньона момент силы F относительно оси z равен:

М_z(F) = F₁R.

Момент силы, приложенной к диску, относительно оси вращения называется вращающим моментом, и, согласно стандарту ИСО, обозначается буквой Т:

Т = М_z(F), следовательно, W = Tφ.

Работа постоянной силы, приложенной к вращающемуся телу, равна произведению вращающего момента на угловое перемещение.

***

Пример решения задачи

Задача: рабочий вращает рукоятку лебедки силой F = 200 Н, перпендикулярной радиусу вращения.
Найти работу, затраченную в течение времени t = 25 секунд, если длина рукоятки r = 0,4 м, а ее угловая скорость ω = π/3 рад/с.

Решение.
Прежде всего определим угловое перемещение φ рукоятки лебедки за 25 секунд:

φ = ωt = (π/3)×25 = 26,18 рад.

Далее воспользуемся формулой для определения работы силы при вращательном движении:

W = Tφ = Frφ = 200×0,4×26,18 ≈ 2100 Дж ≈ 2,1 кДж.

***

Мощность

Работа, совершаемая какой-либо силой, может быть за различные промежутки времени, т. е. с разной скоростью. Чтобы охарактеризовать, насколько быстро совершается работа, в механике существует понятие мощности, которую обычно обозначают буквой P.

Мощностью называется работа, совершаемая в единицу времени.

Если работа совершается равномерно, то мощность определяют по формуле

P = W/t.

Если направление силы и направление перемещения совпадают, что эту формулу можно записать в иной форме:

P = W/t = Fs/t   или   P = Fv.

Мощность силы равна произведению модуля силы на скорость точки ее приложения.

Если работа совершается силой, приложенной к равномерно вращающемуся телу, то мощность в этом случае может быть определена по формуле:

P = W/t = Tφ/t    или    P = Tω.

Мощность силы, приложенной к равномерно вращающемуся телу, равна произведению вращающего момента на угловую скорость.

Единицей измерения мощности является ватт (Вт):

Ватт = работа/время = джоуль в секунду.

***

Понятие об энергии и КПД

Способность тела при переходе из одного состояния в другое совершать работу называется энергией. Энергия есть общая мера различных форм движения материи.

В механике для передачи и преобразования энергии применяются различные механизмы и машины, назначение которых – выполнение заданных человеком полезных функций. При этом энергия, передаваемая механизмами, называется механической энергией, которая принципиально отличается от тепловой, электрической, электромагнитной, ядерной и других известных видов энергии. Виды механической энергии тела мы рассмотрим на следующей странице, а здесь лишь определимся с основными понятиями и определениями.

При передаче или преобразовании энергии, а также при совершении работы, имеют место потери энергии, поскольку механизмы и машины, служащие для передачи или преобразования энергии преодолевают различные силы сопротивления (трения, сопротивления окружающей среды и т. п.). По этой причине часть энергии при передаче безвозвратно теряется и не может быть использована для выполнения полезной работы.

Коэффициент полезного действия

Часть энергии, потерянная при ее передаче на преодоление сил сопротивления, учитывается при помощи коэффициента полезного действия механизма (машины), передающего эту энергию.
Коэффициент полезного действия (КПД) обозначается буквой η и определяется, как отношение полезной работы (или мощности) к затраченной:

η = W₂/W₁ = P₂/P₁.

Если коэффициент полезного действия учитывает только механические потери, то его называют механическим КПД.

Очевидно, что КПД – всегда правильная дробь (иногда его выражают в процентах) и его значение не может быть больше единицы. Чем ближе значение КПД к единице (100 %), тем экономичнее работает машина.

Если энергия или мощность передаются рядом последовательных механизмов, то суммарный КПД может быть определен, как произведение КПД всех механизмов:

η = η₁η₂η₃ ….η_n,

где: η₁, η₂, η₃, …. η_n– КПД каждого механизма в отдельности.

***

Теоремы и законы динамики материальной точки



§ 4. Мощность силы и мощность механизмов — ЗФТШ, МФТИ

Для того чтобы характеризовать скорость совершения работы, вводится понятие мощности. Точнее, вводится даже несколько близких и связанных друг с другом понятий, ключевое слово в которых «мощность».

есть отношение работы `DeltaA` к промежутку времени `Deltat`, в течение которого она совершена:

`P_»ср»=(DeltaA)/(Deltat)`.

(4.1)

Как и средняя скорость движения, средняя мощность есть довольно грубая характеристика быстроты совершения работы. За достаточно большой промежуток времени интенсивность совершения работы могла то возрастать, то убывать. Для учёта этого вводится понятие мгновенной мощности силы (или просто мощности) в момент времени `t`, которая определена как предел отношения (4.1) при `Deltat->0` (когда интервал рассматриваемых времён вблизи момента времени  стягивается к нулю):

`P(t)=lim_(Deltat->0)(DeltaA)/(Deltat)=lim_(Deltat->0)(vecF(t)*Deltavecr)/(Deltat)=` `=vecF(t)*lim_(Deltat->0)(Deltavecr)/(Deltat)=vecF(t)*vecv(t)`.

(4.2)

Единица мощности в СИ есть ватт:  `1`Вт`=1`Дж/с.

До сих пор говорилось о мощности силы. В быту мы часто слышим о мощности механизмов – насоса, автомобиля, электровоза. И это ещё не всё. Иногда говорят о потребляемой мощности, в других случаях – о полезной мощности (причём и о средних их значениях, и о мгновенных мощностях). Усугубляет сложности то, что в конкретном механизме не всегда легко указать (показать в виде явной стрелки) силу, которая что-то движет.

называют количество энергии, которое получает в единицу времени машина для своей работы (автомобиль или аэросани – от сгорания бензина в двигателе, электровоз – от электрической сети):

`P_»потребл»-DeltaE_»потребл»//Deltat`.

(4.3)

(при `Deltat->0` говорят о мгновенной потребляемой мощности). Не вся потреблённая энергия `DeltaE_»потребл»` тратится именно на то, что нужно (говорят – «на совершение полезной работы»). Часть её (иногда – значительная) расходуется впустую: например, из-за трения в различных частях  сложного механизма автомобиля или аэросаней происходит разогрев деталей машины (к чему никто не стремился). Пусть нам надо, чтобы аэросани перевезли какой-то груз. Для этого (даже без всяких подъёмов) нужно преодолеть силу трения о снег. Энергия, которая будет истрачена на разгон саней и преодоление силы трения о снег (для поддержания конечной скорости), считается истраченной с пользой. Сила тяги двигателя аэросаней совершит полезную работу `DeltaA_»полезн»`.

называют отношение

`P_»полезн»=DeltaA_»полезн»//Deltat`.

(4.4)

Полезная работа всегда меньше потреблённой механизмом энергии: `DeltaA_»полезн»<DeltaE_»потребл»`.  Долю потреблённой энергии, пошедшую на совершение полезной работы, называют коэффициентом полезного действия

`»КПД»=(DeltaA_»полезн»)/(DeltaE_»потребл»)*100%=(P_»полезн»)/(P_»потребл»)*100%`.

(4.5)

Величина КПД всегда меньше ста процентов. У бензиновых двигателей КПД порядка  `25%-30%`, у дизельных – `40%-50%`, у ракетных двигателей на жидком топливе он близок к `50%`. У простых механизмов (блок, рычаг) КПД может быть близок к  `100%`.

мощность силы — это… Что такое мощность силы?



мощность силы

мощность силы; мощность

Величина, равная скалярному произведению силы на скорость точки её приложения

Политехнический терминологический толковый словарь. Составление: В. Бутаков, И. Фаградянц. 2014.

• мощность на валу компрессора
• мощность

Смотреть что такое «мощность силы» в других словарях:

• мощность силы — power of a force Скалярное произведение силы и скорости точки ее приложения. Шифр IFToMM: 3.3.24 Раздел: ДИНАМИКА МЕХАНИЗМОВ …   Теория механизмов и машин

• мощность — силы; мощность Величина, равная скалярному произведению силы на скорость точки её приложения …   Политехнический терминологический толковый словарь

• Мощность — Размерность L2MT−3 Единицы измерения СИ Вт СГС …   Википедия

• Мощность (физика) — Мощность  физическая величина, равная отношению работы, выполняемой за некоторый промежуток времени, к этому промежутку времени. Эффективная мощность, мощность двигателя, отдаваемая рабочей машине непосредственно или через силовую передачу.… …   Википедия

• Мощность локомотива — одна из основных характеристик, которая выражает тяговые и скоростные качества локомотива. Мощность локомотива есть объём выполненной локомотивом работы отнесённый к потраченному на его выполнение времени. В основном определяют касательную… …   Википедия

• Мощность двигателя — характеризует полезную работу, производимую двигателем в единицу времени. Мощность газотурбинного двигателя Ne = GB/Nуд зависит от секундного расхода воздуха GB и удельной мощности Nуд (при GB = 1 кг/с), определяемой параметрами… …   Энциклопедия техники

• МОЩНОСТЬ ЧЕЛОВЕКА — МОЩНОСТЬ ЧЕЛОВЕКА, количество механической работы, выполняемой человеком в единицу времени (напр. в 1 сек.). По данным ряда авторов средняя М. человека равна х/10 г17 лошадиной силы и в пересчете на кзм колеблется в пределах от 7,5 до 11… …   Большая медицинская энциклопедия

• МОЩНОСТЬ — (1) энергетическая характеристика, выражаемая отношением (см.) к промежутку (см.), в течение которого она совершена. Единицей мощности в СИ является (см.), обозначается Вт; (2) М. звука энергия, передаваемая звуковой волной через какую либо… …   Большая политехническая энциклопедия

• МОЩНОСТЬ ЛОШАДИ — кол во работы, выполненной л. в единицу времени. Измеряется лошадиной силой (л. с.). Зависит от типа и п ды л., ее живой массы, тренированности и т. д. Хорошая л. массой 500 кг развивает М., равную 75 кГм/с, т. е. 1 л. с. М. мелких л. всего 0,6 …   Справочник по коневодству

• Мощность — [power; capacity] физическая величина, измеряющая количеством работы в единицу времени. В теплотехнике применяют понятие «тепловая мощность» в качестве теплотехнического параметра печи Рп, характеризующего максимальное количество теплоты,… …   Энциклопедический словарь по металлургии

5.3. Мощность силы

нальности (∂f 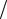∂ϕ)2 . Отсюда видно, что коэффициент инерции объекта зави-

сит от выбора обобщенной координаты и может быть пересчитан.

КЭ нестационарной голономной одностепенной системы имеет струк-

туру квадратного полинома относительно обобщенной скорости q&, коэффи-

циенты которой в общем случае зависят от q и t:

2T = aq&2 +2a1q& +2a0 , при a = a(q,t), a1 = a1 (q,t), a0 = a0 (q,t) (5.10)

Размерность коэффициентов a, a0 ,a1 определяем по принципу Л.Эйлера: все слагаемые в выражениях должны иметь одинаковую размерность.

Область пространства, в которой к материальному объекту приложена сила, называется векторным силовым полем. Эта область может быть трехмерной (например-шаровой), либо двумерной, либо представлять отрезок прямой или кривой линии. Обычно считают, что сила зависит только от координат (x, y, z) точки приложения силы, либо — от одной или двух координат, либо – постоянная по модулю и направлению. Допускаются также случаи, когда силы зависят и от скорости точки и от времени, т.е. сила задана в области пространства координат, скоростей, времени. Встречаются случаи, ко-

гда сила зависит от ускорения.

в мгновение t в системе отсчета Oxyz называется

Мощностью силы F

скаляр, равный скалярному произведению силы

на скорость точки прило-

F

жения силы v в этой системе:

м/c=Вт)

(5.11)

=

=

=

+

+

=

& +

& +

&

P

F

v

Fv cos(F,v )

Xvx

Yvy

Zvz

Xx

Yy

Zz,(Н

Согласно данному определению мощность силы есть положительный скаляр, если угол между силой и скоростью острый (в этом случае сила способствует движению, нарастанию кинетической энергии) и отрицательна, если угол тупой.(когда сила замедляет движение). Мощность силы равна нулю, если сила перпендикулярна к скорости точки приложения силы, или в случае, если точка приложения силы не имеет скорости.

Мощности в двух системах отсчета различны в случае, если системы движутся одна относительно другой, поэтому следует указывать систему отсчета, в которой вычисляется мощность сил.

Мощность сил трения, также как и других диссипативных сил, направленных против движения, отрицательна.

Мощность силы сцепления колеса с дорогой (если нет проскальзывания колеса) равна нулю, поскольку точка приложения силы не имеет скорости.

Рассмотрим случай, когда силы зависят только от положения точки при-

ложения и мощность			&
	P = Xx +Yy + Zz приводится к виду P =U , где
	& &	&

U (x, y, z) — функция положения точки приложения силы, т.е. – функция декартовых (или обобщенных) координат. В этом случае силу F(x, y, z) называют потенциальной, а “силовую функцию” U с обратным знаком, называют

74

потенциальной энергией: П(x, y, z) = −U (x, y, z) . Область пространства, в ко-

торой на тело действует потенциальная сила, называется потенциальным силовым полем. Под знаком производной можно добовлять любую константу, поэтому силовая функция и потенциальная энергия определяется с точностью до константы, определяющей уровень отсчета. В общем случае, потенциальную энергию можно определить как функцию П(q1,…, qn ) , получаемую

путем преобразования мощности к виду: P = −П&(q1,…, qn ) , где qs – обобщен-

ные координаты.

Пусть тело произвольно движется в пространстве, т.е. оно перемещается вместе с полюсом O со скоростью vO и вращается с угловой скоростью ω.

Мощность пары сил, приложенной к твердому телу, не зависит от скорости полюса. Она равна скалярному произведению момента пары сил и угловой скорости.

							(5.12)
P = M		ω	= Mω cos(M ,ω			) = M xωx + M yωy + M zωz ,

где M — момент пары сил, ω — угловая скорость твердого тела, которая, как известно, не зависит от выбора полюса. Мощность диссипативных пар сил отрицательна. Мощность пары сил не зависит от места приложения её к телу. Мощность пары сил трения в подшипнике отрицательная, поскольку момент трения и угловая скорость вращения противонаправлены.

Мощность системы сил, приложенных к твердому телу, равна скалярному произведению главного вектора R системы на скорость любого полюса тела, сложенному со скалярным произведением главного момента M 0 сил относительно этого полюса на угловую скорости тела:

P =

R

vO + M

O ω

при R = ∑Fi , MO = ∑ri ×Fi .

(5.13)

5.4. Работа и потенциальная энергия

Элементарной работой силы в выбранной системе координат Oxyz (неподвижной или подвижной) называется бесконечно малая величина, равная скалярному произведению силы на элементарное перемещение точки приложения силы в этой системе:

					(5.14)
d ′A = F		dr = Xdx +Ydy + Zdz = F | dr | cos(F,dr ), (Н м=Дж)

Здесь через d΄A обозначена бесконечно малая работа, совершаемая силой за бесконечно малый интервал времени, dr — элементарное перемещение, сонаправленное со скоростью точки. Штрихом отмечено, что d΄A не всегда является полным дифференциалом от некоторой функции.

Очевидно, что произведение Pdt равно элементарной работе d΄A:

и наоборот, мощность равна отношению элементарной работы к элементар-

ному времени:
P=d΄A/dt .	(5.16)
	75

Мощность, умноженная на малый интервал времени ∆t, есть приближенное значение работы ∆A силы за этот интервал, мощность приближенно равна работе силы за 1 сек. Работой силы за конечный интервал времени [t1, t2] называется определенный интеграл от мощности по времени:

t2	t2			(5.17)
A12 = ∫Pdt = ∫			vdt при v = r& = dr / dt .
		F
t1	t1

Для расчета работы по данной общей формуле необходимо знать мощность как функцию времени или силу и скорость в виде функций только времени t. Но в некоторых частных случаях (случай потенциальной силы, случай постоянной силы трения при неизменном направлении движения) возможно вычисление работы без применения кинематических уравнений движения точки приложения силы, достаточно знать только начальное и конечное положение точки.

Рассмотрим движение точки приложения силы по отношению к двум системам отсчета, движущимся одна относительно другой. Скорость точки в двух системах различна, поэтому и мощность силы будет различной. Таким образом, понятия мощность, работа, формулируется по отношению к конкретной системе отсчета, преимущественно – по отношению к ИСО или ПСО (инерционной или поступательной системам отсчета).

Определение Сила F называется потенциальной, а ее силовое поле —

потенциальным силовым полем, если выполнены два условия:

1) Сила удовлетворяет одному из следующих условий: сила постоянна по величине и направлению F = const или зависит только от координат точки (всех трех или части) ее приложения, т.е. F = F(x, y, z).

2) Элементарная работа d′A силы есть полный дифференциал от некоторой функции координат, либо мощность силы в любой момент времени равна полной производной по времени от некоторой функции Π(x, y, z)

(с выделенным знаком минус) :		(5.18)
′	&
d A = −dΠ(x, y, z) или P = −Π(x, y, z).

Функция П(x,y,z), получаемая посредством преобразования выражения элементарной работы, либо из выражения мощности, называется по-

тенциальной энергией потенциального силового поля в точке M(x, y, z).

Тем самым векторному силовому полю силы F (x, y, z) сопоставляется

математически более простое поле скалярной функции трех переменных П(x, y, z), либо — функции двух переменных П(x,y), либо — функции одной переменной П(x)

Потенциальная энергия может быть представлена не только в декартовой системе координат, но также — в цилиндрической, сферической системах координат, в общем она является функцией некоторых обобщенных коорди-

нат П(q1, q2, q3).

76

Поверхности, определенные уравнением П(q1, q2, q3)=C, где C — произвольно назначаемый постоянный параметр, называются эквипотенциальными поверхностями.

Заметим, что под знаком дифференциала всегда можно прибавить или вычесть любую константу, так что функция П в формуле (5.18) определяется с точностью до константы. Константу произвольно назначают, например, полагают равной нулю, выбирая тем самым уровень отсчета семейства эквипотенциальных поверхностей.

Мощность потенциальной силы равна взятой со знаком минус произ-

водной по времени от потенциальной энергии P = −Π& . Подставим это выражение в определенный интеграл (5.17). Получим выражение работы потенциальной силы на конечном перемещении точки приложения силы, осуществленном за конечный промежуток времени:

A12 = П(x1, y1, z1) – П(x2, y2, z2) = П1 – П2.

(5.19)

Таким образом, работа потенциальной силы при ее перемещении за ин-

тервал [t1, t2] из точки M1(x1, y1, z1) в точку M2(x2, y2, z2) по любой траектории равна убыли потенциальной энергии на этом перемещении, т.е. равна разно-

сти потенциальных энергий в первой и второй точках потенциального поля. Работа потенциальной силы не зависит от формы траектории, соединяющей две точки. В частности, работа потенциальной силы на любой замкнутой траектории равна нулю, а работа при переходе точки приложения силы с эквипотенциальной поверхности П=С1 на поверхность П=С2 равна разно-

сти констант: А12=С1-С2.

Частный случай В качестве начальной точки M1(x1, y1, z1) возьмем любую точку M(x, y, z) потенциального поля, а в качестве M2(x2, y2, z2) возьмем такую точку поля M(xO, yO, zO), в которой потенциальная энергия принята равной

нулю. В этом случае формула (5.19) принимает вид
П(x, y, z) = AMO = –AOM.	(5.20)

Получаем следующую физическую интерпретацию. Потенциальная энергия в любой точке M потенциального поля равна работе приложенной силы при перемещении ее точки приложения из положения M по любой гладкой или негладкой траектории в такое положение, в котором потенциальная энергия принята равной нулю, а также равна взятой со знаком минус работе силы на перемещении в положение M(x,y,z) из “нулевого” положения, в котором потенциальная энергия принята равной нулю.

Пример 1 Найдем потенциальную энергию силы тяжести G = −Gk , про-

тивонаправленной с ортом k вертикальной оси Oz системы Oxyz. Методом элементарной работы получаем:

d΄A = Gxdx + Gydy + Gzdz = –Gdz = – d(Gz) => П = Gz.

Методом мощности получаем

P = Gx x& +Gy y& +Gz z& = −Gz& = −(Gz) Π = Gz.

Таким образом, потенциальная энергия силы тяжести равна произведению веса материальной точки на высоту расположения точки M над плоскостью Oxy, удовлетворяющей условию z = 0. Здесь плоскость Oxy назначена

77

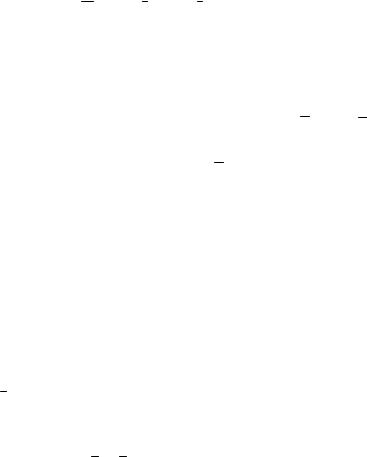
нулевой эквопотенциальной плоскостью. Потенциальная энергия силы тяжести отрицательна в точках, расположенных под плоскостью Oxy, при z < 0. На любых горизонтальных плоскостях данная потенциальная энергия одинакова во всех точках, т.е. горизонтальные плоскости являются эквипотенциальными поверхностями. Работа силы тяжести на перемещении с плоскости уровня z = z1 на плоскость z = z2 определяется по формуле:

A12 = П1 – П2 = G(z1 – z2) = ± Gh при h = |z1–z2|.

Эта работа пропорциональна разности (убыли) уровней, она отрицательна, если первый уровень ниже, чем второй.

Замечание. В случае если ось Oz направлена вниз, получаем формулу с обратным знаком: П = –Gz.

Пример 2. Потенциальная энергии силы упругости пружины. Силовое поле горизонтальной пружины имеет вид горизонтальной оси Ox. Начало оси совместим со свободным концом недеформированной пружины, x — деформация растяжения пружины при x > 0, или сжатия пружины при x < 0. Упругая сила пружины F = −cxi , где i — орт оси x. Она всегда направлена противоположно деформации. Методом мощности находим потенциальную энергию силы упругости

P = Fx x = −c x x = −(c x		2	&	, отсюда	Π = cx	2	/ 2
			/ 2)
&	&

Вообразим, что пружина очень медленно растягивается внешней силой,

медленно нарастающей от нуля до значения F вн = cxi . Считаем, что в каждый момент времени упругая сила пружины уравновешивает внешнию силу.

Среднее значение величины силы F вн на интервале [0, x] равно: Fcр = cx / 2 .

Упругая сила пружины, совершая при этом отрицательную работу по сопротивлению растягиванию, запасает в пружине положительную потенциальную

энергию, равную Π = F x = cx2 / 2.
			ср
Работа упругой силы на деформации				= x2 − x1 равна A12 = (x22 – x12)c/2.
Очевидно, что A12 < 0 при x1 < x2 и A12 > 0 при x1 > x2
Пример	3. Сила тяготения Земли			по закону «обратных квадратов»:
F =γm m / r2 ,			= −γm mr / r3 , где r — радиус-вектор материальной точки в
	F
1	1

геоцентрической системе отсчета, γ = 6,672·10–11 (м3/(кг·с2) — постоянная тя-

готения, r / r = e — орт радиус-вектора тела (материальной точки), проведенного из центра Земли, m1 = 6·1024 (кг)— масса Земли, m — масса тела, γm1 =

3986·1011 (м3/с2) — геоцентрическая гравитационная постоянная. Учитывая

тождества r r = r2 ,

r

dr

= rdr

находим ,

′

γm1m

γm1m

γm1m

γm1m

d A = −

r3

r dr = −

r2

dr = d (−

r

)

Π(r) = −

r

.

Отметим, что П(r)→0 при r→∞, следовательно, потенциальная энергия

на бесконечности принята равной нулю.

Пример 4. Работа постоянной по величине и направлению силы

на

F

прямолинейном векторе перемещения s

,

образующим с силой угол α. Име-

ем работу на перемещении [0, s]:

78