определение, единицы измерения, пример решения задач

п.1. Определение мощности

При оценке эффективности работы обычно важна скорость её выполнения.

Например, лошадь и трактор вспашут одно и то же поле – совершат одну и ту же работу — за разное время; трактор справится в десятки раз быстрее лошади.

Мощность – это отношение совершенной работы к промежутку времени, за который она была совершена: $$ N=\frac At $$

п.2. Единицы измерения мощности

В системе СИ (см. §2 данного справочника) работа измеряется в джоулях, время – в секундах. А для измерения мощности используется «ватт».

Единицей работы в системе СИ является ватт (1 Вт) – мощность, при которой за 1 секунду совершается работа равная 1 Дж: $$ 1\ \text{Вт}=\frac{1\ \text{Дж}}{1\ \text{с}} $$

Для измерения мощности также используется множество внесистемных единиц, например: 1 ккал/ч – 1 килокалория в час (1 калория = 4,184 джоуля), 1 л. 3}=\frac{50}{4}=12,5\ (\text{м/с}) \end{gather*} Ответ: 12,5 м/с

Какую среднюю мощность и силу тяги должен развивать электровоз, чтобы состав массой

Условие задачи:

Какую среднюю мощность и силу тяги должен развивать электровоз, чтобы состав массой 1000 т через 2 мин после начала равноускоренного движения по горизонтальному пути приобрел скорость 72 км/ч? Коэффициент силы сопротивления движению 0,005.

Задача №2.7.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=1000\) т, \(t=2\) мин, \(\upsilon=72\) км/ч, \(k=0,005\), \(F-?\), \(N_{ср}-?\)

Решение задачи:

Начнем с определения величины силы тяги. Для этого запишем второй закон Ньютона в проекции на горизонтальную ось \(x\):

\[F – {F_{сопр}} = ma\]

Силу сопротивления движению \(F_{сопр}\) найдем по следующей формуле (\(N=mg\) из первого закона Ньютона в проекции на вертикальную ось \(y\)):

\[{F_{сопр}} = kN = kmg\]

\[F – kmg = ma\]

\[F = m\left( {a + kg} \right)\]

Так как движение равноускоренное без начальной скорости, и за время \(t\) скорость состава с электровозом станет равной \(\upsilon\), то легко найти ускорение:

\[\upsilon  = at\]

\[a = \frac{\upsilon }{t}\]

Окончательная формула для расчета силы тяги такая:

\[F = m\left( {\frac{\upsilon }{t} + kg} \right)\]

Средняя мощность равна отношению совершенной работы ко времени (за которое эта работа совершилась):

\[{N_{ср}} = \frac{A}{t}\]

Так как вектор силы тяги \(\overrightarrow F\) сонаправлен с вектором перемещения \(\overrightarrow S\), т. 6}\left( {\frac{{20}}{{120}} + 0,005 \cdot 10} \right) \cdot \frac{{20}}{2} = 2166666,7\;Вт \approx 2,17\;МВт\]

Ответ: 217 кН; 2,17 МВт.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий

Смотрите также задачи:

2.7.25 Какую работу надо совершить, чтобы поднять груз массой 3000 кг на высоту 10 м
2.7.27 Камень брошен под углом 30 градусов к горизонту. Кинетическая энергия камня в верхней
2.7.28 Камень массой 100 г бросили под углом 60 градусов к горизонту со скоростью 15 м/с

Как рассчитать мощность на основе силы и скорости

В физике можно рассчитать мощность на основе силы и скорости. Поскольку работа равна силе, умноженной на расстояние, вы можете написать уравнение для мощности следующим образом, предполагая, что сила действует вдоль направления движения:

, где s — пройденное расстояние. Однако скорость объекта, v, , равна всего лишь с , деленная на t, , поэтому уравнение распадается на

.

Интересный результат — мощность равна силе, умноженной на скорость? Да, это то, что он говорит. Однако, поскольку вам часто приходится учитывать ускорение при приложении силы, вы обычно записываете уравнение в терминах средней мощности и средней скорости:

Вот пример. Предположим, ваш брат купил себе новую крутую машину. Вы думаете, что он маленький, но он утверждает, что у него более 100 лошадиных сил. «Хорошо», — говорите вы, доставая блокнот. «Давайте проверим это».

Автомобиль вашего брата имеет массу

На большом треке для физических испытаний на окраине города вы измеряете его ускорение как 4,60 метра в секунду ² за 5,00 секунд, когда машина трогается с места. Сколько это лошадиных сил?

Вы знаете, что

, поэтому все, что вам нужно рассчитать, это средняя скорость и чистая приложенная сила. Возьмите чистую силу в первую очередь. Вы знаете, что F = мА, , поэтому вы можете подставить значения, чтобы получить

Итак, сила, приложенная для постоянного ускорения автомобиля, составляет 5060 ньютонов. Теперь все, что вам нужно, это средняя скорость. Скажем, начальная скорость была v _i , а конечная скорость v _f . Вы знаете, что v _i

= 0 м/с, так что же такое v _f ? Ну, вы также знаете, что, поскольку ускорение было постоянным, верно следующее уравнение:

v _f = v _i + на

Так получилось, что вы знаете, что ускорение и время разгона автомобиля превысили:

v _f = 0 м/с + (4,60 м/с ² )(5,00 с) = 23,0 м/с

Поскольку ускорение было постоянным, средняя скорость равна

.

Поскольку v _i = 0 м/с, это разбивается на

Подставив числа, вы получите среднюю скорость:

Отлично — теперь вы знаете приложенную силу и среднюю скорость. Вы можете использовать уравнение

, чтобы найти среднюю мощность.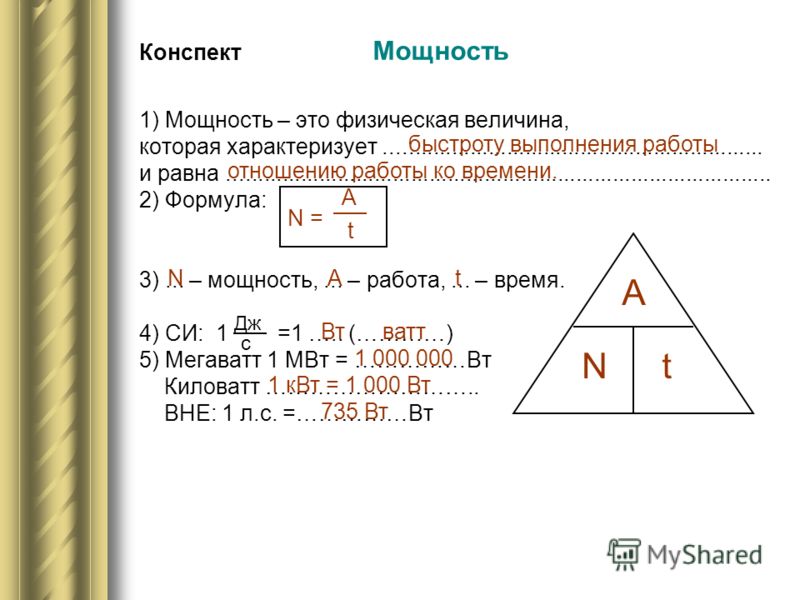 В частности

Вам все еще нужно преобразовать в лошадиные силы. Одна лошадиная сила = 745,7 Вт, поэтому

Следовательно, машина развивала в среднем 78,0 лошадиных сил, а не 100 лошадиных сил. «Крысы», — говорит твой брат. «Я требую пересчета».

Итак, вы согласны считать мощность другим способом. Вы знаете, что вы также можете рассчитать среднюю мощность как работу, деленную на время:

.

А работа, совершаемая автомобилем, равна разности начальной и конечной кинетических энергий:

W = KE _f – KE _i

Автомобиль тронулся с места, поэтому KE _i = 0 Дж. Остается вычислить только конечную кинетическую энергию:

Подстановка чисел дает:

Так потому что

и проделанная работа составила

вы получаете следующее:

И, как прежде

«Двойные крысы», — говорит твой брат.

Расчет мощности с перемещением — GeeksforGeeks

Мощность определяется как ориентированное на время значение, которое вычисляет скорость выполнения работы. Она определяется как скорость, с которой над телом совершается работа. Оно прямо пропорционально приложенной силе и перемещению тела, но изменяется обратно пропорционально времени. Его можно интерпретировать как силу, приложенную к телу, чтобы сместить его из исходного положения. Его формула равна произведению силы и перемещения, деленному на затраченное время. Он обозначается символом P. Его стандартной единицей измерения являются ватты (Вт), а размерная формула дается [M ¹ L ² T ^-3 ].

Смещение с помощью питания формулы

P = FD/T

, где

• P — мощность,
• F является применением силы,
• D. DAMSISION 9010. 9013. DABSISION 9010. 9010. 9010. 9010. 9010. 9010. 9010. 9010. 9010. 9010. 9010. 9010. затраченное время.

Вывод

Нам нужно найти значение смещения, d.

Известно, что мощность находится по формуле

P = Fd/t

Разделив обе части на F, получим,

P/F = Fd/Ft

P/F = d/t

Умножив обе части на t, получим,

Pt/F = (d/t) t

d = Pt/F

Это дает формулу смещения с силой, которая говорит, что смещение объекта равно произведению мощности и времени, деленному на приложенную силу.

Примеры задач

Задача 1. Вычислить перемещение, если к объекту прикладывалась сила 12 Н в течение 2 с для получения мощности 100 Вт. 

Решение:

,

P = 100

T = 2

F = 12

Используя формулу, мы получаем,

D = PT/F

= (100 × 2 )/12

= 200/12

= 16,67 м 

Задача 2. Вычислить перемещение, если к объекту прикладывалась сила 10 Н в течение 3 с для получения мощности 50 Вт. Решение:

Имеем,

P = 50

T = 3

F = 10

Используя формулу, которую мы получаем,

D = Pt/F

= (50 × 3)/10

= 150/10

= 15 М

Задача 3. Рассчитайте мощность, вырабатываемую, если к объекту приложена сила 20 Н в течение 5 с, а его перемещение равно 10 м.

Решение:

Имеем,

F = 20

t = 5

d = 10

= Ft3/9000

= (20) (10)/5

= 200/5

= 40 Вт

Задача 4. Рассчитайте мощность, вырабатываемую, если к объекту приложена сила 15 Н в течение 3 с, а перемещение равно 20 м.

Решение:

,

F = 15

T = 3

D = 20

Используя формулу,

P = FD/T

= (15) (

P = FD/T

= (15) 20)/3

= 100 Вт

Задача 5. Рассчитайте приложенную силу, если мощность 70 Вт генерируется в течение 11 с, а перемещение равно 7 м.

Решение:

Мы имеем,

P = 70

T = 11

D = 7

Используя формулу, мы получаем,

P = FD/T

=> F = Pt /d

= 70 (11)/7

= 110 Н

Задача 6. Рассчитайте приложенную силу, если в течение 20 с генерируется мощность 120 Вт, а перемещение равно 5 м.

Решение:

Имеем,

P = 120

t = 20

d = 5

Используя формулу, получаем Задача 7.