3. Моменты инерции тел различной формы.
Рассчитаем моменты инерции некоторых тел при различном расположении оси вращения.
1.Кольцо (тонкостенный цилиндр), ось вращения проходит через центр масс. (рис.3).
Рис.3а. Рис.3б.
Пусть кольцо (цилиндр) имеет радиус и массу. Для расчета используем формулу. В этом случаедля всех элементарных масс. Поэтому.
2. Однородный стержень, ось вращения проходит через конец стержня.
Разобьем стержень на несколько частей длинойс массой, расположенных на разных расстоянияхот оси вращения. Чем больше разбиений, тем точнее можно сосчитать момент инерции (рис.4). Поэтому удобней сумму заменить интегрированием:
где
— масса всего стержня. Введем плотность
и выразим через нее массу.
Рис.4.
,
где — объем элемента стержня площадью поперечного сеченияи длины. Тогда,
где — длина стержня. После интегрирования получаем:
,
где — объем всего стержня. Таким образом
.
Если ось вращения стержня проходит через центр масс стержня, то
.
В таблице 1 приведены значения моментов инерции некоторых тел.
Таблица 1
Тело | Положение оси вращения | Момент инерции |
Полый тонкостенный цилиндр радиусом R | Ось симметрии | mR2 |
Сплошной цилиндр или диск радиусом R | Ось симметрии | (1/2)mR2 |
Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его середину | (1/12)ml2 |
Прямой тонкий стержень длиной l | Ось перпендикулярна стержню и проходит через его конец | (1/3)ml2 |
Шар радиусом R | Ось проходит через центр шара | (2/5)mR2 |
(15)
Момент инерции твердого тела относительно
любой оси равен моменту инерции
относительно оси параллельной данной
и проходящей через центр масс тела плюс
произведение массы тела на квадрат
расстояния между осями.
Рис.5.
Применим теорему Штейнера для определения момента инерции однородного стержня, длиной . Пусть. Величина( смотри таблицу). Тогда
Рис.6.
.
4. Момент силы относительно неподвижной точки.
Моментом силы относительно неподвижной точки 0 называется физическая величина, определяемая векторным произведением радиуса-вектора, проведенного из точки 0 в точкуаприложения силы, на силу
(16)
Рис.7.
Направление вектора совпадает с направлением поступательного движения правого винта при его вращении отк. Модуль момента силы равен
,
где — угол междуи, а- кратчайшее расстояние между линией действия силы и точкой 0 называется плечом силы.
5. Момент силы относительно неподвижной оси.
Моментом силы относительно неподвижной оси zназывается скалярная величина, равная проекции на эту ось вектора момента силы, определенного относительно произвольной точки 0 данной осиz. Значение моментане зависит от выбора точки 0 на осиz.
Рис. 8.
В частном случае, если ось zсовпадает с направлением вектора М, величина момента силы относительно точки, совпадает с моментом силы относительно оси.
Рассмотрим систему материальных точек, к которым приложены силы. Моментом всех сил, действующих на систему материальных точек относительно неподвижной точки, называется векторная сумма моментов отдельных сил относительно той же точки.
(18)
Моментом всех сил, действующих на систему материальных точек относительно неподвижной оси называется алгебраическая сумма моментов отдельных сил относительно той же оси,
(19)
Курс физики (Грабовский Р.
И.) Курс физики (Грабовский Р.И.)
ОглавлениеПредисловиеВведение § 1. 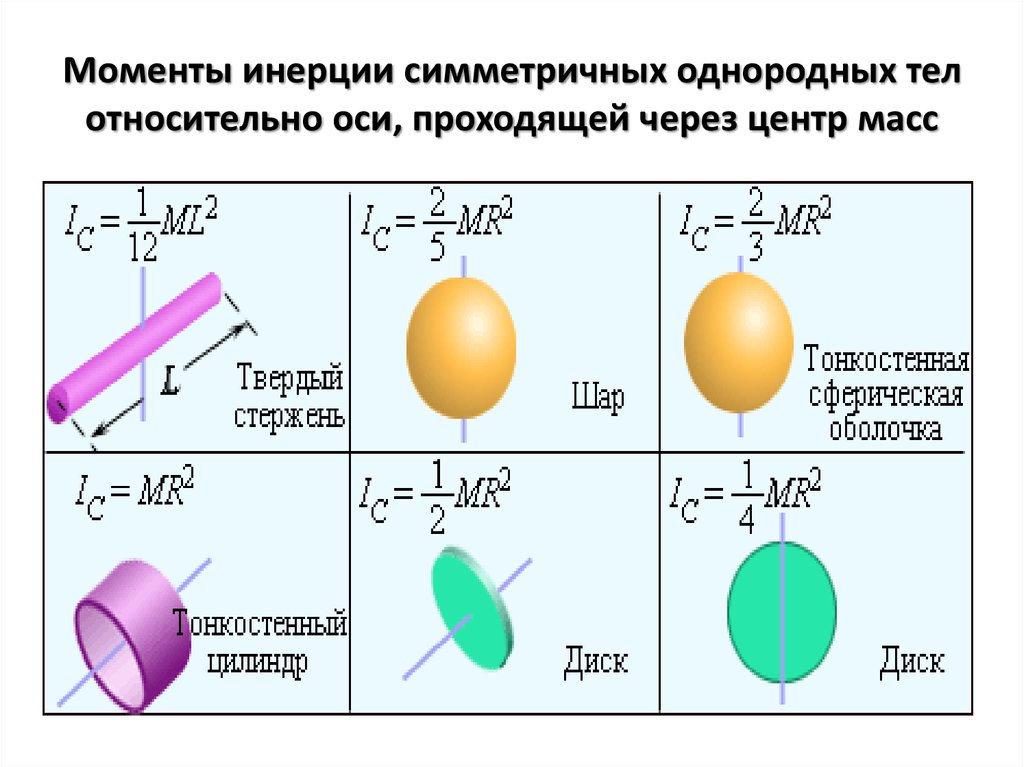 § 2. О единицах измерения и размерности физических величин § 3. О некоторых математических понятиях и символах 1. Физические основы механики § 4. Общий случай криволинейного движения материальной точки; основные характеристики движения § 5. Прямолинейное движение материальной точки § 6. Движение материальной точки по окружности Глава II. Основные законы динамики § 7. Законы Ньютона. Масса и сила § 8. Закон изменения количества движения (импульса) § 9. Закон сохранения количества движения в изолированной системе § 11. Силы трения § 12. Силы тяготения (гравитационные силы) § 13. Центростремительная сила § 14. Инерциальные и неинерциальные системы отсчета. Силы инерции § 15. Вес тел. Ускорение силы тяжести. Невесомость Глава III. Работа и энергия § 16. Работа и мощность § 17. Энергия § 18. Закон сохранения и превращения энергии § 19. 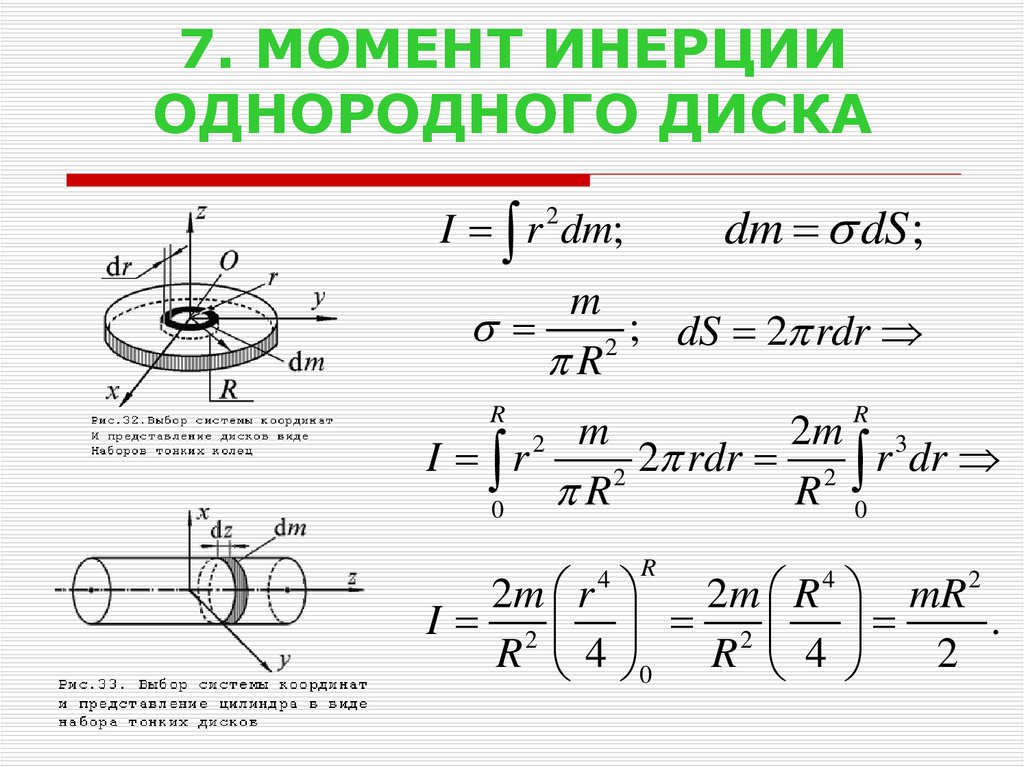 О космических скоростях§ 20. Границы применимости классической механики Глава IV. Вращательное движение твердого тела § 21. Основной закон динамики вращения § 22. Моменты инерции некоторых тел Глава V. Движение жидкости § 24. Основные определения. Уравнение неразрывности § 25. Уравнение Бернулли § 26. О некоторых приложениях уравнения Бернулли Глава VI. Колебания и волны § 27. Гармоническое колебание и его характеристики § 28. Сложение гармонических колебаний § 29. Динамика колебательного движения. Маятник § 30. О затухающих и вынужденных колебаниях § 31. Волновой процесс § 32. Уравнение волны. Интенсивность волны § 33. Интерференция волн. Стоячие волны § 34. Фронт волны. Принцип Гюйгенса-Френеля 2. Молекулярная физика и термодинамика § 35. Основные положения молекулярно-кинетической теории § 37. 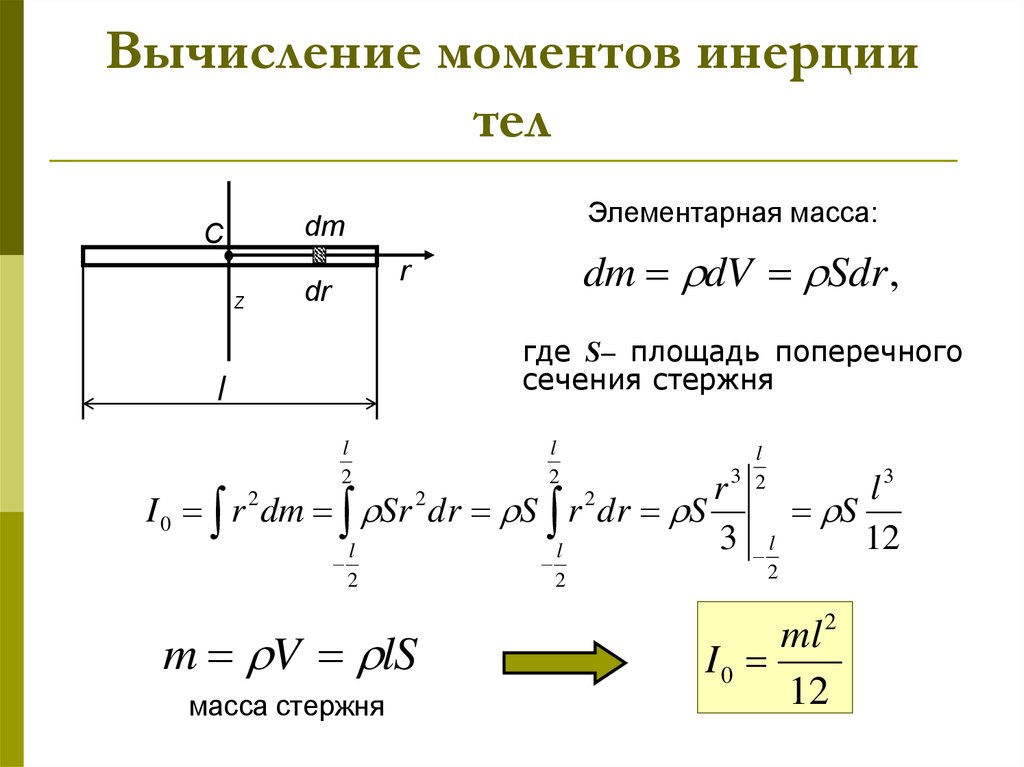 О теплоте и температуре§ 38. О предмете и методах молекулярной физики Глава VIII. Газы § 39. Экспериментальные газовые законы: Бойля-Мариотта, Гей-Люссака, Дальтона, Авогадро. Абсолютная температура § 40. Уравнение Клапейрона — Менделеева. Универсальная газовая постоянная § 41. Основное уравнение кинетической теории идеального газа § 42. Средняя кинетическя энергия поступательного движения молекулы идеального газа § 44. Теплоемкости газа. Физический смысл универсальной газовой постоянной § 45. Скорость поступательного движения молекул газа. Распределение числа молекул по скоростям § 46. Средняя длина свободного пробега молекул § 47. Явления переноса в газах. Уравнение переноса § 48. Диффузия § 49. Теплопроводность § 50. Внутреннее трение (вязкость) Глава IX. Жидкости и твердые тела § 51. Особенности строения жидкостей и твердых тел § 52. Деформация твердого тела § 53. 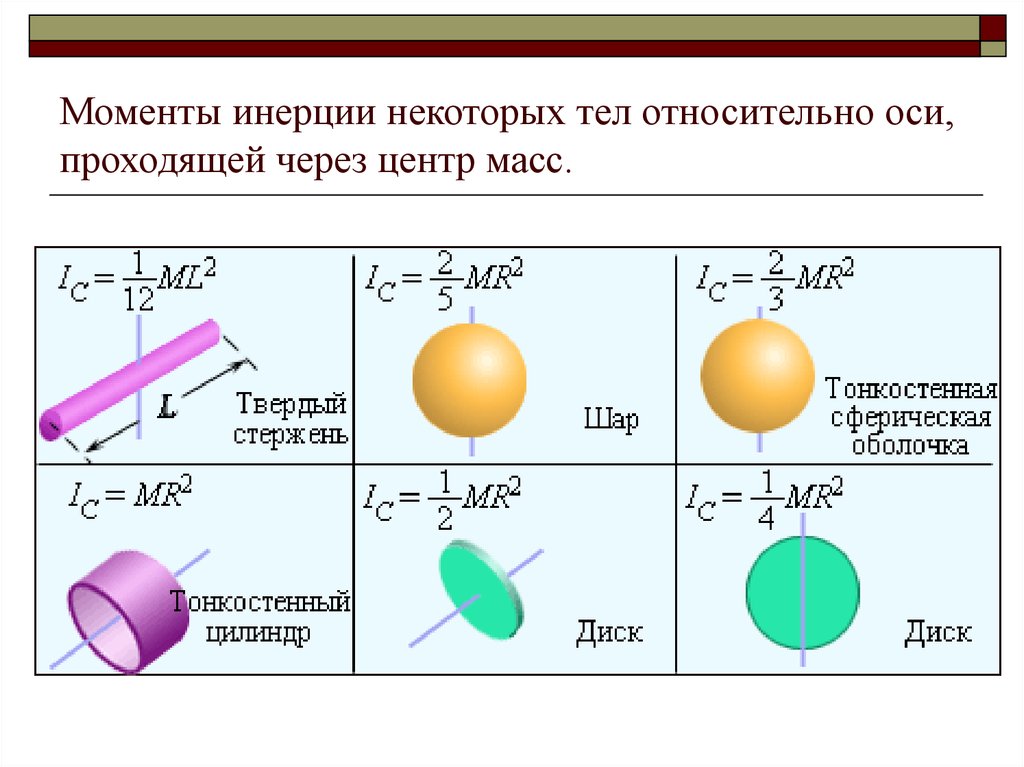 Тепловое расширение твердых и жидких тел§ 54. Теплоемкость твердых и жидких тел § 55. Диффузия в жидких и твердых телах § 56. Осмос § 57. Теплопроводность жидких и твердых тел § 58. Вязкость жидкости. Турбулентное движение жидкости § 59. Внутреннее давление в жидкости. Поверхностное натяжение и свободная энергия поверхности жидкости § 60. Дополнительное давление под искривленной поверхностью жидкости. Формула Лапласа § 61. Капиллярные явления; формула Жюрена Глава X. Изменение агрегатного состояния вещества (фазовые превращения) § 62. Понятие о фазовых превращениях и диаграмме состояний вещества § 63. Реальный газ. Уравнение Ван-дер-Ваальса § 64. Опыт Эндрюса. Критическая температура § 65. Сжижение газов. Эффект Джоуля-Томсона § 66. Испарение и конденсация. Кипение § 67. Упругость насыщенного пара над искривленной поверхностью жидкости и над раствором § 68. Плавление и затвердевание (кристаллизация). Возгонка Глава XI.  Основы термодинамики§ 69. О некоторых общих понятиях термодинамики. Первое начало термодинамики § 70. Работа, совершаемая при изменении объема газа. Адиабатические процессы § 71. Цикл Карно. Второе начало термодинамики § 72. Энтропия § 73. О статистическом смысле энтропии и второго начала термодинамики 3. Электричество и магнетизм § 74. Электризация тел. Электрический заряд § 75. Взаимодействие электрических зарядов в вакууме. Электрическое поле и его напряженность § 76 Электрический диполь. Поле диполя § 77. Теорема Остроградского-Гаусса и ее приложения § 78. Работа перемещения заряда в электрическом поле. Потенциал § 79. О неустойчивости статических систем электрических зарядов § 80. Проводники в электрическом поле. Электроемкость. Энергия заряженного проводника § 81. Диэлектрики в электрическом поле. Поляризация диэлектриков § 82. Электрическое поле в диэлектрике. Диэлектрическая проницаемость. Вектор электрической индукции § 83. 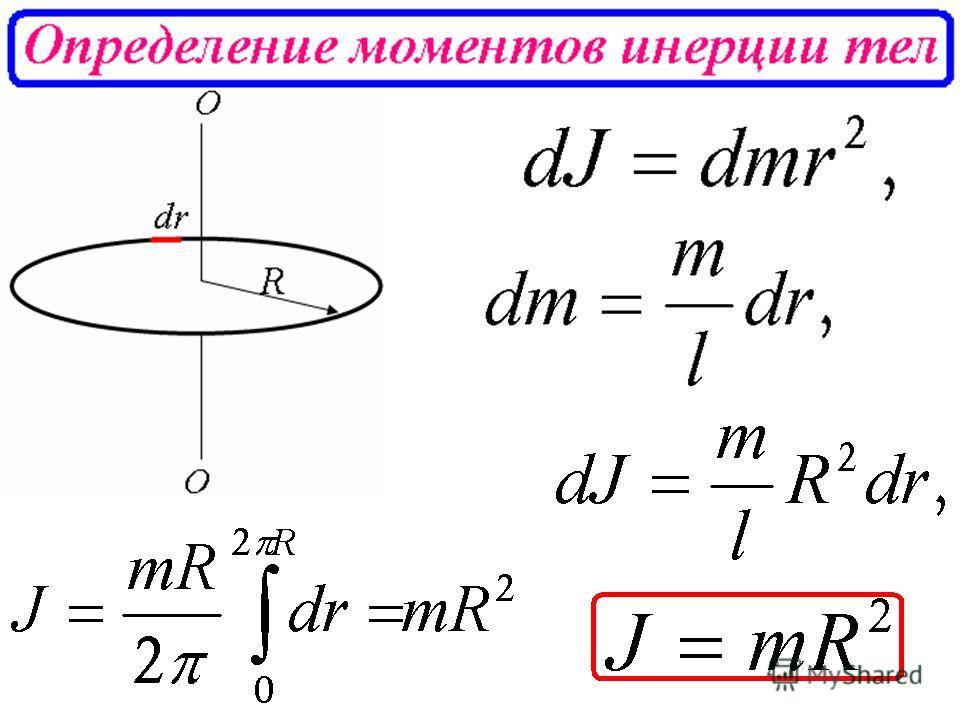 Конденсатор. Энергия электрического поляГлава XIII. Постоянный электрический ток § 84. Электрический ток. Сила тока. Электродвижущая сила. Напряжение § 85. Ток в металлических проводниках. Сопротивление. Законы Ома. Работа и мощность тока § 86. Разветвленная электрическая цепь. Правила Кирхгофа § 87. Контактная разность потенциалов. Термоэлектрические явления § 88. Эмиссия электронов. Термоэлектронная эмиссия. Электронные лампы § 89. Ток в полупроводниках. Собственная и примесная проводимости полупроводников § 90. Запирающий слой. Полупроводниковые выпрямители, усилители и термоэлектрические батареи § 91. Ток в жидкостях. Электролиз. Законы Фарадея § 92. Ток в газах. Несамостоятельный и самостоятельный газовые разряды § 93. Типы самостоятельного газового разряда Глава XIV. Электромагнетизм § 94. Постоянный магнит и круговой ток. Магнитные поля магнитов и токов § 95. Магнитное взаимодействие токов в вакууме; закон Ампера § 96.  Напряженность магнитного поля. Формула Ампера. Закон Био-Савара-Лапласа§ 97. Некоторые приложения закона Био-Савара-Лапласа § 98. Магнитные поля соленоида и тороида § 99. Диамагнитные, парамагнитные и ферромагнитные вещества. Магнитная проницаемость. Магнитная индукция. Поток магнитной индукции § 100. Действие магнитного поля на проводник с током. Определение ампера § 101. Движение заряженных частиц в электрическом и магнитном полях. Определение удельного заряда и массы электрона § 102. О некоторых приборах и установках, основанных на движении заряженных частиц в электрическом и магнитном полях Глава XV. Электромагнитная индукция и переменный ток § 103. Электромагнитная индукция. Закон Фарадея. Правило Ленца. Токи Фуко § 104. Взаимная индукция и самоиндукция § 105. Энергия магнитного поля. Понятие об электромагнитной теории Максвелла § 106. Контур, вращающийся в магнитном поле. Синусоидальный переменный ток. Работа и мощность переменного тока § 107.  Емкостное и индуктивное сопротивления§ 108. Обобщенный закон Ома. Электрический резонанс. Коэффициент мощности электрической цепи § 109. Понятие о трехфазном токе Глава XVI. Электрические колебания и электромагнитные волны § 110. Электромагнитные волны § 111. Закрытый колебательный контур § 112. Вибратор Герца. Автоколебательный контур. О диапазоне частот электромагнитных волн § 113. Радиосвязь 4. Оптика и атомная физика § 114. Природа света § 115. Отражение и преломление света. Полное отражение § 116. Дисперсия света. Спектры § 117. Тонкие линзы. Микроскоп § 118. Глаз как оптическая система. Спектральная чувствительность глаза § 119. Основные фотометрические характеристики § 120. Поглощение света. О физиологическом действии света Глава XVIII. Волновые свойства света § 121. Интерференция света. Интерферометр § 122. Об интерференции света, отраженного от прозрачных пленок § 123. Дифракция света. Разрешающая способность оптических приборов § 124.  Дифракция от щелей. Дифракционные спектры. Дифракционная решетка. О рассеянии света в мутной среде§ 125. Дифракция рентгеновских лучей. Формула Вульфа-Брэггов § 126. О дифракции микрочастиц и волнах де-Бройля § 127. Поляризация света. Естественный и поляризованный свет. Поляризация света в турмалине. Поляроиды § 128. Двойное лучепреломление. Поляризация света в исландском шпате. Призма Николя 129. Вращение плоскости колебаний поляризованного света. Поляриметр Глава XIX. Квантовые свойства света и строение атома § 130. Тепловое лучеиспускание и лучепоглощение. Абсолютно черное тело. Закон Кирхгофа § 131. Законы излучения абсолютно черного тела. Квантовый характер излучения. Формула Планка § 132. Строение атома (ядерная модель). Дискретность энергетических состояний атома. Постулаты Бора § 133. Квантовая теория строения атома водорода (по Бору). Объяснение спектров излучения и поглощения водорода § 134. Понятие о строении многоэлектронных атомов и образовании оптических и рентгеновских (характеристических) спектров § 135.  Люминесценция. Законы фотолюминесценции и некоторые ее практические применения§ 136. Фотоэффект. Законы фотоэффекта. Фотоэлементы § 137. Масса и импульс фотона. Световое давление. Эффект Комптона. Флуктуации света Глава XX. Атомное ядро и внутриядерные процессы § 138. Общие сведения об атомных ядрах. Изотопы § 139. Естественная радиоактивность. Альфа-, бета- и гамма-лучи. Законы радиоактивного распада § 140. О методах наблюдения и регистрации микрочастиц § 141. Ядерные реакции. Искусственная радиоактивность § 142. Энергия связи и дефект массы атомного ядра § 143. Реакция деления. Цепная реакция. Ядерный реактор § 144. Реакция синтеза (термоядерная реакция). Энергия звезд § 145. Космические лучи. Элементарные частицы § 146. Об использовании ядерной энергии |
Вращательная динамика — Почему момент инерции тела не равен моменту инерции его центра масс?
$\begingroup$
Момент инерции представляет собой сумму (или интегрирование, в случае сплошных тел) произведения квадрата перпендикулярного расстояния всех отдельных частиц в системе от оси вращения и их соответствующих масс.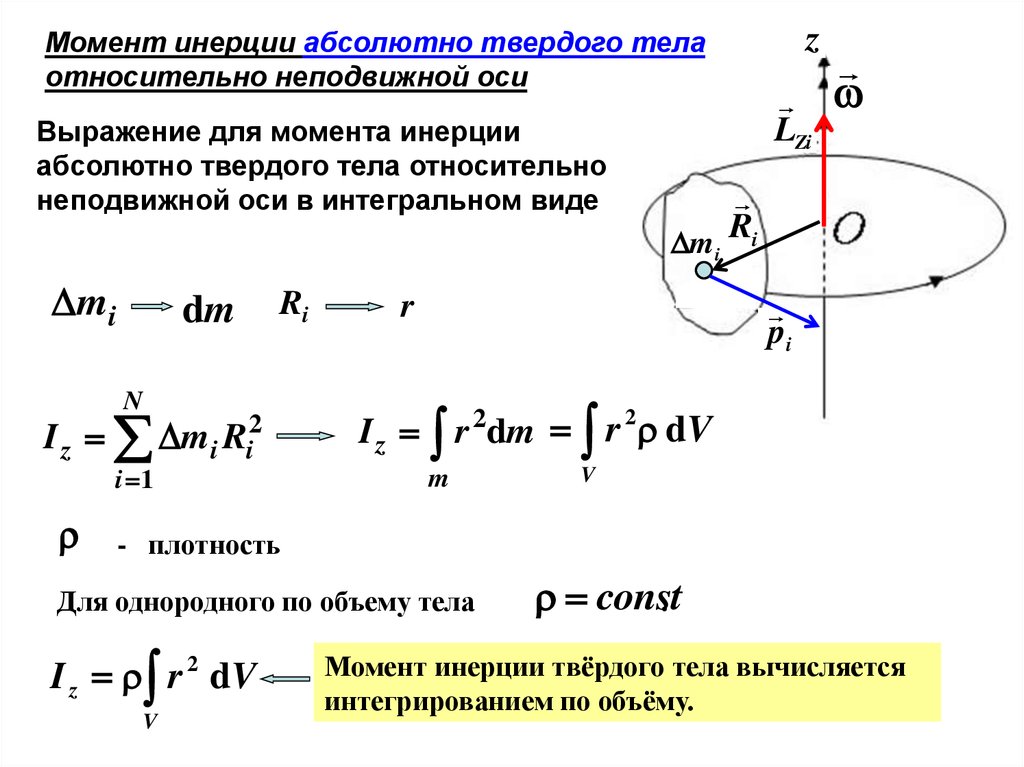
Но для объекта размером с точку он должен быть равен квадрату его перпендикулярного расстояния от оси вращения. Итак, момент инерции системы должен быть равен моменту инерции ее центра масс, так как можно сказать, что вся масса тела сосредоточена там, но этого не происходит. Почему это так?
- вращательная динамика
- системы отсчета
- момент инерции
$\endgroup$
1
$\begingroup$
Если вы поместите тело с центром масс в начало координат и повернете его, оно все равно будет испытывать момент инерции массы. Это почему?
Потому что все отдельные частицы все еще движутся (имея собственный импульс) на расстоянии от оси вращения. 92 + {\bf I}_\text{центр масс} $$
$\endgroup$
$\begingroup$
Я думаю, что ваша проблема в утверждении «вся масса тела, можно сказать, сосредоточена там» — в общем-то это не всегда верно.
Когда мы имеем дело с гравитационным притяжением (при условии, что мы используем ньютоновскую схему), мы можем сказать, что тела ведут себя так, как если бы вся их масса была сосредоточена в их центре масс. Однако, когда дело доходит до вращения, два тела с одним и тем же центром масс, но с разным распределением массы, могут иметь очень разные вращательные свойства (например, тело будет иметь больший момент инерции, если большая часть его массы сосредоточена дальше от центра тяжести). центр). Ведь если бы тело вело себя так, как его центр масс под всех обстоятельств, момент инерции всегда будет $0$, что вообще не имеет особого смысла.
$\endgroup$
1
$\begingroup$
Нам разрешено свободно выбирать ось вращения. Эта ось не обязательно должна проходить через центр масс. Для такой оси мы должны вычислить момент инерции, и вполне логично, что расстояние каждой бесконечно малой массы относительно этой оси вращения используется для вычисления момента инерции.
Вы не согласны?
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
моментов инерции крыльев и тела летучей мыши | Журнал экспериментальной биологии
Пропустить пункт назначения навигации
СТАТЬЯ В ЖУРНАЛЕ| 01 июля 1991 г.
МИКАЭЛЬ ТОЛЛЕССОН,
УЛЛА М. НОРБЕРГ
Информация об авторе и статье
Принято: 27 марта 1991 г.
Номер для печати в Интернете: 1477-9145
Номер для печати: 0022-0949
© 1991 by Company of Biologist
1991
J Exp Biol (1991) 158 (1): 19–35.
https://doi.org/10.1242/jeb.158.1.19
История статьи
Принято:
27 марта 1991
- Разделенный экран
- Просмотры
- Содержание артикула
- Рисунки и таблицы
- Видео
- Аудио
- Дополнительные данные
- Экспертная оценка
- Делиться
- Твиттер
- MailTo
- Инструменты
Получить разрешения
Иконка Цитировать Цитировать
- Поиск по сайту
Citation
МИКАЭЛЬ ТОЛЛЕССОН, УЛЛА М.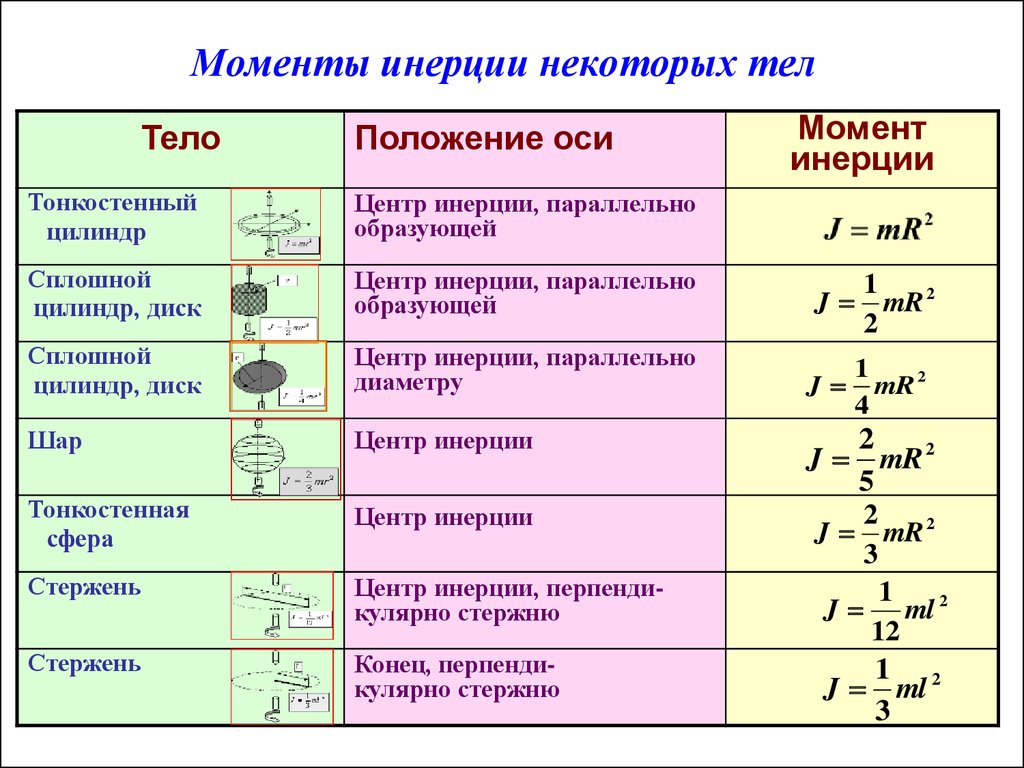
НОРБЕРГ; Моменты инерции крыльев и тела летучих мышей. J Exp Biol 1 июля 1991 г.; 158 (1): 19–35. doi: https://doi.org/10.1242/jeb.158.1.19
Скачать файл цитирования:
- Рис (Зотеро)
- Менеджер ссылок
- EasyBib
- Подставки для книг
- Менделей
- Бумаги
- КонецПримечание
- РефВоркс
- Бибтекс
Расширенный поиск
С помощью полосового анализа оценены моменты инерции крыльев относительно плечевого сустава и относительно оси крена у восьми видов летучих мышей. Момент инерции туловища летучей мыши относительно оси крена оценивали, считая тело и голову эллипсоидами. Наклоны регрессий момента инерции одного крыла относительно плечевого сустава ( J w ) по сравнению с массой тела ( m до ), размахом крыльев ( b ) и площадью крыльев (S) были ожидаемыми для геометрически сходных животных разного размера.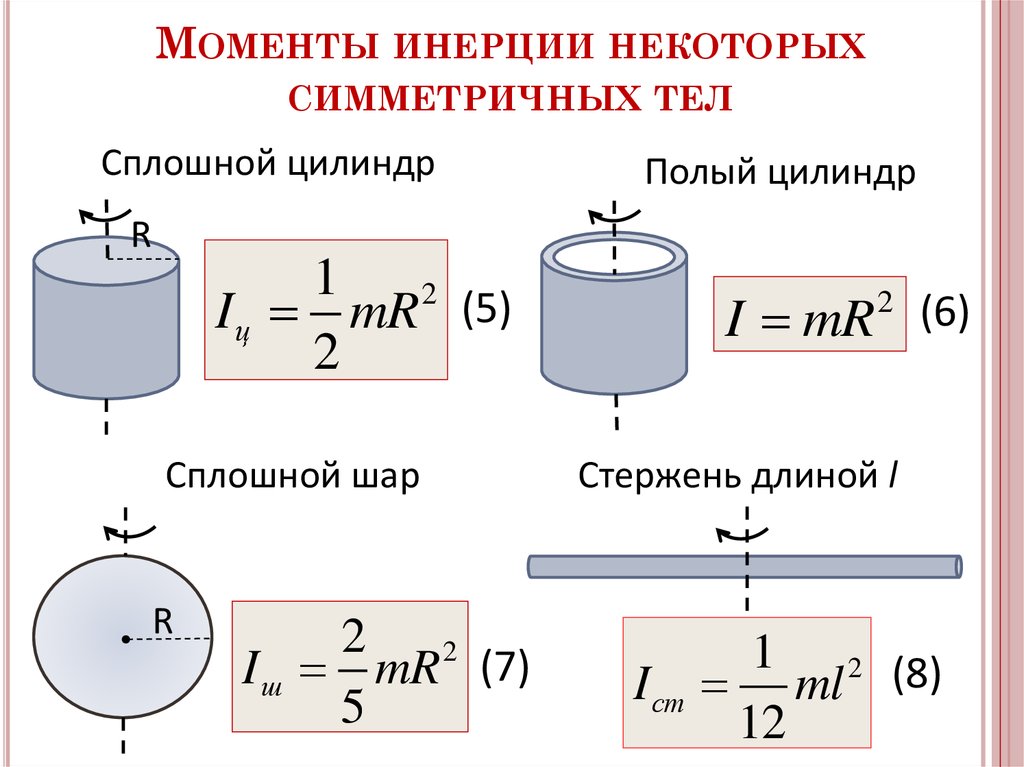
Показатель степени для J w по сравнению с массой тела у летучих мышей отличается от найденного для птиц, а показатель степени для J w по сравнению с размахом крыльев не отличается. Множественная регрессия использовалась, чтобы показать, что J w можно оценить по:
j W = 4,49 × 10 −3 M TOT 0,53 B 2,15 S 9029929.10239.
Среднее значение момента инерции от туловища составляет 7 % от полного момента инерции летучей мыши (крыльев и тела вместе взятых) относительно оси крена. Масса одного крыла (90 037 m 90 038 90 199 w 90 200) была нанесена на график в зависимости от массы тела для восьми видов летучих мышей, что дает: 90 003 90 004 м ш = 0,112 м итого 1 11 .
Наклон для наших летучих мышей, 1,11, аналогичен полученному для птиц, 1,10.
