1.1.3. Момент силы относительно точки и оси. Пара сил

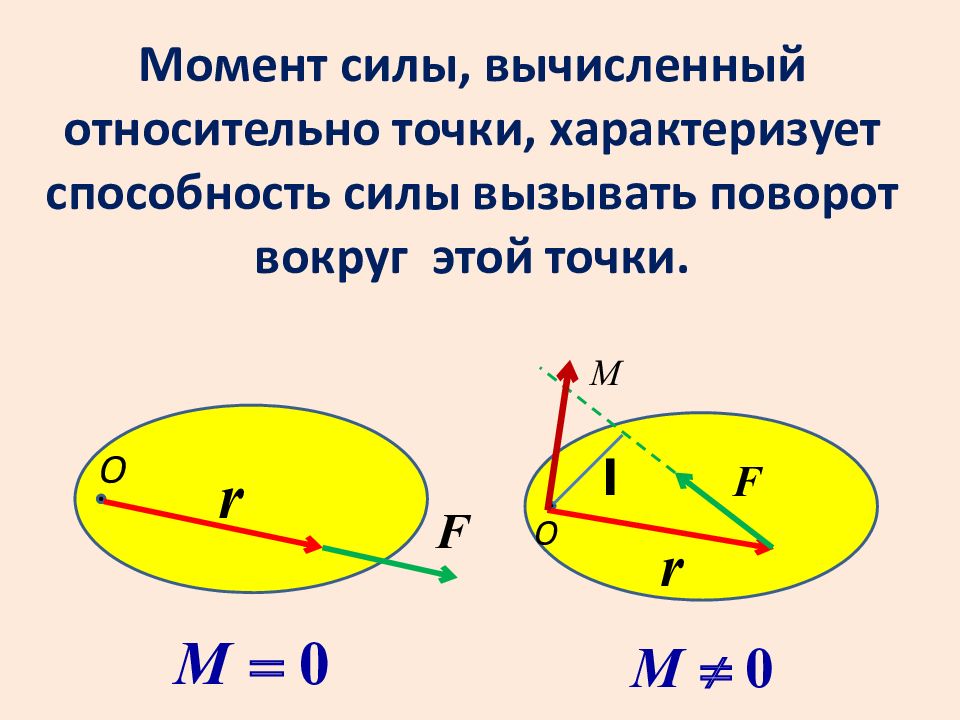
Момент силы относительно центра. Опыт 
показывает, что эффект дей-ствия силы, приложенной к телу (например, к рычагу, 
штурвалу) на разных расстояниях от точки закрепления тела, зависит от так 
называемого м о м е н т а 
с и л ы относительно точки закрепления.
Моментом силы относительно центра О называется произведение модуля силы на 
кратчайшее расстояние от центра О до линии действия силы. 
                  (1.6)
где h — кратчайшее расстояние от центра О до линии действия 
силы 
Момент силы считается 
положительным, если сила стремится повернуть тело вокруг центра О против хода 
часовой стрелки и отрицательным, если по ходу часовой стрелки (рис. 1.24, 1.25). 
Размерность момента силы Н*м.
                            Рис. 1.24                      Рис. 1.25
Момент 
силы не изменяется при переносе точки приложения силы вдоль ее линии действия.  
Момент силы относительно центра О равен нулю, если сила равна нулю или, если 
линия действия силы проходит через центр О (плечо рав-но нулю). Графически 
абсолютная величина момента силы относительно центра О вы-ражается удвоенной 
площадьюОАВ
= 2SОАВ
Момент 
силы относительно центра как векторное произведение. Введенного 
понятия «момент силы относительно центра как алгебраическая ве-личина» 
оказывается недостаточно в случае сил, произвольно расположенных в пространстве. 
Плоскости поворота у разных сил будут различными и должны задаваться 
дополнительно. Удобно ввести понятие «момент силы относительно центра как в е к 
т о р», модуль которого равен произведению модуля силы на ее плечо, а 
направление перпендикулярно плоскости, проходящей через линию действия силы и 
центр момента.
 Вектор момента силы прикладывают в центре момента и направляют в сторону, откуда сила 
видна вращающей тело в направлении, противоположном ходу часовой стрелки (рис. 
1.26). Соединим центр момента О с точкой приложения силы радиусом-вектором и 
найдем векторное произведение
 По определению векторного произведения его модуль
||= 2SОАВ
Модуль вектора момента силы акже равен удвоенной площади ОАВ
=
Направление векторного 
произведения также совпадает с направлением вектора момента. Следовательно, 
вектор-момент силыотносительно центра О можно 
рассматривать как векторное произведение радиус-векторапроведенного из этой точки в точку 
приложения силы, на вектор силы 

 
Рис. 1.26                       Рис. 1.27
Момент силы относительно оси. Чтобы охарактеризовать 
вращательный эффект, создаваемый силой, стремящейся повернуть тело вокруг 
некоторой оси, вводится понятие «момента силы относительно оси». Рассмотрим 
твердое тело, которое может вращаться вокруг оси OZ (рис.1.27). Пусть на тело 
действует сила приложенная в точке 
А. Проведем через точку А плоскость OXY, перпендикулярную оси OZ, и разложим 
силу на две составляющие:параллельную оси OZ, и  , лежащую в плоскости XY.  Составляющая, 
параллельная оси OZ, крутящего момента не создает, а, следовательно, весь 
вращательный эффект, создаваемый силой  ,будет вызван ее составляющей 

Моментом силы относительно оси называют момент проекции 
этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси 
с этой плоскостью. Момент силы относительно 
оси считается положительным, если смотря навстречу оси Z, можно видеть проекцию 
< стремящейся вращать плоскость XY вокруг оси Z в сторону, противополож-ную 
вращению часовой стрелки. 
 Момент силы относительно оси равен нулю: 
 
1) если=0, т.е. линия 
действия силы параллельна оси OZ;
2) если h = 0, т.е. линия действия силы 
пересекает ось OZ.
Следовательно, если сила и ось лежат в одной 
плоскости, то момент силы относительно этой оси равен нулю. Пара сил. Момент 
пары. Система двух равных по модулю, параллельных и противоположно направленных 
сил  называется п а р о й с и л 
(рис.
  1.28). 
Пара сил не имеет равнодействующей и силы пары не 
уравновешиваются. 
Действие пары на тело характеризуется ее моментом. 
1. 
Вектор-момент перпендикулярен плоскости действия пары. 
2. Направлен в ту 
сторону, чтобы, смотря с его конца, вращение было происходящим против хода 
часовой стрелки. 
3. Величина вектора равна в выбранном масштабе численному значению момента 
пары.
Вектор-момент пары равен векторному произведению радиуса-вектора  на ту из сил пары, к началу которой 
направлен вектор 
 (1.10)
или
 (1.11)
по 
модулю
 (1.12)
Пары сил в 
пространстве эквивалентны, если их моменты геометрически равны. Геометрическая 
сумма моментов составляющих пар сил равна моменту эквивалентной им парыт.е. ()
 (1.13)

Пары сил, произвольно расположенные в 
пространстве, взаимно уравно-вешиваются в том случае, если геометрическая сумма 
их моментов равна нулю. Если пары сил расположены в одной плоскости, то моменты 
этих пар сил, на-правленные по одной прямой, складываются а л г е б р а и ч е с 
к и. Момент пары сил, эквивалентный системе пар сил на плоскости, равен 
алгеб-раической сумме моментов составляющих пар (рис. 1.29).
 где  . Пары сил, расположенные в одной 
плоскости, взаимно уравновешиваются, если алгебраическая сумма их моментов равна 
нулю 
Рис. 1.28                          Рис. 1.29
Силовое 
воздействие на самолет часто приводится к паре сил. Например, аэродинамические 
силы (силы сопротивления воздуха вращению) воздушного винта складываются в пару, 
называемую аэродинамическим (реактивным) мо-ментом винта Мв (рис. 1.30). Чем 
большую мощность развивает двигатель, тем больше реактивный момент, вызывающий 
крен самолета. Этот момент уравно-вешивают некоторым отклонением элеронов; 
аэродинамические силы  и Y составляют 
пару с моментом, равным значению реактивного момента воздушного винта и обратным 
его направлению. 
 
 Рис. 1.30               Рис. 1.31             Рис. 1.32


 
Момент силы.
Теоретическая механика
  
Момент силы
Говорят, что когда-то великий Архимед изрек фразу: «Дайте мне точку опоры, и я переверну Землю». Современная физика утверждает, что с практической точки зрения, мудрый грек, конечно же, погорячился – даже сдвинуть на доли миллиметра такой массив, как планета с помощью мускульной силы человека – занятие не одного года, а уж перевернуть Землю… 

Тем не менее, с теоретической точки зрения Архимед прав – если найти соответствующую точку опоры, то с помощью рычага Землю сдвинуть с места может даже комар. Дело в том, что здесь играет роль не сила, как таковая, а ее момент.
 
Что же такое – момент силы? Следует сразу оговориться, что момент силы — понятие относительное, поскольку без указания того, относительно какой точки он рассматривается, понятие момента силы теряет смысл (не путать с моментом пары сил, о котором речь пойдет в следующих статьях).
Рассмотрим гайку, которую затягивают гаечным ключом определенной длины, прикладывая к концу ключа мускульное усилие. 

Если взять более длинный ключ, то гайку можно завернуть значительно сильнее, прикладывая одинаковое усилие. Из этого следует, что одной и той же силой можно выполнить различное по эффективности вращающее действие на какое-либо тело. В этом и кроется понятие момента силы – это вращающее действие силы относительно какой-либо точки в пространстве.
 
Понятие момента силы относительно точки ввел гениальный итальянец Леонардо да Винчи (1452-1519), который известен потомкам не только, как великий художник, но и видный ученый своего времени.
Итак, по определению, момент силы относительно точки – это произведение модуля силы на ее плечо. 

Плечом в данном случае называется кратчайшее расстояние от рассматриваемой точки до линии действия силы, т. е. перпендикуляр, опущенный из точки на линию действия силы (см. рисунок 
 b). 

Математически это определение можно представить в виде формулы:
М0(F) = Fh,     где h – плечо силы относительно точки 0.
Точка, относительно которой рассматривается момент силы, называется центром момента.
Из приведенной выше формулы очевидно, что единицей измерения момента силы является  ньютон × метр (Нм).
 
Теперь можно оценить справедливость высказывания Архимеда относительно возможности перевернуть Землю — при определенном плече силы, которую способны развить человеческие мускулы, это сделать теоретически возможно, но рука Архимеда должна была описать путь длиной в сотни тысяч километров для того, чтобы сдвинуть земной шар на доли миллиметра, поскольку потребовался бы огромной длины рычаг. Как вы понимаете, практически осуществить подобный подвиг нереально даже для такого уважаемого гения, как Архимед.
 
Впрочем, бытующее утверждение о трудностях, связанных с перемещением Земли человеческой рукой не совсем безгрешны. Ведь мы, как обыватели, привыкли рассматривать Землю, как весомый предмет, забывая что она, будучи в космическом пространстве, обладает совсем другими весовыми категориями. Поэтому справедливее будет рассматривать не расстояние, на которое мог бы сдвинуть земной шар Архимед, а ускорение, с которым он попытался бы сдвинуть планету со своего места, т. е. фактически — побороть силу инерции Земли, как тела. 

И тогда ему не потребовался бы рычаг непомерной длины — прикладывая незначительную силу, сдвинуть Землю можно было бы и двухметровой палкой, но здесь уже возник бы вопрос о времени, в течении которого необходимо было давить на рычаг, чтобы побороть инертность земного шара (как вы понимаете, мускульная сила человека не способна придать планете существенного ускорения). 

Опять же, возникает еще одна проблема — Архимеду потребовался бы надежный упор для ног, способный противостоять возмущению Земли на нахальную попытку Архимеда сдвинуть ее с места, а где его найти в открытом космосе?…
Осталось разобраться со знаками для момента силы, ведь он, как и сила, является векторной величиной, т. е. характеризуется не только модулем, но и направлением своего вращающего действия.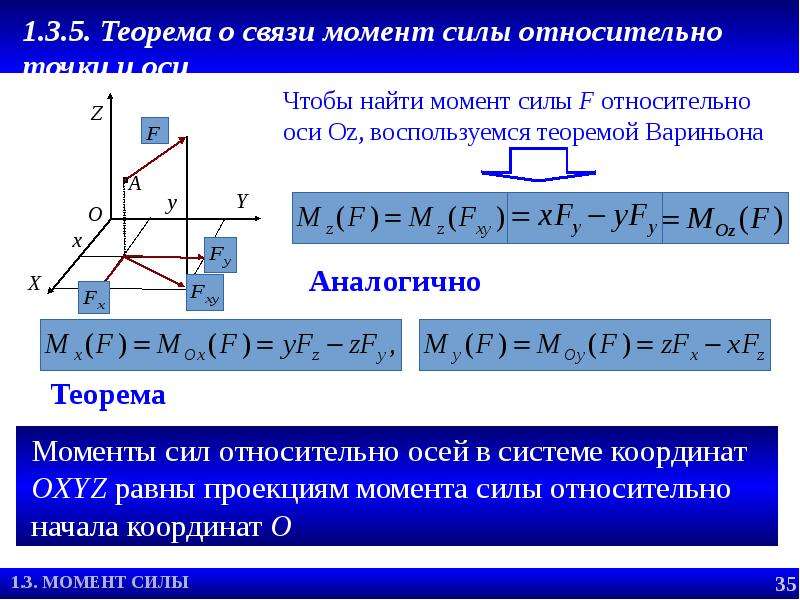 

При расчетах в технической механике условно считают, что если момент силы стремиться вращать свое плечо вокруг центра момента против часовой стрелки, то он является положительным, если по часовой стрелке — отрицательным (см. рисунок a).
Одна и та же сила относительно разных точек может вызывать и положительный, и отрицательный момент (см. рисунок a).
Отдельный случай, когда рассматриваемая точка (центр момента) лежит на линии действия силы. Очевидно, что в этом случае момент силы относительно этой точки будет равен нулю, поскольку плечо отсутствует (расстояние от линии действия силы до точки равно нулю).
И еще одна важная деталь, которая следует из определения момента силы относительно точки: если переносить силу вдоль линии ее действия, то момент силы относительно любой точки не изменится, поскольку не изменится и расстояние от этой точки до линии действия силы, т. е. плечо (см. рисунок с).
***
Плоская система пар сил
 
Главная страница
 

Дистанционное образование
 
Специальности
 
Учебные дисциплины
 
Олимпиады и тесты
 
Момент силы относительно центра [wiki.
 eduVdom.com]
Внимание! Этот раздел может иметь неточности в формулировках. 
Вскоре он будет доработан.
 Рассмотрим тело, которое закреплено в центре О и может  поворачиваться
вокруг  оси,  проходящей  через  точку  О  и  перпендикулярной  к  плоскости
чертежа. Приложим в точке А этого тела силу P и  выясним,  чем  определяется
вращательное действие этой силы (Рис.1).
 
Рис.1
 
 Очевидно, что воздействие силы на тело будет зависеть не только от  ее
величины, но и от того,  как  она  направлена,  и  в  конечном  итоге  будет
определяться ее моментом относительно центра О.
 Определение 1. Моментом силы  Р  относительно  центра  О  называется
взятое со знаком $\pm$ произведение модуля силы на ее плечо – то есть  длину
перпендикуляра, опущенного из моментной точки на линию действия силы.
 Правило  знаков: момент  силы  считается положительным,  если  сила
стремится повернуть тело против хода часовой стрелки и  отрицательным,  если
она вращает тело по ходу часовой стрелки. 
 В соответствии  с  данным  определением  момент  силы  численно  равен
удвоенной площади  треугольника  OAB,  построенного  на  векторе  силы  P  с
вершиной в моментной точке: $M_0(P) = P\cdot d = 2S\Delta_{OAB}$ .
 Отметим, что момент силы относительно точки О равен нулю,  если  линия
действия силы проходит через моментную точку.
 Рассмотренное определение момента силы  подходит  только  для  плоской
системы  сил.  В  общем  случае  для  однозначного  описания   вращательного
действия силы введем следующее определение.
 Определение  2. Вектор-моментом  силы  Р  относительно  центра   О
называется вектор, который:
 приложен  в  моментной  точке  О   перпендикулярно   к   плоскости треугольника, построенного на векторе силы с вершиной в моментной точке;
 направлен по правилу право винта;
 равен по модулю моменту силы Р относительно центра О (Рис. 1а).
 Правило правого винта, известное также из  курса  физики  как правило
буравчика, означает, что если смотреть навстречу  вектор-моменту  $\vec{М_0}(\vec{P})$ ,  мы
увидим вращение силой $\vec{P}$ плоскости своего действия, происходящим против  хода
часовой стрелки.
 Обозначим через $\vec{r}$ радиус-вектор точки приложения  силы $\vec{P}$ и  докажем, что справедлива следующая
 Теорема 1. Вектор-момент  силы  $\vec{P}$  относительно  центра О равен
векторному произведению радиус-вектора $\vec{r}$ и вектора силы $\vec{P}$ :
 $$\vec{M_0}(\vec{P}) = ( \vec{r} \times \vec{P})$$
 Напомним, что векторным произведением векторов  $\vec{a}\text{ и }\vec{b}$ называется вектор $\vec{c}$ , который (Рис.2б):
 
Рис.2
 
 перпендикулярен к векторам $\vec{a}\text{ и }\vec{b}$ ;
 образует с ними правую тройку  векторов,  то  есть,  направлен  так, что, смотря навстречу этому вектору, мы увидим поворот от вектора $\vec{a}$ к  вектору $\vec{b}$ на наименьший угол происходящим против хода часовой стрелки;
 равен по модулю  удвоенной  площади  треугольника,  построенного  на этих векторах:
 $$|\vec{c}| = |\vec{a} \times \vec{b}| = |\vec{a}|\cdot|\vec{b}|\cdot\sin(\vec{a},\,\vec{b})$$
 Для доказательства теоремы  отметим, во-первых,  что  вектор,  равный векторному произведению векторов $\vec{r}\text{ и }\vec{P}$  будет  коллинеарным  вектору  $\vec{M_0}(\vec{P})$. {i=n}M_{0\,\,i}(\vec{P_i})$$
Момент силы относительно точки — Энциклопедия по машиностроению XXL
 

 
 
 
 
 Значения тангенциальных составляющих реакций Fii и F-U можно определить из уравнений моментов сил относительно точки В, составляемых для каждого звена отдельно. Для звена 2 
 [c.148]
МОМЕНТЫ СИЛЫ ОТНОСИТЕЛЬНО точки и оси
 [c.24]
Для рассмотрения различных систем сил необходимо ввести понятия алгебраического и векторного моментов силы относительно точки и момента силы относительно оси. Введем эти характеристики действия силы на твердое тело и рассмотрим их свойства.
 [c.24]
 
 

 
 

 
 
 
 
 
 I. АЛГЕБРАИЧЕСКИЙ МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ
 [c.24]
При рассмотрении плоской системы сил, приложенных к твердому телу, используется понятие алгебраического момента силы относительно точки. 
 [c.24]
Алгебраическим моментом силы относительно точки называют произведение модуля силы на плечо силы относительно этой точки (рис. 19), взятое со знаком плюс или минус.
 [c.25]
Из определения алгебраического момента силы относительно точки следует, что он не зависит от переноса силы вдоль ее линии действия. Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через моментную точку. Сумма алгебраических моментов относительно точки двух равных по модулю, но противоположных по направлению сил, действующих вдоль одной прямой, равна нулю. Численно алгебраический момент относительно точки равен удвоенной площади треугольника, построенного на силе А В и моментной точке 
 [c.25]
СВЯЗЬ МОМЕНТА СИЛЫ ОТНОСИТЕЛЬНО ОСИ С ВЕКТОРНЫМ МОМЕНТОМ СИЛЫ ОТНОСИТЕЛЬНО ТОЧКИ НА ОСИ
 [c.28]
Для векторных моментов сил относительно точки О имеем
 [c.89]
Рассмотрим условия равновесия элемента (рис. 83) — суммы проекций всех сил на оси АВ н О К соответственно и сумму моментов сил относительно точки В 
 [c.72]
 
 

 
 
 
 
 
 Введем важное понятие о моменте силы относительно точки. Точку, относительно которой берется момент, называют центром момента, а момент силы относительно этой точки — моментом относительно центра. Если под действием приложенной силы тело
 [c.31]
Точно так же берем сумму моментов сил, относительно точки О для
 [c.221]
Если рассматриваются только силы, лежащие в одной плоскости, то их моменты относительно точек этой плоскости должны быть направлены по перпендикулярам к этой плоскости в ту или иную сторону. Поэтому моменты сил относительно точки плоскости тождественны
 [c.56]
Момент силы относительно точки считается положительным, если сила Р стремится повернуть плоскость чертежа вокруг точки О 56
 [c. 56]
 
 

 
 

 
 
 
 
 
 Момент силы относительно точки можно определить удвоенной площадью треугольника АОВ
 [c.57]
В обоих случаях главный момент сил относительно точки О равен моменту пары сил (см. 14 о парах сил, лежащих в одной плоскости) 
 [c.58]
Что называется моментом силы относительно точки 
 [c.58]
Как определяется на плоскости момент силы относительно точки 
 [c.58]
И. Какая зависимость существует между моментом силы относительно точки и моментом той же силы относительно оси, проходящей через эту точку 
 [c.58]
При составлении алгебраической суммы моментов сил относительно точки пользуемся правилом знаков, изложенным в 25. При этом сумму моментов сил составляем относительно точки, в которой приложена одна из неизвестных сил. В этом случае сила, приложенная в этой точке, не имеет момента относительно нее и уравнение содержит только одну неизвестную величину. 
 [c.68]
Составляем сумму моментов сил относительно точки В 
 [c.68]
Векторы, направления которых зависят от принятой системы координат, называются псевдовекторами. Примерами псевдовекторов, кроме угловой скорости, могут служить также момент силы относительно точки и момент пары сил. При сложении псевдовекторов действительны правила параллелограмма и многоугольника ( П7).
 [c.208]
Для определения S4 составим уравнение моментов сил относительно точки F, где пересекаются линии действия сил и Sq (точки Риттера
 [c.17]
I. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО точки КАК ВЕКТОР И МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ
 [c.84]
Кроме момента силы относительно точки, при изучении системы сил в пространстве приходится рассматривать также и момент силы относительно той или иной оси.
 [c.85]
Для определения проекций Foix, Fiw, з4л-, / з4у необходимо составить уравнения равновесия сил, денствую1цих на группу, и моментов сил относительно точки В отдельно для каждого звена. 
 [c.142]
Векторным моментом силы относительно точки называют вектор, приложенный в этой точке и равный по модулю произведению силы на плечо силы относителыю этой точки. Векторный момент силы направлен перпендикулярно плоскости, в которой лежат сила и моментная точка, таким образом, что с его конца можно видеть стремление силы вращать тело против движения часовой стрелки (рис. 20).
 [c.25]
Эгу зависимость между моментом силы относительно оси и векюрным моментом силы относительно точки на оси можно принять за определение момента силы относительно оси.
 [c.29]
Используя связь момента силы относительно оси с векторным моментом силы относительно точки на оси, можно получить формулы для вычисления моментов огносительно осей координат, если даны проекции силы на оси координаг и координаты точки приложения силы.
 [c.29]
Для определения Y,, составим условие равновесия для сил, приложенных к егрежню НС, в форме суммы моментов сил относительно точки С. В )то условие НС войду неизвестные силы Х(- и которые определять не
 [c.65]
Че гырьмя неопределенными параметрами являются момент и силы Р I j и P(.. Сила Рд связана с ними условием равенства нулю суммы моментов сил относительно точки Е.
 [c.449]
Как направлен пектор момента силы относительно точки и как определяется его модуль 
 [c.58]
В разделе Статика ( 44 и 45) введены и широко использо-взЕгы понятая моментов силы относительно точки и относительно оси. Так как количество движения материальной точки mv является вектором, ТО можно определить его моменты относительно центра н относительно оси таким же путем, как определяются моменты силы.
 [c.145]
Рассмотрим систему уравновешивающихся сил, приложенных о всей конструкции (рис. 21). Составим уравнение моментов сил относительно точки В. Для упрощения вычисления момента силы i разложиsi te на вертикальную и горизонтальную составляющие P l = Pi os 60° = 2,5 кН Pi = P. sin 60° = 4,33 kH,
 [c.22]
Момент силы относительно точки центра)
 Моментом силы относительно точки (центра) О называется вектор, численно равный произведению модуля силы на плечо (расстояние от центра до линии действия силы) н направленный перпендикулярно плоскости, проходящей через точку О и линию действия силы в ту сторону, откуда сила видна направленной относительно точки О против хода часовой стрелки. Если точка приложения силы F определяется радиусом-вектором г относительно точки О, то Мо Р) = гХ , т. е. момент силы равен векторному произведению вектора г на вектор Х. Проекция в тора момента силы Мо (Р) на ось называется моментом силы Г относительно оси. Момент равнодействующей силы относительно оси равен алгебраической сумме моментов сил данной системы сил относительно этой оси.
 [c.50] 
 

 
 

 
 
 
 
 
 Моментом силы относительно точки центра момента) назовем вектор, равный по величине произведению силы на кратчайшее расстояние линии действия ее
 [c. 37]
Момент силы относительно точки (центра)
 [c.70]
Момент силы относительно точки (центра) 47, 53, 104, 105, 109 Моменты инерции главные 341 Мощность 271, 374
 [c.475]
Теория пар сил. Момент силы относительно точки (центра) как вектор. Пара сил. Момент пары сил как вектор. Теорема о сумме моментов сил, образующих пару, относительно любого центра. Теоремы об эквивалентности пар. Сложение пар, произвольно расположенных в пространстве. Условия равновесия системы пар.
 [c.5]
Введем важное понятие о моменте силы относительно точки. Точку, относительно которой берется момент, называют центром момента, а момент силы относительно этой точки — моментом относительно центра. Если под действием приложенной силы тело
 [c.31]
Как видно из рис. 1.44, б, в результате последовательного приведения заданных сил к точке образовались система сходящихся сил и система присоединенных пар с моментами, равными моментам заданных сил относительно точки (центра) приведения.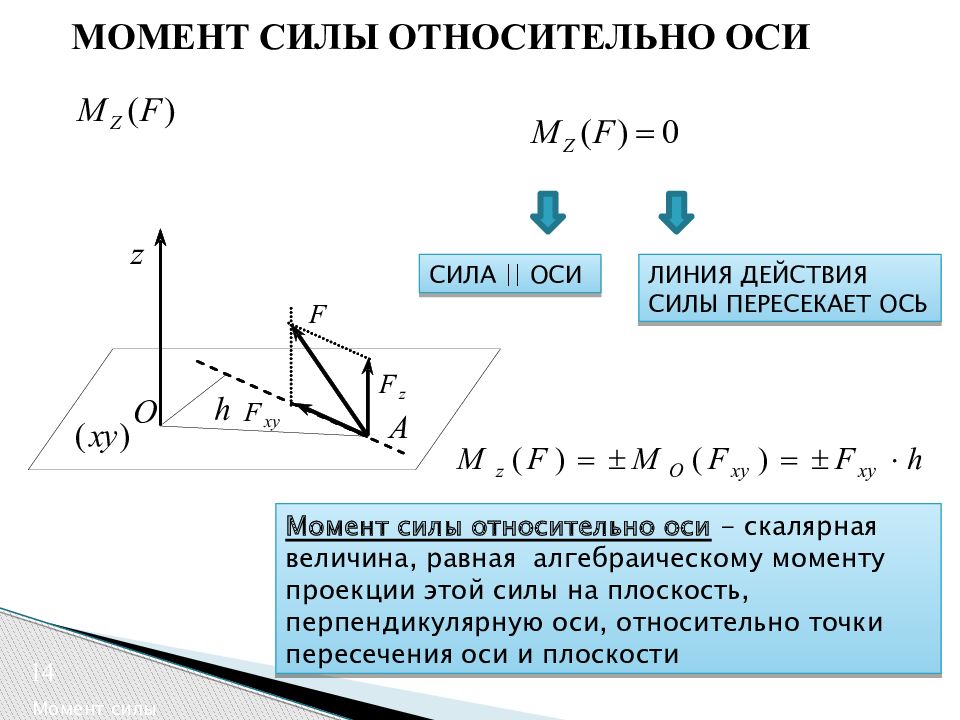 
 [c.36]
При составлении суммы моментов сил относительно точки С сила Р, приложенная в центре катка О, разложена на две составляющие — горизонтальную (Р os а) и вертикальную (Р sin а), и использована теорема Вариньона. При этом, как принято всегда делать, при вычислении момента горизонтальной составляющей силы Р мы пренебрегли изменением ее плеча, считая, что оно равно радиусу катка г.
 [c.111]
Очевидно, что когда центр О лежит на линии действия силы, то момент силы относительно этого центра равен нулю (так как плечо равно нулю).
 [c.224]
Выражение момента силы относительно точки в виде вектора вполне соответствует физической сущности этого понятия, и если силы расположены в различных плоскостях, то моменты сил относительно точки складывают по правилу параллелограмма. Только при рассмотрении системы сил, расположенных в одной плоскости, можно игнорировать направление вектора момента, а учитывать его величину и знак, т. е. определять момент по формулам (14), (15) или (16). В такой системе, когда все силы и центр моментов расположены в одной плоскости, векторы моментов различных сил относительно какой-либо точки О направлены от точки О перпендикулярно к этой плоскости в ту или другую сторону, и в этом случае их складывают алгебраически.
 [c.59]
Словами это равенство можно прочитать так момент равнодействующей системы сходящихся сил относительно какой-либо точки равен сумме моментов всех сил относительно той же точки. Момент силы относительно точки есть вектор, поэтому сумма является геометрической. В частном случае, если все силы и центр моментов
 [c.60]
 
 
Момент пары сил не имеет фиксированной, определенной точки приложения. Он является свободным вектором, т. е. он имеет свой модуль и свое направление, но приложить его можно в любой точке твердого тела, на которое действует пара сил. В этом заключается принципиальное отличие момента пары от момента силы относительно точки, являющегося прикрепленным вектором, приложенным в центре момента, или от скользящего вектора, примером которого является сила. 
 [c.82]
Таким образом, опуская из какой-нибудь точки О перпендикуляр на линию действия силы F и умножая модуль силы на длину этого перпендикуляра, получим момент силы F относительно этой точки О. Знак момента будем определять, руководствуясь следующим правилом если мысленно, закрепив центр момента и действуя на плечо в направлении силы, будем поворачивать плечо против хода часовой стрелки, то момент силы относительно данного центра положителен, если же по ходу часовой стрелки, то момент отрицателен.
 [c.137]
Словами это равенство можно прочитать так момент равнодействующей системы сходящихся сил относительно какой-либо точки равен сумме моментов всех сил относительно той же точки. Момент силы относительно точки есть вектор, поэтому сумма является геометрической. В частном случае, если все силы и центр моментов лежат в одной плоскости, то все векторы моментов направлены по
 [c.232]
Центральная сила может быть притягивающей (направленной к центру) и отталкивающей (направленной от центра). Так как для центральной силы момент силы относительно своего центра равен нулю, т. е. Мо = О, то, следовательно, по теореме об изменении кинетического момента для точки (23),
 [c.306]
В правой системе координат момент силы относительно точки положителен, если направление силы соответствует направлению вращения вокруг центра моментов против хода часовой стрелки.
 [c.264]
Таким образом, момент силы относительно оси, проходящей через центр момента относительно точки, равен проекции момента силы относительно точки на ось.
 [c.69]
Так же как и момент пары, момент силы относительно точки можно изобразить в виде вектора, приложенного в центре момента
 [c.46]
Напомним, что в этом учении момент силы относительно точки рассматривался в плоскости, проходящей через линию действия силы и точку, называемую центром момента , и определялся алгебраической величиной произведения величины силы на плечо, т. е. кратчайшее расстояние линии действия силы от центра момента эта величина бралась со знаком плюс либо минус в зависимости от того, в какую сторону стремилась повернуть тело приложенная к нему сила.
 [c.36]
Направление плоскости в пространстве, как известно, может быть задано перпендикуляром к этой плоскости. Чтобы одновременно определить величину момента силы относительно точки и направление плоскости, проходящей через линию действия силы и центр момента, естественно рассматривать момент силы то(Р) относительно точки О (рис. 26) как вектор, приложенный в этой точке, равный по абсолютной величине произведению величины силы Р на кратчайшее расстояние к линии действия силы от центра момента, т. е. плечо, и направленный по перпендикуляру к плоскости, содержащей линию действия
 [c.36]
Легко видеть (рис. 26), что по численной величине момент силы относительно точки равен удвоенной площади 2S треугольника, построенного на силе как на основании и с вершиной в центре момента.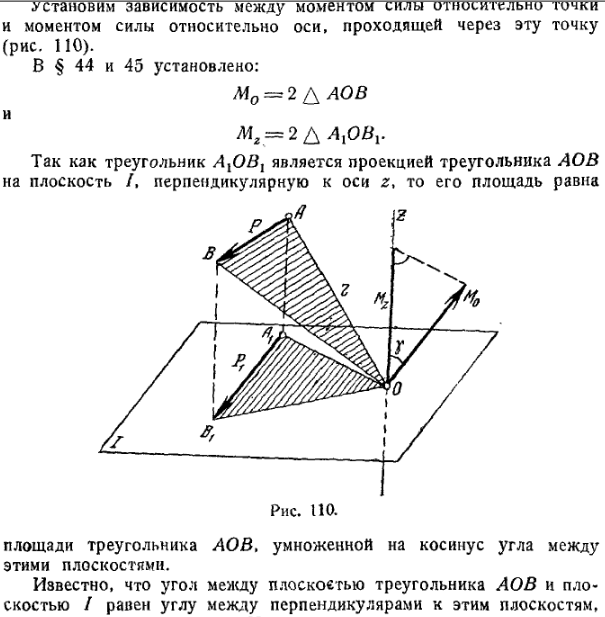 Вместо удвоенной площади треугольника можно взять площадь параллелограмма со сторонами, равными силе и отрезку г, соединяющему центр моментов с точкой приложения силы, так что
 [c.38]
Итак, момент силы относительно некоторого центра равен векторному произведению вектор-радиуса точки приложения силы на вектор силы.
 [c.39]
 
 

 
 

 
 
 
 
 
 Мы уже показали, что линия действия реакции Pgs проходит через точку Р, так что мы, воспользовавшись уравнением (б), можем определить ее величину. При развертывании уравнения (б) надо иметь в виду, что момент силы, приложенной к стороне многоугольника, равен произведению величины силы на длину части стороны от центра момента до точки приложения силы и на синус разности углов наклона к оси х векторов силы и указанной стороны многоугольника. Например, момент силы относительно точки Е (см. рис. 108, а) равен
 [c.158]
УРАВНЕНИЯ ДВИЖЕНИЯ. Пусть в точках P.e g , t=l,. … .., N, приложены силы Fi. Введем две векторные величины формальную сумму сил F = SF, и суммарный момент сил относительно точки А—Ол = Е[ЛР,хР,]. Векторы F и Gg могут зависеть от положения и ориентации тела, его угловой скорости и скорости центра масс и от времени. Уравнения движения свободного твердого тела имеют вид
 [c.205]
Момент силы относительно точки. Моментом силы Р относительно некоторой точки О называется произведение величины силы Р на ее плечо й относительно этой точки (т. е. кратчайшее расстояние от этой точки, называемой центром момента, до линии действия силы). Численно момент равен
 [c.363]
Центр давления результирующей силы Р определяется из уравнения моментов сил относительно точки О 
 [c.45]
Обозначим через к расстояние между центрами тяжести полок, а через кх и — расстояния от центра сдвига 5 до центров тяжести полок. Тогда величины этих расстояний можно определить, приравняв нулю сумму моментов сил относительно точки 5 
 [c. 318]
Точка О. относительно которой берется момент силы, называется центром момента расстояние р центра момента от линии действия силы называется плечом силы относительно этой точки. Итак, момент силы относительно точки — это произведение силы на ее плечо.
 [c.44]
Реактивная сила R меняет и направление. Примем для простоты, что сила R проходит через центр колеса и, перенеся ее в центр, разложим на составляющие вертикальную Q и горизонтальную Кг-Из условия равновесия сил имеем, что Q = П. Сила К2, как внешняя сила и направленная в сторону, обратную движению, будет сопротивлением от качения колеса по рельсу. Составим уравнение моментов сил относительно точки опоры А
 [c.73]
Далее доказывается теорема об изменении кинетической энергии системы, изучаются свойства кинетической энергии системы, указываются способы вычисления ее для твердого тела при различных случаях движения. В связи с последним рассматриваются осевые моменты инерции и их свойства. Затем доказывается теорема об элементарной работе сил, действующих на абсолютно твердое тело на основании определения работы сил, действующих на точки материальной системы, и теоремы о распределении линейных скоростей в свободном твердом теле. Здесь естественно вводятся понятия о К/ оменте силы относительно центра и оси, о главном векторе и главном моменте сил относительно произвольного центра.
 [c.69]
МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ТО КИ (ЦЕНТРА) — величина, равная векторному произведению радиус-век-тора, проведенного из данной точки О в точку приложения силы А, на эту силу 
 [c.226]
Для определения отклонения гирлянды из условия ее статического равновесия напишем уравнение моментов сил относительно точки ее подвеса В (рис. 3-3). Заметим, что вес провода составляет лишь ро1/2, так как провод в смежном пролете оборван вес гирлянды Gp приложен в ее центре тяжести, т. е. на плече i/2. Уравнение моментов сил
 [c.79]
Обозначим и, V горизонтальную и вертикальную составляющие скорости центра тяжести, а через со — угловую скорость одного из верхних стержней сразу же после удара. Тогда эффективные силы одного из стержней будут эквивалентны вертикальной слагающей импульса т (v—V) и его горизонтальной слагающей ти, приложенным в центре тяжести, и импульсивной паре с моментом mk ti), стремящейся увеличить угол а. Пусть R — ударный импульс в точке С, направление которого, по соображениям симметрии, будет горизонтальным. Чтобы избежать введения в наши уравнения реакции в точке В, возьмем для стержня ВС моменты сил относительно точки В. Получим
 [c.158]
Пример 3. Шар радиусом а катится по земле со скоростью U и ударяется под прямым углом о вертикальную стену. Коэффициенты трения и восстановления равны [I и е. Показать, что при условии (1 + е) ц> 2/7 скольжение прекращается перед окончанием удара и шар отскакивает с горизонтальной скоростью — Ue и вертикальной скоростью 2I//7 (это можно получить, если вычислять моменты сил относительно точки соприкосновения). Центр шара затем описывает параболу, и шар ударяется о землю Предполагается, что земля неупругая и имеет коэффициент трення [i удара центр шара будет иметь скорость —и (е— и угловую скорость (2 — 5ц ) t//(7a). Учитывая, что
 [c.177]
Как было показано в п. 205, если пренебрегать квадратами малых величин, то можно брать моменты сил относительно мгновенных центров как относительно неподвижных точек. Обычно неизвестные реакции таковы, что их линии действия проходят через эту точку, и тогда их моменты равны нулю и, таким образом, уравнение будет содержать только известные величины.
 [c.385]
В разделе Статика ( 44 и 45) введены и широко использо-взЕгы понятая моментов силы относительно точки и относительно оси. Так как количество движения материальной точки mv является вектором, ТО можно определить его моменты относительно центра н относительно оси таким же путем, как определяются моменты силы.
 [c.145]
 
 

 
 

 
 
 
 
 
 Если сила Р и центр моментов О лежат в координатной плоскости Оху, то Л4д.(Р)=Л4 2,(Р)=0, а момент силы Мо(Р) будет колли-неарен с осью Ог. В этом случае момент силы Мц(Р) полностью определяется своей проекцией Л1г(Р) на ось Ог. Поэтому при исследовании системы сил на плоскости момент силы относительно точки рассматривают как скалярную величину, собственно, заменяя этот момент его проекцией на ось, перпендикулярную к плоскости, в которой лежат сила и центр моментов.
 [c.264]
Момент силы относительно точки изображается вектором, перпендикулярным к Г[лоскости, проходящей через силу и центр момента так, чтобы из его конца вращение силы вокруг точки представлялось [фоисходящим против часовой стрелки
 [c.363]
Закон площадей — прообраз и частный случай общего закона моментов количеств движения — был установлен впервые Кеплером для движения планет. Кеплер показал, что его второй закон справедлив как для теории Коперника, так и для теорий Птолемея и Тихо Браге. Возможно, что это обстоятельство побудило Ньютона к дальнейшему обобщению. В Началах он доказал и то, что закон площадей для планетных орбит является следствием закона тяготения (планет к Солнцу) в принятой Ньютоном форме, и то, что этот закон справедлив при движении тела под действием любой силы постоянного направления, проходящей через неподвижный центр. Но переход к более общей закономерности не был напрашивающимся, так как момент силы относительно этого центра тождественно равен нулю и в случае, который рассматривал Ньютон. Этот переход был облегчен развитием статики — оперирование моментами (сил) относительно ося или точки как алгебраическими величинами стало там обычным благодаря трудам Вариньона. Все же новое обобщение закона площадей было получено только в работах 40-х годов XVIII в. Все эти работы связаны с задачами о движении тел на движущихся поверхностях. Подобные задачи ставились и в земной, и в небесной механике. Иоганн и Даниил Бернулли начали изучение таких вопросов для случая, когда движущаяся поверхность — наклонная плоскость. Клеро немало содействовал успеху в этой тогда новой области механики своими результатами по теории относительного движения. Вслед за ним Эйлер в большой работе О движениях тел по подвижным поверхностям от-
 [c.125]
Нормальную нагрузку на ведущее колесо Ry можно найти из уравения моментов сил относительно точки А, находящейся на пересечении линии действия касательной силы тяги Рк с нормалью к поверхности пути, проходящей через центр поддерживающего колеса 
 [c.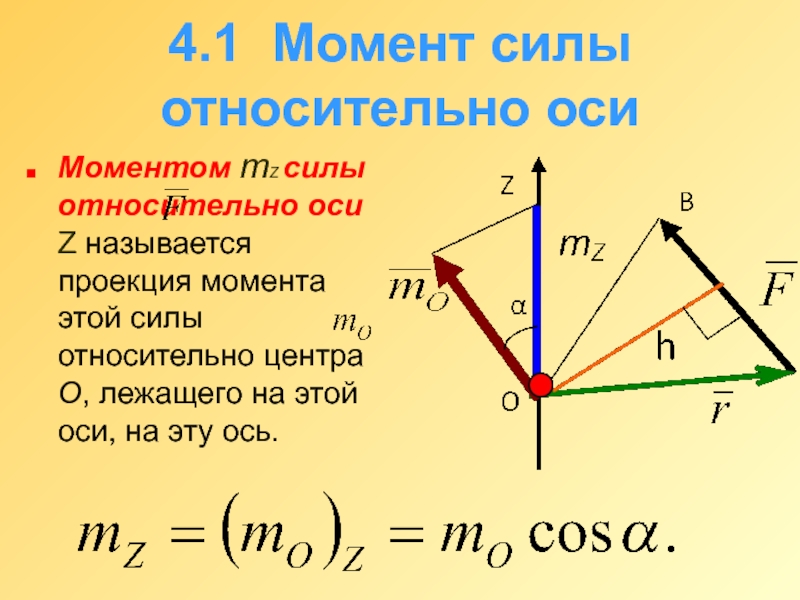 246]
Очевидно, что сила является вектором, переменным по модулю с линией действия, совпадающей с линией возвратно-поступательного движения центра тяжести ползуна. В ряде случаев при расчетах полагают, что центр тяжест(1 комплекта деталей ползуна совпадает с центром шарнира В (см. рис. 1.8), пренебрегая моментом силы относительно точки В .
 [c.28]
Момент сил инёрции относительно центра масс равен нулю, так как угловое ускорение равно нулю. Прикладываем искомый момент Мд. Записываем систему уравнений равновесия в виде проекций сил на оси J и у и момента сил относительно точки О 
 [c.229]
Момент силы — определение и свойства
Момент силы относительно точки
Определение момента
Момент силы относительно точки O
– это векторное произведение вектора , проведенного из точки O в точку приложения силы A, на вектор силы :
(1)   .
 Если выбрать прямоугольную систему координат Oxyz с центром в точке O, то момент силы будет иметь следующие компоненты:
(1. 1)   ;
(1.2)   ;
(1.3)   .
Здесь  – координаты точки A в выбранной системе координат:
.
Компоненты  представляют собой значения момента силы относительно осей , соответственно.
Определение плеча силы
Плечо силы относительно точки
– это расстояние между линией действия силы и точкой, относительно которой определяется плечо. То есть плечо силы – это длина перпендикуляра, опущенного из точки на линию действия силы.
Свойства
 Если точку приложения силы переместить вдоль линии ее действия, то момент, при таком перемещении, не изменится.
Доказательство ⇓
 Абсолютная величина момента силы относительно некоторой точки равна произведению абсолютного значения силы на плечо этой силы относительно выбранной точки.
Доказательство ⇓
 Момент относительно точки O, от силы, линия действия которой проходит через эту точку, равен нулю.
Доказательство ⇓
 Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
Доказательство ⇓
 Тоже самое относится и к силам, чьи линии продолжения пересекаются в одной точке. При этом в качестве точки приложения суммы сил берется точка пересечения линий их действия.
 Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
Доказательство ⇓
 Момент силы является псевдовектором или, что то же самое, аксиальным вектором.
 Это свойство следует из свойства векторного произведения. Поскольку векторы  и  являются истинными (или полярными) векторами, то их векторное произведение является псевдовектором. Это означает то, что мы можем определить только абсолютное значение и ось, вдоль которой направлено векторное произведение. Само же направление по этой оси мы задаем произвольным образом, используя правило правого винта. То есть мы мысленно откладываем векторы  и  из одного центра. Затем поворачиваем ручку из положения  в положение . В результате правый винт смещается в направлении, перпендикулярном плоскости, в которой расположены векторы. Это направление мы и берем за направление векторного произведения.
 Но если бы мы определили направление по правилу левого винта, то векторное произведение было бы направлено в противоположную сторону. При этом никакого противоречия не возникает. То есть фактически, аксиальные векторы могут иметь два взаимно противоположных направления. Чтобы не усложнять математические формулы, мы выбираем одно из них, применяя правило правого винта. По этой причине, псевдовекторы нельзя геометрически складывать с истинными векторами. Но их можно перемножать, используя скалярное или векторное произведение.
Момент силы относительно оси
Определение
 Часто встречаются случаи, когда нам не нужно знать все компоненты момента силы относительно выбранной точки, а нужно знать только момент силы относительно выбранной оси.
Момент силы относительно оси
– это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси.
 Пусть  – единичный вектор, направленный вдоль оси. И пусть O – произвольная точка, принадлежащая ей. Тогда момент силы относительно оси является скалярным произведением:
.
Такое определение возможно, поскольку для любых двух точек O и O′, принадлежащих оси, проекции моментов относительно этих точек на ось равны. Покажем это.
 Воспользуемся векторным уравнением :

;
.
Умножим это уравнение скалярно на единичный вектор , направленный вдоль оси:
.
Поскольку вектор  параллелен оси, то . Отсюда
.
То есть проекции моментов на ось, относительно точек O и O′, принадлежащих этой оси, равны.
Свойства
 Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
Доказательство ⇓
 Момент относительно оси от силы, параллельной этой оси равен нулю.
Доказательство ⇓
Доказательство свойств
Перемещение точки приложения силы вдоль линии ее действия
 Все свойства ⇑ Если точку приложения силы переместить вдоль линии действия силы, то момент, при таком перемещении, не изменится.
 Доказательство
 Пусть сила  приложена в точке A. Через точку A проведем прямую, параллельную вектору силы. Эта прямая является линией ее действия. Переместим точку A приложения силы в точку A′, принадлежащую линии действия. Тогда
.
Вектор  проведен через две точки линии действия. Поэтому его направление совпадает или противоположно направлению вектора силы . Тогда , где λ – параметр; .   , если точка A′ смещена относительно A в направлении вектора . В противном случае .
 Таким образом, вектор, проведенный из O в A′, имеет вид:
.
Найдем момент силы, приложенной в точке A′, применяя свойства векторного произведения:

.
Мы видим, что момент не изменился:
.
 Свойство доказано.
Абсолютная величина момента силы
 Все свойства ⇑ Абсолютная величина момента силы относительно некоторой точки равна произведению абсолютного значения силы на плечо этой силы относительно выбранной точки.
 Доказательство
Абсолютное значение момента M относительно точки O равно произведению силы F на ее плечо d = |OD|.
 Пусть мы имеем силу , приложенную в точке A. Рассмотрим момент этой силы относительно некоторой точки O. Заметим, что точки O, A и вектор  лежат в одной плоскости. Изобразим ее на рисунке. Через точку A, в направлении вектора  проводим прямую AB. Эта прямая называется линией действия силы . Через точку O опустим перпендикуляр OD к линии действия. И пусть D является точкой пересечения линии действия и перпендикуляра. Тогда  – плечо силы относительно центра O. Обозначим его буквой . Воспользуемся предыдущим свойством ⇑, согласно которому точку приложения силы можно перемещать вдоль ее линии действия. Переместим ее в точку D. Момент силы:
.
Поскольку векторы  и  перпендикулярны, то по свойству векторного произведения, абсолютное значение момента:
,
где  – абсолютное значение силы.
 Заметим, что вектор момента  перпендикулярен плоскости рисунка. Его направление определяется по правилу правого винта. Если мы будем вращать винт, проходящий через точку O перпендикулярно плоскости рисунка, в направлении силы F, то он будет перемещаться на нас. Поэтому вектор момента перпендикулярен плоскости рисунка и направлен на нас.
 Свойство доказано.
Момент относительно точки от силы, проходящей через эту точку
 Все свойства ⇑ Момент относительно точки O, от силы, линия действия которой проходит через эту точку, равен нулю.
 Доказательство
 Пусть линия действия силы  проходит через точку O. Тогда плечо этой силы относительно O равно нулю: . Согласно предыдущему свойству ⇑, абсолютное значение момента силы относительно выбранной точки равно нулю:
.
 Свойство доказано.
Момент суммы сил, приложенных в одной точке
 Все свойства ⇑ Момент от векторной суммы сил, приложенных к одной точке тела, равен векторной сумме моментов от каждой из сил, приложенных к этой же точке:
.
 Доказательство
 Пусть силы  приложены в одной точке A. Пусть  – векторная сумма этих сил. Находим момент относительно некоторой точки O от векторной суммы , приложенной в точке A. Для этого применяем свойства векторного произведения:

.
 Свойство доказано.
Момент системы сил, векторная сумма которых равна нулю
 Все свойства ⇑ Если векторная сумма сил равна нулю:
,
то сумма моментов от этих сил не зависит от положения центра, относительно которого вычисляются моменты:
.
 Доказательство
 Пусть силы  приложены в точках , соответственно. И пусть точки O и C обозначают два центра, относительно которых мы будем вычислять моменты. Тогда имеют место следующие векторные уравнения:
.
Используем их при вычислении суммы моментов относительно точки O:



.
Здесь мы воспользовались тем, что по условию,
.
 Свойство доказано.
Момент относительно оси от силы, проходящей через эту ось
 Все свойства ⇑ Момент относительно оси от силы, линия действия которой проходит через эту ось, равен нулю.
 Доказательство
 В определении ⇑ указано, что момент силы относительно оси – это проекция вектора момента силы относительно произвольной точки, принадлежащей этой оси, на направление оси. В качестве такой точки возьмем точку пересечения линии действия силы с осью. Но, согласно доказанному выше ⇑, момент относительно этой точки равен нулю. Поэтому равна нулю и его проекция на эту ось.
 Свойство доказано.
Момент относительно оси от силы, параллельной этой оси
 Все свойства ⇑ Момент относительно оси от силы, параллельной этой оси равен нулю.
 Доказательство
 Пусть O – произвольная точка на оси. Рассмотрим момент силы относительно этой точки. Согласно определению:
.
Согласно свойству векторного произведения, вектор момента  перпендикулярен вектору силы . Поскольку вектор силы параллелен оси, то вектор момента ей перпендикулярен. Поэтому проекция момента относительно точки O на ось равна нулю.
 Свойство доказано.
Автор: Олег Одинцов.     Опубликовано: 20-09-2019
Глава 10. Статика
Статика — это раздел динамики, в котором рассматривается равновесие тел, и формулируются условия, при выполнении которых тела находятся в равновесии. Для успешного решения задач «на статику» необходимо уметь вычислять моменты сил, знать и уметь использовать условия равновесия тел. При этом следует помнить, что при вычислении моментов распределенных сил (тяжести, трения, реакции) возникает понятие центра тяжести тела, как точки, к которой надо приложить суммарную распределенную силу для вычисления ее момента.
 Момент силы определяется по отношению к некоторой точке, которую будем называть началом отсчета моментов, и которая выбирается произвольно. Моментом силы  называется произведение модуля силы на ее «плечо» , которое определяется как длина перпендикуляра, опущенного из начала отсчета момента на прямую, вдоль которой действует сила

(10.1)
Например, плечом силы  относительно точки  (см. рисунок) является отрезок . Знак момента определяется следующим образом. Надо представить, что через точку  проходит ось вращения тела, на которое действует сила . Если сила  стремится закрутить тело по часовой стрелке относительно этой оси, то момент силы  отрицателен, если против часовой стрелки — положителен. (Следует иметь в виду, что знак момента можно было выбирать и наоборот. Дело в том, что момент силы — это вектор. В школьном курсе, однако, определение вектора момент не вводится, и рассматриваются только такие ситуации, когда векторы момента направлены вдоль одной оси. Данное выше определение момента — это определение проекции вектора момента на эту ось. А поскольку направление оси никак не определяется, то важен только относительный знак проекций момента.) Из определения момента (10.1) следует, что момент силы равняется нулю, если прямая, вдоль которой она действует, проходит через начало отсчета момента.
Если на неточечное тело действуют силы, у которых нет определенной точки приложения, например, сила тяжести, сила трения, сила реакции (такие силы принято называть распределенными), то для вычисления их моментов можно поступить следующим образом. Необходимо разбить это тело на бесконечно малые элементы, вычислить момент силы, действующей на каждый элемент, просуммировать полученные моменты. Оказывается, что если распределенные силы пропорциональны массам элементов и одинаково направлены, для вычисления момента распределенной силы нужно суммарную распределенную силу приложить к некоторой точке, которая называется центром тяжести тела. Центр тяжести тела, обладающего центральной симметрией (а только такие тела и могут встретиться школьникам), находится в геометрическом центре тела.
Тело находится в равновесии по отношению к инерциальной системе отсчета, если сумма всех сил, действующих на тело, равна нулю

(10.2)
и сумма моментов этих сил, вычисленных относительно произвольного начала отсчета, равна нулю

(10.3)
Условия (10.2), (10.3) можно использовать для определения сил, действующих на тело, которое находится в равновесии.
В задаче 10.1.1 начало отсчета моментов (точка ) лежит на линии действия силы . Поэтому момент этой силы относительно точки  равен нулю (ответ 3).
На рисунке числами 1, 2, 3 и 4 отмечены отрезки (толстые сплошные линии), которые представляют собой плечи сил , ,  или  (задача 10.1.2) относительно точки  (линии действия сил показаны тонким пунктиром). Из этого рисунка видим, что из этих сил наибольшее плечо имеет сила  (правильный ответ в этой задаче – 2).
Для момента первой силы из задачи 10.1.3 имеем
Тогда для момента второй силы получаем
т.е. момент второй силы в  раз больше момента первой силы (ответ 1).
По определению плечо силы — это перпендикуляр опущенный из начала отсчета момента (точки  в задаче 10.1.4) на линию действия силы. Поэтому плечо силы реакции — отрезок  (или , который равен отрезку ). Следовательно, плечо силы реакции вертикальной стенки, действующей на лестницу, равно длине отрезка . Правильный ответ в задаче – 1.
Плечо силы  в задаче 10.1.5 равно отрезку  (см. рисунок). Из прямоугольного треугольника  получаем для плеча силы — . Поэтому момент силы  равен
(ответ 1).
На тело массой , находящееся на наклонной плоскости с углом наклона  (задача 10.1.6), со стороны плоскости действует сила реакции, направленная перпендикулярно плоскости и равная . Поэтому момент этой силы относительно основания плоскости длиной   (см. рисунок в условии задачи) равен  (ответ 2).
Чтобы рычаг был в равновесии сумма моментов всех сил, действующих на рычаг, должна равняться нулю, причем относительно любой точки — начала отсчета моментов. На рычаг в задаче 10.1.7 действуют: сила 3 Н на плечо длиной 0,1 м, искомая сила  — на плечо длиной 0,3 м и сила со стороны оси вращения. Помещая начало отсчета моментов на оси вращения и находя моменты сил, действующих на плечи рычага, получаем из условия равновесия (10.3)
(момент силы, действующей на рычаг со стороны оси вращения равен нулю относительно выбранного начала). Отсюда находим, что  (ответ 1).
Ось вращения стержня в задаче 10.1.8 надо расположить в такой точке, чтобы сумма моментов сил  и  относительно этой оси равнялась бы нулю. При этом очевидно, что ось должна располагаться справа от точки приложения силы . Поскольку величина силы  втрое больше величины силы , то плечо силы  должно быть втрое меньше плеча силы . Поэтому правильный ответ в задаче — 4.
Приравнивая величины моментов сил тяжести, действующих на тела, относительно опоры (задача 10.1.9), получим
где  — расстояние от опоры до левого груза. Отсюда находим  (ответ 2). Аналогично в задаче 10.1.10 получим  (ответ 4).
В задаче 10.2.1 на невесомый стержень действуют две силы натяжения нитей  и , и сила со стороны груза, равная его силе тяжести  (см. рисунок). Используем условие равновесия стержня (10.3). Моменты удобно вычислять относительно начала отсчета , помещенного около правого конца стержня. Относительно этого начала имеем , ,  (здесь использовано, что точка крепления груза делит стержень в отношении 1:3). Поэтому из условия (10.3) получаем . Отсюда 4 кг (ответ 4).
Из условия равенства моментов, вращающих рычаг в задаче 10.2.2 по и против часовой стрелки, получаем  (ответ 4).
Как отмечалось во введении к настоящей главе, для нахождения момента распределенной силы (в данном случае момента силы тяжести) нужно силу тяжести, действующую на весь стержень, «приложить» к геометрическому центру стержня (к его середине) и вычислять момент этой силы так, как будто бы она является сосредоточенной (см. рисунок). Поэтому плечо силы тяжести относительно точки  в задаче 10.2.3 равно — длина стержня), и момент силы тяжести относительно точки  равен  — ответ 3. Здесь  — масса стержня.
Используя это значение момента силы тяжести, можно найти силу натяжения нити в задаче 10.2.4. Условие равновесия (10.3) относительно точки  дает
где  — момент силы натяжения относительно точки . Отсюда находим  (ответ 3).
С одной стороны, если к стержню приложена минимальная необходимая для переворота сила (задача 10.2.5), сила реакции, действующая на стержень со стороны стола, будет приложена к точке, находящейся над самым краем. С другой стороны, если к концу стержня приложена именно такая сила, стержень практически находится в равновесии. Поэтому в том случае, когда на тело действует минимальная необходимая для переворота сила, сумма моментов силы тяжести и искомой силы  относительно края стола равна нулю
Отсюда находим  (ответ 2).
На стержень из задачи 10.2.6 действуют сила тяжести , реакции стенки  и пола , а также сила трения со стороны пола, направленная так, как показано на рисунке, причем сила тяжести приложена к середине стержня. Используем условие равенства нулю суммы моментов внешних сил (10.3) относительно нижней точки стержня. Поскольку моменты силы трения и силы реакции  относительно нижней точки стержня равны нулю, условие (10.3) дает
где  — угол между стержнем и горизонтальной поверхностью (отмечен на рисунке дугой). Отсюда находим
Поскольку для рассматриваемого случая   , , то  (ответ 1).
При приложении к концу стержня минимально необходимой для отрыва этого конца от поверхности (задача 10.2.7) силы  одновременно выполнены два следующих условия. Поскольку стержень 
 
практически находится в равновесии, то еще выполнены уравнения статики — сумма моментов сил, действующих на стержень, равна нулю. С другой стороны, в этот момент стержень уже начинает отрываться от поверхности, и сила реакции опоры  будет приложена к другому концу стержня (см. рисунок). Поэтому сумма моментов силы  и силы тяжести относительно левого конца стержня должна равняться нулю . Отсюда (ответ 4).
При приложении к бруску минимально необходимой для его переворота силы  (задача 10.2.8) сумма моментов сил тяжести  и  относительно упора (см. рисунок в условии) равна нулю. Этот вывод обосновывается так же, как и в предыдущей задаче. Поэтому  (ответ 3).
В задаче 10.2.9 проще всего сравнить силы реакции упоров, из условия равенства нулю суммы всех сил, действующих на стержень (формула (10.2)). На стержень действуют три силы: тяжести , и две силы реакции  и  (см. рисунок), сумма которых равна нулю, или . Поэтому сила реакции нижнего упора  больше, чем верхнего  (ответ 2).
Треугольник в задаче 10.2.10 находится в равновесии, если его центр тяжести лежит на вертикальной прямой, проходящей через шарнир. Это связано с тем, что на треугольник действуют две силы — тяжести и реакции шарнира — и, чтобы выполнялось условие моментов относительно шарнира, момент силы тяжести относительно шарнира должен равняться нулю. Докажем, что центр тяжести треугольника лежит в точке пересечения его медиан. Действительно, если разбить треугольник на тонкие полоски, параллельные одной из сторон, то центр тяжести каждой из них лежит в ее середине. Поэтому и центры тяжести всех полосок (а, значит, и всего треугольника) лежат на его медиане (см. рисунок; медиана показана пунктиром). А поскольку треугольник можно разделить на слои, параллельные второй и третьей его стороне, то центр тяжести лежит и на этих медианах, т.е. в точке их пересечения (правильный ответ 1).
 Что такое момент? 
 Что такое момент?
 
 Что такое момент?
  Момент  силы
это мера его тенденции заставлять тело вращаться вокруг определенного
точка или ось. Это отличается от тенденции тела двигаться или
перевести, в направлении силы. Чтобы на мгновение развиваться,
сила должна действовать на тело таким образом, чтобы тело начало
крутить. Это происходит каждый раз, когда прикладывается сила, поэтому она не
проходят через центр тяжести тела.Момент возникает из-за силы, не имеющей
равная и противоположная сила прямо вдоль линии его действия.
 Представьте, что два человека толкают дверь у дверной ручки с противоположных сторон.
Если они оба толкают с одинаковой силой, то есть состояние
равновесие. Если один из них внезапно отпрыгнет от двери,
толчок другого человека больше не будет иметь никакого сопротивления, и дверь
качнулся бы прочь. Человек, который все еще толкал дверь, создал
момент. 
 Элементы момента
 Величина момента силы, действующей вокруг точки или оси, равна
прямо пропорционально расстоянию силы от точки или оси.Он определяется как произведение силы (F) и плеча момента (d). В  плечо рычага  или  плечо рычага  — перпендикулярное расстояние между
линия действия силы и центр моментов. 
  Момент = Сила x Расстояние  или  M
= (F) (г) 
 Центр моментов   может быть точкой, относительно которой
сила вызывает вращение. Это также может быть контрольная точка или ось, вокруг которой
сила может рассматриваться как вызывающая вращение.Это не имеет значения, пока
как конкретная точка всегда принимается за точку отсчета. Последний случай
Это гораздо более распространенная ситуация в задачах структурного проектирования.
 Момент выражается в фут-фунтах, кип-футах,
ньютон-метры или килоньютон-метры. Момент тоже имеет смысл; По часовой стрелке
вращение вокруг центра моментов будет считаться положительным моментом;
в то время как вращение против часовой стрелки вокруг центра моментов будет считаться
отрицательный. Самый распространенный способ выразить момент — 
 
 В этом примере показан гаечный ключ, применяемый к гайке.100-фунтовая сила — это
применяется к нему в точке C, центре гайки. Сила применяется при
расстояние x 12 дюймов от гайки. Центром моментов может быть
точка C, но также могут быть точки A, B или D.
  Момент около точки C  
 Плечо момента для расчета момента вокруг точки C составляет 12 дюймов. В
величина момента относительно точки C равна 12 дюймам, умноженным на силу
100 фунтов, чтобы получить общий момент 1200 дюйм-фунтов (или 100 фунт-футов).
 Рычаг момента (d) = 12 дюймов
 Звездная величина (F) = 100 фунтов
  Момент = M = 100 фунтов x 12 дюймов= 1200 дюйм-фунтов 
 Точно так же мы можем найти моменты относительно любой точки пространства.
  Момент @ 
  А 
  В 
  D 
 Рычаг момента
 8 дюймов
 2 дюйма
 0 дюймов
 Величина F
100 фунтов
100 фунтов
100 фунтов
  Общий момент 
 800 фунтов
 200 фунтов
 0 дюймов
 Момент вызывает вращение вокруг точки или оси.Если настало время
быть взятой около точки из-за силы F, затем, чтобы на мгновение развиться,
линия действия не может пройти через эту точку. Если линия действий
проходит через эту точку, момент равен нулю, потому что величина
плечо момента равно нулю. Так было с точкой D предыдущего ключа.
проблема. Полный момент был равен нулю, потому что плечо момента также было нулевым.
 
 В качестве другого примера предположим, что к
гаечный ключ, как указано.Момент силы 200 фунтов, приложенной к точке C, равен нулю.
потому что:
  M = F x d = 200 фунтов x 0 дюймов = 0 дюймов-фунтов 
 Другими словами, у 200-фунтовой силы нет тенденции вызывать
гаечный ключ для вращения гайки. Можно было увеличить величину силы
пока болт окончательно не сломался (разрушение при сдвиге).
 Момент относительно точек X, Y и Z также будет равен нулю, потому что они также
лежать на линии действия. 
 
 Момент также можно рассматривать как результат сил, отклоняющихся от
прямая линия, проведенная между точкой нагрузки системы и ее опорами.В этом случае синяя сила — это эксцентрическая сила. Чтобы он достиг
основание колонны, необходимо сделать обход по балке. Чем больше
объезд, тем важнее момент. Самые эффективные конструкционные системы
иметь как можно меньше объездов. Об этом будет сказано подробнее
подробно в Лекции 37 и
более поздние курсы.
 Есть случаи, когда легче вычислить моменты
компоненты силы вокруг определенной точки, чем для расчета
момент самой силы.Возможно, определение перпендикуляра
расстояние силы сложнее, чем определение перпендикуляра
расстояние составляющих силы. Момент нескольких сил о
точка — это просто алгебраическая сумма составляющих их моментов относительно
та же точка. При добавлении моментов компонентов нужно учитывать большие
заботиться о чувстве каждого момента. Часто благоразумно
отмечать смысл ближайшего момента при решении подобных задач.
 Комбинированный
Моменты 
 Моменты
на балке
  Распространенные ошибки  
 При добавлении моментов компонентов нужно очень внимательно следить за их согласованностью.
со смыслом каждого момента.Часто благоразумно отметить следующий смысл.
на тот момент, когда брались за такие проблемы.
  Часто задаваемые вопросы  
 Любые трудности с вычислением момента обычно связаны с одним из
следующие:
 Центр моментов установлен неправильно или четко
 понял.
 Предполагаемое плечо момента не является ПЕРПЕНДИКУЛЯРНЫМ расстоянием между
 линия действия силы и центр моментов.
 Направление или направление вращения было проигнорировано или неправильно понято.
  Вопросы для размышления  
 Каков момент относительно точки B и точки D для обоих случаев
показано в приведенном выше примере гаечного ключа? Как можно было добавить расширение к
конец гаечного ключа поможет вывернуть заржавевший болт? Какие конструктивные системы
будет наименьшее количество «объездных путей»?
  Проблемы  
  Сопутствующие показания  
 Shaeffer, R.E.  Элементарные конструкции для архитекторов и строителей. С. 33-39.
 Авторские права © 1995, 1996 Крис Х. Любкеман и
Дональд Петинг 
 Авторские права © 1996, 1997, 1998 Крис Х. Любкеман
 Карта механики — момент около точки 
 Момент  силы  — это тенденция некоторых сил вызывать вращение. Любой простой способ визуализировать концепцию — это поставить коробку на гладкую поверхность. Если бы вы приложили силу к центру коробки, она просто скользила бы по поверхности, не вращаясь. Если вместо этого вы нажмете на одну сторону коробки, она начнет вращаться при движении.Несмотря на то, что силы имеют одинаковую величину и одинаковое направление, они вызывают разные реакции. Это связано с тем, что нецентральная сила имеет другую точку приложения и оказывает момент вокруг центра коробки, тогда как сила в центре коробки не оказывает момента вокруг центральной точки коробки.
 Если мы толкнем коробку в центре, она просто начнет скользить. Если мы толкнем коробку не по центру, мы приложим момент, и коробка будет вращаться в дополнение к скольжению.
 Как и силы, моменты имеют величину (степень вращения, которую он может вызвать) и направление (ось, вокруг которой будет вращаться тело).Определение величины и направления этих моментов относительно данной точки является важным шагом в анализе систем твердых тел (твердых тел, в которых силы не действуют одновременно). Приведенный ниже скалярный метод — самый простой способ сделать это в простых двумерных задачах, в то время как альтернативные векторные методы лучше всего работают в более сложных трехмерных системах.
 Скалярный метод в двух измерениях 
 Обсуждая, как вычислить момент силы относительно точки с помощью скалярных величин, мы начнем с примера силы, действующей на простой рычаг, как показано ниже.В этом простом рычаге на конце рычага действует сила на расстоянии d от центра вращения рычага (точка A), где сила имеет величину F.
 Величина момента силы F относительно точки A на этом рычаге будет равна величине силы, умноженной на расстояние d.
 При использовании скалярных величин величина момента будет равна расстоянию по перпендикуляру между линией действия силы и точкой, в которой мы принимаем момент.
 Чтобы определить знак момента, мы определяем, какой тип вращения вызовет сила. В этом случае мы можем видеть, что сила заставит рычаг вращаться против часовой стрелки вокруг точки A. Вращения против часовой стрелки вызываются положительными моментами, а вращение по часовой стрелке — отрицательными моментами.
 Еще один важный фактор, о котором следует помнить, это то, что величина d — это перпендикулярное расстояние от силы до точки, в которой мы принимаем момент. Мы могли бы измерить расстояние от точки A до головы вектора силы, или хвоста вектора силы, или действительно любой точки вдоль линии действия силы F.Однако расстояние, которое нам нужно использовать для расчета скалярного момента, является кратчайшим расстоянием между точкой и линией действия силы. Это всегда будет линия, перпендикулярная линии действия силы, идущая в точку, о которой мы принимаем момент.
 Расстояние d всегда должно быть наименьшим расстоянием между линией действия силы и точкой, в которой мы принимаем момент. Это расстояние будет перпендикулярно линии действия силы.
 Скалярный метод в трех измерениях 
 Для трехмерных скалярных вычислений мы все равно найдем величину момента таким же образом, умножив величину силы на перпендикулярное расстояние между точкой и линией действия силы.Это перпендикулярное расстояние снова является минимальным расстоянием между точкой и линией действия силы. В некоторых случаях найти это расстояние может быть очень сложно.
 Для моментов в трех измерениях вектор момента всегда будет перпендикулярен как вектору силы F, так и вектору расстояния d. Чтобы использовать правило правой руки, выровняйте правую руку, как показано, так, чтобы ваш большой палец совпадал с осью вращения для момент и ваши скрученные пальцы указывают в направлении вращения на ваш момент.Если вы сделаете это, ваш большой палец будет указывать в направлении вектора момента. Адаптировано из изображения Public Domain от Schorschi2.
 Еще одним сложным фактором в трехмерных скалярных задачах является определение оси вращения, поскольку теперь это более сложно, чем просто «по часовой стрелке или против часовой стрелки». Ось вращения будет линией, проходящей через точку, в которой мы принимаем момент, которая перпендикулярна как вектору силы, так и вектору перпендикулярного смещения (вектор, идущий от точки, в которой мы принимаем момент, до точки приложения сила.Хотя это возможно в любой ситуации, это становится очень трудным, если векторы силы или смещения не лежат в одном из трех координатных направлений.
 Для дальнейшего определения направления вектора момента (который будет действовать вдоль установленной линии для оси вращения) мы воспользуемся правилом правой руки в измененной форме. Оберните пальцы правой руки вокруг оси вращения, согнув кончики пальцев в направлении вращения тела. Если вы сделаете это, ваш большой палец должен указывать вдоль линии в направлении вектора момента.Это важный последний шаг, потому что мы можем вращаться по часовой стрелке или против часовой стрелки вокруг любой заданной оси вращения. Имея вектор конечного момента, мы знали не только ось вращения, но и то, как тело будет вращаться вокруг этой оси.
 Динамика вращательного движения: вращательная инерция 
 Цели обучения 
 К концу этого раздела вы сможете:
 Поймите взаимосвязь между силой, массой и ускорением.
 Изучите вращающий эффект силы.
 Изучите аналогию между силой и крутящим моментом, массой и моментом инерции, а также линейным ускорением и угловым ускорением.
 Если вы когда-либо крутили колесо велосипеда или толкали карусель, вы знаете, что для изменения угловой скорости требуется сила, как показано на рисунке 1. На самом деле ваша интуиция надежна в предсказании многих факторов, которые участвуют в этом процессе. . Например, мы знаем, что дверь открывается медленно, если мы нажимаем слишком близко к ее петлям.Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше от оси приложена сила, тем больше угловое ускорение; другое значение состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.
 Рис. 1. Для вращения колеса велосипеда требуется сила. Чем больше сила, тем больше угловое ускорение. Чем массивнее колесо, тем меньше угловое ускорение. Если вы надавите на спицу ближе к оси, угловое ускорение будет меньше.
 Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу  F  к точечной массе  м , которая находится на расстоянии  r  от точки поворота, как показано на рисунке 2.Поскольку сила перпендикулярна  r , ускорение [латекс] a = \ frac {F} {m} [/ latex] получается в направлении  F . Мы можем переписать это уравнение так, чтобы  F  =  ma , а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что  a  =  rα , и мы подставляем это выражение в  F  =  ma , что дает
  F  =  mrα 
 Напомним, что  крутящий момент  — это эффективность силы поворота при повороте.В этом случае, поскольку F перпендикулярно  r , крутящий момент просто равен  τ  =  Fr . Итак, если мы умножим обе части приведенного выше уравнения на  r , мы получим крутящий момент в левой части. То есть
  rF  =  mr   2   α 
 или
  τ  =  mr   2   α .
 Это последнее уравнение является вращательным аналогом второго закона Ньютона ( F = ma ), где крутящий момент аналогичен силе, угловое ускорение аналогично поступательному ускорению, а  mr   2  аналогично массе (или инерции).Величина  mr   2  называется  вращательной инерцией  или  моментом инерции  точечной массы  m  на расстоянии  r  от центра вращения.
 Рис. 2. Объект поддерживается горизонтальным столом без трения и прикреплен к точке поворота шнуром, который обеспечивает центростремительную силу. Сила  F  применяется к объекту перпендикулярно радиусу  r , заставляя его ускоряться относительно точки поворота.Усилие держится перпендикулярно к  р. 
 Установление соединений: динамика вращательного движения 
 Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика связана с силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силе и массе, которые ведут себя так, как мы ожидали из нашего предыдущего опыта.
 Инерция вращения и момент инерции 
 Прежде чем мы сможем рассматривать вращение чего-либо, кроме точечной массы, подобной показанной на рисунке 2, мы должны распространить идею инерции вращения на все типы объектов.{2} [/ латекс]. Здесь  I  аналогичен  м  в поступательном движении. Из-за расстояния  r  момент инерции любого объекта зависит от выбранной оси. Фактически, вычисление  I  выходит за рамки этого текста, за исключением одного простого случая — обруча, вся масса которого находится на одинаковом расстоянии от оси. Таким образом, момент инерции обруча вокруг своей оси равен  MR   2 , где  M,  — его общая масса, а  R  — его радиус.(Мы используем  M  и  R  для всего объекта, чтобы отличить их от  m  и  r  для точечных масс.) Во всех других случаях мы должны обращаться к рисунку 3 (обратите внимание, что таблица является произведением искусства, которое имеет формы, а также формулы) для формул для  I , которые были получены интегрированием по непрерывному телу. Обратите внимание, что  I  имеет единицы массы, умноженные на квадрат расстояния (кг⋅м  2 ), как и следовало ожидать из его определения.
 Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением равно
.
 нетто τ =  Iα 
 или
 [латекс] \ alpha = \ frac {net {\ tau}} {I} [/ latex]
, где net  τ  — полный крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только моменты, действующие под действием сил в плоскости вращения. Такие моменты могут быть положительными или отрицательными и складываются как обычные числа. Соотношение в net τ =  Iα,  [latex] \ alpha = \ frac {\ text {net} {\ tau}} {I} [/ latex] является вращательным аналогом второго закона Ньютона и очень широко применимо.Это уравнение действительно справедливо для  любого крутящего момента , приложенного к  любому объекту , относительно  любой оси .
 Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением состоит в том, что чем больше момент инерции, тем меньше угловое ускорение.Но есть еще один нюанс. Момент инерции зависит не только от массы объекта, но и от его  распределения  массы относительно оси, вокруг которой он вращается. Например, карусель, полную детей, будет намного легче разогнать, если они будут стоять близко к ее оси, чем если все они будут стоять у внешнего края. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на грани.
 Эксперимент на вынос 
 Вырежьте из плотного картона круг радиусом около 10 см.На краю круга напишите числа от 1 до 12, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси через его центр, как колесо. (Вы можете свободно прибить круг к стене.) Держите круг неподвижно и с номером 12, расположенным вверху, прикрепите кусок синей замазки (липкий материал, используемый для крепления плакатов к стене) под номером 3. Насколько велик шишка должна быть просто кружить круг? Опишите, как можно изменить момент инерции круга.Как это изменение повлияет на количество синей замазки, необходимое для числа 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.
 Стратегия решения проблем для динамики вращения 
  Изучите ситуацию, чтобы определить, что крутящий момент и масса участвуют во вращении . Нарисуйте тщательный набросок ситуации.
  Определите интересующую систему .
  Нарисуйте схему свободного тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую систему.
  Примените net τ = Iα, α = net τI, вращательный эквивалент второго закона Ньютона, чтобы решить задачу . Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент относительно точки вращения.
  Как всегда, проверьте правильность решения .
 Выполнение подключений 
 В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует.При вращательном движении чистый крутящий момент является причиной углового ускорения, как и во втором законе движения Ньютона для вращения.
 Рис. 3. Некоторые инерции вращения.
 Пример 1. Расчет влияния распределения массы на карусель 
 Представьте, что отец толкает карусель на детской площадке на рис. 4. Он прилагает силу 250 Н к краю 50,0 кг карусели, имеющей радиус 1,50 м. Рассчитайте угловое ускорение, возникающее (а), когда никто не находится на карусели, и (б), когда он равен 18.Ребенок 0 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с незначительным тормозящим трением.
 Рис. 4. Отец толкает карусель на детской площадке за край и перпендикулярно ее радиусу, чтобы добиться максимального крутящего момента.
 Стратегия 
 Угловое ускорение напрямую выражается выражением [latex] \ alpha = \ frac {\ text {net} \ tau} {I} [/ latex]:
 [латекс] \ alpha = \ frac {\ tau} {I} [/ латекс]
 Чтобы решить для  α , мы должны сначала вычислить крутящий момент  τ  (который одинаков в обоих случаях) и момент инерции  I  (который больше во втором случае).{2}} [/ латекс].
 Решение для (b) 
 Мы ожидаем, что угловое ускорение для системы в этой части будет меньше, потому что момент инерции больше, когда ребенок находится на карусели. Чтобы найти полный момент инерции  I , мы сначала находим момент инерции ребенка  I   c , считая ребенка эквивалентом точечной массы на расстоянии 1,25 м от оси. Затем
  I   c  =  MR   2  = (18.0 кг) (1,25 м)  2  = 28,13 кг м  2 .
 Полный момент инерции — это сумма моментов инерции карусели и ребенка (относительно одной оси). Чтобы оправдать эту сумму, изучите определение  I :
.
  I  = 28,13 кг м  2  + 56,25 кг м  2  = 84,38 кг м  2 .
 Подстановка известных значений в уравнение для  α  дает
 [латекс] \ alpha = \ frac {\ tau} {I} = \ frac {\ text {375 N} \ cdot \ text {m}} {\ text {84.{2}} [/ латекс].
 Обсуждение 
 Угловое ускорение меньше, когда ребенок находится на карусели, чем когда карусель пуста, как и ожидалось. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось незначительным. Если, например, отец продолжал толкать перпендикулярно в течение 2,00 с, он дал бы карусели угловую скорость 13,3 рад / с, когда она пуста, и только 8,89 рад / с, когда на ней сидит ребенок.В оборотах в секунду эти угловые скорости составляют 2,12 об / с и 1,41 об / с соответственно. В первом случае отец разгонялся до 50 км / ч. Летние Олимпийские игры, вот он! Подтверждение этих чисел оставлено читателю в качестве упражнения.
 Проверьте свое понимание 
 Крутящий момент — аналог силы, а момент инерции — аналог массы. Сила и масса — это физические величины, которые зависят только от одного фактора. Например, масса связана исключительно с количеством атомов различных типов в объекте.Одинаково ли просты крутящий момент и момент инерции?
 Решение 
 № Крутящий момент зависит от трех факторов: величины силы, направления силы и точки приложения. Момент инерции зависит как от массы, так и от ее распределения относительно оси вращения. Таким образом, хотя аналогии точны, эти вращательные величины зависят от большего числа факторов.
 Сводка раздела 
 Чем дальше от оси приложена сила, тем больше угловое ускорение; угловое ускорение обратно пропорционально массе.
 Если мы приложим силу  F  к точечной массе  м , которая находится на расстоянии  r  от точки поворота, и поскольку сила перпендикулярна  r , ускорение a = F / m будет получено в направление  F . Мы можем переписать это уравнение так, чтобы
  F  =  ма ,
, а затем поищите способы связать это выражение с выражениями для вращательных величин. Заметим, что  a  =  rα , и мы подставляем это выражение в  F  =  ma , что дает
  F = mrα 
 Крутящий момент — это эффективность силы поворота при повороте.В этом случае, поскольку  F  перпендикулярно  r , крутящий момент равен просто  τ = rF . Если мы умножим обе части приведенного выше уравнения на  r , мы получим крутящий момент в левой части. Это,
  rF = mr   2   α 
 или
  τ = mr  2  α .
 Концептуальные вопросы 
 1. Момент инерции длинного стержня, закрученного вокруг оси через один конец, перпендикулярный его длине, составляет  ML   2 /3.Почему этот момент инерции больше, чем он был бы, если бы вы вращали точечную массу  M  в месте расположения центра масс стержня (на  L /2)? (Это будет  ML   2 /4.)
 2. Почему момент инерции обруча с массой  M  и радиусом  R  больше, чем момент инерции диска с такой же массой и радиусом? Почему момент инерции сферической оболочки с массой  M  и радиусом  R  больше, чем у твердой сферы с такой же массой и радиусом?
 3.Приведите пример, в котором малая сила вызывает большой крутящий момент. Приведите другой пример, в котором большая сила вызывает небольшой крутящий момент.
 4. При уменьшении массы гоночного велосипеда наибольшая выгода достигается за счет уменьшения массы шин и колесных дисков. Почему это позволяет гонщику достичь большего ускорения, чем такое же уменьшение массы рамы велосипеда?
 Рисунок 5.
 5. Мяч скользит по трапу без трения. Затем его катят без проскальзывания и с той же начальной скоростью по другой рампе без трения (с тем же углом наклона).В каком случае он достигает большей высоты и почему?
 Задачи и упражнения 
 1. В этой задаче рассматриваются дополнительные аспекты примера 1: Расчет влияния распределения массы на карусель. а) Сколько времени нужно отцу, чтобы дать карусели угловую скорость 1,50 рад / с? б) Сколько оборотов он должен совершить, чтобы получить эту скорость? (c) Если он приложит замедляющую силу 300 Н в радиусе 1,35 м, сколько времени ему потребуется, чтобы остановить их?
 2.Рассчитайте момент инерции фигуриста с учетом следующей информации. (а) Фигурист весом 60,0 кг приблизительно представляет собой цилиндр с радиусом 0,110 м. (b) Фигурист с вытянутыми руками представляет собой цилиндр, примерно равный 52,5 кг, радиус 0,110 м и две руки длиной 0,900 м, каждая по 3,75 кг, которые выходят прямо из цилиндра, как стержни, вращающиеся вокруг своей оси. заканчивается.
 3. Трехглавая мышца задней части плеча разгибает предплечье. Эта мышца у профессионального боксера имеет силу 2.00 × 10  3  Н с эффективным перпендикулярным плечом рычага 3,00 см, обеспечивающим угловое ускорение предплечья 120 рад / с  2 . {2} [/ latex] Что это сила, прилагаемая мышцей, если ее эффективное перпендикулярное плечо рычага равно 1.90 см?
 5. Предположим, вы прилагаете усилие 180 Н по касательной к точильному камню с радиусом 0,280 м и весом 75,0 кг (твердый диск). а) Какой крутящий момент прилагается? (b) Какое угловое ускорение предполагает незначительное встречное трение? (c) Каково угловое ускорение, если существует противодействующая сила трения 20,0 Н, действующая на 1,50 см от оси?
 6. Рассмотрим колесо мотоцикла массой 12,0 кг, показанное на рисунке 6. Предположим, что это примерно кольцевое кольцо с внутренним радиусом 0.280 м и внешний радиус 0,330 м. Мотоцикл стоит на центральной подставке, так что колесо может свободно вращаться. (a) Если приводная цепь оказывает усилие в 2200 Н на радиусе 5,00 см, каково угловое ускорение колеса? (б) Каково тангенциальное ускорение точки на внешнем крае шины? (c) Сколько времени требуется, начиная с состояния покоя, для достижения угловой скорости 80,0 рад / с?
 Рис. 6. Момент инерции колеса мотоцикла приблизительно равен моменту инерции кольцевого кольца.
 7. Зорч, заклятый враг Супермена, решает замедлить вращение Земли до одного раза в 28,0 ч, приложив противодействующую силу на экваторе и параллельно ему. Супермен не сразу обеспокоен, потому что он знает, что Зорч может проявлять силу только 4,00 × 10  7  Н (немного больше, чем тяга ракеты Сатурн V). Как долго Зорч должен продвигаться с этой силой, чтобы достичь своей цели? (Этот период дает Супермену время, чтобы посвятить его другим злодеям.) Ясно покажите, как вы следуете шагам, описанным в разделе «Стратегия решения проблем  для динамики вращения»  (выше).
 8. Автомобильный двигатель может развивать крутящий момент 200 Н ∙ м. Рассчитайте угловое ускорение, возникающее, если 95,0% этого крутящего момента приложено к ведущему валу, оси и задним колесам автомобиля, учитывая следующую информацию. Автомобиль подвешен так, чтобы колеса могли свободно вращаться. Каждое колесо действует как диск массой 15,0 кг с радиусом 0,180 м. Стенки каждой шины действуют как кольцевое кольцо массой 2,00 кг с внутренним радиусом 0,180 м и внешним радиусом 0,320 м. Протектор каждой шины действует как 10.{2} [/ латекс]. а) Сколько времени требуется ей, чтобы полностью изменить свое вращение? б) Что неразумного в результате? (c) Какие посылки необоснованны или непоследовательны?
 11.  Необоснованные результаты  В рекламе утверждается, что автомобилю массой 800 кг помогает его маховик массой 20,0 кг, который может разогнать автомобиль от состояния покоя до скорости 30,0 м / с. Маховик представляет собой диск радиусом 0,150 м. (a) Рассчитайте угловую скорость, которую должен иметь маховик, если 95,0% его энергии вращения используется для того, чтобы автомобиль набрал скорость.б) Что неразумного в результате? (c) Какая предпосылка является необоснованной, а какие несовместимы?
 Глоссарий 
 крутящий момент:
 токарная эффективность силы
 инерция вращения:
 сопротивление изменению вращения. Чем больше инерция вращения у объекта, тем труднее его повернуть на
 момент инерции:
 масса, умноженная на квадрат расстояния по перпендикуляру от оси вращения; для точечной массы это    I  =  mr   2  и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции
 Избранные решения проблем и упражнения 
 1.{2} \ end {array} [/ latex]
 10. (a) 2,0 мс (b) Временной интервал слишком короткий. (c) Момент инерции слишком мал на один-два порядка. Крутящий момент [латекс] \ text {500 Н} \ cdot \ text {m} [/ latex] является разумным.
 11. (a) 17 500 об / мин (b) Эта угловая скорость очень велика для диска такого размера и массы. Радиальное ускорение на краю диска> 50 000 gs. (c) Масса и радиус маховика должны быть намного больше, с учетом более низкой скорости вращения (угловой скорости).
 центр тяжести | Определение и факты 
  Центр тяжести , в физике, воображаемая точка в теле материи, в которой для удобства некоторых вычислений можно считать, что общий вес тела сосредоточен. Эта концепция иногда полезна при проектировании статических конструкций (например, зданий и мостов) или при прогнозировании поведения движущегося тела при воздействии на него силы тяжести.
  центр тяжести
 Когда барабан стоит вертикально, его центр тяжести (CG) прочно поддерживается, и барабан находится в устойчивом равновесии (A).Если барабан слегка наклонен в любую сторону (B), сила тяжести в этом центре создает крутящий момент или вращающую силу вокруг новой точки опоры и возвращает барабан обратно в устойчивое положение. Барабан, балансирующий на ободе (C), находится в неустойчивом равновесии. Даже небольшое смещение (D) создаст крутящий момент, который повернёт барабан дальше от неустойчивого положения.
  Encyclopædia Britannica, Inc. 
 В однородном гравитационном поле центр тяжести идентичен центру масс — термин, предпочитаемый физиками.Однако эти два понятия не всегда совпадают. Например, центр масс Луны находится очень близко к ее геометрическому центру (это не совсем точно, потому что Луна не является идеальной однородной сферой), но ее центр тяжести немного смещен к Земле из-за более сильной гравитационной силы, действующей на луну. ближняя сторона.
 Расположение центра тяжести тела может совпадать с геометрическим центром тела, особенно у объекта симметричной формы, состоящего из однородного материала.Однако асимметричный объект, состоящий из множества материалов с разной массой, скорее всего, будет иметь центр тяжести, расположенный на некотором расстоянии от его геометрического центра. В некоторых случаях, таких как полые тела или объекты неправильной формы, центр тяжести (или центр масс) может находиться в пространстве в точке, внешней по отношению к физическому материалу, например, в центре теннисного мяча или между ногами кресло.
 В опубликованных таблицах и справочниках перечислены центры тяжести наиболее распространенных геометрических фигур.Для треугольной металлической пластины, такой как изображенная на рисунке, расчет будет включать суммирование моментов весов всех частиц, составляющих металлическую пластину, относительно точки A. Приравнивая эту сумму к весу пластины W, умноженному на по неизвестному расстоянию от центра тяжести G до AC можно определить положение G относительно AC. Суммирование моментов можно легко и точно получить с помощью интегрального исчисления.
  центр тяжести
 Центр тяжести.Красная точка — центр тяжести G.
  Encyclopædia Britannica, Inc.  Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
 Центр тяжести любого тела также можно определить с помощью простой физической процедуры. Например, для пластины на рисунке точка G может быть определена путем подвешивания пластины за шнур, прикрепленный к точке A, а затем за шнур, прикрепленный к точке C. Когда пластина подвешена к точке A, линия AD является вертикальной; когда он подвешен к C, линия CE вертикальна.Центр тяжести находится на пересечении AD и CE. Когда объект подвешен в одной точке, его центр тяжести находится непосредственно под этой точкой.
 механика | Определение, примеры, законы и факты 
  Механика , наука, изучающая движение тел под действием сил, включая особый случай, когда тело остается в покое. В первую очередь проблема движения — это силы, которые тела действуют друг на друга. Это приводит к изучению таких тем, как гравитация, электричество и магнетизм, в зависимости от природы задействованных сил.Учитывая силы, можно искать способ, которым тела движутся под действием сил; это предмет собственно механики.
 Британская викторина
 Викторина «Все о физике»
 Кто был первым ученым, проведшим эксперимент по управляемой цепной ядерной реакции? Какая единица измерения для циклов в секунду? Проверьте свою физическую хватку с помощью этой викторины.
 Исторически механика была одной из первых возникших точных наук. Его внутренняя красота как математической дисциплины и ранний замечательный успех в количественном учете движений Луны, Земли и других планетных тел оказали огромное влияние на философскую мысль и послужили толчком для систематического развития науки.
 Механику можно разделить на три части: статика, которая имеет дело с силами, действующими на покоящееся тело и в нем; кинематика, описывающая возможные движения тела или системы тел; и кинетика, которая пытается объяснить или предсказать движение, которое произойдет в данной ситуации.В качестве альтернативы механику можно разделить по типу изучаемой системы. Простейшей механической системой является частица, определяемая как настолько маленькое тело, что его форма и внутренняя структура не имеют значения в данной задаче. Более сложным является движение системы из двух или более частиц, которые действуют друг на друга и, возможно, испытывают силы, действующие со стороны тел вне системы.
 Принципы механики были применены к трем общим областям явлений.Движение таких небесных тел, как звезды, планеты и спутники, можно предсказать с большой точностью за тысячи лет до того, как они произойдут. (Теория относительности предсказывает некоторые отклонения от движения в соответствии с классической или ньютоновской механикой; однако они настолько малы, что их можно наблюдать только с помощью очень точных методов, за исключением задач, затрагивающих всю или большую часть обнаруживаемой Вселенной. ) Как вторая область, обычные объекты на Земле вплоть до микроскопических размеров (движущиеся со скоростью намного ниже скорости света) правильно описываются классической механикой без значительных исправлений.Инженер, проектирующий мосты или самолеты, может с уверенностью использовать ньютоновские законы классической механики, даже если силы могут быть очень сложными, а вычислениям не хватает прекрасной простоты небесной механики. Третья область явлений включает поведение материи и электромагнитного излучения в атомном и субатомном масштабах. Хотя вначале были достигнуты ограниченные успехи в описании поведения атомов в терминах классической механики, эти явления должным образом рассматриваются в квантовой механике.
 Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту.
Подпишитесь сейчас
 Классическая механика занимается движением тел под действием сил или равновесием тел, когда все силы уравновешены. Этот предмет можно рассматривать как разработку и применение основных постулатов, впервые сформулированных Исааком Ньютоном в его книге  Philosophiae Naturalis Principia Mathematica  (1687), широко известной как  Principia . Эти постулаты, называемые законами движения Ньютона, изложены ниже.Их можно использовать для предсказания с большой точностью самых разных явлений, от движения отдельных частиц до взаимодействий очень сложных систем. В этой статье обсуждается множество этих приложений.
 В рамках современной физики классическую механику можно понять как приближение, вытекающее из более глубоких законов квантовой механики и теории относительности. Однако такой взгляд на место объекта сильно недооценивает его важность в формировании контекста, языка и интуиции современной науки и ученых.Наш современный взгляд на мир и место человека в нем прочно укоренен в классической механике. Более того, многие идеи и результаты классической механики выживают и играют важную роль в новой физике.
 Центральными понятиями классической механики являются сила, масса и движение. Ни сила, ни масса не очень четко определены Ньютоном, и оба они были предметом многих философских спекуляций со времен Ньютона. Оба они наиболее известны своими эффектами. Масса — это мера склонности тела сопротивляться изменениям в состоянии движения.С другой стороны, силы ускоряют тела, то есть они изменяют состояние движения тел, к которым они приложены. Взаимодействие этих эффектов — основная тема классической механики.
 Хотя законы Ньютона фокусируют внимание на силе и массе, три другие величины приобретают особое значение, потому что их общее количество никогда не меняется. Эти три величины — энергия, (линейный) импульс и угловой момент. Любой из них может быть перемещен из одного тела или системы тел в другое.Кроме того, энергия может менять форму, будучи связанной с единственной системой, проявляясь как кинетическая энергия, энергия движения; потенциальная энергия, энергия позиции; тепло или внутренняя энергия, связанная со случайными движениями атомов или молекул, составляющих любое реальное тело; или любая комбинация из трех. Тем не менее полная энергия, импульс и угловой момент во Вселенной никогда не меняются. Этот факт выражается в физике, говоря, что энергия, импульс и угловой момент сохраняются.Эти три закона сохранения вытекают из законов Ньютона, но сам Ньютон их не выражал. Их нужно было обнаружить позже.
 Примечателен тот факт, что, хотя законы Ньютона больше не считаются фундаментальными и даже не совсем правильными, три закона сохранения, выведенные из законов Ньютона — сохранение энергии, импульса и углового момента — остаются в точности верными даже в квантовая механика и теория относительности. Фактически, в современной физике сила больше не является центральным понятием, а масса — лишь одним из множества атрибутов материи.Однако энергия, импульс и угловой момент по-прежнему прочно занимают центральное место. Сохраняющаяся важность этих идей, унаследованных от классической механики, может помочь объяснить, почему этот предмет сохраняет такое большое значение в современной науке.
 Крутящий момент и угловое ускорение | Безграничная физика 
 Взаимосвязь между крутящим моментом и угловым ускорением 
 Крутящий момент равен моменту инерции, умноженному на угловое ускорение.
 Цели обучения 
 Выразите взаимосвязь между крутящим моментом и угловым ускорением в форме уравнения
 Основные выводы 
 Ключевые моменты 
 Когда к объекту прикладывается крутящий момент, он начинает вращаться с ускорением, обратно пропорциональным его моменту инерции.
 Это соотношение можно рассматривать как второй закон Ньютона для вращения. Момент инерции — это вращательная масса, а крутящий момент — это вращательная сила.
 Угловое движение подчиняется Первому закону Ньютона. Если на объект не действуют никакие внешние силы, объект в движении остается в движении, а объект в состоянии покоя остается в покое.
 Ключевые термины 
  угловое ускорение : Скорость изменения угловой скорости, часто обозначаемая α.
  крутящий момент : вращательное или скручивающее действие силы; (Единица СИ ньютон-метр или Нм; британская единица измерения фут-фунт или фут-фунт)
  инерция вращения : Тенденция вращающегося объекта оставаться вращающимся, если к нему не приложен крутящий момент.
 Крутящий момент и угловое ускорение связаны следующей формулой, где — момент инерции объекта, а [latex] \ alpha [/ latex] — угловое ускорение.
 
  Крутящий момент, угловое ускорение и роль церкви во Французской революции : Почему вещи меняют свою угловую скорость? Скоро ты узнаешь.
 Так же, как Второй закон Ньютона, согласно которому сила равна массе, умноженной на ускорение, крутящий момент подчиняется аналогичному закону.Если вы замените крутящий момент силой, а инерцию вращения — массой, а угловое ускорение — линейным ускорением, вы получите второй закон Ньютона. Фактически, это уравнение является вторым законом Ньютона, примененным к системе частиц, вращающихся вокруг данной оси. Он не делает никаких предположений о постоянной скорости вращения.
 Чистый крутящий момент вокруг оси вращения равен произведению инерции вращения вокруг этой оси и углового ускорения, как показано на рисунке 1.
  Рисунок 1 : Взаимосвязь между векторами силы (F), крутящего момента (τ), импульса (p) и углового момента (L) во вращающейся системе
 Подобно Второму закону Ньютона, угловое движение также подчиняется Первому закону Ньютона.Если на объект не действуют никакие внешние силы, объект в движении остается в движении, а объект в состоянии покоя остается в покое. С вращающимися объектами мы можем сказать, что, если не будет приложен внешний крутящий момент, вращающийся объект будет продолжать вращаться, а объект в состоянии покоя не начнет вращаться.
 Если бы поворотный стол вращался против часовой стрелки (если смотреть сверху), и вы приложили пальцы к противоположным сторонам, поворотный стол начал бы замедлять свое вращение. По крайней мере, с точки зрения поступательного движения, к поворотному столу не будет прилагаться результирующая сила.Сила, указывающая на одну сторону, будет отменена силой, указывающей на другую. Силы двух пальцев компенсируются. Следовательно, поворотный стол будет в поступательном равновесии. Несмотря на это, скорость вращения будет уменьшена, что означает, что ускорение больше не будет нулевым. Из этого мы можем заключить, что только потому, что вращающийся объект находится в поступательном равновесии, он не обязательно находится в вращательном равновесии.
 Электрическая потенциальная энергия (U) и Электрический потенциал (В): (Примечания из C 
   Электрическая потенциальная энергия (U) и электрический потенциал
(V): (    Записки К.Лекции Erkals PHYS 221    )  
 Рассмотрим конденсатор с параллельными пластинами, который производит однородную
электрическое поле между его большими пластинами.
Это достигается путем подключения каждой пластины к одному из выводов
источник питания (например, аккумулятор).
 Рисунок 1: Электрическое поле создается заряженными пластинами.
разделенные расстоянием l. Обвинения
на пластинах есть + Q и Q.
 Рисунок 2: Электрический заряд q перемещается из точки A в сторону
точка B с внешней силой T против электрической силы qE.
 Рис. 3, 4: Когда он перемещается на расстояние d, его
потенциальная энергия в точке B равна qEd относительно точки A.
 Рисунок 5: При отпускании из B (T = 0) он будет ускоряться
к нижней пластине. Как он движется
по направлению к нижней пластине его потенциальная энергия уменьшается, а кинетическая энергия
увеличивается.Когда он достигает нижнего
пластина (где мы можем выбрать потенциальную энергию равной нулю), ее потенциал
энергия в точке A полностью преобразуется в кинетическую энергию в точке B:
  
 Обратите внимание, что qEd — это работа, выполняемая полем в качестве заряда
движется под действием силы qE от B к A.
Здесь m — масса заряда q, а v — его скорость при достижении
точка А. Здесь мы предположили, что электрическая
поле однородное! Работы по E field:
  
 Давайте вспомним теорему о кинетической энергии-работе (рабочая энергия
принцип):
  
, где мы ввели понятие потенциальной энергии и
консервативная сила (сила, под которой можно определить потенциальную энергию так
что проделанная работа зависит только от разницы потенциальной энергии
функция оценивается в конечных точках).
  Практическое правило определения того, является ли EPE
увеличение: 
 Если заряд движется в том направлении,
при нормальном движении его электрическая потенциальная энергия уменьшается. Если заряд движется в направлении, противоположном
к тому, что он обычно двигался бы, его электрическая потенциальная энергия увеличивается. Эта ситуация похожа на ситуацию
постоянное гравитационное поле (g = 9,8 м / с  2 ). Когда вы поднимаете предмет, вы
увеличивая его гравитационную потенциальную энергию.Точно так же, когда вы опускаете объект, его гравитационная энергия равна
уменьшается.
 Общая формула потенциальной разницы:
 Работа, выполняемая полем E, когда оно действует на заряд q для перемещения.
он от точки A до точки B определяется как разность электрических потенциалов между
точки A и B:
  
 Ясно, что потенциальную функцию V можно сопоставить каждому
точка в пространстве, окружающем распределение заряда (например, параллельное
тарелки).Приведенная выше формула обеспечивает
простой рецепт для расчета работы, проделанной при перемещении заряда между двумя точками
где мы знаем значение разности потенциалов. Приведенные выше утверждения и формула действительны независимо от
путь, по которому перемещается заряд.
Особый интерес представляет потенциал точечного заряда Q. Его можно найти, просто выполнив
интегрирование по простому пути (например, по прямой) из точки A
расстояние от Q которого равно r до бесконечности.Путь выбирается по радиальной линии, так что   становится просто Edr.
Поскольку электрическое поле Q равно kQ / r  2 ,
 
 Этот процесс определяет электрический потенциал точечного
заряжать. Обратите внимание, что потенциальная функция
скалярная величина в отличие от электрического поля, являющегося векторной величиной. Теперь мы можем определить электрический потенциал
энергия системы зарядов или зарядовых распределений.Предположим, мы вычисляем проделанную работу относительно
электрические силы при перемещении заряда q из бесконечности в точку на расстоянии r от
заряд Q. Работу выдал:
  
 Обратите внимание, что если q отрицательное, его знак должен использоваться в
уравнение! Следовательно, система
состоящий из отрицательного и положительного точечного заряда, имеет отрицательный
потенциальная энергия.
 Отрицательная потенциальная энергия означает, что работа должна быть выполнена
против электрического поля при раздвижении зарядов!
 Теперь рассмотрим более общий случай, связанный с
потенциал в окрестности ряда зарядов, как показано на рисунке
ниже:
 Пусть r  1 , r  2 , r  3  будет
расстояния зарядов до точки поля А, а r  12 , r  13 ,
r  23  представляют собой расстояние между зарядами.Электрический потенциал в точке А равен:
.
  
  Пример: 
 Если мы принесем заряд Q из бесконечности и поместим его в точку A
проделанная работа будет:
  
 Общая электрическая потенциальная энергия этой системы
обвинения, а именно, работа, необходимая для того, чтобы привести их на нынешнее положение, может быть
рассчитывается следующим образом: сначала приведите q1 (нулевая работа, так как нет заряда
еще), затем в поле q1 вывести q2, затем в поля q1 и q2
принести q3.Добавьте всю работу, необходимую для
вычислить общую работу. Результат
будет:
  
 Обнаружение электрического поля по электрическому потенциалу:
 Компонент E в любом направлении является отрицательным
скорость изменения потенциала с расстоянием в этом направлении:
  
 Символ называется Градиент.
Электрическое поле — это градиент электрического потенциала.Линии электрического поля всегда
перпендикулярно эквипотенциальным поверхностям.
  Поверхности равнополостного хвоста: 
 Это воображаемые поверхности, окружающие заряд.
распределение. В частности, если
распределение заряда сферическое (точечный заряд или однородно заряженная сфера),
поверхности сферические, концентрические с центром заряда
распределение. Линии электрического поля
всегда перпендикулярно эквипотенциальным поверхностям.Уравнение   означает, что из-за
отрицательный знак, направление E противоположно направлению, в котором V
увеличивается; E направлен с более высоких уровней V на более низкие (с более высоких
потенциал для снижения потенциала). Другой
словами, градиент скаляра (в данном случае E-поля) нормален к поверхности
постоянного значения (эквипотенциальная поверхность) скаляра и в направлении
максимальная скорость изменения постоянного скаляра.
Запомните это утверждение, когда мы проводим эксперимент.