Момент силы относительно точки — Лекции и примеры решения задач технической механики
Если под действием приложенной силы твердое тело может совершать вращение вокруг некоторой точки, то для того, чтобы охарактеризовать вращательный эффект силы вводится понятие – момент силы относительно точки (или центра).
Определение
Моментом относительно точки (рисунок 1.1) называется векторное произведение радиус-вектора точки приложения силы на вектор силы.
MО(F) = r × F
Рисунок 1.1
Вектор момента направлен перпендикулярно плоскости, в которой лежат сила и точка, в ту сторону, откуда поворот от действия силы виден происходящим против хода часовой стрелки.
Наш короткий видеоурок про момент силы с примерами:
Момент силы (видео)
Вычисление момента
Вектор момента характеризует положение плоскости и направление вращательного действия силы, а также дает меру этого действия:
|MО(F)| = F⋅ r⋅ sin α = F⋅ h,
где h – плечо силы (кратчайшее расстояние от точки
Момент силы относительно точки не меняется от переноса силы вдоль линии ее действия.
Если силы расположены в одной плоскости, то используется понятие алгебраического момента силы.
Алгебраическим моментом силы относительно точки (или центра) называется взятое со знаком плюс или минус произведение модуля силы на плечо (рисунок 1.2).
Правило знаков
Знак плюс выбирается в том случае, если сила стремится поворачивать плоскость относительно центра момента против хода часовой стрелки.
Рисунок 1.2
Если сила F задана своими проекциями на оси координат
Проекции момента силы на оси координат равны:
>> Момент силы относительно оси
Момент силы относительно точки | ПроСопромат.ру
Моментом силы относительно точки называется произведение величины силы на длину перпендикуляра, опущенного из точки на линию действия силы (рис. а).

Если бы тело было закреплено в точке О, то сила Р стремилась бы вращать тело вокруг этой точки. Точка О, относительно которой берется момент, называется центром
момента, а перпендикуляр а называется плечом силы относительно центра момента.
Таким образом,
М = сила×плечо.
Момент силы Р относительно О обозначается
М0
Моменты сил измеряют в ньютонометрах (Нм) или килограммометрах (кГм) или в соответствующих кратных и дольных единицах, как и моменты пар.
Принято считать момент положительным, если сила стремится вращать тело по часовой стрелке (рис. а), и отрицательным — против часовой стрелки (рис. б).
Установленное правило знаков для моментов сил, как и для моментов пар, условно.
Когда линия действия силы проходит через данную точку, ее
Между моментом пары и моментом силы есть одно существенное различие. У момента пары сил величина и направление не зависят от положения этой пары в пространстве. У момента силы величина и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.
Момент силы относительно точки и оси
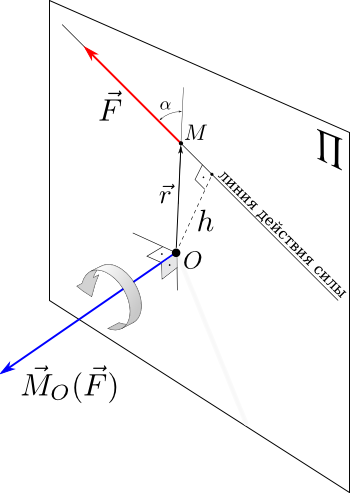
рис.1.2
Если известен
радиус-вектор 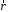 точки
приложения силы
точки
приложения силы 
 .
(1.8)
.
(1.8)
Действительно, модуль этого векторного произведения:
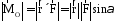 .
(1.9)
.
(1.9)
В соответствии
с рисунком 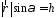
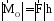 |.
(1.10)
|.
(1.10)
Вектор 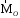 ,
как и результат векторного произведения,
перпендикулярен векторам
,
как и результат векторного произведения,
перпендикулярен векторам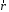 и
и ,
которые принадлежат плоскости Π.
Направление вектора
,
которые принадлежат плоскости Π.
Направление вектора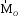
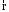 к
к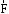 происходит по часовой стрелке. Другими
словами, вектор
происходит по часовой стрелке. Другими
словами, вектор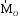 достраивает
систему векторов (
достраивает
систему векторов (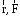 ) до
правой тройки.
) до
правой тройки.Зная координаты точки приложения силы в системе координат, начало которой совпадает с точкой О, и проекцию силы на эти оси координат, момент силы может быть определен следующим образом:
 .
(1.11)
.
(1.11)
Момент силы относительно оси
Проекция момента силы относительно точки на некоторую ось, проходящую через эту точку, называется моментом силы относительно оси.
 рис.1.3
рис.1.3
Момент силы
относительно оси вычисляется как момент
проекции силы 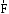 на плоскость Π, перпендикулярную
оси, относительно точки пересечения
оси с плоскостью Π:
на плоскость Π, перпендикулярную
оси, относительно точки пересечения
оси с плоскостью Π:
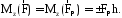 (1.12)
(1.12)
Знак момента определяется направлением вращения, которое стремится придать телу сила F⃗ Π. Если, глядя по направлению оси Oz сила вращает тело по часовой стрелке, то момент берется со знаком «плюс», иначе — «минус».
1.2 Постановка задачи.
Определение реакций опор и шарнира С.
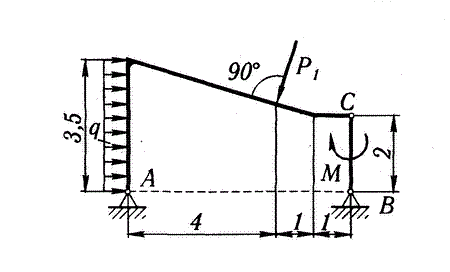
P1, кН | q, кН/м | |
5,0 | 24,0 | 0,8 |
1.3 Алгоритм решения задачи.
Разделим конструкцию на части и рассмотрим равновесие каждой из конструкции.
Рассмотрим равновесие всей конструкции в целом. (рис.1.1)
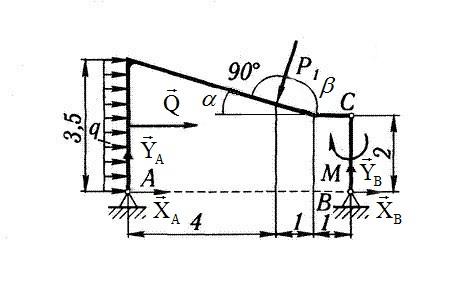
рис. 1.1
Составим 3 уравнения равновесия для всей конструкции в целом:
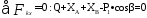
(1)

(2)
 (3)
(3)
Рассмотрим равновесие правой части конструкции.(рис 1.2)
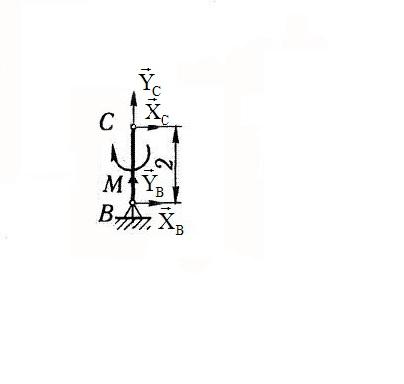
рис.1.2
Составим 3 уравнения равновесия для правой части конструкции:
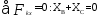 (4)
(4)
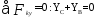 (5)
(5)
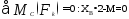 (6)
(6)
Из уравнения 3 находим YA
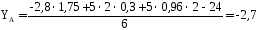 кН
кН
Найдем Q:
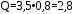 кН/м
кН/м
Найдем угол β:
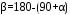
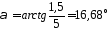
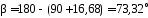
Из уравнения 2 находим YB
 кН
кН
Из уравнения 6 находим XB
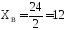 кН
кН
Из уравнения 5 находим YC
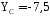 кН
кН
Из уравнения 4 находим XC
 кН
кН
Из уравнения 1 находим XA
 кН
кН
Составим уравнение проверки:
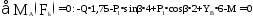

Момент силы. Формула, определение и примеры расчета
Моментом силы называют вращательное усилие создаваемое вектором силы относительно другого объекта (оси, точки).
Размерность — [Н∙м] (Ньютон на метр) либо кратные значения [кН∙м]
Аналогом момента силы является момент пары сил.
Обязательным условием возникновения момента является то, что точка, относительно которой создается момент не должна лежать на линии действия силы.
Определение
Момент определяется как произведение силы F на плечо h:
M(F)=F∙h
Плечо силы h, определяется как кратчайшее расстояние от точки до линии действия силы.
Наш короткий видеоурок про момент силы с примерами:
Момент силы (видео)
Например, сила величиной 7 кН приложенная на расстоянии 35см от рассматриваемой точки дает момент M=7×0,35=2,45 кНм.
Пример момента силы
Наиболее наглядным примером момента силы может служить поворачивание гайки гаечным ключом.
Гайки заворачиваются вращением, для этого к ним прикладывается момент, но сам момент возникает при воздействии нашей силы на гаечный ключ.
Вы конечно интуитивно понимаете — для того чтобы посильнее закрутить гайку надо взяться за ключ как можно дальше от нее.
В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения её плеча (h3>h2).
Плечом при этом служит расстояние от центра гайки до точки приложения силы.
Плечо момента силы
Рассмотрим порядок определения плеча h момента:
Пусть заданы точка A и некоторая произвольная сила F, линия действия которой не проходит через эту точку. Требуется определить момент силы.
Покажем линию действия силы F (штриховая линия)
Проведем из точки A перпендикуляр h к линии действия силы
Длина отрезка h есть плечо момента силы F относительно точки A.
Момент принимается положительным, если его вращение происходит против хода часовой стрелки (как на рисунке).
Так принято для того, чтобы совпадали знаки момента и создаваемого им углового перемещения.
Примеры расчета момента силы
Сила расположена перпендикулярно оси стержня
Расстояние между точками A и B — 3 метра.
Момент силы относительно точки A:
МA=F×AB=F×3м
Сила расположена под углом к оси стержня
Момент силы относительно точки B:
MB=F×cos300×AB=F×cos300×3м
Известно расстояние от точки до линии действия силы
Момент силы относительно точки B:
MB=F×3м
См. также:
Обсуждение:Момент силы — Википедия
«(cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in)» — ну что это за извращение? Еще непонимаю, к чему посклицательный знак в «где F — сила, действующая на частицу, а r — радиус-вектор частицы!» ? Еще смущают фразы типа «Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:» и формулы в виде «МОМЕНТ СИЛЫ * УГОЛ»… Статью стоит переработать, текущая выглядит как рассказ школьника. 83.234.227.14 14:14, 30 мая 2009 (UTC)
Как определить знак для момента сил?[править код]
Если сила направлена в противоход часовой стрелке, то момент силы будет со знаком +.217.64.141.5 18:16, 4 сентября 2010 (UTC)
ответ: определение знака для момента сил[править код]
Нашел ответ:
а) моментом силы относительно точки называется произведение модуля силы на ее плечо;
б) момент силы считается положительным, если сила стремится повернуть тело относительно точки в направлении против часовой стрелки и … отрицательным, если по часовой;
в) момент силы относительно точки равен нулю, если линия действия силы проходит через точку.
216.117.134.180 13:02, 26 декабря 2007 (UTC)
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент)
Товарищи, момент силы, крутящий, вращательный момент не синонимы. Крутящий и вращательный моменты — это моменты силы, а момент силы не обязательно крутящий или вращающий. Предлагаю удалить это неверное уточнение. —Ruglen 16:25, 14 июля 2009 (UTC)
Добавьте, плиз, оговорку, что в технике названия моментов отличают по принципу действия вызвавшей силы относительно «стержня».
- Например, вращающий момент приложенный к косозубой шестерне вызывает в сечении крутящий(вокруг оси, вызванный окружной силой) и изгибающие моменты (осевой, вызванный давлением перпендикулярно поверхности зуба; и радиальный, вызванный давлением перпендикулярным оси вала).
- — Дунаев, Леликов расчет и конструирование дет. маш. глава 2.1.1. пункты 10-11.
85.26.234.120 21:26, 17 февраля 2013 (UTC)
Кто-то, наверное, очень гордится своей «моргалкой»[править код]
«Моргалкой» называются картинки, которые «моргают», «прыгают», «дергаются» и всячески раздражают. Но человеку, который хочет понять термин, который он никогда не понимал, эта «моргалка» самое то, чтобы закрыть тему или поискать другой источник. Зачем мне все эти формулы со значками, похожими на тараканов, если я просто хочу понять, зачем в характеристиках автомобиля нужна строка «крутящий момент», и что эта строка дает простому человеку, не разбирающемуся в этих «тараканьих» формулах?
95.84.179.30 00:22, 7 декабря 2010 (UTC) Александр Иванов, который не понимает, что такое "крутящий момент", и зачем он нужен в характеристиках автомобиля.
Исключительно ради наведения порядка в статьях по классической механике предлагаю заменить обозначение момента с тау греческого на М большое латинское с сохранением значка вектора.Это более соответствует традиционным обозначениям, принятым в российской специальной литературе и вообще пойдёт на пользу делу усиления связности . Возможно, для этого придётся пожертвовать «моргалкой», если в её файл нельзя залезть без нарушения авторских амбиций. Витольд Муратов (обс, вклад) 17:51, 9 мая 2011 (UTC)
- Поддерживаю, тем более что в файл можно залезть, там свободная лицензия. —Rasim 18:00, 9 мая 2011 (UTC)
- Спасибо за поддержку.Как только разберусь со своими долгами — так сразу. Витольд Муратов (обс, вклад) 14:37, 10 мая 2011 (UTC)
Заменил обозначение момента и убрал анимацию, которая, действительно, раздражает читателя. Витольд Муратов (обс, вклад) 17:53, 11 мая 2011 (UTC)
что необходимо уточнение: «… широкого радиус-вектора …» С уважением, (извините, но и к «сопромату»), андроид 91.205.25.30 18:20, 10 июля 2013 (UTC)
Для человека, который не имеет дела в повседневном обращении с механикой, но имеет необходимость разобраться в некоторых понятиях необходимы элементарные чертежи (это касается раздела «предыстория»). Несколько затруднительно представлять себе и додумываться как автор располагает свою систему в пространстве и как там располагаются всякие углы
26. Момент силы относительно оси. Аналитическое выражение момента силы относительно оси.
Моментом силы относительно осиназывается момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью
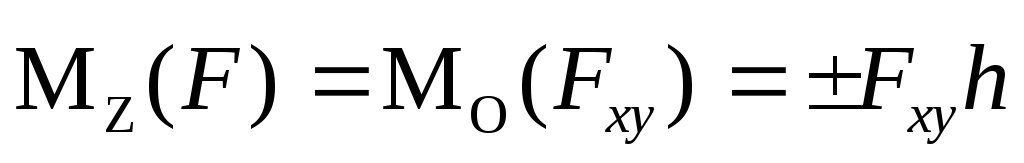
Момент относительно оси положителен, если сила стремится вращать плоскость перпендикулярную оси против часовой стрелки, если смотреть навстречу оси.
Момент силы относительно оси равен 0 в двух случаях:
Если линия действия и ось лежат в одной плоскости, то момент силы относительно оси равен 0.
27. Связь между моментом силы относительно оси и векторным моментом силы относительно точки.
Mz(F)=Mo(F)*cosαМомент силы, относительно оси равен прекции вектора момента сил, относительно точки оси на эту ось.
28. Основная теорема статики о приведении системы сил к заданному центру (теорема Пуансо). Главный вектор и главный момент системы сил.
Всякую пространственную систему сил в общем случае можно заменить эквивалентной системой, состоящей из одной силы, приложенной в какой-либо точке тела (центре приведения) и равной главному вектору данной системы сил, и одной пары сил, момент которой равен главному моменту всех сил относительно выбранного центра приведения.

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:
R = F1 + F2 +
… + Fn = 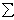 Fi.
Fi.
Для плоской системы сил ее главный вектор лежит в плоскости действия этих сил.
Главным моментом системы сил относительно центра O называется вектор LO, равный сумме векторных моментов этих сил относительно точки О:
LO = MO(F1)
+ MO(F2)
+ … + MO(Fn)
=  MO(Fi).
MO(Fi).
Вектор R не зависит от выбора центра О, а вектор LO при изменении положения центра О может в общем случае изменяться.
Теорема Пуансо: Произвольную пространственную систему сил можно заменить одной силой главным вектором системы сил и парой сил с главным моментом не нарушая состояния твердого тела. Главный вектор представляет собой геометрическую сумму всех сил действующих на твердое тело и расположен в плоскости действия сил. Главный вектор рассматривается через его проекции на оси координат.
Чтобы привести силы к заданному центру приложенному в некоторой точке твердого тела необходимо: 1) перенести параллельно силу самой себе к заданному центру не изменяя модуля силы; 2) в заданном центре приложить пару сил, векторный момент которой равен векторному моменту перенесенной силы относительного нового центра, эту пару называют присоединенной парой.
Зависимость главного момента от выбора центра приведения. Главный момент относительно нового центра приведения равен геометрической сумме главного момента относительно старого центра приведения и векторного произведения радиуса-вектора, соединяющего новый центр приведения со старым, на главный вектор.
29 Частные случаи приведения пространственной системы сил
№ | Значения главного вектора и главного момента | Результат приведения |
1 | | Система сил
приводится к паре сил, момент которой
равен главному моменту |
2 | | Система сил
приводится к равнодействующей,
равной |
3 | | Система сил
приводится к равнодействующей |
4 | | Система сил
приводится к динаме (силовому винту)
– совокупности силы |
5 | | Система сил, приложенных к твердому телу, является уравновешивающейся. |
30. Приведение к
динаме.Динамой в механике
называют такую совокупность силы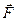 и
пары сил (
и
пары сил ( ) действующих
на твердое тело, у которой сила
перпендикулярна плоскости действия
пары сил. Используя векторный момент
) действующих
на твердое тело, у которой сила
перпендикулярна плоскости действия
пары сил. Используя векторный момент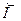 пары
сил
пары
сил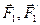 , можно
также определить динаму как совокупность
силы и пары, у которы сила параллельна
векторному моменту пары сил.
, можно
также определить динаму как совокупность
силы и пары, у которы сила параллельна
векторному моменту пары сил.
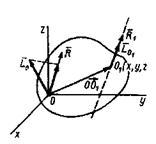 Уравнение
центральной винтовой осиПредположим,
что в центре приведения, принятом за
начало координат, получены главный
вектор
Уравнение
центральной винтовой осиПредположим,
что в центре приведения, принятом за
начало координат, получены главный
вектор 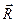 с
проекциями на оси координат
с
проекциями на оси координат 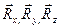 и
главный момент
и
главный момент 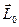 с
проекциями
с
проекциями  При
приведении системы сил к центру
приведения О1 (рис.
30) получается динама с главным вектором
При
приведении системы сил к центру
приведения О1 (рис.
30) получается динама с главным вектором  и
главным моментом
и
главным моментом 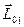 ,
Векторы
,
Векторы  и
и  как
образующие линаму. параллельны и поэтому
могут отличаться только скалярным
множителем k0. Имеем,, так
как
как
образующие линаму. параллельны и поэтому
могут отличаться только скалярным
множителем k0. Имеем,, так
как 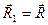 .Главные
моменты и
.Главные
моменты и  , удовлетворяют
соотношению
, удовлетворяют
соотношению
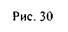
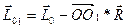
Подставляя 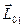 ,
получим
,
получим
Координаты
точки О1 в
которой получена динама, обозначим
х, у, z.
Тогда проекции вектора  на
оси координат равны координатам х,
у, z.
Учитывая это, (*) можно выразить в форме
на
оси координат равны координатам х,
у, z.
Учитывая это, (*) можно выразить в форме
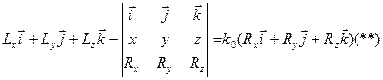
где i.
j ,k — единичные
векторы осей координат, а векторное
произведение 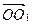 *
*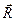 представлено
определителем. Векторное уравнение
(**) эквивалентно трем скалярным, которые
после отбрасывания
представлено
определителем. Векторное уравнение
(**) эквивалентно трем скалярным, которые
после отбрасывания  можно
представить в виде
можно
представить в виде
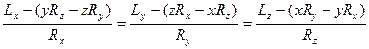
Полученные линейные уравнения для координат х, у, z являются уравнениями прямой линии — центральной винтовой оси. Следовательно, существует прямая, в точках которой система сил приводится к динаме.
Момент силы относительно точки и относительно оси — Мегаобучалка
Момент пары сил
Моментом силы относительно какой-либо точки (центра) называется вектор, численно равный произведению модуля силы на плечо, т.е. на кратчайшее расстояние от указанной точки до линии действия силы, и направленный перпендикулярно плоскости, проходящей через выбранную точку и линию действия силы в ту сторону, откуда «вращение», совершаемое силой вокруг точки, представляется происходящим против хода часовой стрелки. Момент силы характеризует ее вращательное действие.
Если О – точка, относительно которой находится момент силы F, то момент силы обозначается символом Мо(F). Покажем, что если точка приложения силыFопределяется радиус-вектором r, то справедливо соотношение
Мо(F)=r×F. (3.6)
Согласно этому соотношению момент силы равен векторному произведению вектора r на вектор F.
В самом деле, модуль векторного произведения равен
Мо(F)=rFsin=Fh, (3.7)
где h – плечо силы. Заметим также, что вектор Мо(F) направлен перпендикулярно плоскости, проходящей через векторы rи F, в ту сторону, откуда кратчайший поворот вектора rк направлению вектора Fпредставляется происходящим против хода часовой стрелки. Таким образом, формула (3.6) полностью определяет модуль и направление момента силы F.
Иногда формулу (3.7) полезно записывать в виде
Мо(F)=2S, (3.8)
где S – площадь треугольника ОАВ.
Пусть x, y, z – координаты точки приложения силы, а Fx, Fy, Fz – проекции силы на координатные оси. Тогда, если точка О находится в начале координат, момент силы выражается следующим образом:
. (3.9)
Отсюда следует, что проекции момента силы на координатные оси определяются формулами:
MOx(F)= yFz-zFy,
MOy(F)= zFx-xFz,
MOy(F)= xFy-yFx. (3.10)
Введем теперь понятие проекции силы на плоскость.
Пусть даны сила Fи некоторая плоскость. Опустим из начала и конца вектора силы перпендикуляры на эту плоскость.
Проекцией силы на плоскость называется вектор, начало и конец которого совпадают с проекцией начала и проекцией конца силы на эту плоскость.
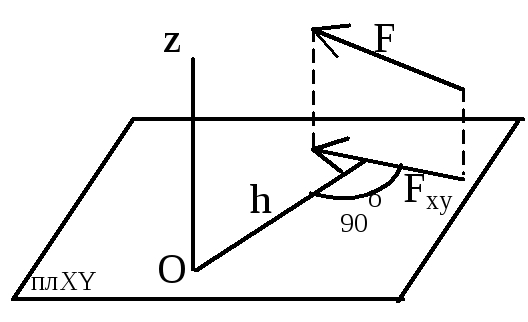
Если в качестве рассматриваемой плоскости принять плоскость хОу, то проекцией силы Fна этуплоскость будет вектор Fху.
Момент силы Fху относительно точки О (точки пересечения оси z с плоскостью хОу) может быть вычислен по формуле (3.9), если в ней принять z=0, Fz=0. Получим
MO(Fху)=(xFy-yFx)k.
Таким образом, момент направлен вдоль оси z, а его проекция на ось z в точности совпадает с проекцией на ту же ось момента силы Fотносительно точки О. Другими словами,
MOz(F)=MOz(Fху)= xFy-yFx. (3.11)
Очевидно, тот же результат можно получить, если спроектировать силуFна любую другую плоскость, параллельную хОу. При этом точка пересечения оси z с плоскостью будет уже иной (обозначим новую точку пересечения через О1). Однако все входящие в правую часть равенства (3.11) величины х, у, Fх, Fуостанутся неизменными, и, следовательно, можно записать
MOz(F)=MO1z(Fху).
Другими словами, проекция момента силы относительно точки на ось, проходящую через эту точку, не зависит от выбора точки на оси. Поэтому в дальнейшем вместо символа MOz(F) будем применять символ Mz(F). Эта проекция момента называется моментом силы относительно оси z. Вычисление момента силы относительно оси часто бывает удобнее производить посредством проектирования силы F на плоскость, перпендикулярную оси, и вычисления величины M z(Fху).
В соответствии с формулой (3.7) и учитывая знак проекции, получим:
Mz(F)=Mz(Fху)=±Fху·h*. (3.12)
Здесь h* – плечо силы Fху относительно точки О. Если наблюдатель видит со стороны положительного направления оси z, что сила Fху стремится повернуть тело вокруг оси z против хода часовой стрелки, то берется знак «+», и в противном случае – знак «–».
Формула (3.12) дает возможность сформулировать следующее правило для вычисления момента силы относительно оси. Для этого нужно:
· выбрать на оси произвольную точку и построить плоскость, перпендикулярную оси;
· спроектировать на эту плоскость силу;
· определить плечо проекции силы h*.
Момент силы относительно оси равен произведению модуля проекции силы на ее плечо, взятому с соответствующим знаком (см. изложенное выше правило).
Из формулы (3.12) следует, что момент силы относительно оси равен нулю в двух случаях:
· когда проекция силы на плоскость, перпендикулярную оси, равна нулю, т.е. когда сила и ось параллельны;
· когда плечо проекции h* равно нулю, т.е. когдалиния действия пересекает ось.
Оба эти случая можно объединить в один: момент силы относительно оси равен нулю тогда и только тогда, когда линия действия силы и ось находятся в одной плоскости.
Задача 3.1.Вычислить относительно точки О момент силы F, приложеннойк точке А и направленной по диагонали грани куба со стороной а.
При решении подобных задач целесообразно сначала вычислить моменты силы Fотносительно координатных осей x, y, z. Координаты точки А приложения силы F будут
, , .
Проекции силы Fна координатные оси:
, , .
Подставляя эти значения в равенства (3.10), найдем
, , .
Эти же выражения для моментов силы Fотносительно координатных осей можно получить, пользуясь формулой (3.12). Для этого спроектируем силу F на плоскости, перпендикулярные оси х и у. Очевидно, что . Применяя изложенное выше правило, получим, как и следовало ожидать, те же выражения:
, , .
Модуль момента определится равенством
.
Введем теперь понятие момента пары. Найдем сначала, чему равна сумма моментов сил, составляющих пару, относительно произвольной точки. Пусть О – произвольная точка пространства, а F и F’ –силы, составляющие пару.
Тогда Мо(F)=ОА×F, Мо(F’)=ОВ×F’,
откуда
Мо(F)+ Мо(F’)= ОА×F+ ОВ×F’,
но так как F= -F’, то
Мо(F)+ Мо(F’)= ОА×F— ОВ×F=(ОА—ОВ)×F.
Принимая во внимание равенство ОА-ОВ=ВА, окончательно находим:
Мо(F)+ Мо(F’)= ВА×F.
Следовательно, сумма моментов сил, составляющих пару, не зависит от положения точки, относительно которой берутся моменты.
Векторное произведение ВА×Fи называется моментом пары. Обозначается момент пары символом М(F, F’), причем
М(F, F’)= ВА×F= АВ×F’,
или, короче,
М= ВА×F= АВ×F’. (3.13)
Рассматривая правую часть этого равенства, замечаем, что момент пары представляет собой вектор, перпендикулярный плоскости пары, равный по модулю произведению модуля одной сил пары на плечо пары (т.е. на кратчайшее расстояние между линиями действия сил, составляющих пару) и направленный в ту сторону, откуда «вращение» пары видно происходящим против хода часовой стрелки. Если h – плечо пары, то М(F, F’)=h×F.
Из самого определения видно, что момент пары сил представляет собой свободный вектор, линия действия которого не определена (дополнительное обоснование этого замечания следует из теорем 2 и 3 этой главы).
Для того, чтобы пара сил составляла уравновешенную систему (систему сил, эквивалентную нулю), необходимо и достаточно, чтобы момент пары равнялся нулю. Действительно, если момент пары равен нулю, М=h×F, то либо F=0, т.е. нет сил, либо плечо пары h равно нулю. Но в этом случае силы пары будут действовать по одной прямой; так как они равны по модулю и направлены в противоположные стороны, то на основании аксиомы 1 они составят уравновешенную систему. Обратно, если две силы F1иF2, составляющие пару, уравновешены, то на основании той же аксиомы 1 они действуют по одной прямой. Но в этом случае плечо пары h равно нулю и, следовательно, М=h×F=0.
Теоремы о парах
Докажем три теоремы, с помощью которых становятся возможными эквивалентные преобразования пар. При всех рассмотрениях следует помнить, что они относятся к парам, действующим на какое-либо одно твердое тело.
Теорема 1. Две пары, лежащие в одной плоскости, можно заменить одной парой, лежащей в той же плоскости, с моментом, равным сумме моментов данных двух пар.
Для доказательства этой теоремы рассмотрим две пары (F1,F’1) и (F2,F’2) и перенесем точки приложения всех сил вдоль линий их действия в точки А и В соответственно. Складывая силы по аксиоме 3, получим
R=F1+F2 и R’=F’1+F’2,
но F1=-F’1 и F2=-F’2.
Следовательно, R=- R’, т.е. силы Rи R’ образуют пару. Найдем момент этой пары, воспользовавшись формулой (3.13):
М=М(R, R’)=ВА× R=ВА×(F1+F2)=ВА×F1+ВА×F2. (3.14)
При переносе сил, составляющих пару, вдоль линий их действия ни плечо, ни направление вращения пар не меняются, следовательно, не меняется и момент пары. Значит,
ВА×F1=М(F1,F’1)=М1, ВА×F2= М(F2,F’2)=М2
и формула (3.14) примет вид
М=М1+М2, (3.15)
что и доказывает справедливость сформулированной выше теоремы.
Сделаем два замечания к этой теореме.
1. Линии действия сил, составляющих пары, могут оказаться параллельными. Теорема остается справедливой и в этом случае, но для ее доказательства следует воспользоваться правилом сложения параллельных сил.
2. После сложения может получиться, что М(R, R’)=0; на основании сделанного ранее замечания из этого следует, что совокупность двух пар (F1,F’1, F2,F’2)=0.
Теорема 2. Две пары, имеющие геометрически равные моменты, эквивалентны.
Пусть на тело в плоскости I действует пара (F1,F’1) с моментом М1. Покажем, что эту пару можно заменить другой с парой (F2,F’2), расположенной в плоскости II, если только ее момент М2равен М1(согласно определению (см. 1.1) это и будет означать, что пары (F1,F’1) и (F2,F’2) эквивалентны). Прежде всего заметим, что плоскости I и II должны быть параллельны, в частности они могут совпадать. Действительно, из параллельности моментов М1 и М2(в нашем случае М1=М2) следует, что плоскости действия пар, перпендикулярные моментам, также параллельны.
Введем в рассмотрение новую пару (F3,F’3) и приложим ее вместе с парой (F2,F’2) к телу, расположив обе пары в плоскости II. Для этого, согласно аксиоме 2 нужно подобрать пару (F3,F’3) с моментом М3 так, чтобы приложенная система сил (F2,F’2, F3,F’3) была уравновешена. Это можно сделать, например, следующим образом: положим F3=-F’1 и F’3=—F1и совместим точки приложения этих сил с проекциями А1 и В1 точек А и В на плоскость II. В соответствии с построением будем иметь: М3= -М1или, учитывая, что М1= М2,
М2+М3=0.
Принимая во внимание второе замечание к предыдущей теореме, получим (F2,F’2, F3,F’3)=0. Таким образом, пары (F2,F’2) и (F3,F’3) взаимно уравновешены и присоединение их к телу не нарушает его состояния (аксиома 2), так, что
(F1,F’1)= (F1,F’1, F2,F’2, F3,F’3). (3.16)
С другой стороны, силы F1 и F3, а также F’1 и F’3 можно сложить по правилу сложения параллельных сил, направленных в одну сторону. По модулю все эти силы равны друг другу, поэтому их равнодействующие R и R’ должны быть приложены в точке пересечения диагоналей прямоугольника АВВ1А1; кроме того, они равны по модулю и направлены в противоположные стороны. Это означает, что они составляют систему, эквивалентную нулю. Итак,
(F1,F’1, F3,F’3)=(R, R’)=0.
Теперь мы можем записать
(F1,F’1, F2,F’2, F3,F’3)=(F3,F’3). (3.17)
Сравнивая соотношения (3.16) и (3.17), получим (F1,F’1)=(F2,F’2), что и требовалось доказать.
Из этой теоремы следует, что пару сил можно перемещать в плоскости ее действия, переносить в параллельную плоскость; наконец, в паре можно менять одновременно силы и плечо, сохраняя лишь направление вращения пары и модуль ее момента (F1h1= F2h2).
В дальнейшем мы будем широко пользоваться такими эквивалентными преобразованиями пары.
Теорема 3. Две пары, лежащие в пересекающихся плоскостях, эквивалентны одной паре, момент которой равен сумме моментов двух данных пар.
Пусть пары (F1,F’1) и (F2,F’2) расположены в пересекающихся плоскостях I и II соответственно. Пользуясь следствием теоремы 2, приведем обе пары к плечу АВ, расположенному на линии пересечения плоскостей I и II. Обозначим трансформированные пары через (Q1,Q’1) и (Q2,Q’2). При этом должны выполняться равенства
М1=М(Q1,Q’1)=М(F1,F’1) и М2=М(Q2,Q’2)=М(F2,F’2).
Сложим по аксиоме 3 силы, приложенные в точках А и В соответственно. Тогда получим R=Q1+Q2и R’= Q’1+Q’2. Учитывая, что Q’1=-Q1и Q’2=-Q2, получим R=-R’. Таким образом , мы доказали, что система двух пар эквивалентна одной паре (R,R’).
Найдем момент Мэтой пары. На основании формулы (3.13) имеем
М(R,R’)=ВА×(Q1+Q2)=ВА×Q1+ВА×Q2=
=М(Q1,Q’1)+М(Q2,Q’2)=М(F1,F’1)+М(F2,F’2)
или
М=М1+М2,
т.е. теорема доказана.
Заметим, что полученный результат справедлив и для пар, лежащих в параллельных плоскостях. По теореме 2 такие пары можно привести к одной плоскости, а по теореме 1 их можно заменить одной парой, момент которой равен сумме моментов составляющих пар.
Доказанные выше теоремы о парах позволяют сделать важный вывод: момент пары является свободным вектором и полностью определяет действие пары на абсолютно твердое тело. В самом деле, мы уже доказали, что если две пары имеют одинаковые моменты (следовательно, лежат в одной плоскости или в параллельных плоскостях), то они друг другу эквивалентны (теорема 2). С другой стороны, две пары, лежащие в пересекающихся плоскостях, не могут быть эквивалентны, ибо это означало бы, что одна из них и пара, противоположная другой, эквивалентны нулю, что невозможно, так как сумма моментов таких пар отлична от нуля.
Таким образом, введенное понятие момента пары чрезвычайно полезно, так как оно полностью отражает механическое действие пары на тело. В этом смысле можно сказать, что момент исчерпывающим образом представляет действие пары на твердое тело.
Для деформируемых тел изложенная выше теория пар неприменима. Две противоположные пары, действующие, например, по торцам стержня, с точки зрения статики твердого тела эквивалентны нулю. Между тем их действие на деформируемый стержень вызывает его кручение, и тем большее, чем больше модули моментов.
Перейдем к решению первой и второй задач статики, когда на тело действуют только пары сил.



 (главный
момент системы сил не зависит от выбора
центра приведения О).
(главный
момент системы сил не зависит от выбора
центра приведения О).
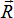 ,
проходящей через центр О.
,
проходящей через центр О.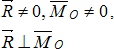
 ,
равной главному вектору
,
равной главному вектору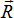 и
параллельной ему и отстоит от него на
расстоянии
и
параллельной ему и отстоит от него на
расстоянии .
Положение линии действия равнодействующей
должно быть таким, чтобы направление
ее момента относительно центра
приведения О совпадало с
направлением
.
Положение линии действия равнодействующей
должно быть таким, чтобы направление
ее момента относительно центра
приведения О совпадало с
направлением относительно
центра О.
относительно
центра О.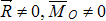 ,
причем векторы
,
причем векторы 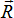 и
и не
перпендикулярны
не
перпендикулярны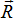 и
пары сил, лежащей в плоскости,
перпендикулярной к этой силе.
и
пары сил, лежащей в плоскости,
перпендикулярной к этой силе.