Что такое момент силы в физике. Момент силы

Представьте, что вы футболист и перед вами футбольный мяч. Чтобы он полетел, его нужно ударить. Всё просто: чем сильнее ударите, тем быстрее и дальше полетит, и бить будете, скорее всего, в центр мяча (см. рис. 1).

А чтобы мяч в полете вращался и летел по искривленной траектории, вы ударите не в центр мяча, а сбоку, что и делают футболисты, чтобы обмануть соперника (см. рис. 2).

Рис. 2. Кривая траектория полета мяча

Здесь уже важно, в какую точку бить.

Еще один простой вопрос: в каком месте нужно взять палку, чтобы она при подъеме не перевернулась? Если палка равномерная по толщине и плотности, то возьмем мы её посередине. А если она с одного края массивнее? Тогда мы возьмем её ближе к массивному краю, иначе он перевесит (см. рис. 3).

Рис. 3. Точка подъема

Представьте: папа сел на качели-балансир (см. рис. 4).

Рис. 4. Качели-балансир

Чтобы его перевесить, вы сядете на качели поближе к противоположному концу.

Во всех приведённых примерах нам важно было не просто подействовать на тело с некоторой силой, но и важно, в каком месте, на какую именно точку тела действовать. Эту точку мы выбирали наугад, пользуясь жизненным опытом. А если на палке будет три разных груза? А если поднимать ее вдвоем? А если речь идёт о подъемном кране или вантовом мосте (см. рис. 5)?

Рис. 5. Примеры из жизни

Для решения таких задач интуиции и опыта недостаточно. Без четкой теории их решить уже нельзя. О решении таких задач сегодня и пойдёт речь.

Обычно в задачах у нас есть тело, к которому приложены силы, и мы их решаем, как всегда до этого, не задумываясь над точкой приложения силы. Достаточно знать, что сила приложена просто к телу. Такие задачи встречаются часто, мы умеем их решать, но бывает, что недостаточно приложить силу просто к телу, — становится важно, в какую точку.

Пример задачи, в которой размеры тела не важны

Например, на столе лежит маленький железный шарик, на который действует сила тяжести 1 Н. Какую силу нужно приложить, чтобы его поднять? Шарик притягивается Землей, мы будем действовать на него вверх, прикладывая некоторую силу.

Силы, действующие на шарик, направлены в противоположные стороны, и, чтобы поднять шарик, нужно подействовать на него с силой, большей по модулю, чем сила тяжести (см. рис. 6).

Рис. 6. Силы, действующие на шарик

Сила тяжести равна , значит, на шарик нужно подействовать вверх с силой:

Мы не задумывались, как именно мы берем шарик, мы его просто берем и поднимаем. Когда мы показываем, как мы поднимали шарик, мы вполне можем нарисовать точку и показать: мы воздействовали на шарик (см. рис. 7).

Рис. 7. Действие на шарик

Когда мы можем так поступить с телом, показать его на рисунке при объяснении в виде точки и не обращать внимания на его размеры и форму, мы считаем его материальной точкой. Это модель. Реально же шарик имеет форму и размеры, но мы на них в этой задаче не обращали внимания. Если тот же шарик нужно заставить вращаться, то просто сказать, что мы воздействуем на шарик, уже нельзя. Здесь важно, что мы толкали шарик с краю, а не в центр, заставляя его вращаться. В этой задаче тот же шарик уже нельзя считать точкой.

Мы уже знаем примеры задач, в которых нужно учитывать точку приложения силы: задача с футбольным мячом, с неоднородной палкой, с качелями.

Точка приложения силы важна также в случае с рычагом. Пользуясь лопатой, мы действуем на конец черенка. Тогда достаточно приложить небольшую силу (см. рис. 8).

Рис. 8. Действие малой силы на черенок лопаты

Что общего между рассмотренными примерами, где нам важно учитывать размеры тела? И мяч, и палка, и качели, и лопата — во всех этих случаях речь шла о вращении этих тел вокруг некоторой оси. Мяч вращался вокруг своей оси, качели поворачивались вокруг крепления, палка — вокруг места, в котором мы ее держали, лопата — вокруг точки опоры (см. рис. 9).

Рис. 9. Примеры вращающихся тел

Рассмотрим поворот тел вокруг неподвижной оси и увидим, что заставляет тело поворачиваться. Будем рассматривать вращение в одной плоскости, тогда можно считать, что тело поворачивается вокруг одной точки О (см. рис. 10).

Рис. 10. Точка вращения

Если мы захотим уравновесить качели, у которых балка будет стеклянной и тонкой, то она может просто сломаться, а если балка из мягкого металла и тоже тонкая — то согнуться (см. рис. 11).

Такие случаи мы рассматривать не будем; будем рассматривать поворот прочных жестких тел.

Неправильно будет сказать, что вращательное движен

Ответы@Mail.Ru: Что такое момент силы

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению) , на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов) . В физике момент силы можно понимать как «вращающая сила» . В системе СИ единицами измерения для момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение: m=r x F где F — сила, действующая на частицу, а r— радиус-вектор частицы.

Момент силы [править] Материал из Википедии — свободной энциклопедии Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению) , на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).

А когда с торцевым гаечным ключом с помощью воротка закручиваешь болт или гайку, усилие, прикладываемое к концу воротка и есть момент силы.

парпарапрарарарарарарара

Роман, спасибо, объяснил

Момент силы — это… Что такое Момент силы?

Момент силы, приложенный к гаечному ключу. Направлен от зрителя

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).

Общие сведения

В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является Ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:

где  — сила, действующая на частицу, а  — радиус-вектор частицы.

Предыстория

Строго говоря, вектор, обозначающий момент сил, введен искусственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси.

Работа, совершаемая при действии силы на рычаг , совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.

Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол между вектором и вектором силы .

Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .

Теперь попытаемся выразить модуль вектора через радиус-вектор , а проекцию вектора силы на вектор , через угол .

Так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , используя соотношения для прямоугольного треугольника, можно записать следующее равенство: , где в случае малого угла справедливо и следовательно

Для проекции вектора силы на вектор , видно, что угол , а так как , получаем, что .

Теперь запишем бесконечно малую работу через новые равенства или .

Теперь видно, что произведение есть не что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуль вектора момента силы .

Теперь полная работа записывается очень просто: или .

Единицы

Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является ньютон-метр. Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н·м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н·м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически

,

где Е — энергия, M— вращающий момент, θ — угол в радианах.

Специальные случаи

Формула момента рычага

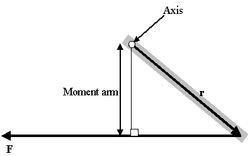Момент рычага

Очень интересен особый случай, представляемый как определение момента силы в поле:

= МОМЕНТ_РЫЧАГА * СИЛА

Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален

= РАССТОЯНИЕ_ДО_ЦЕНТРА * СИЛА

Сила под углом

Если сила F направлена под углом θ к рычагу r, то M = r*F*sinθ, где θ это угол между рычагом и приложенной силой

Статическое равновесие

Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении ΣM=0.

Момент силы как функция от времени

Момент силы — производная по времени от момента импульса,

,

где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.

,

То есть, если I постоянная, то

,

где α — угловое ускорение, измеряемое в радианах в секунду за секунду.

Отношение между моментом силы и мощностью

Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.

= МОМЕНТ_СИЛЫ * УГЛОВАЯ_СКОРОСТЬ

В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.

Отношение между моментом силы и работой

= МОМЕНТ_СИЛЫ * УГОЛ

В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в радианах.

Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .

Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:

= МОМЕНТ_СИЛЫ * *

Момент силы относительно точки

Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющего точки и , на вектор силы :

.

Момент силы относительно оси

Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.

Единицы измерения

Момент силы измеряется в ньютон-метрах. 1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.

Измерение момента

На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM, Lorenz (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).

Ссылки

См. также

Физический маятник — Википедия

Физи́ческий ма́ятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.

Момент инерции относительно оси, проходящей через точку подвеса:

I=m(r2+h3){\displaystyle I=m\left(r^{2}+h^{2}\right)}.

Дифференциальное уравнение движения физического маятника[править | править код]

Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:

Id2θdt2=−mghsin⁡θ{\displaystyle I{\frac {d^{2}\theta }{dt^{2}}}=-mgh\sin \theta }.

Полагая r2h+h=l{\displaystyle {\frac {r^{2}}{h}}+h=l}, предыдущее уравнение можно переписать в виде:

ld2θdt2=−gsin⁡θ{\displaystyle l{\frac {d^{2}\theta }{dt^{2}}}=-g\sin \theta }.

Последнее уравнение аналогично уравнению колебаний математического маятника длиной l{\displaystyle l}. Величина l{\displaystyle l} называется приведённой длиной физического маятника.

Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.

Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии l{\displaystyle l} от точки подвеса. Эта точка и будет центром качания маятника.

Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен I=ml2{\displaystyle I=ml^{2}}, а момент силы тяжести относительно той же оси −mglsin⁡θ{\displaystyle -mgl\sin \theta }. Легко заметить, уравнение движения не изменится.

Теорема Гюйгенса[править | править код]

Формулировка[править | править код]

Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.

Доказательство[править | править код]

Вычислим приведенную длину для нового маятника:

l1=r2r2/h+r2h=h+r2h=l{\displaystyle l_{1}={\frac {r^{2}}{r^{2}/h}}+{\frac {r^{2}}{h}}=h+{\frac {r^{2}}{h}}=l}.

Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.

Период колебаний физического маятника[править | править код]

Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания.
Для этого умножим левую ld2θdt2=lddt(dθdt){\displaystyle l{\frac {d^{2}\theta }{dt^{2}}}=l{\frac {d}{dt}}\left({\frac {d\theta }{dt}}\right)} и правую часть этого уравнения на dθ{\displaystyle d\theta }. Тогда:

ldθdtd(dθdt)=−gsin⁡θdθ{\displaystyle l{\frac {d\theta }{dt}}d\left({\frac {d\theta }{dt}}\right)=-g\sin \theta \,d\theta }.

Интегрируя это уравнение, получаем.

l(dθdt)2=2gcos⁡θ+C{\displaystyle l\left({\frac {d\theta }{dt}}\right)^{2}=2g\cos \theta +C},

где C{\displaystyle C} произвольная постоянная. Её можно найти из граничного условия, что в моменты θ=±α,dθdt=0{\displaystyle \theta =\pm \alpha \,\,\,,{\frac {d\theta }{dt}}=0}. Получаем: C=−2gcos⁡α{\displaystyle C=-2g\cos \alpha }. Подставляем и преобразовываем получившееся уравнение:

dθdt=2glsin2⁡α2−sin2⁡θ2{\displaystyle {\frac {d\theta }{dt}}=2{\sqrt {\frac {g}{l}}}{\sqrt {\sin ^{2}{\frac {\alpha }{2}}-\sin ^{2}{\frac {\theta }{2}}}}}.

Отделяем переменные и интегрируем это уравнение:

glt=∫0θ2d(θ2)sin2⁡α2−sin2⁡θ2{\displaystyle {\sqrt {\frac {g}{l}}}t=\int \limits _{0}^{\frac {\theta }{2}}{\frac {d\left({\frac {\theta }{2}}\right)}{\sqrt {\sin ^{2}{\frac {\alpha }{2}}-\sin ^{2}{\frac {\theta }{2}}}}}}.

Удобно сделать замену переменной, полагая sin⁡θ2=sin⁡α2sin⁡φ{\displaystyle \sin {\frac {\theta }{2}}=\sin {\frac {\alpha }{2}}\sin \varphi }. Тогда искомое уравнение принимает вид:

t=lg∫0φdφ1−sin2⁡α2sin2⁡φ=lgF(φ∖α/2){\displaystyle t={\sqrt {\frac {l}{g}}}\int \limits _{0}^{\varphi }{\frac {d\varphi }{\sqrt {1-\sin ^{2}{\frac {\alpha }{2}}\sin ^{2}\varphi }}}={\sqrt {\frac {l}{g}}}F\left(\varphi \setminus \alpha /2\right)}.

Здесь F(φ∖α){\displaystyle F\left(\varphi \setminus \alpha \right)} — нормальный эллиптический интеграл Лежандра 1-го рода. Для периода колебаний получаем формулу:

T=4lg∫0π/2dφ1−sin2⁡α2sin2⁡φ=4lgK(sin⁡α2){\displaystyle T=4{\sqrt {\frac {l}{g}}}\,\int \limits _{0}^{\pi /2}{\frac {d\varphi }{\sqrt {1-\sin ^{2}{\frac {\alpha }{2}}\sin ^{2}\varphi }}}=4{\sqrt {\frac {l}{g}}}\,K\left(\sin {\frac {\alpha }{2}}\right)}.

Здесь K(sin⁡α2){\displaystyle K\left(\sin {\frac {\alpha }{2}}\right)} — полный нормальный эллиптический интеграл Лежандра 1-го рода. Раскладывая его в ряд, можно получить удобную для практических вычислений формулу:

T=2πlg{1+(12)2sin2⁡(α2)+(1⋅32⋅4)2sin4⁡(α2)+⋯+[(2n−1)!!(2n)!!]2sin2n⁡(α2)+…}{\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}\left\{1+\left({\frac {1}{2}}\right)^{2}\sin ^{2}\left({\frac {\alpha }{2}}\right)+\left({\frac {1\cdot 3}{2\cdot 4}}\right)^{2}\sin ^{4}\left({\frac {\alpha }{2}}\right)+\dots +\left[{\frac {\left(2n-1\right)!!}{\left(2n\right)!!}}\right]^{2}\sin ^{2n}\left({\frac {\alpha }{2}}\right)+\dots \right\}}.

Период малых колебаний физического маятника[править | править код]

Если амплитуда колебаний α{\displaystyle \alpha } мала, то корень в знаменателе эллиптического интеграла приближенно равен единице. Такой интеграл легко берется, и получается хорошо известная формула малых колебаний:

T=2πlg=2πImgh{\displaystyle T=2\pi {\sqrt {\frac {l}{g}}}=2\pi {\sqrt {\frac {I}{mgh}}}}.

Эта формула даёт результаты приемлемой точности (ошибка менее 1 %) при углах, не превышающих 4°.

Следующий порядок приближения можно использовать с приемлемой точностью (ошибка менее 1 %) при углах до 1 радиана (≈60°)

T≈2πlg(1+14sin2⁡(α2))=π4lg(9−cos⁡α){\displaystyle T\approx 2\pi {\sqrt {\frac {l}{g}}}\left(1+{\frac {1}{4}}\sin ^{2}\left({\frac {\alpha }{2}}\right)\right)={\frac {\pi }{4}}{\sqrt {\frac {l}{g}}}\left(9-\cos {\alpha }\right)}.