9.Момент силы и момент импульса.Момент инерции.

Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудахАрхимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения.

Более точно, момент силы частицы определяется как векторное произведение:

где — сила, действующая на частицу, а—радиус-вектор частицы.

Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количествовращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.

Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.

Момент импульса замкнутой системы сохраняется.

Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения в Международной системе единиц (СИ): кг·м².

Обозначение: I или JМоментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех 

n материальных точек системы на квадраты их расстояний до оси:

,

где: m_i — масса i-й точки,

r_i — расстояние от i-й точки до оси.

11. Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этиммомент импульса замкнутой системы в любой системе координат не изменяется со временем.

Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.

В упрощённом виде: , если система находится в равновесии.

Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законымеханики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.

Сила. Момент силы. Закон Гука – онлайн-тренажер для подготовки к ЕНТ, итоговой аттестации и ВОУД

Запомнить

Восстановить пароль

Регистрация

Конспект

Сила – векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная к массивному телу сила является причиной изменения его скорости или возникновения в нем деформаций и напряжений.

Сила как векторная величина характеризуется

модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе в векторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором. В физике эти векторы называются свободными векторами. В механике чрезвычайно распространено представление о связанных векторах, начало которых закреплено в определенной точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы).

Также используется понятие линия действия силы, обозначающее проходящую через точку приложения силы прямую, по которой направлена сила.

Второй закон Ньютона гласит, что в инерциальных системах отсчета ускорение материальной точки по направлению совпадает с равнодействующей всех сил, приложенных к телу, а по модулю прямо пропорционально модулю силы и обратно пропорционально массе материальной точки. {-2}\), единицей измерения в Международной системе единиц (СИ) является ньютон (N, Н), в системе СГС – дина.

Момент силы (иногда применяют синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) – векторная физическая величина, равная векторному произведению радиус-вектора (проведенного от оси вращения к точке приложения силы – по определению), на вектор этой силы. Характеризует вращательное действие силы на твердое тело.

Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» – внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов). В физике момент силы можно часто понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами.

В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создает такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:

\(\vec M = \left[ \vec r \times \vec F \right]\), где \(\vec F\) – сила, действующая на частицу, а \(\vec r\) – радиус-вектор частицы.

Закон Гука – это основной закон, выражающий связь между напряженным состоянием и деформацией упругого тела. Установлен англ. физиком Р. Гуком в \(1660\) для простейшего случая растяжения или сжатия стержня в форме: абсолютное удлинение (укорочение) \(ΔI\) цилиндрического стержня прямо пропорционально растягивающей (сжимающей) силе N, т. е. \(ΔI = kN\), где \(k = \frac I{\frac{ES} I}\) – длина стержня, \(S\) – площадь его поперечного сечения, \(E\) – модуль продольной упругости, являющийся механической характеристикой (константой) материала.

З.Г. удобно представлять также в форме \(σ= Eε\), где \(σ=\frac NS \) – нормальное напряжение в поперечном сечении, \(\varepsilon = \frac{ΔI}I \) – относительное удлинение (укорочение) стержня. При сдвиге этот закон записывается так: \( τ = \frac Gγ\), где \(τ\) – касательное напряжение, γ – сдвиг, \(G\) – модуль сдвига; при сдвиге касательное напряжение прямо пропорционально сдвигу.

Обобщенный закон Гука – для тела произвольной формы – утверждает, что 6 величин, определяющих напряженное состояние в точке, выражаются линейно через \(6\) величин, определяющих деформацию в окрестности рассматриваемой точки. Коэффициенты пропорциональности в этих соотношениях называются модулями упругости. В анизотропных телах, например в кристаллах, модули упругости различны в разных направлениях, поэтому в общем случае упругие свойства твердого тела характеризуются с помощью \(21\) модуля упругости. Для изотропных тел число независимых упругих постоянных сводится к двум.

Закон не имеет места, когда некоторые напряжения (или деформации) достигают предельных значений, характерных для каждого материала, и тело переходит в упруго-пластическое состояние. Закон Гука является основным соотношением, применяемым при расчете на прочность и деформируемость конструкций и сооружений.

Вопросы

1. Угол между направлением действия силы и плечом силы равен

2. Чтобы невесомый рычаг находился в равновесии, сила \(F\) должна иметь величину

3. Брусок массой 0,3 кг прижат к вертикальной стене горизонтальной силой 8 Н. Коэффициент трения между бруском и стеной равен 0,3. Сила трения скольжения бруска о стену равна

4. Чтобы вес гири увеличился в два раза, ее надо поднимать с ускорением

5. Автомобиль массой 1,5 т движется вверх по дороге с уклоном 30° с ускорением 0,5 м/с². 3\))

6. Тело массой \(m\), двигаясь со скоростью \(υ\), растягивает пружину. Если массу тела уменьшить в 4 раза, а скорость увеличить в 4 раза, то модуль абсолютного удлинения пружины

7. Диаметр стержня равен 0,4 см, в нем возникает напряжение \(\alpha\) = 150 МПа под действием силы

8. Пружины жесткостью 100 Н/м и 300 Н/м соединили параллельно. Эту систему пружин заменили одной пружиной жесткостью

9. Плечо силы \(F_2\) – это отрезок

    

10. Два тела с одинаковыми массами, которые можно считать материальными точками, взаимно притягиваются на определенном расстоянии. Если массу одного из них увеличить на 200 кг, то сила их взаимного притяжения на том же расстоянии увеличится в три раза. Первоначальная масса тел

11. Пружина с коэффициентом жесткости 100 Н/м растянется на 0,02 м под действием силы

12. Мальчик равномерно тянет санки массой \(m\) в результате приложения силы \(F\) к нити, которая составляет угол \(\alpha\) к горизонту. Выражение, по которому определяется работа силы трения при перемещении на расстояние \(s\), имеет вид

13. При растяжении пружины на 4 см возникает сила упругости в 20 Н. Жесткость этой пружины равна

14. На концах рычага действуют силы, направленные перпендикулярно вниз и равные 30 Н и 50 Н. 2}\))

15. Два тела притягиваются друг к другу. Масса каждой – 400 кг. Как изменится сила притяжения на том же расстоянии, если увеличить массу одного из них на 200 кг?

16. На рисунке представлено тело, движущееся в горизонтальном направлении со скоростью \(\vartheta\). Какая пара сил, действующих на тело, не совершает работу?

     

17. Как изменится сила тяготения между телами, размерами которых можно пренебречь, если массу одного из тел увеличить в 2 раза, а расстояние между телами сохранить прежним?

18. Определите массу груза, если при его подъеме с ускорением 4 м/с² трос подъемного крана с жесткостью 20 кН/м удлиняется на 14 см (g ≈ 10 м/c²)

19. Первая пружина имеет жесткость 35 Н/м, жесткость второй пружины – 70 Н/м.  Удлинение первой пружины равно удлинению второй. Чему будет равно отношение потенциальных энергий пружин?

20. Груз массой 2 кг поднимают вверх с ускорением 0,8 м/с на пружине жесткостью 500 Н/м. Определите модуль удлинения этой пружины.

21. Определите жесткость вертикально подвешенной пружины, которая под действием груза массой 300 г растянулась с 12 см до 16 см (g ≈ 10 м/c²)

22. Золотое правило механики состоит в том, что

23. Найдите жесткость вертикально подвешенной пружины, если она под действием груза весом 300 г растянулась от 11 см до 15 см (\(g\approx10\) м/с \(^2\))

24. Под действием какой силы пружина жесткостью 50 кН/м может сжаться на 2 см?

25. Чему равно абсолютное удлинение стальной проволоки длиной 1,5 м, если в ней возникло механическое напряжение 42 МПа? (\(Е_{ст}\) = 210 ГПа)

26. Найдите удлинение горизонтальной пружины жесткостью 50 Н/м, если она сообщает тележке массой 500 г ускорение 2 м/с².

27. Какая мощность необходима, чтобы сжать пружину на 2 см за 1 секунду, если для сжатия ее на 1 см требуется сила 22 кН?

28. Под действием силы 4 Н пружина динамометра удлинилась на 5 мм. Чему равен коэффициент упругости пружины этого динамометра?

Сообщить об ошибке

3.2: Момент силы — Физика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

6940

• Джереми Татум
• Университет Виктории

Во-первых, давайте рассмотрим знакомую двухмерную ситуацию. На рисунке III.1 я нарисовал силу \(\textbf{F}\) и точку O. Момент силы относительно точки O можно определить как

Сила, умноженная на перпендикулярное расстояние от O до линии действия \(\textbf{F}\).

В качестве альтернативы (рисунок III.2) момент может быть одинаково хорошо определен с помощью

Поперечная составляющая силы, умноженная на расстояние от точки O до точки приложения силы.

В любом случае величина момента силы, также известная как крутящий момент , равна \(rF \sin\theta\). Мы можем рассматривать его как вектор, \( \boldsymbol\tau \), перпендикулярный плоскость бумаги:

\begin{equation} \ \boldsymbol\tau = \textbf{r} \times \textbf{F}\tag{3.2.1}\label{eq:3.2.1} \end{equation}

Теперь позвольте задать вопрос. Правильно ли говорить о моменте силы относительно (или «около») точка или относительно (или «около») оси ?

В приведенном выше двумерном примере это не имеет значения, но теперь позвольте мне перейти к трем измерениям, и я попытаюсь внести ясность.

На рисунке III.3 я нарисовал набор прямоугольных осей и силу \(\textbf{F}\), вектор положения которой относительно начала координат равен \(\textbf{r}\).

Момент или крутящий момент \(\textbf{F}\) относительно начала координат это вектор

\begin{equation} \ \boldsymbol\tau = \textbf{r}\times \textbf{F}\tag{3.2.2}\label{eq:3.2.2} \end{equation}

\( x-, y-\) и \( z\) — компоненты \( \boldsymbol\tau \) являются моментами \(\textbf{F}\) относительно \ (x-, y-\) и оси z. Вы можете легко найти компоненты \( \boldsymbol\tau \) путем расширения векторного произведения \( \ref{eq:3.2.2}\):

\[ \boldsymbol\tau = \hat{\textbf{x}}(yF_{z}-zF_{y})+\hat{\textbf{y}}(yF_{x}-xF_{z})+ \шляпа{\textbf{z}}(xF_{y}-yF_{x}) \tag{3.2.3}\label{eq:3.2.3} \]

где \( \bf \hat{x},\hat{y},\hat{z}\) — единичные векторы вдоль осей \(x,y,z\). На рисунке III.4 мы смотрим вниз по оси \(x\), и я нарисовал компоненты \(F_{y}\) и \(F_{z}\), и вы можете видеть, что на самом деле , \( \tau_{x} =yF_{z}-zF_{y}\).

Размерность момента силы или крутящего момента равна ML ² T ^-2 , а единицами СИ являются Н·м. (Лучше оставить единицы измерения Н·м, чем выражать крутящий момент в джоулях.)

---

Эта страница под названием 3.2: Moment of Force распространяется под лицензией CC BY-NC 4.0 и была создана, изменена и/или курирована Джереми Татумом с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Джереми Татум

   Лицензия

   CC BY-NC

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. Сила
   2. Момент силы
   3. источник@http://orca. phys.uvic.ca/~tatum/classmechs.html
   4. крутящий момент

Момент силы

Вы когда-нибудь видели, как вращающиеся колеса генерируют энергию? Или видели, как вращаются автомобильные двигатели для производства энергии? Все подобные явления в физике определяются как момент силы. Сила является важной частью любого движения, которое объясняет физика. Будь то эффект толкания и вытягивания или ось вращения. Важную роль в этом играет сила. Одной из таких частей силы является формула момента силы. Существуют различные примеры практических моментов силы, которые мы наблюдаем в нашей повседневной жизни. Но загвоздка в том, что мы никогда не осознаем этого, поскольку это продолжается.

Понимание момента силы сначала потребует правильной интерпретации силы. В приведенной ниже информации будет уточнение того, что такое сила. Также будет разъяснена формула момента силы и виды момента силы. Кроме того, будут примеры момента силы, чтобы облегчить лучшее понимание концепции и значения момента силы.

Что такое сила с точки зрения физики?

В простом смысле сила является синонимом толкания и притяжения между двумя объектами, которые соприкасаются друг с другом. Если два объекта взаимодействуют или сталкиваются друг с другом, говорят, что они действуют друг на друга. Сила может сохраняться только тогда, когда два объекта вступают в контакт. Без какого-либо контакта нет силы.

Силы могут быть контактными силами или силами, возникающими в результате действий на расстоянии. Когда существует физическое взаимодействие между двумя или более объектами, прилагаемая сила известна как контактная сила. Напротив, когда два объекта не находятся в физическом контакте, присутствующая сила является силой, являющейся следствием действий на расстоянии. Здесь присутствует сила гравитации.

Под контактными силами имеется несколько других видов сил, классифицированных в той же категории. Это сила трения, нормальная сила, приложенная сила, сила сопротивления воздуха и т. д. Под силами, возникающими в результате действия на расстоянии, также существуют классификации. Это магнитная сила, электрическая сила и гравитационная сила.

Сила измеряется в стандартной единице, известной как Ньютон. Это векторная величина, указывающая, что она имеет как направление, так и величину. Это означает, что сила может двигаться в определенном направлении или направлениях. Он может колебаться между низкой, средней и высокой величиной, в зависимости от того, как он был проявлен.

Сила представлена ​​в виде векторных диаграмм, которые указывают направление и величину с помощью нарисованных стрелок. Под силой существует совершенно новая концепция момента силы. В следующем разделе есть подробное объяснение этого.

Что такое момент силы?

Момент силы определяется как поворачивающая способность силы. Это сила, которая вращает тело или объект вокруг определенной оси, конца или точки. Этот момент силы также известен как крутящий момент, сила вращения или эффект поворота. Тем не менее, он варьируется в зависимости от двух областей, физики и механики.

Момент силы измеряет тенденцию, которая вращает тело в определенной точке. Однако эта тенденция сильно отличается от тенденции, которая двигает объект. Здесь сила должна начинаться по шаблону, который начинает вращать объект. Момент силы возникает при отсутствии равной и противоположной силы вдоль направления объекта.

Пример

Если вы и ваш друг толкаете дверь с обоих концов, это создаст силу, но не момент силы. Пока вы оба толкаете, это будет классифицироваться как равная сила. Однако, как только вы отказываетесь от пуша, ваш друг становится единственной силой, оказывающей давление. Когда вы уходите, не применяя никакой силы, дверь поворачивается и распахивается. Здесь поворот распашной двери является моментом силы.

Формула момента силы показывает, что он прямо пропорционален расстоянию до точки.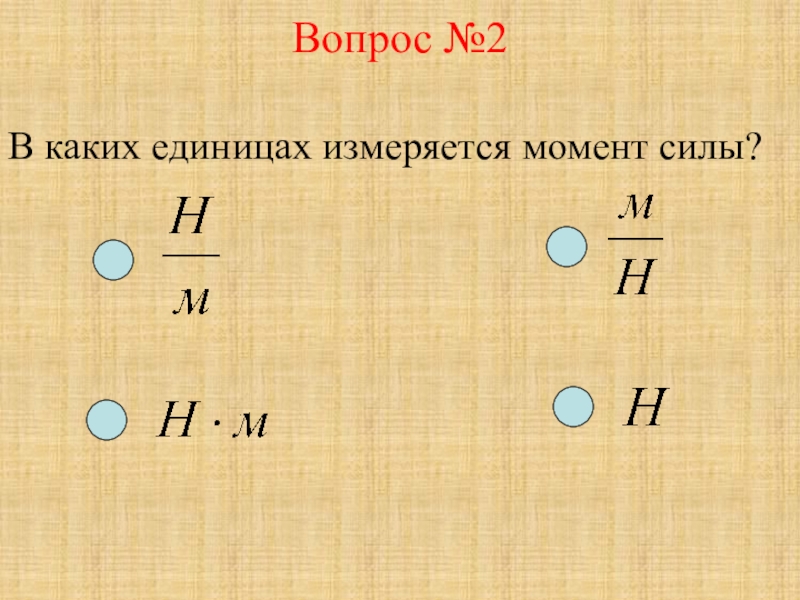 Здесь расстояние силы от фокальной оси или точки. Формула момента силы – это произведение силы и моментного плеча. Сила представлена ​​как F, а плечо момента представлено как d. Плечо момента — это измеренное перпендикулярное расстояние между линией действия силы и центром или ее осью.

Математически формула момента силы может быть представлена ​​в виде 0171 F= силовая линия

d= плечо момента

Кроме того, момент силы выражается в ньютон-метрах, фут-фунтах, кип-футах и ​​килоньютон-метрах. Существуют различные примеры моментов силы. Это вращение дверной ручки, движение гаечного ключа, поворачивающего гайку, и движение качелей.

Помимо этого, существуют различные виды момента силы. Это:

Существуют различные знаки момента силы. Они подробно рассматриваются в следующем разделе.

Значение момента силы

Момент силы играет важную роль в различных приложениях. К ним относятся:

• Кроме того, моменты силы можно наблюдать в различных повседневных предметах, таких как обод чайника, велосипеды и гаечные ключи для ремонта.