Момент силы. Правило моментов

Обратная связь

К оглавлению… Если тело может вращаться относительно некоторой оси, то для его равновесия недостаточно равенства нулю равнодействующей всех сил. Вращающее действие силы зависит не только от ее величины, но и от расстояния между линией действия силы и осью вращения. Длина перпендикуляра, проведенного от оси вращения до линии действия силы, называется плечом силы. Для описания причин вызывающих вращения и условия равновесия тела в статике вводится новое понятие — момент силы. Произведение модуля силы F на плечо d и называется моментом силы M. Таким образом момент силы в статике вычисляется по формуле: Обычно в физике используется следующее правило знаков: если сила поворачивает тело по часовой стрелке, то ее момент считается положительным, а если против – то отрицательным. Момент силы может и равняться нулю, если сила проходит (сама или продолжением) через ось. Обратите внимание: если Вы перепутаете, и возьмете знаки моментов наоборот (по часовой стрелке со знаком минус, а против часовой со знаком плюс), то ничего страшного не произойдет. Поэтому, важно запомнить, что моменты сил, вращающих тело в различных направлениях относительно часовой стрелки, берутся с различными знаками. Обратите внимание, что момент силы зависит не только от величины силы, но и от ее плеча. Следовательно, одно и то же значение момента можно получить двумя способами: взять большую силу и малое плечо или взять малую силу и большое плечо. Вывод: чем больше плечо, тем меньшую силу необходимо прилагать для получения одного и того же результата. Правило моментов: тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю: При записи этого условия в ходе решения конкретной задачи по статике моменты сил необходимо записывать с учётом их знаков. В Международной системе единиц (СИ) моменты сил измеряются в ньютоно-метрах (Н∙м). Обратите внимание: в общем случае, когда тело может двигаться поступательно и вращаться, для равновесия необходимо выполнение обоих условий: равенство нулю равнодействующей силы и равенство нулю суммы всех моментов. Алгоритм решения задач на правило моментов (задач по статике): 1. Нарисовать рисунок. Следует помнить, что сила тяжести, действующая на тело изображается один раз. Если же в задаче идет речь об изломанной палочке, то удобнее рисовать отдельно силы тяжести, действующие на каждую часть палочки, считая массы частей пропорциональными их длинам. В отличие от динамики, где силы изображаются из одной точки, в статике важно точно указать точку приложения силы. 2. Выбрать ось вращения в точке приложения самой ненужной в задаче силы или сил (той силы, которую определять не надо и не хочется из-за природного чувства лени). При этом плечо (и, следовательно, момент) этой силы обратится в нуль независимо от ее величины, и в дальнейших вычислениях эту силу можно не учитывать совсем. 3. Записать правило моментов относительно данной оси, на забывая про правило знаков. 4. При необходимости записать также условие согласно которому равнодействующая сила равна нолю. 5. Выразить искомую силу.   Рычаги и блоки К оглавлению… Как вы знаете из практики, иногда необходимо изменить направление силы, увеличить или уменьшить ее величину. Этой цели служат простые механизмы: устройства, преобразующие величину или направление силы с помощью механических явлений. Для всех простых механизмов справедливо золотое правило механики: выиграл в силе – проиграл в перемещении (или наоборот). Это значит, что при увеличении силы за счет некоторого механизма неизбежно будет уменьшено и перемещение. Рассмотрим основные типы простых механизмов изучаемых в школьной физике: · Равноплечий рычаг (весы). Рычаг, ось вращения которого проходит через его геометрический центр. · Неравноплечий рычаг. Рычаг ось вращения которого проходит через произвольную точку. · Неподвижный блок. Это диск с закрепленной осью, через который переброшена нить. Неподвижный блок используется для изменения направления приложения силы. Если трение в блоке отсутствует, нить невесома, то сила ее натяжения до и после блока не изменяется. Таким образом, неподвижный блок не дает ни выигрыша в силе, ни проигрыша в перемещении. · Подвижный блок. Это диск, ось которого может двигаться поступательно. Подвижный блок позволяет уменьшить силу в два раза, одновременно с этим вдвое увеличивая перемещение. · Наклонная плоскость. Это устройство применяется для поднятия тяжестей. При достаточно малых значениях угла наклона и небольшом коэффициенте трения сила, которую необходимо приложить чтобы поднимать некоторое тело вдоль наклонной плоскости может быть значительно меньше веса тела. Таким образом, подъем становится легче. Естественно, при этом в полном соответствии с «золотым правилом» увеличивается перемещение тела.   Центр тяжести тела К оглавлению… Центр масс (или центр тяжести) – точка к которой приложена сила тяжести, действующая на тело. В общем случае центр тяжести может и не лежать внутри тела, а выходить за его пределы (например, различные изогнутые длинные предметы, кольца, полукольца и так далее). Рассмотрим основные методы определения положения центра масс тел для некоторых конкретных случаев, возникающих при решении задач по статике: 1. У однородных тел правильной формы (шары, прямоугольники, стержни) центр тяжести совпадает с геометрическим центром. Следует запомнить, что центр тяжести однородной треугольной пластины лежит в точке пересечения ее медиан. Для однородных симметричных тел центр тяжести всегда расположен на оси симметрии. 2. Определение положения центра тяжести системы из двух тел с известными центрами тяжести. Здесь можно использовать замечательное свойство центра тяжести. Подперев центр тяжести, мы обеспечим равновесие тела. Таким образом, центр тяжести системы из двух тел лежит на отрезке, соединяющем их центры тяжести, и делит его в отношении, обратном отношению масс тел: где: l1 – расстояние от центра масс до тела с массой m1, а l2 – до тела с массой m2. 3. Определение положения центра тяжести любой системы тел с известными положениями центров тяжести. Необходимо ввести систему координат (естественно, начало координат выбрать в точке, относительно которой необходимо рассчитать положение центра тяжести), определить в ней координаты центров тяжести всех тел и найти координаты центра тяжести системы по формуле: Аналогичные уравнения получаются для остальных координатных осей, если таковые необходимо рассматривать в задаче (просто переменная x меняется на y или z соответственно). 4. Однородное тело правильной формы с вырезом правильной формы. Проще всего свести задачу к обратной: мысленно вставить вырез обратно и получить тело правильной формы с известным положением центра тяжести. Далее представить его в виде двух тел: страшного с вырезом и самого выреза. А теперь все просто. У одного из тел (выреза) мы знаем положения центра тяжести. У другого – нет. Зато знаем положение центра тяжести системы двух тел. Составив уравнение для определения общего центра тяжести получим выражение с одной неизвестной – центром тяжести тела с вырезом. Решив уравнение получим искомый ответ. 5. Теорема Паппа. Применяется для определения положения центра тяжести плоской пластины, которая при вращении вокруг некоторой оси образует тело с легко вычисляемым объемом. Необходимо мысленно повернуть пластину на один оборот, нарисовать рисунок и применить теорему: Формулировка теоремы: объем тела, полученного при вращении пластины, равен произведению ее площади на путь, пройденный центром тяжести при вращении:



Как правильно найти момент силы, формула, решение задач

Оглавление

Время чтения:  7 минут

232

Определение

Момент силы — это крутящий или вращательный момент, который является векторной величиной.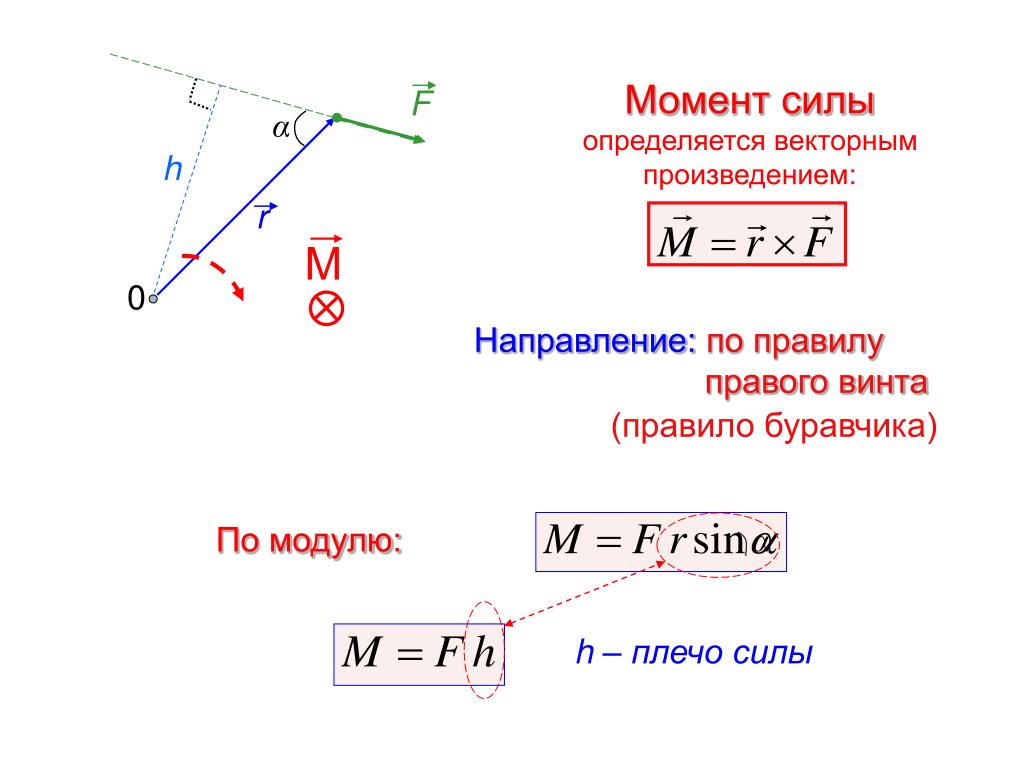

Чтобы определить, чему равен момент силы, нужно получить произведение вектора силы и радиус-вектора, который проводится к точке приложения силы от оси вращения. Поэтому величину можно назвать характеристикой вращательного воздействия силы на твердое тело.

Термины “крутящий” и “вращающий” моменты в данном случае не являются тождественными. Разница между ними состоит в том, что “вращающий” момент воспринимается как внешнее усилие, которое прикладывают к объекту. Термин “крутящий” же рассматривается как внутреннее усилие, которое появляется при приложении конкретных нагрузок (что делает определение схожим с используемым при изучении сопротивления материалов).

Понятие «момент силы»

Физики воспринимают этот термин в качестве так называемой “вращающей силы”. В соответствии с системой СИ, измеряется данная величина в ньютон-метрах. Иногда в литературе можно также встретить понятие “момент пары сил” (такое определение, например, появляется в исследованиях Архимеда над рычагами).

При использовании простых примеров (например, при приложении силы к рычагу в перпендикулярном отношении к нему) величина рассчитывается как произведение расстояния до оси вращения рычага и непосредственно силы, которая на него воздействует.

Пример: На рычаг оказывает воздействие силы в 3 ньютона, которую прикладывают на расстоянии 2 м от оси вращения рычага. В результате момент силы будет равнозначен силе в 1 ньютон, прикладываемой на расстоянии 6 м по отношению к рычагу.

Как определить, чему равен момент силы

Формула

Точно определить момент действия силы частицы удастся, применив следующую векторную формулу:

\[\vec{\mathrm{M}}=\vec{\mathrm{r}} \vec{\mathrm{F}}\]

В данном случае \[\vec{\mathrm{r}}\] — это радиус вектора частицы, а
\[\vec{\mathrm{F}}\] — сила, воздействующая на эту частицу.

Важно помнить, что в физике энергия воспринимается как скалярная величина. В то же время момент силы считается (псевдо)векторной величиной. Поэтому совпадение размерностей указанных величин никогда не бывает случайным. Например, момент силы в 1 Н/м, приложенный через целый оборот, при выполнении механической работы сообщает энергию в 2 Дж. В математическом отображении эта формула момента силы будет выглядеть так:

\[\mathbf{E}=\mathbf{M} \boldsymbol{\theta}\], где:

• \[\mathbf{E}\] — это энергия;
• \[\mathbf{M}\] — это вращающийся момент;
• \[\boldsymbol{\theta}\] — это угол в радианах.

В современных условиях момент силы измеряется при помощи особых датчиков нагрузки, которые могут быть трех типов:

• оптического;
• тензометрического;
• индуктивного.

Применение специальной техники позволяет определить величину предельно точно и избавляет ученых от необходимости производить лишние расчеты.

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Момент силы: формулы

Наиболее интересным в физике считается определение момента силы в поле. Для этого используется следующая формула:

\[\vec{M}=\vec{M_{1}} \vec{F}\]

Где:

\[\vec{M_{1}}\]- это момент рычага;
\[\vec{F}\]- это величина силы, действующей на тело.

У такой формулы момента силы в физике будет один недостаток. С ее помощью не удастся определить, в каком направлении направлен момент силы. Известной станет только его величина. Если сила окажется перпендикулярной вектору, тогда момент рычага окажется равен расстоянию от центра до точки, в которой была приложена сила. В таком случае момент силы достигнет максимального значения:

\[\vec{T}=\vec{r} \quad \vec{F}\]

Если сила совершает какое-либо действие на определенном расстоянии, она параллельно выполняет механическую работу относительно того же объекта. В таком случае в физической практике считается, что и момент силы выполняет работу (при совершении действия через угловое расстояние).

\[\mathrm{P}=\mathrm{M} {\omega}\]

Международная система измерений предлагает определять мощность в Ваттах, при этом момент силы измеряется в радианах в секунду. Для определения величину угловой скорости используется единица “радианы в секунду”).

Как определяется момент действия нескольких сил

Если на тело действуют одновременно две равные по величине и противоположно направленные силы (не лежащие на одной и той же прямой), оно находится в состоянии равновесия. Такая ситуация связана с тем, что результирующий момент данных сил по отношению к любой из осей не обладает нулевым значением. Ведь обе силы направлены в одну сторону момента и являются парой сил.

Если тело закреплено на оси, оно будет вращаться под влиянием пары сил. Когда же пара сил прилагается по отношению к свободному телу, последнее начнет крутиться вокруг той оси, которая проходит через центр тяжести.

В соответствии с правилом моментов сил в физике, момент пары сил считается одинаковым по отношению к любой оси, перпендикулярной плоскости этой пары. При этом суммарный момент пары M всегда определяется как произведение плеча пары (то есть расстояния l между силами) и одной из этих сил F.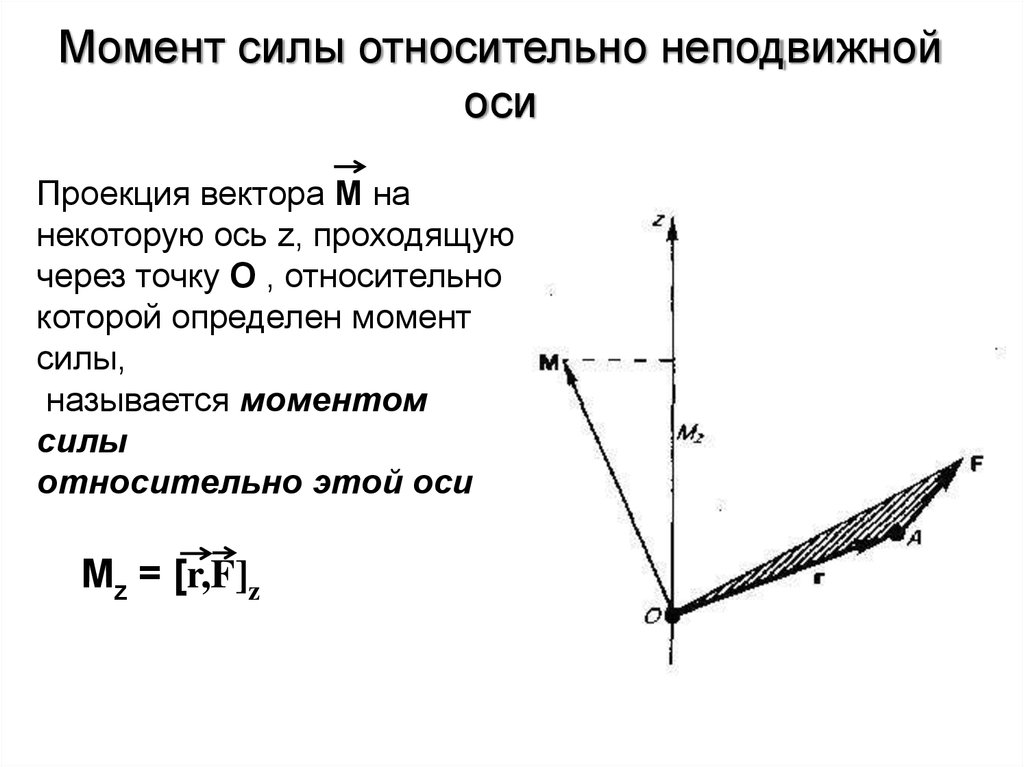 Данный расчет производится независимо от типов отрезков, на которые разделяется положение оси.

\[\mathrm{M}=\mathrm{FL}_{1}+\mathrm{FL}-2=\mathrm{FL}_{1}+\mathrm{L}_{2}=\mathrm{FL}\]

В случае, если равнодействующая момент нескольких сил равняется нулю, он будет одинаковым по отношению ко всем параллельным друг другу осям. Именно поэтому воздействие всех сил на тело можно заменить действием только одной пары сил, имеющих точно такой же момент.

Что означает центр тяжести и момент?| Инструмент выбора для продуктов Motion Design Tech / Sugatsune Kogyo

Что означает центр тяжести и момент?| Инструмент выбора для продуктов Motion Design Tech / Sugatsune Kogyo

Понятие «Центр тяжести» и момент

Что такое центр тяжести?

Центр тяжести — это центр всего веса объекта.

Что такое момент или момент силы?

Это измерение силы, необходимой для вращения чего-либо вдоль оси.

Если створка или дверь имеют постоянную плотность, как показано на рисунке справа, центр тяжести будет их центром.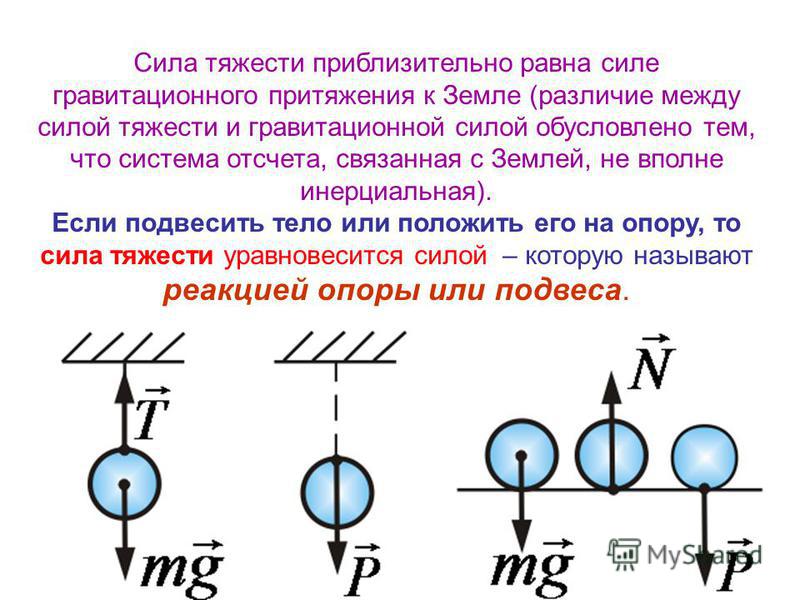
В этом случае X1=L1÷2.

• Вот почему формула в каталоге Сугацунэ — L1÷2.
• Эта формула предназначена для тонкой створки/двери.

Формула момента

На рисунке выше представлена ​​формула для расчета максимального момента.
Момент зависит от угла раскрытия и горизонтального расстояния от центра вращения до «центра тяжести».

Точка выбора петли/ножек

СВОБОДНАЯ ОСТАНОВКА

Если используется несколько петель/ножек, общий крутящий момент будет равен значению, умноженному на их количество

Нажмите здесь, чтобы найти инструменты для СВОБОДНОЙ ОСТАНОВКИ

ДЕМПФИРОВАНИЕ

Если несколько петель/ножек используются, общий крутящий момент будет значением, умноженным на его количество

Щелкните здесь для инструментов SOFT CLOSE

Расчет «Центра тяжести»

Чтобы вычислить центр тяжести L-образного закрылка, сначала разделите фигуру на две простые фигуры и рассчитайте центр тяжести каждой из них. Затем объедините два, добавив их вместе.
*Та же концепция применяется, когда зеркало прикреплено к крышке, где каждое из них может иметь отдельные центры тяжести. Давайте рассмотрим пример, когда
L-образный клапан разделен на 2 части.

ПОПРОБУЙ!

Давайте рассчитаем примерный случай, когда L-образный клапан разделен на 2 части.

Центр тяжести G1 закрылка A

Высота L1 ^*

см

Толщина t1 ^*

см

Введите отрицательные значения, если центр тяжести ниже центра/оси вращения.

Длина блока указана в см для облегчения понимания.

Вес, м1

кг

X1 осевое расстояние

——

см

Осевое расстояние Y1

——

см

Расстояние до центра тяжести G1

——

см

Угол, образованный G1 и
осью X

——

°

Момент в точке А

X1 направление

——

кгс・см

Направление Y1

——

кгс・см

Центр тяжести G2 закрылка B

Высота L2 ^*

см

Толщина t2 ^*

см

Введите отрицательные значения, если центр тяжести ниже центра/оси вращения.

Длина блока указана в см для облегчения понимания.

Вес м2

кг

X2 осевое расстояние

——

см

Y2 осевое расстояние

——

см

Расстояние до центра тяжести G2

——

см

Угол, образованный G2 и
осью X

——

°

Момент в В

X2 направление

——

кгс・см

Направление Y2

——

кгс・см

Общий центр тяжести G

Общий вес

——

кг

Центр тяжести по оси X

——

см

——

мм

Центр тяжести по оси Y

——

см

——

мм

Расстояние от центра вращения до общего центра тяжести

——

см

——

мм

Угол, образованный осью G и
X

——

°

3 знака после запятой будут округлены.

Если центр тяжести неизвестен

Если невозможно рассчитать центр тяжести, так как заслонка/дверь уже установлены, требуемый крутящий момент можно рассчитать с помощью пружинной шкалы. В соответствии с приведенной ниже таблицей вам необходимо измерить значение пружинных весов и расстояние от центра вращения (оси) до точки измерения весов.
L1 × F1 =момент створки/двери
Макс. значение L1 × F1 = макс. момент заслонки/двери

Пример

Если L1 равно 100 см, а F1 равно 2,5 кг, момент створки/двери будет формулироваться как 100 см x 2,5 кг = 250 кгс·см. крутящий момент для свободного останова.
Это означает «крутящий момент на петлях/ножках ≧ 250 кг·см (=24,5 Н·м)».

Примечания: Будет сложно рассчитать центр тяжести, если что-то прикреплено к откидной створке/двери. В этом случае сначала нужно сделать приблизительную оценку веса и центра тяжести и предварительно выбрать шарнир/ногу. Правильный крутящий момент можно определить, используя метод, описанный выше, после сборки. Это означает, что вы можете выбрать подходящие петли/опоры.

Расстояние от центра вращения до точки измерения L1		см
Значение измерения на пружинных весах F1		кг
Момент двери = L1×F1×9,80665÷100	—-	Нм

Расчет другой рабочей силы

Если направление подъема вверх

Для открывания вниз

В центре вращения должен быть центр вала, создающий крутящий момент.

Центр тяжести | Определение и факты

центр тяжести

Смотреть все СМИ

Ключевые люди:

Альберт Саксонский

Похожие темы:

масса центр масс

Просмотреть весь связанный контент →

центр тяжести , в физике воображаемая точка в теле материи, где для удобства некоторых вычислений можно считать, что сосредоточен весь вес тела.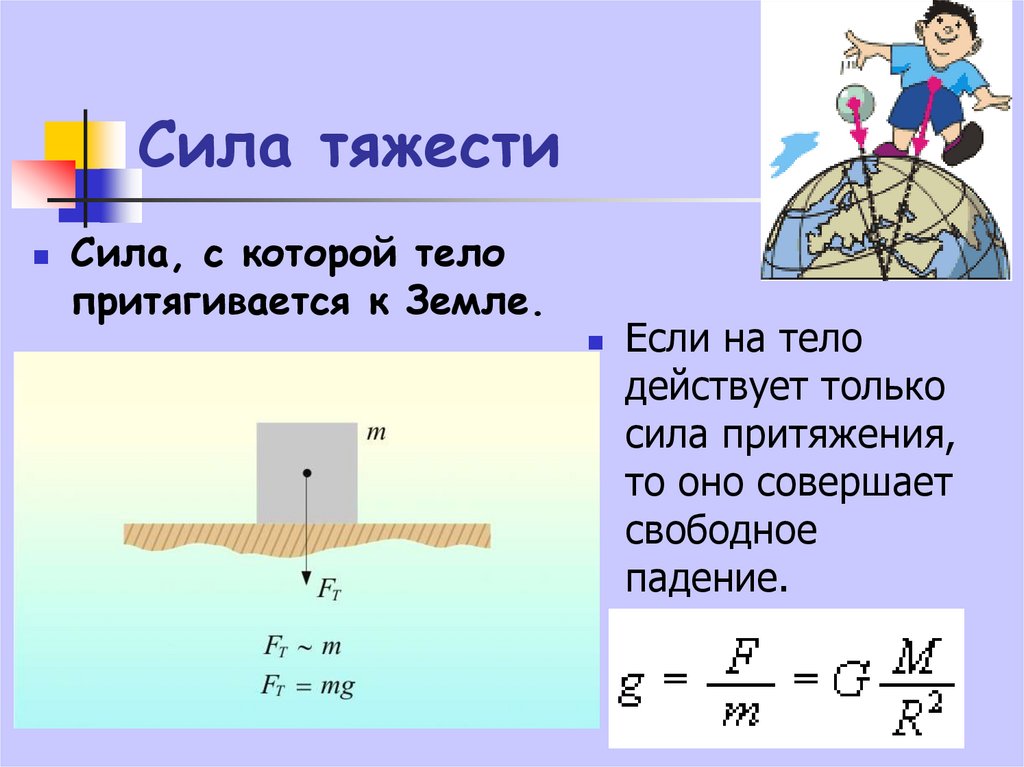 Эта концепция иногда полезна при проектировании статических конструкций (например, зданий и мостов) или при прогнозировании поведения движущегося тела, когда на него действует сила тяжести.

В однородном гравитационном поле центр тяжести идентичен центру масс, термин, предпочитаемый физиками. Однако они не всегда совпадают. Например, центр масс Луны очень близок к ее геометрическому центру (это не точно, потому что Луна не является идеальной однородной сферой), но ее центр тяжести немного смещен к Земле из-за более сильной гравитационной силы на Луне. ближняя сторона.

Расположение центра тяжести тела может совпадать с геометрическим центром тела, особенно в объекте симметричной формы, состоящем из однородного материала. Однако асимметричный объект, состоящий из множества материалов с разными массами, вероятно, будет иметь центр тяжести, расположенный на некотором расстоянии от его геометрического центра. В некоторых случаях, таких как полые тела или объекты неправильной формы, центр тяжести (или центр масс) может находиться в пространстве в точке, внешней по отношению к физическому материалу, например, в центре теннисного мяча или между ножками тела.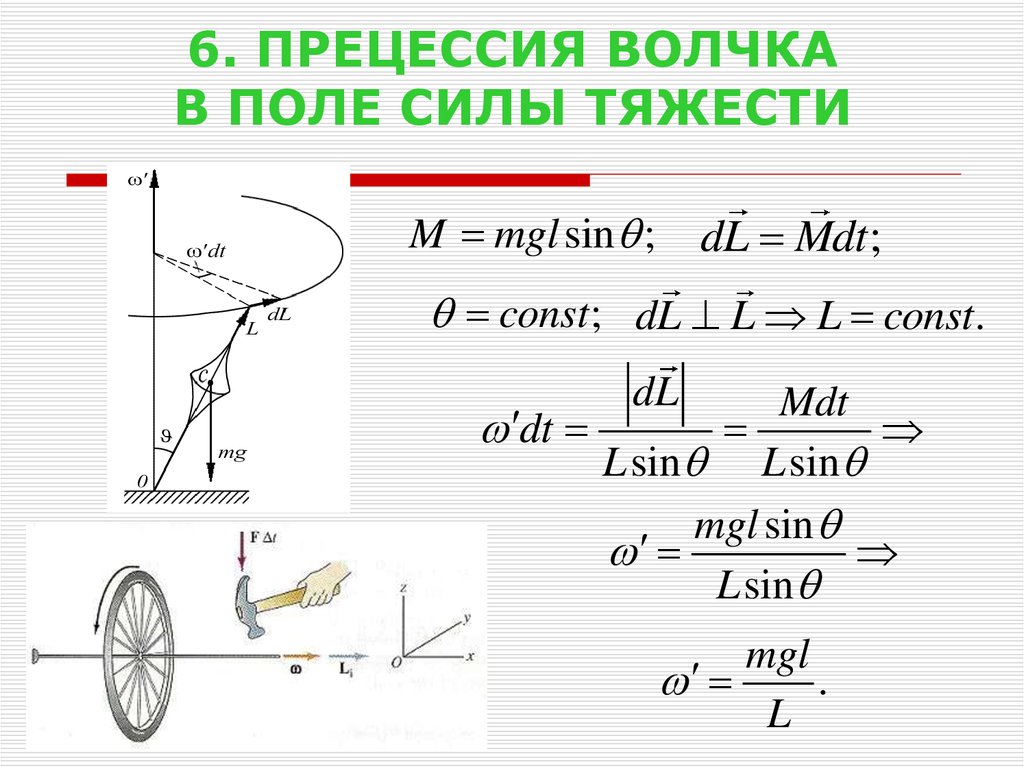 кресло.

В опубликованных таблицах и справочниках указаны центры тяжести наиболее распространенных геометрических фигур. Для треугольной металлической пластины, такой как изображенная на рисунке, расчет будет включать суммирование моментов весов всех частиц, составляющих металлическую пластину, относительно точки A. Приравнивая эту сумму к весу пластины W, умноженному по неизвестному расстоянию от центра тяжести G до АС можно определить положение G относительно АС. Суммирование моментов можно легко и точно получить с помощью интегрального исчисления.

Центр тяжести любого тела также можно определить с помощью простой физической процедуры. Например, для пластины на рисунке точка G может быть расположена путем подвешивания пластины на веревке, прикрепленной в точке А, а затем на веревке, прикрепленной в точке С. Когда пластина подвешена к точке А, линия AD вертикальна; когда он подвешен к C, линия CE вертикальна. Центр тяжести находится на пересечении AD и CE. Когда объект подвешен в какой-либо одной точке, его центр тяжести находится непосредственно под этой точкой.