Определение момента сил трения и момента инерции махового колеса.
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра физики
Методические указания к лабораторной работе №13 по физике
(Раздел «Механика»)
Ростов-на-Дону
2009
Составители: Т.П. Жданова, В.В. Илясов, А.П. Кудря, В.С. Кунаков
УДК 530.1
ОПРЕДЕЛЕНИЕ МОМЕНТА СИЛ ТРЕНИЯ И МОМЕНТА ИНЕРЦИИ МАХОВОГО КОЛЕСА: Метод. указания. — Ростов н/Д: Издательский центр ДГТУ, 2009. — 11 с.
Указания содержат краткое описание рабочей установки и методики определения момента инерции махового колеса.
Методические
указания предназначены для студентов
инженерных специальностей всех форм
обучения при выполнении лабораторного
практикума по физике (раздел «Механика
и молекулярная физика»).
Печатается по решению методической комиссии факультета
«Нанотехнологии и композиционные материалы»
Научный редактор проф., д.т.н. В.С. Кунаков
© Издательский центр ДГТУ, 2009
Лабораторная работа №13
Определение момента сил трения и момента инерции махового колеса.
Цель работы: Определение момента сил трения, момента инерции махового колеса и сравнение его с теоретическим расчётом.
Оборудование: экспериментальная установка, секундомер,
штангенциркуль.
Теоретическая часть.
При изучении вращательного движения твердого тела используют понятие момента инерции. Моментом инерции твердого тела (либо системы тел) относительно некоторой оси называется физическая величина, равная сумме произведения масс материальных точек системы на квадрат их расстояний до оси вращения: ,
где
—
число материальных точек, составляющих
систему тел.
В случае непрерывного распределения масс момент инерции может быть определен интегралом: , где интегрирование ведется по всему объёму тела. Величина — функция положения точки с координатами х, у и z.
Момент инерции зависит от массы тела и формы распределения массы относительно оси вращения.
Момент сил – физическая величина, определяемая векторным произведением радиуса-вектора , проведенного из начало отсчета в точку приложения силы на величину самой силы: ,
где — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от к. Модуль момента силы , где — плечо или кратчайшее расстояние между линией действия силы и точкой относительно, которой определяется момент силы.
Описание экспериментальной установки. Вывод формул для определения момента сил трения и момента инерции махового колеса
4
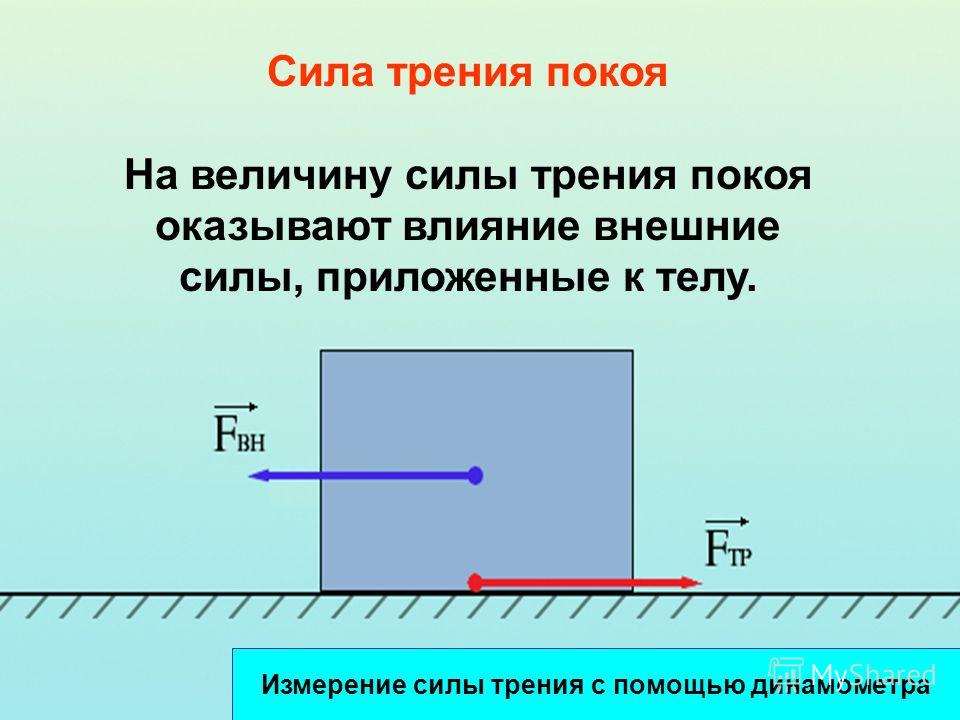
Измерительная
установка состоит из махового колеса
(диска) 1 со шкивом 2, насаженного на вал
3, установленный на шарикоподшипниках
4.
1) Если груз массы опускается с высоты , а поднимается на высоту , то можно сказать, что потенциальная энергия системы «маховое колесо-груз» убывает за счет работы среднего момента сил трения
. (1)
Средний момент сил трения обусловлен трением оси в подшипниках, махового колеса о воздух. Потерей энергии на деформацию нити и трение груза о воздух пренебрегаем.
Работа среднего момента сил трения можно выразить через угловое перемещение колеса :
. (2)
Угловое перемещение равно сумме углового перемещение при опускании и подъёме груза :
, (3)
Угловое перемещение колеса связано с числом его оборотов соотношением . Число оборотов можно найти, зная диаметр шкива и длину нити наматываемой на шкив
и , (4)
С учетом (4) и , а выражение (3) примет вид
. (5)
(5)
Подставим (5) в (2) получим
(6)
Из (1) и (6) получаем выражение для вычисления момента сил трения:
. (7)
2) Если груз из верхней точки опускается в нижнюю, то потенциальная энергия груза () превращается в кинетическую энергию поступательного движения груза (), вращательного движения диска, шкива и вала тел () и работу среднего момента сил трения
. (8)
Работа среднего момента сил трения:
(9)
С учетом (9), уравнение (8) примет вид:
(10)
Учитывая, что линейная скорость движения груза и где — диаметр шкива, на который наматывается нить, — время движения груза до нижней точки, получим выражение для угловой скорости шкива
. (11)
Совместное решение (10) и (11) позволяет определить момент инерции махового колеса:
.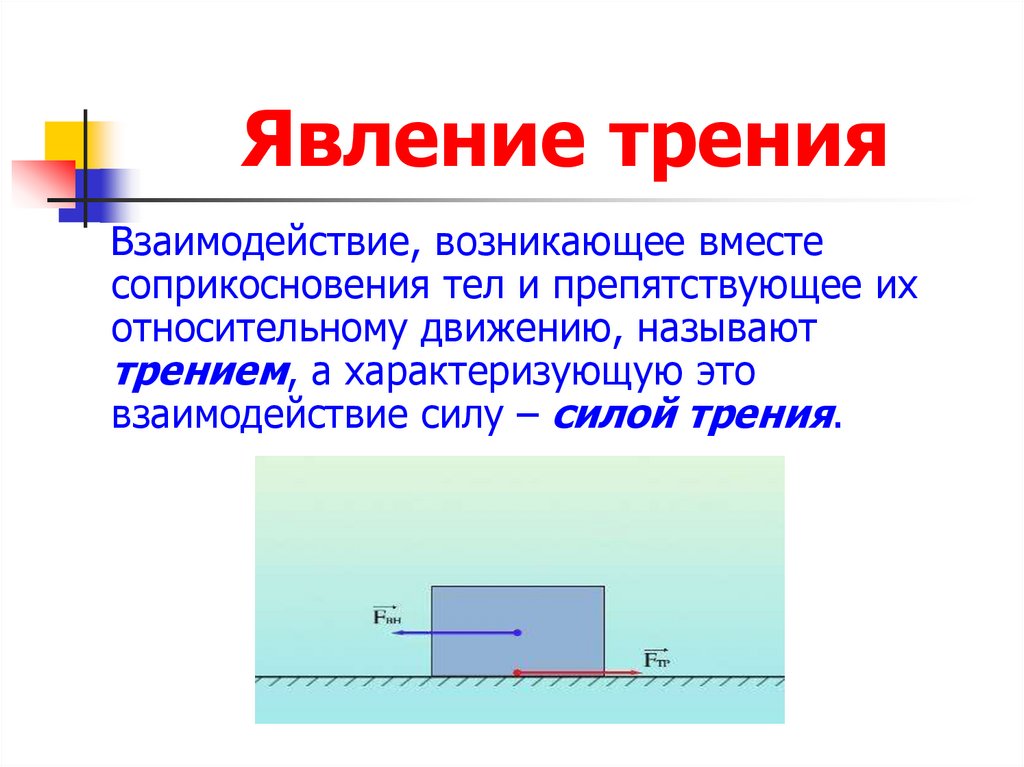 (12)
(12)
|
Заглавная страница
Обратная связь КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 7 из 14Следующая ⇒
Экспериментальная установка (рис. 3) представляет собой вал (1) с диском (2), на котором крепится кольцо (3). Вал установленный на шарикоподшипниках и может вращаться. На вал радиуса наматывается тонкая нить, длиной , до конца которой прикрепленный груз массой . Под действием силы тяготения вся система начинает вращаться. Рассмотрим движение системы с точки зрения закона сохранения энергии. При движении груза из высоты его потенциальная энергия переходит в кинетическую энергию системы
(3) и расходуется на работу против сил трения в подшипниках. Кинетическая энергия системы представляет собой сумму кинетической энергии поступательного движения груза и кинетической энергии вращательного движения диска, кольца и вала. Определим теперь работу сил трения. Поскольку при вращении махового колеса его потенциальная энергия не изменяется, то работа всех внешних сил, которые действуют на него, равняется только увеличению кинетической энергии. Таким образом, элементарная работа сил трения при повороте махового колеса на бесконечно малый угол : или . Соответственно основному уравнению динамики вращательного движения тела вокруг недвижимой оси
. Подставив это выражение в последнее уравнение для и учтя, что , получим , где — угловое перемещение. Работа внешних сил при повороте твердого тела на конечный угол определится как
. Поскольку сила трения является внешней силой, а ее момент постоянный , то работа силы трения будет , здесь , где — число оборотов колеса.
(4) Здесь — момент сил трения, j — полный угол поворота колеса. После того как груз опустится на полную длину нити , колесо будет вращаться по инерции, и нить начнет наматываться на вал. В результате груз поднимается на некоторую максимальную высоту , наверное,
(5) — полный угол поворота колеса при подъеме груза. Учитывая, что , а из равенств (4) и (5) получаем (6) Эта формула разрешает вычислить момент сил трения, если измерить радиус вала и высоты , . Применим теперь динамический метод к изучению движения махового колеса и получим выражение для расчета момента инерции кольца по экспериментальным данным. Уравнение движения системы в проекциях на оси Х и В имеют вид
(7) Общее решение уравнений (6) и (7) дает
(8) Полученное выражение разрешает рассчитать момент инерции всей системы относительно оси вращения , если определить экспериментально время движения груза из высоты . Для определения момента инерции кольца необходимо воспользоваться тем обстоятельством, что момент инерции есть адитивна физическая величина. Если снять кольцо и провести такую же серию опытов по определению времени , движения груза из высоты , то момент инерции системы без кольца (т.е. диска и вала) будет (9) Тогда момент инерции кольца (10) Порядок выполнения работы. 1. Измерить штангенциркулем диаметр вала (1) в разных его точках и определить среднее значение радиуса вала. 2. Поднять груз на высоту , наматывая нить на вал и зафиксировать его подкладкой. 3. Забрать подкладку, дав возможность груза свободно опускаться, и определить с помощью секундомера время движения груза к полному его опусканию на длину нити. Одновременно измерить высоту подъема груза при его движении вверх. Провести не менее 5 измерений и . 4. Снять кольцо (3) (см. рис. 3.) и повторить серию экспериментов по определению времени соответственно пункту 3. 5. Експериментальні даны занести в таблицу и вычислить средние значения измеренных величин. Таблица.
6. По среднему значению измеренных величин вычислить момент силы трения и момент инерции кольца, используя выражения (6) и (10). 7. Измерив внутренний и внешний диаметр кольца, рассчитать его момент инерции (2′) и уравнять с экспериментально полученным (10). 8. Определить погрешности прямых и косвенных измерений.
Контрольные вопросы: 1. Что называется моментом инерции? Какую роль играет момент инерции в динамике вращательного движения? Найдите путем интегрирования момент инерции тела правильной геометрической формы — пустого цилиндра. 2. Дайте определение момента силы. Чему равняется величина момента силы? Как направленный этот вектор? Момент какой силы сообщает маховому колесу угловое ускорение? Как направленный момент этой силы? Что такое момент импульса тела? Как направленный момент импульса? 3. Запишите основное уравнение динамики вращательного движения относительно данной задачи. 4. Изменяется ли направление момента силы, угловой скорости, момента импульса, углового ускорения, если нить начнет наматываться на вал, и тягарець будет подниматься вверх? 5. 6. При каком условии ускорения тягарця равняется тангенциальному ускорению точек на поверхности вала, из которого сматывается нить? 7. Чему при сравнимые значения моменте инерции махового колеса, полученного исследовательским путем, со значением, рассчитанным по формуле , наблюдается расхождение? Как уменьшить это расхождение? Литература: Методические указания. А.Н. Матвеев. Механика и теория относительности, -М., 1976, §22, 23, 48-50. Д.В. Сивухін. Общий курс физики, т. I, -М., 1974, §3, 4, 30, 32, 33, 36.53. С.Э.Хайкін. Физические основы механики, -М., 1971, § 11, 13, 14, 67, 68, 89. С.П. Стрелков. Механика, -М., 1975, §52, 53, 54, 53, 63-65.
Лабораторная работа №9 ⇐ Предыдущая234567891011Следующая ⇒ Читайте также: Алгоритмические операторы Matlab Конструирование и порядок расчёта дорожной одежды Исследования учёных: почему помогают молитвы? Почему терпят неудачу многие предприниматели? |
||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 549; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Простое гармоническое движение: определение и уравнения (с диаграммами и примерами)
Обновлено 28 декабря 2020 г.
Кевин Бек
Некоторые объекты движутся характерным образом ритмично и повторяются, не приводя к какому-либо чистому смещению. Эти объекты перемещаются взад и вперед вокруг фиксированного положения до тех пор, пока трение или сопротивление воздуха не заставят движение остановиться, или на движущийся объект не будет возложена новая «доза» внешней силы.
Примеры: ребенок на качелях, банджи-джампер, подпрыгивающий вверх и вниз, пружина, стягиваемая вниз под действием силы тяжести, маятник часов и игра скучающего малыша, состоящая в том, чтобы держать линейку в одной руке и тянуть верхнюю часть к другой. в сторону и отпуская ее так, чтобы линейка быстро двигалась вперед и назад, прежде чем остановиться в вертикальном положении.
Движение, которое происходит в предсказуемых циклах, называется периодическим движением и включает специальный подтип, называемый простым гармоническим движением, или SHM .
Определение простого гармонического движения
Простое гармоническое движение – это особый вид периодического движения, при котором восстанавливающая сила зависит напрямую от смещения объекта и работает в противоположное направление из них. Иными словами, восстанавливающая сила растет пропорционально увеличению расстояния, а это означает, что чем дальше система уходит от своего положения равновесия, тем труднее ей бороться за его восстановление.
Например, когда вы тянете пружину, подвешенную вертикально сверху, эта сила смещает (растягивает) пружину на определенную величину x ; когда вы отпускаете пружину, сила, возникающая из-за механических характеристик пружины, тянет пружину назад в направлении, противоположном тому, с которого она началась.
Он может даже вернуться в более сжатое состояние, чем то, в котором он начал, снова подпрыгнуть наружу и двигаться вперед и назад несколько раз, пока не остановится в исходном положении покоя.
- Точка или положение равновесия – это положение, в котором результирующая сила равна нулю, поэтому в этом случае ускорение не происходит. (Это также когда кинетическая энергия максимальна.)
- При максимальном перемещении достигается максимальное ускорение. (Это также когда потенциальная энергия максимизируется.)
- График этого смещения с течением времени представляет собой синусоидальную кривую с уменьшающейся амплитудой.
Уравнение простого гармонического движения
Закон Гука или F = – k x, можно использовать для описания простого гармонического движения для приведенных здесь примеров. Константа пропорциональности k, называемая жесткостью пружины , зависит от специфики тестируемой системы. Поищите в Интернете информацию о законе Гука, чтобы сделать собственную пружину.
Поищите в Интернете информацию о законе Гука, чтобы сделать собственную пружину.
Обратите внимание, что восстанавливающая сила всегда действует в направлении, противоположном смещению x , что объясняет отрицательный знак перед k. Для объекта, подвешенного на веревке, восстанавливающая сила от натяжения будет равна вертикальной составляющей силы тяжести:
T = –kx = –mg\cos{\theta}
В любой точке траектории эту силу можно найти с помощью основных тождеств тригонометрии.
Период и частота простого гармонического осциллятора
Период времени T, необходимый для одного полного колебания массы на пружине, определяется как:
T=2\pi \sqrt{\frac{m}{k}}
Аналогично, частота f, или количество колебаний в единицу времени (обычно в секунду, даже если это десятичное число) определяется обратной величиной этого выражения, которая равна:
f = \ frac {1} {2 \ pi} \ sqrt {\ frac { k}{m}}
Таким образом, период и частота зависят от массы объекта, а также от константы k.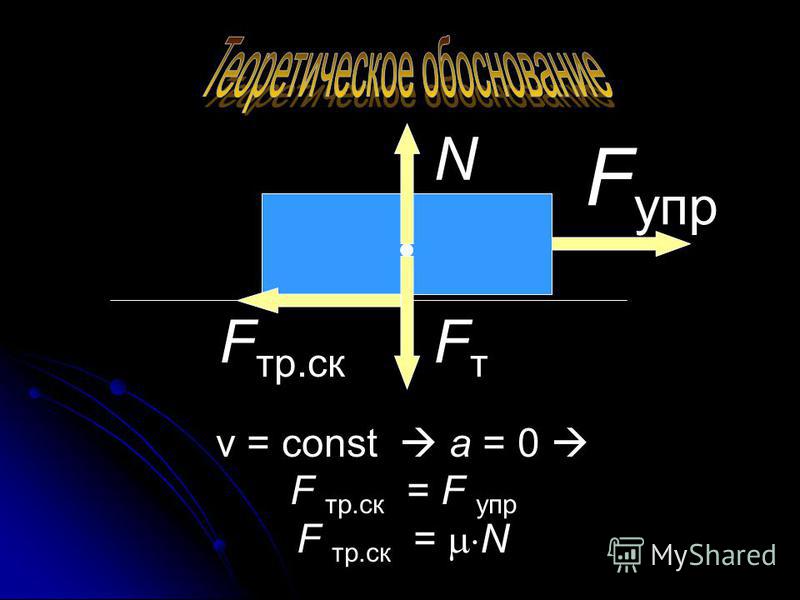
Расчет простого гармонического движения
Можно показать, что значение k для классического простого маятника , в котором масса m подвешена на нити длины L под действием силы тяжести, составляет мг/ L , где г = 9,8 м/с 2 .
Каков период маятника длиной 10 м, подвешенного на массе 100 000 кг?
С заменой k = мг/л приведенное выше выражение для T принимает вид:
T=2\pi \sqrt{\frac{L}{g}}
Где L = 10. Таким образом, период T равен 6,35 с, а не зависит от массы, что исключается из уравнения. (Конечно, для того, чтобы выдержать натяжение этого маятника, потребуется очень прочная струна!)
Как сделать блок для детей
••• Дейл Дэвидсон/Demand Media
Обновлено 24 апреля 2017 г.
Кэрри Perles
Может быть, вы изучаете простые механизмы или просто интересуетесь их работой. В любом случае, отличный способ получить практический опыт работы с простыми машинами — это построить собственный шкив. Вы можете использовать этот блок в качестве простого научного эксперимента, связанного с силами, или вы можете просто построить его, чтобы узнать, как работает блок.
В любом случае, отличный способ получить практический опыт работы с простыми машинами — это построить собственный шкив. Вы можете использовать этот блок в качестве простого научного эксперимента, связанного с силами, или вы можете просто построить его, чтобы узнать, как работает блок.
- Проводной режущий резак
- Wire Hanger
- Пустая капля из нити
- Строка
- Вес (например, книга или игрушка)
- Spring Scale (опциозно делаете шкив в классе, рассмотрите возможность использования флагштока в качестве якоря для вашего шкива. Если якоря нет, попросите одного человека держать верхнюю часть вешалки, а другого тянуть за конец веревки.

••• Dale Davidson/Demand Media
С помощью кусачек обрежьте нижнюю часть проволочной подвески прямо по центру.
••• Дейл Дэвидсон/Demand Media
Наденьте пустую катушку ниток на один из отрезанных концов проволоки. Затем вставьте другой отрезанный конец в катушку с противоположной стороны. Когда катушка надежно закреплена с обеих сторон проволочной подвески, согните отрезанные концы вниз, чтобы катушка осталась на месте.
••• Дейл Дэвидсон/Demand Media
Подвесьте вешалку на вешалку, крючок или другой выступ на стене.
••• Dale Davidson/Demand Media
Привяжите один конец веревки к грузу и наденьте другой конец веревки на катушку. Веревка должна быть примерно в два раза длиннее, чем расстояние от вешалки до пола.
••• Дейл Дэвидсон/Demand Media
Потяните за свободный конец веревки, чтобы поднять вес. Если вы пытаетесь продемонстрировать назначение простых механизмов, используйте пружинные весы, чтобы измерить силу, которую вы прилагаете, чтобы поднять книгу с помощью шкива. (Для этого привяжите свободную нить к одному концу пружинной шкалы и потяните за другой. Проверьте показания на боковой части пружинной шкалы, чтобы узнать силу, которую вы прикладываете.) Затем сравните ее с силой, которую вы прикладываете к поднимите книгу напрямую, используя только веревку.


 Все правила по сольфеджио
Все правила по сольфеджио
 В силу аддитивности момента инерции, под в выражении (3) понимается суммарный момент инерции кольца, диска и вала. Тогда при движении груза вниз до полного разматыванию нити на длину можно записать: .
В силу аддитивности момента инерции, под в выражении (3) понимается суммарный момент инерции кольца, диска и вала. Тогда при движении груза вниз до полного разматыванию нити на длину можно записать: . Тогда закон сохранения энергии при движении рассмотренной системы будет иметь вид
Тогда закон сохранения энергии при движении рассмотренной системы будет иметь вид Зафиксировав в опытах одновременно и высоту подъема груза , можно определить момент сил трения , используя соотношение (6).
Зафиксировав в опытах одновременно и высоту подъема груза , можно определить момент сил трения , используя соотношение (6).
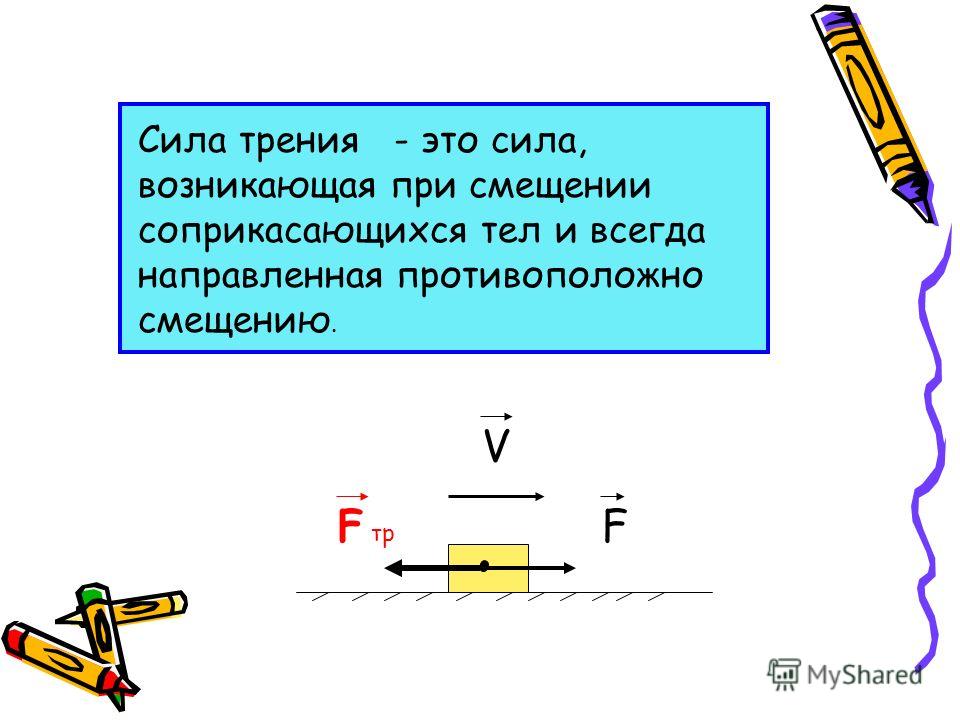 Определить момент инерции кольца без учета сил трения и сравнить результаты.
Определить момент инерции кольца без учета сил трения и сравнить результаты.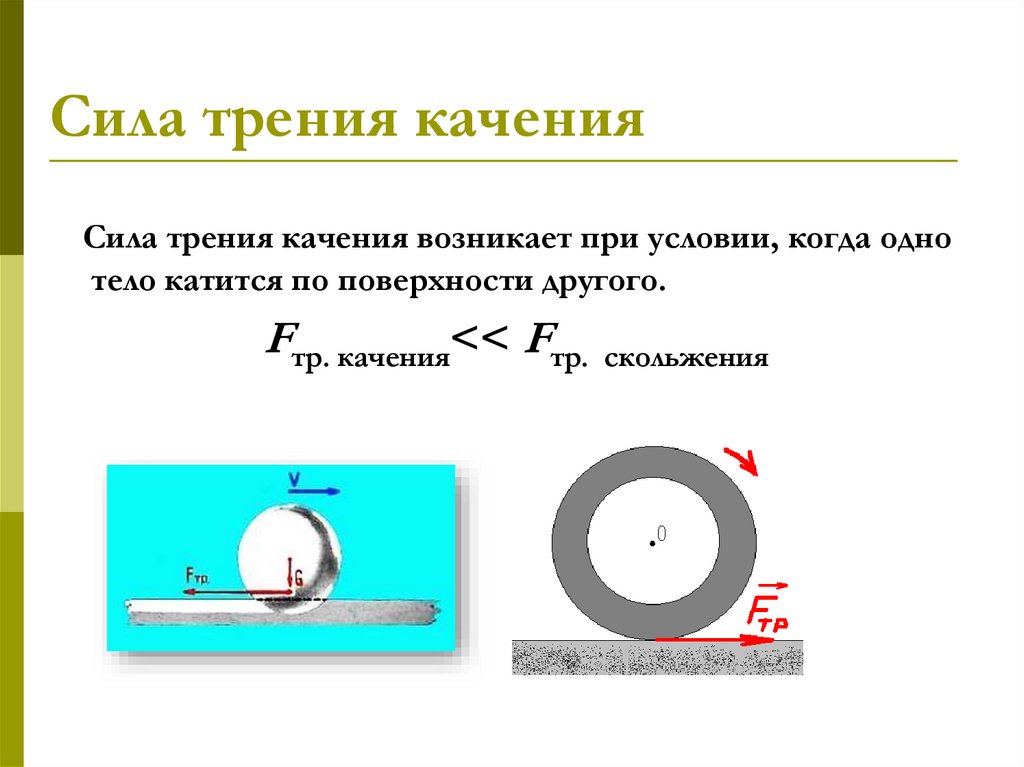 Выведите расчетную формулу для момента инерции махового колеса. Какие законы при этом употребятся?
Выведите расчетную формулу для момента инерции махового колеса. Какие законы при этом употребятся? su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)