Момент силы, условия равновесия рычага, правило, применение рычагов
- Устройство и виды рычагов
- Момент силы
- Правило моментов для двух сил
- Правило моментов для нескольких сил
- Применение рычагов в быту и технике
- Задачи
- Лабораторная работа №9. Проверка условия равновесия рычага
п.1. Устройство и виды рычагов
| Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры. Рычаг состоит из перекладины и опоры. Назначение рычага – получить выигрыш в силе или расстоянии. |
В зависимости от взаимного расположения точки опоры и нагрузки различают три вида рычагов.
| Рычаг 1-го рода Опора располагается между точками приложения сил Даёт выигрыш в силе | Рычаг 2-го рода Точки приложения сил располагаются по одну сторону от опоры, нагрузка приложена между точкой опоры и точкой приложения силы Даёт выигрыш в силе |
| Рычаг 3-го рода Точки приложения сил располагаются по одну сторону от опоры, усилие приложено между точкой опоры и нагрузкой. Проигрыш в силе – выигрыш в расстоянии | |
п.2. Момент силы
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Чтобы найти плечо силы, нужно из точки опоры провести перпендикуляр на линию действия силы.
На рисунке \(l_1\) – плечо силы \(F_1,\ l_2\) — плечо силы \(F_2\).
Силы вращают рычаг вокруг точки опоры – по часовой или против часовой стрелки.
Ось вращения проходит через точку опоры перпендикулярно плоскости вращения.
На рисунке сила \(F_1\) вращает рычаг против часовой стрелки, а сила \(F_2\) — по часовой стрелке.
Момент силы – это произведение силы, вращающей тело, на её плечо. $$ M=Fl $$ В системе СИ единица измерения момента силы — Н·м.
Момент силы определяется не для всего тела, а для некоторой его точки, удалённой от центра (оси) вращения. Эта величина имеет смысл только для вращающихся тел.
п.3. Правило моментов для двух сил
Правило моментов для двух сил
| $$ F_1l_1=F_2l_2 $$ |
п.4. Правило моментов для нескольких сил
Правило моментов для нескольких сил
Рычаг находится в равновесии, если сумма моментов всех сил, вращающих его по ходу часовой стрелки, равен сумме моментов всех сил, вращающих его против хода часовой стрелки.
Например:
| Силы \(F_1,\ F_2,\ F_3\) вращают рычаг против часовой стрелки, а сила \(F_4\) — по часовой стрелке. Поэтому: $$ F_1l_1+F_2l_2+F_3l_3=F_4l_4 $$ |
п.5. Применение рычагов в быту и технике
Рычаги первого рода
Весы Предмет, вес которого нужно измерить, — это нагрузка, а гиря создает усилие. Они равны, так как находятся на одном расстоянии от точки опоры. | Рычажные весы Точка опоры смещена относительно центра. Грузило передвигается по основанию, пока не уравновесит взвешиваемый объект. |
Гвоздодёр Усилие ручки увеличивается плечом и вытаскивает гвоздь. Нагрузкой здесь является сопротивление гвоздя. | Ручная тележка Небольшое усилие, прикладываемое к ручкам тележки, позволяет поднимать тяжелый груз. |
Плоскогубцы Составной рычаг, пара простых рычагов, соединенных в точке опоры.  Нагрузка — сопротивление предмета захвату инструментом. Нагрузка — сопротивление предмета захвату инструментом. | Ножницы Составной рычаг первого рода, развивают мощное режущее действие очень близко к месту крепления. Нагрузка — сопротивление материала лезвиям. |
Рычаги второго рода
Тачка Небольшое усилие, приложенное к ручкам тачки, поднимает тяжелый груз, расположенный ближе к колесу. | Открывалка Давление на ручку преодолевает сопротивление крышки бутылки. | Щипцы для орехов Составной рычаг второго рода. Нагрузка — сопротивление скорлупы. |
Рычаги третьего рода
Молоток Точка опоры — плечевой сустав (рука — продолжение рукоятки), а нагрузка — сопротивление дерева. Во время удара по гвоздю головка молотка двигается быстрее, чем рука с рукояткой. | Удочка Одна рука прикладывает усилие для движения удочки, вторая становится точкой опоры.  Нагрузка — это вес рыбы, который поднимается на большую высоту легким движением руки. Нагрузка — это вес рыбы, который поднимается на большую высоту легким движением руки. |
Пинцет Составной рычаг третьего рода. На кончиках пинцета усилие меньше, чем со стороны пальцев, так что можно захватывать хрупкие предметы. Нагрузка — сопротивление предмета. | |
п.6. Задачи
Задача 1. Для каждого положения тела укажите плечо силы.
При необходимости достраиваем линию действия силы и опускаем на неё перпендикуляр из точки опоры. Этот перпендикуляр и есть искомое плечо.
Задача 2. Грузы уравновешены на рычаге. Отношение плеч рычага 1:5. Масса большего груза 2,5 кг. Найдите массу меньшего груза.
Дано:
\(\frac{l_1}{l_2}=\frac 15\)
\(m_1=2,5\ \text{кг}\)
__________________
\(m_2-?\)
По правилу моментов \begin{gather*} F_1l_1=F_2l_2 \end{gather*} На обоих концах рычага действуют силы тяжести: $$ F_1=m_1g,\ \ F_2=m_2g $$ Получаем: \begin{gather*} m_1gl_1=m_2gl_2\\[7pt] m_2=\frac{m_1l_1}{l_2} \end{gather*} Подставляем: $$ m_2=2,5\cdot \frac 15=0,5\ (\text{кг}) $$ Ответ: 0,5 кг
Задача 3. На концах рычага действуют силы 15 Н и 60 Н, направленные вниз. Рычаг находится в равновесии. Расстояние между точками приложения сил 1 м. Где расположена точка опоры?
На концах рычага действуют силы 15 Н и 60 Н, направленные вниз. Рычаг находится в равновесии. Расстояние между точками приложения сил 1 м. Где расположена точка опоры?
Дано:
\(F_1=15\ \text{Н}\)
\(F_2=60\ \text{Н}\)
\(l_1+l_2=1\ \text{м}\)
__________________
\(l_1,\ l_2-?\)
По правилу моментов \begin{gather*} F_1l_1=F_2l_2. \end{gather*} Получаем систему уравнений \begin{gather*} \left\{ \begin{array}{l l} 15l_1=60l_2 \\ l_1+l_2=1 \end{array} \right. \Rightarrow \left\{ \begin{array}{l l} l_1=4l_2 \\ l_1+l_2=1 \end{array} \right. \Rightarrow \left\{ \begin{array}{l l} l_1=4l_2 \\ 4l_2+l_2=1 \end{array} \right. \Rightarrow \\[7pt] \Rightarrow \left\{ \begin{array}{l l} l_1=4l_2 \\ 5l_2=1 \end{array} \right. \Rightarrow \left\{ \begin{array}{l l} l_1=0,8 \\ l_2=0,2 \end{array} \right. \end{gather*} Ответ: 0,8 м от точки приложения первой силы и 0,2 м от точки приложения второй силы.
Задача 4*. К балке, расположенной на двух опорах А и В подвешен груз массой 500 кг. 2\)
2\)
\(OB=4OA\)
__________________
\(F_A,\ F_B-?\)
Сила тяжести \(F_{\text{т}}=mg\), направленная вниз, уравновешивается силами реакции опор \(F_A\) и \(F_B\), направленными вверх. \begin{gather*} F_A+F_B=mg \end{gather*} По правилу моментов при равновесии \begin{gather*} F_A\cdot OA=F_B\cdot OB=F_B\cdot 4OA\Rightarrow F_A=4F_B \\[7pt] F_A+F_B=5F_B=mg\Rightarrow F_B=\frac{mg}{5} \end{gather*} Получаем: \begin{gather*} F_B=\frac{500\cdot 10}{5}=1000\ \text{Н}=1\ \text{кН},\ \ F_A=4\cdot 100=4000\ \text{Н}=4\ \text{кН} \end{gather*} Ответ: 4 кН и 1 кН
п.7. Лабораторная работа №9. Проверка условия равновесия рычага
Цель работы
Исследовать условия равновесия рычага под действием двух параллельных сил.
Теоретические сведения
Рычаг – это твёрдое тело, которое может вращаться вокруг неподвижной опоры.
В работе используется рычаг 1-го рода, в котором опора располагается между точками приложения сил.
Плечо силы – это кратчайшее расстояние между точкой опоры и прямой, вдоль которой сила действует на рычаг.
Момент силы – это произведение силы, вращающей тело, на её плечо: \(M=Fl\).
Правило моментов для двух сил
Рычаг находится в равновесии под действием двух сил, если момент силы, вращающей его по ходу часовой стрелки, равен моменту силы, вращающей его против хода часовой стрелки.
| \begin{gather*} M_1=M_2\\[7pt] F_1l_1=F_2l_2 \end{gather*} |
В работе используется лабораторный рычаг с отверстиями диаметром 4 мм, находящимися на расстоянии 5 см друг от друга. Отверстий нечетное количество; центральное отверстие (центр тяжести) используется для подвеса рычага на штативе в положении равновесия. Абсолютную погрешность определения плеча на данном рычаге принимаем равной половине диаметра отверстия $$ \Delta l=\frac D2=2\ \text{мм} $$
Для измерения веса груза используется динамометр с ценой деления $$ d=0,1\ \text{Н}. $$
$$
Абсолютная погрешность определения веса $$ \Delta_F=\frac d2=0,05\ \text{Н}. $$
Относительные погрешности измерений: $$ \delta_l=\frac{\Delta_l}{l},\ \ \delta_F=\frac{\Delta_F}{F},\ \ \delta_M=\delta_l+\delta_F $$
Абсолютная погрешность определения момента силы $$ \Delta_M=M\cdot \delta_M $$
Погрешности определения отношений сил и плечей: \begin{gather*} r_F=\frac{F_1}{F_2},\ \ \delta_{rF}=\frac{\Delta_F}{F_1}+\frac{\Delta_F}{F_2},\ \ \Delta_{rF}=\frac{F_1}{F_2}\cdot \delta_{rF}\\[7pt] r_l=\frac{l_2}{l_1},\ \ \delta_{rF}=\delta_{rl}\frac{\Delta_l}{l_1}+\frac{\Delta_l}{l_2},\ \ \Delta_{rl}=\frac{l_2}{l_1}\cdot \delta_{rl} \end{gather*}
Приборы и материалы
Лабораторный рычаг, штатив, стержень, динамометр, набор грузов.
Ход работы
1. Закрепите стержень в штативе, наденьте на него рычаг. Если стержень проходит через центральное отверстие рычага, он находится в равновесии.
3. Подвесьте грузы слева от оси вращения рычага на расстоянии 5 см.
4. С помощью динамометра определите, какую силу нужно приложить на расстоянии 15 см справа от оси вращения, чтобы удерживать рычаг в равновесии.
5. Как направлены в этом случае силы, действующие на рычаг? Запишите длину плеч этих сил.
6. Найдите моменты сил \(M_1\) и \(M_2\), их относительные и абсолютные погрешности.
7. Вычислите отношение сил \(\frac{F_1}{F_2}\) и плеч \(\frac{l_2}{l_1}\) для этого случая, погрешности их определения.
Результаты измерений и вычислений
| \(F_1,\ \text{Н}\) | \(l_1,\ \text{см}\) | \(F_2,\ \text{Н}\) | \(l_2,\ \text{см}\) | \(F_1/F_2\) | \(l_2/l_1\) |
| 2,9 | 5 | 1,0 | 15 | 2,9 | 3,0 |
Погрешности прямых измерений: $$ \Delta_l=2\ \text{мм}=0,2\ \text{см},\ \ \Delta_F=0,05\ \text{Н} $$ Найдем моменты сил и погрешности вычислений: \begin{gather*} M_1=F_1\cdot l_1=2,9\cdot 5=14,5\ (\text{Н}\cdot \text{м})\\[7pt] \delta_{M1}=\frac{\Delta_l}{l_1}+\frac{\Delta_F}{F_1}=\frac{0,2}{5}+\frac{0,05}{2,9}\approx 0,04+0,017=0,057=5,7\text{%} \\[7pt] \Delta_{M1}=M_1\cdot \delta_{M1}=14,5\cdot 0,057\approx 0,8\ (\text{Н}\cdot \text{м})\\[7pt] M_1=(14,5\pm 0,8)\ \text{Н}\cdot \text{м}\\[7pt] \\[7pt] M_2=F_2\cdot l_2=1,0\cdot 15=15,0\ (\text{Н}\cdot \text{м})\\[7pt] \delta_{M2}=\frac{\Delta_l}{l_2}+\frac{\Delta_F}{F_2}=\frac{0,2}{15}+\frac{0,05}{1,0}\approx 0,013+0,05=0,063=6,3 \text{%} \\[7pt] \Delta_{M2}=M_2\cdot \delta_{M2}=15,0\cdot 0,063\approx 0,9\ (\text{Н}\cdot \text{м})\\[7pt] M_2=(15,0\pm 0,9)\ \text{Н}\cdot \text{м} \end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ M_1=M_2 $$
Погрешность вычислений для \(\frac{F_1}{F_2}\) \begin{gather*} \delta_{rF}=\frac{\Delta_F}{F_1}+\frac{\Delta_F}{F_2}=\frac{0,05}{2,9}+\frac{0,05}{1,0}\approx 0,017+0,05=0,067=6,7\text{%}\\[7pt] \Delta_{rF}=\frac{F_1}{F_2}\cdot \delta_{rF}=2,9\cdot 0,067\approx 0,2\\[7pt] \frac{F_1}{F_2}=2,9\pm 0,2 \end{gather*}
Погрешность вычислений для \(\frac{l_2}{l_1}\) \begin{gather*} \delta_{rl}=\frac{\Delta_l}{l_1}+\frac{\Delta_l}{l_2}=\frac{0,2}{5}+\frac{0,2}{15}\approx 0,04+0,013=0,053=5,3\text{%}\\[7pt] \Delta_{rl}=\frac{l_2}{l_1}\cdot \delta_{rl}=3,0\cdot 0,053\approx 0,2\\[7pt] \frac{l_2}{l_1}=3,0\pm 0,2 \end{gather*} Таким образом, с учетом вычисленных погрешностей: $$ \frac{F_2}{F_2}=\frac{l_2}{l_1} $$
Выводы
На основании проделанной работы можно сделать следующие выводы.
Моменты сил, приложенных слева и справа от оси вращения рычага, равны $$ M_1=(14,5\pm 0,8)\ \text{Н}\cdot \text{м},\ \ M_2=(15,0\pm 0,9)\ \text{Н}\cdot \text{м} $$ Таким образом, с учетом вычисленных погрешностей, \(M_1=M_2\) — правило моментов выполняется.
Отношения сил и плечей равны \begin{gather*} \frac{F_1}{F_2}=2,9\pm 0,2,\ \ \frac{l_2}{l_1}=3,0\pm 0,2 \end{gather*}
Таким образом, с учетом вычисленных погрешностей \(\frac{F_1}{F_2}=\frac{l_2}{l_1}\) — правило отношений выполняется.
Эксперименты подтвердили условие равновесия рычага.
Рейтинг пользователей
за неделю
- за неделю
- один месяц
- три месяца
Помогай другим
Отвечай на вопросы и получай ценные призы каждую неделю
См. подробности
Задачи с рычагами (момент силы)
Репетитор
по физике
916 478 1032
Репетитор
по алгебре
916 478 1032
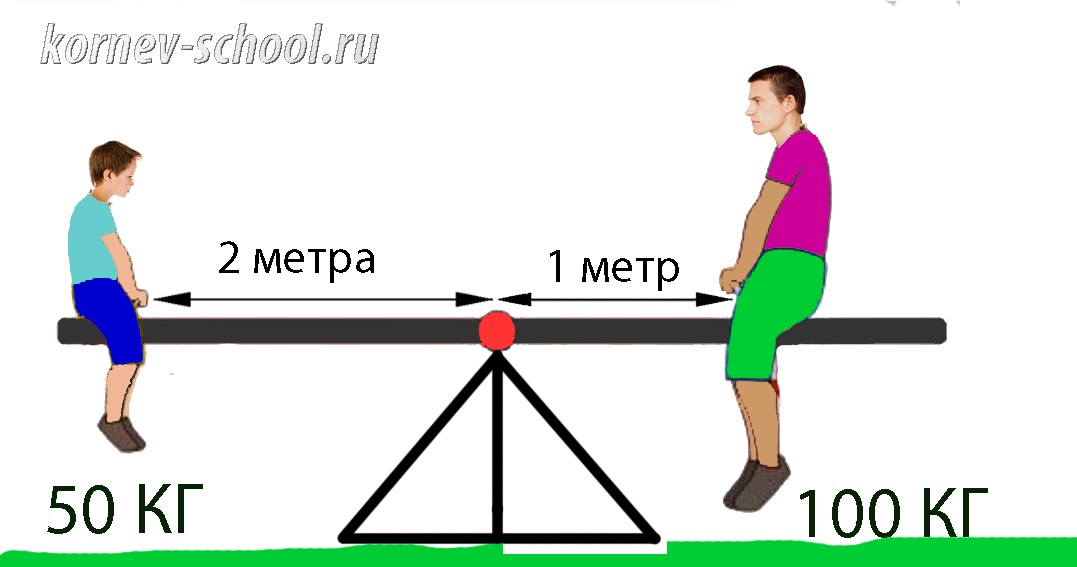
Почему легкий мальчик и взрослый тяжелый мужчина уравновешивают друг друга?
Условие равновесия рычага:
\(F_1l_1=F_2l_2\)
Для решения простейших задач на рычаги достаточно того, что написано выше
Ниже будет приведено подробное объяснение.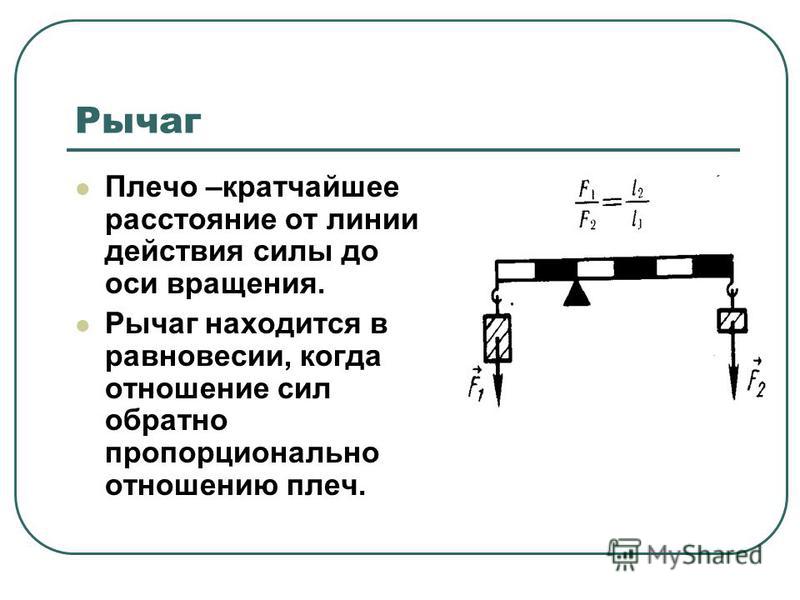
Репетитор по физике
8 916 478 10 32
Плечом силы называют кратчайшее расстояние между линией действия силы и точкой опоры.
\( l_1 \) — плечо силы \(F_1 \;\;\;\;\; \) \( \;\;\; l_2 \) — плечо силы \(F_2 \)
Моментом силы называют произведение (умножение) силы на ее плечо:
\(M=Fl\) .
Момент силы \( F_1 \) пытается закрутить рычаг против часовой стрелки
Момент силы \( F_2 \) пытается закрутить рычаг по часовой стрелке
Условие равновесия:
Рычаг будет находиться в равновесии если сумма моментов, закручивающих его по часовой стрелке будет равна сумме моментов, закручивающих его против часовой стрелки.
На нашем рисунке один момент закручивает рычаг по часовой,а другой против часовой стрелки, по этому
условие равновесия для нашего случая выглядит вот так:
\(M_1=M_2 \)
\(F_1l_1=F_2l_2\)
Задача 1.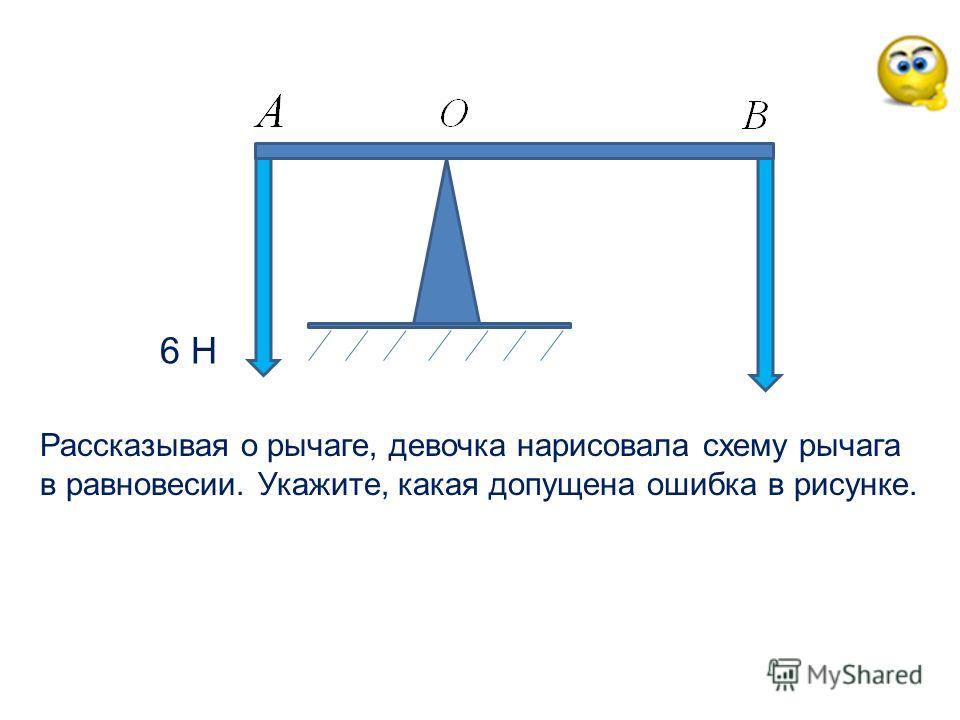
Рычаг изображенный на рисунке находится в равновесии.
Сила \(F_2=100Н \) , плечо этой силы \(l_2=2м\).
Найти силу \(F_1\) , если ее плечо \(l_1=4м\).
Показать ответ
Показать решение
Видеорешение
Ответ: \( F_1=50Н \)
Первое решение приведено для тех, кому хочется попроще:
Запишем условие равновесия рычага:
Дано:
\( F_2=100Н \)
\( l_2=2м \)
\(l_1=4м\)
\(F_1-?\)
\(F_1l_1=F_2l_2\)
\(F_1 \cdot 4 =100 \cdot 2 \)
\(F_1 \cdot 4 =200 \)
\(F_1=200:4 =50 Н \)
Второе решение в общем виде (рекомендуется): Запишем условие равновесия рычага: \(F_1l_1=F_2l_2\) \(F_1=\dfrac{F_2l_2}{l_1} \) \(F_1=\dfrac{100Н \cdot 2м}{4м}=50Н \) Ответ: \(F_1=50Н \)
Задача 2.
Рычаг изображенный на рисунке находится в равновесии.
Сила \(F_2=6Н \) , плечо этой силы \(l_2=0,8м\).
Найти силу \(F_1\) , если ее плечо \(l_1=1,6м\).
Показать ответ
Показать решение
Видеорешение
Ответ: \( F_1=3Н \)
Первое решение приведено для тех, кому хочется попроще:
Запишем условие равновесия рычага:
Дано:
\( F_2=6Н \)
\( l_2=0,8м \)
\(l_1=1,6м\)
\(F_1-?\)
\(F_1l_1=F_2l_2\)
\(F_1 \cdot 1,6 =6 \cdot 0,8 \)
\(F_1 \cdot 1,6 =4,8 \)
\(F_1=4,8:1,6 =3 Н \)
Второе решение в общем виде (рекомендуется): Запишем условие равновесия рычага: \(F_1l_1=F_2l_2\) \(F_1=\dfrac{F_2l_2}{l_1} \) \(F_1=\dfrac{6Н \cdot 0,8м}{1,6м}=3Н \) Ответ: \(F_1=3Н \)
Задача 3.
Рычаг изображенный на рисунке находится в равновесии.
Сила \(F_1=70Н \) , плечо этой силы \(l_1=6м\).
Найти силу \(F_2\) , если ее плечо \(l_2=1,5м\).
Показать ответ
Показать решение
Видеорешение
Ответ: \( F_2=280Н \)
Первое решение приведено для тех, кому хочется попроще:
Запишем условие равновесия рычага:
Дано:
\( F_1=70Н \)
\( l_1=6м \)
\(l_2=1,5м\)
\(F_2-?\)
\(F_1l_1=F_2l_2\)
\(70 \cdot 6 =F_2 \cdot 1,5 \)
\(420 =F_2 \cdot 1,5 \)
\(F_2 \cdot 1,5 =420\)
\(F_2 =420:1,5\)
\(F_2 =280 Н\)
Второе решение в общем виде (рекомендуется): \(F_1l_1=F_2l_2\) \(F_2=\dfrac{F_1l_1}{l_2} \) \(F_2=\dfrac{70Н \cdot 6м}{1,5м}=280Н \) Ответ: \(F_2=280Н \)
Задача 5.
Отец и сын сидят на качелях, при этом они оба не касаются земли и качели находятся в равновесии.
Масса отца составляет 80 килограмм, при этом он сидит на расстоянии \(l_2=0,9 м \) от точки опоры качелей.
Найти массу сына, если он сидит на расстоянии \(l_1=1,8 м \) от точки опоры качелей.
Показать ответ
Показать решение
Видеорешение
Ответ: \( m_1=40 кг \)
Первое решение приведено для тех, кому хочется попроще:
Запишем условие равновесия рычага:
Дано:
\( m_2=80 кг \)
\( l_2=0,9 м \)
\(l_1=1,8м\)
\(m_1-?\)
\(F_1l_1=F_2l_2\)
\(m_1gl_1=m_2gl_2 \)
\(m_1 \cdot 10 \cdot 1,8 =80 \cdot 10 \cdot 0,9 \)
\(18m_1 =720 \)
\(m_1 =720:18 \)
\(m_1 =40 кг \)
Второе решение в общем виде (рекомендуется): Запишем условие равновесия рычага: \(F_1l_1=F_2l_2\) \(m_1gl_1=m_2gl_2 \) \(m_1l_1=m_2l_2 \) \(m_1=\dfrac{m_2l_2}{l_1} \) \(m_1=\dfrac{80кг \cdot 0,9м}{1,8м}=40 кг \) Ответ: \(m_1=40 кг \)
Задача 6.
Отец и сын сидят на качелях, при этом они оба не касаются земли и качели находятся в равновесии.
Масса отца составляет 90 килограмм, при этом он сидит на расстоянии \(l_2=0,7 м \) от точки опоры качелей.
На каком расстоянии от точки опоры сидит ребенок, если его масса составляет 30 килограмм ?
Показать ответ
Показать решение
Видеорешение
Ответ: \( l_1=2,1 м \)
Первое решение приведено для тех, кому хочется попроще:
Запишем условие равновесия рычага:
Дано:
\( m_2=90 кг \)
\( l_2=0,7 м \)
\( m_1=30 кг \)
\(l_1-?\)
\(F_1l_1=F_2l_2\)
\(m_1gl_1=m_2gl_2 \)
\(30 \cdot 10 \cdot l_1 =90 \cdot 10 \cdot 0,7 \)
\(300 l_1 =630 \)
\(l_1 =630:30 \)
\(l_1=2,1 м\)
Второе решение в общем виде (рекомендуется): Запишем условие равновесия рычага: \(F_1l_1=F_2l_2\) \(m_1gl_1=m_2gl_2 \) \(m_1l_1=m_2l_2 \) \(l_1=\dfrac{m_2l_2}{m_1} \) \(l_1=\dfrac{90кг \cdot 0,7м}{30кг}= 2,1 м\) Ответ: \(l_1=2,1 м \)
Момент силы.
 Условие равновесия рычага » Народна Освіта
Условие равновесия рычага » Народна ОсвітаПроведите опыт. Возьмите длинную линейку и разместите ее на опоре так, как показано на рисунке. Ближе к опоре положите (или подвесьте) любой груз, а рукой нажмите на другой конец линейки (подальше от опоры), — вы легко удержите груз. А теперь передвиньте груз дальше от опоры, а руку положите ближе к ней. Почему в этом случае вам приходится прилагать больше усилий, ведь груз остался тем же? Вернитесь к этому вопросу после изучения материала этого параграфа, и вы легко сможете на него ответить.
используем рычаг
Давно известно, что тяжелое тело поднять значительно легче, если просунуть под него крепкий стержень — лом. В данном случае лом играет роль простого механизма — рычага.
Рычаг — это твердое тело, которое может вращаться вокруг неподвижной оси — оси вращения.
Лом, лопата (рис. 34.1), линейка, которой мы удерживали груз во время опыта, — все это примеры рычагов.
Рычаг — простейший механизм, которой люди пользуются тысячи лет. Изображение рычага можно найти на скалах и в пещерах, на стенах древних храмов и в папирусах. И сегодня применение рычага мы наблюдаем повсюду (рис. 34.2). Чаще всего в качестве рычага используют длинный стрежень с закрепленной осью вращения.
Изображение рычага можно найти на скалах и в пещерах, на стенах древних храмов и в папирусах. И сегодня применение рычага мы наблюдаем повсюду (рис. 34.2). Чаще всего в качестве рычага используют длинный стрежень с закрепленной осью вращения.
Выясняем условие равновесия рычага
Выясним, при каком условии рычаг находится в равновесии. Для этого воспользуемся лабораторным рычагом. С помощью проволочных крючков будем подвешивать к рычагу грузы. Передвигая крючки, будем изменять плечи сил, действующих на рычаг (рис. 34.3).
Плечо силы — это наименьшее расстояние от оси вращения рычага до линии, вдоль которой сила действует на рычаг.
Например, подвесим слева от оси вращения на расстоянии d1 = 30 см груз весом Р1 = F1 = 1 Н. Справа от оси вращения подвесим грузы общим весом Р2 = F2 = 3 Н и будем передвигать этот крючок, пока не добьемся равновесия рычага. Это произойдет, когда грузы общим весом 3 Н окажутся на расстоянии d2 = 10 см от оси вращения.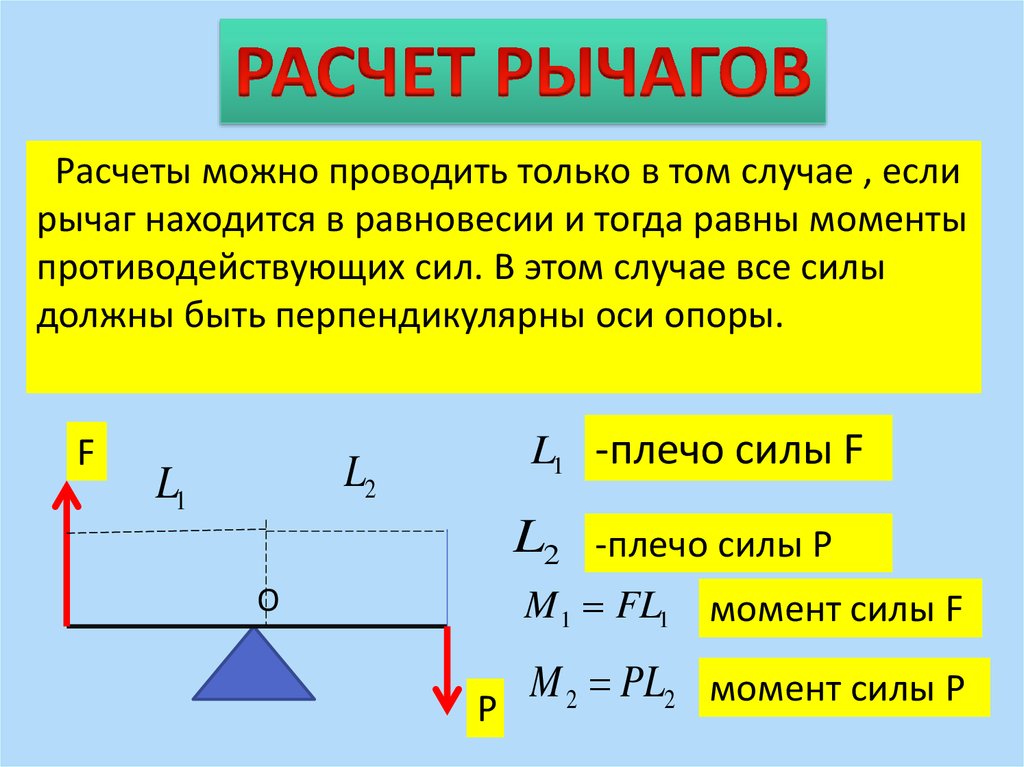 ), поэтому, когда человек с помощью рычага поднимает тяжелое тело даже на небольшую высоту, рука преодолевает значительное расстояние.
), поэтому, когда человек с помощью рычага поднимает тяжелое тело даже на небольшую высоту, рука преодолевает значительное расстояние.
И наоборот, действуя на короткое плечо рычага, мы проиграем в силе, но во столько же раз выиграем в расстоянии (рис. 34.5, б).
Рассмотрите рис. 34.6. Какой рычаг применяют для выигрыша в силе, а какой — для выигрыша в расстоянии?
Знакомимся с моментом силы
Для характеристики способности силы вращать твердое тело введена физическая величина момент силы.
Момент силы — физическая величина, равная произведению силы, действующей на тело, на плечо этой силы:
где M — момент силы; F — значение силы; d — плечо силы.
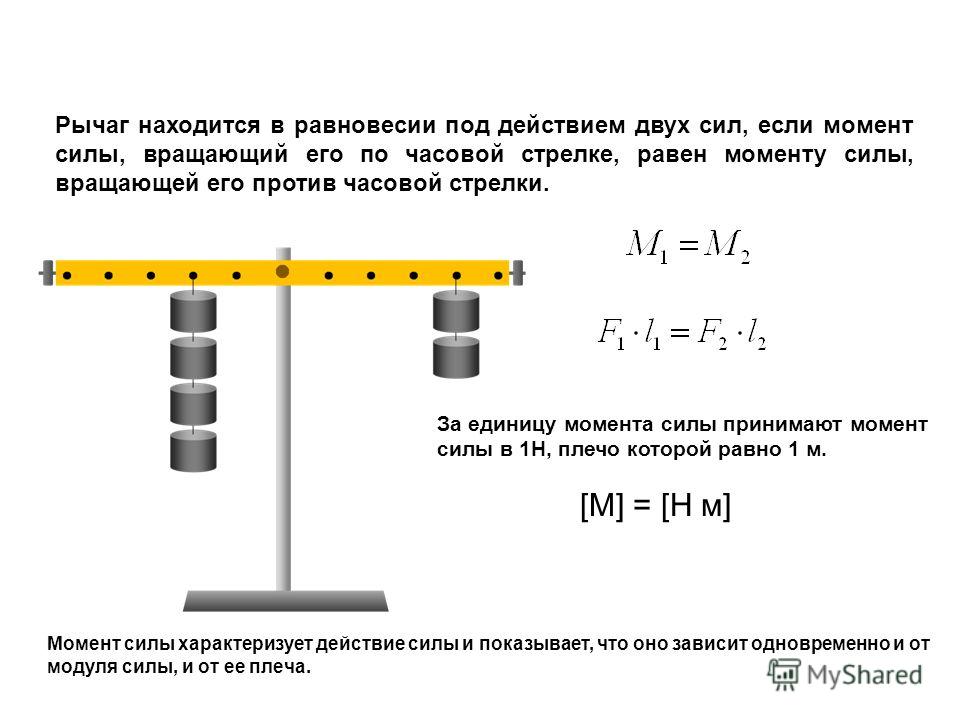
Единица момента силы в СИ — ньютонметр:
Сила 1 Н создает момент силы 1 Н-м, если плечо силы равно 1 м.
Открываем правило моментов
Воспользуемся свойством пропорции и запишем правило рычага
Поскольку произведение силы F на плечо d силы — это момент силы (М), получим:
Итак, условие равновесия рычага при действии двух вращающих сил можно сформулировать следующим образом: рычаг находится в равновесии, если момент силы, вращающей рычаг против хода часовой стрелки, равен моменту силы, вращающей рычаг по ходу часовой стрелки.
Чаще всего на рычаг действуют более двух сил. В общем случае условие равновесия рычага (правило моментов) формулируется так:
Рычаг находится в равновесии, если сумма моментов сил, вращающих рычаг против хода часовой стрелки, равен сумме моментов сил, вращающих рычаг по ходу часовой стрелки.
Например, когда на плечи рычага действуют три силы (рис. 34.7), условие его равновесия будет выглядеть так: М1 = М2 + М3.
Обратите внимание!
1. На рычаг (рис. 34.7) кроме сил Р1, Р2 и Р3, пытающихся его вращать, действуют еще сила тяжести Ртяж (рычаг имеет массу) и сила нормальной реакции опоры N. Но плечи этих сил, а следовательно, их моменты равны нулю, поэтому данные силы не влияют на вращение рычага.
2. Рычаг неподвижен. Это означает, что силы, действующие на рычаг, скомпенсированы: F1 + F2 + F3 + Fтяж = N. Понятно, что силы будут скомпенсированы для любого рычага, который находится в равновесии.
Учимся решать задачи
Задача. Определите массу груза 1 (см. рисунок), если масса груза 2 равна 4 кг. Массой рычага пренебречь.
Анализ физической проблемы. На плечи изображенного на рисунке рычага действуют две силы: вес груза 1 (сила ) и вес груза 2 (сила Е2). Эти силы пытаются вращать рычаг в противоположных направлениях: сила Е1 — против хода часовой стрелки, сила Е2 — по ходу часовой стрелки. Из рисунка видно, что плечи этих сил таковы: d1 = 5а, d2 = 3а, где a — длина одного отрезка. Грузы неподвижны, поэтому вес каждого из них можно определить по формуле: F = mg. Рычаг находится в равновесии, поэтому можем воспользоваться правилом рычага.
Подводим итоги
Рычаг — это твердое тело, которое может вращаться вокруг неподвижной оси.
Плечо силы — кратчайшее расстояние от оси вращения рычага до линии действия силы.
Момент силы — физическая величина, характеризующая вращающее действие силы и равная произведению силы F, вращающей тело, на плечо d этой силы: М = Fd.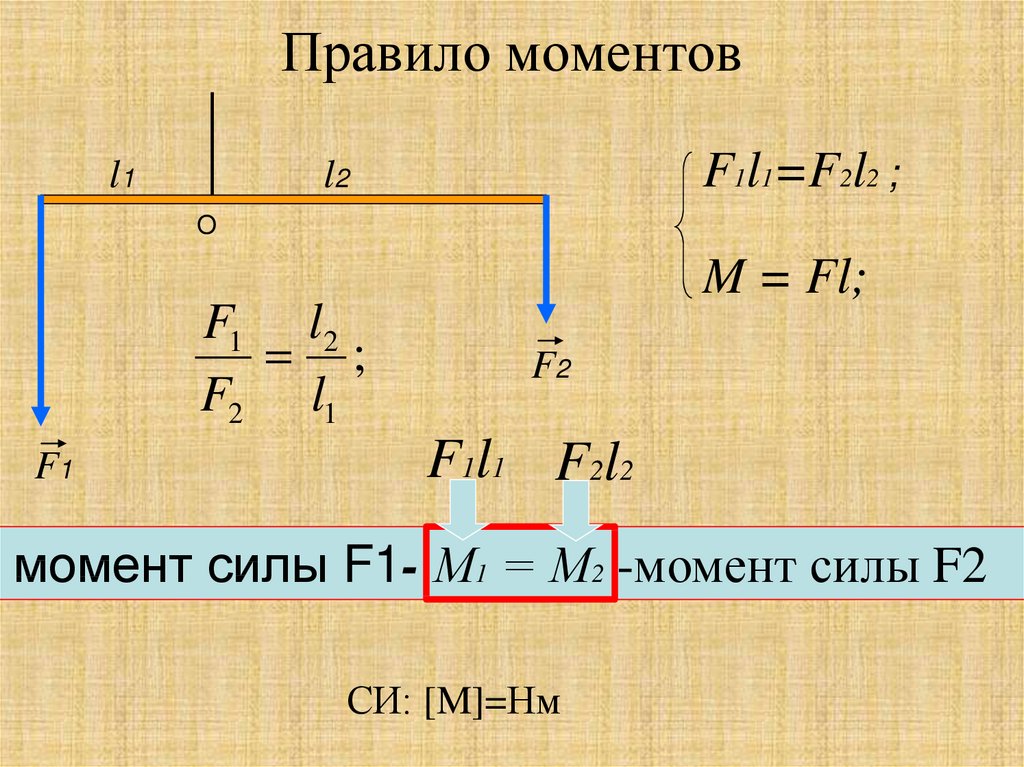
Рычаг находится в равновесии, если сумма моментов сил, вращающих рычаг против хода часовой стрелки, равна сумме моментов сил, вращающих рычаг по ходу часовой стрелки.
‘1. Что такое рычаг? 2. Приведите примеры применения рычага. 3. Дайте определение плеча силы. 4. Каким равенством записывают правило рычага? 5. Всегда ли рычаг применяют для получения выигрыша в силе? Приведите примеры. 6. Дайте определение момента силы. 7. Какова единица момента силы в СИ? 8. Сформулируйте правило моментов.
Упражнение № 34
В заданиях 1-7 массой рычага следует пренебречь.
1. Масса какого человека на рис. 1 больше? Поясните свой ответ.
2. Вес груза 1 равен 90 Н (рис. 2). Определите вес груза 2.
3. Определите массу груза (рис. 3), если сила, действующая на правый конец рычага, равна 40 Н.
4. Общая масса грузов — 48 кг (рис. 4).
Определите массу каждого груза.
5. К концам тонкого однородного стержня длиной 2 м подвешены грузы массами 14 и 26 кг. На каком расстоянии от середины стержня нужно разместить опору, чтобы стержень находился в равновесии?
6. Объясните принцип действия устройств, изображенным хна рис.б.В ыполн и вне-обходимыеизм ерениыы ,определите, какой наибольший выигрыш в силе можно получить с помощью этих устройств.
Объясните принцип действия устройств, изображенным хна рис.б.В ыполн и вне-обходимыеизм ерениыы ,определите, какой наибольший выигрыш в силе можно получить с помощью этих устройств.
7. Масса груза 1 — 10 кг, г руза 2 — 5 кг (рис. 6). Определите массу груза 3. С какой силой рычаг давит на опору?
8. Решите задачу, рассмотренную в § 34, с учетом того, что масса р чага равна 500 г.
9. Воспользуйтесь дополнительными источник ами информации и н айдите сведения о рым агах в теле человека. Составьте задачу, опираясь на полученные сведения, и решите ее.
1. С помощью карандаша и трех монет по 5 копеек измерьте массу линейки. Считайте, что сила тяжести, действующая на линейку, приложена к ее середине. Масса одной пятикопеечной монеты равна 4,3 г.
2. Найдите у себя дома несколько устройств, действие которых основано на условии равновесия рычага (ножницы, пассатижи, гаечный ключ и т. п.). Проведите необходимые измерения и вычисления и определите, какой наибольший выигрыш в силе (или расстоянии) можно получить с помощью этих устройств.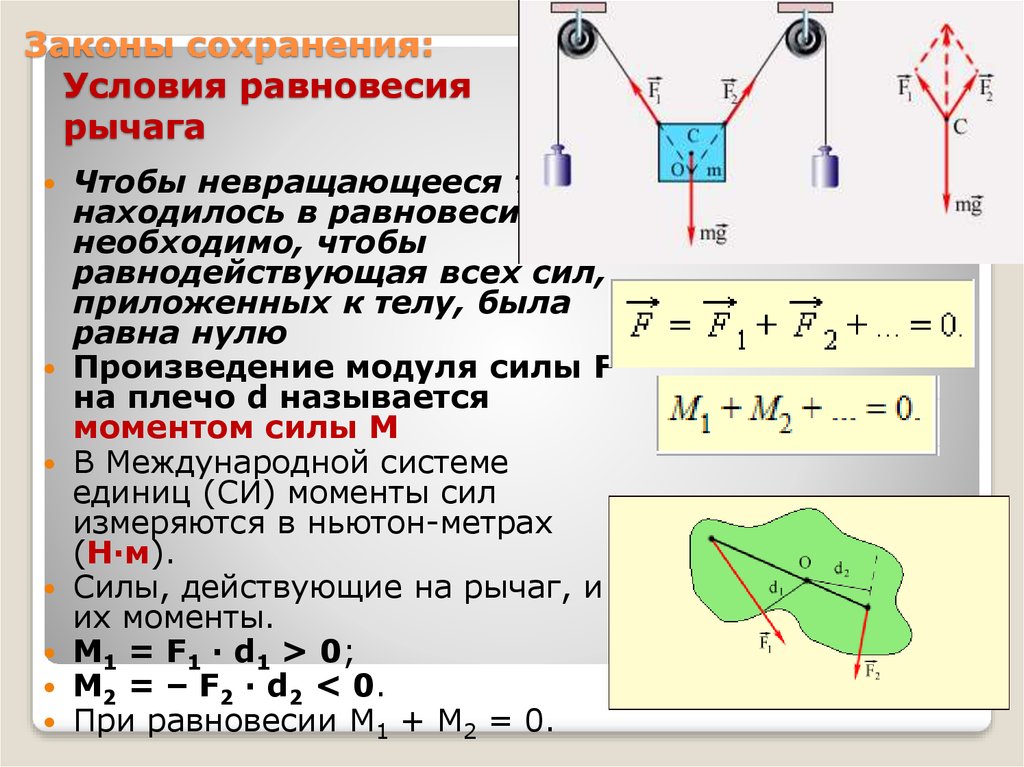
Видеоопыт. Посмотрите видеоролик, воспроизведите опыт и попробуйте его объяснить.
лабораторная работа № 11
тема. Выяснение условия равновесия рычага.
цель: проверить опытным путем, каким должно быть соотношение сил и их плеч, чтобы рычаг находился в равновесии.
оборудование: рычаг; штатив с муфтой и лапкой; набор грузов массой по 100 г; динамометр; ученическая линейка.
указания к работе
Подготовка к эксперименту
1. Прежде чем приступить к выполнению работы, вспомните ответы на следующие вопросы.
1) Что называют рычагом и где применяют рычаги?
2) Что называют плечом силы?
3) Что такое момент силы?
2. Определите цены делений шкал измерительных приборов.
3. Закрепите на лапке штатива рычаг и уравновесьте его с помощью регулировочных гаек.
Эксперимент
Строго соблюдайте инструкцию по безопасности (см. форзац). Результаты измерений сразу заносите в таблицу.
1. С одной стороны от оси вращения рычага подвесьте один груз, а с другой стороны — два груза.
1) найдите отношение сил — и отношение плеч —2;
2) вычислите момент М1 силы, вращающей рычаг против хода часовой стрелки, и момент М2 силы, вращающей рычаг по ходу часовой стрелки.
2. Завершите заполнение таблицы.
Анализ эксперимента и его результатов
На основании проведенных опытов сравните отношение сил, действующих на рычаг, и отношение его плеч. Сделайте вывод, в котором: 1) сформулируйте условие равновесия рычага; 2) проанализируйте, какие факторы повлияли на точность измерений.
творческое задание
Соберите устройство, как показано на рис. 4. Выполните необходимые измерения и определите моменты сил, действующих на рычаг. Найдите сумму моментов. Сделайте вывод об условии равновесия рычага в данном эксперименте.
Это материал учебника Физика 7 класс Барьяхтар, Довгий
моментов, рычаги и шестерни: принцип и пример | StudySmarter
Моменты очень часто встречаются в повседневной жизни. Возможно, у вас уже есть интуитивное представление о моментах, и вы можете использовать его в своих интересах, даже если вы не знакомы с его физической теорией. Например, мы применяем понятие момента, когда играем на качелях на детской площадке и измеряем массу с помощью неравноплечевых весов. При правильном использовании моменты могут помочь нам использовать нашу силу и тяжелые предметы, которые мы не можем переместить в одиночку. Знаменитый греческий математик и философ Архимед так увлекся таким способом применения моментов, что сказал: «Дайте мне точку опоры, и я переверну мир!» Возможно, вы видели, как люди уравновешивают предметы так, что кажется, будто они бросают вызов гравитации, например, те наклонные держатели для бутылок. Да, это еще одно применение понятия моментов! Продолжайте читать, чтобы узнать больше о значении, принципе и причинах Моменты, выбывшие и шестеренки.
Возможно, у вас уже есть интуитивное представление о моментах, и вы можете использовать его в своих интересах, даже если вы не знакомы с его физической теорией. Например, мы применяем понятие момента, когда играем на качелях на детской площадке и измеряем массу с помощью неравноплечевых весов. При правильном использовании моменты могут помочь нам использовать нашу силу и тяжелые предметы, которые мы не можем переместить в одиночку. Знаменитый греческий математик и философ Архимед так увлекся таким способом применения моментов, что сказал: «Дайте мне точку опоры, и я переверну мир!» Возможно, вы видели, как люди уравновешивают предметы так, что кажется, будто они бросают вызов гравитации, например, те наклонные держатели для бутылок. Да, это еще одно применение понятия моментов! Продолжайте читать, чтобы узнать больше о значении, принципе и причинах Моменты, выбывшие и шестеренки.
Бутылка балансируется без усилий благодаря продуманному использованию моментов в конструкции держателя бутылки, StudySmarter Originals
Что означает момент в физике?
Когда мы прикладываем силу к объекту в определенном направлении, мы можем заставить его вращаться. Точка, вокруг которой происходит вращение, называется точкой разворота . Моменты посвящены пониманию и количественной оценке эффективности силы, заставляющей объект поворачиваться.
Точка, вокруг которой происходит вращение, называется точкой разворота . Моменты посвящены пониманию и количественной оценке эффективности силы, заставляющей объект поворачиваться.
Момент — это название, которое мы даем в физике вращательному действию силы, заставляющей объект вращаться вокруг оси.
Чтобы количественно определить момент силы, мы умножаем приложенную силу на перпендикулярное расстояние линии действия силы от точки поворота.
Поскольку единицами силы являются ньютоны, а единицами измерения расстояния являются метры, мы измеряем момент в ньютон-метрах.
На следующем рисунке показано, как создать момент в гайке с помощью разводного ключа, прикладывая усилие в правильном направлении. В этом случае центр гайки является точкой поворота.
Сила, приложенная к гаечному ключу, вызывает момент, заставляющий гайку вращаться вокруг своего центра, StudySmarter Originals
В качестве эксперимента попробуйте открыть дверь, толкая ее на разном расстоянии от петли.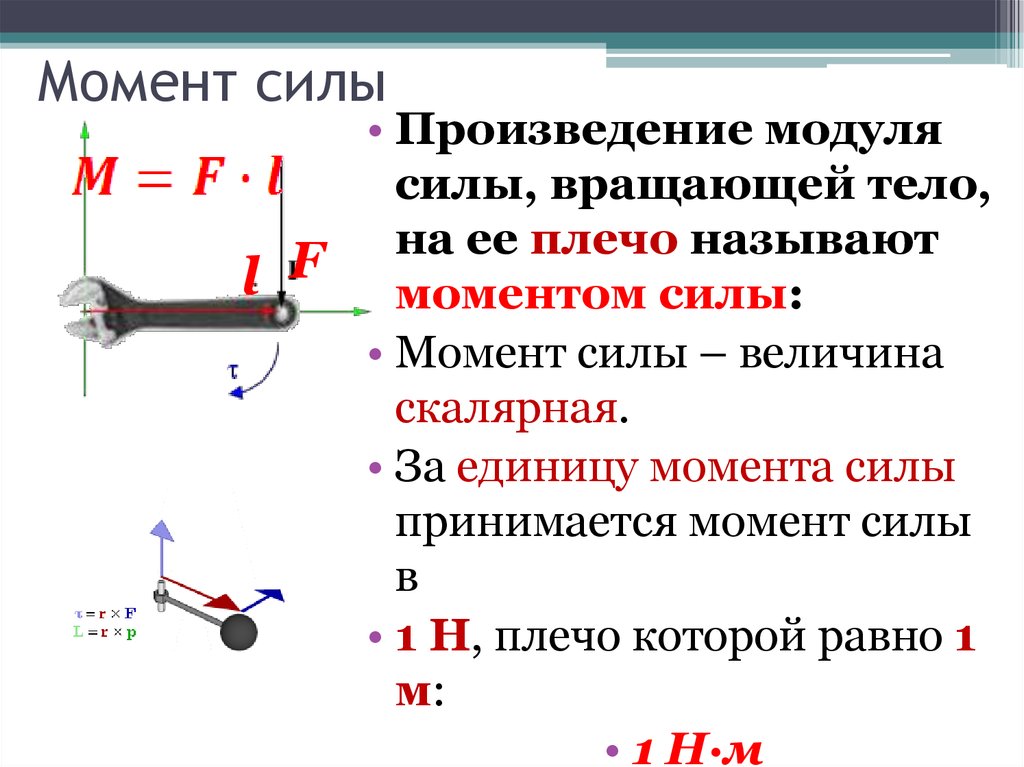 Вы обнаружите, что чем дальше от петли вы нажимаете, тем легче будет сдвинуть дверь. Вам нужно меньше силы, когда вы находитесь дальше от шарнира, потому что вы увеличиваете перпендикулярное расстояние от линии действия силы — вашего толчка — до оси вращения — шарнира. Таким образом, момент становится больше, что делает поворотное воздействие на дверь более эффективным.
Вы обнаружите, что чем дальше от петли вы нажимаете, тем легче будет сдвинуть дверь. Вам нужно меньше силы, когда вы находитесь дальше от шарнира, потому что вы увеличиваете перпендикулярное расстояние от линии действия силы — вашего толчка — до оси вращения — шарнира. Таким образом, момент становится больше, что делает поворотное воздействие на дверь более эффективным.
Набор грузов общей массой a помещается на балку, уравновешенную в точке опоры, как показано на рисунке ниже. Этот набор размещается на расстоянии от оси вращения. Чему равен момент, обусловленный набором масс?
Набор грузов на балке над точкой опоры создает момент. GCSE
Для этого вопроса нам нужно использовать приведенное выше уравнение для момента:
Приложенная сила — это вес набора. Поскольку груз действует вниз, заданное расстояние перпендикулярно линии действия груза. Обе величины уже указаны в единицах СИ, поэтому мы можем напрямую использовать уравнение, чтобы найти момент.
Момент, создаваемый набором масс.
Причины моментов
Из приведенного выше определения мы знаем, что сила вызывает момент. Но не всякой силой! Например, обратите внимание, что если линия действия силы проходит через точку опоры, момента не будет, так как перпендикулярное расстояние равно нулю. Следовательно, в таком случае нет вращения.
Линия действия силы проходит через точку вращения. В этом случае ключ не заставляет гайку проворачиваться, так как момент отсутствует. StudySmarter Originals
Используя эту идею, мы можем балансировать объекты так, чтобы они не падали. Нам просто нужно убедиться, что их вес, который направлен вниз, действует в направлении, которое проходит через точку опоры конструкции, которую мы пытаемся уравновесить, — точку опоры. Вы помните определение центра масс?
центр масс — это точка, в которой мы можем считать, что сосредоточена вся масса объекта. Его расположение зависит от распределения массы объекта.
Сбалансировать объект легко, если мы знаем, где находится центр масс. Рассмотрим бутылку, показанную в начале. Если бутылка наклонена, ее центр масс не совпадает с точкой опоры. Поэтому его вес будет действовать на некотором перпендикулярном расстоянии от оси вращения, создавая момент. В этот момент бутылка поворачивается к поверхности, на которой она стоит, и падает.
Вес бутылки создает момент, потому что центр масс не совмещен с точкой вращения. StudySmarter Originals
Однако наклонный держатель для бутылок сконструирован таким образом, что центр масс системы держатель для бутылок и бутылок находится непосредственно над точкой опоры. Таким образом, вес системы не создает момента.
Центр масс системы бутылкодержатель-бутылка совмещен с точкой поворота. Следовательно, система не подвержена никакому моменту из-за своего веса. StudySmarter Originals
Вы можете попробовать это дома. Если у вас есть две одинаковые вилки, две зубочистки и солонка, вы можете сбалансировать вилки удивительным образом. Сначала заблокируйте зубцы вил, как показано на рисунке ниже.
Сначала заблокируйте зубцы вил, как показано на рисунке ниже.
Блокировка зубцов вил, оригиналы StudySmarter
Теперь вставьте зубочистку в одну из прорезей в блокируемых вилках, пока она не станет твердой. Если все сделано правильно, у вас получится конструкция с центром масс, расположенным на вертикальной линии, проходящей через невставленный конец зубочистки. Из-за этого вы должны быть в состоянии сбалансировать всю конструкцию на одном из ваших пальцев от невставленного конца зубочистки.
Конструкция легко балансируется с невставленного конца зубочистки, так как центр масс находится прямо под ним. StudySmarter Originals
Но мы можем сделать лучше! Закрепите вторую зубочистку в одном из отверстий солонки. Аккуратно сбалансируйте структуру вилки-зубочистки на второй зубочистке вместо пальца. Эта установка будет работать и сбалансирована, потому что центр масс системы вилок выровнен с вертикальной зубочисткой, не создавая момента, чтобы заставить вилки упасть.
Поскольку вес конструкции действует по линии, проходящей через точку вращения — второй конец зубочистки, — нет момента, чтобы заставить вилки упасть.
Принцип моментов
Теперь мы знаем, что моменты могут вызывать вращение объекта, но, как и в предыдущих примерах, иногда мы можем предпочесть, чтобы наша система оставалась статической. Рассмотрим конструкции, поднятые во время строительства. Очень важно, чтобы эти конструкции не раскачивались, потому что это было бы слишком опасно. Однако мы не всегда можем сбалансировать объекты, используя их центр масс. В таких случаях нам нужно сбалансировать моменты , и принцип моментов может помочь нам с этим .
Принцип моментов утверждает, что система сбалансирована , если сумма моментов по часовой стрелке равна сумме моментов против часовой стрелки.
Объект будет вращаться, только если существует дисбаланс моментов по часовой стрелке и против часовой стрелки. Следовательно, мы можем предотвратить нежелательный момент, вызывающий вращение по часовой стрелке, уравновешивая его, используя момент против часовой стрелки той же величины.
Следовательно, мы можем предотвратить нежелательный момент, вызывающий вращение по часовой стрелке, уравновешивая его, используя момент против часовой стрелки той же величины.
Когда система находится в равновесии, говорят, что она находится в равновесии. Примером этого может служить ситуация, когда два человека одинаковой массы сидят по обе стороны от качелей. Поскольку их веса равны, равны и расстояния от центра вращения до обеих сил. Генерируемые моменты равны из-за равных сил — одинаковых весов — и перпендикулярных расстояний до оси вращения. Следовательно, эффекты поворота от двух сил компенсируют друг друга, и качели не вращаются. Обратите внимание, что в точке поворота также действует сила реакции (представленная на диаграмме ниже). Однако это не вызывает никакого момента, потому что перпендикулярное расстояние для него равно нулю.
Моменты, возникающие у каждого ребенка на качелях, зависят от их массы и расстояния от оси вращения, philschatz
Двое детей сидят по обе стороны от качелей. Система находится в равновесии и не движется. Момент, приложенный к качелю ребенком с левой стороны, равен . Масса ребенка справа равна. Какова общая длина качелей?
Система находится в равновесии и не движется. Момент, приложенный к качелю ребенком с левой стороны, равен . Масса ребенка справа равна. Какова общая длина качелей?
Можно предположить, что качели расположены горизонтально, а силы, действующие от веса детей, перпендикулярны ему, так как направлены вниз. Уравнение момента, вызванного силой, имеет вид:
,
где F — сила в ньютонах и расстояние по перпендикуляру линии действия силы от оси вращения в метрах. Мы можем изменить это выражение, чтобы изолировать расстояние от опорной точки:
.
Нам нужно рассчитать вес ребенка справа, так как система находится в равновесии, поэтому она вызовет тот же момент, что и ребенок слева. Сила веса ребенка равна:
,
, принимая g за:
Теперь мы можем подставить этот результат в уравнение для расстояния.
.
Однако мы должны быть осторожны. Вопрос касается длины качелей. Эта длина равна , удвоенному по расстоянию от точки опоры до любого из дочерних элементов, и так оно и есть.
Другие примеры и применение моментов: рычаги и шестерни
С рассмотренными примерами вы, возможно, уже начали понимать, как часто моменты присутствуют в повседневной жизни. Некоторые другие приложения моментов включают ножницы и кусачки, которые мы можем использовать, чтобы разрезать даже металл силой наших рук. Другой пример — удаление гвоздя с помощью головки молотка и нажатия или вытягивания рукоятки молотка. Пример молотка и гвоздя показан ниже. Помните, что мы должны учитывать перпендикулярное расстояние от оси вращения до линии действия силы, а не расстояние от точки вращения до места приложения силы.
Молоток, удаляющий гвоздь, представляет собой приложение моментов, StudySmarter Originals
Все эти конкретные приложения моментов известны как рычаги . Давайте посмотрим, как они работают более подробно.
Что такое рычаг и как он работает? Рычаг состоит из жесткого стержня или балки, опирающейся на шарнир (также называемый точкой опоры).
Мы можем использовать рычаги, чтобы легче поднимать тяжести. Рычаги работают по тому принципу, что мы можем создать больший момент (и, следовательно, больший вращательный эффект), применяя меньшую силу на большем расстоянии от оси вращения. Идея состоит в том, чтобы точка опоры находилась ближе к грузу — весу, который мы хотим поднять, — чем к точке приложения силы или усилия. Посмотрите на картинку ниже. В данном случае груз представляет собой большой камень. Вес камня создает момент в системе рычагов. Однако мы можем создать момент, равный или больший, используя меньшую силу, потому что расстояние, на котором прикладывается усилие, больше.
Рычаг использует моменты для подъема тяжелого веса. Поднимаемый груз вызывает момент. Однако мы можем вызвать больший момент, приложив меньшую силу, чем вес груза, если приложим ее на большем расстоянии от точки опоры. StudySmarter Originals
Тачка — еще один пример применения рычагов. Грузы, которые слишком тяжелы для прямой перевозки, вместо этого можно перевозить с помощью тачек. Груз размещается внизу над колесом, а к нему подходят два руля. Эти рули можно поднимать с меньшим усилием, чем сам груз, поскольку усилие прикладывается дальше от оси вращения, чем груз.
Груз размещается внизу над колесом, а к нему подходят два руля. Эти рули можно поднимать с меньшим усилием, чем сам груз, поскольку усилие прикладывается дальше от оси вращения, чем груз.
P представляет собой тяговое усилие или «усилие», прилагаемое человеком, а R представляет сопротивление нагрузки из-за его веса. Шарнир расположен в центре колеса, tec.amordediocadiz
На приведенной выше диаграмме показаны силы, действующие в этой ситуации. Обе силы действуют слева от оси системы, которая находится в центре колеса. Однако эти силы действуют в противоположных направлениях. Вес груза вызывает момент против часовой стрелки. С другой стороны, сила, которую человек прикладывает, дергая за руль, — усилие — создает момент по часовой стрелке.
Мы видим, что рычаги очень полезны, но это не единственное применение моментов. Мы также применяем эту концепцию при использовании передач.
Что такое шестерня и как она работает? Шестерни представляют собой зубчатые колеса (они имеют небольшие выступы по краям), которые могут сцепляться друг с другом.
Возможно, вы видели шестерни в разных местах, например, на велосипедах и шкивах. Шестерни, хотя и простые, могут быть очень полезными, поскольку они имеют разные применения. Например, когда шестерни соединены друг с другом, они могут вращаться с разной скоростью, потому что для того, чтобы большая шестерня могла совершить один оборот, меньшей шестерне необходимо совершить больше оборотов. Точное количество оборотов зависит от размеров шестерен. Обратите внимание, что если одна шестерня вращается против часовой стрелки, это заставляет подсоединенную шестерню вращаться по часовой стрелке. Следовательно, мы можем использовать их для изменения направления вращения объекта.
Если одна шестерня вращается в одном направлении, это приведет к тому, что другая повернется в противоположном направлении, Wikimedia commons
Но как именно здесь применяется понятие момента? В месте контакта зубьев шестерен действуют силы, равные и противоположные друг другу. Однако, поскольку их радиусы различны, моменты, действующие на каждую шестерню, также различны. Приложение силы к меньшей шестерне вызовет больший момент на большей шестерне, потому что сила, приложенная к ней, будет такой же, но ее радиус больше.
Приложение силы к меньшей шестерне вызовет больший момент на большей шестерне, потому что сила, приложенная к ней, будет такой же, но ее радиус больше.
Ключевые выводы
Момент — это вращательный эффект силы, которая заставляет объект вращаться вокруг оси.
Мы вычисляем момент силы, умножая приложенную силу на расстояние по перпендикуляру от оси вращения до линии действия силы.
Принцип моментов гласит, что когда система находится в равновесии, сумма моментов по часовой стрелке равна сумме моментов против часовой стрелки относительно оси вращения.
Сила, действующая непосредственно через стержень системы, не создает момента относительно стержня.
Рычаги выгодно используют моменты и могут использоваться для увеличения момента, чтобы что-то повернуть или поднять тяжелый предмет.
Шестерни различных размеров могут быть соединены для увеличения или уменьшения величины момента.

Рычаги
Рычаг — это механизм, который можно использовать для приложения большой силы на небольшом расстоянии к одному концу рычага путем приложения небольшой силы на большом расстоянии к другому концу.
Моментное действие с обеих сторон рычага равна и может быть выражено как
F E D E = F L D L (1) 240240234240240234024024024024024024024024024024024024024024024024024024024024024024024024024024023н. где
F e = сила усилия (Н, фунты)
F l = сила нагрузки (Н, фунты) (обратите внимание, что вес является силой)
3 l13 расстояние от силы нагрузки до точки опоры (м, фут)
D E = Расстояние от силы усилия до точки зрения (M, FT)
Сила усилий может быть рассчитана путем модификации (1) до
F E =
F E = F L F E = F L F E = F L F E = F L F E . D L / D E
D L / D E
= M A G DL / DE (1B)
, где
9029 MASS 2
9 29029.0230 г = ускорение свободного падения (9,81 м/с 2 , 32,17 фут/с 2 )
Калькулятор рычага
Этот калькулятор можно использовать для расчета силы усилия рычага. Его можно использовать как для метрических, так и для имперских единиц, если использование единиц согласовано.
F l — сила нагрузки (Н, кг, фунт)
d l — расстояние от силы нагрузки до точки опоры (м, фут)
0 сила — 1 d 90 усилие от
до точки опоры (м, фут )
- Обратите внимание, что кг — это единица измерения массы в системе СИ. Подробнее о массе и весе (силе)
Пример — самодельный автомобильный подъемник как показано на рисунке выше. При расстоянии нагрузки до точки опоры
0,2 м , расстоянии силы усилия до точки опоры 2 м и нагрузке на рычаг — половине веса автомобиля 2000 кг — силу усилия можно рассчитать F e = (0.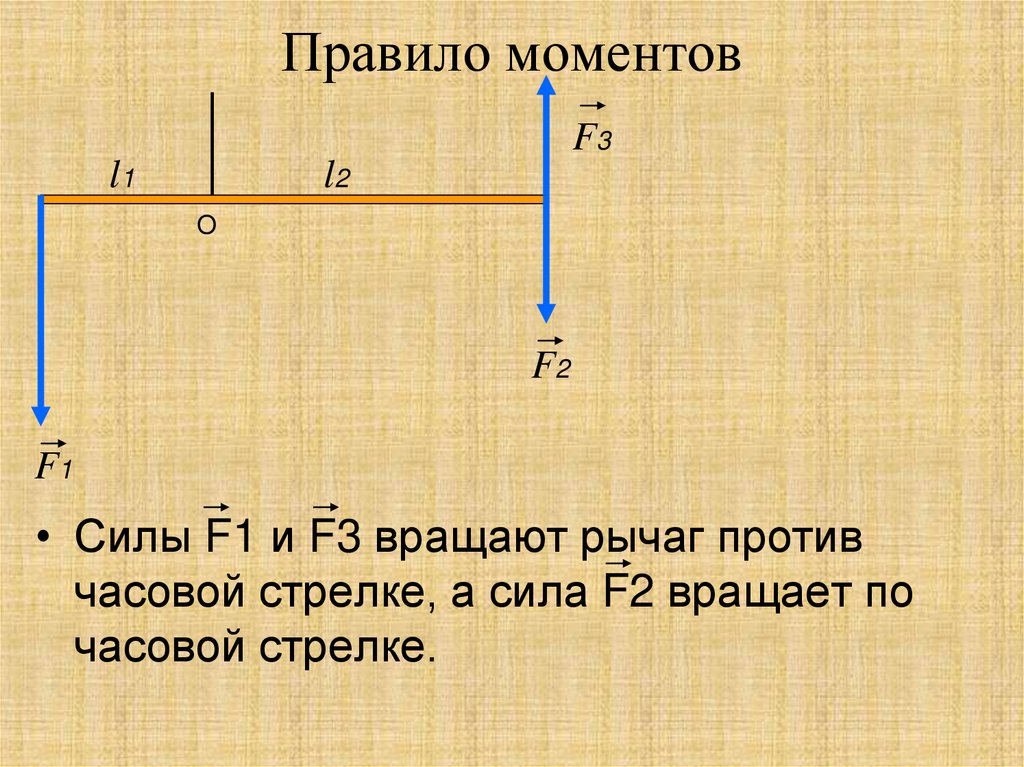 5 2000 kg) (9.81 m/s 2 ) (0.2 m) / (2 m)
5 2000 kg) (9.81 m/s 2 ) (0.2 m) / (2 m)
= 981 N
≈ 100 kg
Orders of Рычаги
Рычаги первого порядка
- точка опоры расположена между усилием и грузом
- усилие меньше груза
- усилие перемещается дальше груза
- рычаг можно рассматривать как усилитель силы
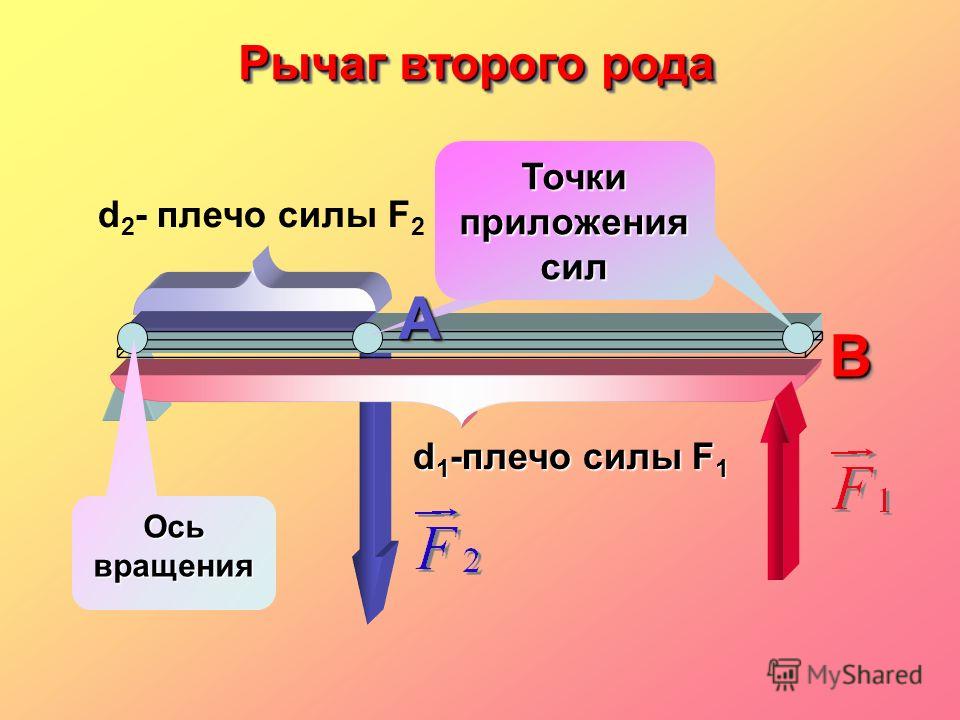
Рычаги второго порядка
- усилие и нагрузка расположены по одну сторону от точки опоры, но приложены в противоположных направлениях
- нагрузка расположена между усилием и точкой опоры
- усилие меньше нагрузки усилие перемещается дальше груза
- рычаг можно рассматривать как усилитель силы
Рычаги третьего порядка
- усилие лежит между грузом и точкой опоры
- усилие больше, чем нагрузка
- груз перемещается дальше, чем усилие
- рычаг можно рассматривать как увеличитель расстояния
Пример — Рычаг первого класса (порядок) — сила (вес)
1 фунт действует на конец рычага на расстоянии 1 фут от точки опорыСила усилия на расстоянии 2 фута от точки опоры может быть рассчитана как
F e = (1 фунт ) (1 фут) / (2 фута)
= 0,5 (lb)
Формула (1) может быть изменена, чтобы выразить требуемую нагрузку, если известно усилие, или требуемое расстояние от точки опоры, если известны нагрузка и усилие, и т.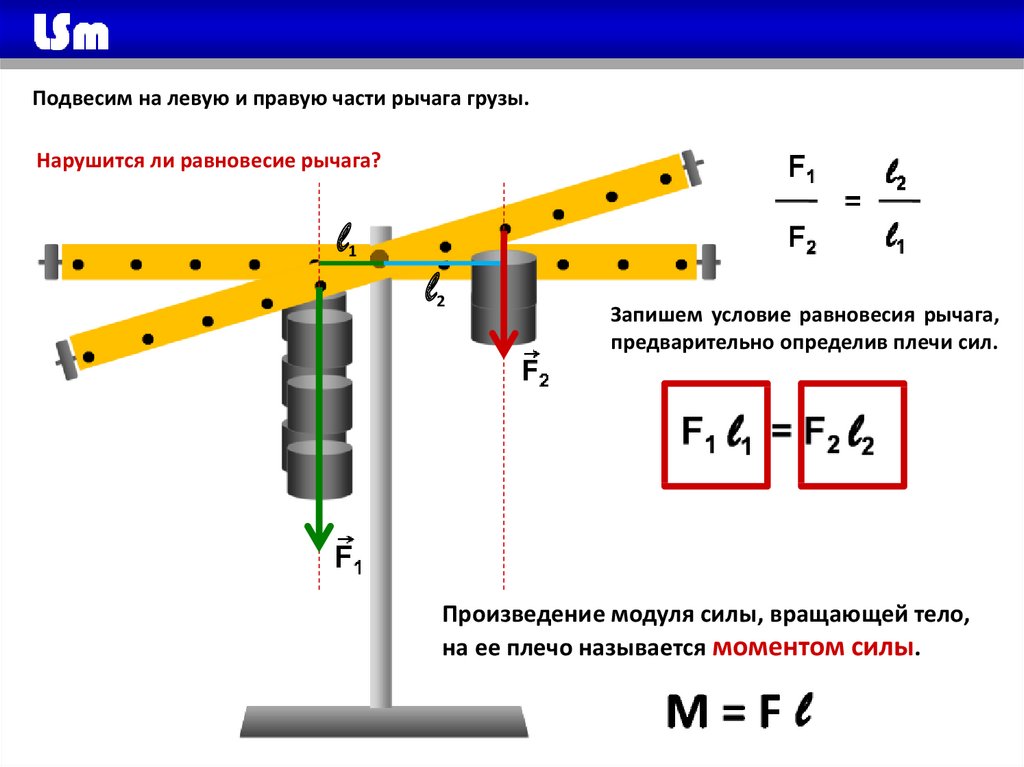 д.
д.
Уровень выше, где точка опоры расположена между нагрузкой и усилием, часто характеризуется как первоклассный механизм уровня .
Уровень, на котором нагрузка и усилие расположены по одну сторону от точки опоры, часто характеризуется как механизм уровня второго класса .
Пример — Рычаг второго класса (порядок)
Сила (вес) 1 фунт действует на расстоянии 1 фут от точки опоры.
Сила усилия на расстоянии 2 фута от точки опоры может быть рассчитана как
F e = (1 фунт) (1 (фут) / (2 фута)
. lb)
Пример — Расчет рычага в единицах СИ — вес
1 кг масса, действующая 1 м от точки опорыСила усилия на расстоянии 2 м от точки опоры может быть рассчитана как
F e = (1 кг/м) s 2 ) (1 м) / (2 м)
= 4,9 Н
Рычажный механизм, в котором входное усилие превышает выходную нагрузку, часто характеризуется как рычаг третьего класса механизм.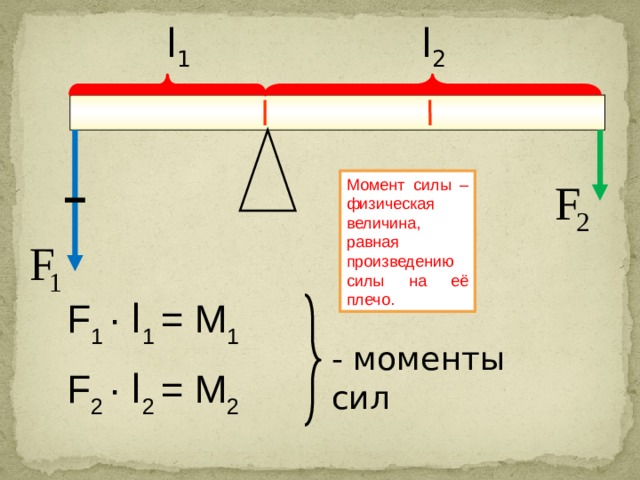
Пример — рычаг третьего класса (порядка)
Сила (вес) 1 фунт действует на расстоянии 2 фута от точки опоры.
The effort force at a distance of 1 ft from the fulcrum can be calculated as
F e = F l d l / d e
= ( 1 фунт) (2 фута) / (1 фут)
= 2 (фунта)
Одна или несколько сил, действующих на рычаг
Рычаг с двумя действующими силами нагрузки и одним усилием показан на рисунке ниже:
Общее уравнение для одного усилия с одним или несколькими действующими усилиями нагрузки может быть выражено как
F e = (F LA D LA + F LB D LB + .. + F LN D LN ) / D E (2) ). три действующие нагрузки ниже.
Пример.
Рычаг с тремя действующими нагрузками и одной силой усилия
Груз A из 1 фунт действует на расстоянии 1 фут от точки опоры. Вес B из 2 фунта приложен на расстоянии 2 фута от точки опоры, а вес C из 3 фунта приложен на расстоянии 3 фута от точки опоры.
Сила усилия на расстоянии 2 фута от точки опоры может быть рассчитана как
F e = (F lA d lA + F lB d lB + F l C d lC ) / d e
= ((1 фунт) (1 фут) + (2 фунта) (2 фута) + (3 фунта) (3 фута)) / (2 фута)
= 7 (фунт)
Простые машины
Простые машиныКлючевые термины
эксцентриковый шкив
механическое преимущество
рычаг
рычаг
мощность
крутящий момент
колесо и ось«Дайте мне точку опоры и я переверну землю».
.. Архимед
Поскольку сила человека ограничена, умные люди построили машины, которые позволить подвиги, ранее невозможные. Один из самых простых (и, скорее всего, первый) автомат это рычаг . Я уверен, что вы обнаружили магия рычага в детстве, когда вы играли на качелях. Каким-то образом младшая сестра может противостоять весу старшего брата, осторожно позиционирование на аппарате. Это может показаться очень интуитивным, но тем не менее это устройство, которое нужно было изобрести. Применение рычага может быть можно найти повсюду в вашем доме.
Рычаг состоит из жесткого стержня, который может поворачиваться в одной точке. Эта точка вращения известна как точка опоры. Сила приложена в какой-то точка от точки опоры (обычно называется усилием ). Этот сила инициирует тенденцию вращать стержень вокруг точки опоры. Идея заключается в предоставлении другой силы для подъема или перемещения какого-либо объекта (обычно называемого загрузить ).
Рассмотрим анимацию ниже. Для того, чтобы поднять вес слева (нагрузка) требуется направленное вниз усилие с правой стороны рычаг. Здравый смысл подсказывает вам, что количество требуемой силы усилия поднять груз зависит от где применяется сила. Я уверен, что вы знаете, что задача будет проще всего, если приложить силу усилия как можно дальше от точки опоры.
The Simple (1 ст класс) Рычаг (анимация)Допустим, груз (выше) составляет 200 фунтов, и вам нужно поднять его на 1 фут. земля. Это потребовало бы 200 * 1 = 200 футо-фунтов работы (в отсутствие трения). Используя рычаг, вы можете поднять его с большим меньшая сила… в зависимости от того, где приложена сила усилия. Факт что вы можете поднять что-то тяжелое с небольшим усилием, является ключом к любому простому машина. Большинство простых механизмов (таких как рычаг) дают вам механическое преимущество (множитель силы = сила нагрузки/сила усилия).
Однако ни на секунду не думайте, что простая машина как-то нарушает законы сохранения энергии. Количество энергии, которое вы получаете, равно точно равно энергии, которую вы вкладываете. То есть, поскольку энергия не может быть создан или уничтожен, вы всегда найдете:
Энергия (выход) = Энергия (вход)
Для упрощения мы не будем учитывать вес стержня себя и рассматривать только ситуации без трения (без потерь, которые приводят к нагревать). Таким образом
Работа (из) = Работа (в)
СИЛА НАГРУЗКИ * расстояние (вверху) = сила усилия * РАССТОЯНИЕ (вниз)
200 фунтов * 1 фут = 25 фунтов * 8 футов
или
200 фунтов * 1 фут = 100 фунтов * 2 фута
Ключ, таким образом, заключается в обмене силой на расстояние. Вы можете поднять Нагрузите 200 фунтов на короткое расстояние (1 фут вверх), прилагая меньшее усилие.
сила над большее расстояние. Однако, куда бы вы ни обратились сила усилия потребует 200 футо-фунтов работы.
Рассмотрим пример, когда вы поднимаете груз весом 200 фунтов вверх на 1 фут (в пример выше). Попробуйте ответить на следующие вопросы. Нажмите здесь, чтобы увидеть ответы.
Вопрос №1 — Своими словами; объясните где усилие необходимо приложить, чтобы убедиться, что усилие равно 200 фунтам.
Вопрос №2. В чем заключается механическое преимущество в данном случае?
Вопрос №3 — Своими словами; объясните где усилие должны быть приложены, чтобы гарантировать, что сила усилия составляет менее 200 фунтов.
Вопрос № 4. Если вы приложите усилие в 50 фунтов, через что (вертикальное) расстояние применяется?
Классы рычагов
Рычаги относятся к 1-му, 2-му и 3-му классу. изображения ниже демонстрируют каждый тип с силой усилия, показанной стрелкой и нагрузка представлена черной сферой.
Старинный открывалка для бутылок и традиционный щелкунчик (анимация)
- Рычаг 3-го класса дает механический недостаток , но позволяет широко Диапазон движения груза. Многие гидравлические системы используют 3-й класс рычаг, потому что выходной поршень (куда действует приложенная сила) может двигаться только (физически) на короткое расстояние. Другим примером может быть ваша собственная челюсть, где мышцы челюсти обеспечивают силу усилия и «нагрузку» приложил к зубам… пережевывая пищу.
Адаптировано из Викисклад
Можете ли вы назвать несколько примеров рычагов каждого класса?
Вопрос № 6. К какому классу рычагов вы бы отнесли (а) плоскогубцы (б) руку тормоза на велосипеде (c) пинцет (d) хоккейная клюшка (e) дверь автомобиля … груз масса дверцы (ж) мышеловки
Крутящий момент
Теперь должно быть очевидно, что расстояние усилия (и нагрузки) от точка опоры становится важным фактором, связанным с рычагом.
Чем дальше сила усилия прикладывается со стороны шарнира, тем легче произвести вращение. Эти факторы включены в термин под названием крутящий момент . Ты возможно уже было ощущение, что крутящий момент имел дело с поворотным эффектом сила.
Два способа достижения одинакового крутящего момента (анимация)
Тот, кто хоть раз пытался открутить ржавую гайку гаечным ключом знает о крутящем моменте. На анимации выше показаны два способа выполнения цель… приложить большую силу рядом с ржавой гайкой или приложить меньшую силу дальше от оси вращения. Сколько из вас добавили кусок трубы к концу вашего гаечного ключа, чтобы убедить его двигаться? Фактически, многие гайки должны быть затянуты в соответствии с очень специфическими спецификациями. Этот это когда вы используете динамометрический ключ (специальный инструмент, правильная степень затяжки).
Динамометрический ключ затянет болт с нужным усилием из «поворота».
Предоставлено Викисклад
Крутящий момент и работают два разные вещи. Рассмотрим силу, приложенную перпендикулярно металлическому стержню. (как видно на изображении ниже):
Крутящий момент = прилагаемое усилие * плечо рычага Работа = Сила * Расстояние
Если плечо рычага составляет 8 футов, а приложенная сила составляет 10 фунтов, результирующий крутящий момент составляет 80 фут-фунтов (независимо от того, вращается ли система). Фактическая работа , выполненная в этом примере, равна силе, умноженной на физическое расстояние, на которое он перемещается (показано как смещение в 1 фут). Если полоса не двигается в общем, никакой работы не делается, но у вас все еще есть крутящий момент в 80 ft-lbs в системе.
То есть проделанная работа и созданный крутящий момент являются разными величинами… но измеряются в одних и тех же единицах. Вы можете думать о крутящий момент как «закручивающие эффекты» силы и работают как энергия, используемая при движении что-нибудь.
При рассмотрении рычага (без трения):
Работа (из) = Работа (в)
Крутящий момент (выходной) = крутящий момент (внутренний)
Рабочие номера:
(анимация)
Анализ с точки зрения работы
Концепция любой простой машины состоит в том, чтобы выполнить задачу, применяя меньшее усилие на большем расстоянии. Рассмотрим пример показано ниже. Предположим, вам нужно поднять 60-фунтовый предмет по вертикали. расстояние 1 фут. Это требует 60 футов-фунтов работы. Вы можете не быть способным поднять 60 фунтов (или получить боль в спине при попытке).
Однако рычаг позволяет поднять объект с гораздо меньшим усилием. Рассмотрим рисунок ниже, где груз весом 60 фунтов поднимается на вертикальное расстояние. 1 фут (показан розовым цветом рядом с грузом). Чтобы поднять вес, вы можете приложите силу в 12 фунтов на расстояние 5 футов, чтобы поднять объект… или сила 15 фунтов на расстоянии 4 футов … и т. д. Это дает вам механическое преимущество потому что вы прикладываете силу менее 60 фунтов. рассчитывается как отношение выходной силы к входной силе. Если это требуется 12 фунтов, чтобы поднять груз весом 60 фунтов, механическое преимущество равно 5. (60/12 = 5) … если требуется 15 фунтов, чтобы поднять груз весом 60 фунтов, механическое преимущество равно 4. Во всех случаях вы выполняете одинаковый объем работы. На изображении ниже сила в 10 фунтов должна быть приложена на расстоянии 6 футов для производства 60 футо-фунтов работы.
Анимация рычага, в которой MA = 6
Примечание.
Мы проанализировали ситуацию, предполагая отсутствие убытков трение. В реальном мире механическое преимущество рассчитывается таким образом. может быть немного ниже, потому что сила усилия будет немного выше, чем идеальный случай.
Анализ с точки зрения крутящего момента
Анимация рычага
Теперь проанализируем тот же рычаг с точки зрения крутящего момента. Предполагать расстояние между (красными) точками вдоль рычага равно 2 футам. 60 нагрузка в фунтах опирается на 2 фута от точки опоры, создавая против часовой стрелки крутящий момент 120 футо-фунтов вокруг точки поворота. Сила в 10 фунтов приложенный в 12 футах от точки опоры произведет такое же количество по часовой стрелке крутящий момент … достаточный для вращения. отношение плеча входного рычага к плечо выходного рычага даст механическое преимущество , равное 12/2 = 6. Таким образом, можно оценить механическое преимущество от прямого наблюдение.
Если плечо входного рычага в 6 раз больше длины выходного плечо рычага, система дает механическое преимущество в 6, а это означает, что для на каждый фунт, который вы нажимаете на рычаг, вы можете поднять 6 фунтов груза.
Более длинное плечо входного рычага (место усилия) обеспечивает более высокое механическое преимущество. Это в соответствии с идеей здравого смысла, что вы обычно прикладываете усилие как как можно дальше от точки опоры.
Используйте эту картинку, чтобы ответить на эти вопросы (ответы ниже)
Вопрос № 7. Предположим, этот рычаг первого класса используется для подъема 100-фунтового предмета. (нагрузку), прикладывая направленную вниз силу усилия в точке B. механическое преимущество? Какая сила требуется?
Вопрос №8 — Если сила усилия приложена в точке А и груз перемещается на 1 фут вверх, на сколько футов должна опуститься точка А? Какая работа совершается при подъеме этого масса?
Еще немного о крутящем моменте
При вращении педалей на велосипеде вы можете , а не передавать постоянный крутящий момент на педали.
Крутящий момент — это не только произведение приложенной силы, умноженной на плечо рычага … это также зависит от направления прилагаемой силы.
Когда вы крутите педали на велосипеде, есть части «цикла педалирования», в которых вы находитесь. ничего не делайте для подачи мощности на колеса, потому что вы не создаете крутящий момент на педали.. В результате мощность, которую вы придать колесам на самом деле выглядит как половина синусоиды, как бы вы ни старались нажимайте на педали (если только у вас нет тех «прищепок», которые гонщики использовать привязку ноги к педали). Вы найдете тот же эффект в двигатель и электродвигатель.
Колесо и ось
Вы когда-нибудь использовали лебедку для подъема лодки на прицеп? … или же вытащить ведро воды из глубокого колодца? … или поймать этот приз мускусный с вашей удочкой и катушкой? Если у вас есть, вы использовали простую машину известный как колесо и ось.
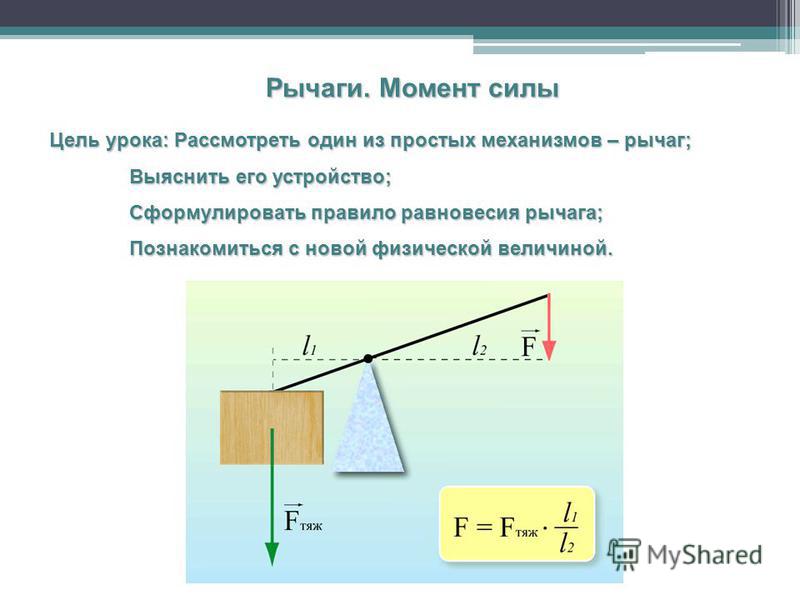
Колесо и ось — это еще одна форма простого рычага. Видишь Почему? К какому классу рычагов он относится?
Колесо и ось — это просто замаскированный рычаг
Примечание: «Колесо и ось» не следует путать с видом вы найдете на фургоне … который представляет собой просто колесо , прикрепленное к оси. Колесо (то, которое вы катите) — это просто устройство предназначен для уменьшения трения. «Колесо и ось» — это то, к чему вы обращаетесь получить механическое преимущество. Обычный лебедка (см. изображение ниже) является примером «колеса и ось». Используя только одного человека, вы можете притянуть лодку к вершине прицеп с этим приспособлением (а еще у вас есть колеса на которых едет лодка во время этого процесса, чтобы уменьшить трение).
Вот несколько примеров «колеса и оси», которые я нашел вокруг своего дом:
Вы должны быть в состоянии придумать множество других распространенных примеров «колеса и ось».
Одинарные шкивы
Один шкив не дает вам механического преимущества (на самом деле MA = 1) … но позволяет поднять тяжелый объект легко с помощью противовеса . Если противовес соответствует нагрузке … все, что вам нужно сделать, это преодолеть трение, облегчение подъема. Большинство лифтов имеют противовес, равный к весу лифта плюс 40% его максимальной нагрузки.
Специальный тип шкива, называемый 9.0435 эксцентриковый шкив, дает вам механическое преимущество, потому что центр вращения не находится в геометрической центр шкива. Это можно найти на блочном луке. если ты когда-либо использовали блочный лук, вы обнаружите, что изначально лук очень трудно оттянуть назад, но как только оттянут достаточно далеко, становится вполне легко держать и устойчиво. Почему мы упоминаем этот тип шкива здесь (в разделе рычаги)? Это связано с тем, что эксцентриковый шкив представляет собой замаскированный рычаг первого класса. Сначала, когда вы впервые рисуете стрелку, вы обычно ожидаете, что легкое усилие, но на самом деле это довольно сложно.
Эксцентриковый шкив производит механический dis преимущество в этой позе и действительно надо напрячься первый. Однако, как только вы потянете стрелу назад (и ожидайте наибольшей борьбы с луком)… становится легко держать и устойчиво. Это связано с тем, что шкив вращается, давая вам механическое преимущество.
Эксцентриковый шкив — это всего лишь замаскированный рычаг.
Составной лук — вы видите, что эксцентриковый шкив точно рычаг?
Мощность
Мощность есть не что иное, как скорость выполнения работы (насколько быстро энергия использовался). Распространенными единицами являются ватт и лошадиная сила. концепция мощности была рассмотрена в предыдущем разделе, но снова требует нашего внимания из-за того, как это связано с крутящим моментом.
Автомобильный двигатель может производить ограниченную мощность. Эта сила может быть доставляется на колеса автомобиля одним из двух способов.
.. крутящего момента и оборотов (число оборотов в минуту). На самом деле формула выглядит так:
Мощность (л.с.) = Крутящий момент (фут-фунт) * об/мин 5252
Это означает, что выходная мощность двигателя должна регулироваться либо создавать высокий крутящий момент на низкой скорости или низкий крутящий момент на высокой скорости. Это где вступает в действие трансмиссия автомобиля. Она предназначена для передачи крутящий момент и скорость на колеса с помощью систем зубчатых передач.
Гораздо проще использовать обычный велосипед, чтобы проиллюстрировать это. В этом случае и являются устройством, обеспечивающим выходную мощность на колеса. Велосипед имеет цепь, которая передает мощность от педалей на заднее колесо. Если на велосипеде нет сменных передач … он становится очень простым … если вы хотите ехать быстрее… вам нужно сильнее крутить педали (производить больше выходной мощности). Кроме того, вам придется сильнее крутить педали, если вы начинаете подниматься в гору (нужен больший крутящий момент на колеса).
Gears позволяет вам напрягаться примерно так же, но позволяет обменять скорость на крутящий момент или порок наоборот При установке цепи педалью на наименьшую передачу и задняя ось (колесо) устанавливается на самую большую передачу, вы обмениваете скорость на крутящий момент. Вы будете ехать очень медленно, но обеспечите высокий крутящий момент на колесах (для движения вверх по склону). холм). При спуске с горы требуется очень небольшой крутящий момент на колесах. так что вы переключаете передачи и получаете много скорости. Тоже самое происходит с вашей машиной. Выходная мощность двигателя может быть довольно постоянной но трансмиссия играет в ту же игру крутящего момента против скорости, что и шестерни на велосипед. Если вы хотите подняться на крутой холм, вам нужно больше крутящего момента на колеса, поэтому вам нужно пожертвовать скоростью (об/мин), чтобы выполнить задачу.
2001, 2004, 2007, 2009, 2016 Джим Михал — Все права защищены
Никакая часть не может быть распространена без явного письменного разрешения автора
ответов
Вопрос №1.
Силу усилия необходимо прикладывать как можно точки опоры, так как нагрузка исходит от точки опоры. То есть правила симметрии, поэтому правая сторона является зеркальным отражением левой стороны.
Вопрос № 2. MA равен 1. Нет ни преимущества, ни недостатка. Механическое преимущество — это отношение нагрузки/усилия… 200/200 = 1
Вопрос №3. Усилие должно быть приложено дальше от точки опоры, чем нагрузка от точки опоры.
Вопрос № 4. 200 футо-фунтов = x футы * 50 фунтов х = 4 фута
Вопрос № 5. В некоторых случаях вас больше интересует свобода движения, а не умножения силы. В этом случае вы предоставляете большая сила усилия на коротком расстоянии, чтобы обеспечить меньшую силу на большее расстояние. Во многих гидравлических системах необходимо применять этот тип рычага. потому что выходной поршень не перемещается очень далеко. Посмотрите внимательно на некоторые тяжелая строительная техника, снегоочистители и/или землеройные машины.




 Рычаг с тремя действующими нагрузками и одной силой усилия
Рычаг с тремя действующими нагрузками и одной силой усилия ..
Архимед
..
Архимед Рассмотрим анимацию ниже. Для того, чтобы поднять вес
слева (нагрузка) требуется направленное вниз усилие с правой стороны
рычаг. Здравый смысл подсказывает вам, что количество требуемой силы усилия
поднять груз зависит от где применяется сила. Я
уверен, что вы знаете, что задача будет проще всего, если приложить силу усилия
как можно дальше от точки опоры.
Рассмотрим анимацию ниже. Для того, чтобы поднять вес
слева (нагрузка) требуется направленное вниз усилие с правой стороны
рычаг. Здравый смысл подсказывает вам, что количество требуемой силы усилия
поднять груз зависит от где применяется сила. Я
уверен, что вы знаете, что задача будет проще всего, если приложить силу усилия
как можно дальше от точки опоры.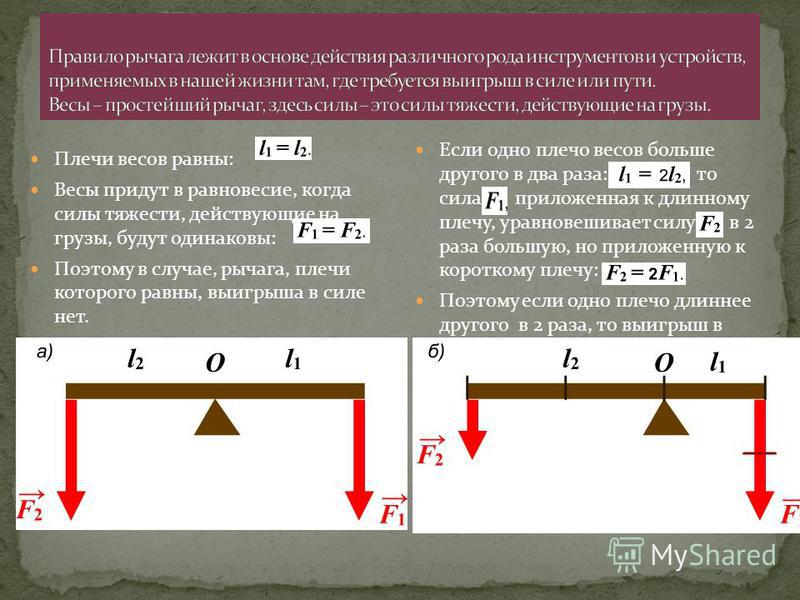 Однако ни на секунду не думайте, что простая машина как-то нарушает
законы сохранения энергии. Количество энергии, которое вы получаете, равно
точно равно энергии, которую вы вкладываете. То есть, поскольку энергия не может быть
создан или уничтожен, вы всегда найдете:
Однако ни на секунду не думайте, что простая машина как-то нарушает
законы сохранения энергии. Количество энергии, которое вы получаете, равно
точно равно энергии, которую вы вкладываете. То есть, поскольку энергия не может быть
создан или уничтожен, вы всегда найдете: 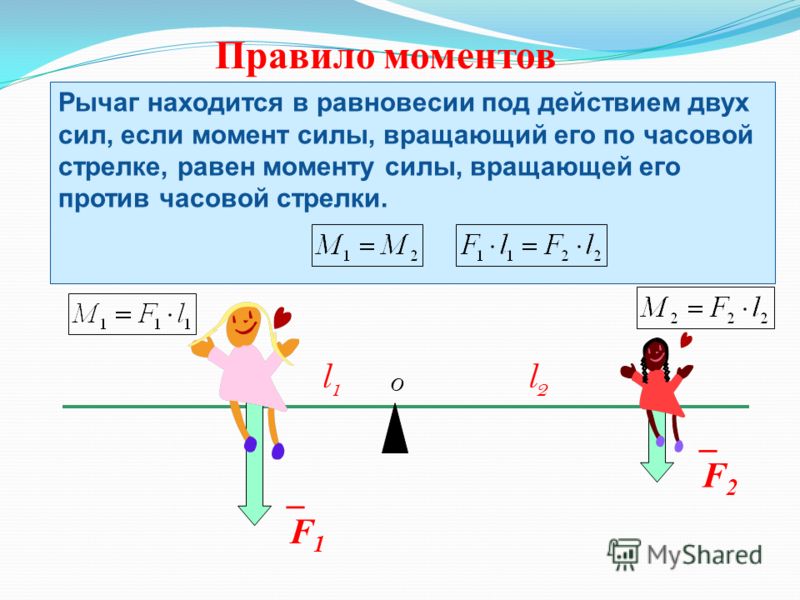 сила над большее расстояние. Однако, куда бы вы ни обратились
сила усилия потребует 200 футо-фунтов работы.
сила над большее расстояние. Однако, куда бы вы ни обратились
сила усилия потребует 200 футо-фунтов работы.
 Чем дальше
сила усилия прикладывается со стороны шарнира, тем легче произвести вращение. Эти
факторы включены в термин под названием крутящий момент . Ты возможно
уже было ощущение, что крутящий момент имел дело с поворотным эффектом сила.
Чем дальше
сила усилия прикладывается со стороны шарнира, тем легче произвести вращение. Эти
факторы включены в термин под названием крутящий момент . Ты возможно
уже было ощущение, что крутящий момент имел дело с поворотным эффектом сила.
 То есть проделанная работа и созданный крутящий момент являются разными величинами… но измеряются в одних и тех же единицах. Вы можете думать о крутящий момент как
«закручивающие эффекты» силы и работают как энергия, используемая при движении
что-нибудь.
То есть проделанная работа и созданный крутящий момент являются разными величинами… но измеряются в одних и тех же единицах. Вы можете думать о крутящий момент как
«закручивающие эффекты» силы и работают как энергия, используемая при движении
что-нибудь.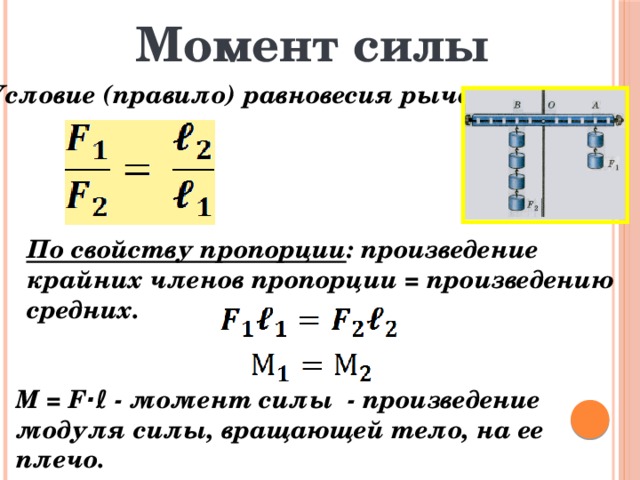 Однако рычаг позволяет поднять объект с гораздо меньшим усилием.
Рассмотрим рисунок ниже, где груз весом 60 фунтов поднимается на вертикальное расстояние.
1 фут (показан розовым цветом рядом с грузом). Чтобы поднять вес, вы можете
приложите силу в 12 фунтов на расстояние 5 футов, чтобы поднять объект… или
сила 15 фунтов на расстоянии 4 футов … и т. д. Это дает вам механическое преимущество потому что вы прикладываете силу менее 60 фунтов.
рассчитывается как отношение выходной силы к входной силе. Если это
требуется 12 фунтов, чтобы поднять груз весом 60 фунтов, механическое преимущество равно 5.
(60/12 = 5) … если требуется 15 фунтов, чтобы поднять груз весом 60 фунтов, механическое
преимущество равно 4. Во всех случаях вы выполняете одинаковый объем работы.
На изображении ниже сила в 10 фунтов должна быть приложена на расстоянии 6
футов для производства 60 футо-фунтов работы.
Однако рычаг позволяет поднять объект с гораздо меньшим усилием.
Рассмотрим рисунок ниже, где груз весом 60 фунтов поднимается на вертикальное расстояние.
1 фут (показан розовым цветом рядом с грузом). Чтобы поднять вес, вы можете
приложите силу в 12 фунтов на расстояние 5 футов, чтобы поднять объект… или
сила 15 фунтов на расстоянии 4 футов … и т. д. Это дает вам механическое преимущество потому что вы прикладываете силу менее 60 фунтов.
рассчитывается как отношение выходной силы к входной силе. Если это
требуется 12 фунтов, чтобы поднять груз весом 60 фунтов, механическое преимущество равно 5.
(60/12 = 5) … если требуется 15 фунтов, чтобы поднять груз весом 60 фунтов, механическое
преимущество равно 4. Во всех случаях вы выполняете одинаковый объем работы.
На изображении ниже сила в 10 фунтов должна быть приложена на расстоянии 6
футов для производства 60 футо-фунтов работы. Мы проанализировали ситуацию, предполагая отсутствие убытков
трение. В реальном мире механическое преимущество рассчитывается таким образом.
может быть немного ниже, потому что сила усилия будет немного выше, чем
идеальный случай.
Мы проанализировали ситуацию, предполагая отсутствие убытков
трение. В реальном мире механическое преимущество рассчитывается таким образом.
может быть немного ниже, потому что сила усилия будет немного выше, чем
идеальный случай.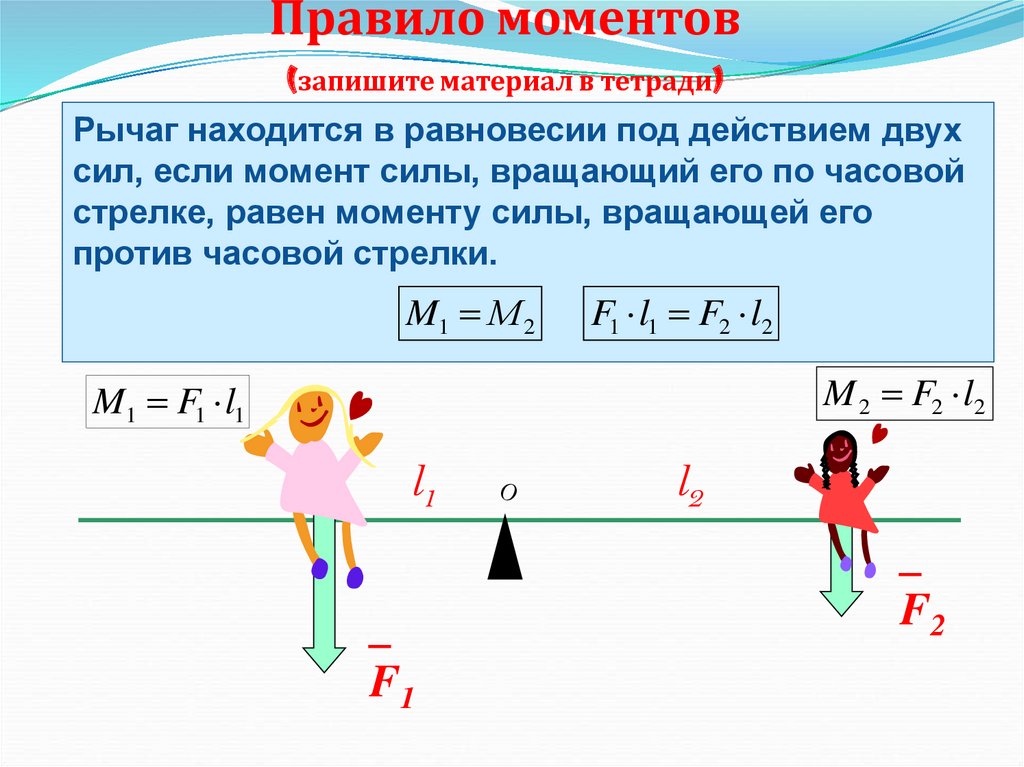 Если плечо входного рычага в 6 раз больше длины выходного
плечо рычага, система дает механическое преимущество в 6, а это означает, что для
на каждый фунт, который вы нажимаете на рычаг, вы можете поднять 6 фунтов груза.
Если плечо входного рычага в 6 раз больше длины выходного
плечо рычага, система дает механическое преимущество в 6, а это означает, что для
на каждый фунт, который вы нажимаете на рычаг, вы можете поднять 6 фунтов груза.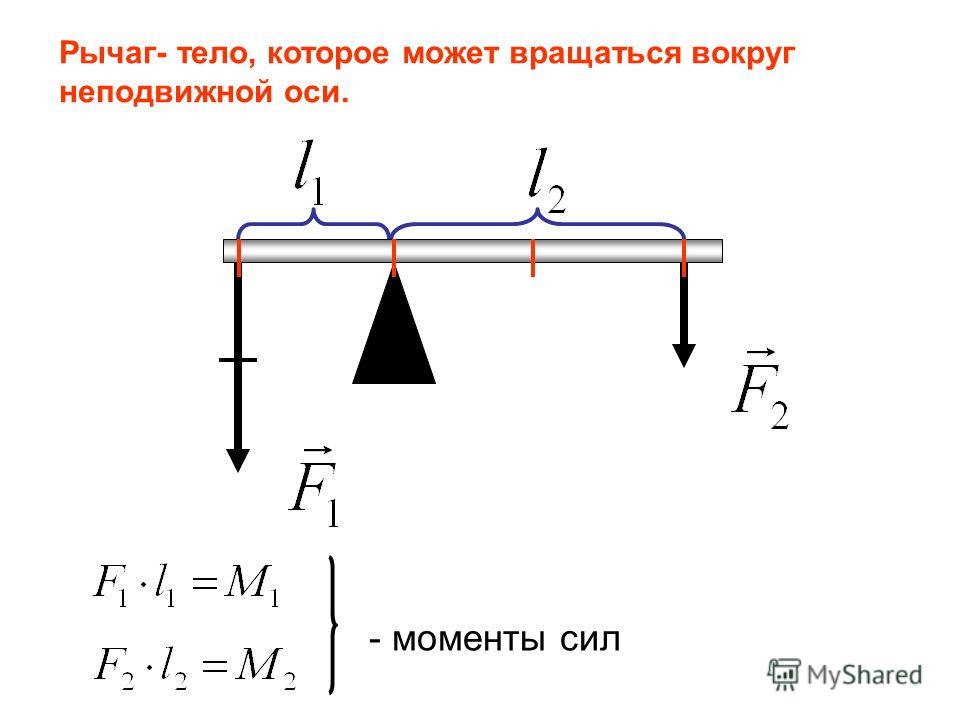 Крутящий момент — это не только произведение приложенной силы, умноженной на
плечо рычага … это также зависит от направления прилагаемой силы.
Крутящий момент — это не только произведение приложенной силы, умноженной на
плечо рычага … это также зависит от направления прилагаемой силы. Колесо и ось — это еще одна форма простого рычага. Видишь
Почему? К какому классу рычагов он относится?
Колесо и ось — это еще одна форма простого рычага. Видишь
Почему? К какому классу рычагов он относится?
 Эксцентриковый шкив
производит
механический dis преимущество в этой позе и действительно надо напрячься
первый.
Однако, как только вы потянете
стрелу назад (и ожидайте наибольшей борьбы с луком)… становится легко
держать и устойчиво. Это связано с тем, что шкив вращается, давая вам
механическое преимущество.
Эксцентриковый шкив
производит
механический dis преимущество в этой позе и действительно надо напрячься
первый.
Однако, как только вы потянете
стрелу назад (и ожидайте наибольшей борьбы с луком)… становится легко
держать и устойчиво. Это связано с тем, что шкив вращается, давая вам
механическое преимущество. .. крутящего момента и оборотов
(число оборотов в минуту). На самом деле формула выглядит так:
.. крутящего момента и оборотов
(число оборотов в минуту). На самом деле формула выглядит так: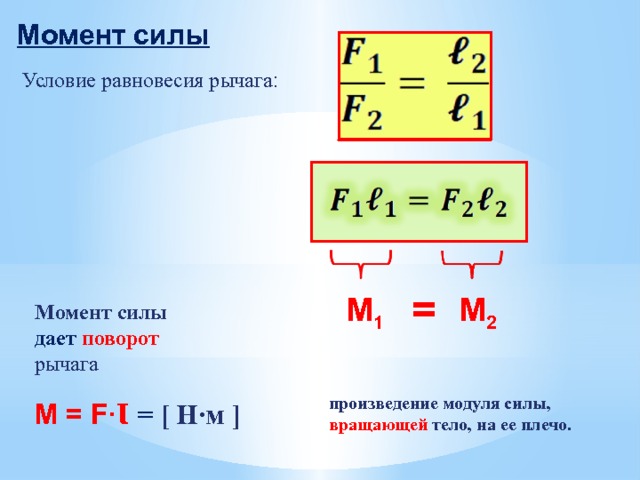 Gears позволяет вам
напрягаться примерно так же, но позволяет обменять скорость на крутящий момент или порок
наоборот При установке цепи педалью на наименьшую передачу и
задняя ось (колесо) устанавливается на самую большую передачу, вы обмениваете скорость на крутящий момент.
Вы будете ехать очень медленно, но обеспечите высокий крутящий момент на колесах (для движения вверх по склону).
холм). При спуске с горы требуется очень небольшой крутящий момент на колесах.
так что вы переключаете передачи и получаете много скорости. Тоже самое
происходит с вашей машиной. Выходная мощность двигателя может быть довольно постоянной
но трансмиссия играет в ту же игру крутящего момента против скорости, что и шестерни на
велосипед. Если вы хотите подняться на крутой холм, вам нужно больше крутящего момента на
колеса, поэтому вам нужно пожертвовать скоростью (об/мин), чтобы выполнить задачу.
Gears позволяет вам
напрягаться примерно так же, но позволяет обменять скорость на крутящий момент или порок
наоборот При установке цепи педалью на наименьшую передачу и
задняя ось (колесо) устанавливается на самую большую передачу, вы обмениваете скорость на крутящий момент.
Вы будете ехать очень медленно, но обеспечите высокий крутящий момент на колесах (для движения вверх по склону).
холм). При спуске с горы требуется очень небольшой крутящий момент на колесах.
так что вы переключаете передачи и получаете много скорости. Тоже самое
происходит с вашей машиной. Выходная мощность двигателя может быть довольно постоянной
но трансмиссия играет в ту же игру крутящего момента против скорости, что и шестерни на
велосипед. Если вы хотите подняться на крутой холм, вам нужно больше крутящего момента на
колеса, поэтому вам нужно пожертвовать скоростью (об/мин), чтобы выполнить задачу. Силу усилия необходимо прикладывать как можно
точки опоры, так как нагрузка исходит от точки опоры. То есть правила симметрии, поэтому
правая сторона является зеркальным отражением левой стороны.
Силу усилия необходимо прикладывать как можно
точки опоры, так как нагрузка исходит от точки опоры. То есть правила симметрии, поэтому
правая сторона является зеркальным отражением левой стороны.