ОглавлениеОТ ИЗДАТЕЛЬСТВАВВЕДЕНИЕ Глава I.  Кинематика§ 1. Движение тел § 2. Кинематика. Относительность движения и покоя. § 3. Траектория движения § 4. Поступательное и вращательное движения тела § 5. Движение точки § 6. Описание движения точки § 7. Измерение длины § 8. Измерение промежутков времени § 9. Равномерное прямолинейное движение и его скорость § 10. Знак скорости при прямолинейном движении § 11. Единицы скорости § 12. Графики зависимости пути от времени § 13. Графики зависимости скорости от времени § 14. Неравномерное прямолинейное движение § 15. Мгновенная скорость § 16. Ускорение при прямолинейном движении § 18. Знак ускорения при прямолинейном движении § 19. Графики скорости при прямолинейном равноускоренном движении § 20. Графики скорости при произвольном неравномерном движении § 21. Нахождение пути, пройденного при неравномерном движении, при помощи графика скорости § 22.  Путь, пройденный при равнопеременном движении§ 23. Векторы § 24. Разложение вектора на составляющие § 25. Криволинейное движение § 26. Скорость криволинейного движения § 27. Ускорение при криволинейном движении § 29. Кинематика космических движений Глава II. Динамика § 30. Задачи динамики § 31. Закон инерции § 32. Инерциальные системы отсчета § 33. Принцип относительности Галилея § 34. Силы § 35. Уравновешивающиеся силы. О покое тела и о движении по инерции § 36. Сила — вектор. Эталон силы § 37. Динамометры § 38. Точка приложения силы § 39. Равнодействующая сила § 40. Сложение сил, направленных по одной прямой § 41. Сложение сил, направленных под углом друг к другу § 42. Связь между силой и ускорением § 43. Масса тела § 44. Второй закон Ньютона § 45. Единицы силы и массы § 47. Третий закон Ньютона § 48. Примеры применения третьего закона Ньютона § 49.  Импульс тела§ 50. Система тел. Закон сохранения импульса § 51. Применения закона сохранения импульса § 52. Свободное падение тел § 53. Ускорение свободного падения § 54. Падение тела без начальной скорости и движение тела, брошенного вертикально вверх § 55. Вес тела § 56. Масса и вес § 57. Плотность вещества § 58. Возникновение деформаций § 59. Деформации в покоящихся телах, вызванные действием только сил, возникающих при соприкосновении § 61. Деформации тела, испытывающего ускорение § 62. Исчезновение деформаций при падении тел § 63. Разрушение движущихся тел § 64. Силы трения § 65. Трение качения § 66. Роль сил трения § 67. Сопротивление среды § 68. Падение тел в воздухе Глава III. Статика § 69. Задачи статики § 70. Абсолютно твердое тело § 71. Перенос точки приложения силы, действующей на твердое тело § 72. Равновесие тела под действием трех сил § 73.  Разложение сил на составляющие§ 74. Проекции сил. Общие условия равновесия § 76. Равновесие тела, закрепленного на оси § 77. Момент силы § 78. Измерение момента силы § 79. Пара сил § 80. Сложение параллельных сил. Центр тяжести § 81. Определение центра тяжести тел § 82. Различные случаи равновесия тела под действием силы тяжести § 83. Условия устойчивого равновесия под действием силы тяжести § 84. Простые машины § 85. Клин и винт Глава IV. Работа и энергия § 86. «Золотое правило» механики § 87. Применения «золотого правила» § 88. Работа силы § 89. Работа при перемещении, перпендикулярном к направлению силы § 90. Работа силы, направленной под любым углом к перемещению § 92. Единица работы § 93. О движении по горизонтальной плоскости § 94. Работа силы тяжести при движении по наклонной плоскости § 95.  Принцип сохранения работы§ 96. Энергия § 97. Потенциальная энергия § 98. Потенциальная энергия упругой деформации § 99. Кинетическая энергия § 100. Выражение кинетической энергии через массу и скорость тела § 101. Полная энергия тела § 102. Закон сохранения энергии § 103. Силы трения и закон сохранения механической энергии § 104. Превращение механической энергии во внутреннюю энергию § 106. Мощность § 107. Расчет мощности механизмов § 108. Мощность, быстроходность и размеры механизма § 109. Коэффициент полезного действия механизмов Глава V. Криволинейное движение § 110. Возникновение криволинейного движения § 111. Ускорение при криволинейном движении § 112. Движение тела, брошенного в горизонтальном направлении § 113. Движение тела, брошенного под углом к горизонту § 114. Полет пуль и снарядов § 115. Угловая скорость § 116. Силы при равномерном движении по окружности § 117.  § 118. Разрыв маховиков § 119. Деформация тела, движущегося по окружности § 120. «Американские горки» § 121. Движение на закруглениях пути § 122. Движение подвешенного тела по окружности § 123. Движение планет § 124. Закон всемирного тяготения § 125. Искусственные спутники Земли Глава VI. Движение в неинерциальных системах отсчета и силы инерции § 126. Роль системы отсчета § 127. Движение относительно разных инерциальных систем отсчета § 128. Движение относительно инерциальной и неинерциальной систем отсчета § 129. Поступательно движущиеся неинерциальиые системы § 131. Эквивалентность сил инерции и сил тяготения § 132. Невесомость и перегрузки § 133. Является ли Земля инерциальиой системой отсчета? § 134. Вращающиеся системы отсчета § 135. Силы инерции при движении тела относительно вращающейся системы отсчета § 136. Доказательство вращения Земли § 137.  ПриливыГлава VII. Гидростатика § 138. Подвижность жидкости § 139. Силы давления § 140. Измерение сжимаемости жидкости § 141. «Несжимаемая» жидкость § 142. Силы давления в жидкости передаются во все стороны § 143. Направление сил давления § 145. Мембранный манометр § 146. Независимость давления от ориентации площадки § 147. Единицы давления § 148. Определение сил давления по давлению § 149. Распределение давления внутри жидкости § 150. Закон Паскаля § 151. Гидравлический пресс § 152. Жидкость под действием силы тяжести § 153. Сообщающиеся сосуды § 154. Жидкостный манометр § 155. Устройство водопровода. Нагнетательный насос § 156. Сифон § 157. Сила давления на дно сосуда § 158. Давление воды в морских глубинах § 159. Прочность подводной лодки § 160. Закон Архимеда § 161. Измерение плотности тел на основании закона Архимеда § 162. Плавание тел § 163. Плавание несплошных тел  Устойчивость плавания кораблей§ 165. Всплывание пузырьков § 166. Тела, лежащие на дне сосуда Глава VIII. Аэростатика § 167. Механические свойства газов § 168. Атмосфера § 169. Давление атмосферы § 170. Другие опыты, показывающие существование атмосферного давления § 171. Разрежающие насосы § 172. Влияние атмосферного давления на уровень жидкости в трубке § 173. Максимальная высота столба жидкости § 174. Опыт Торричелли. Ртутный барометр и барометр-анероид § 175. Распределение атмосферного давления по высоте § 176. Физиологическое действие пониженного давления воздуха § 178. Воздушные шары и дирижабли § 179. Применение сжатого воздуха в технике Глава IX. Гидродинамика и аэродинамика § 180. Давление в движущейся жидкости § 181. Течение жидкости по трубам § 182. Закон Бернулли § 183. Жидкость в неинерциальных системах отсчета § 184. Реакция движущейся жидкости и ее использование § 185. 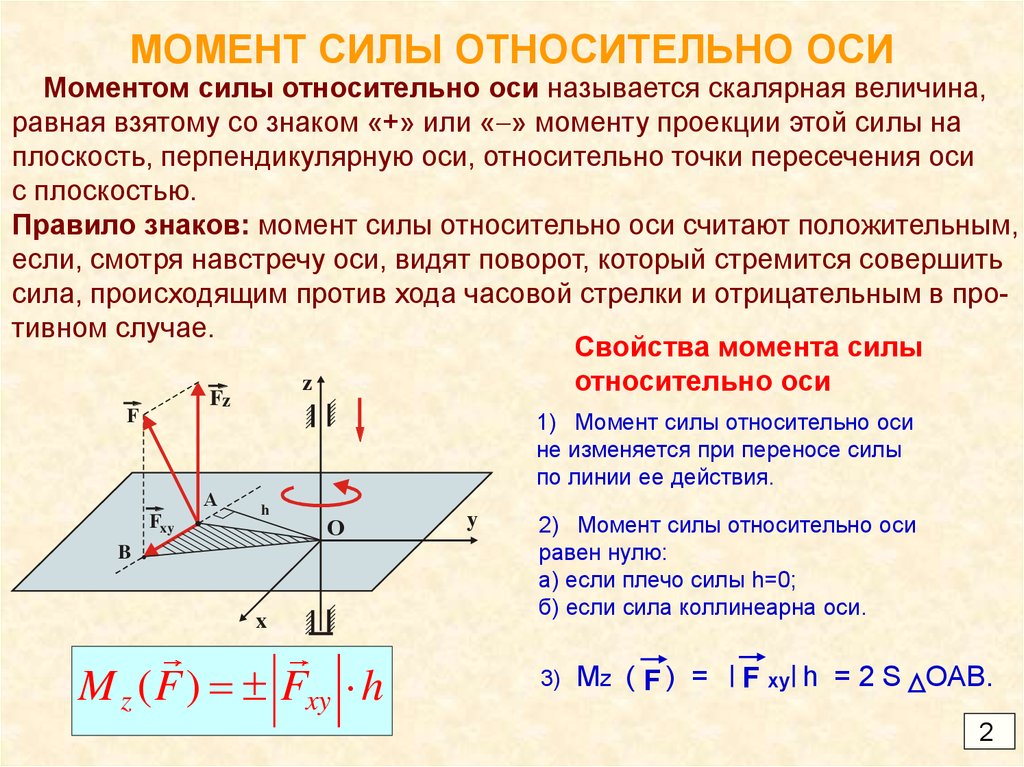 Перемещение на воде§ 186. Ракеты § 187. Реактивные двигатели § 188. Баллистические ракеты § 189. Взлет ракеты с Земли § 190. Сопротивление воздуха § 191. Эффект Магиуса и циркуляция § 192. Подъемная сила крыла и полет самолета § 193. Турбулентность в потоке жидкости или газа § 194. Ламинарное течение РАЗДЕЛ ВТОРОЙ. ТЕПЛОТА. МОЛЕКУЛЯРНАЯ ФИЗИКА Глава X. Тепловое расширение твердых и жидких тел § 195. Тепловое расширение твердых и жидких тел § 196. Термометры § 197. Формула линейного расширения § 198. Формула объемного расширения § 199. Связь между коэффициентами линейного и объемного расширения § 200. Измерение коэффициента объемного расширения жидкостей § 201. Особенности расширения воды Глава XI. Работа. Теплота. Закон сохранения энергии § 202. Изменения состояния тел § 203. Нагревание тел при совершении работы § 204. Изменение внутренней энергии тел при теплопередаче § 205. Единицы количества теплоты § 206. 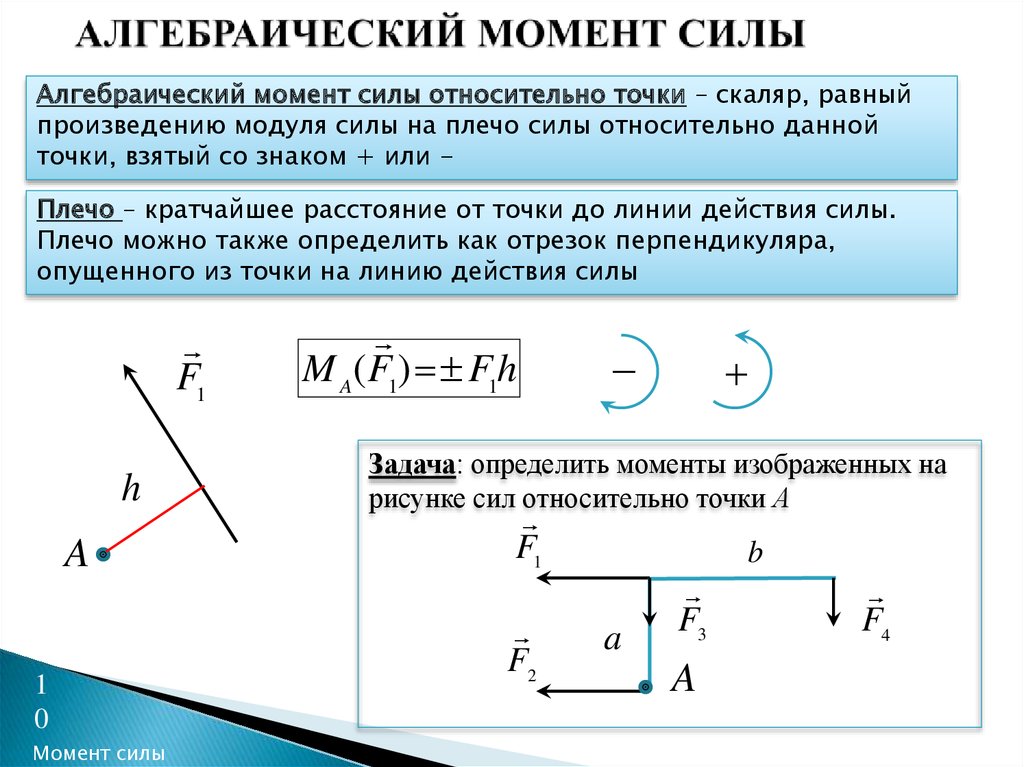 Зависимость внутренней энергии тела от его массы и вещества§ 207. Теплоемкость тела § 208. Удельная теплоемкость § 209. Калориметр. Измерение теплоемкостей § 210. Закон сохранения энергии § 211. Невозможность «вечного двигателя» § 212. Различные виды процессов, при которых происходит передача теплоты Глава XII. Молекулярная теория § 213. Молекулы и атомы § 214. Размеры атомов и молекул § 215. Микромир § 216. Внутренняя энергия с точки зрения молекулярной теории § 217. Молекулярное движение § 218. Молекулярное движение в газах, жидкостях и твердых телах § 219. Броуновское движение § 220. Молекулярные силы Глава XIII. Свойства газов § 221. Давление газа § 222. Зависимость давления газа от температуры § 223. Формула, выражающая закон Шарля § 224. Закон Шарля с точки зрения молекулярной теории § 225. Изменение температуры газа при изменении его объема. Адиабатические и изотермические процессы § 226. Закон Бойля — Мариотта § 227.  Формула, выражающая закон Бойля — Мариотта§ 228. График, выражающий закон Бойля — Мариотта § 229. Зависимость между плотностью газа и его давлением § 230. Молекулярное толкование закона Бойля — Мариотта § 231. Изменение объема газа при изменении температуры § 232. Закон Гей-Люссака § 233. Графики, выражающие законы Шарля и Гей-Люссака § 234. Термодинамическая температура § 235. Газовый термометр § 236. Объем газа и термодинамическая температура § 237. Зависимость плотности газа от температуры § 238. Уравнение состояния газа § 239. Закон Дальтона § 240. Плотность газов § 241. Закон Авогадро § 242. Моль. Постоянная Авогадро § 243. Скорости молекул газа § 244. Об одном из способов измерения скоростей движения молекул газа (опыт Штерна) § 245. Удельные теплоемкости газов § 246. Молярные теплоемкости § 247. Закон Дюлонга и Пти Глава XIV. Свойства жидкостей § 248. Строение жидкостей § 249. Поверхностная энергия § 250. 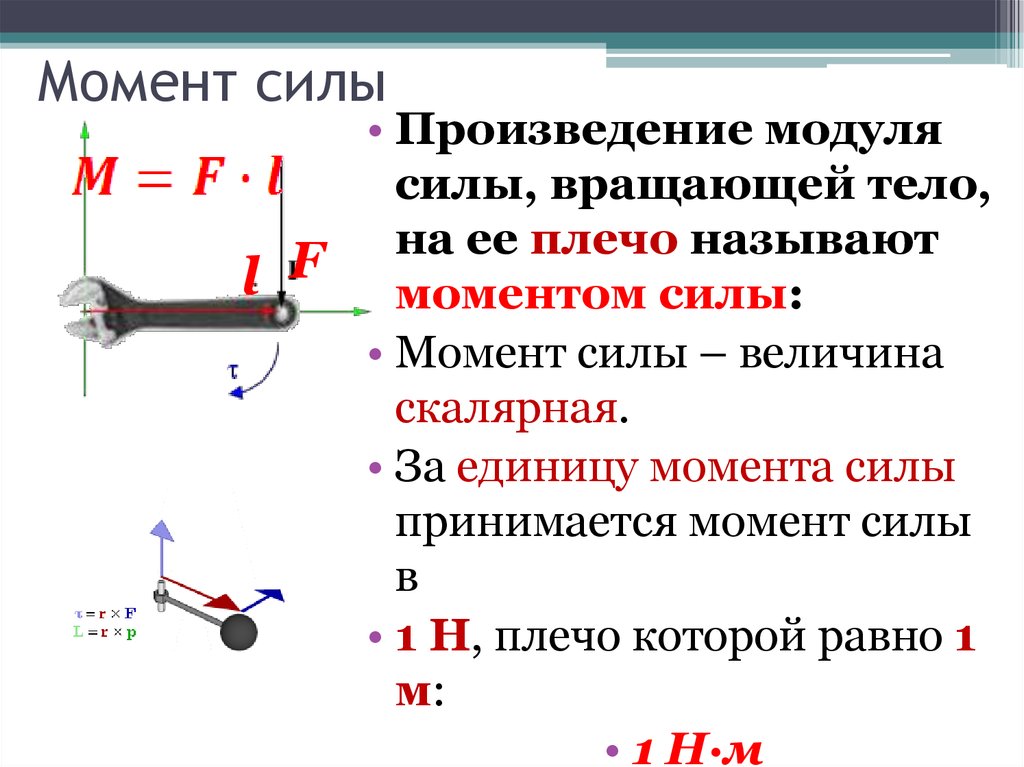 Поверхностное натяжение§ 251. Жидкостные пленки § 252. Зависимость поверхностного натяжения от температуры § 253. Смачивание и несмачивание § 254. Расположение молекул у поверхности тел § 255. Значение кривизны свободной поверхности жидкости § 256. Капиллярные явления § 257. Высота поднятия жидкости в капиллярных трубках § 258. Адсорбция § 259. Флотация § 260. Растворение газов § 261. Взаимное растворение жидкостей § 262. Растворение твердых тел в жидкостях Глава XV. Свойства твердых тел. Переход тел из твердого состояния в жидкое § 263. Введение § 264. Кристаллические тела § 265. Аморфные тела § 266. Кристаллическая решетка § 267. Кристаллизация § 268. Плавление и отвердевание § 269. Удельная теплота плавления § 270. Переохлаждение § 271. Изменение плотности веществ при плавлении § 272. Полимеры § 273. Сплавы § 274. Затвердевание растворов § 275. Охлаждающие смеси § 276. Изменения свойств твердого тела Глава XVI. 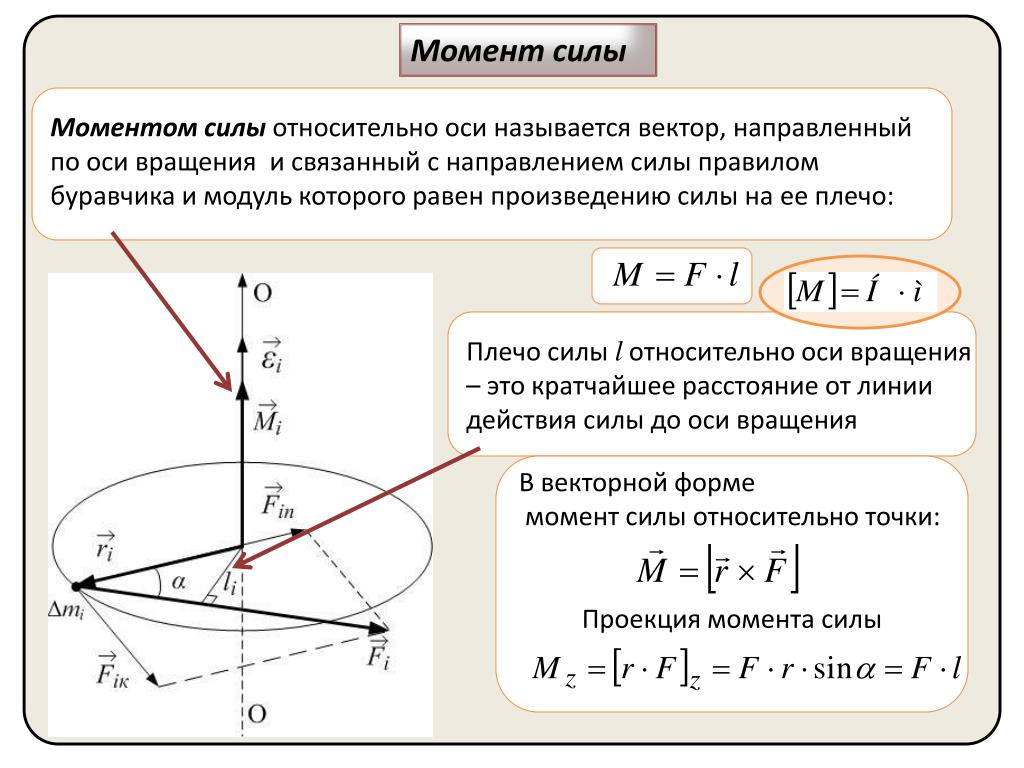 Упругость и прочность§ 277. Введение § 278. Упругие и пластические деформации § 279. Закон Гука § 280. Растяжение и сжатие § 281. Сдвиг § 282. Кручение § 283. Изгиб § 284. Прочность § 285. Твердость § 286. Что происходит при деформации тел § 287. Изменение энергии при деформации тел Глава XVII. Свойства паров § 288. Введение § 289. Пар насыщенный и ненасыщенный § 290. Что происходит при изменении объема жидкости и насыщенного пара § 291. Закон Дальтона для пара § 292. Молекулярная картина испарения § 293. Зависимость давления насыщенного пара от температуры § 294. Кипение § 295. Удельная теплота парообразования § 296. Охлаждение при испарении § 297. Изменение внутренней энергии при переходе вещества из жидкого состояния в парообразное § 298. Испарение при кривых поверхностях жидкости § 299. Перегревание жидкости § 300. Пересыщение паров § 301. Насыщение пара при возгонке § 302. Превращение газа в жидкость § 303.  Критическая температура§ 304. Сжижение газов в технике § 305. Вакуумная техника § 306. Водяной пар в атмосфере Глава XVIII. Физика атмосферы § 307. Атмосфера § 308. Тепловой баланс Земли § 309. Адиабатические процессы в атмосфере § 310. Облака § 311. Искусственные осадки § 312. Ветер § 313. Предсказание погоды Глава XIX. Тепловые машины § 314. Условия, необходимые для работы тепловых двигателей § 315. Паросиловая станция § 316. Паровой котел § 317. Паровая турбина § 318. Поршневая паровая машина § 319. Конденсатор § 320. Коэффициент полезного действия теплового двигателя § 321. Коэффициент полезного действия паросиловой станции § 322. Бензиновый двигатель внутреннего сгорания § 323. Коэффициент полезного действия двигателя внутреннего сгорания § 324. Двигатель Дизеля § 325. Реактивные двигатели § 326. Передача теплоты от холодного тела к горячему Ответы и решения к упражнениям Предметный указатель |
Физика Момент силы.
Второе условие равновесия твёрдого телаМатериалы к уроку
Конспект урока
Одним из условий равновесия твердого тела является геометрическая сумма внешних сил, действующих на тело, которая должна быть равна нулю. Это условие является необходимым, но не является достаточным. Чтобы в этом убедиться проведем опыт. Приложим к дощечке, лежащей на плоской поверхности, в различных точках две силы равные по модулю, но направленные в противоположные стороны. Сумма этих двух сил равна нулю. Но дощечка не останется в равновесии, она будет поворачиваться. Первое условие равновесия твердого тела выполняется, но тело не находится в равновесии.
Другой пример, на руль автомобиля во время поворота действуют две силы, приложенные в двух разных точках. Эти силы одинаковые по модулю и противоположно направленные. Сумма этих двух сил так же равна нулю, а руль не находится в состоянии покоя.
Почему же так происходит? Тело находится в равновесии, если сумма всех приложенных к каждому его элементу сил равна нулю. В наших примерах сумма внешних сил, приложенных к телу, равна нулю. Но если брать каждый отдельный элемент, сумма действующих на него сил может быть не равна нулю. Поэтому и дощечка, и руль в данных случаях не находятся в равновесии.
Для того чтобы выяснить, какое же еще условие должно выполняться, чтобы твердое тело находилось в равновесии, вспомним теорему об изменении кинетической энергии. Изменение кинетической энергии тела за некоторый промежуток времени равно работе, совершенной за то же время силой, действующей на тело.
Рассмотрим пример, при каком условии будет оставаться в равновесии стержень, шарнирно закрепленный на горизонтальной оси в точке 0. Эта конструкция представляет собой обыкновенный рычаг. Пусть к рычагу приложены две перпендикулярные стержню силы F1 и F2. Предположим, что это силы натяжения веревок, к концам которых прикреплены грузы.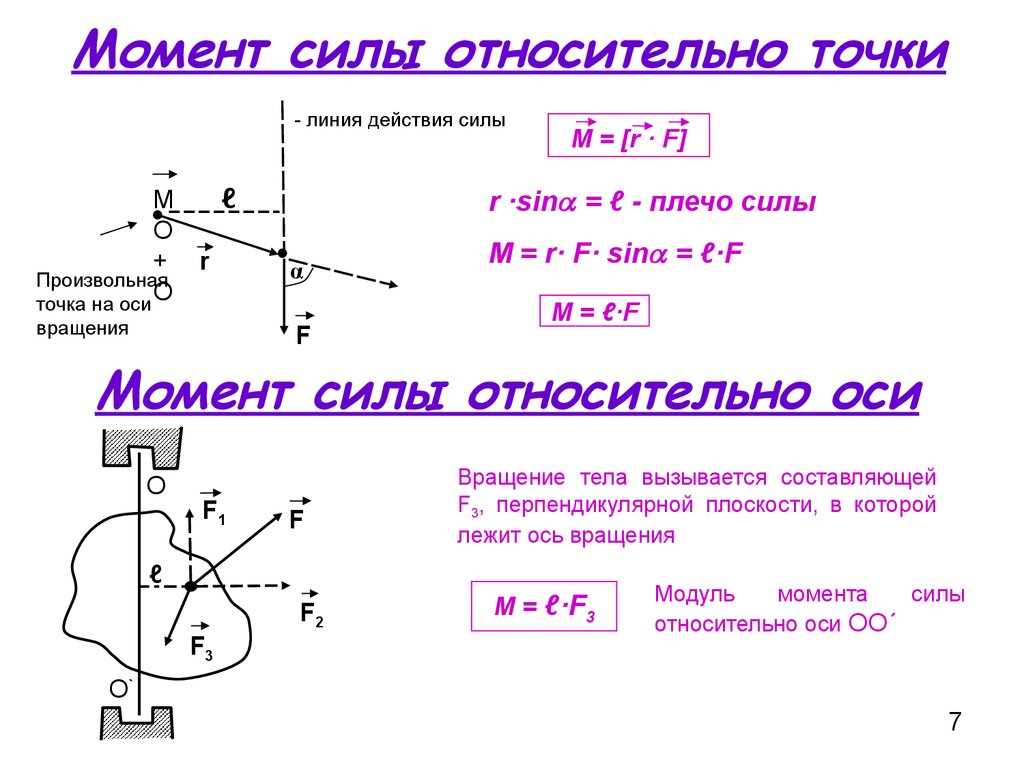
Кроме этих двух сил, на рычаг ещё действует направленная вертикально вверх сила реакции опоры со стороны оси рычага F3. При равновесии рычага сумма всех трех сил равна нулю.
Найдем работу, которую совершают внешние силы при повороте рычага на очень малый угол α. Точка приложения силы F1 пройдет путь равный BB1. А точка приложения силы F2 пройдёт путь равный CC1. Так как угол α невелик, можно считать линии BB1 и CC1 отрезками прямой. Работа силы F1 положительна, потому что точка B перемещается в том же направлении, что и сила, а работа силы F2 отрицательна, так как точка приложения силы C движется в сторону противоположную направлению силы. Сила F3 работы не совершает, потому что точка 0 не перемещается.
Пройденные пути s1 и s2 можно выразить через угол поворота рычага α, измеренный в радианах. Тогда перемещение точки приложения силы F1 равно произведению угла α на длину отрезка BO. А перемещение точки приложения силы F2 равно произведению угла α на длину отрезка СO.
Подставим эти равенства в формулы работы сил F1 и F2. Получим, что работа силы F1 равна произведению модуля силы F1 на угол α и на длину отрезка ВО. Работа силы F2 равна произведению модуля силы F2 на угол α и на длину отрезка СО.
Радиусы ВО и СО дуг окружностей, описываемых точками приложения сил F1 и F2, являются перпендикулярами, опущенными из оси вращения на линии действия этих сил.
Кратчайшее расстояние от оси вращения до линии действия силы называют плечом силы.
Плечо силы обозначим буквой d. Плечо силы F1 равно d1. Плечо силы F2 равно d2.
Тогда выражения для работы сил F1 и F2 примут следующий вид. Работа силы F1 равна произведению модуля силы F1 на угол α и на плечо силы F1. Работа силы F2 равна произведению модуля силы F2 на угол α и на плечо силы F2.
Полученные формулы показывают, что при заданном угле поворота тела работа каждой приложенной к этому телу силы равна произведению модуля силы на плечо взятому со знаком «+» или «-».
Это произведение называют моментом силы.
Моментом силы относительно оси вращения тела называется произведение модуля силы на ее плечо. Момент силы может быть положительным или отрицательным.
Если сила, действующая на тело, направлена так, чтобы повернуть его против часовой стрелки, то момент силы считают положительным, если по часовой, то отрицательным.
В нашем примере момент силы F1 равен произведению модуля силы F1 на плечо силы F1. Момент силы F2 равен произведению модуля силы F2 на плечо силы F2. Сила F1 стремится повернуть стержень против часовой стрелки, значит момент этой силы положительный. Сила F2 стремится повернуть стержень по часовой стрелке, значит момент этой силы отрицательный.
Следовательно, выражения для работы сил F1 и F2 можно записать в таком виде: работа силы F1 равна произведению момента силы F1 на угол α; работа силы F2 равна произведению момента силы F2 на угол α.
Полная работа внешних сил складывается из работы сил F1, F2 и F3.
Работа силы F3 равна нулю, потому что точка 0 не перемещается. Подставим в формулу вместо работы сил F1 и F2 произведения моментов сил на угол поворота. Получаем, что полная работа внешних сил равна произведению суммы моментов сил F1 и F2 на угол α.
Для того чтобы тело пришло в движение, нужно чтобы увеличилась его кинетическая энергия, а для этого внешние силы должны совершить работу.
Согласно полученному уравнению, работа внешних сил может быть отлична от нуля только в том случае, если сумма моментов этих сил не равна нулю. Если же суммарный момент внешних сил, действующих на тело, равен нулю, то их работа равна нулю. Следовательно, кинетическая энергия тела не увеличивается, то есть остается равной нулю. Значит, тело не приходит в движение.
Это есть второе условие, необходимое для равновесия твердого тела.
При равновесии твердого тела сумма моментов всех внешних сил, действующих на него относительно любой оси, равна нулю.
Если же на абсолютно твердое тело действует произвольное число сил, условия равновесия абсолютно твердого тела следующие:
‒ во-первых, геометрическая сумма внешних сил, действующих на тело, равна нулю,
‒ во-вторых, сумма моментов всех внешних сил, действующих на тело относительно любой оси, равна нулю.
Эти условия являются необходимыми и достаточными для равновесия твердого тела. Если они выполняются, то тело остается в равновесии.
Если же тело не является абсолютно твердым, даже при соблюдении двух условий равновесия, это тело может и не оставаться в равновесии.
Это происходит из-за того, что под воздействием приложенных к нему сил тело может деформироваться и тогда сумма всех сил, действующих на каждый его элемент, не будет равна нулю. Возьмем, например, резиновый шнур. Приложим к его концам две силы, равные по модулю и направленные вдоль шнура в противоположные стороны. Под действием этих сил шнур будет растягиваться, а, значит, выйдет из состояния равновесия, несмотря на то, что сумма внешних сил равна нулю и нулю равна сумма их моментов относительно оси, проходящей через любую точку шнура.
Остались вопросы по теме? Наши репетиторы готовы помочь!
Подготовим к ЕГЭ, ОГЭ и другим экзаменам
Найдём слабые места по предмету и разберём ошибки
Повысим успеваемость по школьным предметам
Поможем подготовиться к поступлению в любой ВУЗ
Выбрать репетитораОставить заявку на подбор
Укажите, когда момент силы положительный, а когда отрицательный.
Если вы видите это сообщение, это означает, что JavaScript отключен в вашем браузере , включите JS , чтобы это приложение заработало.Получение изображения
Пожалуйста, подождите…
Предыдущий вопросСледующий вопрос
Вопрос :
Ответ :
Связанный ответ
Когда работа совершается отрицательной силой и когда она совершается отрицательной силой и когда совершается работа отрицательной силой?
Подробнее связанные с вопросами и ответы
3,0K Like
3,0K просмотр
1,5K Акции
3,0K Like
3,0K Просмотры
1,5K Share
3,0K Like
1,5K SHARES
3,0K LIFE
404040404040404040404040404040404040404.
0004.0004.0004.0004.0004.0004 3,0404040404040404040404040404036 1,5K. K Акции
3,0K Like
3,0K Просмотр
1,5K Акции
3.0K Like
3,0K просмотр
1,5K Акции
3,0K Like
3,01K VIEWS
3,0K LIFK
3,01K VIEWS
3,0K
3,0K. k НРАВИТСЯ
3,0K Просмотр
1,5K Акции
3,0K Like
3,0K просмотр
1,5K Акции
3,0K Like
3.013
1,5K SHARES
9001K 3,013 9008.0008 9001K 9001K 9001K 3,011.1,5K Акции
3,0K Like
3,0K Просмотр
1,5K Акции
3,0K Like
3,0K VISIT
3.
0k НРАВИТСЯ
3,0K Просмотр
1,5K Акции
3,0K, такие как
3,0K просмотр
1,5K Акции
3,0K Like
3,0K Views
1,5K Шарес.
1,5K Акции
3,0K Like
3,0K просмотр
1,5K Акции
3,0K любят
3,0K View
1,5K. , Doubtnut не владеет и не контролирует характер и содержание этих вопросов. Doubtnut не несет ответственности за какие-либо расхождения относительно дублирования контента по этим вопросам.
Если моменту силы присвоить отрицательный знак, то будет ли тенденция силы вращаться по часовой стрелке или против часовой стрелки?
Last updated date: 23rd Mar 2023
•
Total views: 270k
•
Views today: 6.
48k
Answer
Verified
270k+ views
Hint: A body has a tendency to вращаться вокруг оси или точки. Это можно назвать моментом силы. Таким образом, тело не будет перемещаться в направлении действия силы.
Полный пошаговый ответ:
Момент силы заставляет тело вращаться вокруг оси. Движение не будет поступательным. К телу приложена сила, которая заставляет тело вращаться вокруг оси. Именно из-за неравной и противоположной силы создается момент.
Величина момента силы прямо пропорциональна приложенной силе и расстоянию силы от оси. Перпендикулярное расстояние между линией действия и центром моментов можно назвать плечом момента. Следовательно,
${\text{Момент}} = F \times d$
Где $F$ — сила, а $d$ — плечо момента.
Центр момента — это точка отсчета, в которой сила вызывает вращение. Если вращение происходит по часовой стрелке вокруг центра момента, мы можем сказать, что момент положительный.
