Момент силы – формула, определение, свойства кратко (7 класс)
4.3
Средняя оценка: 4.3
Всего получено оценок: 86.
Обновлено 4 Марта, 2021
4.3
Средняя оценка: 4.3
Всего получено оценок: 86.
Обновлено 4 Марта, 2021
Из курса физики в 7 классе известно, что сила имеет три параметра: точку приложения, модуль и направление. Для вращательного движения точка приложения приобретает особое значение. В расчетах оказывается целесообразным заменить силу другим, более удобным понятием, учитывающим точку приложения, — моментом силы. Рассмотрим его суть, дадим определение, выведем формулу момента силы.
Сила при вращательном движении
Вращательное движение отличается от поступательного тем, что различные точки проходят различное расстояние и имеют различную мгновенную скорость, в зависимости от расстояния до оси вращения. Сила, приложенная к вращающемуся телу, также по-разному влияет на точки, лежащие на разном расстоянии от оси.
Фактически тело, начинающее вращение под действием силы, представляет собой рычаг второго рода с точкой опоры на оси вращения. И чем дальше от опоры находится точка приложения силы, тем меньшая сила требуется для движения рычага. Если приложить силу вдвое дальше от точки опоры, то для поворота рычага на один и тот же угол потребуется сила вдвое меньше. То есть для одного и того же поворота произведение силы на радиус поворота оказывается одинаковым.
Момент силы
В динамике вращательного движения важна не непосредственно величина силы, а произведение этой величины на расстояние от точки вращения. Это произведение называется моментом силы, обозначается буквой $M$:
$$M=F_\tau R$$
Из приведенной формулы можно получить размерность момента: поскольку сила измеряется в ньютонах, а радиус — в метрах, единица измерения момента силы получается равной ньютон-метру. Радиус вращения при этом нередко называют «плечом силы» $l$.
Момент силы.Обратите внимание, что вращательное движение создает только компонента силы, направленная перпендикулярно радиусу поворота, — тангенциальная составляющая силы:
$$F_\tau = F sin \alpha,$$
где $\alpha$ — это угол между радиус-вектором точки, к которой приложена сила $F$, и вектором приложения этой силы.
В самом деле, если сила направлена от точки приложения точно в сторону оси вращения, никакого вращательного движения создать с помощью этой силы не получится, какой бы модуль у этой силы не был. Формула также подтверждает это — синус угла между вектором силы, направленной точно на ось, и радиус-вектором точки приложения равен нулю, а значит, и тангенциальная составляющая силы также будет равна нулю. Момент такой силы, соответственно, также будет нулевым. Создать вращение будет невозможно.
Вращение невозможно создать также в случае, когда сила приложена непосредственно к оси вращения, независимо от ее направления. Радиус-вектор точки приложения силы при этом равен нулю, и определить тангенциальную составляющую приложенной силы невозможно.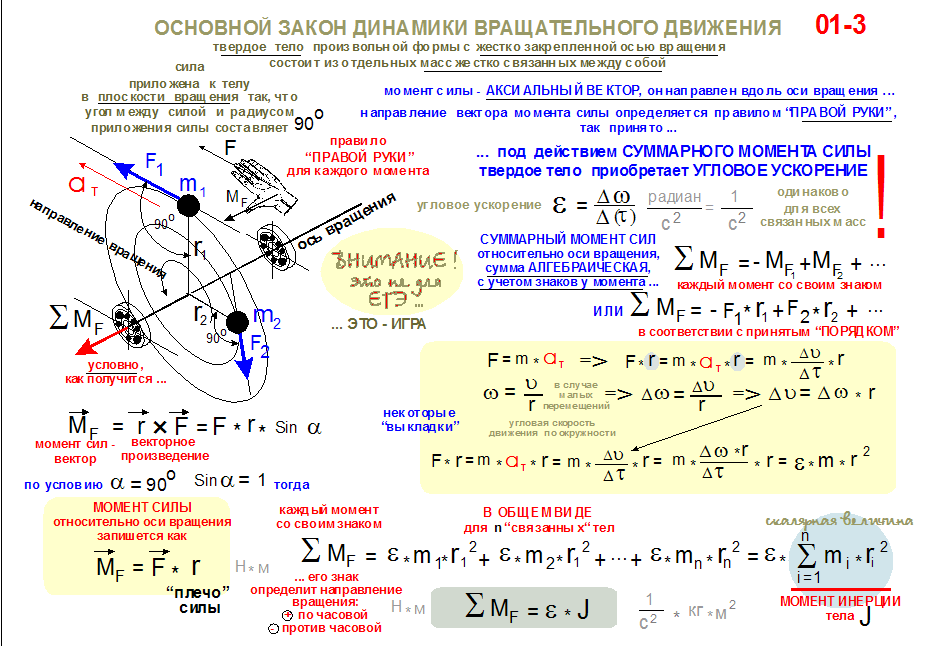
Знак момента силы
Тангенциальная составляющая силы, входящая в формулу момента силы, может иметь два направления. В зависимости от направления такой момент силы может как увеличивать скорость вращения тела, так и уменьшать ее.
Для учета этой разницы вводится такое свойство момента, как знак.
Поскольку угол на координатной плоскости отсчитывается в направлении против часовой стрелки, то момент силы, поворачивающий тело в этом направлении, считается положительным. Если момент силы поворачивает тело по часовой стрелке, он принимается отрицательным.
Что мы узнали?
Для вращательного движения особую роль играет точка приложения силы. Поэтому при исследовании вращательного движения используется не понятие силы, а понятие момента силы, который равен произведению тангенциальной составляющей силы на радиус поворота и измеряется в ньютон-метрах.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.3
Средняя оценка: 4.3
Всего получено оценок: 86.
Момент силы — Лекции по динамике вращательного движения
- Главная страница 🏠
- 📚 Библиотека
- 👉 Механика 👈
- Лекции по динамике вращательного движения
Нужна помощь в написании работы?
Узнать стоимость
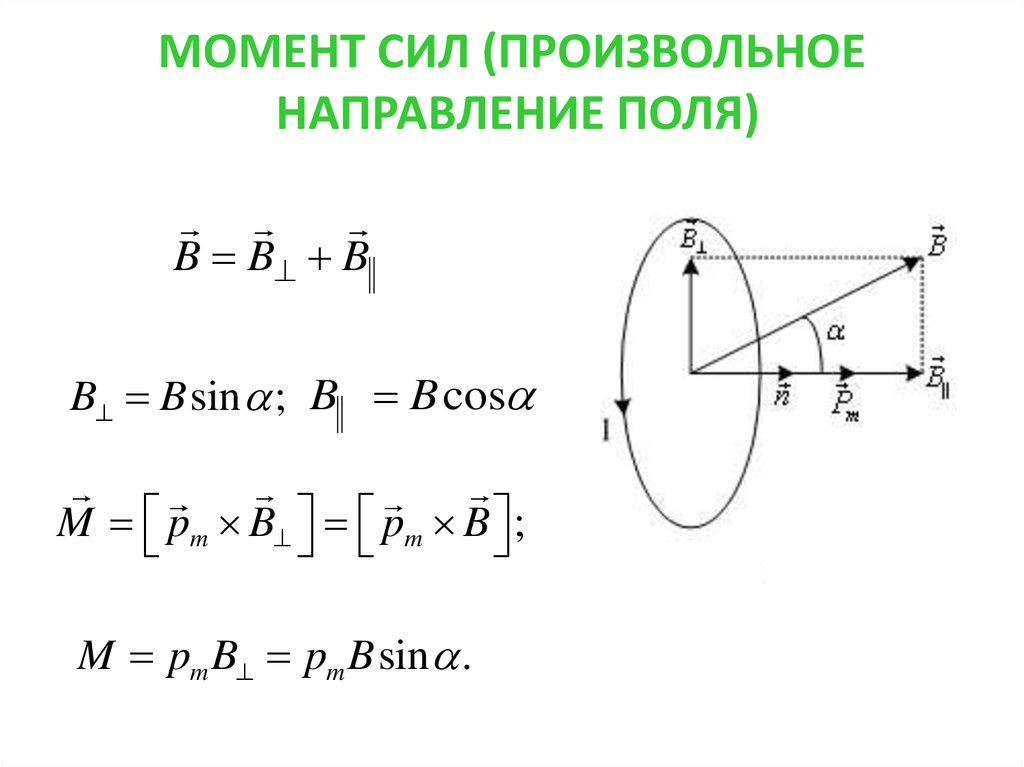
Вектором момента силы относительно полюса называют векторное произведение радиус-вектора и вектора силы:
Направление вектора момента силы находится по правилу правого винта (см. рис): перенесем вектор параллельно самому себе так, чтобы совпадали начала векторов и . Если вращать головку винта в направлении от вектора к вектору , то поступательное движение винта укажет направление вектора момента силы .
Модуль вектора момента силы равен:
,
где — угол между радиус-вектором и линией действия силы.
Момент равнодействующей силы относительно полюса О равен геометрической сумме векторов моментов составляющих сил относительно того же полюса:
или
Поможем написать любую работу на аналогичную тему
Реферат
Момент силы
От 250 руб
Контрольная работа
Момент силы
От 250 руб
Курсовая работа
Момент силы
От 700 руб
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Поделись с друзьями
- Содержание
- Материалы 5
- Меню
Момент инерции материальной точки,
Момент инерции системы материальных точек
Момент силы
Момент импульса материальной точки
Связь вектора момента силы и момента импульса
Связь момента инерции, момента силы и момента импульса и ЗСМИ
Работа, совершаемая телом при вращении.
Кинетическая энергия вращающегося тела
Материалы по теме:
Момент импульса. Момент силы Лекция
Момент импульса. Момент силы Шпаргалка
Момент силы. Лекция
Работа момента силы. Лекция
Момент силы. Плечо силы. Шпаргалка
Добавить в избранное (необходима авторизация)
Подробные объяснения и проблемы — Lambda Geeks
В этой статье мы обсудим, как найти направление крутящего момента и другие его аспекты.
Правило правой руки используется для определения пути вектора крутящего момента. Вектор крутящего момента направлен в плоскость большого пальца, если рука обвивается вокруг плоскости вращения, а пальцы ориентированы по вектору силы.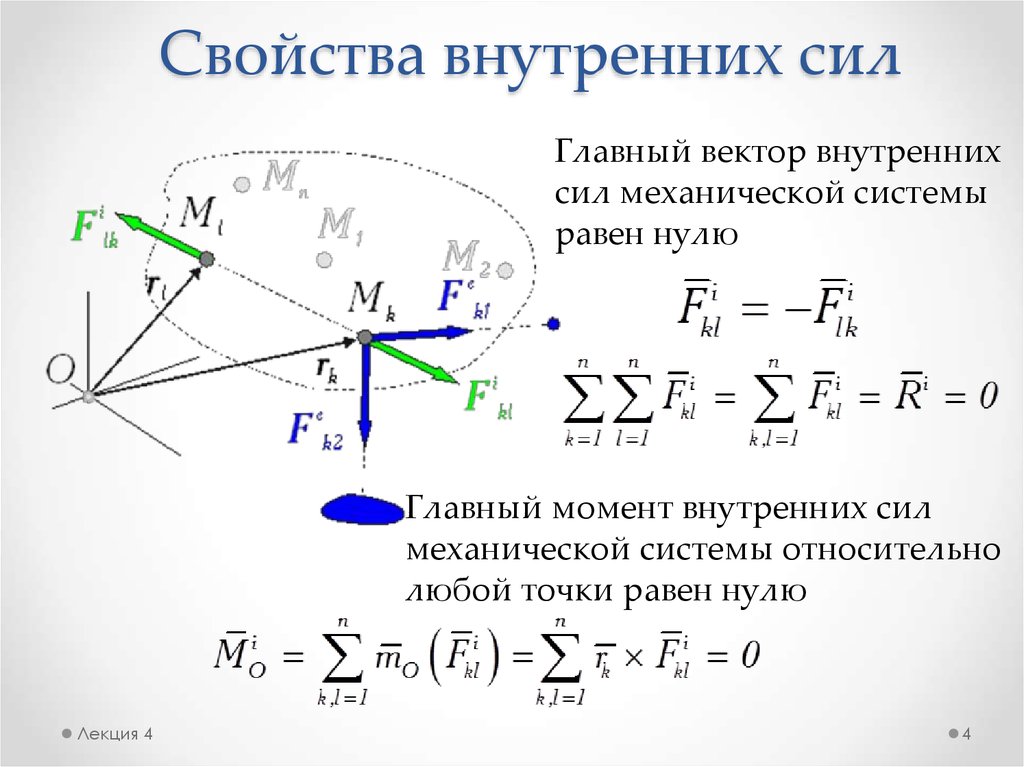
Крутящий момент — это измерение силы, необходимой для вращения предмета вокруг оси. В линейной кинематике сила заставляет объект ускоряться; в угловой кинематике крутящий момент позволяет объекту ускоряться. Крутящий момент — это параметр, который измеряется как вектор. Ориентация вектора крутящего момента определяется силой, действующей на ось.
Крутящий момент интуитивно понятен каждому, кто когда-либо открывал дверь. Открывая дверь, человек нажимает на ту сторону двери, которая находится дальше всего от петель. I t требуется гораздо больше усилий, чтобы нажать на сторону, ближайшую к петлям. Несмотря на то, что труд в обоих случаях одинаков (большее усилие передается по меньшему радиусу), люди предпочитают применять меньшее усилие, поэтому дверная ручка обычно расположена посередине.
Направление крутящего момента: Snappy Goat Термин «статический крутящий момент» относится к крутящему моменту, который не создает углового ускорения.
Поскольку дверь не вращается на петлях независимо от приложенной силы, кто-то, толкая ее, прикладывает к ней статический крутящий момент. Поскольку они не ускоряются, кто-то, крутящий педали велосипеда в постоянном темпе, также применяет статический крутящий момент.
Кинетический крутящий момент передается валом-шестерней спортивного транспортного средства, движущегося со стартового положения, поскольку он должен создавать угловое ускорение колес при условии, что автомобиль движется по трассе. Словарь, используемый для описания крутящего момента, может немного сбить с толку. Ученые часто без разбора используют термины «момент» и «момент силы». Плечо момента относится к радиусу действия силы.
Для вращающейся системы идея вращательного равновесия идентична первому закону Ньютона. Без воздействия внешнего крутящего момента предмет, который не вращается, остается таким. Точно так же, если на него не действует внешний крутящий момент, тело, вращающееся с постоянной угловой скоростью, будет продолжать вращаться.
При решении проблем с несколькими вращающими моментами, воздействующими на вращающийся объект, пригодится идея вращательного равновесия. В этом сценарии важен чистый крутящий момент. Если чистый крутящий момент вращающегося объекта равен нулю, он будет находиться в равновесии вращения и не сможет получить угловое ускорение.
Как найти направление крутящего момента в электрическом поле?Чтобы определить крутящий момент, создаваемый диполем во внешнем поле, представьте себе диполь, расположенный в однородном внешнем поле «E».
Положительный заряд подвергается воздействию электрического давления по верхней оси значения «qE», тогда как отрицательный заряд подвергается воздействию электрической силы по направлению вниз значения «qE».
Можно видеть, что диполь находится в переходном равновесии, поскольку результирующее давление равно нулю. Что, с другой стороны, вращательное равновесие? Диполь в этом случае может оставаться неподвижным, но он вращается с заданной угловой скоростью.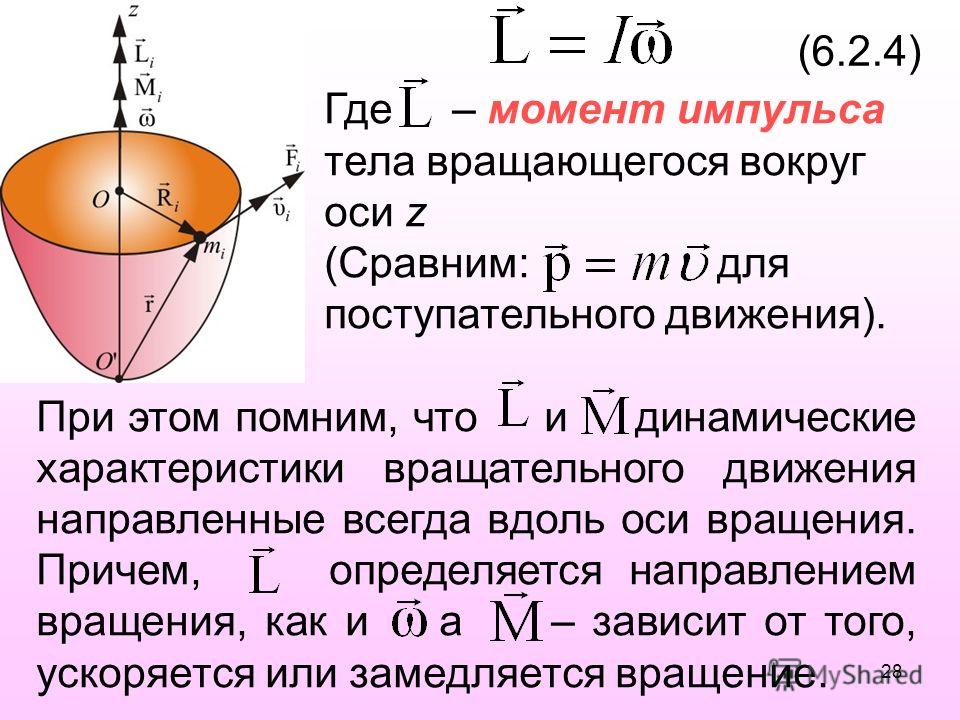
Это было показано эмпирически, указывая на то, что оба электростатических давления (qE) действуют как крутящий момент по часовой стрелке.
В ответ диполь вращается, если его поместить в однородное внешнее электрическое поле. Обычно помните, что крутящий момент всегда применяется парами. величина также является следствием сочетания силы и руки. Пространство, разделяющее место приложения давления и место вращения диполя, можно назвать плечом.
Как найти направление крутящего момента в магнитном поле?Таким же образом, как вычислялся крутящий момент, создаваемый электрическим диполем, вектор крутящего момента можно определить по моменту магнитного диполя:
⇔
Петля поворачивается магнитным полем, и верхняя часть вставляется в страницу. Сгибание пальцев таким образом приводит к тому, что крутящий момент прикладывается к левой стороне. Перекрестное произведение магнитного момента и поля определяет распределение крутящего момента.
Наука — странная тема, которая редко перестает удивлять вас по мере появления новых тем. Мы все знаем, что заряд существует вокруг нас и что он создает широкий спектр природных явлений. Более того, положительные и отрицательные заряды бывают разных форм и размеров, каждый из которых обладает собственным набором свойств при воздействии стимулирующего поля.
Вы когда-нибудь слышали слово «электрический диполь»? Это странное расположение положительных и отрицательных электрических зарядов порождает увлекательную физическую концепцию. Диссоциация положительных и отрицательных зарядов называется электрическим диполем.
Представьте себе пару противоположных знаков, но равных по величине электрических ионов, рассеянных на значительно меньшем расстоянии. В настоящее время наше внимание сосредоточено на поведении электрического диполя при появлении внешнего поля. Переходя к особенностям момента, действующего на электрический диполь в однородном электрическом поле, напомним особенности момента, действующего на электрический диполь в однородном электрическом поле.
Всякий раз, когда диполь помещается в однородное электрическое поле, каждый заряд получает силу из-за ориентации вектора диполя не параллельна ориентации поля. Эти силы имеют одинаковую силу, но они текут в противоположных направлениях. Эти равные и противоположные параллельные давления создают пару.
Эта пара приводит в движение диполь, что приводит к его вращению и выравниванию в плоскости поля. Однако в однородном поле сила обычно равна нулю. Всякий раз, когда диполь помещается в неоднородное поле, как указывалось ранее, возникает крутящий момент.
После ориентации диполя на ось поля силы, действующие на заряды, неодинаковы. Как следствие, диполь будет испытывать результирующую силу в направлении увеличения поля. Как следствие, электрический диполь подвергается неравномерному крутящему моменту и силе.
Отв. AB и CD имеют одинаковый функциональный дипольный момент, т.е. /2)
⇒P
Поскольку результирующий вектор образует угол 30° с осью x, крутящий момент, ощущаемый функциональным диполем, увеличивается, Работает по оси Z.
В результате функциональный дипольный момент равен p, а программный момент равен 1/2pE по оси +z.
Часто задаваемые вопросы | Часто задаваемые вопросы Вопросы. Что означает термин «ориентация крутящего момента»? Отв.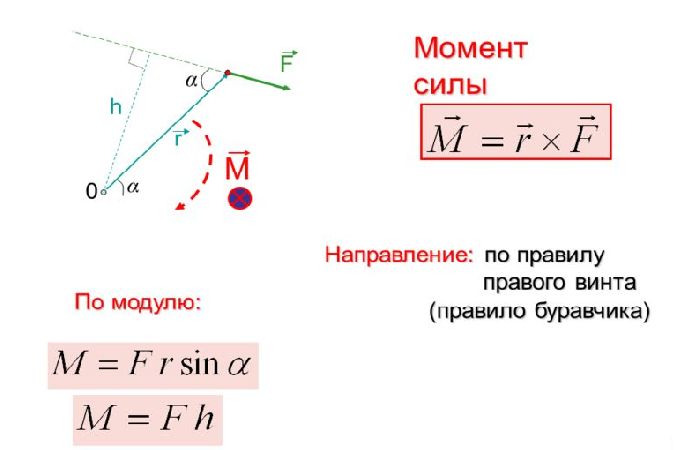
Крутящий момент находится в ориентации угловой скорости, которую он создал бы, если бы не присутствовали другие факторы. Изменение угловой скорости обычно связано с направлением крутящего момента.
Отв. Каждая сила, действующая по часовой стрелке, имеет положительный крутящий момент, а каждая сила, действующая против часовой стрелки, имеет отрицательный крутящий момент. Когда расстояние, сила или ортогональные компоненты больше, крутящий момент также выше.
Вопрос. Крутящий момент – это либо сила, либо момент.Отв. Крутящий момент, также известный как момент силы, — это склонность силы вращать объект, к которому она приложена в физике.
Вопрос. Каково определение крутящего момента по часовой стрелке? Отв. Отрицательный крутящий момент — это тот, который вращает предмет по часовой стрелке.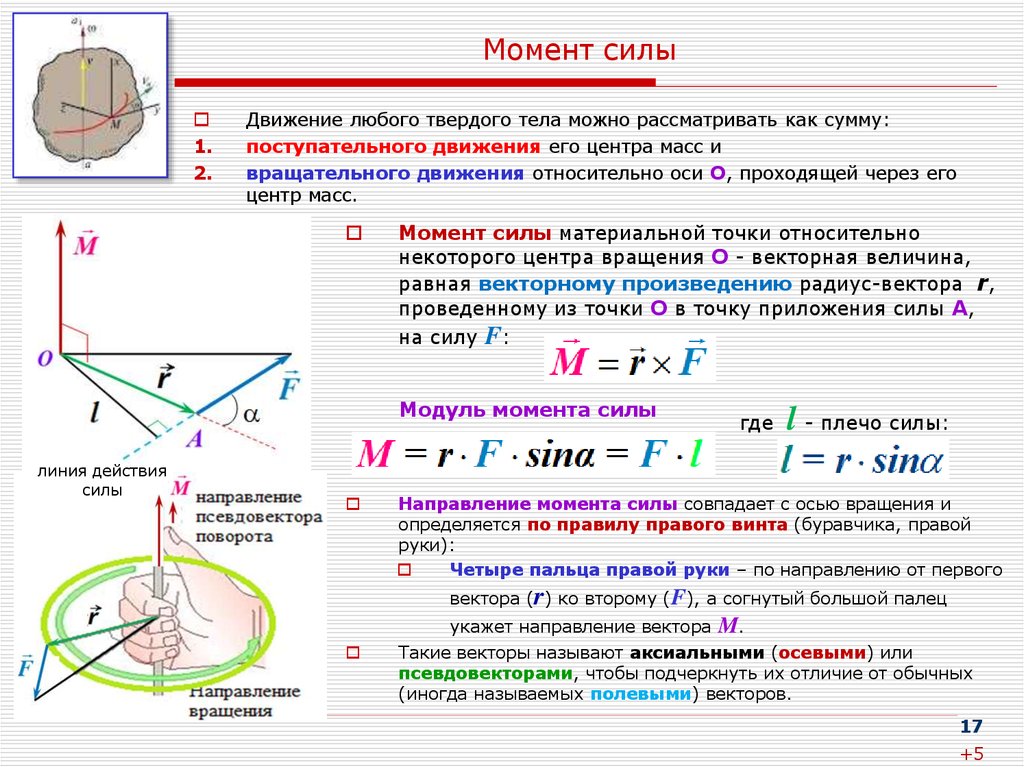
Отв. Ориентация вектора крутящего момента определяется тем, как приложенная сила заставляет систему вращаться. В этом случае ключ вращается против часовой стрелки.
Кроме того, нажмите, чтобы узнать о том, как рассчитать крутящий момент по об/мин.
Указание величины и направления для нагрузок
Указание величины и направления для нагрузок
Выберите один из следующих элементов, чтобы указать величину и направление силы, момента, скорости или ускорения для нагрузки. Обратите внимание, что для большинства нагрузок вы можете ввести любое из обсуждаемых ниже значений в виде действительного числа, арифметического выражения или имени параметра. Однако для нагрузок на подшипники можно использовать только действительные числа.
• Компоненты — введите компоненты силы или момента для каждого направления координат. Creo Simulate определяет направление и величину силы или момента по введенным вами компонентам.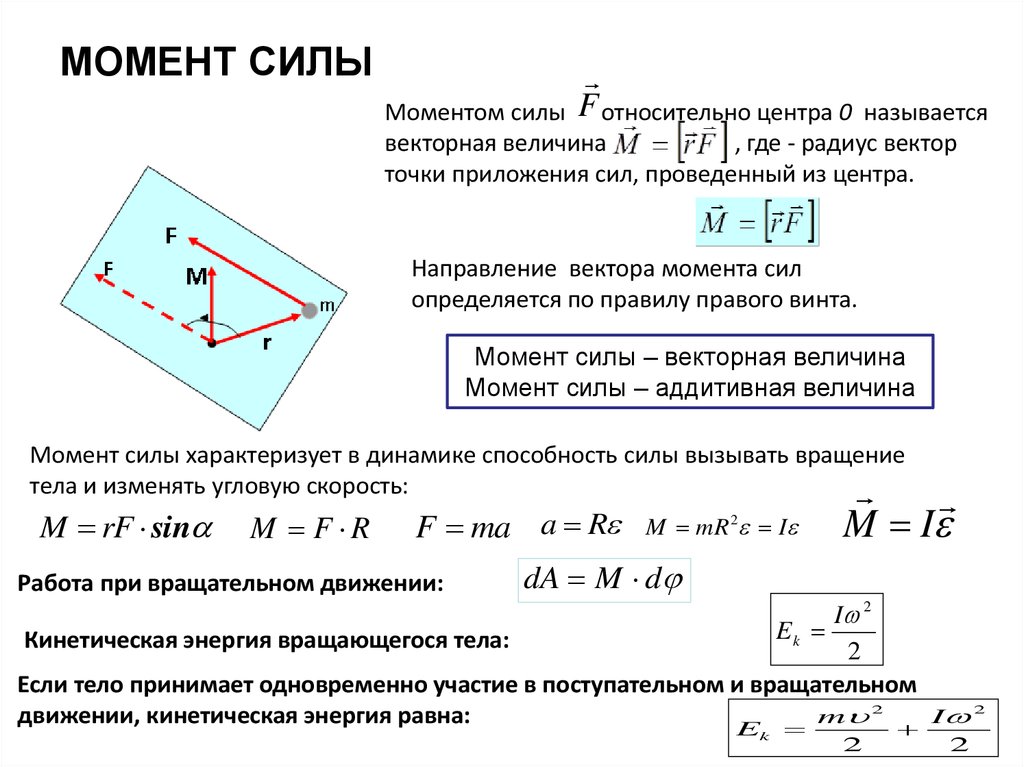
| Если у вас есть 2D-плоская деформация, 2D-плоское напряжение или 2D-осесимметричная модель, вы можете указать только X и Y для силовой нагрузки. |
Если у вас есть плоская 2D-деформация или 2D-осесимметричная модель, вы можете указать только Z для мгновенной нагрузки. Укажите Z только для 2D-оболочек, а не для 2D-тел. Для плоских 2D-моделей напряжений вы не можете задавать моментные нагрузки.
• Направление вектора и магнита — определите направление силы или момента, введя значения единичных векторов выбранной системы координат, и введите величину силы в поле ввода Mag. Если вы введете положительное значение, программа применит силу или момент в том же направлении, что и вектор. Если вы используете отрицательное значение, направление противоположно вектору.
