Момент силы и момент инерции
В динамике поступательного движения материальной точки кроме кинематических характеристик вводились понятия силы и массы. При изучении динамики вращательного движения вводятся физические величины — момент сил и момент инерции, физический смысл которых раскроем ниже.
Пусть некоторое тело под действием силы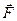 
, приложенной в точке А, приходит во вращение вокруг оси ОО’ (рисунок 5.1).
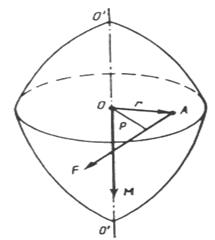
Рисунок 5.1 – К выводу понятия момента силы
Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы. Произведение силы на плечо определяет модуль момента силы относительно точки О:
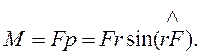
Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы:
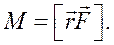(5.2)
Единица момента силы — ньютон-метр (Н.м). Направление вектора момента силы находиться с помощью правила правого винта.
Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, называемая
Момент инерции материальной точки относительно оси вращения — произведение массы этой точки на квадрат расстояния от оси:
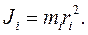(5.3)
Момент инерции тела относительно оси вращения — сумма моментов инерции материальных точек, из которых состоит это тело:
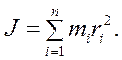(5.4)
В общем случае, если тело сплошное и представляет собой совокупность точек с малыми массами
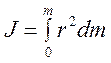, (5.5)
где r — расстояние от оси вращения до элемента массой dm.
Если тело однородно и его плотность ρ = m/V, то момент инерции тела
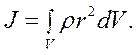(5.6)
Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.
Наиболее просто определяется момент инерции тел, имеющих правильную геометрическую форму и равномерное распределение массы по объему.
Момент инерции однородного стержня относительно оси, проходящей через центр инерции и перпендикулярной стержню,
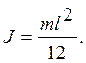(5.7)
Момент инерции однородного цилиндра относительно оси, перпендикулярной его основанию и проходящей через центр инерции,
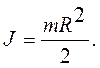(5.8)
Момент инерции тонкостенного цилиндра или обруча относительно оси, перпендикулярной плоскости его основания и проходящей через его центр,
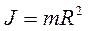(5.9)
Момент инерции шара относительно диаметра
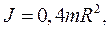(5.10)
Определим момент инерции диска относительно оси, проходящей через центр инерции и перпендикулярной плоскости вращения. Пусть масса диска – m, а его радиус – R.
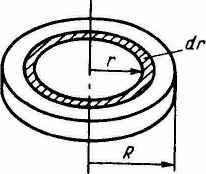
Площадь кольца (рисунок 5.2), заключенного между r и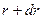 
, равна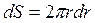 
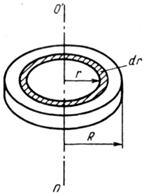
Рисунок 5.2 – К выводу момента инерции диска
Площадь диска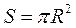 
. При постоянной толщине кольца,
откуда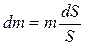 
или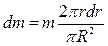 
.
Тогда момент инерции диска,
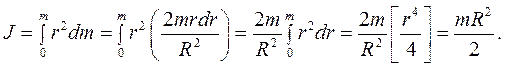
Для наглядности на рисунке 5.3 изображены однородные твердые тела различной формы и указаны моменты инерции этих тел относительно оси, проходящей через центр масс.
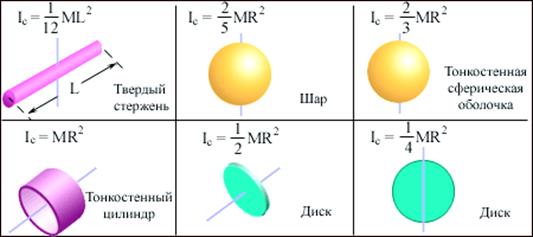
Рисунок 5.3 – Моменты инерции IC некоторых однородных твердых тел.
Теорема Штейнера
Приведенные выше формулы для моментов инерции тел даны при условии, что ось вращения проходит через центр инерции. Чтобы определить моменты инерции тела относительно произвольной оси, следует воспользоваться
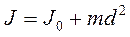(5.12)
где m — масса тела, d — расстояние от центра масс до выбранной оси вращения. Единица момента инерции — килограмм-метр в квадрате (кг . м2).
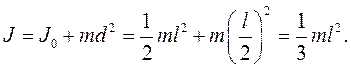(5.13)
Дата добавления: 2017-01-08; просмотров: 25433;
Похожие статьи:
9.Момент силы и момент импульса.Момент инерции.
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудахАрхимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:
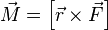
где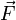 
—
сила, действующая на частицу,
а
—радиус-вектор частицы.
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количествовращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — псевдоскаляр.
Момент
импульса замкнутой
системы сохраняется. 
Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Обозначение: I или JМоментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где: mi — масса i-й точки,
ri — расстояние от i-й точки до оси.
11. Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этиммомент импульса замкнутой системы в любой системе координат не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
В
упрощённом виде: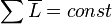 
,
если система находится в равновесии.
16.Постулаты специальной теории относительности.
Специальная теория относительности (СТО; также частная теория относительности) — теория, описывающая движение, законымеханики и пространственно-временные отношения при произвольных скоростях движения, меньших скорости света в вакууме, в том числе близких к скорости света. В рамках специальной теории относительности классическая механика Ньютона является приближением низких скоростей. Обобщение СТО для гравитационных полей называется общей теорией относительности.
Момент силы. Момент импульса.
Пусть некоторое тело под действием силы F, приложенной в точке А, приходит во вращение вокруг оси ОО’ (рис. 1.14).
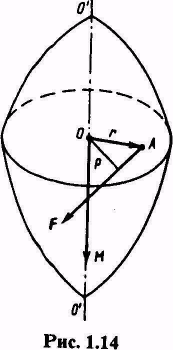Сила действует в плоскости, перпендикулярной оси. Перпендикуляр р, опущенный из точки О (лежащей на оси) на направление силы, называют плечом силы. Произведение силы на плечо определяет модуль момента силы относительно точки О:
М = Fp=Frsinα.
Момент силы есть вектор, определяемый векторным произведением радиуса-вектора точки приложения силы и вектора силы:
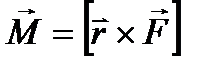(3.1)
Единица момента силы — ньютон-метр (Н • м).
Направление М можно найти с помощью правила правого винта.
Моментом импульса частицы называется векторное произведение радиус-вектора частицы на её импульс:
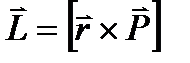или в скалярном виде L = гPsinα
Эта величины векторная и совпадает по направлению с векторами ω.
§ 3.2 Момент инерции. Теорема Штейнера
Мерой инертности тел при поступательном движении является масса. Инертность тел при вращательном движении зависит не только от массы, но и от ее распределения в пространстве относительно оси вращения. Мерой инертности при вращательном движении служит величина, называемая моментом инерции тела относительно оси вращения.
Моментом инерции материальной точки относительно оси вращения называют произведение массы этой точки на квадрат расстояния её от оси:
Ii=miri2 (3.2)
Момент инерции тела относительно оси вращения называют сумму моментов инерции материальных точек, из которых состоит это тело:
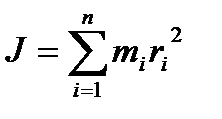(3.3)
Момент инерции тела зависит от того, относительно какой оси оно вращается и как распределена масса тела по объему.
Наиболее просто определяется момент инерции тел, имеющих правильную геометрическую форму и равномерное распределение массы по объему.
· Момент инерции однородного стержняотносительно оси, проходящей через центр инерции и перпендикулярной стержню
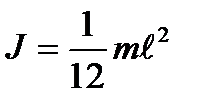(3.6)
· Момент инерции однородного цилиндра относительно оси, перпендикулярной его основанию и проходящей через центр инерции,
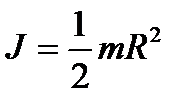(3.7)
· Момент инерции тонкостенного цилиндра или обруча относительно оси, перпендикулярной плоскости его основания и проходящей через его центр,
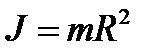(3.8)
· Момент инерции шара относительно диаметра
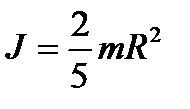(3.9)
Приведенные формулы для моментов инерции тел даны при условии, что ось вращения проходит через центр инерции. Чтобы определить моменты инерции тела относительно произвольной оси, следует воспользоваться теоремой Штейнера: момент инерции тела относительно произвольной оси вращения равен сумме момента инерции тела относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела на квадрат расстояния между осями:
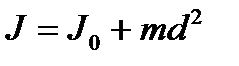(3.11)
[m — масса тела, d — расстояние от центра масс до выбранной оси вращения (расстояние между осями)].
Единица момента инерции — килограмм-метр в квадрате (кг • м2).
Так, момент инерции однородного стержня относительно оси, проходящей через его конец, по теореме Штейнера равен
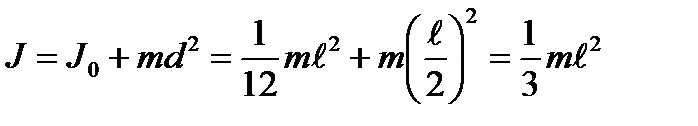(3.12)
§ 3.3 Уравнение динамики вращательного движения твердого тела
Рассмотрим вначале материальную точку А массой m, движущуюся по окружности радиусом г (рис. 1.16). Пусть на нее действует постоянная сила F, направленная по касательной к окружности. Согласно второму закону Ньютона, эта сила вызывает тангенциальное ускорение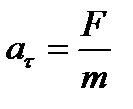 
или F = maτ.
Используя соотношение aτ = βr , получаем F = m βr.
Умножим обе части написанного выше равенства на r.
Fr = m βr 2. (3.13)
Левая часть выражения (3.13) является моментом силы: М= Fr. Правая часть представляет собой произведение углового ускорения β на момент инерции материальной точки А: J= m r 2 .
Угловое ускорение точки при ее вращении вокруг неподвижной оси пропорционально вращающему моменту и обратно пропорционально моменту инерции (основное уравнение динамики вращательного движения материальной точки):
М = β J или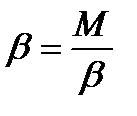 
(3.14)
При постоянном моменте вращающей силы угловое ускорение будет величиной постоянной и его можно выразить через разность угловых скоростей:
(3.15)
Тогда основное уравнение динамики вращательного движения можно записать в виде
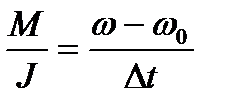или 
(3.16)
[ 
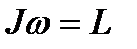—момент импульса (или момент количества движения), МΔt — импульс момента сил (или импульс вращающего момента)].
Основное уравнение динамики вращательного движения можно записать в виде
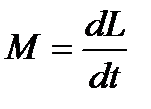(3.17)
§ 3.4 Закон сохранения момента импульса
Рассмотрим частый случай вращательного движения, когда суммарный момент внешних сил равен нулю. При вращательном движении тела каждая его частица движется с линейной скоростью υ = ωr, [r, — радиус окружности, которую описывает частица массой m, ω — угловая скорость, одинаковая для всех точек тела].
Момент импульса вращающегося тела равен сумме моментов
импульсов отдельных его частиц:
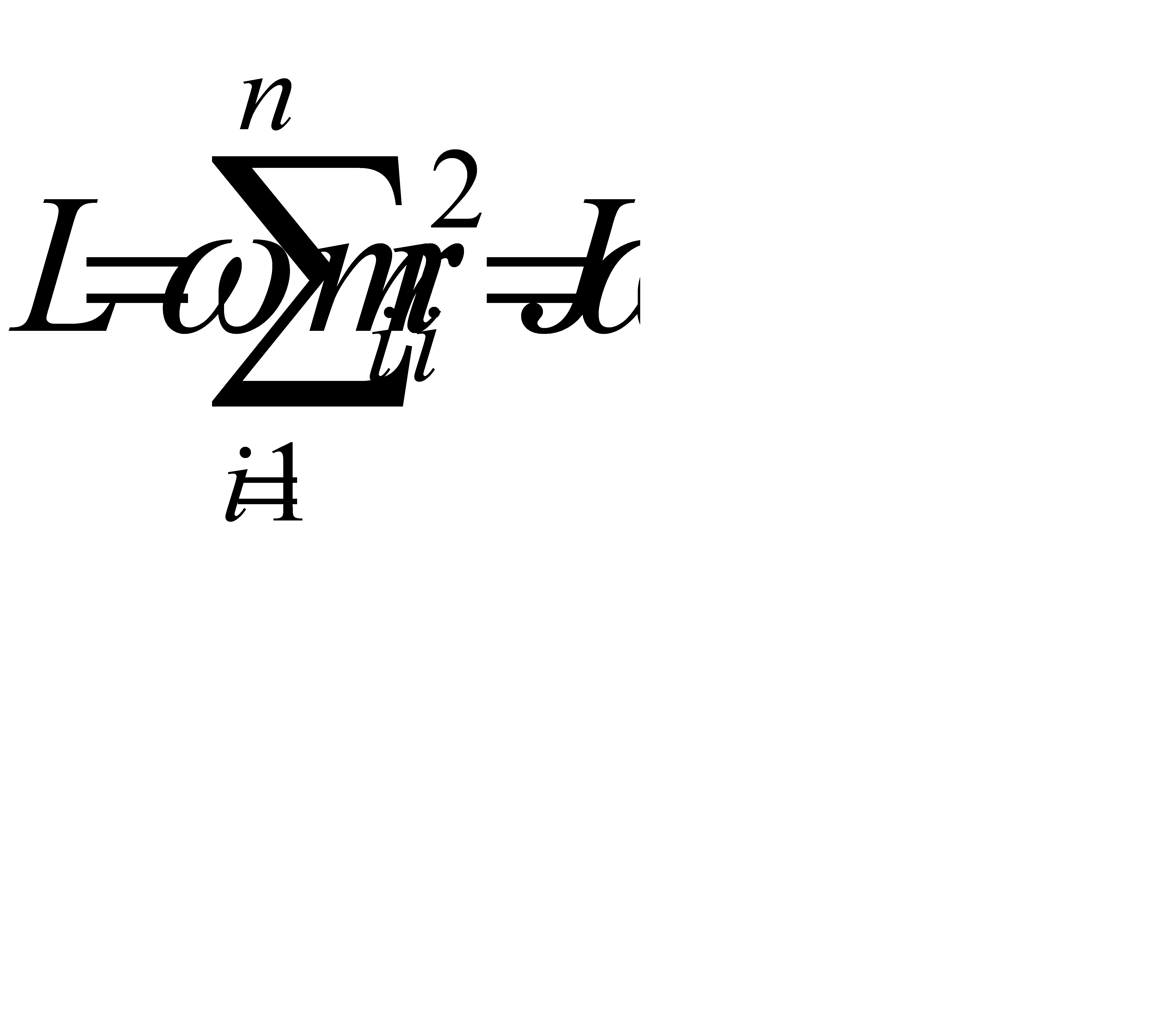(3.18)
Изменение момента импульса равно импульсу момента сил:
dL=d(Jω)=Jdω=Mdt (3.19)
Если суммарный момент всех внешних сил, действующих на систему тела относительно произвольной неподвижной оси, равен нулю, т.е. М=0, то dL и векторная сумма моментов импульсов тел системы не изменяется с течением времени.
Сумма моментов импульсов всех тел изолированной системы сохраняется неизменной (закон сохранения момента импульса):
d(Jω)=0 Jω=const (3.20)
Согласно закону сохранения момента импульса можно записать
J1ω1= J2ω2 (3.21)
где J1 и ω1 — момент инерции и угловая скорость в начальный момент времени, а и J2 и ω2 – в момент времени t.
Из закона сохранения момента импульса следует, что при М=0 в процессе вращения системы вокруг оси любое изменение расстояния от тел до оси вращения должно сопровождаться изменением скорости их обращения вокруг этой оси. С увеличением расстояния скорость вращения уменьшается, с уменьшением – возрастает. Например, гимнаст, совершающий сальто, чтобы успеть сделать в воздухе несколько оборотов, во время прыжка свёртывается клубком. Балерина или фигуристка, кружась в пируэте, разводит руки если хочет замедлить вращение, и, наоборот, прижимает их к телу, когда старается вращаться как можно быстрее.
§ 3.5 Кинетическая энергия вращающегося тела
Определим кинетическую энергию твёрдого тела, вращающегося вокруг неподвижной оси. Разобьем это тело на n материальных точек. Каждая точка движется с линейной скоростью υi=ωri, тогда кинетическая энергия точки
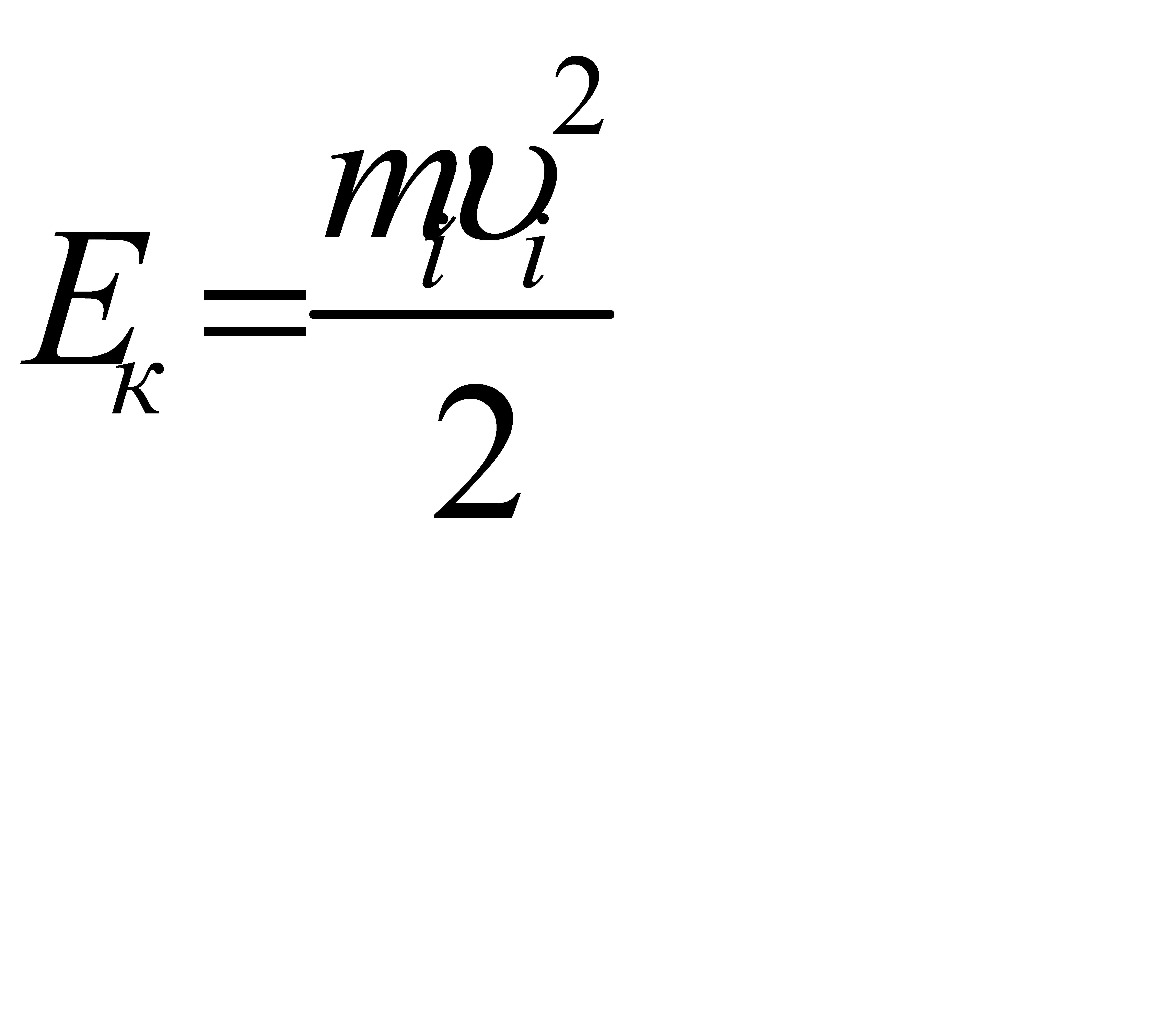или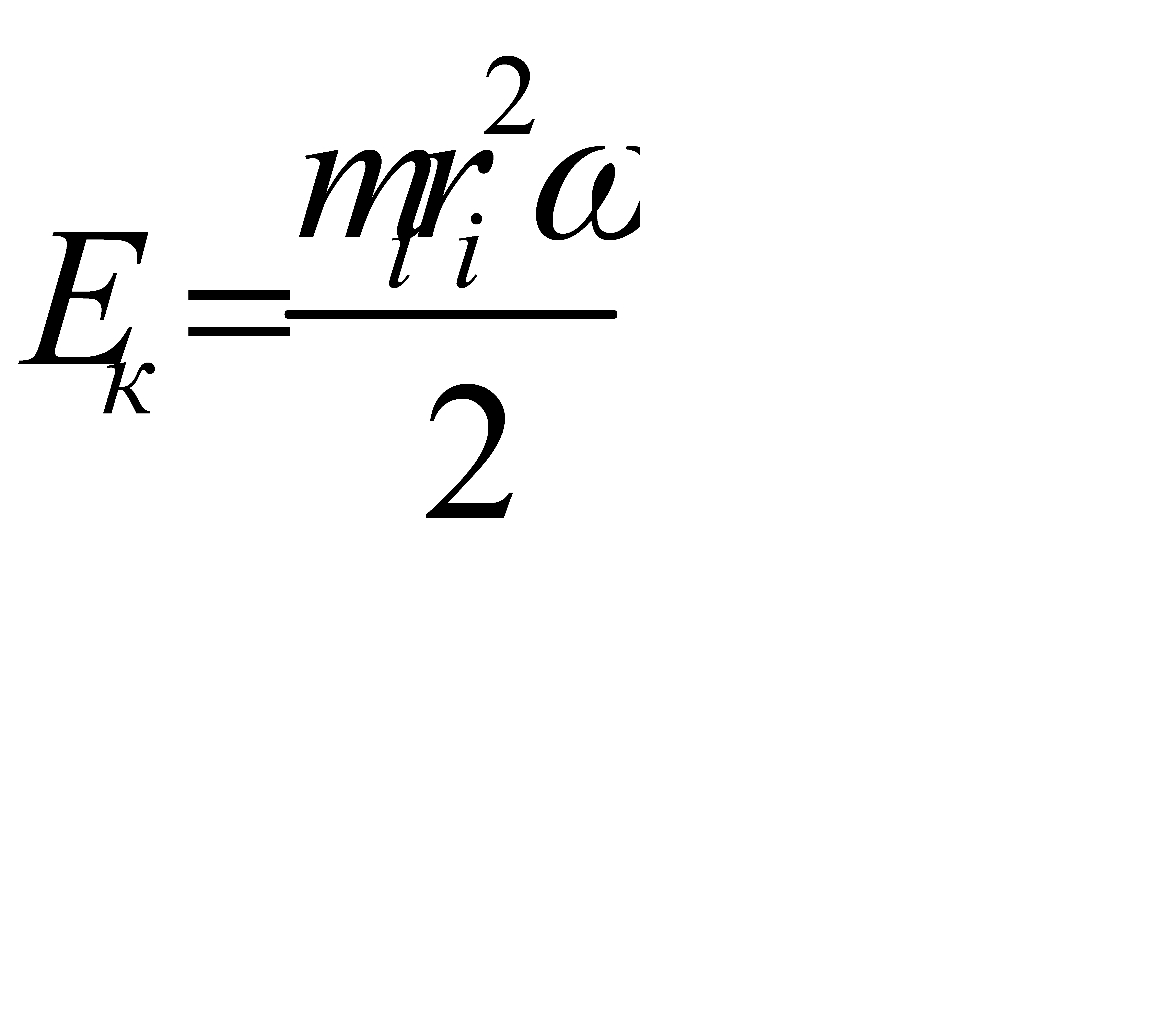 
Полная кинетическая энергия вращающегося твердого тела равна сумме кинетических энергий всех его материальных точек:
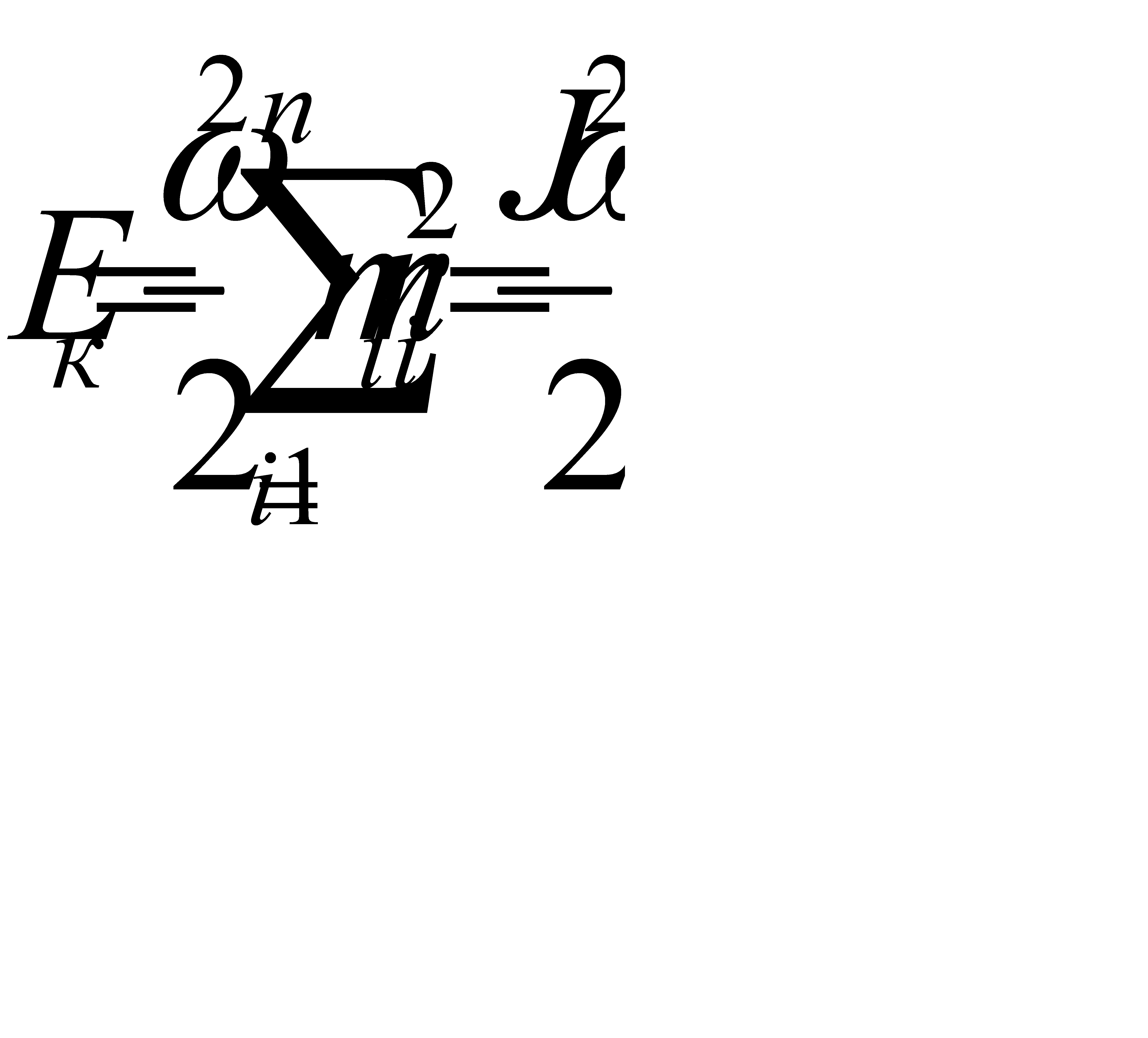(3.22)
(J — момент инерции тела относительно оси вращения)
Если траектории всех точек лежат в параллельных плоскостях (как у цилиндра, скатывающегося с наклонной плоскости, каждая точка перемещается в своей плоскости рис ), это плоское движение. В соответствии с принципом Эйлера плоское движение всегда можно бесчисленным количеством способов разложить на поступательное и вращательное движение. Если шарик падает или скользит вдоль наклонной плоскости, он двигается только поступательно; когда же шарик катится – он ещё и вращается.
Если тело совершает поступательное и вращательное движения одновременно, то его полная кинетическая энергия равна
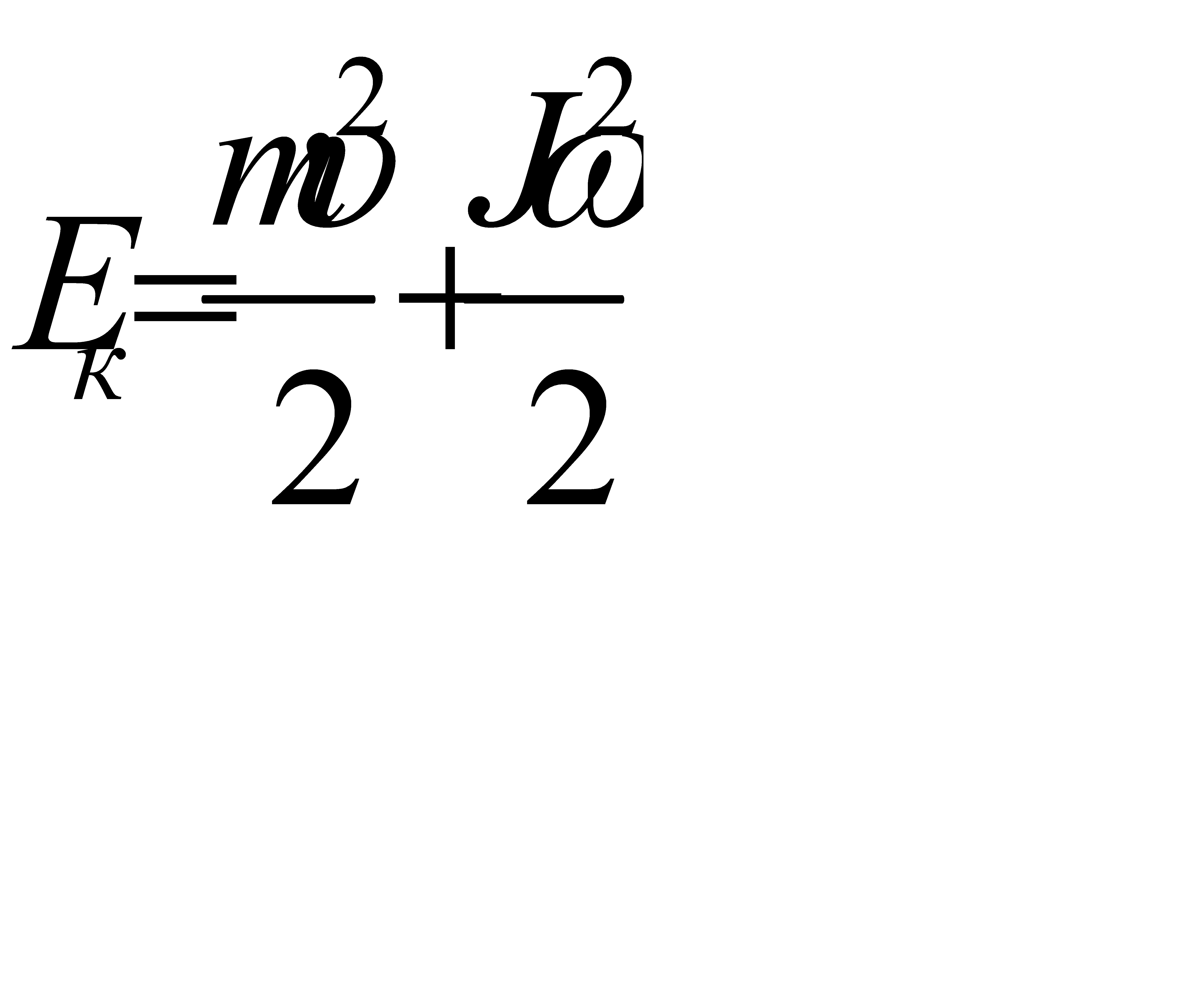(3.23)
Из сопоставления формул кинетической энергии для поступательного и вращательного движений видно, что мерой инертности при вращательном движении служит момент инерции тела.
§ 3.6 Работа внешних сил при вращении твёрдого тела
При вращении твёрдого тела его потенциальная энергия не изменяется, поэтому элементарная работа внешних сил равна приращению кинетической энергии тела:
ΔA = ΔE или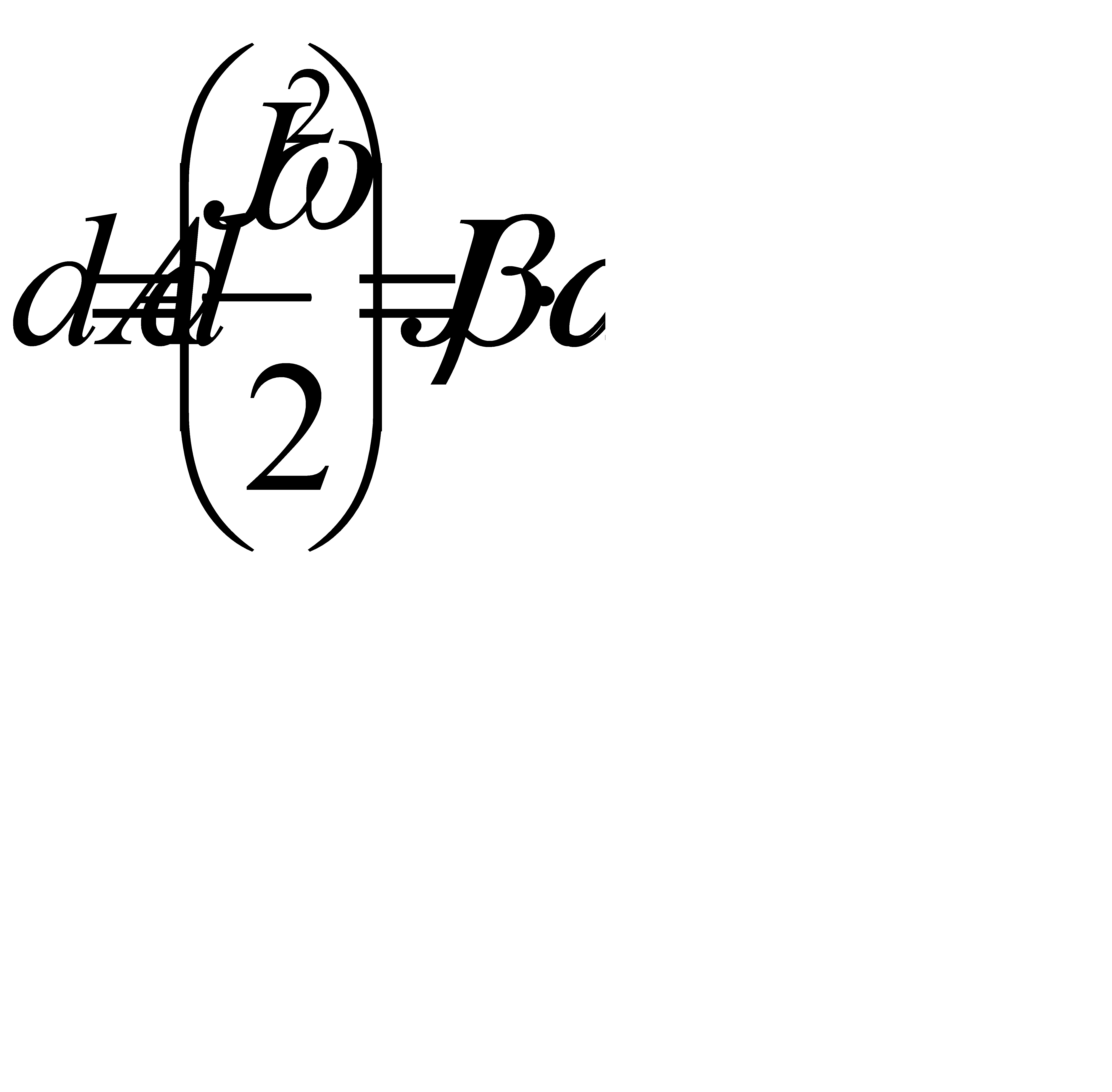 
Учитывая, что Jβ = M, ωdr = dφ, имеем
ΔA =MΔφ (3.24)
Работа внешних сил при повороте твёрдого тела на конечный угол φ равна
При вращении твёрдого тела вокруг неподвижной оси работа внешних сил определяется действием момента этих сил относительно данной оси. Если момент сил относительно оси равен нулю, то эти силы работы не производят.
Дата добавления: 2017-03-12; просмотров: 16296;
Похожие статьи:
16. Момент силы относительно точки и оси.
Твердое тело мы рассматриваем как систему материальных точек, жестко скрепленных друг с другом. Отсутствие такого скрепления существенно затруднило бы описание движения.
Для описания динамики вращательного движения тел необходимо ввести понятие момента сил, при этом необходимо различать: момент силы относительно точки, момент силы относительно оси.
Если
сила 
приложенная к материальной точкеA,
а момент
силы 
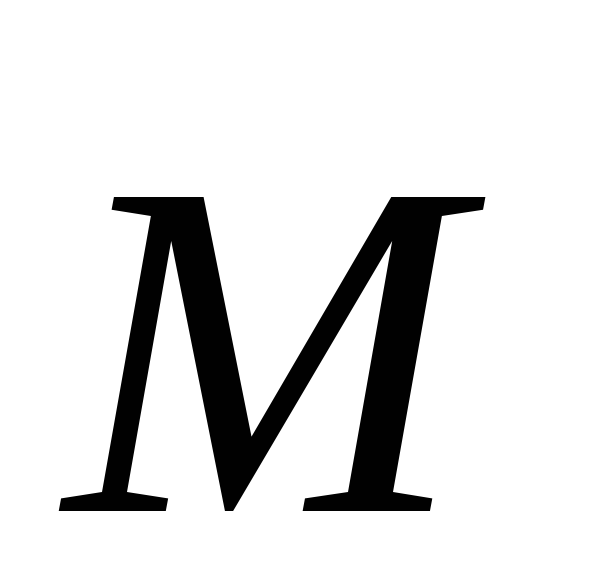,относительно
точки O называется векторное произведение
радиус-вектора (
),
проводимого из точкиО в точку А и вектора силы:
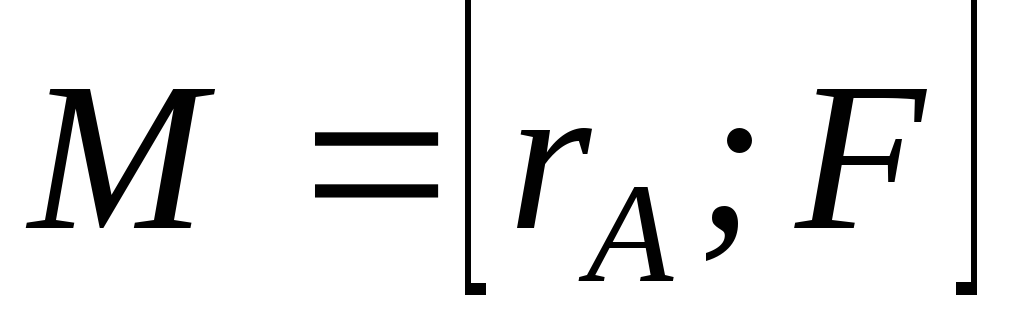Модуль вектора
момента силы: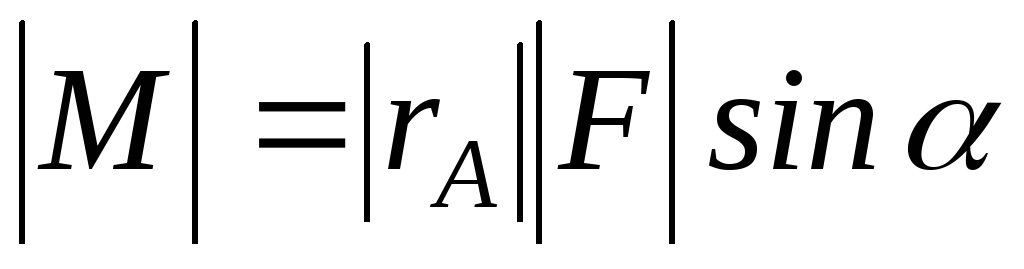 
.
Направление вектора момента силы определяется правилом Буравчика: если вращательное движение головки буравчика совместить с направлением силы, действующей на точку А, то поступательная сила самого буравчика укажет направление вектора момента силы.
Моментом
силы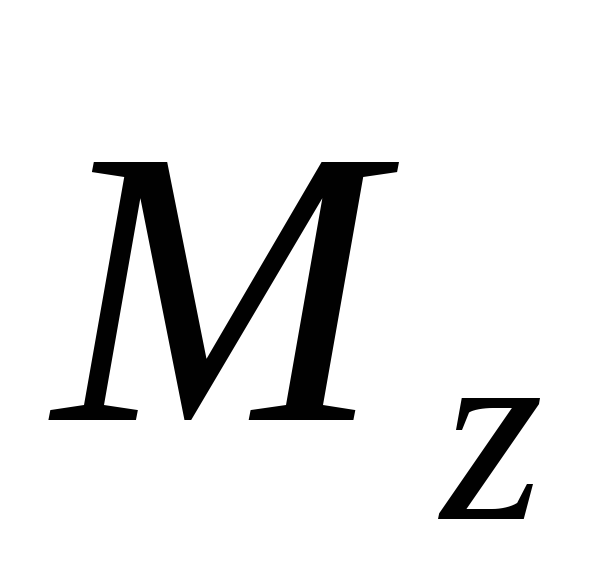 
относительно
произвольной оси z называется
векторное произведение радиус-вектора 
и составляющей ей перпендикулярно силы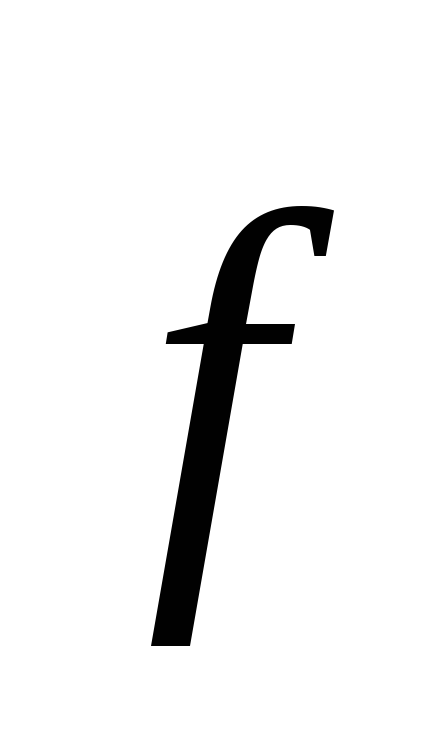
,
приложенной к точкеА.
.
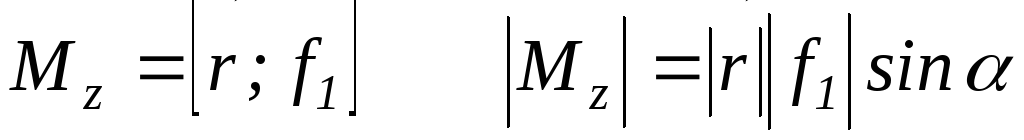17. Момент инерции твердого тела. Теорема Штейнера.
Произведение
массы точки на квадрат ее расстояния
до оси назовем моментом
инерции материальной
точки относительно оси: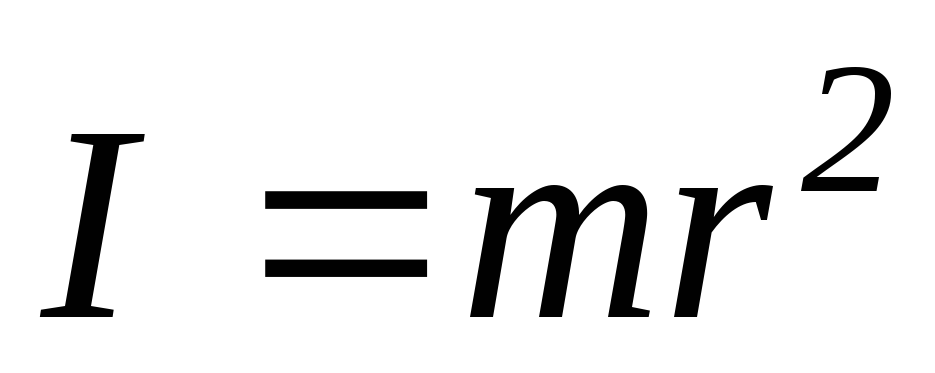
.
Единица момента инерции в СИ — кг.м2.
Твердое тело мы
можем рассматривать как совокупность
частиц с массами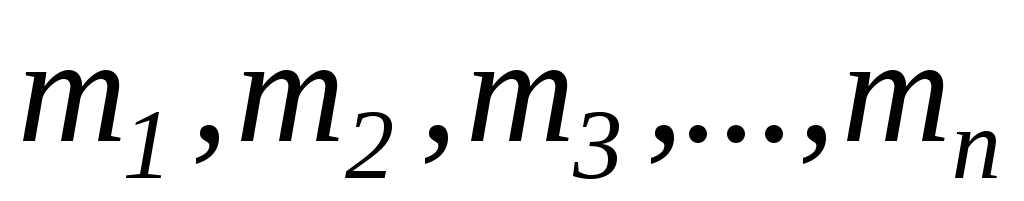 
,
расположенных на расстояниях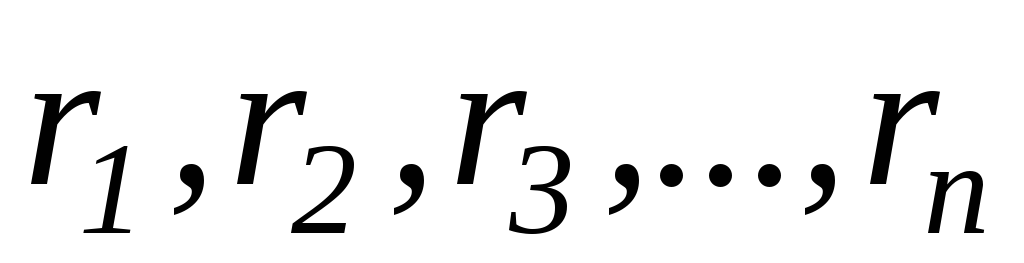
от оси вращения. Момент
инерции твердого тела сумма моментов инерции составляющих
его частиц: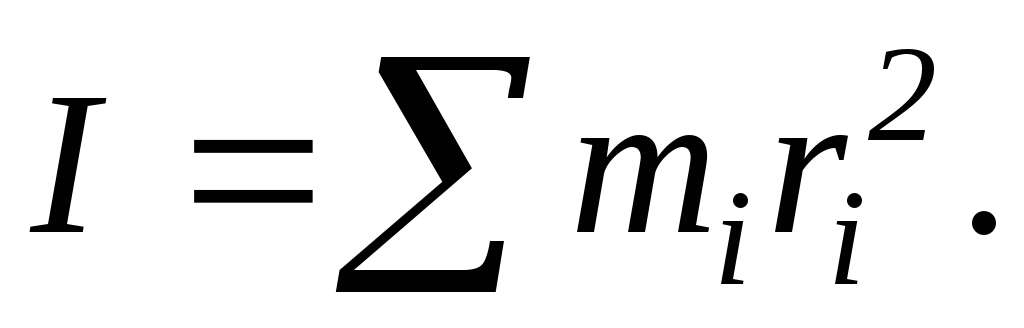 
Для разных осей
вращения момент инерции одного и того
же тела различен. Если известен момент
инерции I0 относительно
любой оси, проходящей через центр масс
тела, то для расчета момента инерции I этого тела относительно другой оси,
параллельной первой и отстоящей от нее
на расстоянии d,
используется соотношение, известное
как теорема
Штейнера: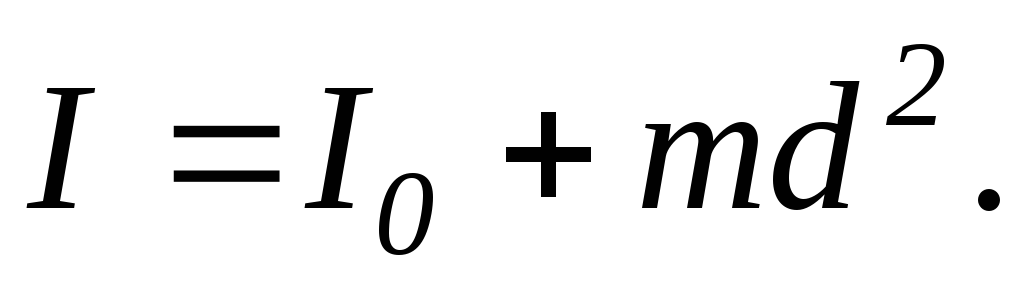 
Тело | Ось вращения проходит | Момент инерции I0 |
Обруч | через центр обруча перпендикулярно плоскости обруча | mR2 |
диск (цилиндр) | через центр диска перпендикулярно плоскости диска | 0,5mR2 |
диск | через центр диска вдоль его диаметра | 0,25mR2 |
Шар | через центр шара | 0,4mR2 |
Стержень длиной 1 | через середину тонкого стержня перпендикулярно ему | 1/12 ml2 |
18. Основное уравнение динамики вращательного движения.
Чтобы получить
искомое уравнение, рассмотрим вначале
простейший случай, когда материальная
точка массой m вращается на невесомом твердом стержне
длиной r вокруг оси.
Второй закон Ньютона для этой точки
запишется так: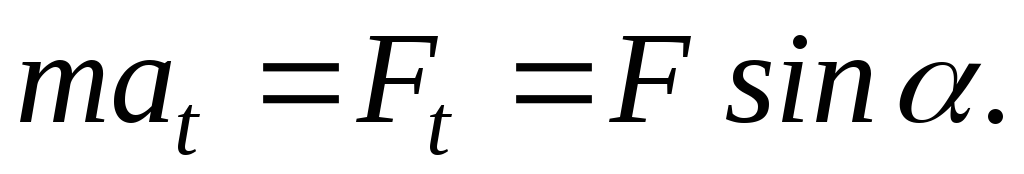 
Но тангенциальное ускорение
.
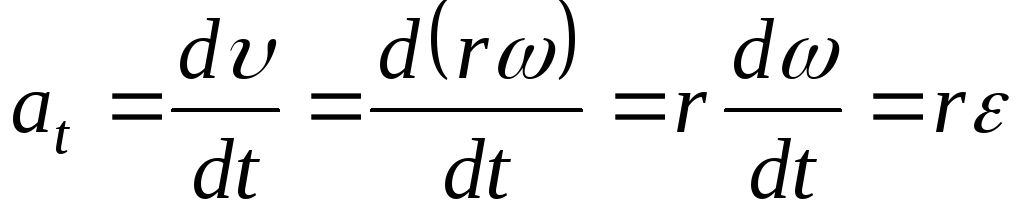Подставив в предыдущую формулу получим: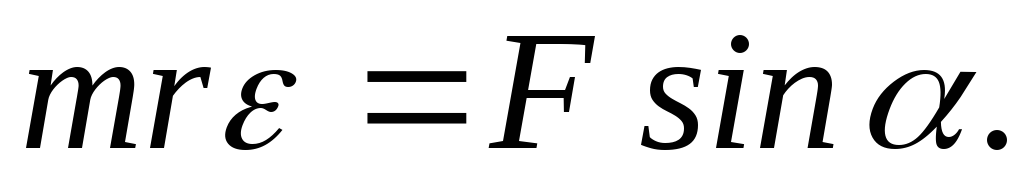
Умножив обе части
этого равенства на r, чтобы свести
действие силы к ее моменту, будем иметь: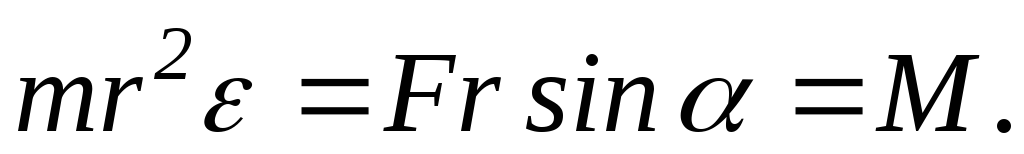
Произведение массы точки на квадрат ее
расстояния до оси назовеммоментом
инерции материальной
точки относительно оси: 
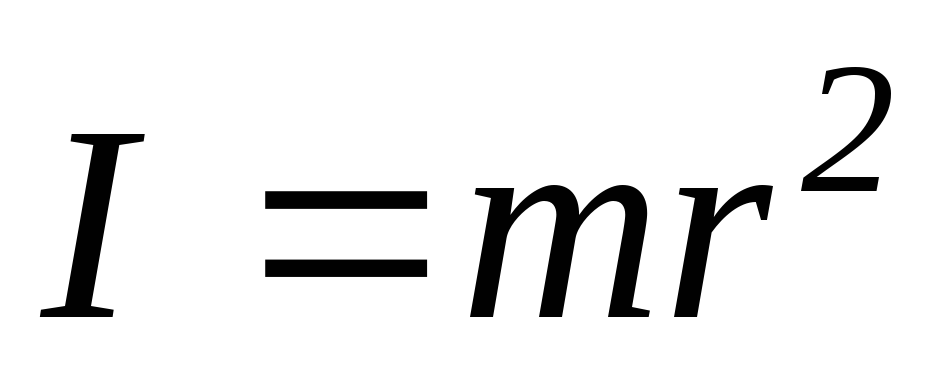.Единица
момента инерции в СИ — кг.м2.
Тогда: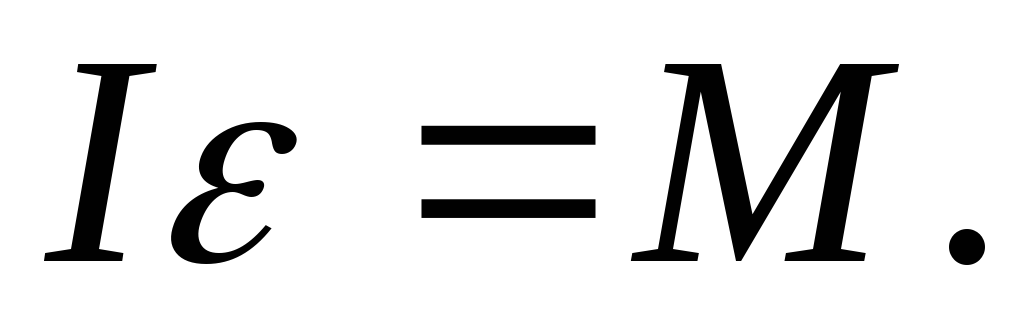 
Поскольку векторы 
и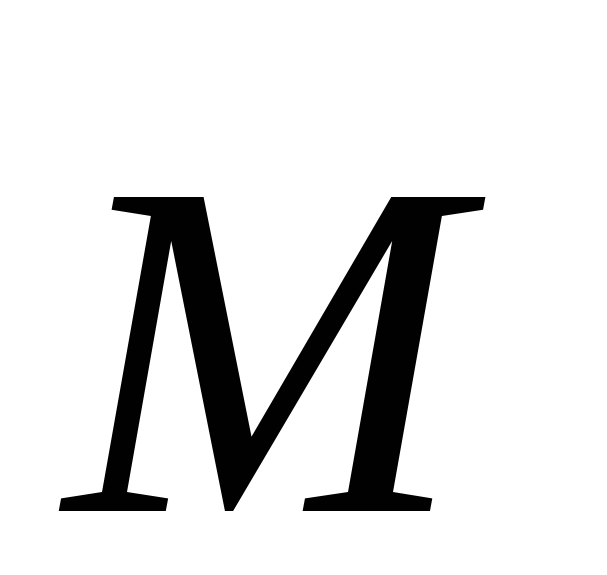
направлены в одну и ту же сторону вдоль
оси вращения, то можно записать в
векторном виде: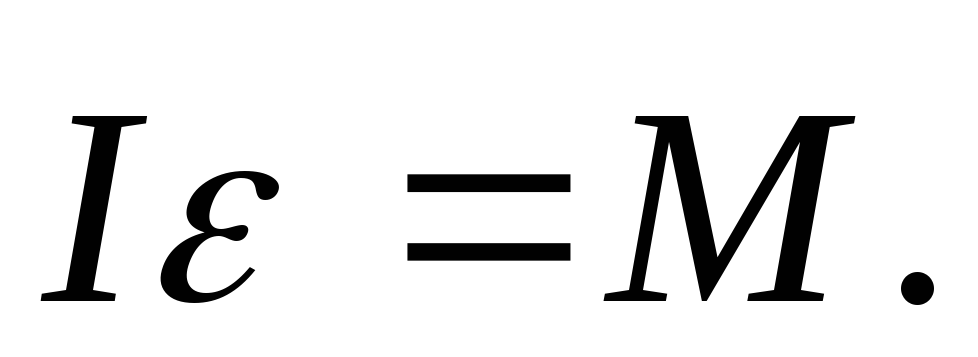
Это и естьосновное
уравнение динамики вращательного
движения.
Динамика вращательного движения. Момент инерции. — Студопедия.Нет
Вращательное движение — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружности и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения может быть подвижной и неподвижной.
Аналогия между параметрами кинематики и динамики:
| S | ϕR | путь |
| V | ω | Скорость — угловая скорость |
| a | β | Ускорение – угловое ускорение |
| F | M=I*β | Сила – момент силы |
| m | I=km 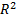 | Масса – момент инерции |
| P=mV | L=p*l | Импульс – момент импульса |
| A=F*S | A=M*ϕ | Работа |
W= 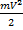 | W= 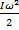 | Энергия |
Момент инерции механической системы относительно неподвижной оси a («осевой момент инерции») — физическая величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
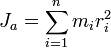
где: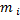 
— масса i-й точки, 
— расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси a подобно тому, как масса тела является мерой его инертности в поступательном движении.
Теорема Штейнера
Момент инерции твёрдого тела вокруг произвольной оси равен моменту инерции тела вокруг оси, проходящей через центр массы данного тела параллельно данной оси, плюс произведение массы тела на квадрат расстояния между осями.
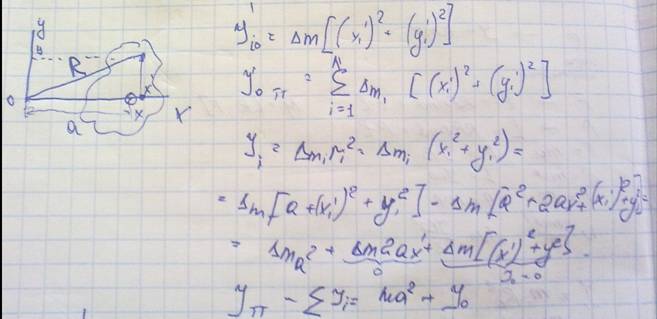
Момент силы. Основной закон динамики вращательного движения.
Момент силы— векторная физическая величина, равная произведению радиус-вектора, проведенного от оси вращения к точке приложения силы, на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
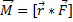
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр.
Основным законом динамики вращательного движения является связь момента силы М с моментом инерции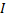 
и угловым ускорением β:
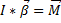
Работа при вращательном движении тела
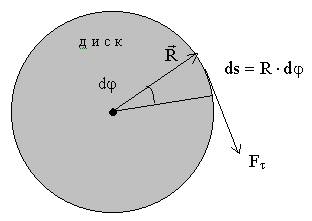
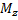— момент силы 
относительно оси вращения z.
— векторное произведение.
Кинетическая энергия при вращательном движении
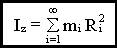
— момент инерции твердого тела, относительно оси z.
Моментом инерции материальной точки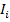 
называется величина:
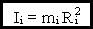
Следовательно,
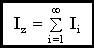
Величина I зависит от положения оси вращения и от распределения масс в теле.
Момент импульса. Закон сохранения момента импульса.
Момент импульса характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Замечание: момент импульса относительно точки — это псевдовектор, а момент импульса относительно оси — скалярная величина.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, оно также обладает моментом импульса. Наибольшую роль момент импульса играет при описании собственно вращательного движения.
Момент импульса замкнутой системы сохраняется.
Момент импульса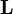 
частицы относительно некоторого начала отсчёта определяется векторным произведением ее радиус-вектора и импульса:
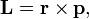
где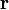 
— радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчета начала отсчёта, 
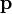— импульс частицы.
В системе СИ момент импульса измеряется в единицах джоуль-секунда; Дж·с.
Моментом импульса вращающегося тела называют физическую величину, равную произведению момента инерции тела I на угловую скорость ω его вращения. Момент импульса обозначается буквой L:
L = Iω
Поскольку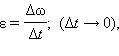 
уравнение вращательного движения можно представить в виде:
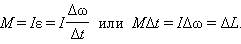
Окончательно будем иметь:
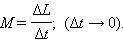
Это уравнение, полученное здесь для случая, когда I = const, справедливо и в общем случае, когда момент инерции тела изменяется в процессе движения.
Если суммарный момент M внешних сил, действующих на тело, равен нулю, то момент импульса L = Iω относительно данной оси сохраняется:
ΔL = 0, если M = 0.
Следовательно,
L = Iω = const.
Это и есть закон сохранения момента импульса. Иллюстрацией этого закона может служить неупругое вращательное столкновение двух дисков, насажанных на общую ось
Неупругое вращательное столкновение двух дисков.
Закон сохранения момента импульса: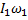 
= ( 
+ 
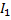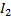)ω
Момент инерции — это… Что такое Момент инерции?
У этого термина существуют и другие значения, см. Момент.Момент инерции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Осевой момент инерции
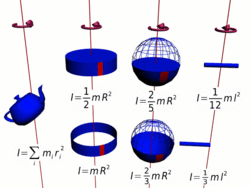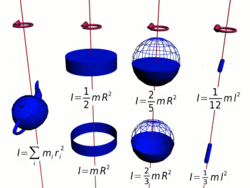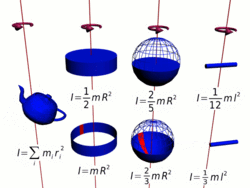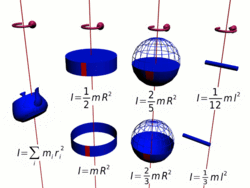Осевые моменты инерции некоторых тел.Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
,
где:
- mi — масса i-й точки,
- ri — расстояние от i-й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
,
где:
Если тело однородно, то есть его плотность всюду одинакова, то
Теорема Гюйгенса-Штейнера
Момент инерции твёрдого тела относительно какой-либо оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси. Согласно теореме Штейнера (теореме Гюйгенса-Штейнера), момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела Jc относительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела m на квадрат расстояния d между осями:
,
где — полная масса тела.
Например, момент инерции стержня относительно оси, проходящей через его конец, равен:
Осевые моменты инерции некоторых тел
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Вывод формулы
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Вывод формулы
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Вывод формулы
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Вывод формулы
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Вывод формулы
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Вывод формулы
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
Тонкий стержень (ось проходит через центр)
Вывод формулы
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
Вывод формулы
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
Безразмерные моменты инерции планет и их спутников
Большое значение для исследований внутренней структуры планет и их спутников имеют их безразмерные моменты инерции. Безразмерный момент инерции тела радиуса r и массы m равен отношению его момента инерции относительно оси вращения к моменту инерции материальной точки той же массы относительно неподвижной оси вращения, расположенной на расстоянии r (равному mr2). Эта величина отражает распределение массы по глубине. Одним из методов её измерения у планет и спутников является определение допплеровского смещения радиосигнала, передаваемого АМС, пролетающей около данной планеты или спутника. Для тонкостенной сферы безразмерный момент инерции равен 2/3 (~0,67), для однородного шара — 0,4, и вообще тем меньше, чем большая масса тела сосредоточена у его центра. Например, у Луны безразмерный момент инерции близок к 0,4 (равен 0,391), поэтому предполагают, что она относительно однородна, её плотность с глубиной меняется мало. Безразмерный момент инерции Земли меньше, чем у однородного шара (равен 0,335), что является аргументом в пользу существования у неё плотного ядра. [3][4]
Центробежный момент инерции
Центробежными моментами инерции тела по отношению к осям прямоугольной декартовой системы координат называются следующие величины:
где x, y и z — координаты малого элемента тела объёмом dV, плотностью ρ и массой dm.
Ось OX называется главной осью инерции тела, если центробежные моменты инерции Jxy и Jxz одновременно равны нулю. Через каждую точку тела можно провести три главные оси инерции. Эти оси взаимно перпендикулярны друг другу. Моменты инерции тела относительно трёх главных осей инерции, проведённых в произвольной точке O тела, называются главными моментами инерции тела.
Главные оси инерции, проходящие через центр масс тела, называются главными центральными осями инерции тела, а моменты инерции относительно этих осей — его главными центральными моментами инерции. Ось симметрии однородного тела всегда является одной из его главных центральных осей инерции.
Геометрический момент инерции
Геометрический момент инерции — геометрическая характеристика сечения вида
где — расстояние от центральной оси до любой элементарной площадки относительно нейтральной оси.
Геометрический момент инерции не связан с движением материала, он лишь отражает степень жесткости сечения. Используется для вычисления радиуса инерции, прогиба балки, подбора сечения балок, колонн и др.
Единица измерения СИ — м4. В строительных расчетах, литературе и сортаментах металлопроката в частности указывается в см4.
Из него выражается момент сопротивления сечения:
- .
Центральный момент инерции
Центральный момент инерции (или момент инерции относительно точки O) — это величина
,
где:
Центральный момент инерции можно выразить через главные осевые или центробежные моменты инерции: .
Момент инерции тела относительно произвольной оси, проходящей через центр масс и имеющей направление, заданное единичным вектором , можно представить в виде квадратичной (билинейной) формы:
- (1),
где — тензор инерции. Матрица тензора инерции симметрична, имеет размеры и состоит из компонент центробежных моментов:
- ,
.
Выбором соответствующей системы координат матрица тензора инерции может быть приведена к диагональному виду. Для этого нужно решить задачу о собственных значениях для матрицы тензора :
,
где — ортогональная матрица перехода в собственный базис тензора инерции. В собственном базисе координатные оси направлены вдоль главных осей тензора инерции, а также совпадают с главными полуосями эллипсоида тензора инерции. Величины — главные моменты инерции. Выражение (1) в собственной системе координат имеет вид:
- ,
откуда получается уравнение эллипсоида в собственных координатах. Разделив обе части уравнения на
и произведя замены:
- ,
получаем канонический вид уравнения эллипсоида в координатах :
Расстояние от центра эллипсоида до некоторой его точки связано со значением момента инерции тела вдоль прямой, проходящей через центр эллипсоида и эту точку:
См. также
Примечания
Литература
- Матвеев. А. Н. Механика и теория относительности. М.: Высшая школа, 1986. (3-е изд. М.: ОНИКС 21 век: Мир и Образование, 2003. — 432с.) http://www.alleng.ru/d/phys/phys108.htm
- Трофимова Т. И. Курс физики. — 7-е изд. — М.: Высшая школа, 2001. — 542 с.
- Алешкевич В. А., Деденко Л. Г., Караваев В. А. Механика твердого тела. Лекции. Издательство Физического факультета МГУ, 1997. http://nature.web.ru/db/msg.html?mid=1186208&s=120000000
- Павленко Ю. Г. Лекции по теоретической механике. М.: ФИЗМАТЛИТ, 2002. — 392с. http://www.alleng.ru/d/phys/phys99.htm
- Яворский Б. М., Детлаф А. А. Физика для школьников старших классов и поступающих в вузы: учебное пособие — М.: Дрофа, 2002, 800с. ISBN 5-7107-5956-3
- Сивухин Д. В. Общий курс физики. В 5 т. Том I. Механика. 4-е изд. М.: ФИЗМАТЛИТ; Изд-во МФТИ, 2005. — 560 с. http://www.alleng.ru/d/phys/phys103.htm
- Беляев Н. М., Сопротивление материалов. Главная редакция физико-математической литературы изд-ва «Наука», 1976. — 608 с.
Ссылки
моменты силы, импульса и инерции
Если линейное перемещение тел описывают в классической механике с помощью законов Ньютона, то характеристики движения механических систем по круговым траекториям вычисляют с помощью специального выражения, которое называется уравнением моментов. О каких моментах идет речь и в чем заключается смысл этого уравнения? Эти и другие вопросы раскрываются в статье.
Момент силы
Всем хорошо известна ньютоновская сила, которая, действуя на тело, приводит к сообщению ему ускорения. Когда же такая сила прилагается к объекту, который закреплен на некоторой оси вращения, то эту характеристику принято называть моментом силы. Уравнение момента силы может быть записано в следующем виде:
M¯ = L¯*F¯
Рисунок, поясняющий это выражение, приведен ниже.
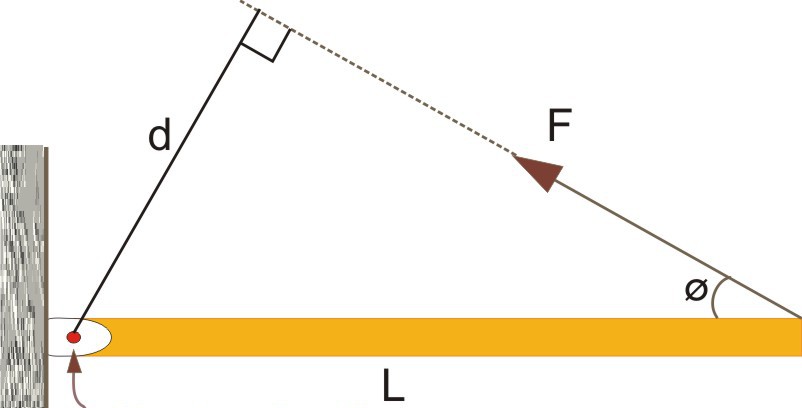
Здесь видно, что сила F¯ направлена к вектору L¯ под углом Φ. Сам же вектор L¯ полагается направленным от оси вращения (указана стрелкой) к точке приложения F¯.
Приведенная выше формула представляет собой произведение двух векторов, поэтому величина M¯ также является направленной. Куда будет повернут момент силы M¯? Это можно определить по правилу правой руки (четыре пальца направлены вдоль траектории от конца вектора L¯ к концу F¯, а отставленный палец большой показывает направление M¯).
На рисунке выше выражение для момента силы в скалярном виде примет форму:
M = L*F*sin(Φ)
Если внимательно всмотреться в рисунок, то можно увидеть, что L*sin(Φ) = d, тогда имеем формулу:
M = d*F
Величина d является важной характеристикой при вычислении момента силы, поскольку она отражает эффективность приложенной F к системе. Эту величину принято называть рычагом силы.
Физический смысл M заключается в способности силы совершить вращение системы. Эту способность может ощутить на себе каждый, если будет открывать дверь за ручку, толкая ее около петель, или же попробует открутить гайку коротким и длинным ключом.
Равновесие системы
Понятие о моменте силы оказывается очень полезным, когда рассматривают равновесие системы, на которую действуют несколько сил, и которая имеет ось или точку вращения. В таких случаях применяют формулу:
∑iMi¯=0
То есть система будет находиться в равновесии, если сумма всех моментов сил, приложенных к ней, нулевая. Заметим, что в этой формуле присутствует знак вектора над моментом, то есть при решении следует не забывать учитывать знак этой величины. Общепринятым правилом считается, что действующая сила, которая вращает систему против часовой стрелки, создает положительный Mi¯.
Ярким примером задач рассматриваемого типа являются проблемы с равновесием рычагов Архимеда.
Момент импульса
Это еще одна важная характеристика движения по окружности. В физике ее описывают произведением количества движения на рычаг. Уравнение момента импульса имеет такой вид:
T¯ = r¯*p¯
Здесь p¯ — вектор импульса, r¯ — вектор, соединяющий вращающуюся материальную точку с осью.
Поясняющий это выражение рисунок приведен ниже.
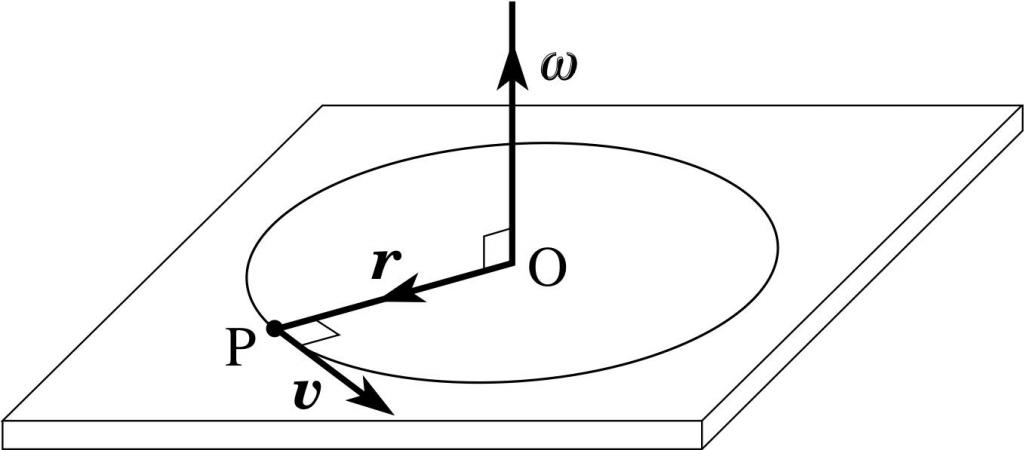
Здесь ω — угловая скорость, которая дальше появится в уравнении моментов. Заметим, что направление вектора T¯ находится по тому же правилу, что и M¯. На рисунке выше T¯ по направлению будет совпадать с вектором угловой скорости ω¯.
Физический смысл величины T¯ является таким же, как и характеристики p¯ в случае линейного движения, то есть момент импульса описывает количество вращательного движения (запасенную кинетическую энергию).
Момент инерции
Третья важная характеристика, без которой невозможно составить уравнение движения вращающегося объекта, — это момент инерции. Появляется он в физике в результате математических преобразований формулы для момента импульса материальной точки. Покажем, как это делается.
Представим величину T¯ в следующем виде:
T¯ = r¯*m*v¯, где p¯ = m*v¯
Пользуясь связью между угловой и линейной скоростями, можно переписать это выражение следующим образом:
T¯ = r¯*m*r¯*ω¯, где v¯ = r¯*ω¯
Последнее выражение запишем в виде:
T¯ = r2*m*ω¯
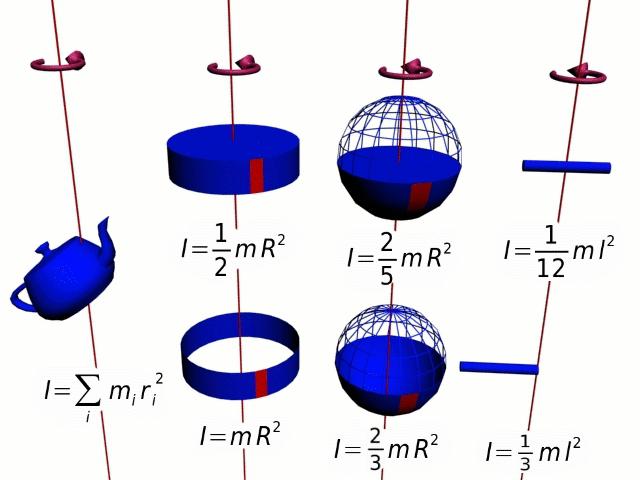
Величина r2*m — это момент инерции I для точки массой m, которая совершает круговое движение вокруг оси на расстоянии от нее r. Этот частный случай позволяет ввести общее уравнение момента инерции для тела произвольной формы:
I = ∫m (r2*dm)
I — это аддитивная величина, смысл которой заключается в инерционности вращающейся системы. Чем больше I, тем труднее раскрутить тело, и необходимо приложить значительные усилия, чтобы его остановить.
Уравнение моментов
Мы рассмотрели три величины, название которых начинается со слова «момент». Это сделано было намеренно, поскольку все они связаны в одно выражение, получившее название уравнения 3 моментов. Выведем его.
Рассмотрим выражение для момента импульса T¯:
T¯ = I*ω¯
Найдем, как изменяется величина T¯ во времени, имеем:
dT¯/dt = I*dω¯/dt
Учитывая, что производная угловой скорости равна таковой для скорости линейной, деленной на r, а также раскрывая величину I, приходим к выражению:
dT¯/dt = m*r2*1/r*dv¯/dt = r*m*a¯, где a¯ = dv¯/dt — линейное ускорение.
Заметим, что произведение массы на ускорение — это не что иное, как действующая внешняя сила F¯. В итоге получаем:
dT¯/dt = r*F¯ = M¯
Мы пришли к интересному выводу: изменение момента импульса равно моменту действующей внешней силы. Это выражение принято записывать в несколько иной форме:
M¯ = I*α¯, где α¯ = dω¯/dt — угловое ускорение.
Это равенство называется уравнением моментов. Оно позволяет рассчитать любую характеристику вращающегося тела, зная параметры системы и величину внешнего воздействия на нее.
Закон сохранения T¯
Полученный в предыдущем пункте вывод свидетельствует о том, что если внешний момент сил будет равен нулю, то момент импульса меняться не будет. В таком случае запишем выражение:
T¯ = const. или I1*ω1¯ = I2*ω2¯
Эта формула носит название закона сохранения величины T¯. То есть любые изменения внутри системы суммарный момент импульса не меняют.
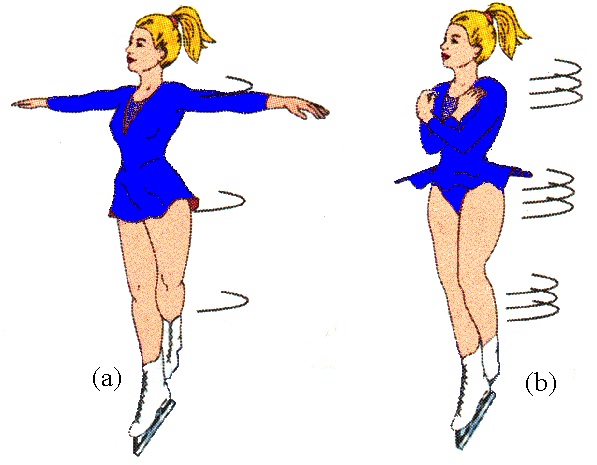
Этот факт используется фигуристами и балеринами во время их выступлений. Также его применяют, если необходимо выполнить поворот вокруг своей оси искусственного спутника, движущегося в космосе.
