момент силы — это… Что такое момент силы?
Момент силы — Размерность L2MT−2 Единицы измерения СИ Ньютон метр … Википедия
МОМЕНТ СИЛЫ — величина, характеризующая вращат. эффект силы при действии её на тв. тело; одно из осн. понятий механики. Различают М. с. относительно центра (точки) и относительно оси. М. с. относительно центра О величина векторная. Его модуль MO=Fh, где F… … Физическая энциклопедия
Момент (силы) — – в статике сооружений произведение величины силы на кратчайшее расстояние от линии действия силы до точки, относительно которой определяется момент. [Полякова, Т.Ю. Автодорожные мосты: учебный англо русский и русско английский… … Энциклопедия терминов, определений и пояснений строительных материалов
МОМЕНТ СИЛЫ — относительно точки (Moment of a force) произведение величин силы на длину перпендикуляра, опущенного из точки на направление силы. М. С. относительно оси произведение проекции силы на плоскость, перпендикулярную оси, на расстояние между осью и… … Морской словарь
момент силы — произведение силы на плечо. вращающий момент. плечо. кручение. см. равновесие … Идеографический словарь русского языка
МОМЕНТ СИЛЫ — МОМЕНТ СИЛЫ, см. ВРАЩАЮЩИЙ МОМЕНТ … Научно-технический энциклопедический словарь
Момент силы — величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают М. с. относительно центра (точки) и относительно оси. М. с. относительно центра О величина … Большая советская энциклопедия
МОМЕНТ СИЛЫ — механич. величина, характеризующая внеш. воздействие на тело (или систему тел) и определяющая изменение вращат. движения тела. М. с. относительно полюса (точки) О (см. рис.) наз. вектор М, равный векторному произведению радиус вектора r,… … Большой энциклопедический политехнический словарь
МОМЕНТ СИЛЫ — величина, характеризующая вращат. эффект силы при действии её на тв. тело. Различают М. с. относительно центра (точки) и относительно осн. М. с. относительно центра О (рис. а) векторная величина, численно равная произведению модуля силы F на… … Естествознание. Энциклопедический словарь
Момент силы — Википедия
Момент силы, приложенный к гаечному ключу. Направлен от зрителя
Моме́нт си́лы (синонимы: кру́тящий момент, враща́тельный момент, вертя́щий момент, враща́ющий момент) — векторная физическая величина, равная векторному произведению вектора силы и радиус-вектора, проведённого от оси вращения к точке приложения этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Общие сведения
В физике момент силы можно понимать как «вращающая сила». В Международной системе единиц (СИ) единицей измерения момента силы является ньютон-метр (Н·м). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как векторное произведение:
- M→=[r→×F→],{\displaystyle {\vec {M}}=\left[{\vec {r}}\times {\vec {F}}\right],}
где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — радиус-вектор частицы (в предположении, что ось вращения проходит через начало координат).
Предыстория
Для того чтобы понять, откуда появилось обозначение момента сил и как к нему пришли, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси. Работа, совершаемая при действии силы F→{\displaystyle {\vec {F}}} на рычаг r→{\displaystyle {\vec {r}}}, совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок dl{\displaystyle dl}, которому соответствует бесконечно малый угол dφ{\displaystyle d\varphi }. Обозначим через d→l{\displaystyle {\vec {d}}l} вектор, который направлен вдоль бесконечно малого отрезка dl{\displaystyle dl} и равен ему по модулю. Угол между вектором силы F→{\displaystyle {\vec {F}}} и вектором d→l{\displaystyle {\vec {d}}l} равен β{\displaystyle \beta }, а угол между векторами r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}} — α{\displaystyle \alpha }.
Следовательно, бесконечно малая работа dA{\displaystyle dA}, совершаемая силой F→{\displaystyle {\vec {F}}} на бесконечно малом участке dl{\displaystyle dl}, равна скалярному произведению вектора d→l{\displaystyle {\vec {d}}l} и вектора силы, то есть dA=F→⋅d→l{\displaystyle dA={\vec {F}}\cdot {\vec {d}}l}.
Теперь попытаемся выразить модуль вектора d→l{\displaystyle {\vec {d}}l} через радиус-вектор r→{\displaystyle {\vec {r}}}, а проекцию вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} — через угол α{\displaystyle \alpha }.
Так как для бесконечно малого перемещения рычага dl{\displaystyle dl} можно считать, что траектория перемещения перпендикулярна рычагу r→{\displaystyle {\vec {r}}}, используя соотношения для прямоугольного треугольника, можно записать следующее равенство: dl=rtgdφ{\displaystyle dl=r\mathrm {tg} \,d\varphi }, где в случае малого угла справедливо tgdφ=dφ{\displaystyle \mathrm {tg} \,d\varphi =d\varphi } и, следовательно, |dl→|=|r→|dφ{\displaystyle \left|{\vec {dl}}\right|=\left|{\vec {r}}\right|d\varphi }.
Для проекции вектора силы F→{\displaystyle {\vec {F}}} на вектор d→l{\displaystyle {\vec {d}}l} видно, что угол β=π2−α{\displaystyle \beta ={\frac {\pi }{2}}-\alpha }, а так как cos(π2−α)=sinα{\displaystyle \cos {\left({\frac {\pi }{2}}-\alpha \right)}=\sin \alpha }, получаем, что |F→|cosβ=|F→|sinα{\displaystyle \left|{\vec {F}}\right|\cos \beta =\left|{\vec {F}}\right|\sin \alpha }.
Теперь запишем бесконечно малую работу через новые равенства: dA=|r→|dφ|F→|sinα{\displaystyle dA=\left|{\vec {r}}\right|d\varphi \left|{\vec {F}}\right|\sin \alpha }, или dA=|r→||F→|sin(α)dφ{\displaystyle dA=\left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin(\alpha )d\varphi }.
Теперь видно, что произведение |r→||F→|sinα{\displaystyle \left|{\vec {r}}\right|\left|{\vec {F}}\right|\sin \alpha } есть не что иное, как модуль векторного произведения векторов r→{\displaystyle {\vec {r}}} и F→{\displaystyle {\vec {F}}}, то есть |r→×F→|{\displaystyle \left|{\vec {r}}\times {\vec {F}}\right|}, которое и было принято обозначить за момент силы M{\displaystyle M}, или модуль вектора момента силы |M→|{\displaystyle \left|{\vec {M}}\right|}.
Теперь полная работа записывается просто: A=∫0φ|r→×F→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {r}}\times {\vec {F}}\right|d\varphi }, или A=∫0φ|M→|dφ{\displaystyle A=\int \limits _{0}^{\varphi }\left|{\vec {M}}\right|d\varphi }.
Единицы
Момент силы имеет размерность «сила, умноженная на расстояние» и единицу измерения ньютон-метр в системе СИ. 1 Н·м — это момент, который производит сила 1 Н на рычаг длиной 1 м, приложенная к концу рычага и направленная перпендикулярно ему.
Энергия и механическая работа также имеют размерность «сила, умноженная на расстояние» и измеряются в системе СИ в джоулях. Следует заметить, что энергия — это скалярная величина, тогда как момент силы — величина псевдовекторная. Совпадение размерностей этих величин не случайность: момент силы 1 Н·м, при повороте рычага или вала на 1 радиан совершает работу в 1 Дж, а при повороте на один оборот совершает механическую работу и сообщает энергию 2π{\displaystyle 2\pi } джоуля. Математически:
- E=Mθ,{\displaystyle E=M\theta ,}
где E{\displaystyle E} — энергия, M{\displaystyle M} — вращающий момент, θ{\displaystyle \theta } — угол в радианах.
Специальные случаи
Формула момента рычага
Момент, действующий на рычагОчень интересен особый случай, представляемый как определение момента силы в поле:
- |M→|=|M→1||F→|,{\displaystyle \left|{\vec {M}}\right|=\left|{\vec {M}}_{1}\right|\left|{\vec {F}}\right|,}
где: |M→1|{\displaystyle \left|{\vec {M}}_{1}\right|} — момент рычага, |F→|{\displaystyle \left|{\vec {F}}\right|} — величина действующей силы.
Недостаток такого представления в том, что оно не дает направления момента силы, а только его величину. Если сила перпендикулярна вектору r→{\displaystyle {\vec {r}}}, момент рычага будет равен расстоянию от центра до точки приложения силы и момент силы будет максимален:
- |T→|=|r→||F→|.{\displaystyle \left|{\vec {T}}\right|=\left|{\vec {r}}\right|\left|{\vec {F}}\right|.}
Сила под углом
Если сила F→{\displaystyle {\vec {F}}} направлена под углом θ{\displaystyle \theta } к рычагу r, то M=rFsinθ{\displaystyle M=rF\sin \theta }.
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для двумерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0,ΣV=0{\displaystyle \Sigma H=0,\,\Sigma V=0} и момент силы в третьем измерении ΣM=0{\displaystyle \Sigma M=0}.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
Видеоурок: вращающий момент- M→=dL→dt,{\displaystyle {\vec {M}}={\frac {d{\vec {L}}}{dt}},}
где L→{\displaystyle {\vec {L}}} — момент импульса.
Возьмём твердое тело. Движение твёрдого тела можно представить как движение конкретной точки и вращения вокруг неё.
Момент импульса относительно точки O твёрдого тела может быть описан через произведение момента инерции и угловой скорости относительно центра масс и линейного движения центра масс.
- Lo→=Icω→+[M(ro→−rc→),vc→].{\displaystyle {\vec {L_{o}}}=I_{c}\,{\vec {\omega }}+[M({\vec {r_{o}}}-{\vec {r_{c}}}),{\vec {v_{c}}}].}
Будем рассматривать вращающиеся движения в системе координат Кёнига, так как описывать движение твёрдого тела в мировой системе координат гораздо сложнее.
Продифференцируем это выражение по времени. И если I{\displaystyle I} — постоянная величина во времени, то
- M→=Idω→dt=Iα→,{\displaystyle {\vec {M}}=I{\frac {d{\vec {\omega }}}{dt}}=I{\vec {\alpha }},}
где α→{\displaystyle {\vec {\alpha }}} — угловое ускорение, измеряемое в радианах в секунду за секунду (рад/с2). Пример: вращается однородный диск.
Если тензор инерции меняется со временем, то движение относительно центра масс описывается с помощью динамического уравнения Эйлера:
- Mc→=Icdω→dt+[w→,Icw→].{\displaystyle {\vec {M_{c}}}=I_{c}{\frac {d{\vec {\omega }}}{dt}}+[{\vec {w}},I_{c}{\vec {w}}].}
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Так же и момент силы, если совершает действие через угловое расстояние, он совершает работу.
- P=M→⋅ω→.{\displaystyle P={\vec {M}}\cdot {\vec {\omega }}.}
В системе СИ мощность P{\displaystyle P} измеряется в ваттах, момент силы — в ньютоно-метрах, а угловая скорость — в радианах в секунду.
Отношение между моментом силы и работой
- A=∫θ1θ2|M→|dθ.{\displaystyle A=\int _{\theta _{1}}^{\theta _{2}}\left|{\vec {M}}\right|\mathrm {d} \theta .}
В случае постоянного момента получаем:
- A=|M→|θ.{\displaystyle A=\left|{\vec {M}}\right|\theta .}
В системе СИ работа A{\displaystyle A} измеряется в джоулях, момент силы — в ньютоно-метрах, а угол — в радианах.
Обычно известна угловая скорость ω{\displaystyle \omega } в радианах в секунду и время действия момента t{\displaystyle t}.
Тогда совершённая моментом силы работа рассчитывается как:
- A=|M→|ωt.{\displaystyle A=\left|{\vec {M}}\right|\omega t.}
Момент силы относительно точки
Если имеется материальная точка OF{\displaystyle O_{F}}, к которой приложена сила F→{\displaystyle {\vec {F}}}, то момент силы относительно точки O{\displaystyle O} равен векторному произведению радиус-вектора r→{\displaystyle {\vec {r}}}, соединяющего точки O{\displaystyle O} и OF{\displaystyle O_{F}}, на вектор силы F→{\displaystyle {\vec {F}}}:
- MO→=[r→×F→].{\displaystyle {\vec {M_{O}}}=\left[{\vec {r}}\times {\vec {F}}\right].}
Момент силы относительно оси
Момент силы относительно оси равен алгебраическому значению проекции момента этой силы на плоскость, перпендикулярную этой оси относительно точки пересечения оси с плоскостью, то есть
- Mz(F)=Mo(F′)=F′h′.{\displaystyle M_{z}(F)=M_{o}(F’)=F’h’.}
Измерение момента силы
Измерение момента силы осуществляется с помощью специальных приборов — торсиометров. Принцип их действия обычно основан на измерении угла закручивания упругого вала, передающего крутящий момент, либо на измерении деформации некоторого упругого рычага. Измерения деформации и угла закручивания производится различными датчиками деформации — тензометрическими, магнитоупругими, а также измерителями малых перемещений — оптическими, ёмкостными, индуктивными, ультразвуковыми, механическими.
Существуют специальные динамометрические ключи для измерения крутящего момента затягивания резьбовых соединений и регулируемые и нерегулируемые ограничители крутящего момента, так называемые «трещотки», применяемые в гаечных ключах, шуруповёртах, винтовых микрометрах и др.
См. также
МОМЕНТ СИЛЫ — это… Что такое МОМЕНТ СИЛЫ?
Момент силы — Размерность L2MT−2 Единицы измерения СИ Ньютон метр … Википедия
МОМЕНТ СИЛЫ — величина, характеризующая вращат. эффект силы при действии её на тв. тело; одно из осн. понятий механики. Различают М. с. относительно центра (точки) и относительно оси. М. с. относительно центра О величина векторная. Его модуль MO=Fh, где F… … Физическая энциклопедия
Момент (силы) — – в статике сооружений произведение величины силы на кратчайшее расстояние от линии действия силы до точки, относительно которой определяется момент. [Полякова, Т.Ю. Автодорожные мосты: учебный англо русский и русско английский… … Энциклопедия терминов, определений и пояснений строительных материалов
МОМЕНТ СИЛЫ — относительно точки (Moment of a force) произведение величин силы на длину перпендикуляра, опущенного из точки на направление силы. М. С. относительно оси произведение проекции силы на плоскость, перпендикулярную оси, на расстояние между осью и… … Морской словарь
момент силы — произведение силы на плечо. вращающий момент. плечо. кручение. см. равновесие … Идеографический словарь русского языка
МОМЕНТ СИЛЫ — МОМЕНТ СИЛЫ, см. ВРАЩАЮЩИЙ МОМЕНТ … Научно-технический энциклопедический словарь
момент силы — величина, характеризующая вращательный эффект силы при действии её на твёрдое тело. Различают моменты силы относительно центра (точки) и относительно оси. Момент силы относительно центра O (рис. а) векторная величина, численно равная… … Энциклопедический словарь
Момент силы — величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают М. с. относительно центра (точки) и относительно оси. М. с. относительно центра О величина … Большая советская энциклопедия
момент силы — [moment of force] величина, характеризизующая вращательный эффект силы при действии ее на твердое тело. Момент силы, Н • м, рассчитывается относительно центра (точки) вращения. Смотри также: Момент момент сопротивления сечения момент прокатки … Энциклопедический словарь по металлургии
МОМЕНТ СИЛЫ — величина, характеризующая вращат. эффект силы при действии её на тв. тело. Различают М. с. относительно центра (точки) и относительно осн. М. с. относительно центра О (рис. а) векторная величина, численно равная произведению модуля силы F на… … Естествознание. Энциклопедический словарь
МОМЕНТ СИЛЫ — это… Что такое МОМЕНТ СИЛЫ?
— величина, характеризующая вращательный эффект силы; имеет размерность произведения длины на силу. Различают момент силы относительно центра (точки) и относительно оси.
M. с. относительно центра О наз. векторная величина M0, равная векторному произведению радиуса-вектора r, проведённого из O в точку приложения силы F, на силу M0 = [rF]или в др. обозначениях M0 = r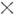 F (рис.). Численно M. с. равен произведению модуля силы на плечо h, т. е. на длину перпендикуляра, опущенного из О на линию действия силы, или удвоенной площади
F (рис.). Численно M. с. равен произведению модуля силы на плечо h, т. е. на длину перпендикуляра, опущенного из О на линию действия силы, или удвоенной площади
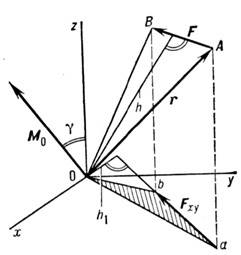
треугольника, построенного на центре O и силе:
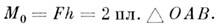
Направлен вектор M0 перпендикулярно плоскости, проходящей через O и F. Сторона, куда направляется M0, выбирается условно (M0 — аксиальный вектор). При правой системе координат вектор M0 направляют в ту сторону, откуда поворот, совершаемый силой, виден против хода часовой стрелки.
M. с. относительно оси z наз. скалярная величина Mz, равная проекции на ось z вектора M. с. относительно любого центра О, взятого на этой оси; величину Mz можно ещё определять как проекцию на плоскость ху, перпендикулярную оси z, площади треугольника OAB или как момент проекции Fxy силы F на плоскость ху, взятый относительно точки пересечения оси z с этой плоскостью. T. о.,
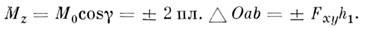
В двух последних выражениях M. с. считается положительным, когда поворот силы Fxy виден с положит. конца оси z против хода часовой стрелки (в правой системе координат). M. с. относительно координатных осей Oxyz могут также вычисляться по аналитич. ф-лам:
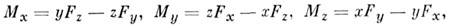
где Fx, Fy, Fz — проекции силы F на координатные оси, х, у, z — координаты точки А приложения силы. Величины Mx, My, Mz равны проекциям вектора M0 на координатные оси.
Если система сил имеет равнодействующую, то момент этой равнодействующей относительно любого центра (или оси) равен сумме моментов всех сил системы относительно того же центра (оси) (см. Вариньона теорема). Понятие о M. с. является одним из осн. понятий механики.
Лит. см. при ст. Статика. С. M. Тарг.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
Момент силы — это… Физический смысл, условие равновесия тел, пример задачи
Динамика вращения является одним из важных разделов физики. Она описывает причины движения тел по окружности вокруг некоторой оси. Одной из важных величин динамики вращения является момент силы, или вращающий момент. Что это — момент силы? Рассмотрим это понятие в данной статье.
Что следует знать о вращении тел?
Прежде чем давать ответ на вопрос, что это — момент силы, охарактеризуем с точки зрения физической геометрии процесс вращения.
Каждый человек интуитивно представляет, о чем идет речь. Вращение подразумевает под собой такое движение тела в пространстве, когда все его точки движутся по круговым траекториям вокруг некоторой оси или точки.
В отличие от линейного перемещения, процесс вращения описывается угловыми физическими характеристиками. Среди них следует назвать угол поворота θ, угловую скорость ω и угловое ускорение α. Величина θ измеряется в радианах (рад), ω — в рад/с, α — в рад/с2.
Примерами вращения являются движение нашей планеты вокруг своей звезды, раскручивание ротора двигателя, движение колеса обозрения и другие.
Понятие о вращающем моменте
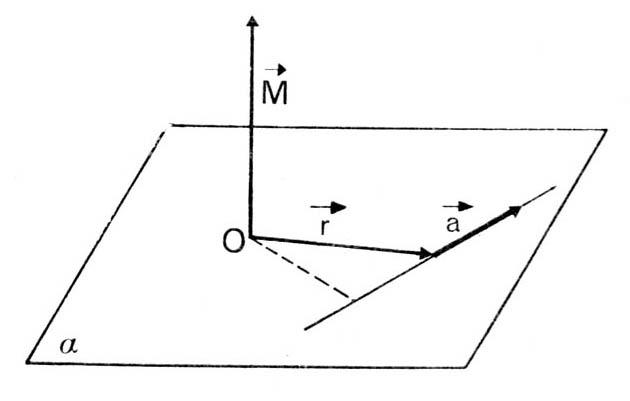
Момент силы — это физическая величина, равная векторному произведению радиус-вектора r¯, направленного от оси вращения к точке приложения силы F¯, и вектора этой силы. Математически это записывают так:
M¯ = [r¯ * F¯].
Как видно, момент силы — это величина векторная. Ее направление определяют по правилу буравчика или правой руки. Величина M¯ направлена перпендикулярно плоскости вращения.
На практике часто возникает необходимость вычисления абсолютного значения момента M¯. Для этого используют такое выражение:
M = r * F * sin(φ).
Где φ является углом между векторами r¯ и F¯. Произведение модуля радиус-вектора r на синус отмеченного угла называется плечом силы d. Последнее представляет собой расстояние между вектором F¯ и осью вращения. Формулу выше можно переписать в виде:
M = d * F, где d = r * sin(φ).
Момент силы измеряется в ньютонах на метр (Н*м). Тем не менее не следует прибегать к использованию джоулей (1 Н*м = 1 Дж), поскольку величина M¯ является не скаляром, а вектором.
Физический смысл величины M¯
Физическое значение момента силы проще всего понять на следующих примерах:
- Предлагаем проделать следующий эксперимент: постараться открыть дверь, толкнув ее вблизи петель. Чтобы проделать эту операцию с успехом, придется приложить большую силу. В то же время за ручку любая дверь открывается достаточно легко. Разница между двумя описанными случаями заключается в длине плеча силы (в первом случае она очень мала, поэтому и создаваемый момент будет небольшим и требует приложения большой силы).
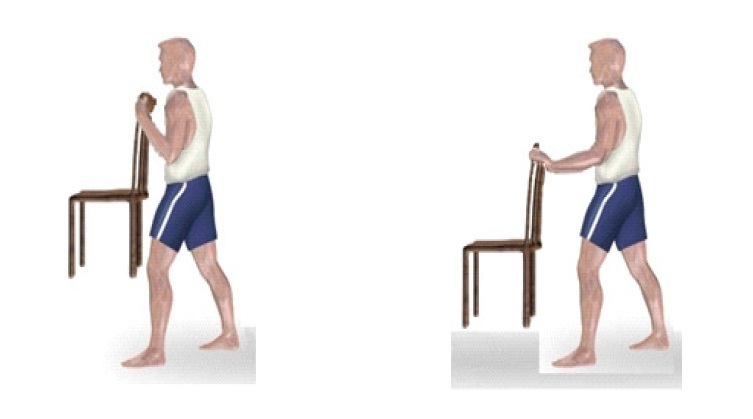
- Еще один эксперимент, показывающий смысл вращающего момента, заключается в следующем: возьмите стул и постарайтесь удержать его на вытянутой вперед руке на весу. Сделать это достаточно сложно. В то же время если прижать руку со стулом к телу, то задача уже не будет казаться непосильной.
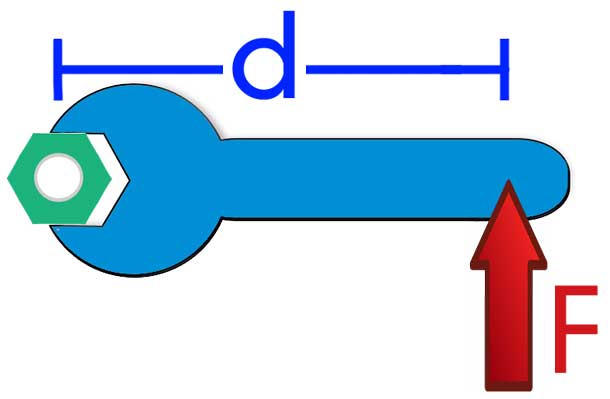
- Каждый человек, связанный с техникой, знает, что открутить гаечным ключом гайку гораздо легче, чем делать это пальцами рук.
Все эти примеры говорят об одном: момент силы отражает способность последней совершить поворот системы вокруг оси. Чем больше вращающий момент, тем выше вероятность, что он выполнит поворот в системе и придаст ей угловое ускорение.
Статика — раздел, занимающийся изучением причин равновесия тел. Если в рассматриваемой системе имеется одна или несколько осей вращения, значит, эта система потенциально может совершать круговое движение. Чтобы этого не происходило и система находилась в состоянии покоя, сумма всех n внешних моментов сил относительно любой оси должна равняться нулю, то есть:
∑i=1nMi = 0.
При использовании этого условия равновесия тел во время решения практических задач следует запомнить, что любая сила, стремящаяся повернуть систему против часовой стрелки, создает положительный вращающий момент, и наоборот.
Очевидно, что если сила приложена к оси вращения, то никакого момента она не создаст (плечо d равно нулю). Поэтому сила реакции опоры никогда не создает момента силы, если его рассчитывать относительно этой опоры.

Пример задачи
Разобравшись, как определить момент силы, решим следующую интересную физическую задачу: предположим, что имеется стол на двух опорах. Длина стола равна 1,5 метра, его масса составляет 30 кг. Груз массой 5 кг положили на расстоянии 1/3 от правого края стола. Необходимо рассчитать, какая сила реакции будет действовать на каждую опору стола с грузом.
Расчет задачи следует проводить в два этапа. На первом рассмотрим стол без груза. На него действуют три силы: две одинаковые реакции опоры и вес тела. Поскольку стол является симметричным, то реакции опор равны друг другу и вместе уравновешивают вес. Значение каждой реакции опоры составляет:
N0 = P / 2 = m * g / 2 = 30 * 9,81 / 2 = 147,15 Н.
Как только кладут груз на стол, то значения реакций опор изменяются. Чтобы их рассчитать, воспользуемся равновесием моментов. Сначала рассмотрим моменты сил, действующие относительно левой опоры стола. Этих моментов два: дополнительная реакция правой опоры без учета веса стола и вес самого груза. Поскольку система находится в равновесии, получаем:
ΔN1 * l — m1 * g * 2 / 3 * l = 0.
Здесь l — длина стола, m1 — масса груза. Из выражения получаем:
ΔN1 = m1 * g * 2 / 3 = 2 / 3 * 9,81 * 5 = 32,7 Н.
Аналогичным способом рассчитаем дополнительную реакцию на левую опору стола. Получаем:
-ΔN2 * l + m1 * g * 1/3 * l = 0;
ΔN2 = m1 * g * 1 / 3 = 1 / 3 * 5 * 9,81 = 16,35 Н.
Чтобы рассчитать реакции опор стола с грузом, необходимо величины ΔN1 и ΔN2 добавить к N0, получаем:
правая опора: N1 = N0 + ΔN1 = 147,15 + 32,7 = 179,85 Н;
левая опора: N2 = N0 + ΔN2 = 147,15 + 16,35 = 163,50 Н.
Таким образом, нагрузка на правую опору стола будет больше, чем на левую.
Момент сил — это… Что такое Момент сил?
Момент силы (синонимы: крутящий момент; вращательный момент; вращающий момент) — физическая величина, характеризующая вращательное действие силы на твёрдое тело.
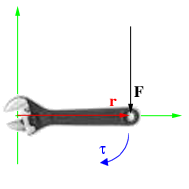
Момент силы приложенный к гаечному ключу
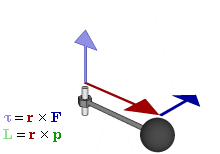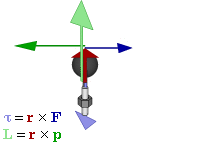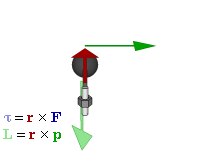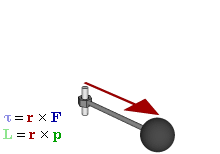
Отношение между векторами силы, момента силы и импульса во вращающейся системе
Момент силы
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является ньютон-метр, хотя сантиньютон-метр (cN•m), футо-фунт (ft•lbf), дюйм-фунт (lbf•in) и дюйм-унция (ozf•in) также часто используются для выражения момента силы. Символ момента силы τ (тау). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. Вращающиеся аналоги силы, массы и ускорения есть момент силы, момент инерции и угловое ускорение соответственно. Сила, приложенная к рычагу, умноженная на расстояние до оси рычага, есть момент силы. Например, сила в 3 ньютона, приложенная к рычагу, расстояние до оси которого 2 метра, это то же самое, что 1 ньютон, приложенный к рычагу, расстояние до оси которого 6 метров. Более точно, момент силы частицы определяется как векторное произведение:
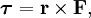
где 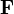 — сила, действующая на частицу, а
— сила, действующая на частицу, а 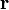 — радиус-вектор частицы!
— радиус-вектор частицы!
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искуственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, относительно неподвижной оси.
Работа, совершаемая при действии силы 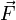 на рычаг
на рычаг 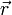 , совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
, совершающего вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок 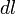 , которому соответствует бесконечно малый угол
, которому соответствует бесконечно малый угол 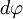 . Обозначим через
. Обозначим через 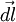 вектор, который направлен вдоль бесконечно малого отрезка
вектор, который направлен вдоль бесконечно малого отрезка 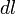
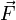 и вектором
и вектором 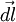 равен
равен 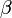 , а угол
, а угол 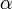
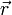 и вектором силы
и вектором силы 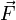
Следовательно, бесконечно малая работа 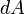 , совершаемая силой
, совершаемая силой 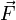 на бесконечно малом участке
на бесконечно малом участке 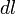 равна скалярному произведению вектора
равна скалярному произведению вектора 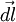 и вектора силы, то есть
и вектора силы, то есть 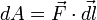 .
.
Теперь попытаемся выразить модуль вектора 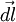 через радиус вектор
через радиус вектор 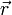 , а проекцию вектора силы
, а проекцию вектора силы 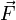 на вектор
на вектор 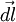 , через угол
, через угол 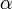 .
.
В первом случае, используя теорему Пифагора, можно записать следующее равенство 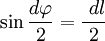 , где в случае малого угла справедливо
, где в случае малого угла справедливо 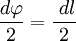 и следовательно
и следовательно 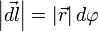
Для проекции вектора силы 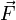 на вектор
на вектор 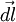 , видно, что угол
, видно, что угол 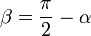 , так как для бесконечно малого перемещения рычага
, так как для бесконечно малого перемещения рычага 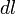 , можно считать, что траектория перемещения перпендикулярна рычагу
, можно считать, что траектория перемещения перпендикулярна рычагу 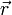 , а так как
, а так как 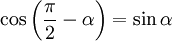 , получаем, что
, получаем, что 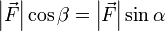 .
.
Теперь запишем бесконечно малую работу через новые равенства 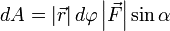 или
или 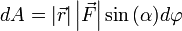 .
.
Теперь видно, что произведение 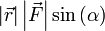 есть ни что иное как модуль векторного произведения векторов
есть ни что иное как модуль векторного произведения векторов 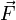 и
и 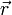 , то есть
, то есть 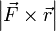 , которое и было принято обозначить за момент силы
, которое и было принято обозначить за момент силы 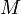 или модуля вектора момента силы
или модуля вектора момента силы 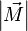 .
.
И теперь полная работа записывается очень просто 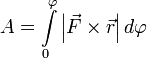 или
или 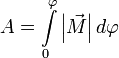 .
.
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является «ньютон-метр». Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н*м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н*м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
 ,
,
где Е — энергия, τ — вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
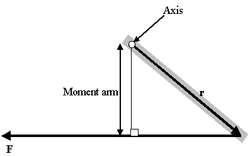
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- τ = МОМЕНТ РЫЧАГА * СИЛУ
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
Сила под углом
Если сила F направлена под углом θ к рычагу r, то τ = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении Στ=0.
Момент силы как функция от времени
Момент силы — производная по времени от момент импульса,
 ,
,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
 ,
,
То есть если I постоянная, то
 ,
,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
 = МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
= МОМЕНТ СИЛЫ * УГЛОВАЯ СКОРОСТЬ
В системе СИ мощность 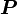 измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
 = МОМЕНТ СИЛЫ * УГОЛ
= МОМЕНТ СИЛЫ * УГОЛ
В системе СИ работа 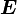 измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в в радианах.
Обычно известна угловая скорость 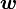 в радианах в секунду и время действия МОМЕНТА
в радианах в секунду и время действия МОМЕНТА 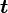 .
.
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
 = МОМЕНТ СИЛЫ *
= МОМЕНТ СИЛЫ *  *
* 
Момент силы относительно точки
Если имеется материальная точка 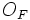 , к которой приложена сила
, к которой приложена сила 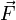 , то момент силы относительно точки
, то момент силы относительно точки  равен векторному произведению радиус-вектора
равен векторному произведению радиус-вектора 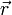 , соединяющий точки O и OF, на вектор силы
, соединяющий точки O и OF, на вектор силы 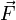 :
:
![\vec M_O = \left[ \vec r \times \vec F \right]](/800/600/https/dic.academic.ru/pictures/wiki/files/48/060f481774ea2ae7875fb856dd7d28d8.png) .
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н•м — момент силы, который производит сила 1 Н на рычаг длиной 1 м.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
См. также
Wikimedia Foundation. 2010.
Момент силы, формулы
Определение 1
Моментом силы представляется крутящий или вращательный момент, являясь при этом векторной физической величиной.
Она определяется как векторное произведение вектора силы, а также радиус-вектора, который проведен от оси вращения к точке приложения указанной силы.
Момент силы выступает характеристикой вращательного воздействия силы на твердое тело. Понятия «вращающий» и «крутящий» моменты не будут считаться при этом тождественными, поскольку в технике понятие «вращающий» момент рассматривают как внешнее, прикладываемое к объекту, усилие.
В то же время, понятие «крутящий» рассматривается в формате внутреннего усилия, возникающего в объекте под воздействием определенных приложенных нагрузок (подобным понятием оперируют при сопротивлении материалов).
Понятие момента силы
Момент силы в физике может рассматриваться в виде так называемой «вращающей силы». В СИ за единицу измерения принимают ньютон-метр. Момент силы также может называться «моментом пары сил», что отмечено в работах Архимеда над рычагами.
Замечание 1
В простых примерах, при приложении силы к рычагу в перпендикулярном отношении к нему, момент силы будет определяться в виде произведения величины указанной силы и расстояния до оси вращения рычага.
К примеру, сила в три ньютона, приложенная на двухметровом расстоянии от оси вращения рычага, создает момент, равнозначный силе в один ньютон, приложенной на 6-метровом расстоянии к рычагу. Более точно момент силы частицы определяют в формате векторного произведения:
$\vec {M}=\vec{r}\vec{F}$, где:
- $\vec {F}$ представляет силу, воздействующая на частицу,
- $\vec {r}$ является радиусом вектора частицы.
В физике следует понимать энергию как скалярную величину, в то время как момент силы будет считаться величиной (псевдо) векторной. Совпадение размерностей подобных величин не будет случайным: момент силы в 1 Н•м, который приложен через целый оборот, совершая механическую работу, сообщает энергию в 2 $\pi$ джоулей. Математически это выглядит так:
$E = M\theta $, где:
- $E$ представляет энергию;
- $M$ считается вращающимся моментом;
- $\theta $ будет углом в радианах.
Сегодня измерение момента силы осуществляют посредством задействования специальных датчиков нагрузки тензометрического, оптического и индуктивного типа.
Формулы расчета момента силы
Интересным в физике является вычисление момента силы в поле, производимого по формуле:
$\vec{M} = \vec{M_1}\vec{F}$, где:
- $\vec{M_1}$ считается моментом рычага;
- $\vec{F}$ представляет величину действующей силы.
Недостатком такого представления будет считаться тот факт, что оно не определяет направление момента силы, а только лишь его величину. При перпендикулярности силы вектору вектору $\vec{r}$ момент рычага будет равен расстоянию от центра до точки приложенной силы. При этом момент силы окажется максимальным:
$\vec{T}=\vec{r}\vec{F}$
При совершении силой определенного действия на каком-либо расстоянии, она совершит механическую работу. Точно также и момент силы (при выполнении действия через угловое расстояние) совершит работу.
$P = \vec {M}\omega $
В существующей международной системе измерений мощность $P$ будет измеряться в Ваттах, а непосредственно момент силы— в ньютон-метрах. При этом угловая скорость определяется в радианах в секунду.
Момент нескольких сил
Замечание 2
При воздействии на тело двух равных, а также противоположно направленных сил, не лежащих при этом на одной и той же прямой, наблюдается отсутствие пребывания этого тела в состоянии равновесия. Это объясняется тем, что результирующий момент указанных сил относительно любой из осей не имеет нулевого значения, поскольку обе представленные силы имеют направленные в одну сторону моменты (пара сил).
В ситуации, когда тело закрепляется на оси, произойдет его вращение под воздействием пары сил. Если пара сил будет приложенной в отношении свободного тела, оно в таком случае станет вращаться вокруг проходящей сквозь центр тяжести тела оси.
Момент пары сил считается одинаковым в отношении любой оси, которая перпендикулярна плоскости пары. При этом суммарный момент $М$ пары всегда будет равным произведению одной из сил $F$ на расстояние $l$ между силами (плечо пары) в независимости от типов отрезков, на которые оно разделяет положение оси.
$M={FL_1+FL-2} = F{L_1+L_2}=FL$
В ситуации, когда равнодействующая момента нескольких сил равнозначна нулю, он будет считаться одинаковым относительно всех параллельных друг другу осей. По этой причине воздействие на тело всех этих сил возможно заменить действием всего лишь одной пары сил с таким же моментом.


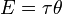 ,
,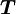 = РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ
= РАССТОЯНИЕ ДО ЦЕНТРА * СИЛУ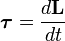 ,
,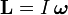 ,
,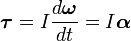 ,
,