Момент силы | это… Что такое Момент силы?
Момент силы, приложенный к гаечному ключу. Направлен от зрителя
Зависимости между силой F, моментом силы τ (M), импульсом p и моментом импульса L в системе, которая была ограничена только в одной плоскости (силы и моменты, обусловленные тяжестью и трением не учитываются)
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Содержание
|
Общие сведения
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является Ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага.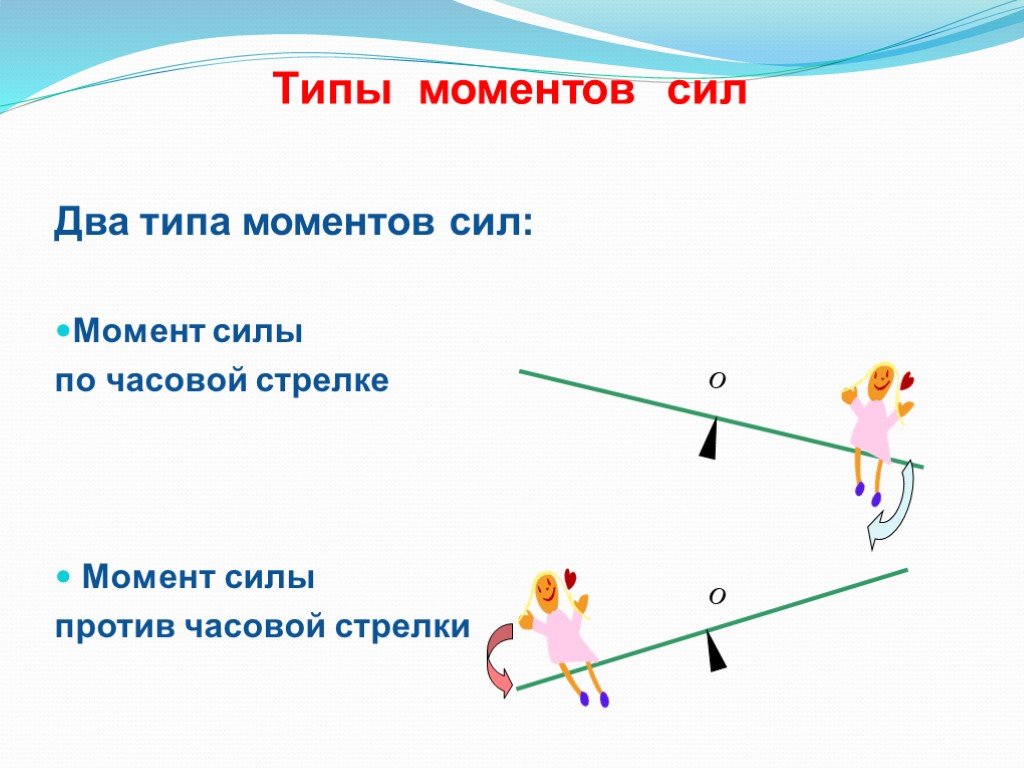
где — сила, действующая на частицу, а — радиус-вектор частицы.
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искусственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол между вектором и вектором силы .
Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол между вектором и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус-вектор , а проекцию вектора силы на вектор , через угол .
Так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , используя соотношения для прямоугольного треугольника, можно записать следующее равенство: , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть не что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуль вектора момента силы .
Теперь полная работа записывается очень просто: или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является ньютон-метр. Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н·м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н·м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, M— вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- = МОМЕНТ_РЫЧАГА * СИЛА
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в. м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ_ДО_ЦЕНТРА * СИЛА
Сила под углом
Если сила F направлена под углом θ к рычагу r, то M = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении ΣM=0.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть, если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.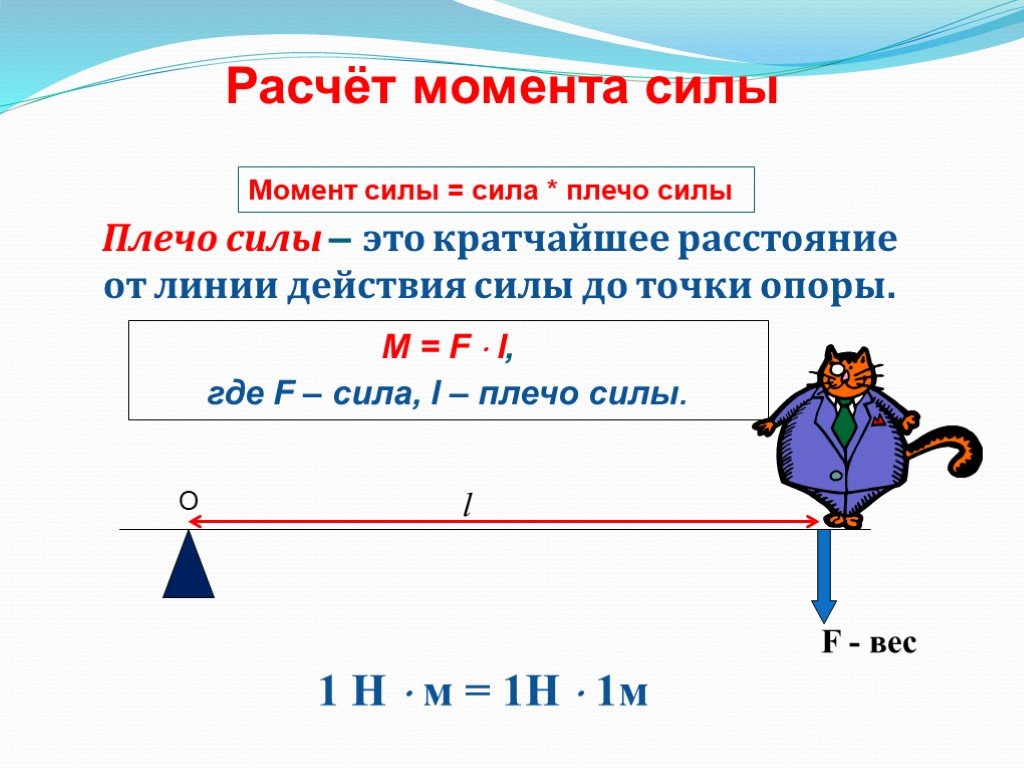
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ_СИЛЫ * УГЛОВАЯ_СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ_СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ_СИЛЫ * *
Момент силы относительно точки
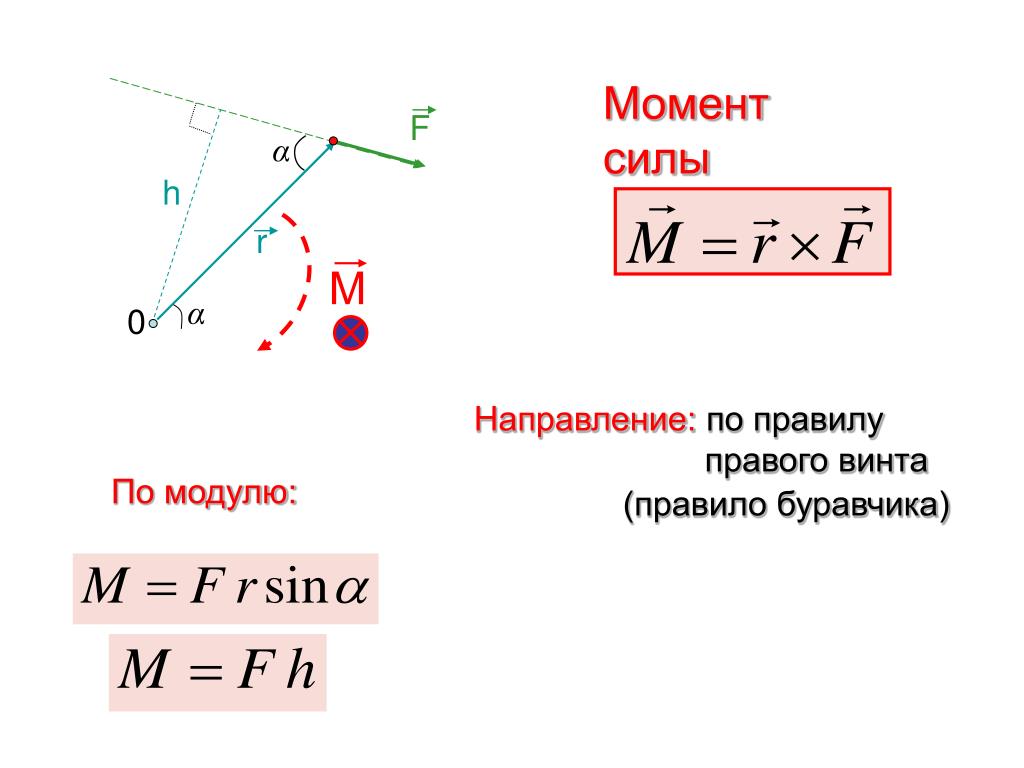
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющего точки и , на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM, Lorenz (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
Ссылки
- Развитие и будущее технологии измерения крутящего момента
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Момент силы | это… Что такое Момент силы?
Момент силы, приложенный к гаечному ключу.
Зависимости между силой F, моментом силы τ (M), импульсом p и моментом импульса L в системе, которая была ограничена только в одной плоскости (силы и моменты, обусловленные тяжестью и трением не учитываются)
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Содержание
|
Общие сведения
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является Ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения.
где — сила, действующая на частицу, а — радиус-вектор частицы.
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искусственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю.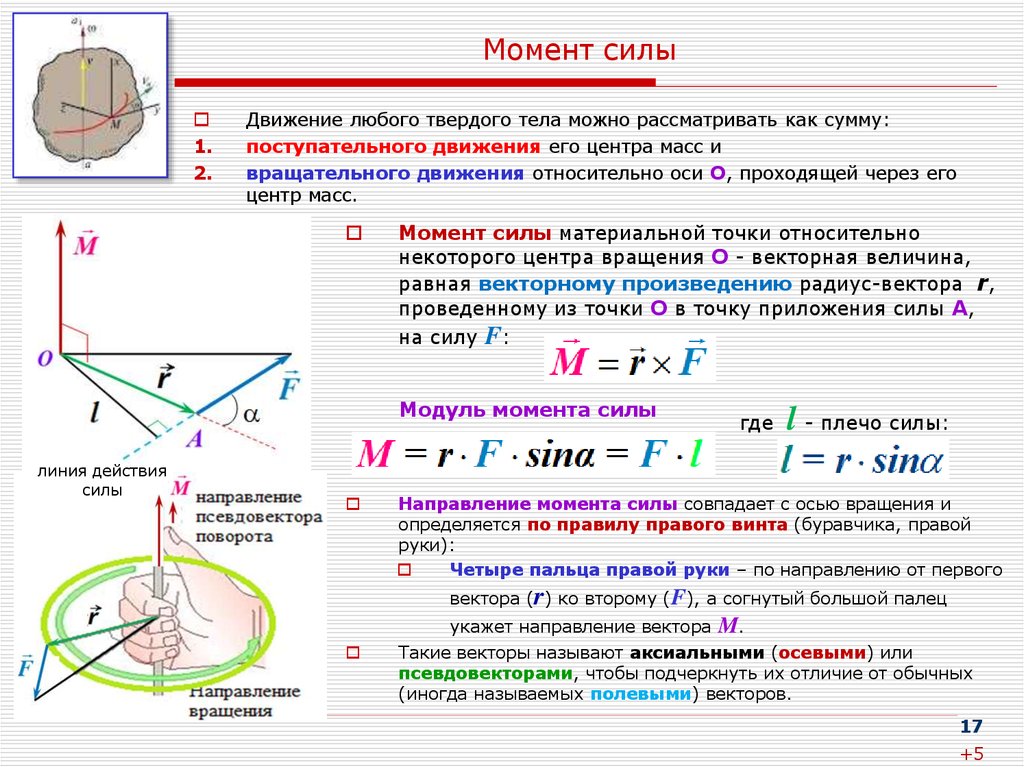 Угол между вектором силы и вектором равен , а угол между вектором и вектором силы .
Угол между вектором силы и вектором равен , а угол между вектором и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус-вектор , а проекцию вектора силы на вектор , через угол .
Так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , используя соотношения для прямоугольного треугольника, можно записать следующее равенство: , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть не что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуль вектора момента силы .
Теперь полная работа записывается очень просто: или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является ньютон-метр. Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н·м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н·м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, M— вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
Момент рычага
Очень интересен особый случай, представляемый как определение момента силы в поле:
- = МОМЕНТ_РЫЧАГА * СИЛА
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.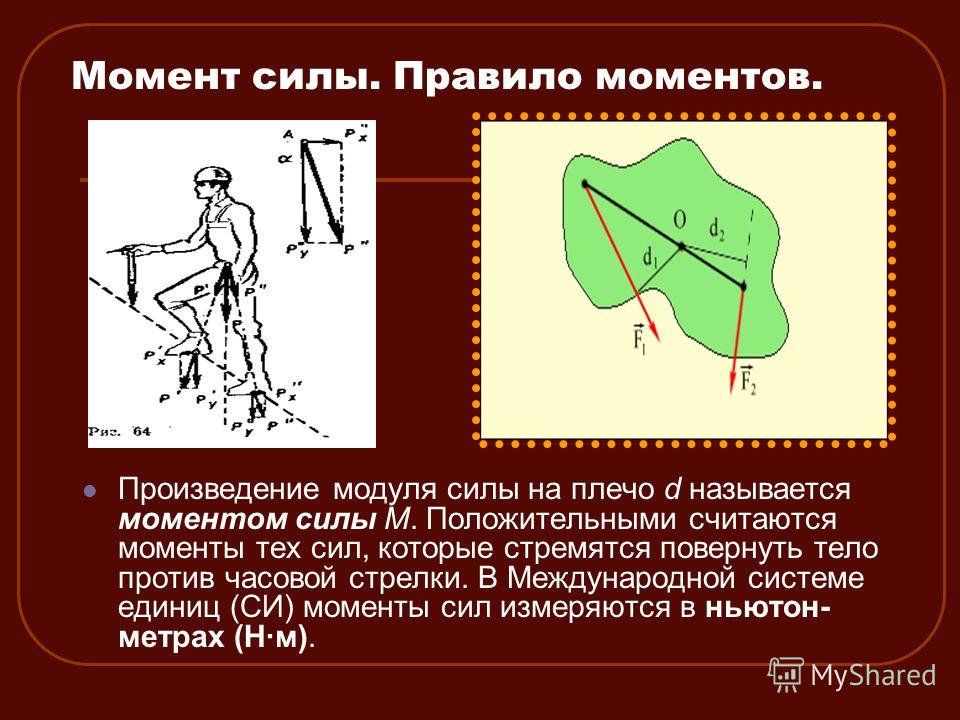 м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ_ДО_ЦЕНТРА * СИЛА
Сила под углом
Если сила F направлена под углом θ к рычагу r, то M = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении ΣM=0.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть, если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.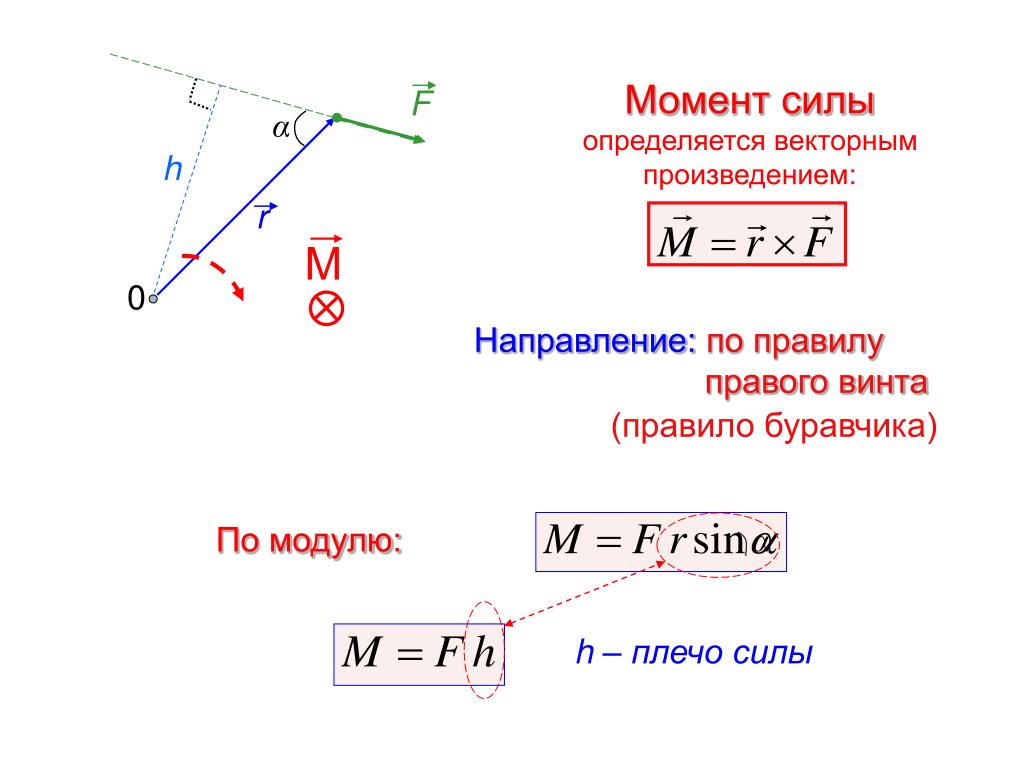
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ_СИЛЫ * УГЛОВАЯ_СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ_СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ_СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющего точки и , на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM, Lorenz (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
Ссылки
- Развитие и будущее технологии измерения крутящего момента
См. также
- Момент инерции
- Момент импульса
- Теорема Вариньона
Момент силы: определение, формула, классификация, примеры момент силы.
 Сила – это воздействие, способное изменить движение объекта. Сила, действующая на объект с массой, может заставить его ускориться или изменить его скорость. Простой способ описать силу — это толчок или притяжение. Поскольку сила имеет как величину, так и направление, она является векторной величиной. Выражается в ньютонах (Н) в системе СИ. F — символ, используемый для обозначения силы.
Сила – это воздействие, способное изменить движение объекта. Сила, действующая на объект с массой, может заставить его ускориться или изменить его скорость. Простой способ описать силу — это толчок или притяжение. Поскольку сила имеет как величину, так и направление, она является векторной величиной. Выражается в ньютонах (Н) в системе СИ. F — символ, используемый для обозначения силы.Вращательное воздействие силы известно как момент силы, который определяется как произведение силы на перпендикулярное расстояние между силой и осью вращения. Момент силы зависит от ее величины и перпендикулярного расстояния между ней и стержнем. Скручивающее воздействие увеличивается по мере увеличения перпендикулярного расстояния (момент).
Скачать формулы для машиностроения GATE — Сопротивление материалов
Содержание
- 1. Определение момента силы
- 2. Формула момента силы
- 3. Классификация момента силы
- 4. Что такое единица СИ для момента силы?
- 5.
 Направление момента силы
Направление момента силы - 6. Примеры момента силы
Прочитать статью полностью
Определение момента силы
Момент — это термин, используемый для описания вращательного действия силы. Это результат умножения силы путем разделения линии действия силы и точки поворота или точки, в которой объект повернется. Единицей СИ для момента силы является ньютон-метр (Нм). Это векторная величина.
Правило правой руки, которое параллельно плоскости действия силы и имеет точку вращения, параллельную оси вращения, определяет его ориентацию.
Момент силы Формула
Момент определяется как эффект вращения силы. Это результат умножения силы на расстояние между линией действия силы и точкой поворота или точкой, в которой объект повернется. Обозначается 𝝉.
𝝉 = F×d
Где,
𝝉 — момент силы
F — сила
d — расстояние по перпендикуляру между линией действия силы и центром вращения.
Загрузить формулы для машиностроения GATE — Конструирование машин
Классификация момента силы
Момент силы относится к действию силы на тело, вращающееся вокруг оси. Он равен произведению величины силы и перпендикулярного расстояния силовой линии от оси вращения. Момент силы классифицируется по следующим категориям:
- Крутящий момент
- Изгибающий момент
- Крутящий момент
Крутящий момент
Этот момент заставляет тело вращаться вокруг точки опоры. В этом сценарии тело может свободно вращаться вокруг точки опоры.
Изгибающий момент
Этот момент заставляет тело изгибаться вокруг одного из закрепленных концов.
Крутящий момент
Это событие заставляет вал закручиваться вокруг одного из его неподвижных концов.
Загрузить формулы для машиностроения GATE — Технология производства и материалы
Что такое единица СИ для момента силы?
Стремление силы заставить тело вращаться вокруг определенной точки или оси измеряется ее моментом силы.
Момент силы = (сила) * (перпендикулярное расстояние от оси вращения)
Ньютон — это единица силы в системе СИ, тогда как метр — это единица измерения расстояния в системе СИ. Итак, ньютон-метр — это единица измерения момента силы в системе СИ.
Направление момента силы
В простейшей форме момент создается путем умножения расстояния до точки на физическую величину (например, силу). Он подразделяется на два типа в зависимости от направления момента.
- Момент по часовой стрелке
- Момент против часовой стрелки
Момент по часовой стрелке
Создаваемый момент называется моментом по часовой стрелке, если сила, действующая на тело, стремится заставить тело вращаться по часовой стрелке.
Момент против часовой стрелки
Момент против часовой стрелки создается, когда сила, действующая на тело, может заставить тело вращаться против часовой стрелки.
Примеры момента силы
Момент возникает в результате действия силы, вращающейся вокруг неподвижной точки вращения. Дверь, открывающаяся вокруг неподвижной петли, качели, ножницы или гаечный ключ, вращающийся вокруг гайки, — вот несколько примеров.
Дверь, открывающаяся вокруг неподвижной петли, качели, ножницы или гаечный ключ, вращающийся вокруг гайки, — вот несколько примеров.
- Чтобы открыть и закрыть дверь, к ручке P, наиболее удаленной от петли, прикладывается сила (толкание или вытягивание), перпендикулярная двери.
- Для того чтобы верхний круглый камень ручной мельницы можно было легко поворачивать вокруг металлического стержня в его центре путем небольшого нажатия на ручку, он снабжен ручкой у края (т. е. на максимальном расстоянии от центра) .
- Сила по касательной воздействует на обод колеса, чтобы повернуть рулевое колесо.
- На велосипеде небольшое усилие прикладывается к педали зубчатого колеса, чтобы повернуть колесо против часовой стрелки.
Часто задаваемые вопросы о моменте силы
Что такое момент силы?
Результат умножения составляющей силы, перпендикулярной линии расстояния, на расстояние между точкой и точкой приложения известен как момент силы .

Какова формула момента силы?
Момент силы = F x d
Момент силы выражается в ньютон-метрах (Нм), где F — приложенная сила, а d — расстояние от неподвижной оси. Как для уравновешенных, так и для неуравновешенных сил момент силы можно рассчитать, используя формулу момента силы.
Приведите пример момента силы?
Например, визуализируйте открытие двери. Дверь вращается вокруг своих петель, когда вы тянете за дверную ручку (петли являются шарниром). Вращение двери было прямым результатом силы, которую вы приложили, толкнув ее.
Почему его называют моментом силы?
Например, момент силы, также известный как крутящий момент, является результатом силы, действующей на объект, и расстояния объекта от контрольной точки. Теоретически любую физическую величину можно умножить на расстояние, чтобы получить момент силы.
Крутящий момент и момент силы одинаковы?
В то время как момент измеряет угол между точкой вращения и линией действия силы, крутящий момент измеряет силу, поворачивающую тело.
 Стремление силы заставить тело вращаться в определенной точке или оси описывается в физике как момент силы.
Стремление силы заставить тело вращаться в определенной точке или оси описывается в физике как момент силы.Что такое момент силы относительно точки?
Величина и расстояние от оси вращения силы определяют ее момент. Момент силы относительно точки равен (величина силы) × (перпендикулярное расстояние линии действия силы от точки).
ESE & GATE ME
Mechanical Engg.GATEGATE MEHPCLBARC SOESEIES MEBARC ExamISRO ExamOther Exams
Избранные статьи
Следите за нашими новостями
Наши приложения
- BYJU’S Exam Prep: приложение для подготовки к экзамену
GradeStack Learning Pvt. Ltd.Windsor IT Park, Tower — A, 2nd Floor,
Sector 125, Noida,
Uttar Pradesh 201303
help@byjusexamprep. com
com
Момент силы: определение, принцип, типы, применение
Kamal Dwivedi 11 мая 2022
Здравствуйте, друзья сегодня я собираюсь обсудить « момент силы », в котором вы будете знать обо всех аспектах, связанных с моментом силы, таких как их классификация, принцип, геометрическое представление, применение и т. д.
Итак, не теряя времени, давайте начнем.
Что такое Момент силы?
Тенденция сил заключается не только в перемещении тела, но и во вращении тела.
Эта вращательная тенденция силы называется моментом или моментом силы.
Математически это можно определить как » Произведение силы на перпендикулярное расстояние от точки до линии действия силы называется моментом силы относительно этой точки».
Может быть обозначено через M.
Итак,
Формула момента силы может быть записана как,
M = F × d
d = Перпендикулярное расстояние
Единицей момента силы в системе СИ является ньютон-метр (Н-м), а в СГС ее можно записать как ньютон-сантиметр (Н-см).
Направление момента
В зависимости от направления момента он делится на два типа.
- Момент по часовой стрелке
- Момент против часовой стрелки
См. на рисунке направление моментов, которые подробно описаны ниже.
Момент по часовой стрелке
Если сила, действующая на тело, стремится повернуть тело по часовой стрелке, то создаваемый момент называется моментом по часовой стрелке.
Момент против часовой стрелки
Если сила, действующая на тело, стремится повернуть тело против часовой стрелки, то создаваемый таким образом момент называется моментом против часовой стрелки.
Классификация момента силы
Существуют следующие классификации моментов:
- Крутящий момент
- Изгибающий момент
- Крутящий момент
См. на рисунке ниже вращающий момент, изгибающий момент и в деталях.
Крутящий момент
Этот момент стремится повернуть тело вокруг точки опоры. В этом случае тело может свободно вращаться вокруг точки опоры.
В этом случае тело может свободно вращаться вокруг точки опоры.
Изгибающий момент
Этот момент стремится согнуть тело вокруг одного из его неподвижных концов.
Крутящий момент
Этот момент закручивает вал вокруг одного из его неподвижных концов.
Геометрическое представление момента силы
Момент силы относительно точки равен удвоенной площади треугольника, образованного таким образом, если принять точку за вершину треугольника и линию за основание треугольника.
Рассмотрим силу F, действующую на тело и представленную вектором AB.
Пусть O будет точкой, относительно которой должен быть рассчитан момент силы.
Тогда,
Момент силы относительно O, M =Fx OC
Момент силы относительно O, M = AB x OC
(Отчетливо видно на рисунке F = AB)
Теперь умножьте и разделите на 2
Тогда
M = 2 x 1/2 AB x OC
Как мы знаем,
Площадь треугольника = 1/2 × основание × высота
Итак,
M = 902 △ОАБПринцип момента силы
Если тело находится в равновесии под действием ряда сил, одновременно действующих на тело, то алгебраическая сумма моментов всех сил относительно точки в их плоскости равна нулю» .
или
Если тело находится в равновесии под действием ряда сил, одновременно действующих на тело, то алгебраическая сумма моментов сил относительно точки по часовой стрелке равна сумме моментов сил против часовой стрелки. силы относительно одной и той же точки».
Это означает, что алгебраическая сумма всех моментов должна быть равна нулю.
ΣM = 0
Рассмотрим четыре копланарные силы F1, F2, F3 и F4, действующие на тело, когда оно находится в равновесии.
Пусть О — точка, вокруг которой может вращаться тело. Пусть d1, d2, d3 и d4 — расстояние по перпендикуляру от точки O до линии действия сил F1, F2, F3 и F4 соответственно.
Тогда
Момент силы F1 = F1 x d1 (против часовой стрелки)
Момент силы F2 = F2 x d2 (против часовой стрелки)
Момент силы F3 = F3 x d3 (по часовой стрелке)
Момент силы F4= F4 x d4 (по часовой стрелке)
Результирующий момент = M
Σ x d1 + F2 x d2 — F3 x d3 — F4 x d4
Согласно принципу момента силы алгебраическая сумма всех моментов должна быть равна нулю.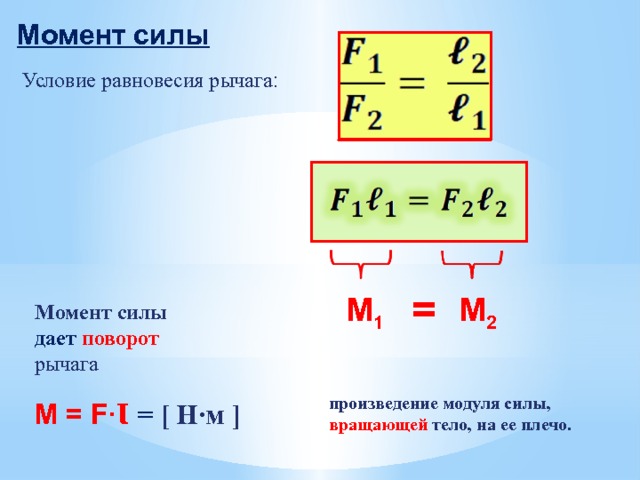


 1 Формула момента рычага
1 Формула момента рычага Направление момента силы
Направление момента силы
 Стремление силы заставить тело вращаться в определенной точке или оси описывается в физике как момент силы.
Стремление силы заставить тело вращаться в определенной точке или оси описывается в физике как момент силы.