Лекция 2. Теория пар
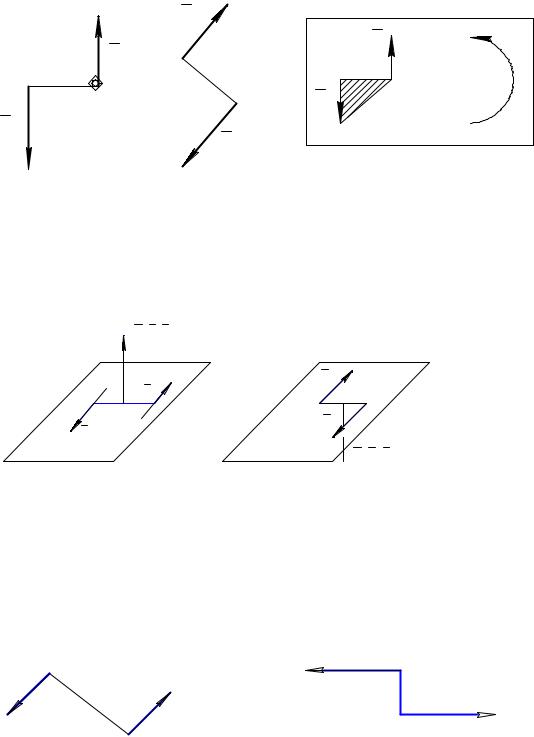
2.1. Момент силы относительно точки и оси
Моментом
силы 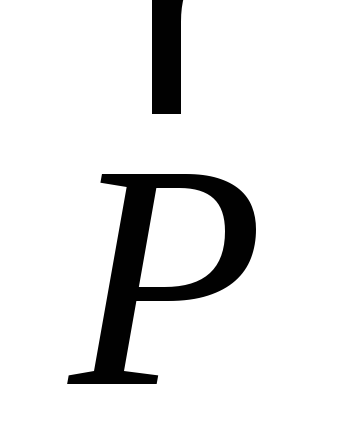 относительно точки O называют величину, равную векторному
произведению радиус-вектора
относительно точки O называют величину, равную векторному
произведению радиус-вектора 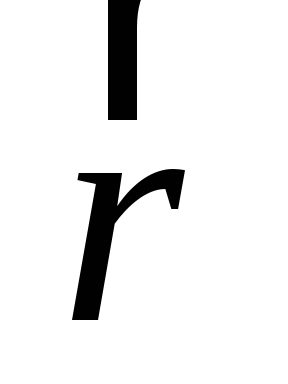 ,
проведенного из точкиO в точку приложения силы (рис. 2.1), на эту
силу
,
проведенного из точкиO в точку приложения силы (рис. 2.1), на эту
силу
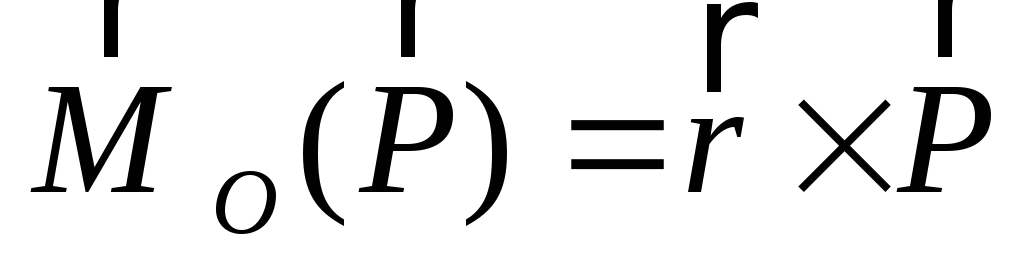 .
(2.1)
.
(2.1)
Этот вектор приложен в точке O и
направлен перпендикулярно плоскости,
содержащей векторы 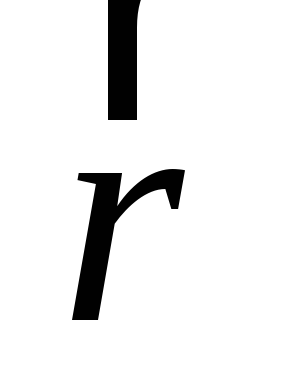 и
и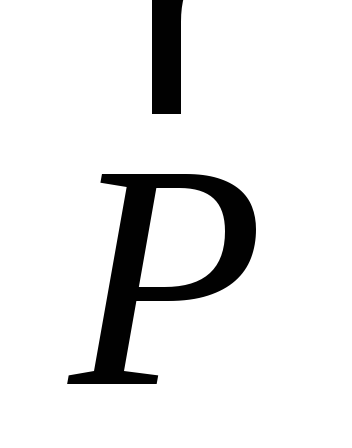 в ту сторону, откуда вращение тела,
вызываемое силой
в ту сторону, откуда вращение тела,
вызываемое силой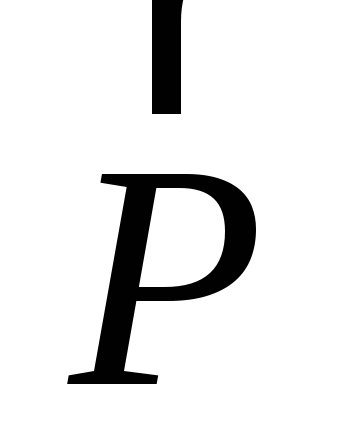
Модуль момента
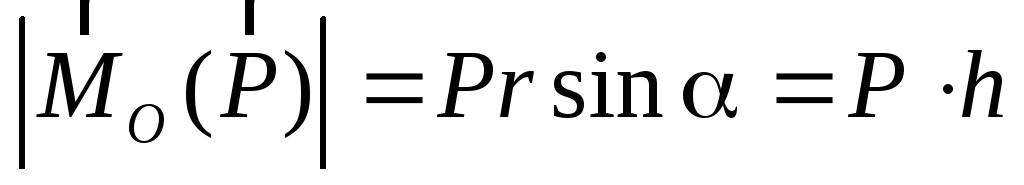 ,
(2.2)
,
(2.2)
где 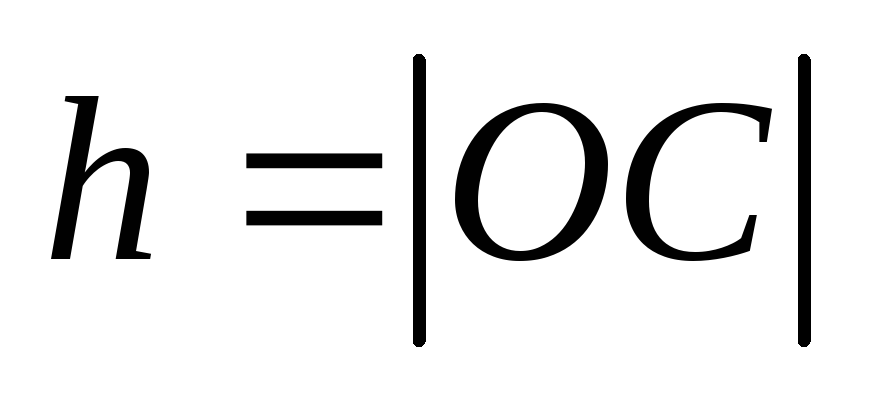 – плечо силы
– плечо силы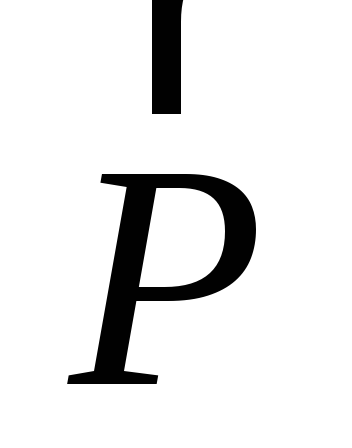
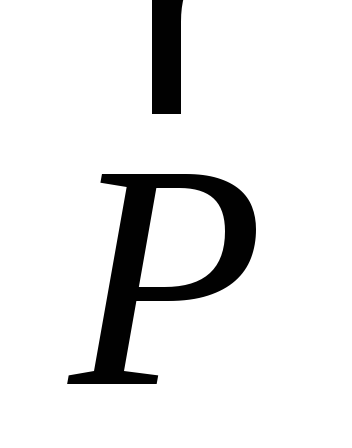 .
Из формулы (2.2) следует, что
.
Из формулы (2.2) следует, что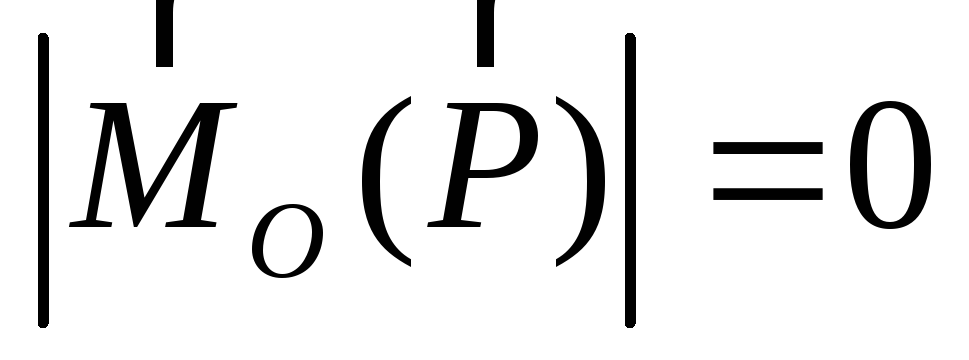 ,
еслиh = 0, т.е. если линия действия силы
,
еслиh = 0, т.е. если линия действия силы 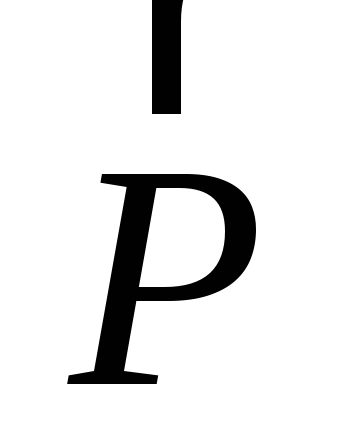 проходит через точкуО.
проходит через точкуО. Обозначим через x,
y, z координаты точки
приложения силы, 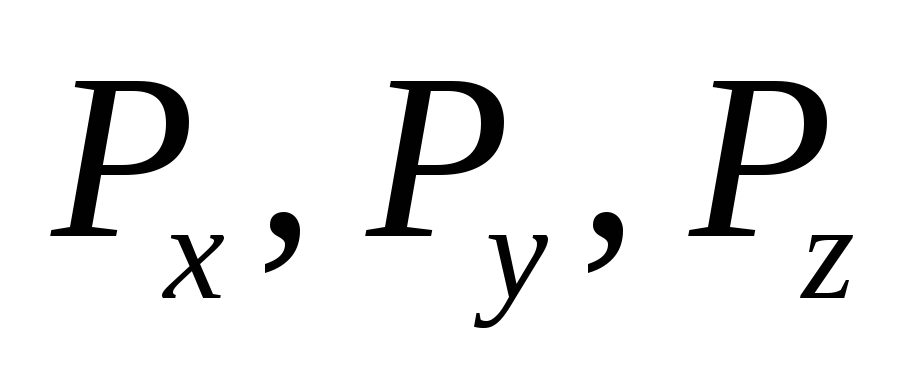 – проекции силы
– проекции силы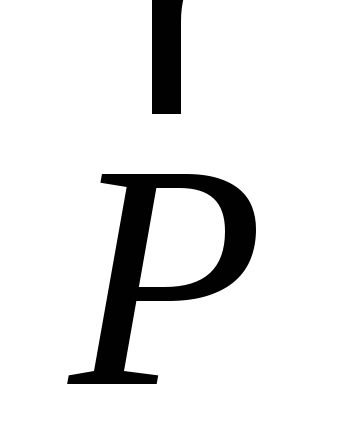
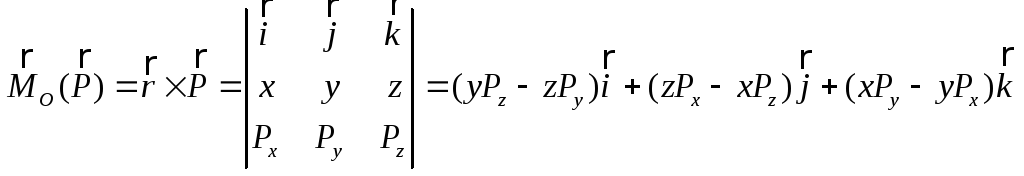 ,
(2.3)
,
(2.3)
откуда следует, что проекции момента силы на координатные оси равны
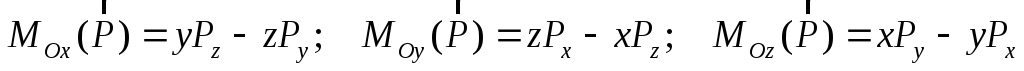 .
(2.4)
.
(2.4)
Моментом силы относительно оси называют величину, равную проекции на эту ось момента силы, взятого относительно некоторой точки оси
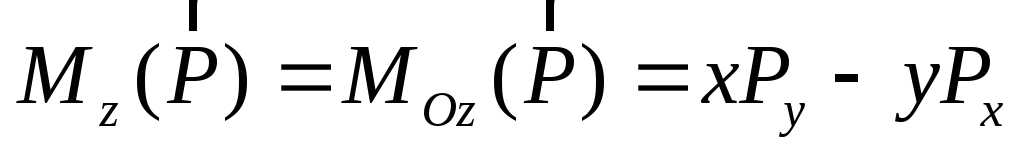
Момент силы относительно оси не зависит от выбора точки O на оси, так как ни одна из величин в правой части формулы (2.5) не зависит от положения начала координат при параллельном перемещении осей x и y.
П роекцией
силы на плоскостьназывают
вектор, начало и конец которого совпадают
с проекциями начала и конца вектора
силы на эту плоскость. На рис. 2.2 показана
проекция
роекцией
силы на плоскостьназывают
вектор, начало и конец которого совпадают
с проекциями начала и конца вектора
силы на эту плоскость. На рис. 2.2 показана
проекция 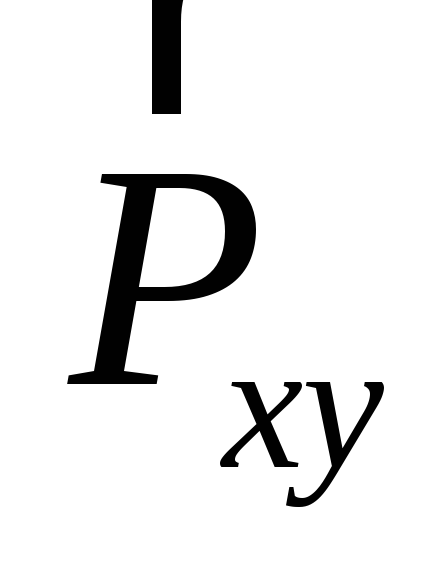 силы
силы
 и
и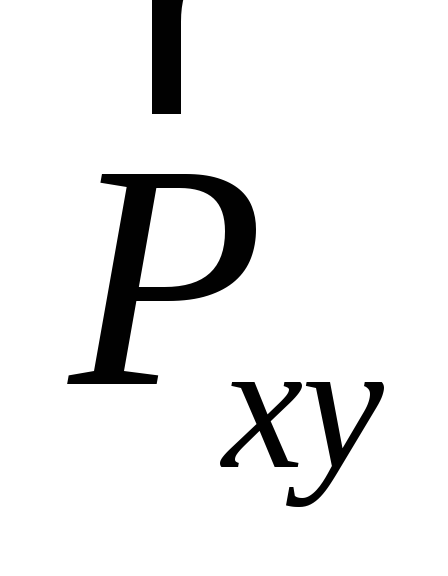 ,
а также точек их приложения на осиx и y одинаковы, момент силы
,
а также точек их приложения на осиx и y одинаковы, момент силы 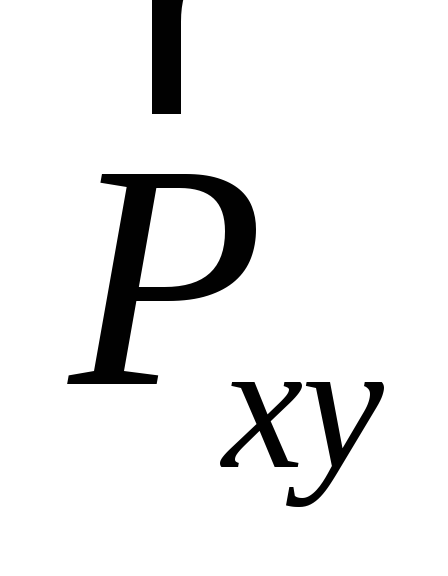 относительно точкиO может быть вычислен по формуле (2.3), где
следует положить, что z = 0 и
относительно точкиO может быть вычислен по формуле (2.3), где
следует положить, что z = 0 и 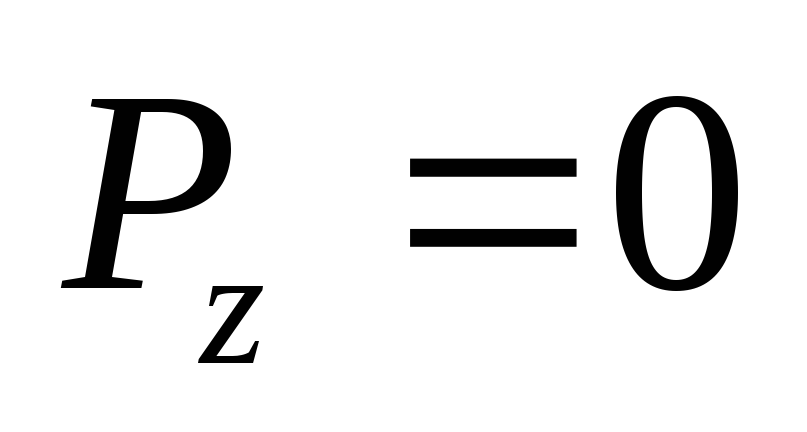 ,
, 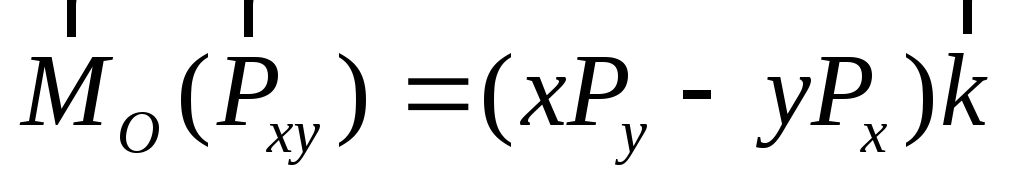
Этот момент направлен вдоль
оси z,
а его проекция на эту ось совпадает с
моментом силы 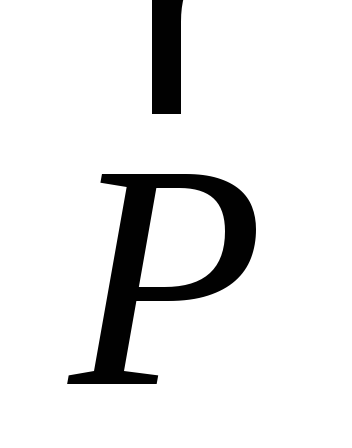 относительно
осиz:
относительно
осиz:
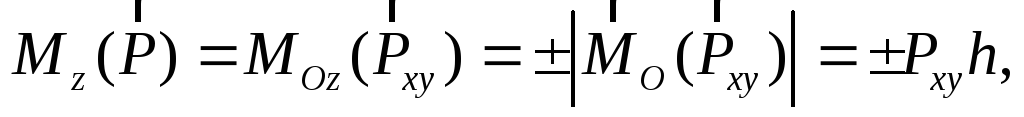
где h – плечо силы 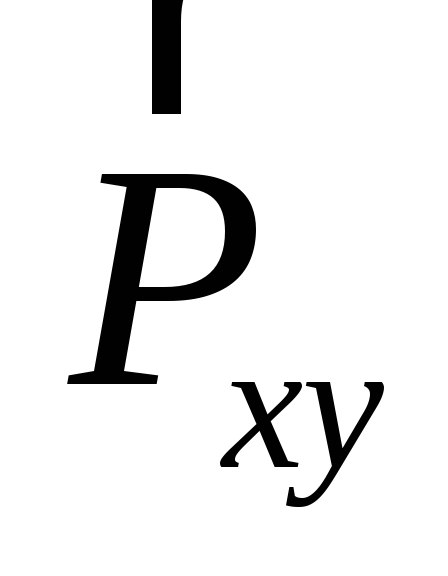 относительно точкиO.
относительно точкиO.
Таким образом, можно сформулировать следующее правило вычисления момента силы относительно оси z:
1) выберем на оси
2) спроецируем силу на эту плоскость;
3) определим плечо проекции силы;
4) вычислим момент силы относительно оси z по формуле
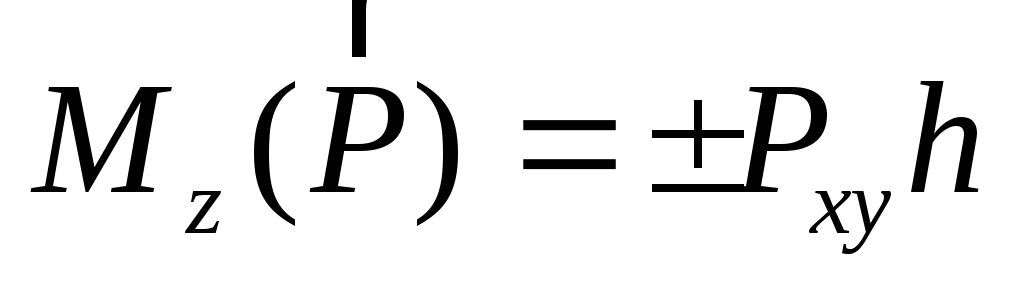 .
(2.6)
.
(2.6)
В формуле (2.6) знак «плюс» ставим в том случае, если с положительного направления оси z поворот тела вокруг этой оси виден направленным против часовой стрелки, знак «минус» – в противном случае. Аналогично вычисляют моменты силы относительно других координатных осей.
Из формулы (2.6) следует, что момент силы относительно оси равен нулю в двух случаях:
1) если сила параллельна оси,
т.е. проекция 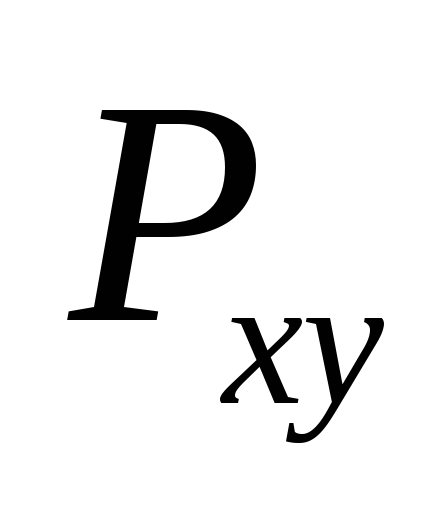 = 0;
= 0;
2) если линия действия силы пересекает ось, т.е. плечо h = 0.
Оба случая можно объединить: момент силы относительно оси равен нулю тогда и только тогда, когда линия действия силы и ось лежат в одной плоскости.
2.2. Пара сил и ее момент
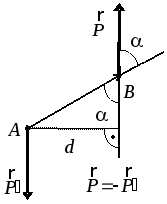
Рис. 2.3.
Парой сил называют систему двух параллельных сил, которые равны по модулю и направлены в противоположные стороны (рис. 2.3). Плоскость, в которой лежат силы пары, называют плоскостью действия пары, а расстояние d между линиями действия сил – плечом пары.Пара сил не имеет равнодействующей и не является уравновешенной системой сил. Она, как и сила, – самостоятельный силовой фактор.
Пара сил оказывает на тело вращательное воздействие, для характеристики которого используют момент пары.
Момент пары сил – это мера механического действия пары, равная моменту одной из сил пары относительно точки приложения другой силы
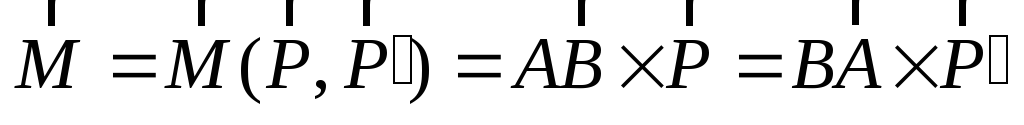 .
(2.7)
.
(2.7)
Э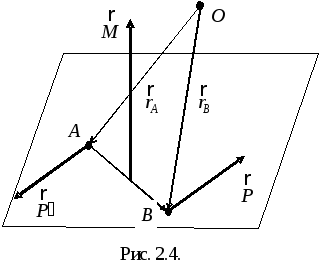 тот
вектор направлен перпендикулярно
плоскости действия пары в ту сторону,
откуда вращение тела под действием сил
пары представляется происходящим против
часовой стрелки (рис. 2.4). Модуль момента
пары (см. рис.2.3) равен
произведению одной из сил пары на ее
плечо
тот
вектор направлен перпендикулярно
плоскости действия пары в ту сторону,
откуда вращение тела под действием сил
пары представляется происходящим против
часовой стрелки (рис. 2.4). Модуль момента
пары (см. рис.2.3) равен
произведению одной из сил пары на ее
плечо
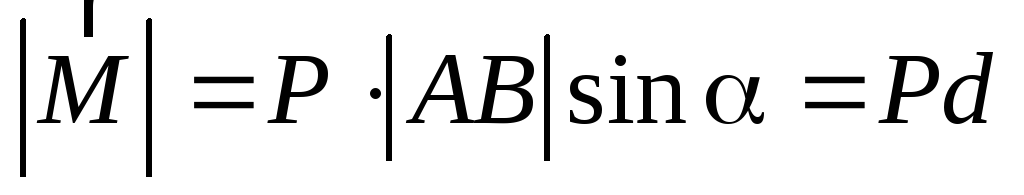 .
(2.8)
.
(2.8)
Вычислим сумму моментов сил пары относительно произвольной точки
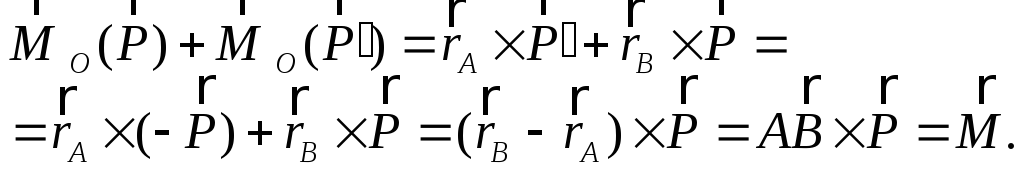
Таким образом, сумма моментов сил пары относительно точки не зависит от выбора этой точки и равна моменту пары.
Глава 3. Теория пар сил на плоскости
3.1. Пара сил. Эквивалентность пар сил
Система двух параллельных сил, равных по модулю и направленных в противоположные стороны, называется парой сил или просто парой (рис. 3.1). Понятие о паре сил ввел в механику французский ученый Луи Пуансон (1777–1859).
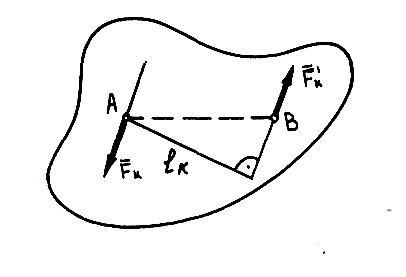
Рис. 3.1. Пара сил
Пара сил – неуравновешенная система и не имеет равнодействующей. Пара сил производит на тело вращательное действие.
Вращательный эффект пары измеряется взятым со знаком «плюс» или «минус» произведением модуля одной из сил пары на ее плечо (момент пары):
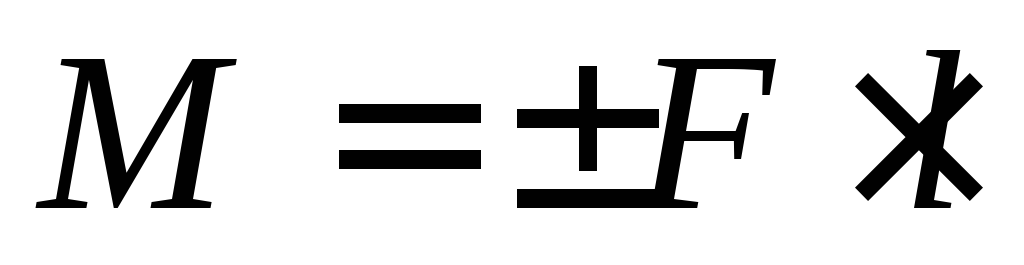 .
.
Знак «плюс» ставится перед числовым значением момента в том случае, если пара стремится повернуть тело против хода часовой стрелки, и знак

Рис. 3.2. Правило знаков момента пары сил
В
Международной системе единиц (СИ) моменты
пар выражаются в 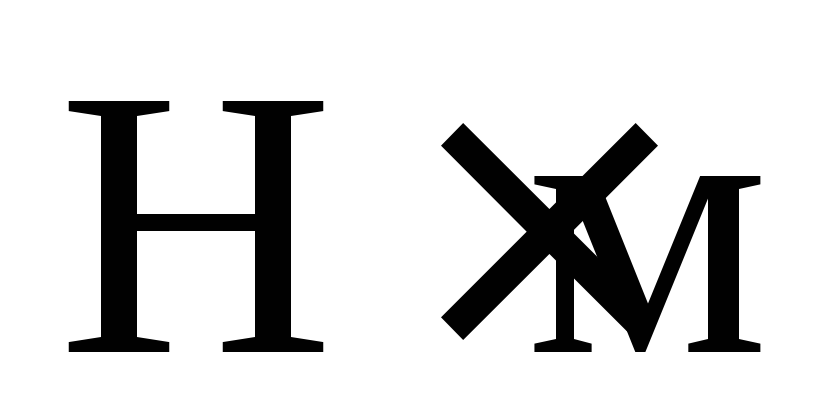 или
или 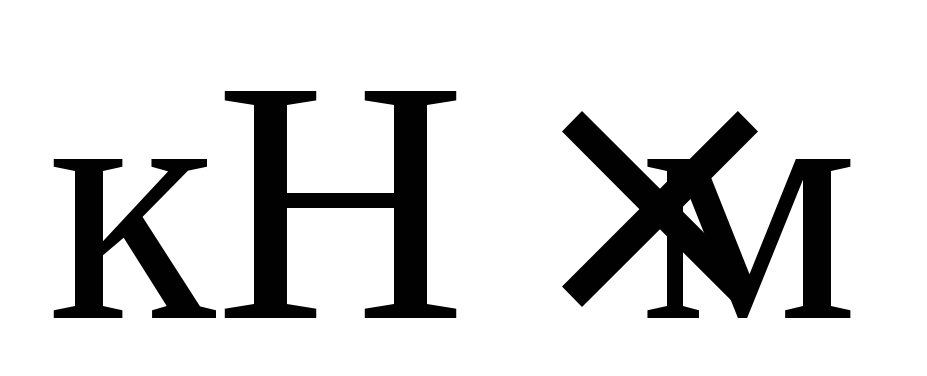 .
.
Вращательное
действие расположенной в данной плоскости
пары зависит только от ее момента,
поэтому для задания пары сил достаточно
указать числовое значение ее момента,
а затем по данному или выбранному
плечу определить силы пары или по силам
подобрать необходимое плечо. Исходя из
этого, на рисунках и схемах пары сил
изображают иногда просто круговой
стрелкой, характеризующей лишь
направление вращающего действия.
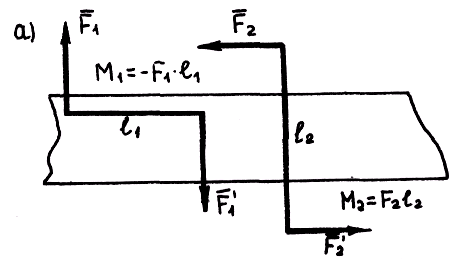
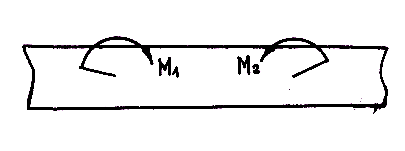
Например, пары (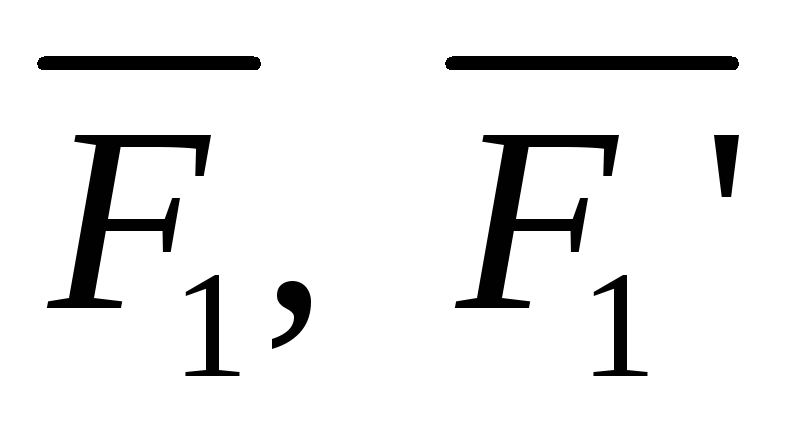 )
и (
)
и (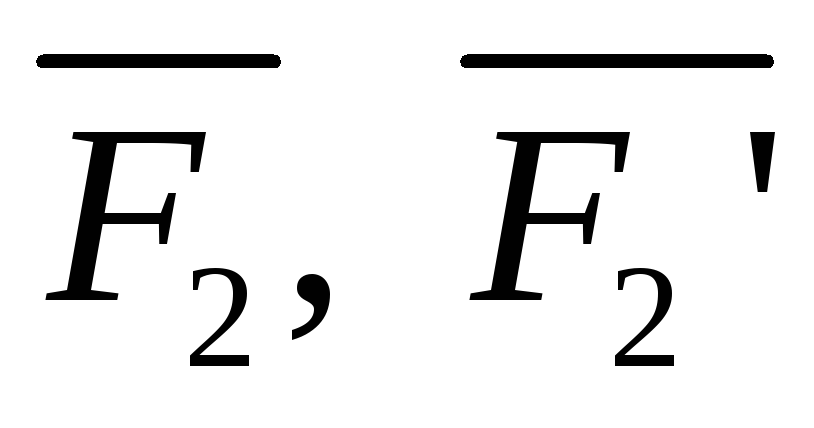 )
(рис. 3.3, а),
приложенные к брусу, можно условно
изобразить круговыми стрелками, обозначив
их M1 и M2 (рис. 3.3, б).
)
(рис. 3.3, а),
приложенные к брусу, можно условно
изобразить круговыми стрелками, обозначив
их M1 и M2 (рис. 3.3, б).
а

б
Рис. 3.3. Изображение пары сил
3.2. Сложение пар сил. Условие равновесия пар
Теорема: Система пар сил, действующих на тело в одной плоскости, эквивалентна паре сил с моментом, равным алгебраической сумме моментов пар системы.
Допустим, на тело действуют три пары, моменты которых M1, M2 и M3 известны (рис. 3.4).

Рис. 3.4. Система пар сил
Момент равнодействующей пары
 ,
,
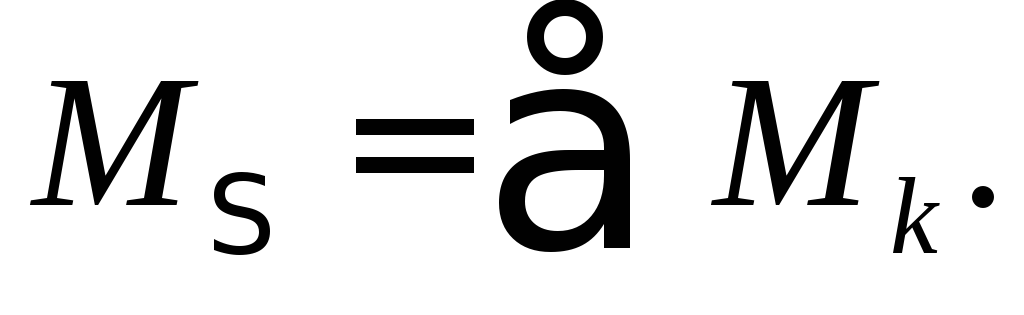
Если
в результате сложения пар 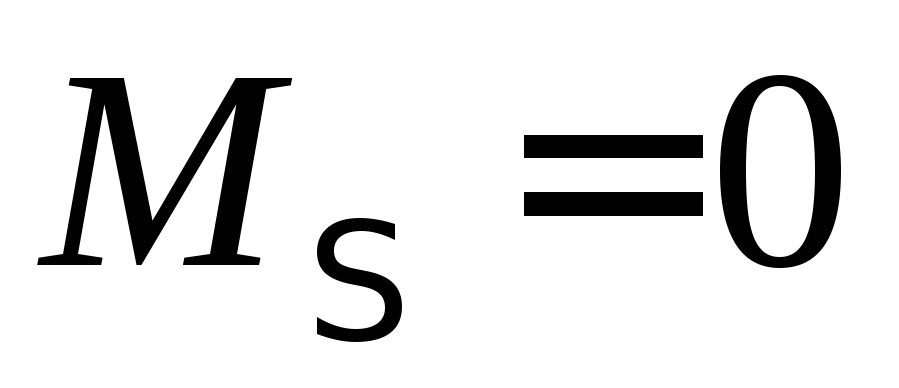 ,
то действующие на тело пары сил образуют
уравновешенную систему. Следовательно,
необходимое и достаточное условие
равновесия системы пар выражается одним
уравнением:
,
то действующие на тело пары сил образуют
уравновешенную систему. Следовательно,
необходимое и достаточное условие
равновесия системы пар выражается одним
уравнением:
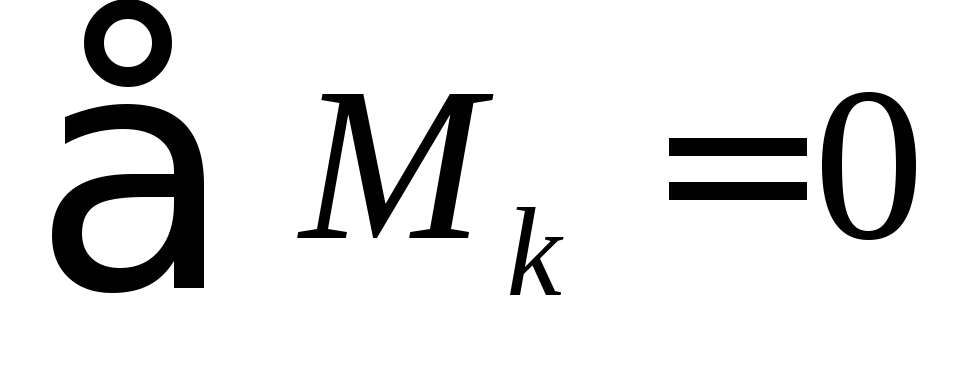 ,
,
т. е. для равновесия системы пар сил, действующих на тело в одной плоскости, необходимо и достаточно, чтобы алгебраическая сумма их моментов была равна нулю.
Значит, систему пар или одну пару можно уравновесить только парой.
3.3. Момент пары относительно точки
Задолго до появления понятия о паре сил и ее моменте в механике возникло понятие о моменте силы относительно точки. Первый, кто обратил внимание на важную роль в механике момента силы относительно точки, был Леонардо да Винчи (1452–1519), современную трактовку понятия момента силы относительно точки дал П. Вариньон (1654–1722).
Моментом силы относительно точки называется взятое со знаком «плюс» или «минус» произведение модуля силы на кратчайшее расстояние от точки до линии действия силы:
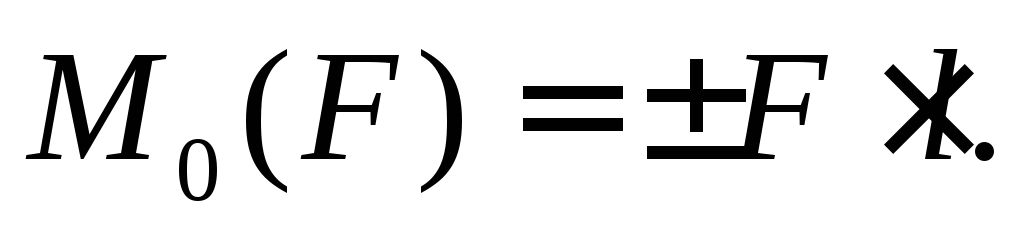
Точка О, относительно которой берется момент силы, называется центром момента. OВ = l – кратчайшее расстояние от центра момента до линии действия силы – называется плечом силы относительно данной точки. Знак «плюс» ставится в случае, если сила F стремится повернуть тело против хода часовой стрелки, а знак «минус» – в противоположном случае (правило знаков то же, что и у моментов пар сил). Момент силы относительно точки О на рис. 3.5 положительный.
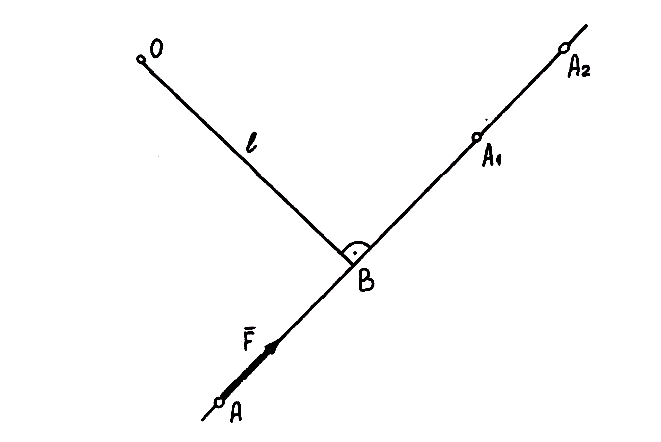
Рис. 3.5. Момент силы относительно точки
Техническая механика. Шпаргалка. 5. Пара сил. Момент силы (Аурика Луковкина, 2009)
5. Пара сил. Момент силы
Парой сил называется система двух сил, равных по модулю, параллельных и направленных в разные стороны.
Пара сил вызывает вращение тела, и ее действие на тело оценивается моментом. Силы, входящие в пару, не уравновешиваются, так как они приложены к двум точкам.
Действие этих сил на тело не может быть заменено одной равнодействующей силой.
Момент пары сил численно равен произведению модуля силы на расстояние между линиями действия сил плеча пары.
Момент считается положительным, если пара вращает тело по часовой стрелке.
M(f,f‘) = Fa; M > 0.
Плоскость, проходящая через линии действия сил пары, называется плоскостью действия пары.
Свойства пар сил.
1. Пару сил можно перемещать в плоскости ее действия.
2. Эквивалентность пар. Две пары, моменты которых равны, эквивалентны (действие их на тело аналогично).
3. Сложение пар сил. Систему пар сил можно заменить равнодействующей парой.
Момент равнодействующей пары равен алгебраической сумме моментов пар, составляющих систему:
MΣ = F1a1 + F2a2 + F3a3 + … + Fna1;
Равновесие пар. Для равновесия пар необходимо и достаточно, чтобы алгебраическая сумма моментов пар системы равнялась нулю:
Момент силы относительно точки. Сила, не проходящая через точку крепления тела, вызывает вращение тела относительно точки, поэтому действие такой силы на тело оценивается моментом.
Момент силы относительно точки численно равен произведению модуля силы на расстояние от точки до линии действия силы. Перпендикуляр, опущенный из точки на линию действия силы, называется плечом силы.
Момент обозначается:
MO= (F) или mO(F).
Момент считается положительным, если сила разворачивается по часовой стрелке.
Термех проба
10
Министерство образования и науки РФ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
Забайкальский государственный университет
Кафедра теоретической механики
Р Е Ф Е Р А Т
По теме: «Эквивалентность пар сил в пространстве и на плоскости, их сложение и условие равновесия»
Студент: Садилов И.А.
Группа: СУС-13-2
Преподаватель: Геллер Ю.А.
г.Чита, 2014 г.
Содержание:
Что такое пара сил…………………………………………………3
Теорема о сумме моментов пары сил…………………………….3
Теорема об эквивалентности пар сил……………………………4
Теорема о переносе пары сил в параллельную плоскость…….5
Теорема о сложении пар сил…………………………………….8
Условия равновесия пар сил……………………………………..8
Выводы…………………………………………………………….9
Список используемой литературы………………………………10
ПАРА СИЛ
Парой сил называется система двух равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.
Плоскостью действия пары сил называется плоскость в которой расположены эти силы.
Плечом пары сил d называется кратчайшее расстояние между линиями действия сил пары.
Моментом пары
сил называется
вектор 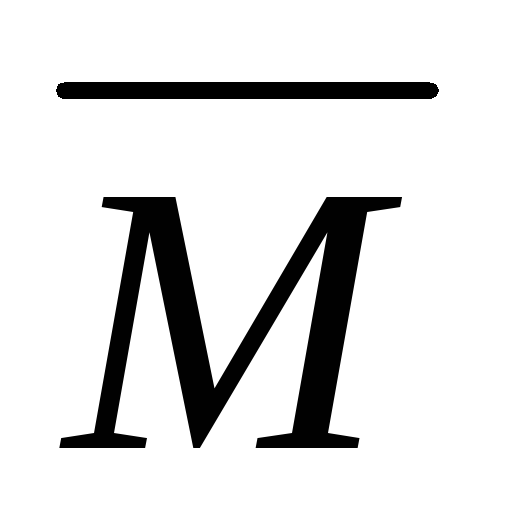 ,
модуль которого равен произведению
модуля одной из сил пары на ее плечо и
который направлен перпендикулярно
плоскости действия сил пары в ту сторону,
откуда пара видна стремящейся повернуть
тело против хода часовой стрелки.
,
модуль которого равен произведению
модуля одной из сил пары на ее плечо и
который направлен перпендикулярно
плоскости действия сил пары в ту сторону,
откуда пара видна стремящейся повернуть
тело против хода часовой стрелки. 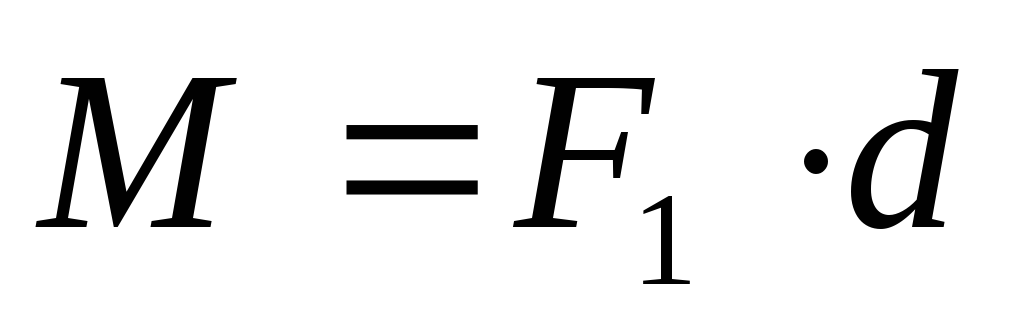
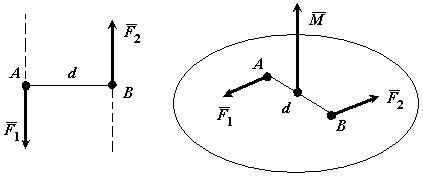
Рис. 4.1
Теорема о сумме моментов пары сил. Сумма моментов сил, входящих в состав пары, относительно любой точки не зависит от выбора этой точки и равна моменту этой пары сил.
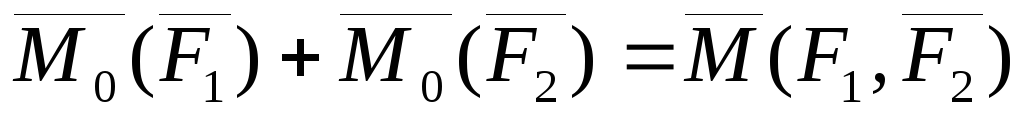
Доказательство: Выберем произвольно точку О. Проведем из нее в точки А и В радиус-векторы (Смотри Рис. 4.2).
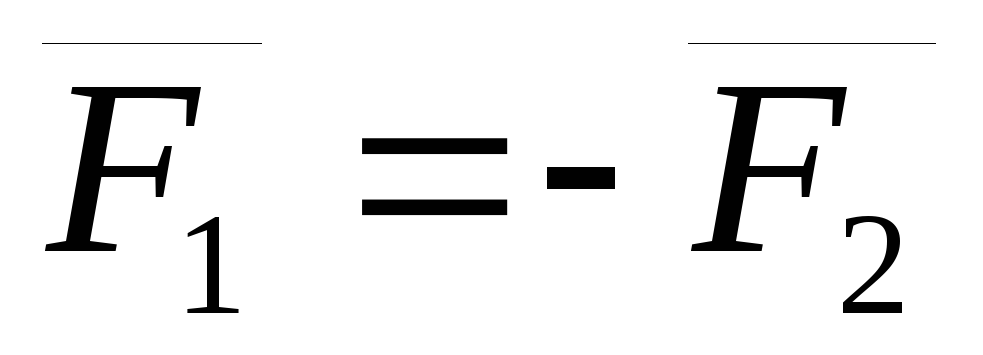 ,
, 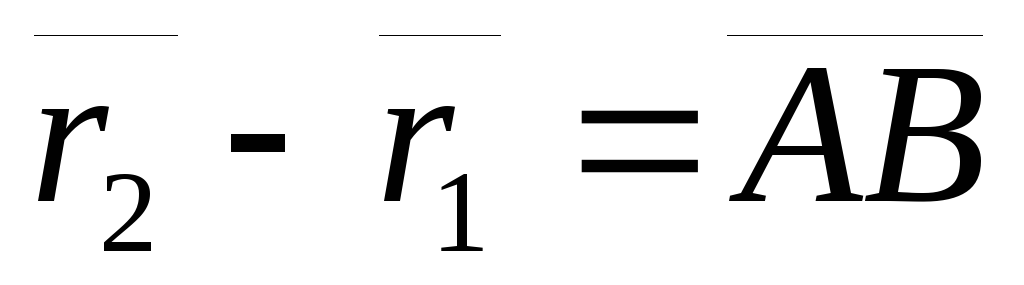
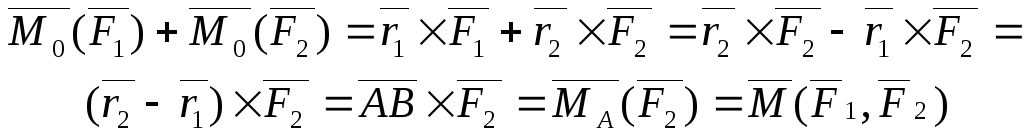
Ч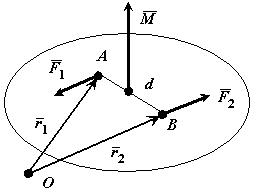 то
и требовалось доказать.
то
и требовалось доказать.
Рис. 4.2
Две пары сил называются эквивалентными, если их действие на твердое тело одинаково при прочих равных условиях.
Теорема об эквивалентности пар сил. Пару сил, действующую на твердое тело, можно заменить другой парой сил, расположенной в той же плоскости действия и имеющий одинаковый с первой парой момент.
Доказательство:
Пусть на твердое тело действует пара
сил 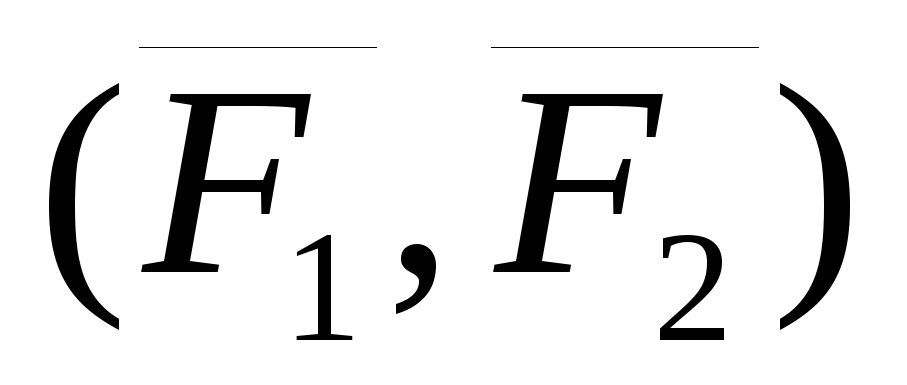 .
.
П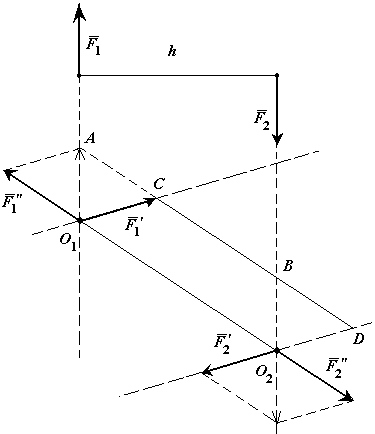 еренесем
силу
еренесем
силу  в точку
в точку  ,
а силу
,
а силу  в точку
в точку  .
Проведем через точки
.
Проведем через точки  две любые параллельные прямые,
пересекающие линии действия сил пары.
Соединим точки
две любые параллельные прямые,
пересекающие линии действия сил пары.
Соединим точки 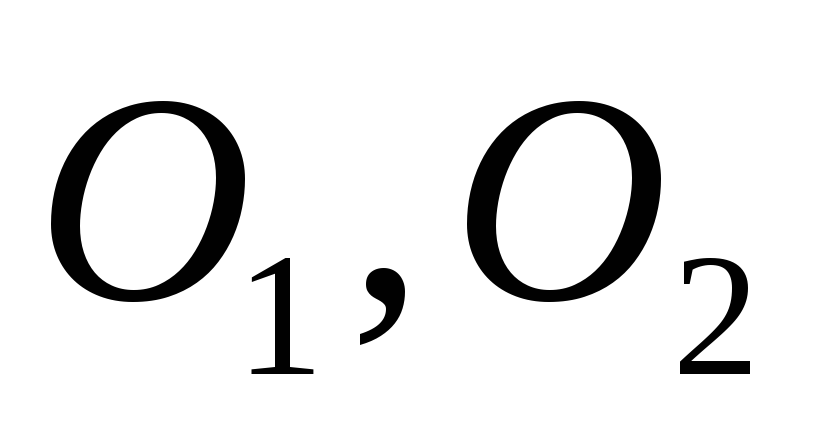 отрезком прямой и разложим силы
отрезком прямой и разложим силы  в
точке
в
точке 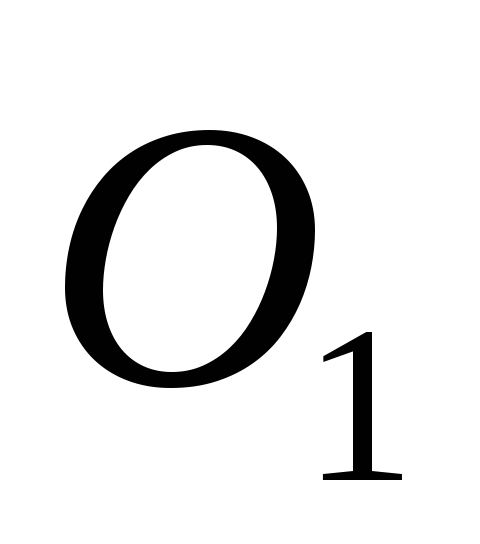 и
и  в точке
в точке 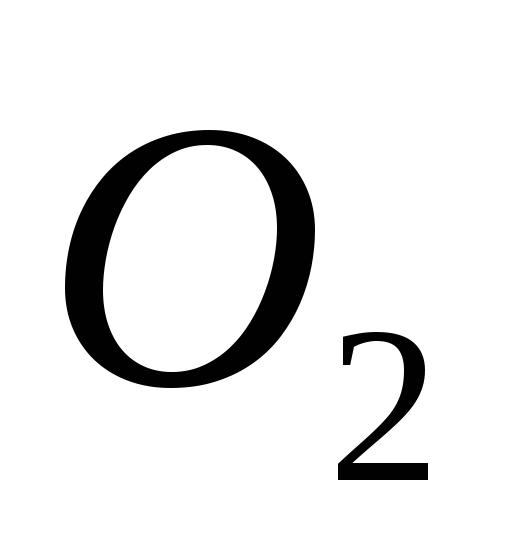 по правилу параллелограмма.
по правилу параллелограмма.
Так как 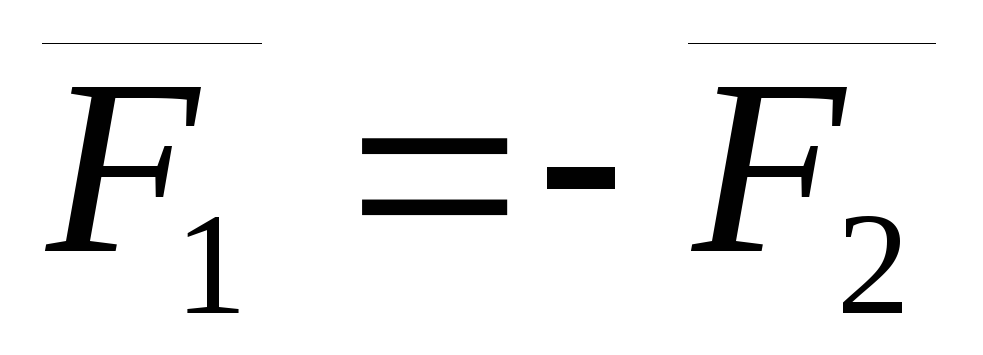 ,
то
,
то
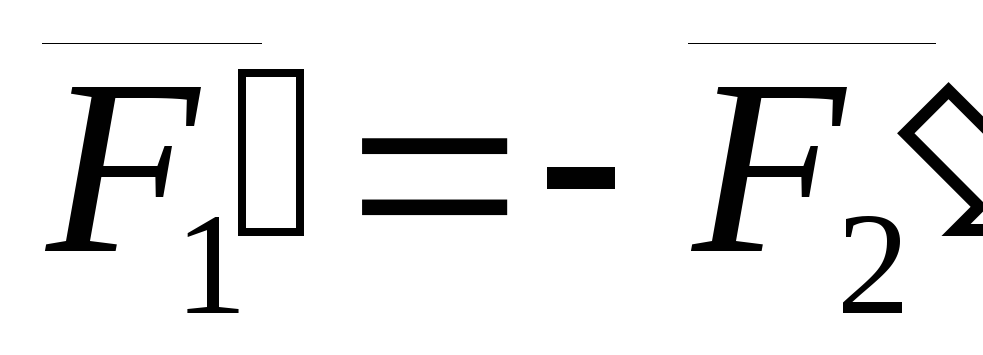 и
и 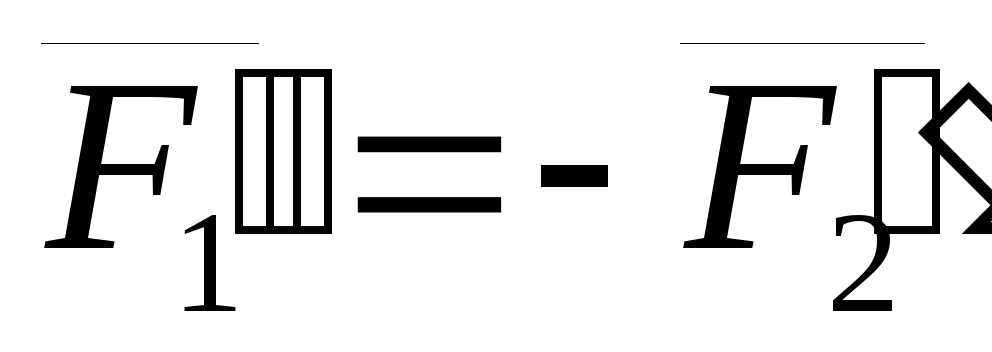
Поэтому 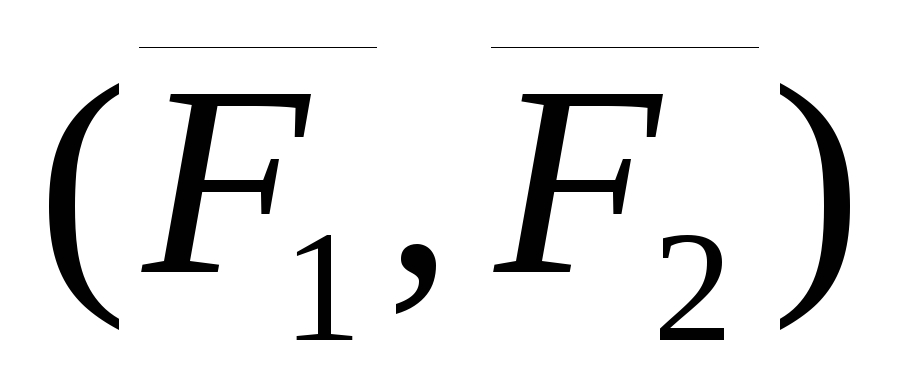 эквивалентна системе
эквивалентна системе 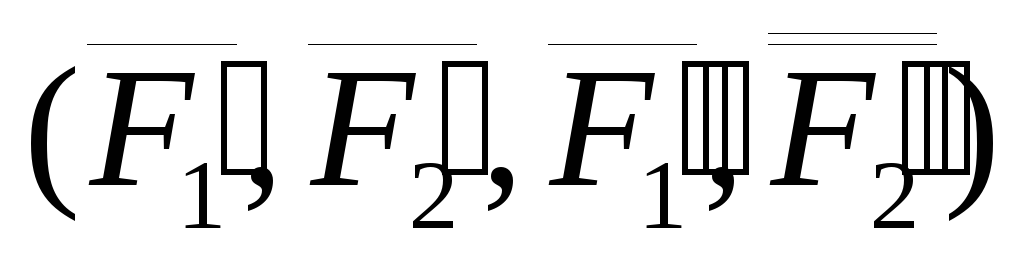 ,
а эта система эквивалентна системе
,
а эта система эквивалентна системе 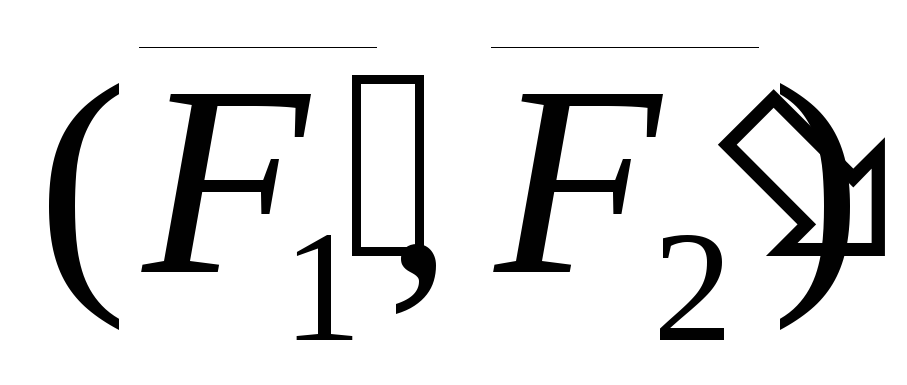 ,
так как
,
так как  эквивалентна нулю.
эквивалентна нулю.
Таким образом мы
заданную пару сил 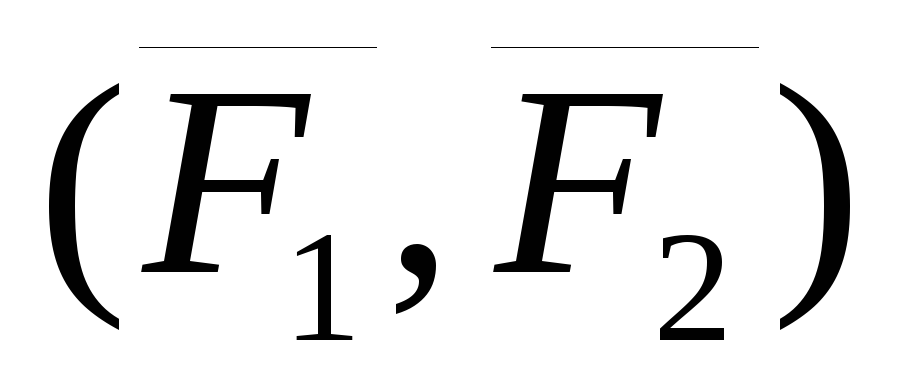 заменили другой парой сил
заменили другой парой сил 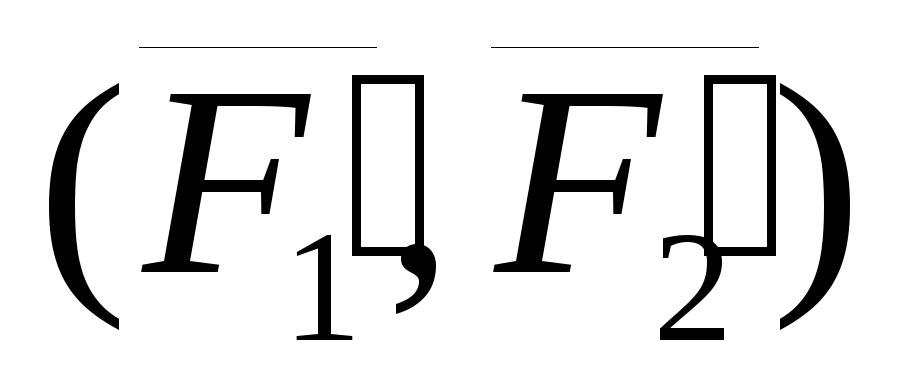 .
Докажем, что моменты у этих пар сил
одинаковы.
.
Докажем, что моменты у этих пар сил
одинаковы.
Момент исходной
пары сил 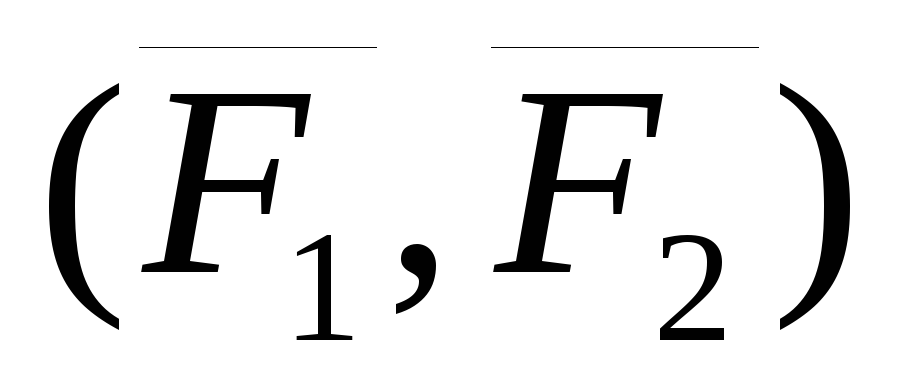 численно равен площади параллелограмма
численно равен площади параллелограмма 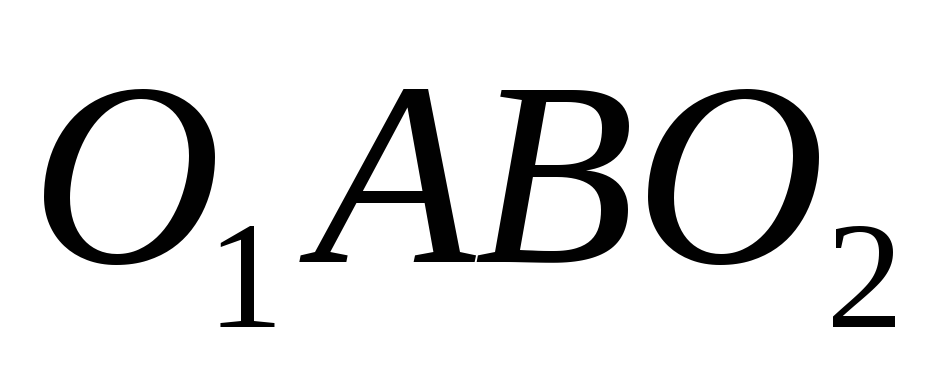 ,
а момент пары сил
,
а момент пары сил 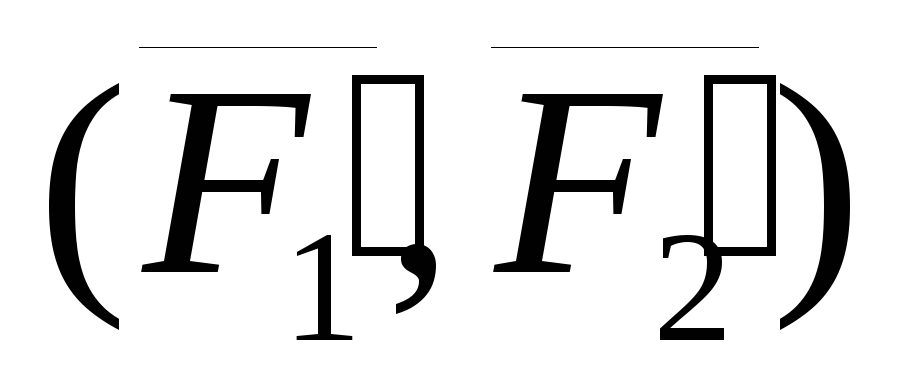 численно равен площади параллелограмма
численно равен площади параллелограмма  .
Но площади этих параллелограммов
равны, так как площадь треугольника
.
Но площади этих параллелограммов
равны, так как площадь треугольника 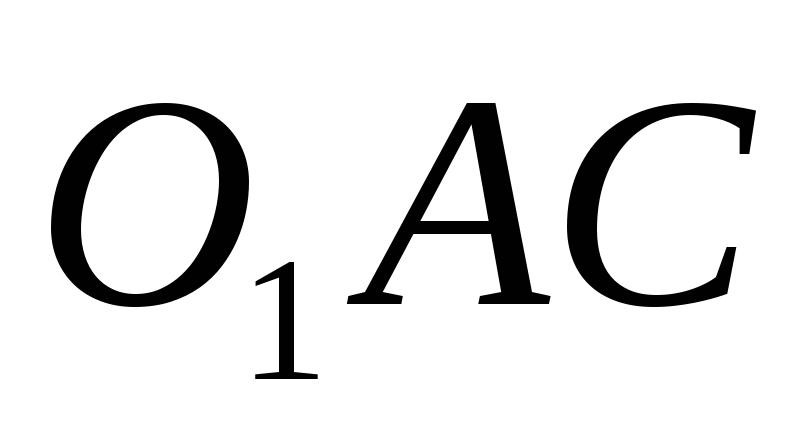 равна площади треугольника
равна площади треугольника 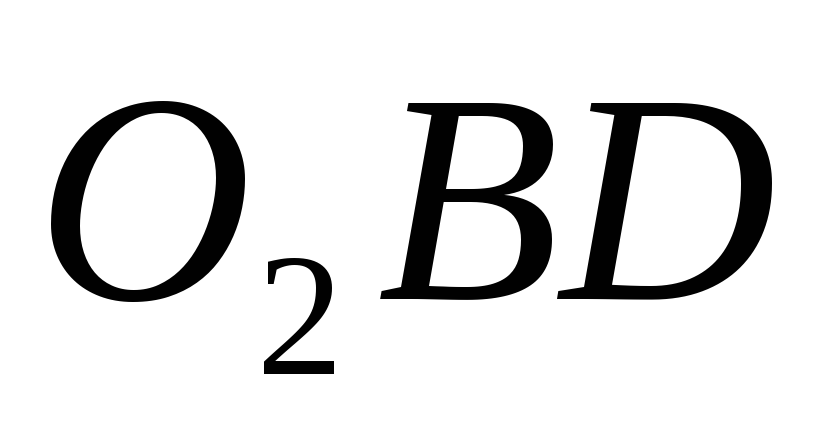 .
.
Что и требовалось доказать.
Теорема о переносе пары сил в параллельную плоскость. Действие пары сил на твердое тело не изменится от переноса этой пары в параллельную плоскость.
Доказательство:
Пусть на твердое тело действует пара
сил 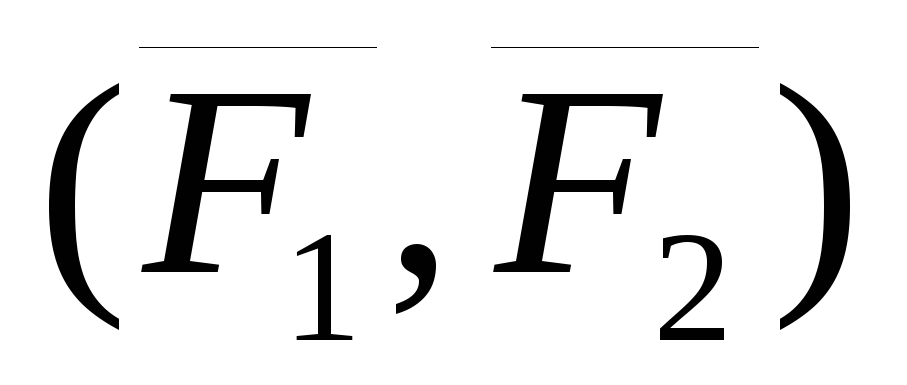 в плоскости
в плоскости 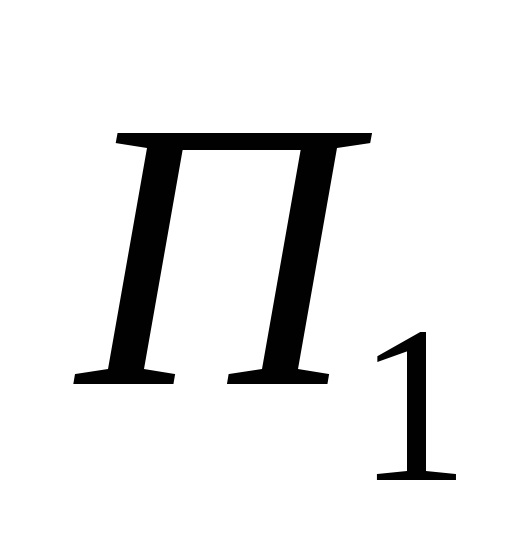 .
Из точек приложения сил А и В опустим
перпендикуляры на плоскость
.
Из точек приложения сил А и В опустим
перпендикуляры на плоскость 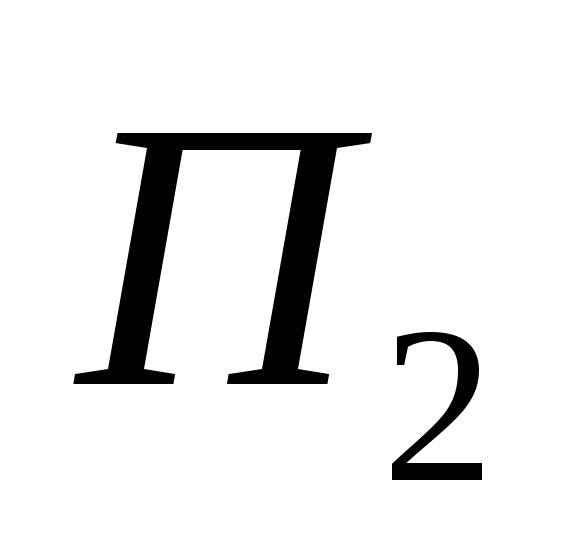 и в точках их пересечения с плоскостью
и в точках их пересечения с плоскостью  приложим две системы сил
приложим две системы сил 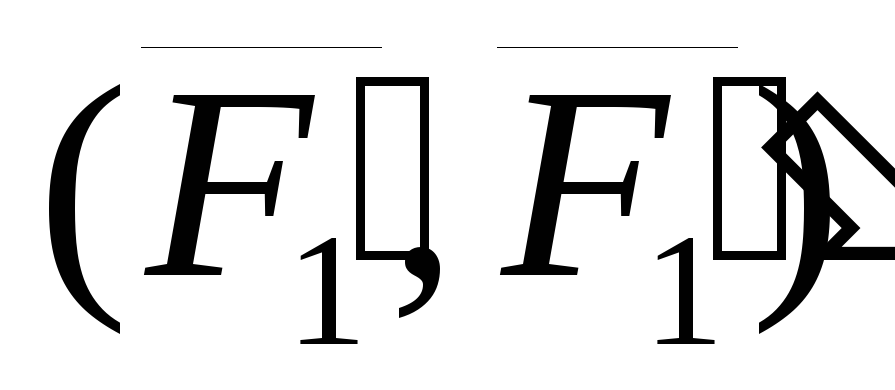 и
и 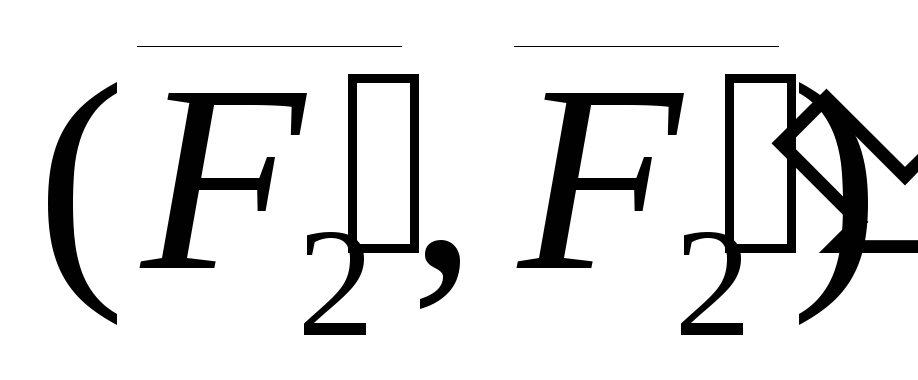 ,
каждая из которых эквивалентна нулю.
,
каждая из которых эквивалентна нулю.
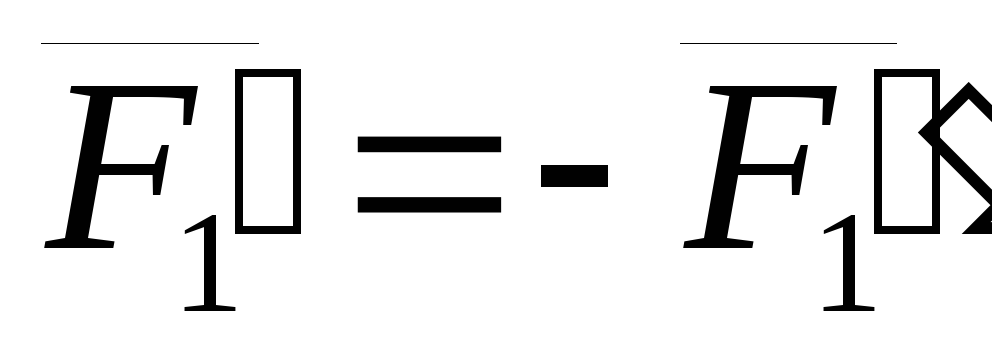
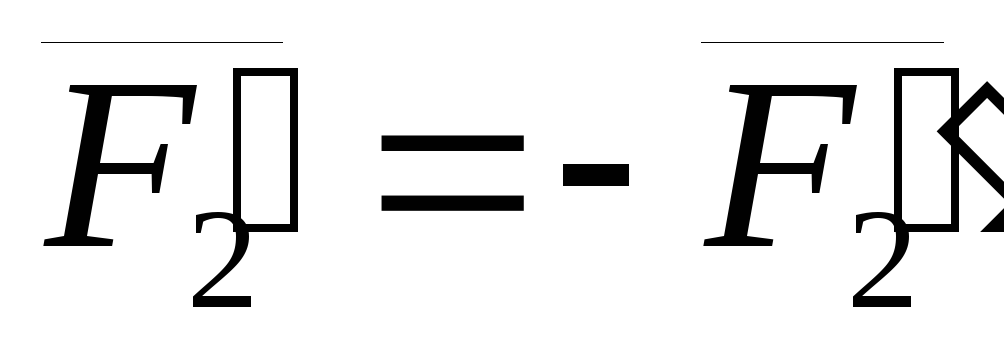
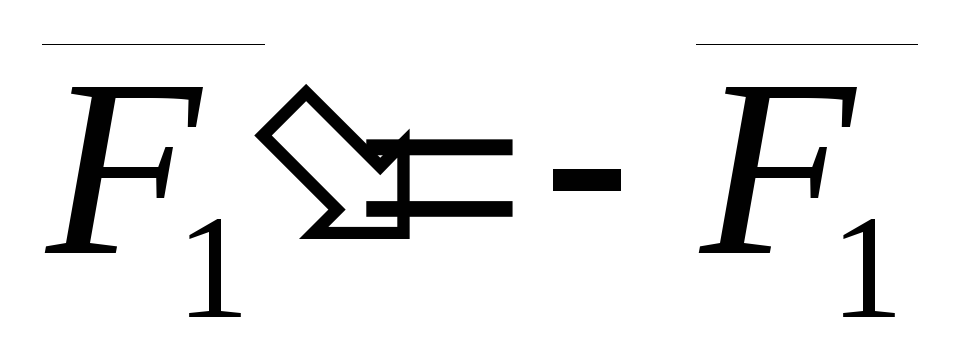
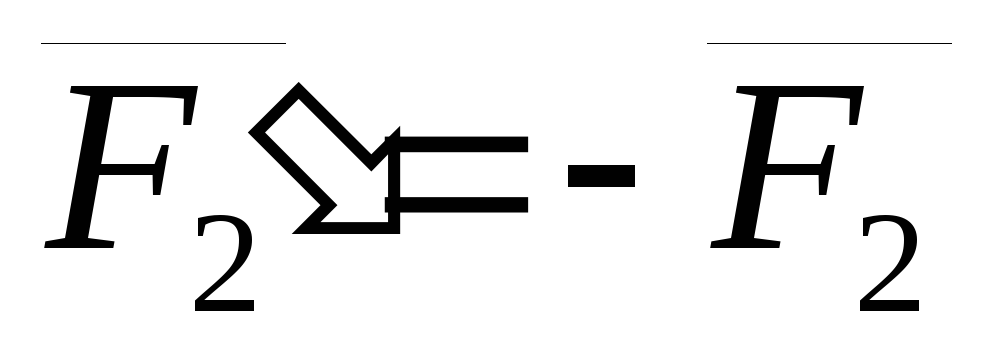
С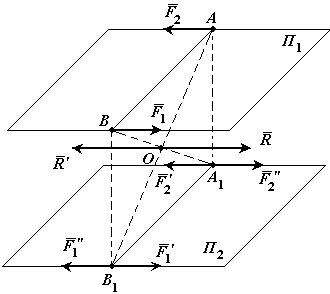 ложим
две равные и параллельные силы
ложим
две равные и параллельные силы  и
и  .
Их равнодействующая
.
Их равнодействующая  параллель-на этим силам, равна их сумме
и приложена посредине отрезка
параллель-на этим силам, равна их сумме
и приложена посредине отрезка 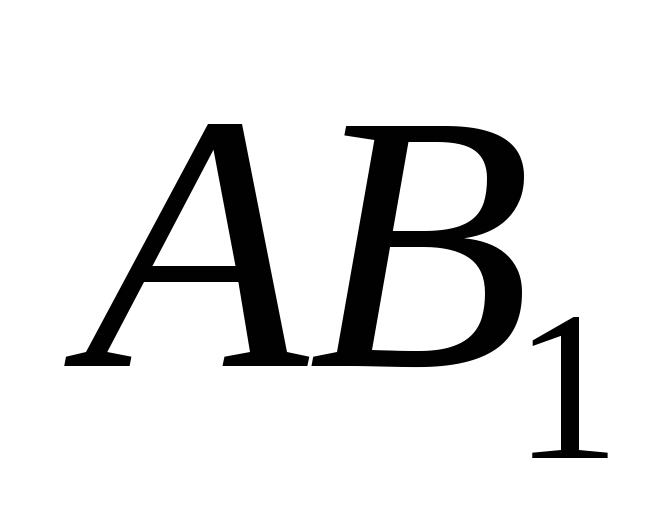 в точке О.
в точке О.
Сложим две равные
и параллельные силы 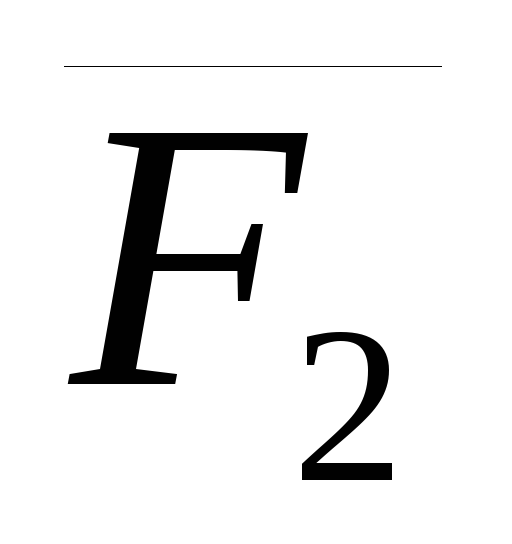 и
и  .
Их равнодействующая
.
Их равнодействующая  параллель-на этим силам, равна их сумме
и приложена посредине отрезка
параллель-на этим силам, равна их сумме
и приложена посредине отрезка  в точке О.
в точке О.
Так как 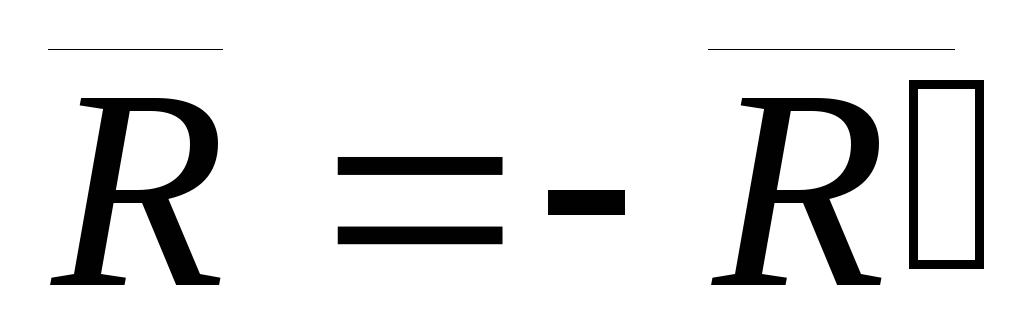 ,
то система сил
,
то система сил 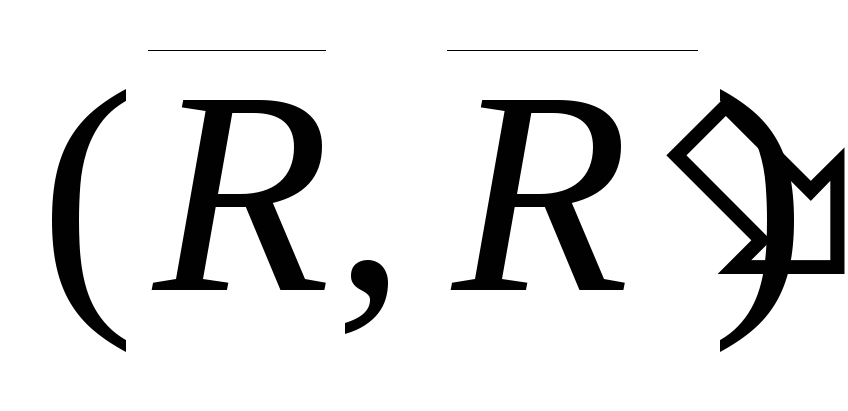 эквивалентна нулю и ее можно отбросить.
эквивалентна нулю и ее можно отбросить.
Таким образом
пара сил 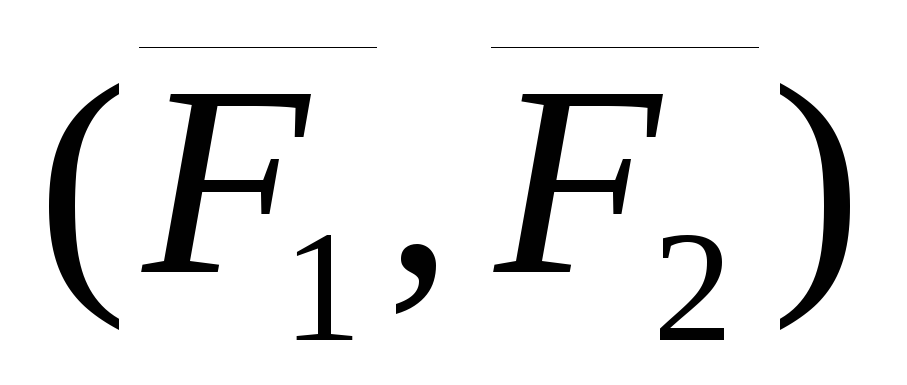 эквивалентна паре сил
эквивалентна паре сил 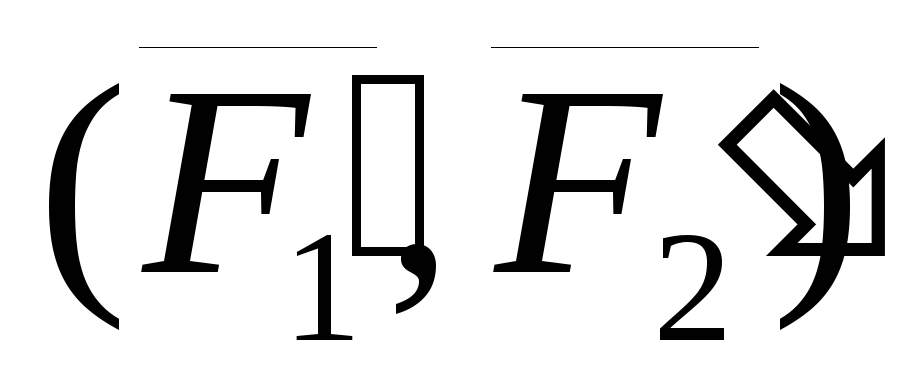 ,
но лежит в другой, параллельной плоскости.
Что и требовалось доказать.
,
но лежит в другой, параллельной плоскости.
Что и требовалось доказать.
Следствие: Момент пары сил, действующий на твердое тело, есть свободный вектор.
Две пары сил, действующих на одно и то же твердое тело, эквивалентны, если они имеют одинаковые по модулю и направлению моменты.
Теорема о
сложении пар сил. Две пары
сил, действующих на одно и то же твердое
тело, и лежащие в пересекающихся
плоскостях, можно заменить одной
эквивалентной парой сил, момент которой
равен сумме моментов заданных пар
сил. 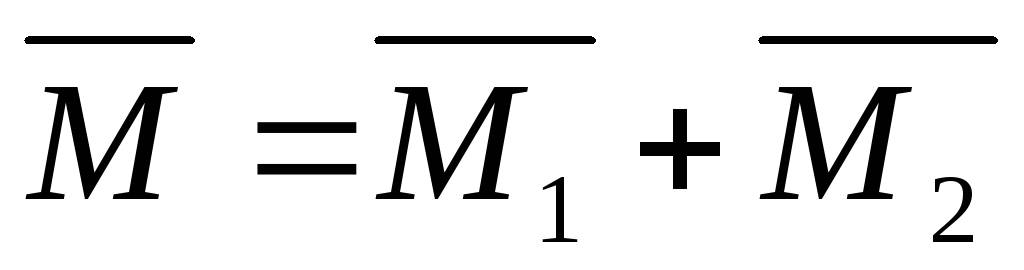
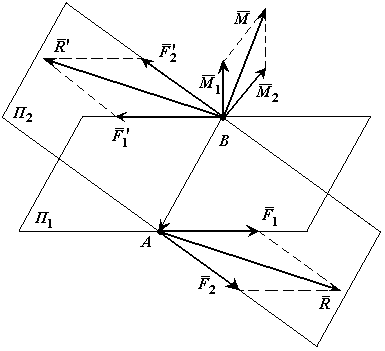
Доказательство:
Пусть имеются две пары сил, расположенные
в пересекающихся плоскостях. Пара сил 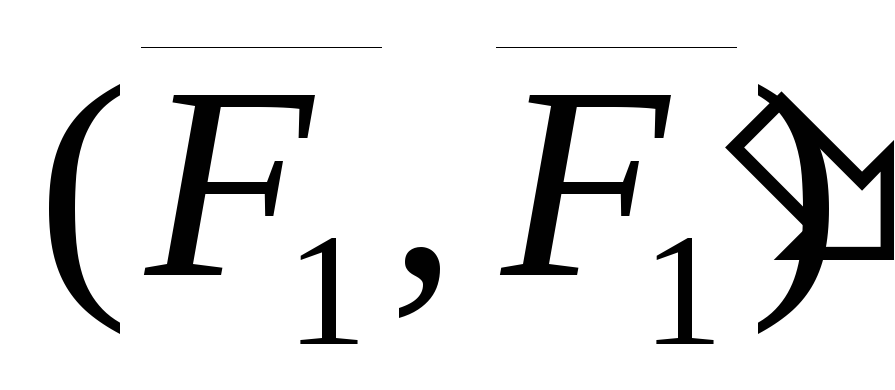 в плоскости
в плоскости 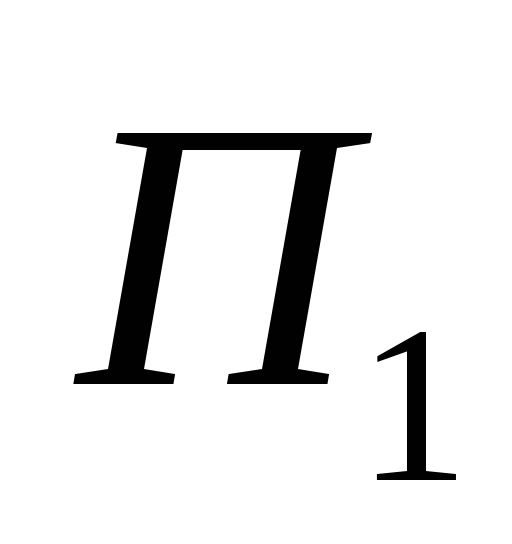 характеризуется моментом
характеризуется моментом 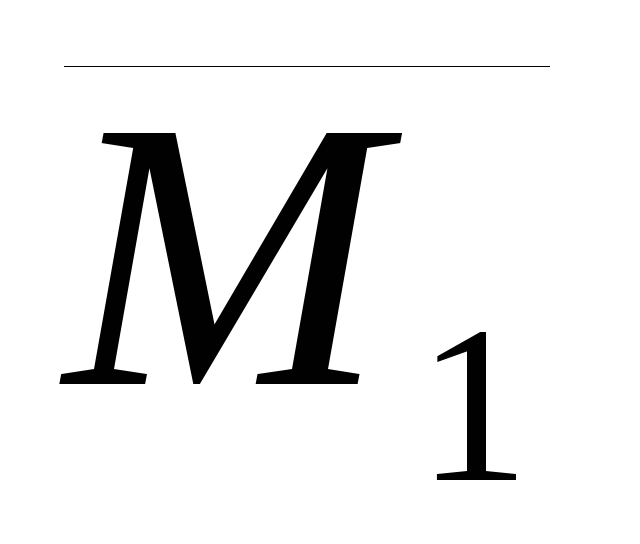 ,
а пара сил
,
а пара сил 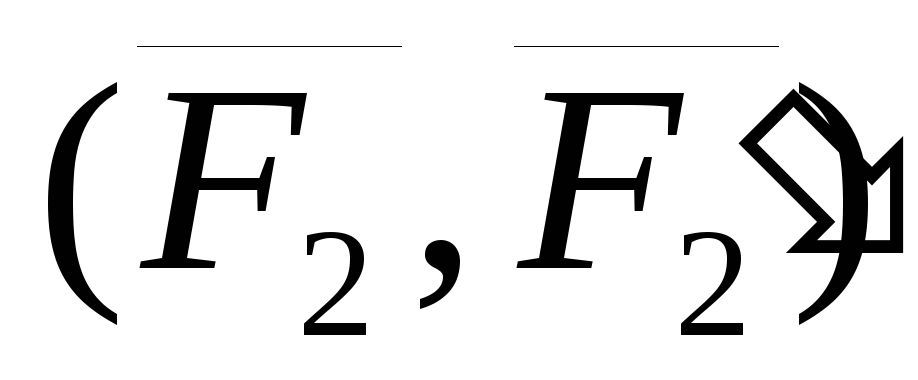 в плоскости
в плоскости 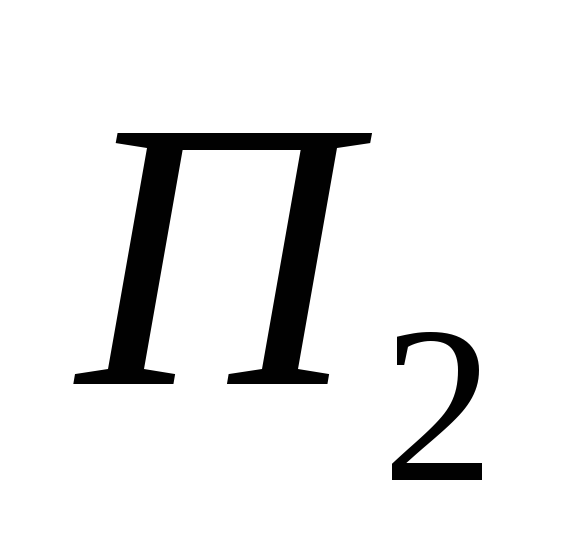 характеризуется моментом
характеризуется моментом 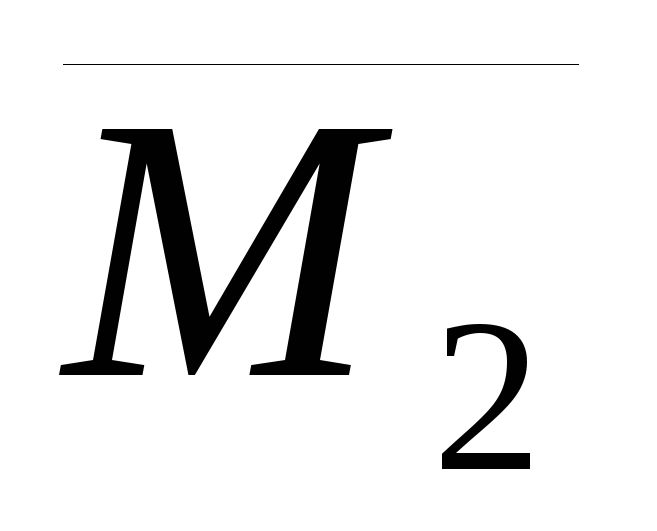 .
.
Расположим пары
сил так, чтобы плечо пар было общим и
располагалось на линии пересечения
плоскостей. Складываем силы, приложенные
в точке А и в точке В, 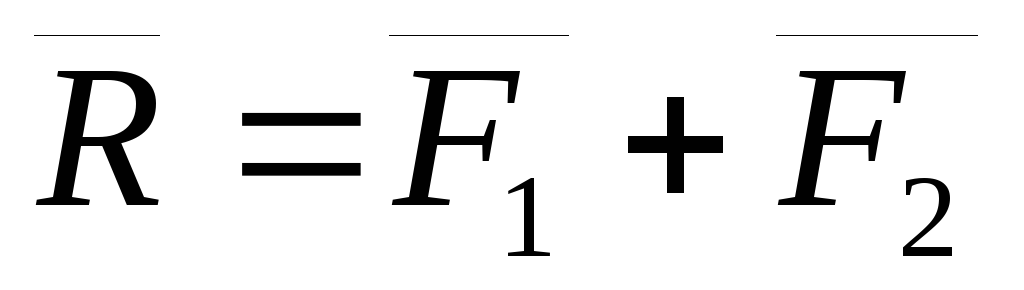
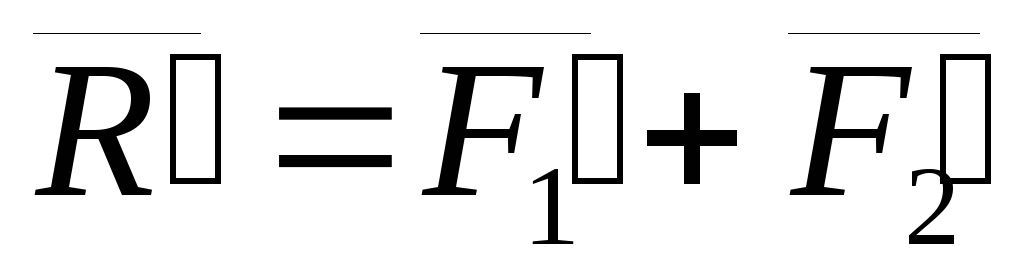 .
Получаем пару сил
.
Получаем пару сил 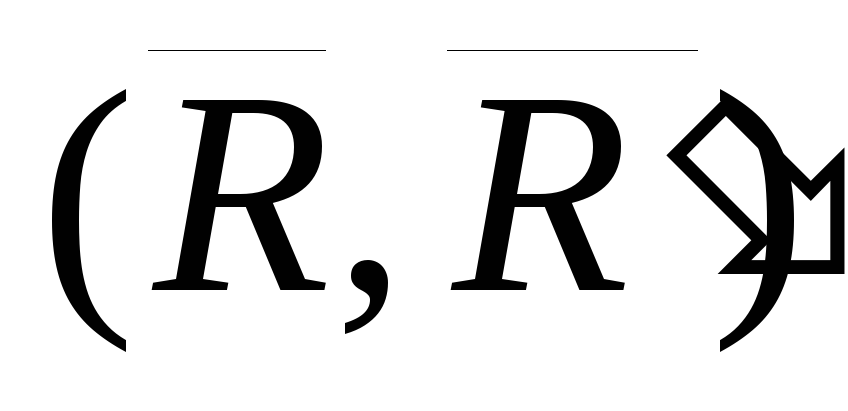 .
.
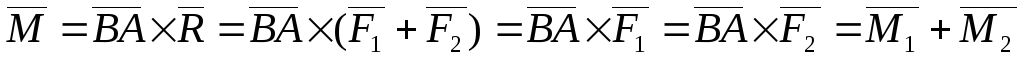
Что и требовалось доказать.
Условия равновесия пар сил
Если на твердое тело действует несколько пар сил, как угодно расположенных в пространстве, то последовательно применяя правило параллелограмма к каждым двум моментам пар сил, можно любое количество пар сил заменить одной эквивалентной парой сил, момент которой равен сумме моментов заданных пар сил.
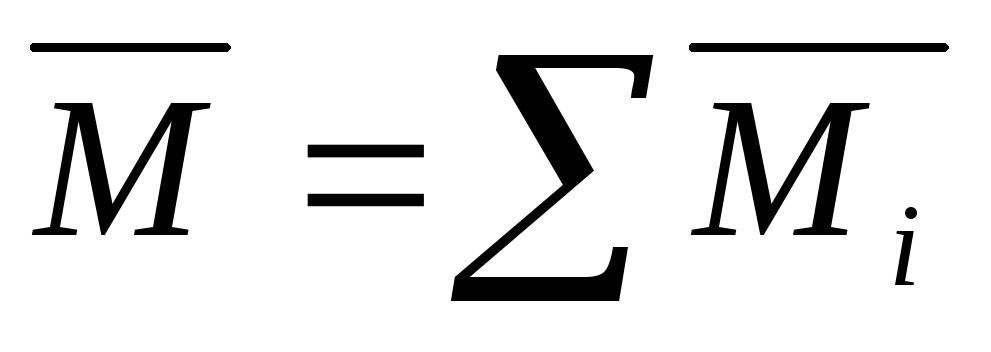
Теорема. Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы момент эквивалентной пары сил равнялся нулю.
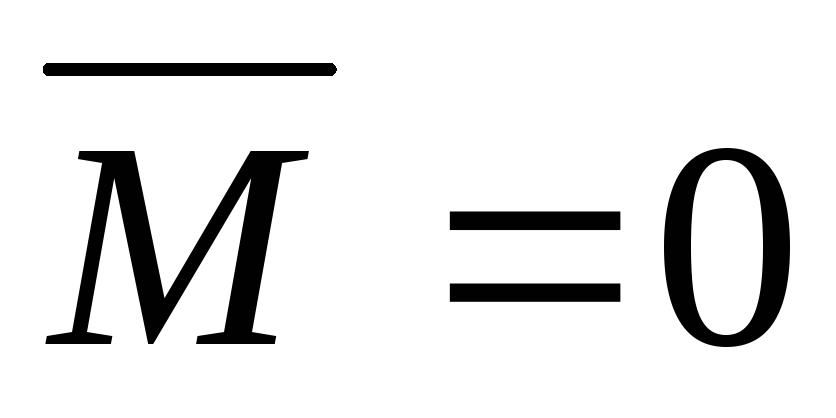
Теорема. Для равновесия пар сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма проекций моментов пар сил на каждую из трех координатных осей была равна нулю.
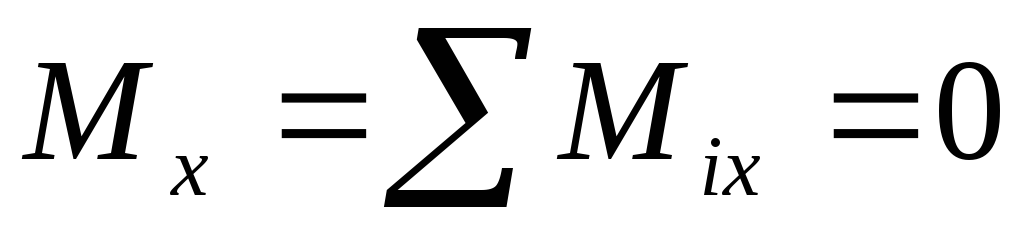
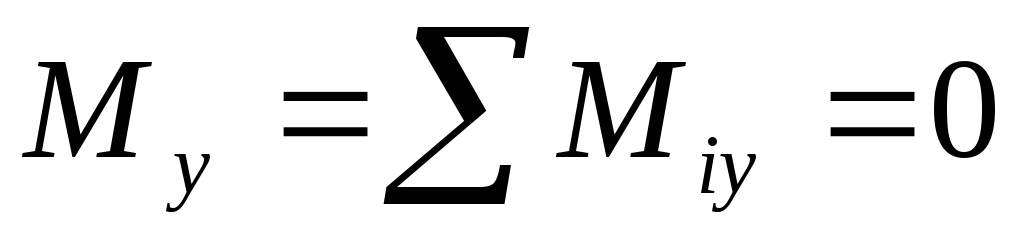
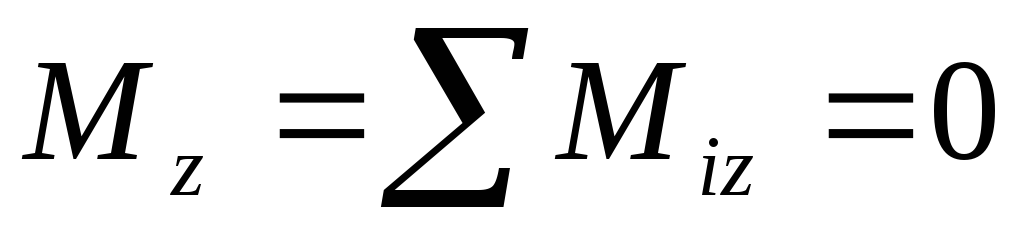
Условия равновесия системы сил
Векторная форма
Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы главный вектор системы сил был равен нулю и главный момент системы сил относительно любого центра приведения также был равен нулю.
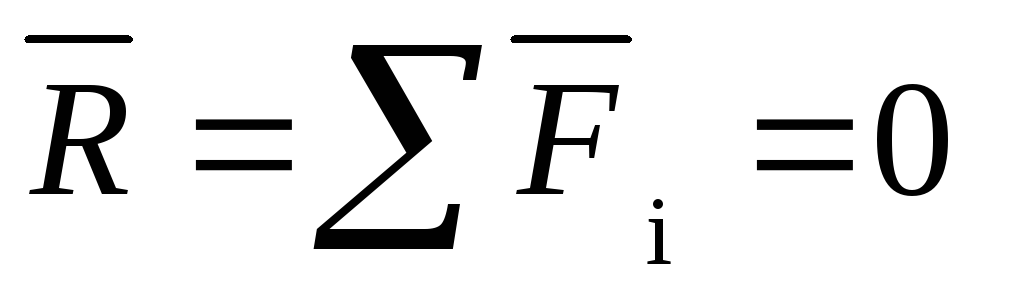
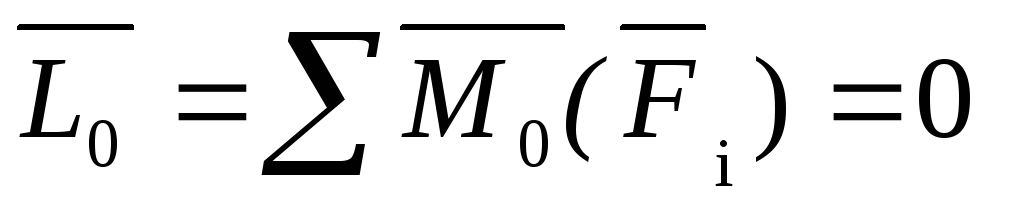
Алгебраическая форма.
Для равновесия произвольной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на оси декартовых координат были равны нулю и три суммы моментов всех сил относительно трех осей координат также были равны нулю.
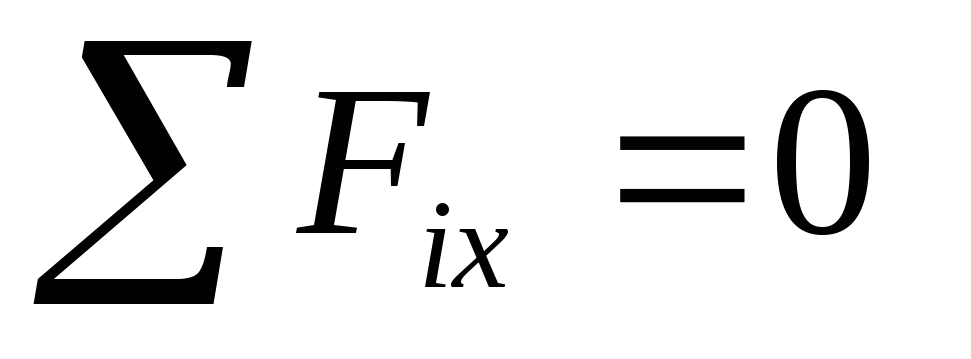
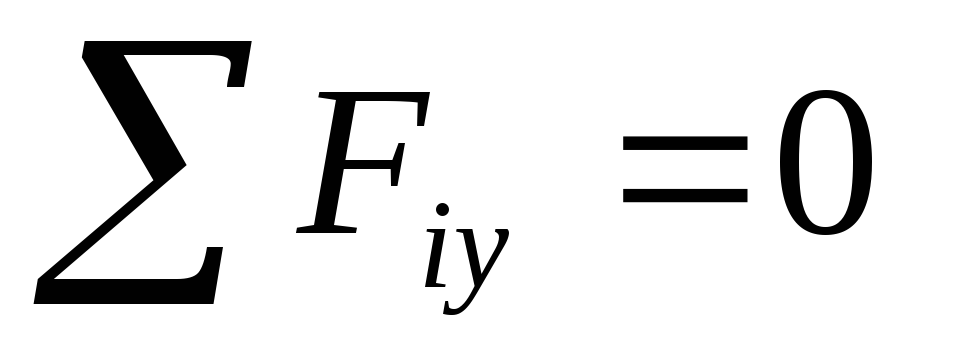
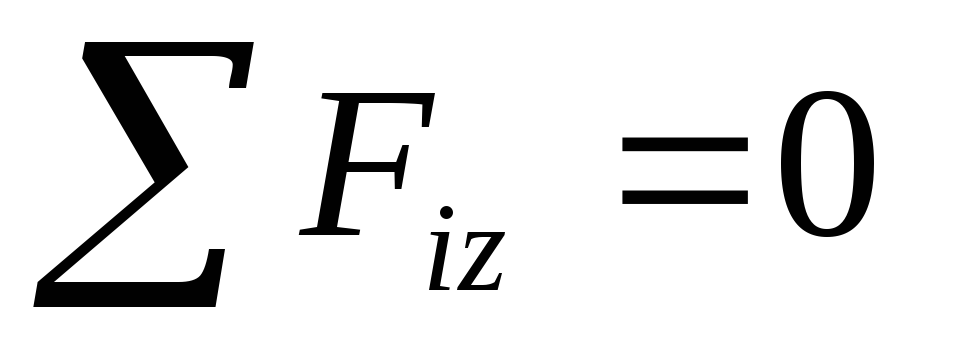
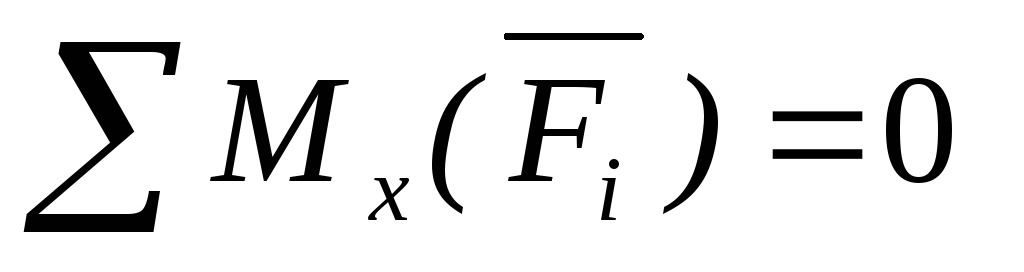
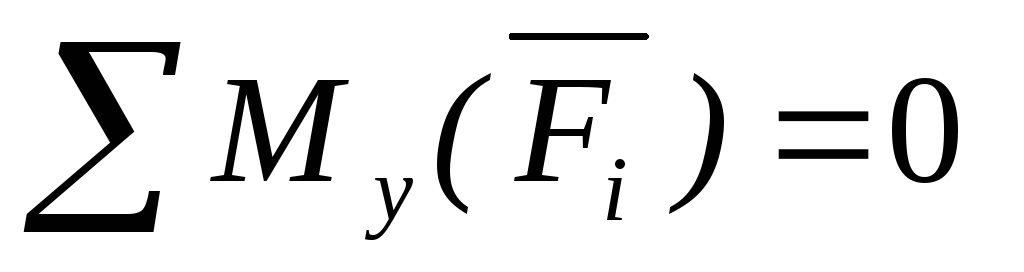
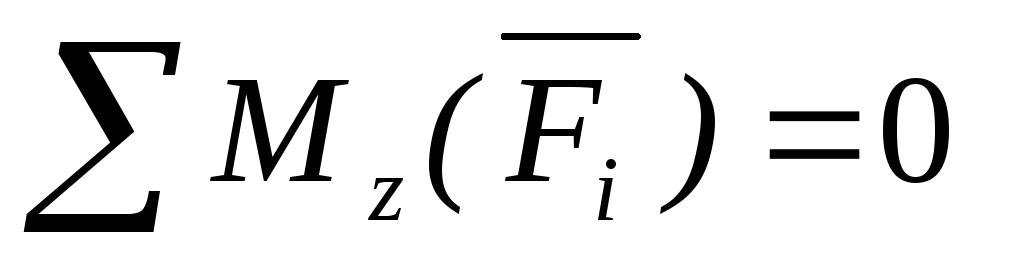
Условия равновесия пространственной системы
параллельных сил
На тело действует система параллельных сил. Расположим ось Oz параллельно силам.
Уравнения 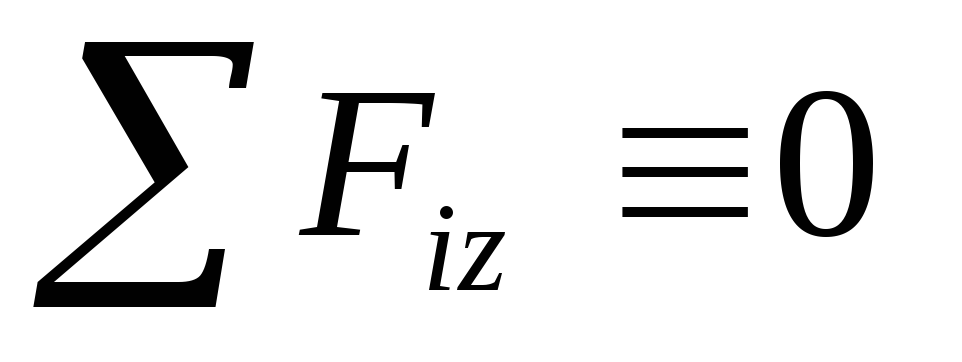
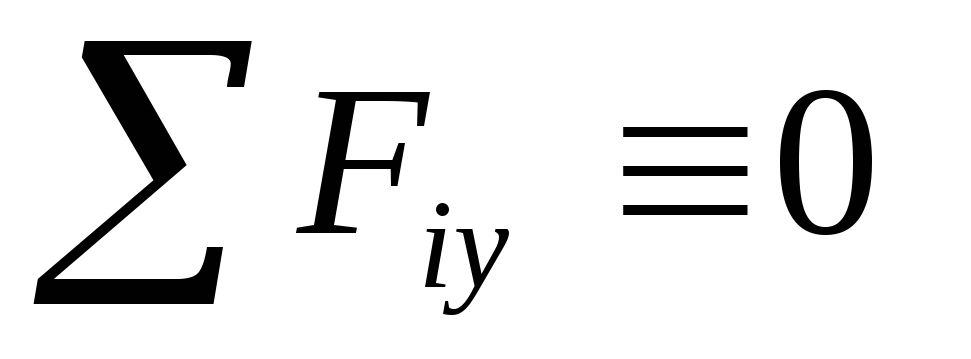
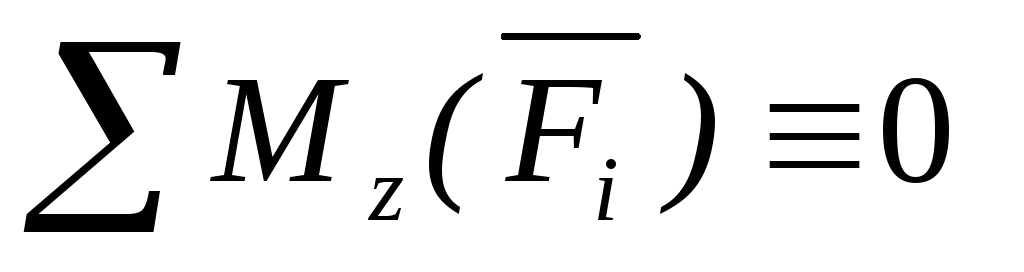
Для равновесия пространственной системы параллельных сил, действующих на твердое тело, необходимо и достаточно, чтобы сумма проекций этих сил была равна нулю и суммы моментов этих сил относительно двух координатных осей, перпендикулярным силам, также были равны нулю.
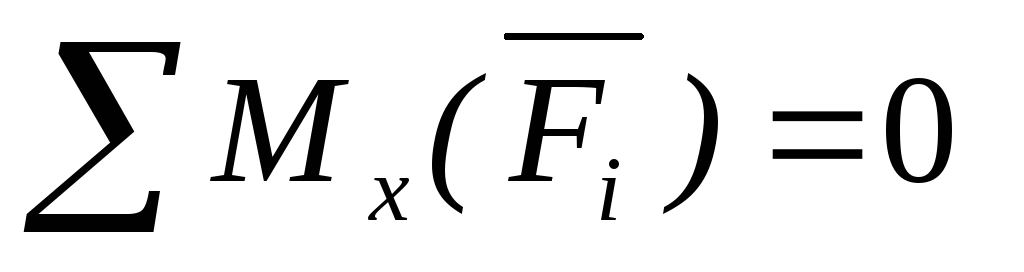
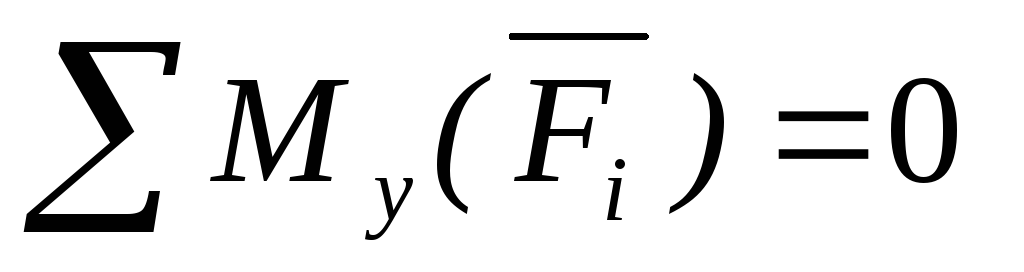
— проекция силы на ось Oz.
Выводы:
Пару сил как жесткую фигуру можно как угодно поворачивать и переносить в ее плоскости действия.
У пары сил можно изменять плечо и силы, сохраняя при этом момент пары и плоскость действия.
3.момент пары является свободным вектором и полностью определяет действие пары на абсолютно твердое тело. Для деформируемых тел теория пар неприменима.
ЛИТЕРАТУРА:
1. Кирсанов М.Н Теоретическая механика. Учебник для самоподготовки.
2.Тарг С.М Курс по Теоретической Механике.
Момент силы. Пара сил и ее свойства (стр. 1 из 2)
1. Плоская система сходящихся сил
Система сходящихся сил находится в равновесии, когда алгебраические суммы проекций ее слагаемых на каждую из двух координатных осей равны нулю.
Проекция силы на ось.
Осью называют прямую линию, которой приписано определенное направление. Проекция вектора на ось является скалярной величиной.
Проекция вектора считается положительной (+), если направление от начала к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (-), если направление от начала проекции к ее концу противоположно положительному направлению оси.
Если сила совпадает с положительным направлением оси, но угол будет тупой – тогда проекция силы на ось будет отрицательною.
Итак, проекция силы на ось координат равна произведению модуля силы на косинус или синус угла между вектором силы и положительным направлением оси.
Силу, расположенную на плоскости хОу, можно спроецировать на две координатные оси Ох и Оу:
; ; .Проекция векторной суммы на ось.
Геометрическая сумма, или равнодействующая, этих сил
определяется замыкающей стороной силового многоугольника: ,где п – число слагаемых векторов.
Итак, проекция векторной суммы или равнодействующей на какую-либо ось равна алгебраической сумме проекций слагаемых векторов на ту же ось.
2. Пара сил
Сумма проекций пары сил на ось х и на ось у равна нулю, поэтому пара сил не имеет равнодействующей. Несмотря на это тело под действием пары сил находится в равновесии.
Способность пары сил производить вращение определяется моментом пары, равным произведению силы на кратчайшее расстояние между линиями действия сил. Обозначим момент пары М, а кратчайшее расстояние между силами а, тогда абсолютное значение момента:
Кратчайшее расстояние между линиями действия сил называется – плечом пары, поэтому можно сказать, что момент пары сил по абсолютному значению равен произведению одной из сил на ее плечо.
Момент пары сил можно показывать дугообразной стрелкой, указывающей направление вращения.
Момент пары сил будем считать положительным, если пара стремится повернуть тело по направлению хода часовой стрелки, и отрицательным, если – против часовой стрелки.
Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой механическое состояние тела не изменяется, т.е. не изменяется движение тела или не нарушается его равновесие.
Эффект действия пары сил на твердое тело не зависит от ее положения в плоскости. Таким образом, пару сил можно переносить в плоскости ее действия в любое положение.
Еще одно свойство пары сил, которое является основой для сложения пар:
− не нарушая состояния тела, можно как угодно изменять модули сил и плечо пары, только бы момент пары оставался неизменным.
По определению пары сил эквивалентны, т.е. производят одинаковое действие, если их моменты равны.
Если, изменив значения сил и плечо новой пары, мы сохраним равенство их моментов М 1 = М 2 или F1 a = F 2 b, то состояние тела от такой замены не нарушится.
Подобно силам пары можно складывать. Пара, заменяющая собой действие данных пар, называется результирующей. Действие пары сил полностью определяется ее моментом и направлением вращения. Исходя из этого, сложение пар производится алгебраическим суммированием их моментов, т.е. момент результирующей пары равен алгебраической сумме моментов составляющих пар.
Момент результирующей пары определится по формуле:
М= М 1 + М 2 +... + М п.=
М і,Где моменты пар, вращающие по часовой стрелке, принимаются положительными, а против часовой стрелки – отрицательными. На основании приведенного правила сложения пар устанавливается условие равновесия системы пар лежащих в одной плоскости, а именно: для равновесия системы пар необходимо и достаточно, чтобы момент результирующей пары равнялся нулю или чтобы алгебраическая сумма моментов пар равнялась нулю:
Момент силы относительно точки и оси.
Момент силы относительно точки определяется произведением модуля силы на длину перпендикуляра, опущенного из точки на линию действия силы.
При закреплении тела в точке О сила
стремится поворачивать его вокруг этой точки. Точка О, относительно которой берется момент, называется центром момента, а длина перпендикуляра а – плечом относительно центра момента.Момент силы
относительно О определяется произведением силы на плечо: .Момент принято считать положительным, если сила стремится вращать тело по часовой стрелке, а отрицательным — против часовой стрелки. Между моментом пары и моментом силы есть одно существенное различие. Численное значение и направление момента пары сил не зависит от положения этой пары в плоскости. Значение и направление (знак) момента силы зависит от положения точки, относительно которой определяется момент.
Если сила расположена в плоскости, перпендикулярной к оси, момент этой силы определяется произведением ее величины на плечо
относительно точки пересечения оси и плоскости:Следовательно, для определения момента силы относительно оси нужно спроектировать силу на плоскость, перпендикулярную оси, и найти момент проекции силы относительно точки пересечения оси с этой плоскостью.
3. Метод кинетостатики
Представим себе материальную точку массой т, движущуюся с ускорением а под действием какой-то системы активных и реактивных сил, равнодействующая которых равна F.
Воспользуемся одной из известных нам формул (основным уравнением динамики) для того, чтобы уравнения движения записать в форме уравнений равновесия (метод кинетостатики):
F = ma.
Перепишем это уравнение в следующем виде:
F + (-/ma) = 0.
Выражение обозначается Кин и называется силой инерции:
Kин= -mа.
Сила инерции есть вектор, равный произведению массы точки на ее ускорение и направленный в сторону, противоположную ускорению.
Это равенство, являющееся математическим выражением принципа, который носит имя французского ученого Даламбера (1717—1783), можно рассматривать как уравнение равновесия материальной точки. Следует подчеркнуть, что полученное равенство, хотя и названо уравнением равновесия, в действительности является видоизмененным уравнением движения материальной точки.
Принцип Даламбера формулируется гак: активные и реактивные силы, действующие на материальную точку, вместе с силами инерции образуют систему взаимно уравновешенных сил, удовлетворяющую всем условиям равновесия.
Следует помнить, что сила инерции приложена к рассматриваемой материальной точке условно, но для связи, вызывающей ускорение, она в определенном смысле является реальной. Обладая свойством инерции, всякое тело стремится сохранять свою скорость по модулю и направлению неизменной, в результате чего оно будет действовать на связь, вызывающую ускорение, с силой, равной силе инерции. В качестве примера действия сил инерции можно привести случаи разрушения маховиков при достижении ими критической угловой скорости. Во всяком вращающемся теле действуют силы инерции, так как каждая частица этого тела имеет ускорение, а соседние частицы являются для нее связями. Отметим, что весом тела называется сила, с которой тело вследствие притяжения Земли действует на опору (или подвес), удерживающую его от свободного падения. Если тело и опора неподвижны, то вес тела равен его силе тяжести.
4. Момент силы относительно точки
Рассмотрим гайку, которую затягивают гаечным ключом определенной длины, прикладывая к концу ключа мускульное усилие. Если взять гаечный ключ в несколько раз длиннее, то прилагая то же усилие, гайку можно затянуть значительно сильнее. Из этого следует, что одна и та же сила может оказывать различное вращательное действие. Вращательное действие силы характеризуется моментом силы.
Понятие момента силы относительно точки ввел в механику итальянский ученый и художник эпохи Возрождения Леонардо да Винчи (1452—1519).
Моментом силы относительно точки называется произведение модуля силы на ее плечо:
М0(¥) = РИ.
Точка, относительно которой берется момент, называется центром момента. Плечом силы относительно точки называется кратчайшее расстояние от центра момента до линии действия силы.
4. 2. Момент силы относительно точки в пространстве
29
Пример 4.1
Определить моменты сил Р1 = 10 кН, Р2 = 20 кН, Р3 = 30 кН, приложенных в вершинах квадрата АВСО (рис. 4. 3, а), относительно точки О, при стороне квадрата а = 0,2 м.
Решение:
1) Определяем момент силы Р1 = 10 кН относительно точки О.
Мо (Р1) = — Р1 . а = -10 . 0,2 = -2 кНм
2) Определяем момент силы Р2 = 20 кН относительно точки О.
Мо (Р2) = Р2 . ОВ = 20 . а√2 = 5,66 кНм
3) Определяем момент силы Р3 = 30 кН относительно точки О.
Мо (Р3) = — Р3 . ОД = -30 . а Соs 30° = -5,20 кНм
Пример 4.2
Определить моменты сил Р1 = 10 кН, Р2 = 15 кН, Р3 = 30 кН, приложенных в вершинах А и В прямоугольного равнобедренного треугольника (рис. 4. 3, б), относительно точки О, при а = 0,3 м.
Решение:
Определяем момент силы Р1 = 10 кН относительно точки О.
Мо (Р1) = Р1 . ОС = 10 . а Sin 45° = 2,12 кНм Определяем момент силы Р2 = 15 кН относительно точки О.
Мо (Р2) = Р2 . ОД = 15 . а Sin 60° = 3,9 кНм Определяем момент силы Р3 = 30 кН относительно точки О.
Мо (Р3) = Р3 . 0 = 0
Пример 4.3
Определить моменты сил Р1 = 15 кН, Р2 = 20 кН, Р3 = 40 кН, приложенных в вершинах А, В, С прямоугольника (рис. 4. 3, в) и треугольников (рис. 4. 3, г, д, е), относительно точки О, при а = 0,6 м самостоятельно.
Результаты решения:
Рис. 3в Мо (Р1) = 9 кНм, Мо (Р2) = -10,39 кНм, Мо (Р3) = -33,94 кНм Рис. 3г Мо (Р1) = -4,5 кНм, Мо (Р2) = -20,78 кНм, Мо (Р3) = 20,78кНм Рис. 3д Мо (Р1) = -7,79 кНм, Мо (Р2) = -12 кНм, Мо (Р3) = 20,78 кНм Рис. 3е Мо (Р1) = -7,79 кНм, Мо (Р2) = -18 кНм, Мо (Р3) = -24 кНм
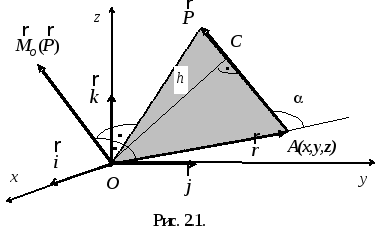
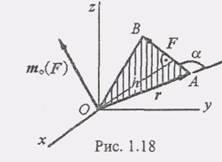
Момент силы относительно точки в пространстве определяется вектором, приложенным в этой точке, модуль которого равен произведению модуля силы на плечо.

30
Этот вектор перпендикулярен к плоскости, проведенной через моментную точку и линию действия силы и направлен так, чтобы вращение плоскости (если смотреть с конца вектора) происходило против хода часовой стрелки (рис. 4.4). Если из моментной точки О в точку приложения силы провести радиус – вектор r (рис. 4.4), то вектор момента силы можно выразить векторным произведением.
|
|
|
|
|
|
Мо (Р) = | r | * | р | (4.3) | |
Модуль момента силы
Мо (Р) = r . р Sin α = Р . d
5. ТЕОРИЯ ПАР СИЛ НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
5. 1. Пара сил. Момент пары сил на плоскости
Парой сил называется совокупность двух параллельных сил (линии действия которых не совпадают), равных по модулю и направленных в противоположные стороны.
Плоскость, в которой действуют силы, называется плоскостью действия пары.
Кратчайшее расстояние d между линиями действия сил, составляющих пару, называется плечом пары.
Если пару сил приложить к телу, находящемуся в покое, то оно будет совершать вращательное движение.
Пару сил нельзя уравновесить силой, так как она не имеет равнодействующей. Уравновесить пару можно только с помощью другой пары.
Вращательное действие пары на твердое тело характеризуют моментом пары.
Момент пары сил на плоскости – это скалярная величина, равная произведению одной из сил на плечо пары со знаком плюс или минус
Мо (Р1, Р1′) = ± Р1 . d
Если вращение плоскости действия пары происходит против хода часовой стрелки, то момент пары считаем положительным, если по ходу часовой стрелки – отрицательным.
Выразим моменты пар сил на плоскости (рис. 5. 1, а):
Мо (Р1, Р1′) = Р1 . d1 Мо (Р2, Р2′) = — Р2 . d2
Поскольку пару сил характеризуют только моментом и в расчетах нужен лишь момент пары сил, то обычно для обозначения пары сил пользуются дуговой стрелкой в плоскости действия пары, которая показывает направление вращения пары и модуль момента М = М (Р1, Р1′) (рис. 5. 1, б). Численно момент пары можно определить как удвоенную площадь треугольника ОАВ,
31
основанием которого является одна из сил Р1, а вершиной О – точка приложения другой силы Р1′ (рис. 5. 1, б).
5. 2. Момент пары сил в пространстве. Эквивалентные пары
Пару сил характеризуют:
-плоскость действия;
-величина момента пары;
-направление вращения.
Момент пары в пространстве зависит от расположения плоскости действия и от направления, в котором пара стремится вращать тело, т.е. является векторной величиной.
Вектор, определяющий момент пары, называют вектор-моментом. Вектормомент пары равен по модулю произведению силы пары на ее плечо и направлен перпендикулярно к плоскости действия пары таким образом, чтобы вращение плоскости происходило против хода часовой стрелки, если смотреть с конца вектора (рис. 5. 2).
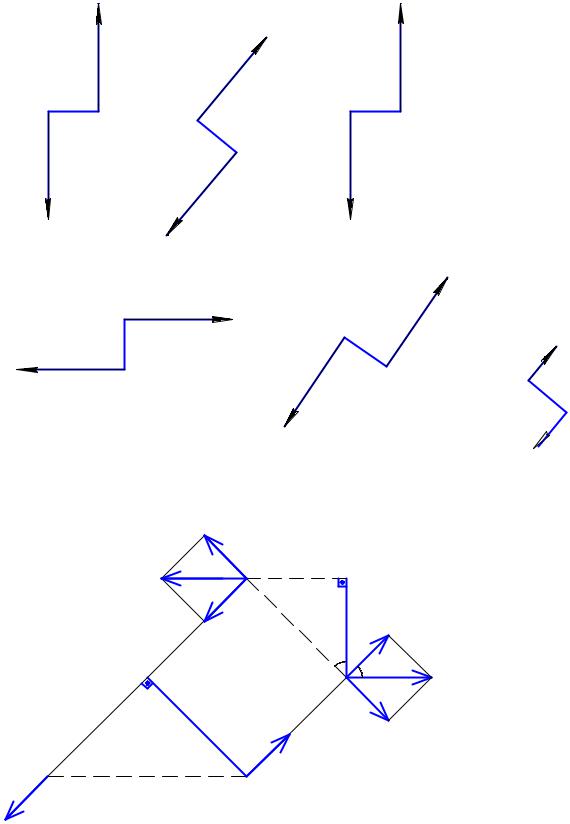
Эквивалентными называются пары, оказывающие на твердое тело одинаковое действие, т.е. вектор-моменты которых геометрически равны. Пары сил, расположенные в одной плоскости эквивалентны, если их моменты численно равны и совпадают по направлению вращения (рис. 5. 3).
Пара (Р1, Р1′) и пара (Р2, Р2′) эквивалентны, так как М (Р1, Р1′) = 20 кНм иМ (Р2, Р2′) = 20 кНм, а направление вращения одинаково (против хода часовой стрелки).
Определить эквивалентные пары на рис. 5. 4 самостоятельно.
Ответ. Первая и третья пары эквивалентны. Четвертая и шестая пары эквивалентны.
5. 3. Теоремы об эквивалентности пар
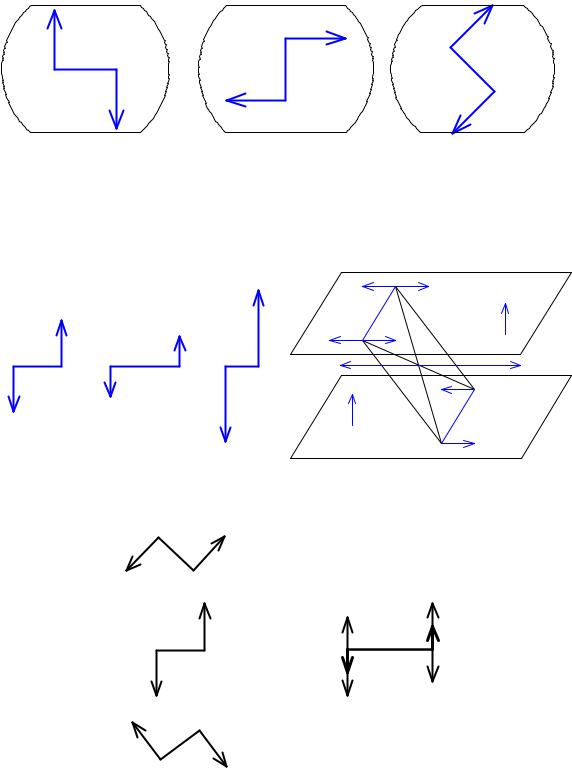
Теорема 1
Всякую пару сил, не изменяя ее действия на твердое тело, можно заменить другой парой, расположенной в той же плоскости, имеющей одинаковое с заданной парой направление вращения и равный по модулю момент.
Доказательство
Пусть на тело действуют пара сил (Р1, Р1′) в точках А и В (рис.5.5). Перенесем эти силы в точки Д и С, лежащие на их линиях действия. Приложим в точках С и Д две взаимно уравновешенные силы Т1 = — Т1′. Найдем равнодействующие:
R1 = Р1 + Т1, R1′ = Р1′ + Т1′
Получим новую пару сил (R1 , R1′). У пар (Р1, Р1′) и (R1 , R1′) одинаковое направление вращения.
Покажем, что обе пары имеют одинаковый по величине момент. M (Р1, Р1′) = Р1 . d1 M (R1, R1′) = R1 . d2
32
Р1 |
|
|
R1 = ———— | d2 = d1 Cos α | |
Cos α |
|
|
| Р1 | . d1. |
M (R1, R1′) = ———- | d1 Cos α = Р1 | |
Cos α
Таким образом, эти пары эквивалентны.
Следствия:
1.Действие пары сил на тело не изменится, если не изменяя момента пары переместить ее или повернуть в любое положение в плоскости действия
(рис.5.6).
2.Действие пары на тело не изменится, если не изменяя момента пары изменить силы пары и ее плечо. Во сколько раз уменьшаем силу, во столько раз увеличиваем плечо, и наоборот (рис. 5. 7).
Теорема
Действие пары сил на твердое тело не изменится, если пару сил перенести из данной плоскости в любую другую параллельную плоскость.
Доказательство
Рассмотрим твердое тело, на которое в плоскости I действует пара сил (Р1, Р1′). В произвольной плоскости II, параллельной плоскости I, проведем отрезок СД, параллельный и равный отрезку АВ (рис. 5. 8). В точках С и Д приложим уравновешенные силы Р2 = — Р2′ и Р3 = — Р3′. Модули этих сил выберем равными модулям сил заданной пары
Р1 = Р1′ = Р2 = Р2′ = Р3 = Р3′
Сложив силы Р′1 и Р3′, а также Р1 и Р2, найдем их равнодействующие R1 и R1′, которые приложены в точке пересечения диагоналей параллелограмма АВСД, равны по модулю и противоположно направлены.
Силы R1 и R1′ образуют уравновешенную систему сил, т.е. R1 + R1′ = 0, поэтому их можно устранить. Оставшаяся пара сил (Р2′, Р3) эквивалентна заданной, но расположена в параллельной плоскости.
Следствие
Вектор-момент пары является свободным вектором, т.е. его точку приложения можно переносить в любую точку тела, не изменяя модуль и направление.
33
| б. |
|
P’ |
|
|
2 |
| M |
d |
| P’1 |
А | d | |
2 | 1 О | |
| P1 | В |
P |
| |
|
| |
2 |
|
|
Рис. 5.1
M (P1,P’1)
P2
P’1 
P1 P’2
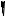 M (P2 ,P’2 )
M (P2 ,P’2 )
Рис.5.2
P1 | =2H |
|
|
| P2 =5Н |
|
| |||
d=10м |
|
|
| d=4м |
| |||||
|
|
|
| |||||||
|
|
|
| |||||||
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
| ||||
|
|
|
|
|
|
|
|
|
|
|
|
|
| P’1 | =2H |
|
|
|
|
| |
|
|
|
|
| P’2 | =5Н |
| |||
|
|
|
|
|
|
|
|
| ||
Рис. 5.3
1.
P1=6H
d=4м
P’1=6H
4.
P’4 =6Н
A
_
P1′
2. 3.
P2 =12Н
d=2м
P’2 =12Н
5.
P4 =6Н
d=3м P5 =6H
P3 =3Н
d=8м
P’3 =3Н
d =3м
d=9м
P’6 =2Н 
|
| Рис.5.4 |
|
|
| _ |
|
|
|
_ | T1′ |
|
|
|
|
|
|
| |
R1′ | _ C |
| _ |
|
| d2 |
| ||
| P1′ | 1 |
| |
|
| a | P |
|
|
| a | _ | |
|
|
| ||
|
| D |
| R1 |
|
|
|
| |
| d1 |
| _ |
|
|
| _ | T1 |
|
|
|
|
| |
| B | P1 |
|
|
_
P1
d
_
P1′
P1=4H
P2=2H
4м 8м
P2’=2H
P1’=4H
Рис. 5.7
_
P1 d1
d2
_
P2
_
P1
d
_
P1′
Рис.5.6
P3=8H
_
P2
2м _
R’
P3’=8H
_
P1′
_
P1
d
_
P1′
_ |
| _ | II |
P3′ |
|
| |
|
| M |
|
O |
|
| _ |
_ |
|
| R |
B |
| I | |
P1 |
|
|
|
d _
A P1′
Рис. 5.8
| _ |
| _ | |
_ |
| Q2′ | ||
Q3 |
| |||
P2′ |
|
| _ | |
A _1 | d | Q1′ | ||
| ||||
| B_ | |||
|
| |||
| Q |
| Q3′ | |
| _ |
| ||
| Q2 |
|
|
_
P3′
Рис.5.9
Векторный момент силы относительно точки (центра).
Векторный момент пары сил – вектор, равный векторному произведению радиус-вектора ρ, соединяющий точки приложения сил на вектор силы и направленный перпендикулярно плоскости действия пары сил таким образом, чтобы, смотря ему навстречу, пара сил стремилась поворачивать плоскость действия против часовой стрелки.
Момент силы относительно оси.
Моментом силы относительно осиназывается момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью
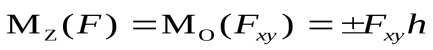
Момент относительно оси положителен, если сила стремится вращать плоскость перпендикулярную оси против часовой стрелки, если смотреть навстречу оси.
Момент силы относительно оси равен 0 в двух случаях:
Если линия действия и ось лежат в одной плоскости, то момент силы относительно оси равен 0.
Зависимость между моментами силы относительно оси и точки, лежащей на этой оси.
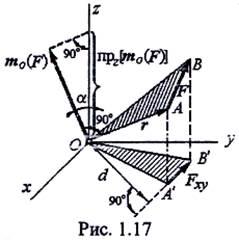

Момент силы относительно оси равен проекции на эту ось вектор-момента силы относительно произвольной точки, лежащей на этой оси.
Аналитические выражения моментов силы относительно координатных осей.
 Если
сила F задана своими проекциями Fx, Fy, Fz
и координатами х, у, z точки приложения,
то момент силы относительно начала
координат может быть представлен в
виде определителя третьего порядка*
Если
сила F задана своими проекциями Fx, Fy, Fz
и координатами х, у, z точки приложения,
то момент силы относительно начала
координат может быть представлен в
виде определителя третьего порядка*
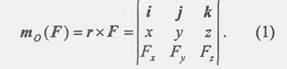
Разлагая этот определитель по элементам первой строки, найдем разложение вектора mo(F) по ортам декартовой системы координат
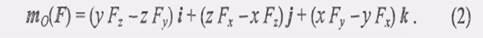
Коэффициенты при единичных ортах в формуле (2) равны проекциям вектор-момента силы на оси координат.
С другой стороны, согласно теореме с связи между моментом силы относительно оси и моментом силы относительно любой точки, лежащей на этой оси проекции вектор-момента силы на оси координат, равны моментам силы относительно этих осей. Таким образом,
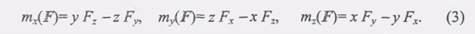
С помощью этих формул момент силы относительно оси можно вычислить, зная проекции силы и координаты точки ее приложения.
Понятие о паре сил как самостоятельной мере механического взаимодействия между телами.
Пара сил называется две равные по модулю антипараллельные силы не лежащие на одной прямой. Пара сил является не упрощенной СС самостоятельной мерой механического взаимодействия между телами, по аксиоме #1, её нельзя уравновесить одной силой то есть является не уравновешенной системой пара сил стремящееся сообщить вращение движения систем.
Алгебраический момент пары сил.
Алгебраический момент силы плоской системы сил относительно точки называется величина, равная со знаком «+» или «-» произведению модуля силы на ее плечо, то есть m0(F)=+-Fn
Векторный момент пары сил
Векторный момент пары силы называется векторная величина равная сумме векторных моментов сил пары относительно произвольной точки или векторному моменту одной из сил пары относительно точки приложения одной силы
m=m0(F1)+m0(F2)
m=+-F1d=+-F2d
Эквивалентность пар. Операции над парами
Две пары сил считаются эквивалентными в том случае, если после замены одной пары другой парой механическое состояние тела не изменяется, т. е. не изменяется движение тела или не нарушается его равновесие.
Эффект действия пары сил на твердое тело не зависит от ее положения в плоскости. Таким образом, пару сил можно переносить в плоскости ее действия в любое положение.
Существует две теоремы об эквивалентности пар:
Теорема 1. ( Об эквивалентности пар на плоскости ). Две пары, лежащие в одной плоскости и имеющие равные по величине и по знаку моменты, эквивалентны.
Теорема 2. ( Об эквивалентности пар в пространстве ). Две пары, лежащие в параллельных плоскостях и имеющие равные по величине и по знаку моменты, эквивалентны.

