Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика

Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика

Андронов В.В. Теоретическая механика. 20 лекций. Ч. 1. Статика. Кинематика: Учебное пособие для студентов очного и заочного обучения. Спец. 260100 и 260200. 2-е изд., доп. и испр. — М: МГУЛ, 2003.- 137 с. Книга содержит материал лекций, которые автор читает в Московском государственном университете леса студентам технологических специальностей. Настоящая, первая часть книги, включает статику и кинематику. Для лучшего усвоения материала в конце каждой лекции приводятся вопросы для самопроверки и упражнения. В интересах студентов заочных форм обучения в книге большое внимание уделяется поясняющим примерам и решению задач. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ. ПРЕДМЕТ И ОСНОВНЫЕ ПОНЯТИЯ ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ СТАТИКА. ЛЕКЦИЯ 1. ЗАДАЧИ СТАТИКИ, АКСИОМЫ СТАТИКИ. СВЯЗИ И РЕАКЦИИ СВЯЗЕЙ Момент силы относительно точки Алгебраический момент силы Основные типы связей и их реакции Упражнения ЛЕКЦИЯ 2. СХОДЯЩИЕСЯ СИЛЫ И ПАРЫ СИЛ Сходящиеся силы. Приведение сходящихся сил к простейшему виду Вычисление и построение равнодействующей Условия равновесия сходящихся сил Теорема о трех силах Теорема Вариньона Пара сил и ее момент Приведение системы пар сил к простейшему виду или сложение пар сил Упражнения ЛЕКЦИЯ 3. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ Момент силы относительно оси Аналитический способ вычисления момента Геометрический способ вычисления момента Преобразование пространственной произвольной системы сил Приведение пространственной произвольной системы сил к данному центру. Главный вектор и главный момент. Основная теорема статики Вычисление и построение главного вектора и главного момента Перемена центра приведения ЛЕКЦИЯ 4. ПРЕОБРАЗОВАНИЕ И РАВНОВЕСИЕ ПРОСТРАНСТВЕННОЙ ПРОИЗВОЛЬНОЙ СИСТЕМЫ СИЛ (продолжение). ЧАСТНЫЕ СЛУЧАИ СИСТЕМЫ СИЛ Случаи приведения к простейшему виду Условия (уравнения) равновесия пространственной произвольной системы сил Частные случаи системы сил Плоская система сил Система параллельных сил Равновесие системы тел Вопросы для самопроверки ЛЕКЦИЯ 5. ЦЕНТР ПАРАЛЛЕЛЬНЫХ СИЛ И ЦЕНТР ТЯЖЕСТИ Центр параллельных сил Распределенные силы Центр тяжести Интегральные формулы для координат центра тяжести Метод разбиения Вопросы для самопроверки ЛЕКЦИЯ 6. ТРЕНИЕ ТВЕРДЫХ ТЕЛ Трение покоя и трение скольжения Трение качения Решение задач статики при учете сил трения Заклинивание Упражнения КИНЕМАТИКА ЛЕКЦИЯ 7. КИНЕМАТИКА ТОЧКИ Способы задания движения точки Определение траектории, скорости и ускорения точки при векторном способе задания движения Определение траектории, скорости и ускорения точки при координатном способе задания движения Определение скорости и ускорения точки при естественном способе задания движения Естественные координатные оси и их орты Определение скорости Определение ускорения Вопросы для самопроверки ЛЕКЦИЯ 8. ПРОСТЕЙШИЕ ДРИЖЕНИЯ ТВЕРДОГО ТЕЛА Поступательное движение Вращательное движение Уравнение вращательного движения. Угловая скорость и угловое ускорение тела Траектории, скорости и ускорения точек тела Векторы угловой скорости и углового ускорения тела Векторные формулы для линейной скорости, касательного и нормального ускорений точки тела Вопросы для самопроверки ЛЕКЦИЯ 9. ПЛОСКОПАРАЛЛЕЛЬНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА Уравнения движения Угловая скорость и угловое ускорение тела при плоскопараллельном движении Определение скоростей точек тела. Метод полюса Мгновенный центр скоростей Определение скоростей точек плоской фигуры через мгновенный центр скоростей Различные случаи определения положения мгновенного центра скоростей Определение ускорений точек тела Вопросы для самопроверки ЛЕКЦИЯ 10. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ Теорема сложения скоростей Теорема сложения ускорений Причины появления ускорения Кориолиса Вычисление и построение ускорения Кориолиса Вопросы для самопроверки ДОБАВЛЕНИЕ. КИНЕМАТИКА ПРОЦЕССА ФУГОВАНИЯ ДРЕВЕСИНЫ Схема и расчетная модель процесса фугования Геометрические характеристики обработанной поверхности при одном ноже в ножевой головке Геометрические характеристики поверхности в случае многоножевой головки РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Теоретическая механика (Голубева О.В.)

Теоретическая механика (Голубева О.В.)

Голубева О. В. Теоретическая механика. Изд-во «Высшая школа». Учебник составлен в соответствии с программой и содержит изложение теоретической механики и элементов специальной теории относительности. Первая часть — «Кинематика» посвящена изложению кинематики точки, произвольной системы и твердого тела. Вторая — центральная часть «Кинетика» включает в себя постулаты классической механики, динамику точки, вопросы приведения системы сил (элементы статики), основные теоремы и законы динамики систем, элементы динамики твердого тела, механики точки переменной массы и удара. В эту часть входит динамика голономных систем, основные принципы механики и теория малых колебаний системы. Последний раздел «Элементы специальной теории относительности» рассматривается как современное развитие и обобщение Ньютонианской механики. В учебнике даны элементы векторной алгебры, анализа и понятие многомерных векторов (тензора первого ранга). Рассмотренные примеры носят принципиальный характер и относятся к естественно научным вопросам (задача двух тел, маятник Фуко, закон Бера и т. д.) и вопросам теоретической физики (формула Резерфорда, теория осциллятора, двойной маятник и т. д.). Предназначается для студентов физико-математических факультетов педагогических институтов. Оглавление ПРЕДИСЛОВИЕ ВВЕДЕНИЕ. НЕКОТОРЫЕ СВЕДЕНИЯ ИЗ ВЕКТОРНОЙ АЛГЕБРЫ И АНАЛИЗА § 1. Векторные величины и некоторые операции над ними § 2. Вектор-функция Часть I. КИНЕМАТИКА § 1. Предмет теоретической механики и ее основные понятия § 2. Уравнение движения точки и ее траектория § 3. Скорость точки § 4. Ускорение точки § 5. Проекции ускорения на естественные оси § 6. Частные случаи движепия точки. Физический смысл тангенциального и нормального ускорения точки § 7. Уравнения движения точки в криволинейных координатах. Проекция скорости и ускорения на осн криволинейных координат ГЛАВА 2. КИНЕМАТИКА НЕСВОБОДНОЙ СИСТЕМЫ МАТЕРИАЛЬНЫХ ТОЧЕК § 1. Механические системы и классификация связей § 2. Ограничения на скорость и ускорение, налагаемые геометрическими связями § 3. Число степеней свободы системы. Обобщенные координаты уравнения движения системы, обобщенные скорости ГЛАВА 3. КИНЕМАТИКА ТВЕРДОГО ТЕЛА ИЛИ НЕИЗМЕНЯЕМОЙ СРЕДЫ § 1. Уравнения движения абсолютно твердого тела § 2. Поступательное движение твердого тела § 3. Вращение твердого тела вокруг неподвижной оси § 4. Вращение тела около неподвижной точки. Теорема Даламбера § 5. Общий случай движения свободного твердого тела. Теорема Шаля Б. СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ И ТВЕРДОГО ТЕЛА ГЛАВА 4 ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 2. Сложение скоростей § 3. Сложение ускорений ГЛАВА 5. СЛОЖНОЕ ДВИЖЕНИЕ ТВЕРДОГО ТЕЛА § 2. Сложение вращений § 3. Плоскопараллельное движение твердого тела § 4. Кривошипно-шатупный механизм Часть II. КИНЕТИКА § 1. Вектор силы § 2. Тяжелая масса тел § 3. Закон инерции. Инерциальные системы координат § 1. Основной закон механики (второй закон Ньютона). Инертная масса. Принцип независимости действия сил § 5. Закон равенства действия и противодействия (третий закон Ньютона) Б. ДИНАМИКА ТОЧКИ § 1. Динамика точки и ее две основные задачи § 2. Характеристика сил § 3. Дифференциальные уравнения движения § 4. Определение уравнения движения точки по заданной силе § 5. Определение силы по заданному уравнению движения § 6. Интегрирование дифференциальных уравнений движения точки в случае сил частного вида ГЛАВА 8. ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ § 1. Уравнение движелия материальной точки в неинерциальной системе координат § 2. Координатные системы, связанные с Землей § 3. Отклонение падающих тел от вертикали ГЛАВА 9. ДВИЖЕНИЕ ТОЧКИ ПОД ДЕЙСТВИЕМ ЦЕНТРАЛЬНОЙ СИЛЫ § 1. Характерные особенности движения точки иод действием центральной силы § 2. Уравнения движения точки, находящейся под действием центральной силы § 3. Закон всемирного тяготения § 4. Задача двух тел § 5. Движение электрона в поле ионизированного атома (центральная отталкивающая сила) Б. СТАТИКА ГЛАВА 10. СТАТИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА И МЕХАНИЧЕСКОЙ СИСТЕМЫ § 2. Активные силы и силы реакции связей § 3. Система сходящихся сил § 4. Система параллельных сил § 5. Центр тяжести и центр масс § 6. Момент силы относительно точки и относительно оси § 7. Свойства пары сил § 8. Приведение произвольной системы сил § 9. Равновесие произвольной системы сил, действующих на твердое тело § 10. Раваовесне системы материальных точек Г. ДИНАМИКА СИСТЕМЫ ГЛАВА 11. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ В ИНЕРЦИАЛЬНОЙ СИСТЕМЕ КООРДИНАТ И ИХ ПЕРВЫЕ ИНТЕГРАЛЫ § 2. Принцип Даламбера. Основные уравнения диижения системы § 3. Теорема о количестве движения системы § 4. Теорема импульсов § 5. Теорема о количестве движения центра инерции системы и примеры ее применения § 6. Теорема о кинетическом моменте ГЛАВА 12. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ В НЕИНЕРЦИАЛЬНОЙ СИСТЕМЕ КООРДИНАТ § 1. Теорема о количестве движения в неинерциальной системе координат § 2. Теорема о кинетическом моменте в неинерциальной системе координат § 3. Законы сохранения § 4. Уравнения движения в расчетной системе координат Д. КОНСЕРВАТИВНЫЕ СИЛЫ ГЛАВА 13. РАБОТА СИЛЫ. ПОТЕНЦИАЛЬНОЕ ПОЛЕ § 2. Силовое поле и его частный случай — потенциальное поле § 3. Работа внутренних сил, действующих в системе ГЛАВА 14. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ § 1. Теорема о кинетической энергии и закон сохранения механической энергии точки § 2. Теорема о кинетической энергии системы § 3. Формула Кенига § 4. Закон сохранения механической энергии системы Е. ДИНАМИКА АБСОЛЮТНО ТВЕРДОГО ТЕЛА § 1. Кинетический момент твердого тела в частных случаях его движения § 2. Вычисление моментов инерции относительно параллельных осей § 3. Эдлипсоид инерции ГЛАВА 16. ДИНАМИКА ПРОСТЕЙШИХ ВИДОВ ДВИЖЕНИЯ ТВЕРДОГО ТЕЛА § 2. Вращение твердого тела вокруг неподвижной оси § 3. Физический и математический маятники ГЛАВА 17. ДИНАМИКА ТЕЛА, ВРАЩАЮЩЕГОСЯ ОКОЛО НЕПОДВИЖНОЙ ТОЧКИ. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ ТЕЛА § 1. Кинематические уравнения Эйлера Углы Эйлера § 2. Динамические уравнения Эйлера § 3. Постановка задачи о движении твердого тела вокруг неподвижной точки § 4. Регулярная прецессия гироскопа § 5. 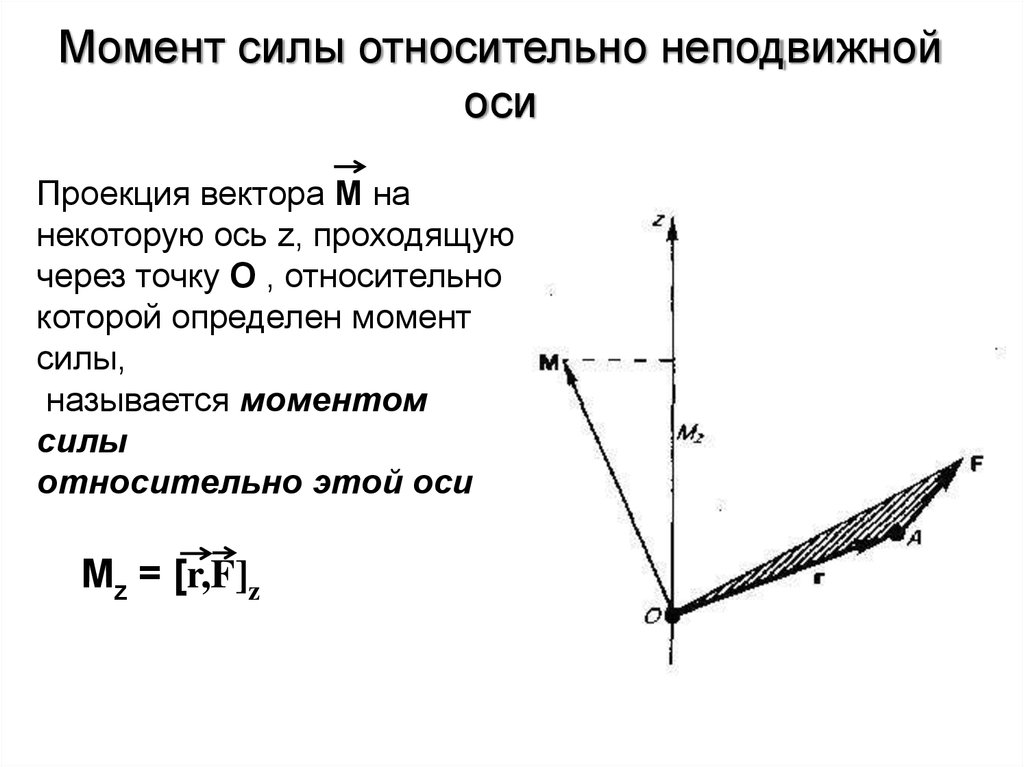Приближенная теория гироскопа § 6. Общий случай движения твердого тела Ж. ПРИМЕНЕНИЕ ОСНОВНЫХ УРАВНЕНИЙ ДИНАМИКИ К НЕКОТОРЫМ СПЕЦИАЛЬНЫМ ВОПРОСАМ МЕХАНИКИ ГЛАВА 18. ДВИЖЕНИЕ ТОЧКИ ПЕРЕМЕННОЙ МАССЫ § 2. Примеры применения уравнения Мещерского. Задачи Циолковского ГЛАВА 19. УДАР § 1. Основное уравнение теории удара § 2. Гипотеза Ньютона § 3. Абсолютно упругий удар точки о сферу § 4. Прямое центральное соударение двух тел З. ДИНАМИКА СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ (АНАЛИТИЧЕСКАЯ МЕХАНИКА) ГЛАВА 20. ЗАДАЧА О ДВИЖЕНИИ СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ § 2. Перемещения и число степенен свободы системы § 3. Идеальные связи (основной постулат аналитической механики) § 4. Уравнения Лагранжа первого рода ГЛАВА 21. УРАВНЕНИЯ ЛАГРАНЖА ВТОРОГО РОДА § 2. Уравнения Лагранжа второго рода § 3. Уравнения Лагранжа второго рода, как уравнения движения точки в 3n-мерном пространстве § 4. Уравнения Лагранжа второто рода для частных случаев сил, действующих на систему § 5. Первые интегралы уравнений движения ГЛАВА 22. КАНОНИЧЕСКИЕ УРАВНЕНИЯ ГАМИЛЬТОНА § 2. Канонические уравнения Гамильтона 3. Первые интегралы канонических уравнений § 4. Скобки Пуассона § 5. Метод Рауса ГЛАВА 23. ОБЩИЕ ПРИНЦИПЫ МЕХАНИКИ § 2. Принцип Лагранжа — Даламбера и принцип виртуальных перемещений Лагранжа § 3. Вариационный интегральный принцип Гамильтона — Остроградского И. КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ ТОЧКИ И МЕХАНИЧЕСКОЙ СИСТЕМЫ ГЛАВА 24. ПРЯМОЛИНЕЙНОЕ КОЛЕБАТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ § 2. Свободные колебания точки при наличии сопротивления среды § 3. Вынужденные колебания точки § 4. Резонанс ГЛАВА 25. ОБЩИЕ УРАВНЕНИЯ МАЛЫХ КОЛЕБАНИЙ МЕХАНИЧЕСКОЙ СИСТЕМЫ § 2. Устойчивое равновесие консервативной системы § 3. Уравнения малых колебаний механических систем § 4. Малые колебания системы с одной степенью свободы ГЛАВА 26. МАЛЫЕ КОЛЕБАНИЯ СИСТЕМЫ С ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ § 2. Собственные колебания системы § 3. Главные координаты § 4. Вынужденные колебания системы с двумя степенями свободы § 5. Двойной математический маятник Часть III. УРАВНЕНИЯ МЕХАНИЧЕСКИХ ДВИЖЕНИИ ТОЧЕК СО СКОРОСТЯМИ, БЛИЗКИМИ К СКОРОСТИ СВЕТА (ЭЛЕМЕНТЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ) ГЛАВА 27. ВВЕДЕНИЕ В СПЕЦИАЛЬНУЮ ТЕОРИЮ ОТНОСИТЕЛЬНОСТИ § 2. Элементарные сведения об ортогональных преобразованиях ГЛАВА 28. СВОЙСТВА ПРОСТРАНСТВА И ВРЕМЕНИ ПРИ СКОРОСТЯХ ТОЧЕК, СРАВНИМЫХ СО СКОРОСТЬЮ СВЕТА (ПЕРВЫЙ ЗАКОН НЬЮТОНА В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ) § 1. Порвый закон Ньютона и свойства пространства и времени ньютонианской маханики § 2. Преобразования Лоренца § 3. Свойства пространства и времени при относительном движении координатных систем, сравнимых со скоростью света § 4. Преобразование скорости и ускорения (теорема сложения скоростей Эйнштейна) ГЛАВА 29. ВТОРОЙ ЗАКОН НЬЮТОНА В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 2. Второй закон Ньютона в специальной теории относительности § 3. Уравнение энергии в специальной теории относительности § 4. Закон взаимной связи массы и энергии ГЛАВА 30. УРАВНЕНИЯ ДВИЖЕНИЯ МЕХАНИЧЕСКИХ СИСТЕМ В СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ § 2. Уравнения движения механических систем ГЛАВА 31. РЕЛЯТИВИСТСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ ТОЧКИ В КРИВОЛИНЕЙНЫХ КООРДИНАТАХ. РЕЛЯТИВИСТСКИЕ УРАВНЕНИЯ ДВИЖЕНИЯ СВЯЗНЫХ МЕХАНИЧЕСКИХ СИСТЕМ § 1. Релятивистские уравнения движения точки в криволинейных координатах § 2. Релятивистские уравнения движения связных механических систем

Вращательная динамика — Момент силы относительно заданной оси (крутящий момент) — Скалярный или векторный?

спросил 5 лет, 6 месяцев назад

Изменено 2 года назад

Просмотрено 5к раз

$\begingroup$

Я изучаю Статику и увидел, что:

Момент силы относительно данной оси (или Крутящий момент) определяется уравнением:

$M_X = (\vec r \times \vec F) \cdot \vec x \ \ \ $ (или $\ \tau_x = (\vec r \times \vec F) \cdot \vec x \ $)

Но на уроке физики я увидел:

$\vec M = \vec r \times \vec F \ \ \ $ (или $\ \vec \tau = \vec r \times \vec F \$)

В первой формуле крутящий момент представляет собой вектор тройного произведения, то есть скалярную величину. 2 } $$ 92} = \vec{r} $$

Это требует, чтобы $\vec{F} \cdot \vec{r}=0$, что верно для точки на прямой, ближайшей к началу координат.

Как для статики, так и для динамики верно, что момент есть просто сила на расстоянии . Только когда результирующая сила равна нулю (пара сил), момент является чистым моментом и не передает никакой информации о местоположении.

$\endgroup$

6

$\begingroup$

Очевидно, что это вектор, как видно из формулы 2.

В первом случае вы получаете компонент $x$ этого вектора. Помните, что скалярное произведение — это проекция одного вектора на направление другого. На самом деле вы должны написать $\hat{x}$ или $\vec{i}$ или $\hat{i}$, чтобы обозначить, что это единичный вектор. Это потому, что единичный вектор удовлетворяет

$\vec{v}\cdot\hat{u}=|v| \cdot |1|\cdot \cos(\alpha)=v \cos(\alpha)$

, так что это проекция самого вектора.

В заключение, момент является вектором, а первая формула улавливает только один из его компонентов, как указано субиндексом.

$\endgroup$

$\begingroup$

В некоторых приложениях нам может понадобиться количественно определить как крутящий момент, который является вектором, так и компонент крутящего момента относительно определенной оси, который является скаляром.

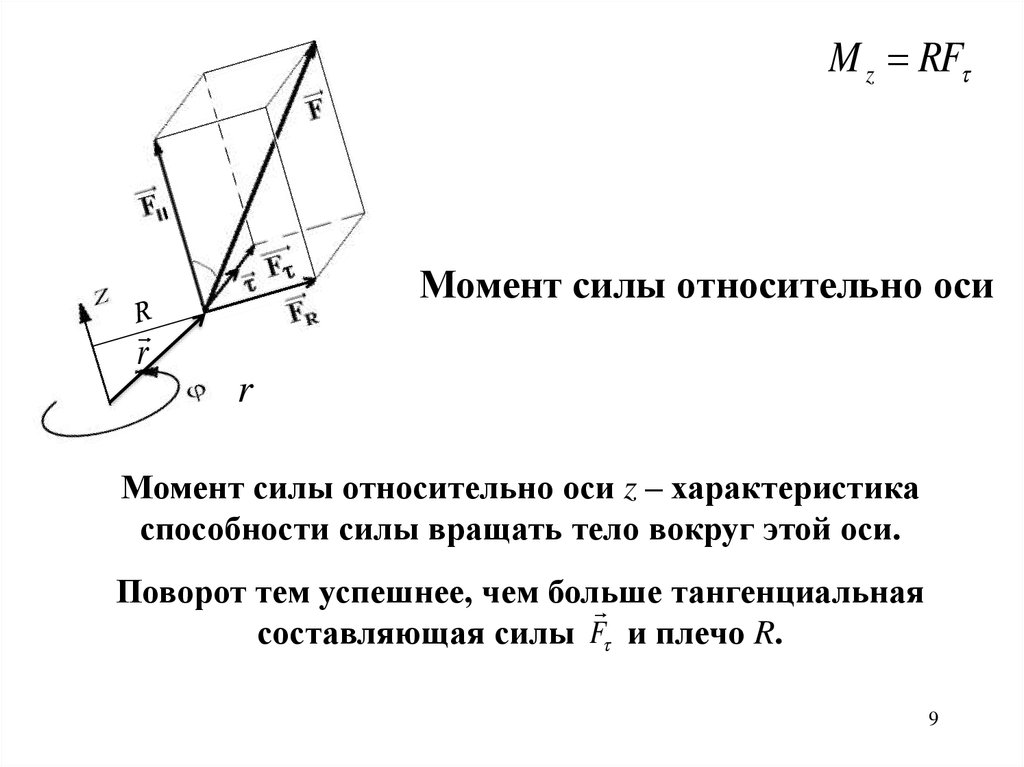
Я иллюстрирую пример этого на рисунке ниже, который взят из 1 и представлен здесь в рамках добросовестного использования в научных целях. Дверь шарнирно закреплена так, что поворачивается только вокруг оси $\mathbf{\widehat{k}}$. При этом дверная ручка находится в позиции $\mathbf{r}$ относительно начала координат. К ручке двери приложена сила $\mathbf{F}$.

Через $\boldsymbol{\tau}$ я обозначаю крутящий момент на дверной ручке, который равен $$\boldsymbol{\tau} = \mathbf{r}\times \mathbf{F}.$$ Через $\tau_z$ я обозначаю скалярную составляющую вектора крутящего момента относительно оси вращения.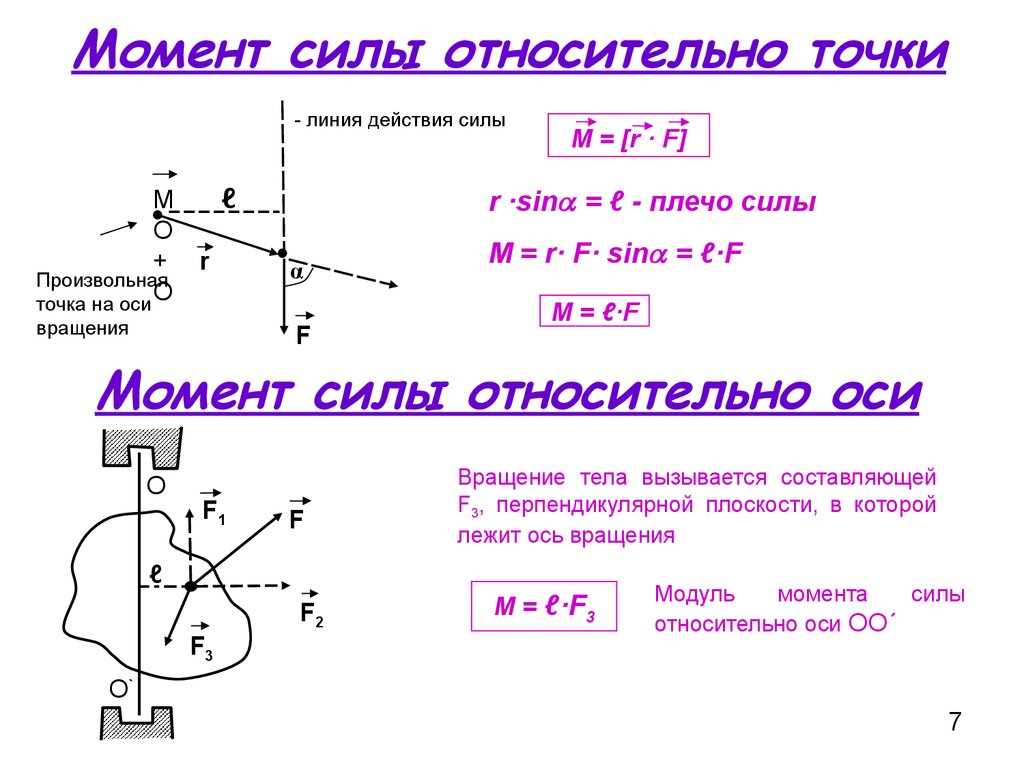 Так, $$\tau_z = \mathbf{\widehat{k}} \cdot \boldsymbol{\tau} = \left(\mathbf{r}\times \mathbf{F}\right)\cdot \mathbf{\widehat{k }}.$$

Библиография

1 Математические методы в физических науках, 3-е издание, Мэри Л. Боас, ISBN: 978-0-471-19826-0 июль 2005 г.

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

. 2$; по какой оси брать момент инерции (относительно центра масс (ЦМ) или относительно оси вращения)? Для чистой катящейся сферы возьмем $I$ относительно ЦМ, которая также является осью вращения, а для стержня, шарнирно закрепленного на одном конце, что должно занимать $I$ (ЦМ или шарнир)?

Кроме того, в $\tau = I \alpha$ какую $I$ брать (о COM или ось, о которой написан крутящий момент)?

Любая помощь приветствуется.

• ньютоновская механика
• система отсчета
• динамика вращения
• момент инерции

$\endgroup$

1

$\begingroup$

Всегда следует рассчитывать кинетическую энергию вращения и крутящий момент относительно точки, вокруг которой происходит только чистое вращение. Таким образом, для шарнирного объекта в шарнире существует только вращательное движение. Следовательно, MOI рассчитывается относительно шарнира. Хотя, в случае крутящего момента можно выбрать любую ось (перпендикулярную плоскости вращения) только , если сумма внешних сил равна нулю.

$\endgroup$

1

$\begingroup$

МВД берется относительно оси вращения. ЕСЛИ ваше тело вращается вокруг своего центра масс, то это ось вращения. Пример кинетической энергии Земли, если для расчета использовать оси, проходящие через северный и южный полюса планеты. Если стержень вращается вокруг оси, то инерция стержня, и крутящий момент должны рассчитываться по шарниру 9.2}$$

В вашем сценарии из этих уравнений совершенно ясно, что $I$ должно быть записано относительно. $com$.

В уравнении $\vec{T_{net}}=I\vec{\alpha}$ $I$ следует писать относительно той оси, относительно которой рассчитывается $\vec{T_{net}}$.

$\endgroup$

1

$\begingroup$

Допустим, здесь самый простой способ выполнить работу — вычислить момент инерции относительно шарнира либо с помощью теоремы Гюйгенса-Штайнера: $$ I_{AOR} = I_{COM} + md^2 $$ ($m$ — масса стержня, $d$ — расстояние от ЦМ до АОР) 92$ и $\tau = I \alpha$, не заботясь о других членах из-за движущихся систем отсчета.