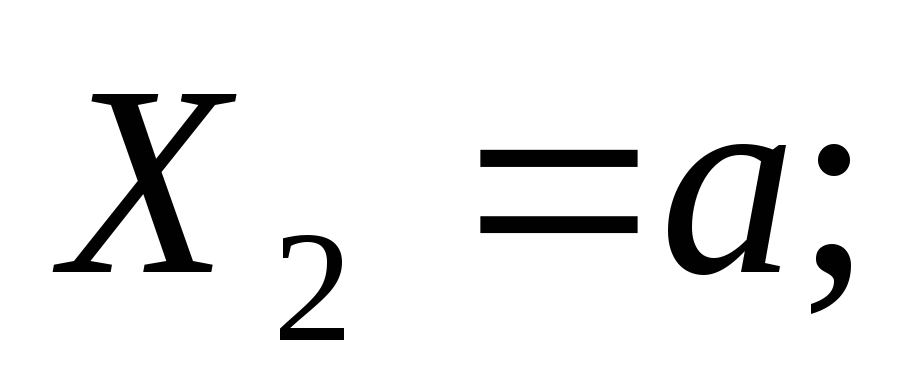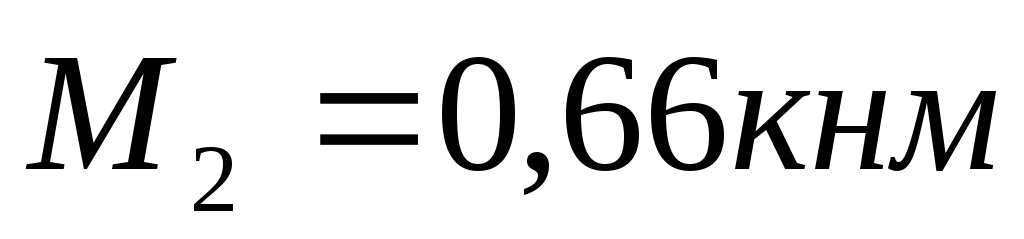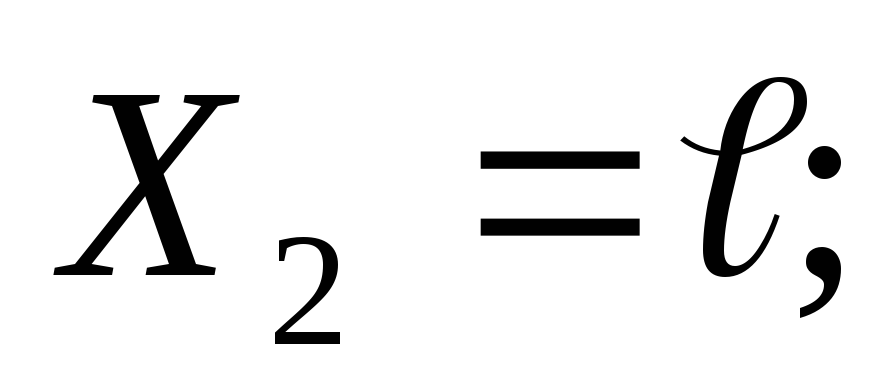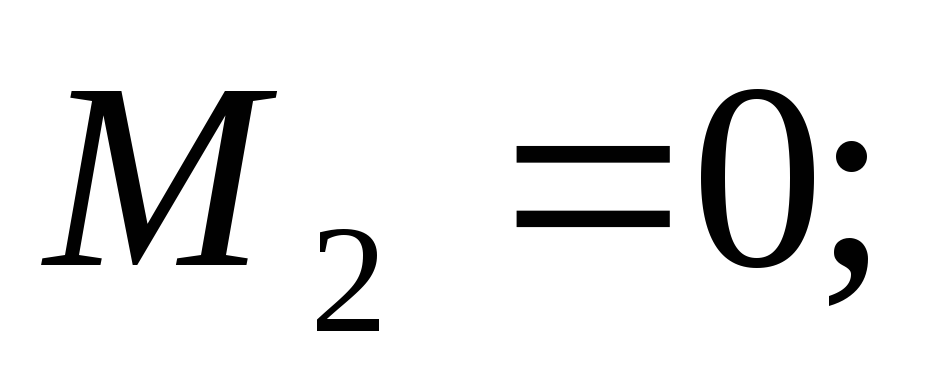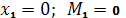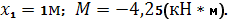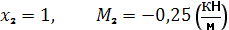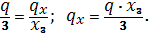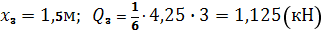Изгибающий момент — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 августа 2016; проверки требуют 5 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 23 августа 2016; проверки требуют 5 правок.Изгибающий момент — момент внешних сил относительно нейтральной оси сечения балки или другого твёрдого тела.
Изгибающий момент вычисляется, как произведение приложенной статической силы (включая реакции опор) на кратчайшее расстояние от вектора этой силы до нейтральной оси сечения. Если таких сил несколько, то изгибающие моменты от каждой силы складываются с учётом знака. Отсюда понятно, что в каждом сечении тела изгибающие моменты могут различаться.
Для сечения, находящегося в равновесии, изгибающий момент равен моменту внутренних сил относительно нейтральной оси сечения. Внутренние силы можно представить, если мысленно удалить часть тела по одну сторону от сечения и заменить её внешними силами так, чтобы оставшаяся часть находилась в равновесии.
Если других воздействий нет (прямой чистый изгиб), то сечение при деформации изгиба остается плоским и поворачивается на малый угол. В реальности изгибающий момент часто сочетается со сдвигающими, растягивающими, крутящими и другими внешними силами.
Определение изгибающего момента является очень важным для расчета конструкций на прочность. При изгибающем воздействии часть стержня (волокна), расположенная по одну сторону от нейтральной оси, растягивается, а другая — сжимается. Наибольшие напряжения возникают в крайних волокнах стержня. Если они превышают прочность материала, конструкция разрушается. Связь между внутренними напряжениями и изгибающим моментом была впервые математически выражена Ш. Кулоном в 1773 году
Простейшие случаи вычисления изгибающего момента[править | править код]
Для консоли длиной l с нагрузкой P на конце консоли изгибающий момент увеличивается от нуля на конце консоли до P*l.
Для консоли, равномерно загруженной нагрузкой q, изгибающий момент увеличивается от нуля на конце консоли до q l2 / 2.
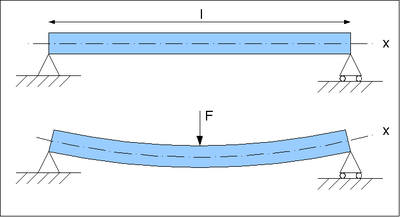
Для балки, изображенной на рисунке,
- My(x=l/2)=F/2⋅l/2=Fl/4{\displaystyle M_{y}(x=l/2)=F/2\cdot l/2=Fl/4} .
- Волновой изгибающий момент; определяется на миделе судна, находящегося на волне
- Положительный изгибающий момент; в машиностроении принято считать положительным момент на сжатых волокнах балки, в строительстве — на растянутых
- Отрицательный изгибающий момент
- ↑ Атапин В.Г. Сопротивление материалов / Учебник и практикум для академического бакалавриата. М.:Юрайт, 2016. — 342 с. ISBN:978-5-9916-5203-2
Изгибающий момент – внутренний силовой фактор

Здравствуйте. Здорово, что Вы проявляете интерес к нашему проекту SoproMats, спасибо! Эта статья будет посвящена внутреннему силовому фактору – изгибающему моменту. Фактору, который возникает в поперечных сечениях балок, работающих на изгиб. Здесь поделимся информацией как он обозначается, измеряется, определяется и т.д. В общем все, что нужно знать об изгибающем моменте. Также в конце статьи поделимся ссылочками, на важные материалы про изгибающий момент.
Что такое изгибающий момент?
Изгибающий момент – это внутренний силовой фактор, возникающий в элементах конструкций, деталях, работающих на изгиб: такие конструктивные элементы как балка, рама, плита и т.д.
Зачем нужен?
Зная изгибающий момент в сечении, а также геометрические размеры этого сечения, можно определить нормальное напряжение в его конкретной точке и исследовать ее напряженно-деформированное состояние. Определение изгибающих моментов является неотъемлемой частью любого прочностного расчета деталей, работающих на изгиб. Для наглядной визуализации распределения изгибающих моментов строят эпюры, которые позволяют выявить наиболее подверженные к разрушению места балки. Как правило, то сечение, в котором изгибающий момент имеет максимальное значение, является самым опасным у балки. За редкими исключениями. Поэтому так важно уметь определять эту величину.
Как обозначается?
Изгибающий момент обозначается буквой M с индексом, который указывает на название оси, относительного которой происходит изгиб. Обычно это ось x, поэтому в этой статье будем использовать такое обозначение — M
Как определяется?
Для определения этой величины используется метод сечений. По которому считается, что если балка находится в равновесии, то и отдельные части балки также будут находится в равновесии, если действие каждой части друг на друга, заменить равными силовыми факторами. Используя этот метод в совокупности с уравнениями равновесия статики, можно определить изгибающий момент в любом сечении, более подробно посмотрим этот процесс на примере ниже.
В чем измеряется?
Данная величина измеряется в Н·м. В расчетах, в основном, используется размерность — кН·м, и этот вариант будем использовать в этой статье. Иногда считают в кгс·м и т·м.
Статьи про изгибающие моменты:
Как построить эпюру изгибающего момента? В материале этой статьи написано, как можно построить эпюру различными методами.

Поперечная сила и изгибающий момент.
В поперечных сечениях балки возникает поперечная сила Q и изгибающий моментM.
| Разрежем балку на расстоянии Заменим действие отброшенной части (правой) внутренними усилиями Q и M; рассмотрим левую часть балки. Q – поперечная сила — результирующая всех внутренних усилий алгебраически равна сумме всех сил, расположенных левее сечения. M – изгибающий момент результирующий момент всех внешних сил, численно равен алгебраической сумме моментов всех усилий, расположенных левее сечения. Составим уравнения равновесия для левой части: |
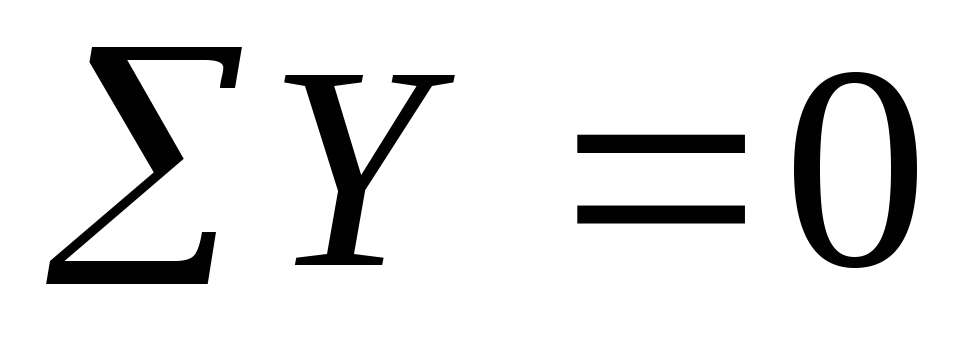 →
→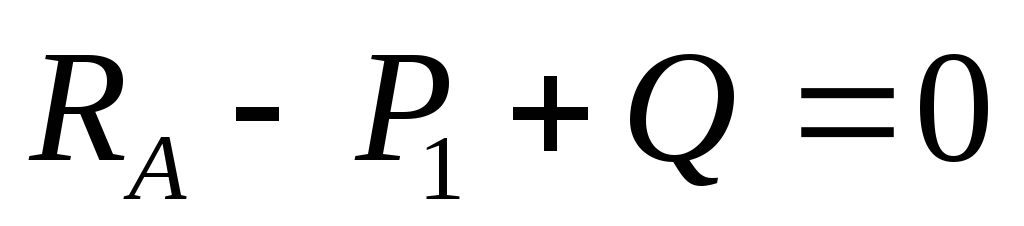 →
→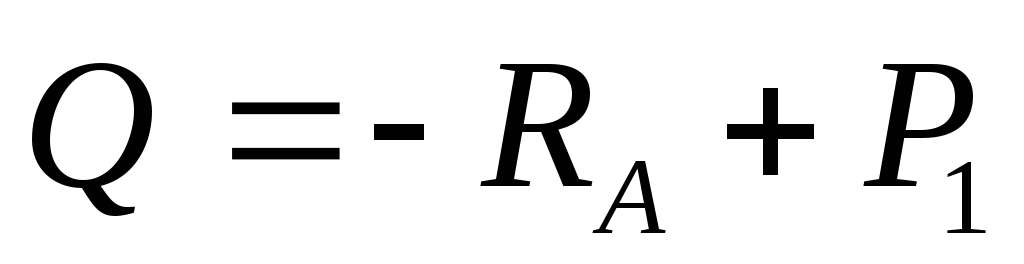
∑МсечХ=0;
→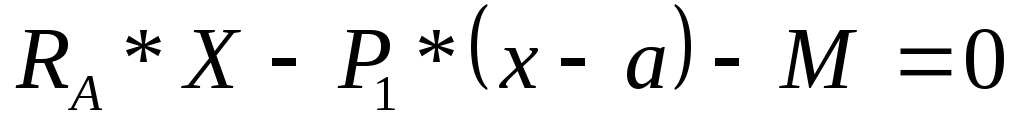 →
→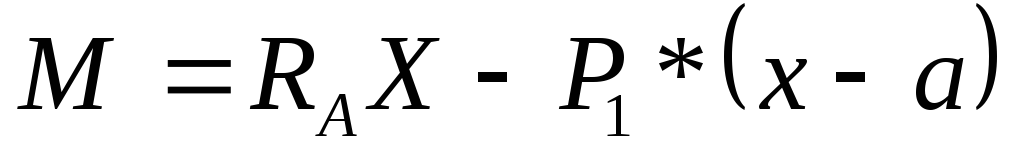 ;
;
Можно вместо левой части рассмотреть правую часть. Результат будет тот же, но с обратным знаком.
В связи с этим для того, чтобы в одном и том же сечении
ПРАВИЛО ЗНАКОВ (см. рисунок):
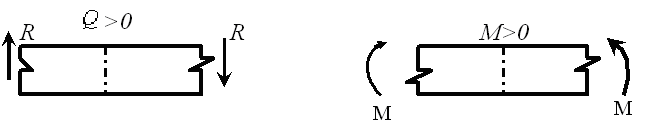
Поперечную силу будем считать положительной, если равнодействующая сила левее сечения направлена вверх, а правее сечения направлена вниз.
Изгибающий момент будет считаться положительным, если равнодействующий момент левых сил направлен по ходу часовой стрелки, а правых – против часовой стрелки.
Зависимость
между изгибающим моментом, поперечной
силой и интенсивностью распределенной
нагрузки.
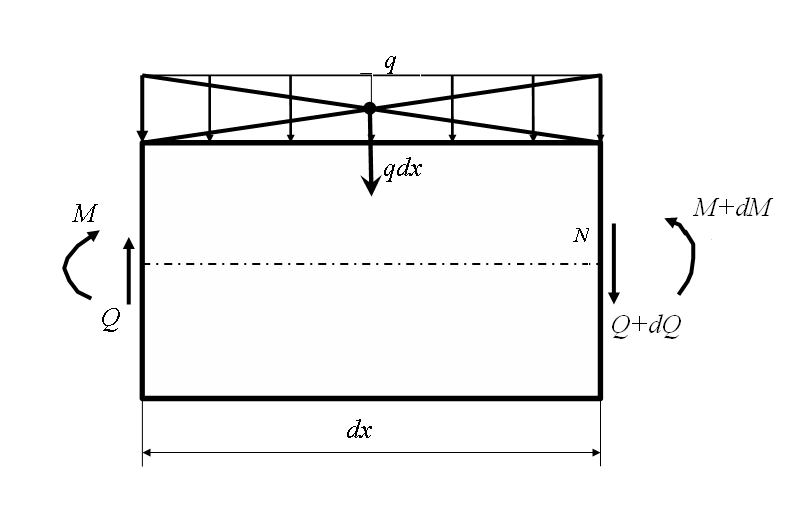
| Выделим из балки участок бесконечно малой длины так чтобы по границам этого участка и по самом участке сосредоточенные силы отсутствовали. Ввиду малости участка распределенную
нагрузку Составим уравнения равновесия:
|
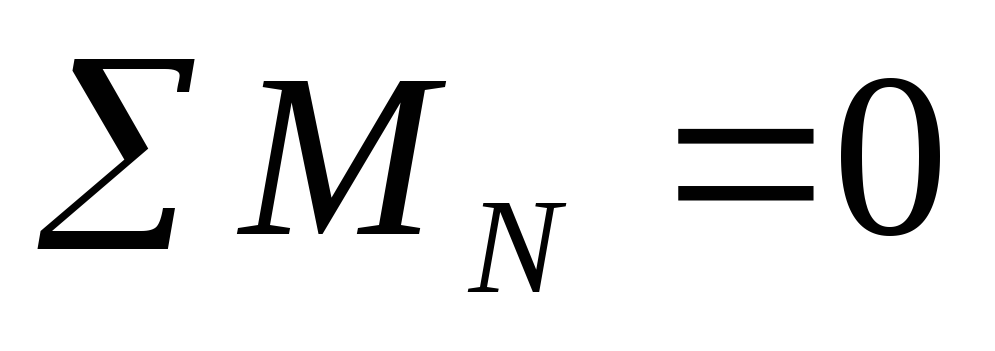
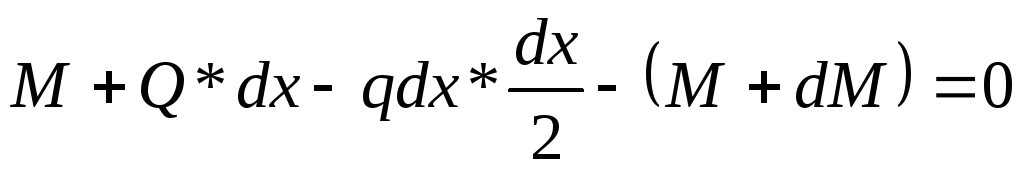 ;
;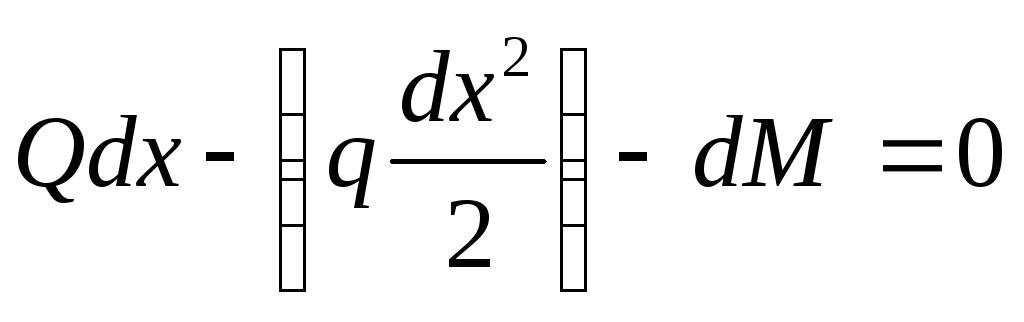
Пренебрегая бесконечно
малыми величинами второго порядка,
получаем: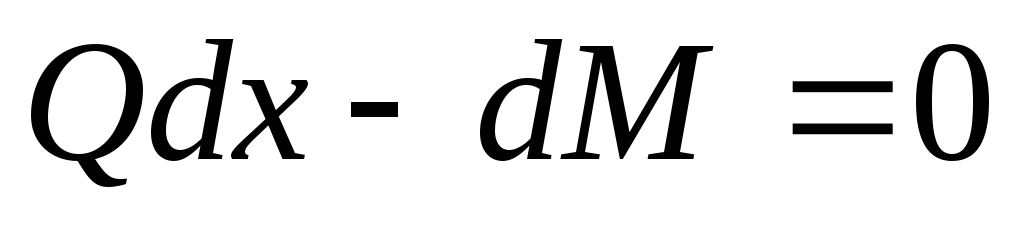 или
или
Продифференцировав последнее
выражение по Х, получаем: 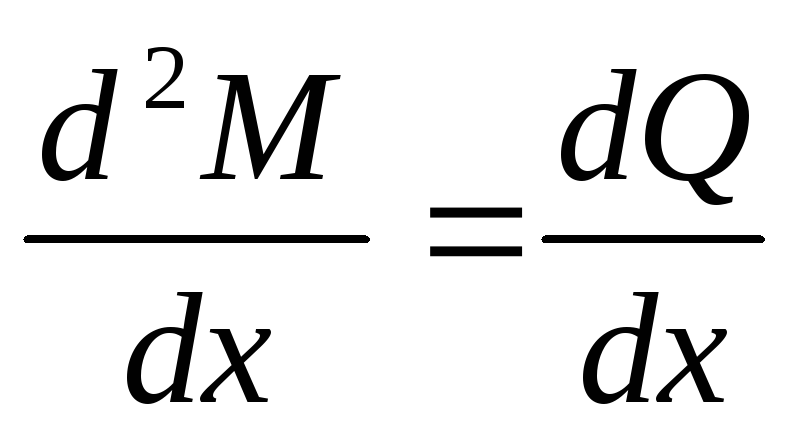 ;или
;или
Построение эпюр изгибающих моментов и поперечных сил.
Внутренние усилия Q и M зависят от координатыХ,поэтому удобно иметь графики зависимостиQ и M от расстоянияХ,эти графики называютсяэпюрамипоперечных сил и изгибающих моментов. Построение эпюрQ и M рассмотрим на частных примерах.
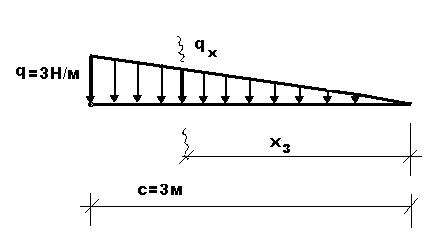
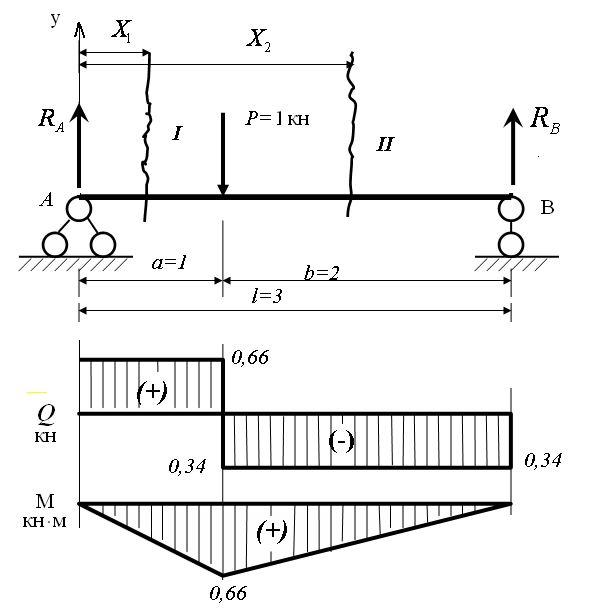
Положительные изгибающие моментыбудем откладывать в сторону растянутых волокон. | Пример 1. Построить эпюры Q иM. 1) Определяем опорные реакции: 2) Разбиваем балку на участки. Рассмотрим отдельные участки. 3) Участок 1: (рассекаем на расстоянии Х1) Участок 2: (рассекаем на расстоянии Х2) при . |
Пример 2. Построить эпюры Q иM.
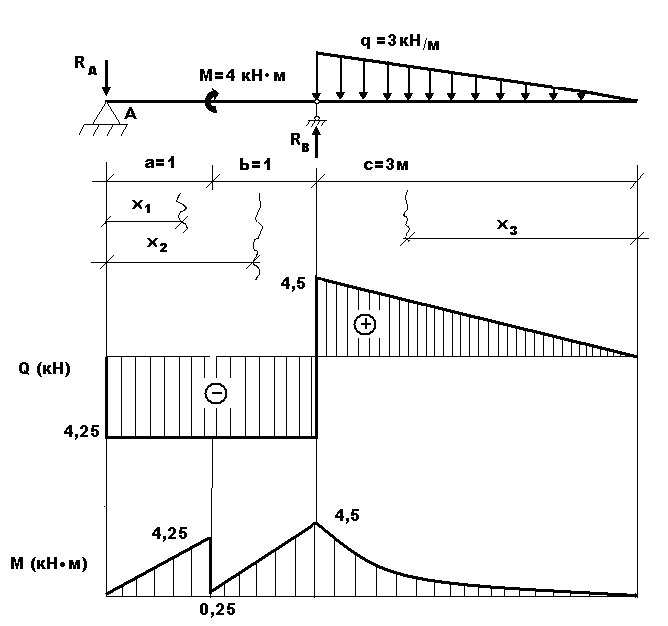
Определим опорные реакции:
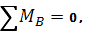
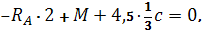
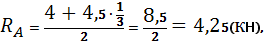
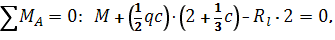
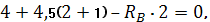
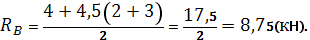
Проверка
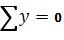
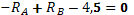 ,
,
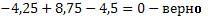
Следовательно, опорные реакции определены верно.
2) Построим эпюры QиM:
Участок I: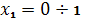
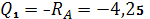
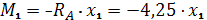
Участок II: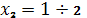
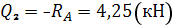
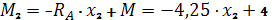
Участок III: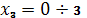
| Идем справа налево Из подобия треугольников . находим: |
Ньютон-метр — Википедия
Материал из Википедии — свободной энциклопедии
 Момент силы F относительно точки О равен F.b, пунктир — линия действия силы.
Момент силы F относительно точки О равен F.b, пунктир — линия действия силы.Ньютон-метр (русское обозначение Н·м; международное: N·m) — единица измерения момента силы в Международной системе единиц (СИ). Один ньютон-метр равен моменту силы, создаваемому силой, равной 1 Н, относительно точки, расположенной на расстоянии 1 м от линии действия силы.
По правилам форматирования, принятым в СИ, буквенные обозначения единиц, входящих в произведение, разделяются точкой на средней линии (знаком умножения). Допускается также разделять их пробелом, если это не может вызвать недоразумения. Символ «х» для этих целей не используется[1].
За основу единицы был принят ньютон.
| Кратные | Дольные | ||||||
|---|---|---|---|---|---|---|---|
| величина | название | обозначение | величина | название | обозначение | ||
| 101 Н·м | деканьютон-метр | даН·м | daN·m | 10−1 Н·м | дециньютон-метр | дН·м | dN·m |
| 102 Н·м | гектоньютон-метр | гН·м | hN·m | 10−2 Н·м | сантиньютон-метр | сН·м | cN·m |
| 103 Н·м | килоньютон-метр | кН·м | kN·m | 10−3 Н·м | миллиньютон-метр | мН·м | mN·m |
| 106 Н·м | меганьютон-метр | МН·м | MN·m | 10−6 Н·м | микроньютон-метр | мкН·м | µN·m |
| 109 Н·м | гиганьютон-метр | ГН·м | GN·m | 10−9 Н·м | наноньютон-метр | нН·м | nN·m |
| 1012 Н·м | тераньютон-метр | ТН·м | TN·m | 10−12 Н·м | пиконьютон-метр | пН·м | pN·m |
| 1015 Н·м | петаньютон-метр | ПН·м | PN·m | 10−15 Н·м | фемтоньютон-метр | фН·м | fN·m |
| 1018 Н·м | эксаньютон-метр | ЭН·м | EN·m | 10−18 Н·м | аттоньютон-метр | аН·м | aN·m |
| 1021 Н·м | зеттаньютон-метр | ЗН·м | ZN·m | 10−21 Н·м | зептоньютон-метр | зН·м | zN·m |
| 1024 Н·м | иоттаньютон-метр | ИН·м | YN·m | 10−24 Н·м | иоктоньютон-метр | иН·м | yN·m |
| применять не рекомендуется | |||||||
1 килограмм-сила-метр (кгс·м; kp·m, Kilopond · Meter) = 9,80665 Н·м
1 кгс·см, kp·cm = 0,0980665 Н·м
1 дюйм-унция-сила = 7,0615518 мН·м
1 дина-сантиметр = 10−7 Н·м
0,7375621 ft·lb (Foot-pound) = 1 Н·м
1 ft·lb = 1,3558179483314004 Н·м
Поперечная сила Q и изгибающий момент М. Эпюры поперечных сил Q и изгибающих моментов М.
Цели занятий:Рассмотреть деформацию изгиб, где в технике встречается данный вид деформации, какие внутренние силовые факторы возникают при изгибе, показать, каким образом они определяются.
План занятий:
1. Основные понятия и определения прямого изгиба.
2. Определение значений поперечных сил Q и построение эпюры поперечных сил Q.
3. Определение значений изгибающих моментов М и построение эпюры изгибающих моментов М.
Если на стержень действуют силы перпендикулярные оси, то такое нагружение называется изгибом. Первоначально прямая ось искривляется. Мы будем рассматривать в этой лекции случай, когда силы лежат в одной плоскости. Изгиб называется чистым изгибом, если в поперечных сечениях возникает лишь один внутренний силовой фактор – изгибающий момент.
Если помимо изгибающих моментов возникают еще и поперечные силы, то изгиб называется поперечным.
Стержень, работающий на изгиб называется балками.
Поперечная сила Q – это алгебраическая сумма всех сил, действующих относительно рассматриваемого сечения.
Изгибающий момент М – это алгебраическая сумма всех изгибающих моментов, действующих относительно рассматриваемого сечения.
Эпюры поперечных сил и изгибающих моментов – это графики распределения поперечных сил и изгибающих моментов по длине бруса.
Основная литература: 1;2
Дополнительная литература: 1;2
Контрольные вопросы.
1. Какие внутренние силовые факторы возникает при изгибе?
2. Дайте определение поперечной силы.
3. Как обозначается поперечная сила и в каких единицах она измеряется?
4. Дайте определение изгибающего момента.
5. Как обозначается изгибающий момент и в каких единицах он измеряется?
6. Что такое эпюра поперечных сил?
7. Что такое эпюра изгибающих моментов?
Лекция №13.
Цели занятия:
1. Ознакомить с дифференциальной зависимостью при изгибе между изгибающим моментом М, поперечной силой Q и интенсивностью распределённой нагрузки q, где применяется данная дифференциальная зависимость.
2. Рассмотреть деформацию чистый изгиб, практическое применение чистого изгиба.
План занятия:
1. Дифференциальная зависимость при изгибе между изгибающим моментом М, поперечной силой Q и интенсивностью распределённой нагрузки q.
2. Чистый изгиб.
Дифференциальные зависимости при изгибе между изгибающим моментом М, поперечной силой Q и интенсивностью распределённой нагрузки q.
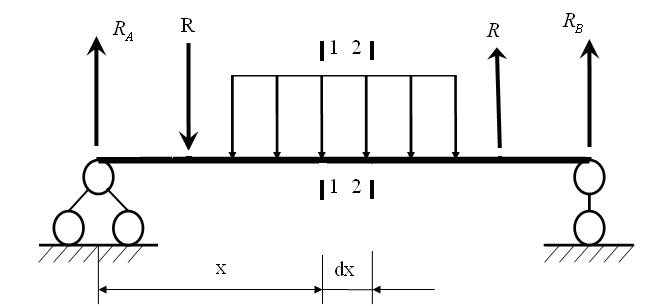
Рассмотрим балку, загруженную произвольной распределенной нагрузкой. Двумя сечениями, отстоящими друг от друга на малую величину , выделим элементы. Внутренние силы, действующие в сечениях статически эквивалентны изгибающему моменту и поперечной силе. Мы рассматриваем и как функции z. При изменении независимой переменной на малую величину . и получат приращения, которые можно рассматривать как дифференциалы данных функций. Рассмотрим равновесие элемента.
Производная от поперечной силы по координате равняется по модулю интенсивности нагрузки, действующей на балку.
Пренебрегая малой второго порядка малости, получаем:
Производная от изгибающего момента по координате равняется поперечной силе.
При помощи данных формул проверяется правильность вычислений поперечных сил Q и изгибающих моментов М.
Чистый изгиб.
Допустим, что в данном случае в поперечных сечениях действуют лишь нормальные напряжения. Рассмотрим балку, загруженную таким образом, что возникает нагружение чистого изгиба.
1. Рассмотрим вначале статическую сторону задачи.
Из 6 уравнений 3 удовлетворяются тождественно при любых значениях
Остаются 3 уравнения:
1)
2)
3)
Напряжения, рассматриваемые как функция координат:
должны удовлетворять статическим уравнениям (1-3).
Однако статических уравнений недостаточно для того, чтобы получить решение для напряжений. Надо рассмотреть еще деформации и принять закон, связывающие деформации и напряжения.
2. Геометрическая сторона задачи.
Характер деформации балки можно было бы наблюдать на модели из сильно деформируемого материала, например резины.
Изгибая резиновый брус с сеткой нанесенной на боковой поверхности мы бы увидели картину, похожую на ту, что показана на рисунке.
Мы видим, что поперечные сечения, оставаясь прямыми и нормальными к искривленным поперечным линиям, наклоняются друг к другу.
Этот факт был замечен еще в 1705 г. Я.Бернулли, многократно подтвержден экспериментами и сформулирован в форме гипотезы плоских сечений, положенный в основу технической теории изгиба:
Сечения плоские и нормальные к оси балки до изгиба остаются плоскими и нормальными к изогнутой оси балки.
Пользуясь этой гипотезой, мы установим закон изменения удлинений волокон по высоте балки (под волокном понимаем мыслимый геометрический объект, а отнюдь не настаиваем на волокнистом строении материала).
Рассмотрим малый элемент. Очевидно, что верхние и нижние
волокна будут иметь разные по знаку деформации (в случае, показан-
ном на рисунке верхние волокна будут сжиматься, а нижние растягиваться), и т.к. деформация по своей сути – величина непрерывная, то
безусловно, где-то будет находиться слой не испытывающий деформации – нейтральный слой.
Пусть — радиус кривизны нейтрального слоя, а — координата, отсчитываемая от нейтрального слоя.
Удлинение произвольного волокна равняется:
В нашем случае а
(Напомним, что кривизна положительна, когда положительна координата кривизны). Чтобы привести знаки в соответствие с физическим смыслом запишем аналитическая запись гипотезы плоских сечений.
3. Физическая сторона задачи.
Мы уже не раз говорили о том, что между напряжениями и деформациями существует связь, которая может быть установлена экспериментальным путем. Примем эту связь простейшей, т.е. будем считать, что материал линейно упруг, т.е. следует закону Гука.
Допустим, что волокна не давят друг на друга, а это для случая чистого изгиба совершенно точный факт, подтвержденный точным решением методами теории упругости, то тогда оказывается, что каждое волокно работает либо на растяжение, либо на сжатие, и в этой ситуации можно применить закон Гука:
Вернемся к статическим уравнениям (1-3) и подставим в них
выражение (5). Мы получим 3 уравнения, содержащие одну неизвестную величину .
Эта система будет совместна только при некоторых условиях.
Подставим в (1): , т.к. (балка деформировалась и кривизна отлична от нуля), то , т.е. если поместить начало координат в центр тяжести сечения, то первое условие совместности будет удовлетворительно. Вспомним, что координата отсчитывалась от нейтрального слоя. Отсюда вывод: при изгибе нейтральный слой проходит через центр тяжести. Подставим в (2):
т.е. оси, в которых рассматривается изгиб, должны быть главными.
Итак! Приняв оси и за главные, центральные оси мы удовлетворяем уравнениям (1) и (2).
Осталось уравнение (3)
— основная зависимость при изгибе.
Произведение модуля упругости на момент инерции называется жесткостью при изгибе.
Основную зависимость при изгибе можно сформулировать: кривизна прямо пропорциональна изгибающему моменту и обратно пропорциональна жесткости при изгибе.
Обратим внимание. Если чистый изгиб, то М-const и тогда изогнутая ось – дуга окружности. Подставим выражение для в (5) и получим закон распределения нормальных напряжений:
Чаще всего в дальнейшем мы знаки напряжений будем расставлять по физическому смыслу и запишем, как это обычно принято в сопротивлении материалов.
Проанализируем полученный закон распределения нормальных напряжений.
1. Мы видим, что напряжения не зависят от координаты , следовательно, по ширине сечения распределяются равномерно.
2. По высоте сечения нормальные напряжения распределяются линейно. На уровне центра тяжести они равны нулю, а максимальны по модулю в точке наиболее удаленной от нейтральной оси (следа на плоскости сечения нейтрального слоя). Если обозначить
, где — расстояние от нейтральной оси до наиболее удаленной точки, то максимальное по модулю напряжение в сечении находится по формуле:
Основная литература: 1;2
Дополнительная литература: 1;2
Контрольные вопросы.
1. Чему равна интенсивность распределённой нагрузки?
2. Чему равна поперечная сила Q?
3. Какой внутренний силовой фактор возникает при чистом изгибе?
4. Какое напряжение возникает при чистом изгибе?
5. По какой формуле определяется напряжение при чистом изгибе?
6. Как обозначается жёсткость при изгибе?
7. Где при чистом изгибе напряжение имеет максимальное и минимальное значения?
Лекция №14.
Цели занятия:
1. Рассмотреть деформацию поперечный изгиб, практическое применение поперечного изгиба.
2. Ознакомить с условием прочности и жёсткости при изгибе.
План занятия:
1. Поперечный изгиб.
2. Условие прочности при изгибе.
3. Условие жёсткости при изгибе.
Поперечный изгиб.
При поперечном изгибе, помимо изгибающего момента, в поперечном сечение имеется также и поперечная сила, которая является результирующей элементарных усилий, действующих в плоскости сечения. Т.е. помимо нормальных напряжений возникают и касательные напряжения.
Касательные напряжения искривляют поперечные сечения и гипотеза плоских сечений, вообще говоря, не выполняется. Однако если длина велика по сравнению с высотой балки, то искривления по перечных сечений и возникающее в случае поперечного изгиба взаимное нажатие волокон не оказывают существенного влияния на величину нормальных напряжений, и нормальные напряжения при поперечном изгибе будут определяться по тем же формулам, что и при чистом изгибе.
Дадим грубую оценку касательных напряжений при изгибе.
Пусть — длина балки, а
— характерный размер поперечного сечения.
Если сечение не является тонкостенным, то площадь его отличается от величины числовым множителем порядка единицы. Тогда среднее касательное напряжение в сечении имеет порядок
Оценим порядок нормальных напряжений.
Наибольший момент имеет порядок , а момент сопротивления порядок (например для прямоугольного сечения ). Таким образом нормальное напряжение имеет следующий порядок: , откуда видно, что если длина стержня велика по сравнению с характерным размером поперечного сечения , то касательные напряжения при расчетах на прочность обычно не принимаются во внимании. Однако, исключения составляют случаи:
1. Тонкостенные стержни.
2. В случае конструкций, выполненных из материалов с малым сопротивлением межслойному сдвигу, например, древесина, или, получающие в настоящее время большое распространение армированные пластики, когда касательные напряжения могут оказаться более опасными, чем нормальные.
3. Для расчета соединений (поясных швов, заклепок) в металлических балках составного сечения.
Имея это ввиду, мы приведем формулу для определения касательных напряжений при изгибе, полученную нашим соотечественником Д.И.Журавским в середине прошлого века. , где — касательные напряжения в слое, отстоящим от нейтральной оси на расстоянии .
— поперечная сила в сечении.
— статический момент части сечения, расположенной выше слоя в котором определяются касательные напряжения относительно оси .
— момент инерции относительно оси .
Следует иметь ввиду, что формула приближена и дает приемлемые результаты для высоких узких сечений.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Момент силы — это… Что такое Момент силы?
Момент силы, приложенный к гаечному ключу. Направлен от зрителя
Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора, (проведенного от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов).
Общие сведения
В физике момент силы можно понимать как «вращающая сила». В системе СИ единицами измерения для момента силы является Ньютон-метр. Момент силы иногда называют моментом пары сил, это понятие возникло в трудах Архимеда над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метров от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров до оси вращения. Более точно, момент силы частицы определяется как векторное произведение:
где — сила, действующая на частицу, а — радиус-вектор частицы.
Предыстория
Строго говоря, вектор, обозначающий момент сил, введен искусственно, так как является удобным при вычислении работы по криволинейному участку относительно неподвижной оси и удобен при вычислении общего момента сил всей системы, так как может суммироваться. Для того, чтобы понять откуда появилось обозначение момента сил и как до него додумались, стоит рассмотреть действие силы на рычаг, поворачивающийся относительно неподвижной оси.
Работа, совершаемая при действии силы на рычаг , совершающий вращательное движение вокруг неподвижной оси, может быть рассчитана исходя из следующих соображений.
Пусть под действием этой силы конец рычага смещается на бесконечно малый отрезок , которому соответствует бесконечно малый угол . Обозначим через вектор, который направлен вдоль бесконечно малого отрезка и равен ему по модулю. Угол между вектором силы и вектором равен , а угол между вектором и вектором силы .
Следовательно, бесконечно малая работа , совершаемая силой на бесконечно малом участке равна скалярному произведению вектора и вектора силы, то есть .
Теперь попытаемся выразить модуль вектора через радиус-вектор , а проекцию вектора силы на вектор , через угол .
Так как для бесконечно малого перемещения рычага , можно считать, что траектория перемещения перпендикулярна рычагу , используя соотношения для прямоугольного треугольника, можно записать следующее равенство: , где в случае малого угла справедливо и следовательно
Для проекции вектора силы на вектор , видно, что угол , а так как , получаем, что .
Теперь запишем бесконечно малую работу через новые равенства или .
Теперь видно, что произведение есть не что иное как модуль векторного произведения векторов и , то есть , которое и было принято обозначить за момент силы или модуль вектора момента силы .
Теперь полная работа записывается очень просто: или .
Единицы
Момент силы имеет размерность сила на расстояние, и в системе СИ единицей момента силы является ньютон-метр. Джоуль, единица СИ для энергии и работы, тоже определяется как 1Н·м, но эта единица не используется для момента силы. Когда энергия представляется как результат «сила на расстояние», энергия скалярная, тогда как момент силы — это «сила, векторно умноженная на расстояние» и таким образом она (псевдо) векторная величина. Конечно, совпадение размерности этих величин не простое совпадение; момент силы 1Н·м, приложенный через целый оборот, требует энергии как раз 2*π джоулей. Математически
- ,
где Е — энергия, M— вращающий момент, θ — угол в радианах.
Специальные случаи
Формула момента рычага
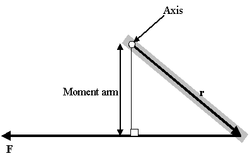 Момент рычага
Момент рычагаОчень интересен особый случай, представляемый как определение момента силы в поле:
- = МОМЕНТ_РЫЧАГА * СИЛА
Проблема такого представления в том, что оно не дает направления момента силы, а только его величину, поэтому трудно рассматривать в.м. в 3-хмерном случае. Если сила перпендикулярна вектору r, момент рычага будет равен расстоянию до центра и момент силы будет максимален
- = РАССТОЯНИЕ_ДО_ЦЕНТРА * СИЛА
Сила под углом
Если сила F направлена под углом θ к рычагу r, то M = r*F*sinθ, где θ это угол между рычагом и приложенной силой
Статическое равновесие
Для того чтобы объект находился в равновесии, должна равняться нулю не только сумма всех сил, но и сумма всех моментов силы вокруг любой точки. Для 2-хмерного случая с горизонтальными и вертикальными силами: сумма сил в двух измерениях ΣH=0, ΣV=0 и момент силы в третьем измерении ΣM=0.
Момент силы как функция от времени
Момент силы — производная по времени от момента импульса,
- ,
где L — момент импульса. Момент импульса твердого тела может быть описан через произведение момента инерции и угловой скорости.
- ,
То есть, если I постоянная, то
- ,
где α — угловое ускорение, измеряемое в радианах в секунду за секунду.
Отношение между моментом силы и мощностью
Если сила совершает действие на каком-либо расстоянии, то она совершает механическую работу. Также если момент силы совершает действие через угловое расстояние, он совершает работу.
- = МОМЕНТ_СИЛЫ * УГЛОВАЯ_СКОРОСТЬ
В системе СИ мощность измеряется в Ваттах, момент силы в ньютон-метрах, а УГЛОВАЯ СКОРОСТЬ в радианах в секунду.
Отношение между моментом силы и работой
- = МОМЕНТ_СИЛЫ * УГОЛ
В системе СИ работа измеряется в Джоулях, момент силы в Ньютон * метр, а УГОЛ в радианах.
Обычно известна угловая скорость в радианах в секунду и время действия МОМЕНТА .
Тогда совершенная МОМЕНТОМ силы РАБОТА рассчитывается как:
- = МОМЕНТ_СИЛЫ * *
Момент силы относительно точки
Если имеется материальная точка , к которой приложена сила , то момент силы относительно точки равен векторному произведению радиус-вектора , соединяющего точки и , на вектор силы :
.
Момент силы относительно оси
Моментом силы относительно оси называется момент проекции силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью.
Единицы измерения
Момент силы измеряется в ньютон-метрах. 1 Н·м — момент силы, который производит сила 1 Н на рычаг длиной 1 м. Сила приложена к концу рычага и направлена перпендикулярно ему.
Измерение момента
На сегодняшний день измерение момента силы осуществляется с помощью тензометрических, оптических и индуктивных датчиков нагрузки. В России при решении задач измерения момента в основном используется оборудование зарубежных производителей (HBM, Lorenz (Германия), Kyowa (Япония), Dacell (Корея) и ряда других).
Ссылки
См. также
Поперечная сила — внутренний силовой фактор

Привет! Спасибо, что изучаешь материалы нашего проекта – SoproMats. В этой статье расскажем ВСЕ о поперечной силе: что это такое, зачем она нужна, как вычисляется и в чем измеряется. В конце этой статьи, дадим ссылочки на материалы, которые связаны с поперечной силой. Например, дадим ссылку на урок по построению эпюры от этой величины, примеры решения задач и т.д.
Что такое поперечная сила?
Поперечная сила – это один из внутренних силовых факторов, возникающий в поперечных сечениях элементов конструкций, работающих на поперечный изгиб. Как правило, на поперечный изгиб работают балки, и именно одну из таких будем сегодня рассчитывать в нашем уроке.
Поперечная сила обозначается как Q и к этой букве приписывается индекс, совпадающий с названием координатной оси, которая параллельна поперечной силе. Обычно это ось y, поэтому дальше в статье и на сайте будем использовать обозначение поперечной силы — Qy.
Зачем нужно рассчитывать поперечную силу?
Эта величина используется при расчетах на прочность, в частности, при вычислении касательных напряжений, взять ту же формулу Журавского, где поперечная сила занимает важное место:

Построив эпюру, мы можем однозначно определить то сечение, где поперечная сила максимальная и рассчитать именно его. Сами по себе эти силы, за редкими исключениями, на прочность балок влияют незначительно. Например, для такой балки:

По эпюрам видно, что максимальная поперечная сила в сечении A равна 11,25 кН, а изгибающий момент, в сечении С, равен 12.66 кНм. Предположим, что балка имеет в сечении двутавр №16 по ГОСТ 8239-89. Выполнив расчет, получим: максимальное касательное напряжение, зависящее от поперечной силы равно 27.68 МПа. В свою очередь нормальное напряжение, от изгибающего момента, равно 116.11 МПа. Таким образом, напряжение от момента получилось в 4 раза больше.
Поэтому, при подборе сечения балок, расчет ведут только по нормальным напряжениям. После вычисления размеров, делают проверку с учетом касательных напряжений. И в большинстве случаев сечения проходят эту проверку. Исключениями могут быть расчетные схемы, у которых значительные нагрузки, а расстояния между опорами небольшое, либо имеется короткая консоль. Тем самым, получаются существенные расчетные значения касательных напряжений.
Так вот, очень важно при расчете эпюр определить максимальное нормальное напряжение. Если на балку действует распределенная нагрузка, как в нашем примере, то значение поперечной силы, в пределах одного участка, может меняться с положительного на отрицательное и наоборот. То есть эпюра, в таком случае, пересекает нулевую линию. А там, где это происходит, на эпюрах изгибающих моментов, находятся экстремальные значения, эти места еще называют точками перегиба эпюры. Как раз, эти значения, часто, оказываются теми самыми наибольшими величинами, которые идут в расчет. Но не всегда так! Однако, проверять экстремумы у эпюр моментов, нужно. И помочь в этом, может эпюра поперечных сил. В данном уроке, мы не будем вычислять экстремумы, так как это история для следующего урока про эпюры изгибающих моментов.
Статьи про поперечную силу:
Как построить эпюру поперечных сил? Прочитав этот материал, Вы узнаете, как это сделать тремя методами: подробным, упрощенным и быстрым. Все методики показаны на примере одной и той же балки.



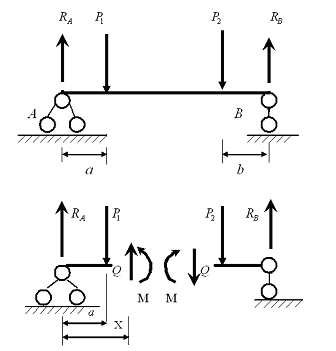
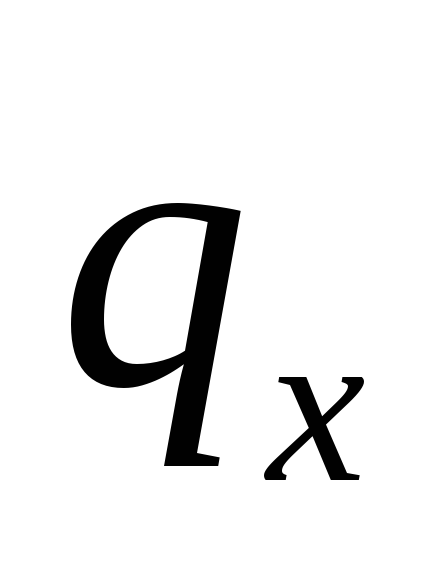 примем равномерно распределенной
примем равномерно распределенной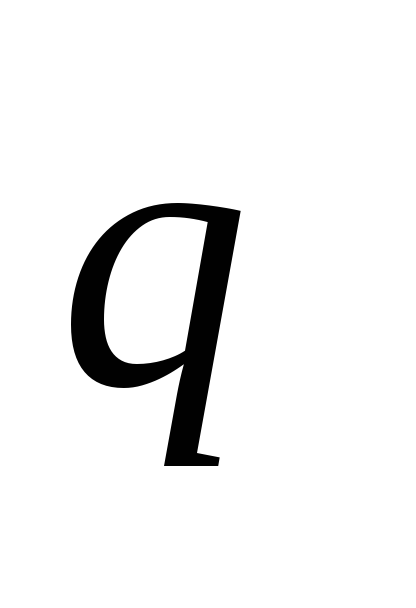
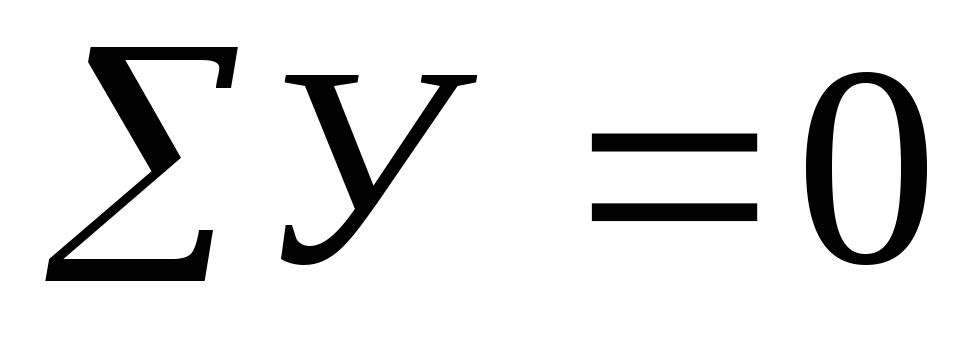 ;
;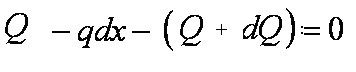
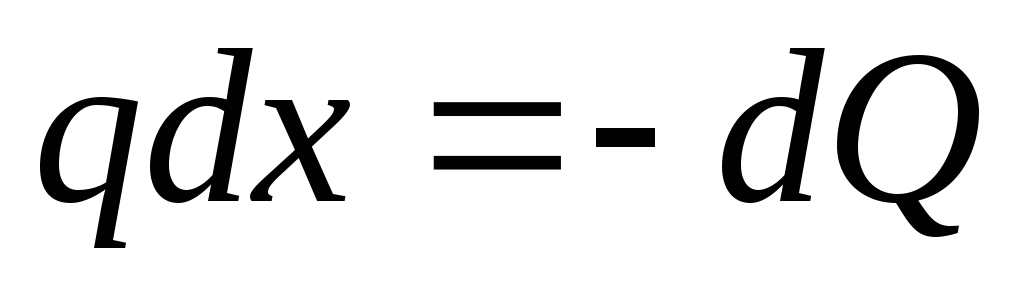 или
или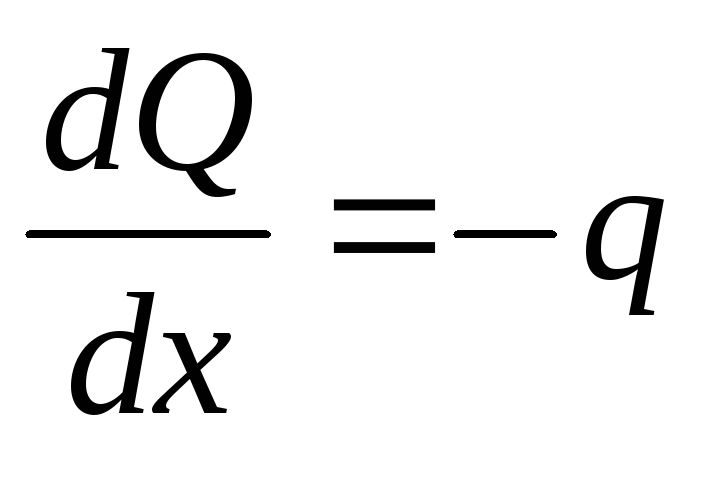
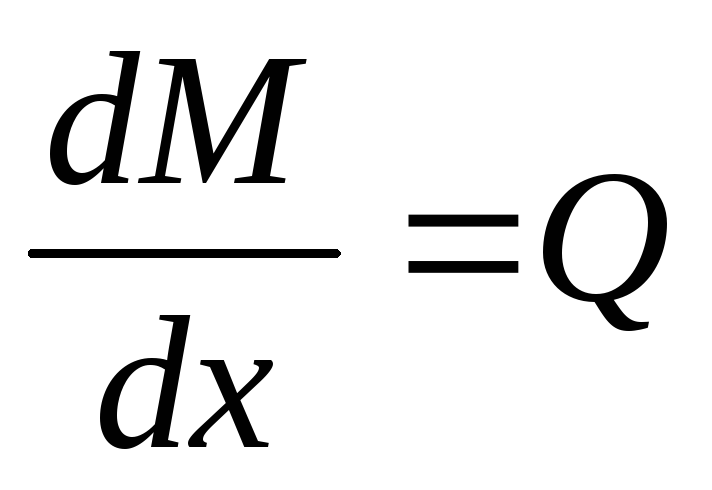
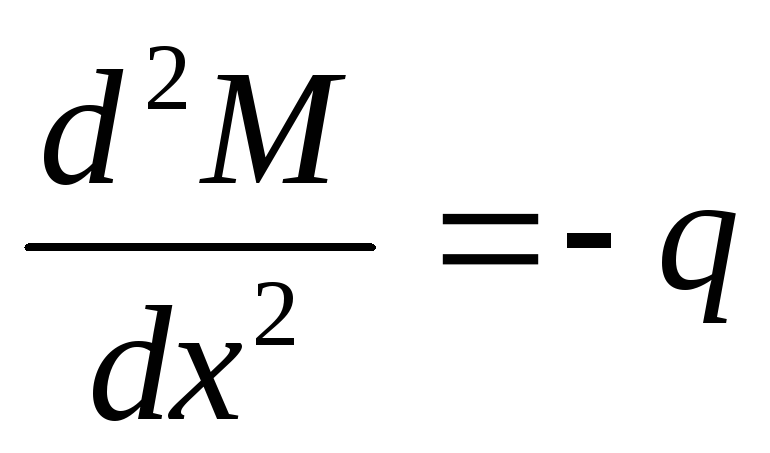
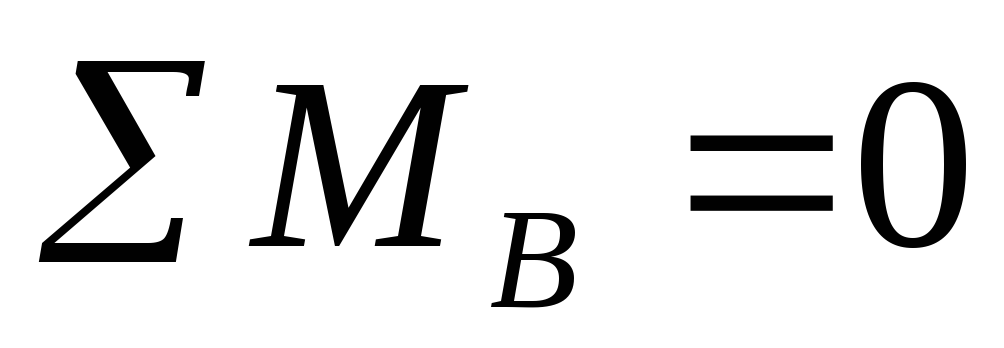 ;
;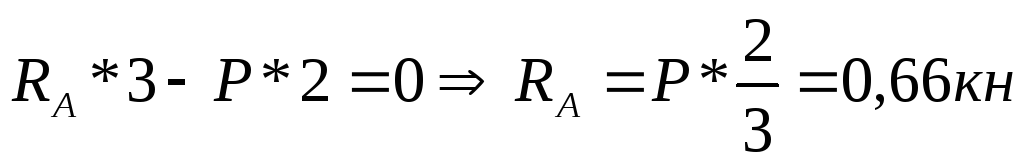
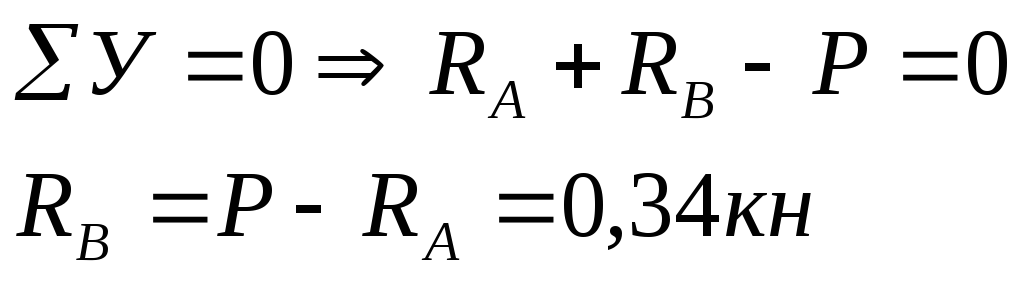
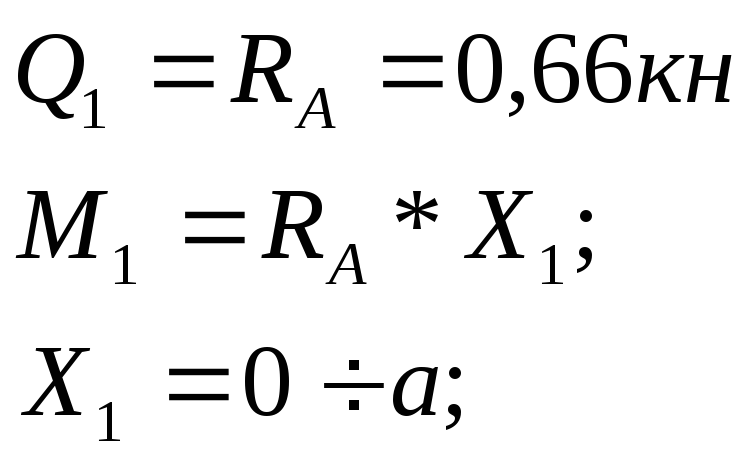

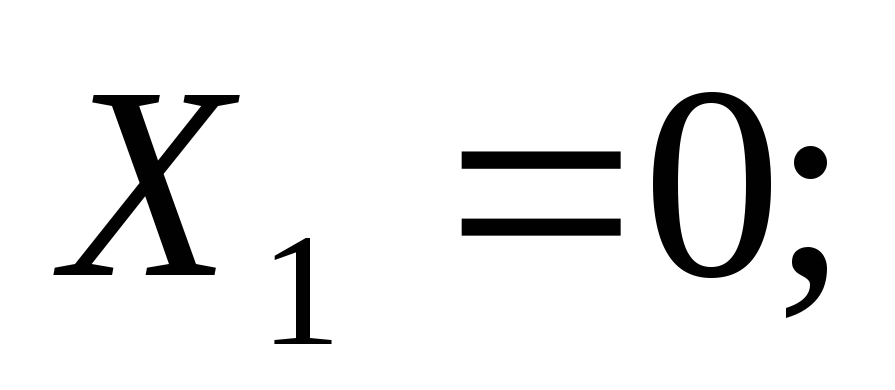
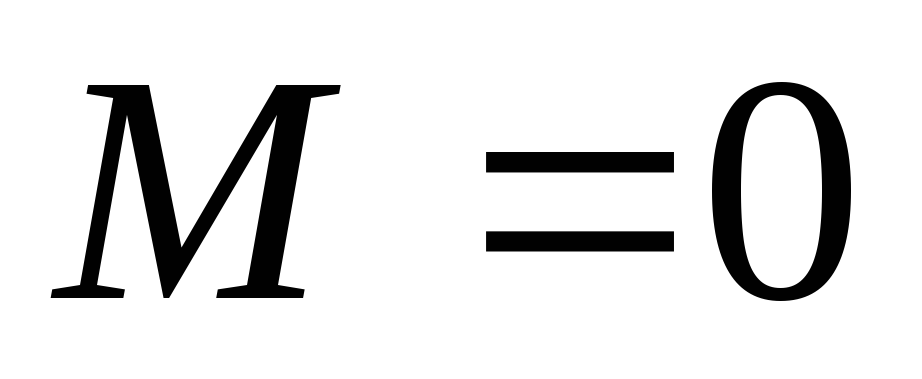
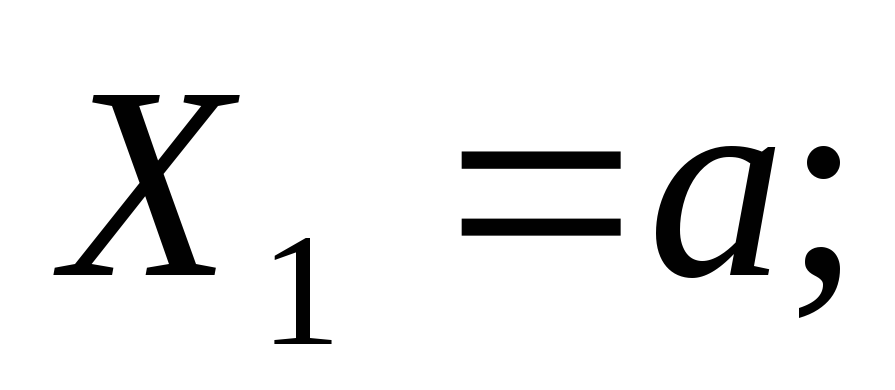
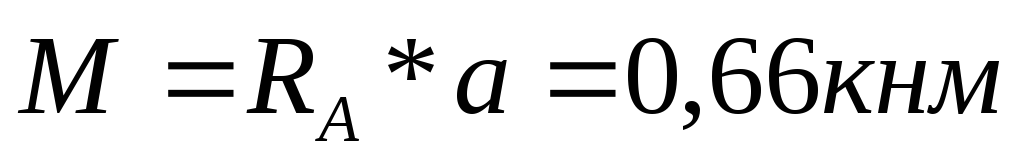
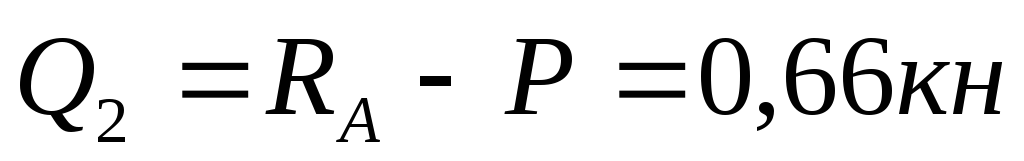
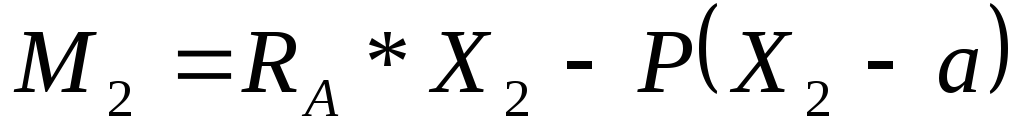
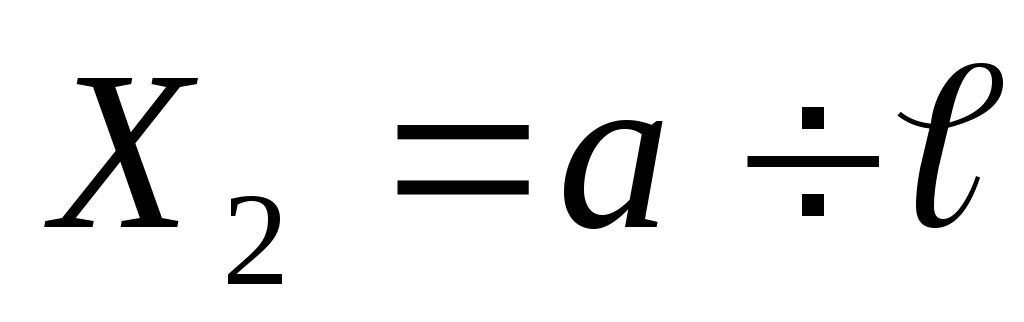
 при
при