формулы для стержня и колеса

Любые перемещения тел в пространстве, траектория которых является окружностью, предполагают знание не только угловой скорости, но и момента инерции для описания этого движения. Что такое момент инерции, а также чему он равен для стержня и колеса, ответит данная статья.

Вращение и момент инерции

Физическая величина, которая называется моментом инерции, обозначается, как правило, буквой I и появляется в физике при рассмотрении момента импульса материальной точки, которая вращается вокруг оси. Момент импульса L в скалярной форме записывается следующим выражением:

L = r*m*v

Здесь r — дистанция до оси материальной точки, m — ее масса, v — линейная скорость. Используя связь последней со скоростью угловой ω, получаем выражение:

L = r2*m*ω, где ω = v/r

Отвечая на вопрос о том, что такое момент инерции, следует сказать, что это величина I = r2*m. То есть она зависит от массы вращающегося объекта, быстро растет с увеличением расстояния до оси и измеряется в кг*м2.

Общее выражение для момента инерции

Введенная в предыдущем пункте формула для величины I справедлива, если размеры объекта пренебрежимо малы по сравнению с дистанцией до оси r (вращение Земли вокруг нашей звезды). Если же линейные размеры объекта становятся сравнимыми с расстоянием r, тогда необходимо для вычисления I пользоваться более общей формулой, которая дана ниже:

I = ∫m(r2*dm)

Из нее видно, что подынтегральное выражение представляет собой момент инерции материальной точки. Сумма же всех моментов от точек с массой dm составляет полный момент инерции I для всего тела.

Эта формула является мощным инструментом для определения I тела абсолютно любой формы. Согласно формуле величина I является аддитивной, то есть позволяет разбить тело на отдельные части, вычислить их моменты инерции, а затем сложить полученные результаты для получения величины I тела.

Физический смысл величины I

Зная, что такое момент инерции, необходимо сказать несколько слов о том, как его значение отражается на поведении и характеристиках вращения реальных объектов.

Большая величина I приводит к тому, что тело очень тяжело раскрутить вокруг оси. Для этого приходится выполнить значительную работу и приложить существенные усилия. Примером тела с большим I является автомобильный маховик — тяжелый металлический диск, жестко закрепленный на коленвале двигателя. Наоборот, если величина I системы невелика, то ее можно быстро раскрутить и так же быстро и легко остановить. Примером для этого случая является алюминиевый обод велосипедного колеса.

Приведенное выше обсуждение говорит о том, что момент инерции характеризуется инерционностью процесса вращения, то есть выполняет ту же самую роль, что и масса тела при приложении к ней силы с целью придания ускорения.

Отличие массы и момента инерции заключается не только в единицах измерения, но и в том, что последний является функцией вращательной системы, а не только геометрии тела и его массы.

Момент инерции относительно оси вращения, пересекающей центр масс стержня

Рассмотрим пример использования интегральной формулы для решения реальных задач. Первым делом решим простую проблему: имеется стержень тонкий длиной l и массой m. Вращения оси проходит перпендикулярно этому стержню через центр массы объекта. Необходимо определить величину I для этой системы.

Выпишем общую формулу для инерции момента стержня относительно оси, имеем:

I = ∫m(r2*dm)

Поскольку ось перпендикулярна рассматриваемому телу, и сам стержень имеет бесконечно малую толщину, то можно мысленно разрезать его на тонкие слои плоскостями, параллельными оси. В таком случае получаем, что элемент массой dm может быть представлен следующим равенством:

dm = ρ*S*dr

Здесь ρ — плотность материала, S — поперечное сечение, которое является постоянной величиной и стремится к нулю (стержень бесконечно тонкий). Подставим это выражение в общую формулу:

I = ρ*S*∫+l/2-l/2(r2*dr)

Заметим, что подставленные пределы интегрирования по r соответствуют условию задачи (ось делит стержень на две равные части). Выполняя интегрирование, получаем:

I = ρ*S*(r3/3)|+l/2-l/2 = m*l2/12, где m = ρ*S*l

Таким образом, момент инерции стержня тонкого, когда ось проходит через центр масс, в 12 раз меньше такового для материальной точки той же массы, находящейся на расстоянии l от оси.

Величина I для стержня с осью вращения на конце объекта

Рассмотрим, что такое момент инерции, в несколько иной ситуации. Имеем тот же самый объект (тонкий стержень), но теперь ось проходит через конец. Как изменится момент инерции в этом случае? Применяем тот же метод разбиения стержня и последующего интегрирования, как в предыдущем пункте, получаем:

I = ρ*S*∫l0(r2*dr)

Заметим, что изменились лишь пределы интегрирования. Решением будет следующее равенство:

I = m*l2/3

Выражение показывает, что тот же самый стержень будет обладать в 4 раза большим моментом инерции (труднее раскрутить), если ось вращения переместить с его центра на край.

Рассматривая решение этих двух задач, следует сделать важный вывод: при расчете величины I нельзя сводить всю массу объекта в его центр и выполнять расчет, как для материальной точки. Вычисление следует проводить только с использованием интегрального выражения.

Значение I для колеса со спицами

Момент инерции колеса можно определить, используя свойство аддитивности рассматриваемой величины. Для этого мысленно разберем колесо на отдельные части, которые представляют собой спицы и обод. Поскольку спица — это тонкий стержень, и ось ее вращения проходит через конец, то для нее справедлива формула, полученная в предыдущем пункте.

Что касается обода колеса, то его момент инерции аналогичен таковому для материальной точки, находящейся на расстоянии радиуса колеса и имеющей массу обода.

Складывая моменты инерции всех элементов, получаем:

I = n*mc*r2/3 + mo*r2

Здесь mc и mo — массы спицы и обода, соответственно, n — число спиц. Если все спицы весят намного меньше обода, тогда момент инерции колеса будет равен:

I =mo*r2, если n*mc

Знание величины I для колеса является важным при расчете скорости угловой и момента импульса вращения колес любого транспортного средства (автомобиля, велосипеда).

формулы для стержня и колеса :: SYL.ru

Любые перемещения тел в пространстве, траектория которых является окружностью, предполагают знание не только угловой скорости, но и момента инерции для описания этого движения.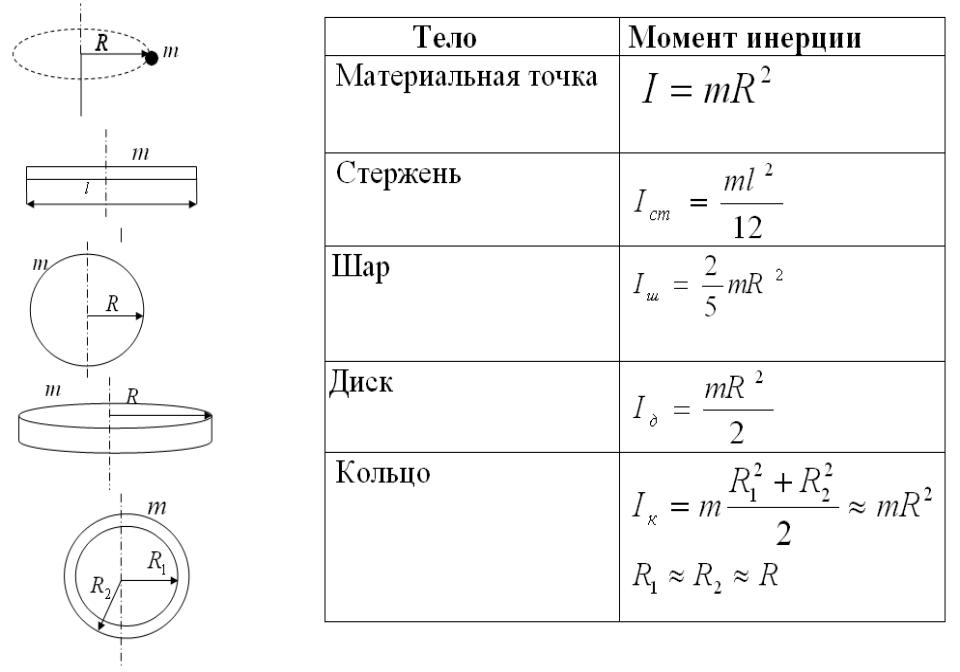 Что такое момент инерции, а также чему он равен для стержня и колеса, ответит данная статья.

Вращение и момент инерции

Физическая величина, которая называется моментом инерции, обозначается, как правило, буквой I и появляется в физике при рассмотрении момента импульса материальной точки, которая вращается вокруг оси. Момент импульса L в скалярной форме записывается следующим выражением:

L = r*m*v

Здесь r — дистанция до оси материальной точки, m — ее масса, v — линейная скорость. Используя связь последней со скоростью угловой ω, получаем выражение:

L = r²*m*ω, где ω = v/r

Отвечая на вопрос о том, что такое момент инерции, следует сказать, что это величина I = r²*m. То есть она зависит от массы вращающегося объекта, быстро растет с увеличением расстояния до оси и измеряется в кг*м².

Общее выражение для момента инерции

Введенная в предыдущем пункте формула для величины I справедлива, если размеры объекта пренебрежимо малы по сравнению с дистанцией до оси r (вращение Земли вокруг нашей звезды). Если же линейные размеры объекта становятся сравнимыми с расстоянием r, тогда необходимо для вычисления I пользоваться более общей формулой, которая дана ниже:

I = ∫_m(r²*dm)

Из нее видно, что подынтегральное выражение представляет собой момент инерции материальной точки. Сумма же всех моментов от точек с массой dm составляет полный момент инерции I для всего тела.

Эта формула является мощным инструментом для определения I тела абсолютно любой формы. Согласно формуле величина I является аддитивной, то есть позволяет разбить тело на отдельные части, вычислить их моменты инерции, а затем сложить полученные результаты для получения величины I тела.

Физический смысл величины I

Зная, что такое момент инерции, необходимо сказать несколько слов о том, как его значение отражается на поведении и характеристиках вращения реальных объектов.

Большая величина I приводит к тому, что тело очень тяжело раскрутить вокруг оси. Для этого приходится выполнить значительную работу и приложить существенные усилия. Примером тела с большим I является автомобильный маховик — тяжелый металлический диск, жестко закрепленный на коленвале двигателя. Наоборот, если величина I системы невелика, то ее можно быстро раскрутить и так же быстро и легко остановить. Примером для этого случая является алюминиевый обод велосипедного колеса.

Приведенное выше обсуждение говорит о том, что момент инерции характеризуется инерционностью процесса вращения, то есть выполняет ту же самую роль, что и масса тела при приложении к ней силы с целью придания ускорения.

Отличие массы и момента инерции заключается не только в единицах измерения, но и в том, что последний является функцией вращательной системы, а не только геометрии тела и его массы.

Момент инерции относительно оси вращения, пересекающей центр масс стержня

Рассмотрим пример использования интегральной формулы для решения реальных задач. Первым делом решим простую проблему: имеется стержень тонкий длиной l и массой m. Вращения оси проходит перпендикулярно этому стержню через центр массы объекта. Необходимо определить величину I для этой системы.

Выпишем общую формулу для инерции момента стержня относительно оси, имеем:

I = ∫_m(r²*dm)

Поскольку ось перпендикулярна рассматриваемому телу, и сам стержень имеет бесконечно малую толщину, то можно мысленно разрезать его на тонкие слои плоскостями, параллельными оси. В таком случае получаем, что элемент массой dm может быть представлен следующим равенством:

dm = ρ*S*dr

Здесь ρ — плотность материала, S — поперечное сечение, которое является постоянной величиной и стремится к нулю (стержень бесконечно тонкий). Подставим это выражение в общую формулу:

I = ρ*S*∫^+l/2_-l/2(r²*dr)

Заметим, что подставленные пределы интегрирования по r соответствуют условию задачи (ось делит стержень на две равные части). Выполняя интегрирование, получаем:

I = ρ*S*(r³/3)|^+l/2_-l/2 = m*l²/12, где m = ρ*S*l

Таким образом, момент инерции стержня тонкого, когда ось проходит через центр масс, в 12 раз меньше такового для материальной точки той же массы, находящейся на расстоянии l от оси.

Величина I для стержня с осью вращения на конце объекта

Рассмотрим, что такое момент инерции, в несколько иной ситуации. Имеем тот же самый объект (тонкий стержень), но теперь ось проходит через конец. Как изменится момент инерции в этом случае? Применяем тот же метод разбиения стержня и последующего интегрирования, как в предыдущем пункте, получаем:

I = ρ*S*∫^l₀(r²*dr)

Заметим, что изменились лишь пределы интегрирования. Решением будет следующее равенство:

I = m*l²/3

Выражение показывает, что тот же самый стержень будет обладать в 4 раза большим моментом инерции (труднее раскрутить), если ось вращения переместить с его центра на край.

Рассматривая решение этих двух задач, следует сделать важный вывод: при расчете величины I нельзя сводить всю массу объекта в его центр и выполнять расчет, как для материальной точки. Вычисление следует проводить только с использованием интегрального выражения.

Значение I для колеса со спицами

Момент инерции колеса можно определить, используя свойство аддитивности рассматриваемой величины. Для этого мысленно разберем колесо на отдельные части, которые представляют собой спицы и обод. Поскольку спица — это тонкий стержень, и ось ее вращения проходит через конец, то для нее справедлива формула, полученная в предыдущем пункте.

Что касается обода колеса, то его момент инерции аналогичен таковому для материальной точки, находящейся на расстоянии радиуса колеса и имеющей массу обода.

Складывая моменты инерции всех элементов, получаем:

I = n*m_c*r²/3 + m_o*r²

Здесь m_c и m_o — массы спицы и обода, соответственно, n — число спиц. Если все спицы весят намного меньше обода, тогда момент инерции колеса будет равен:

I =m_o*r², если n*m_c<<m_o

Знание величины I для колеса является важным при расчете скорости угловой и момента импульса вращения колес любого транспортного средства (автомобиля, велосипеда).

Вращательная инерция – College Physics

Глава 10 Вращательное движение и угловой момент

Резюме

• Понять взаимосвязь между силой, массой и ускорением.
• Изучите вращающее действие силы.
• Изучите аналогию между силой и крутящим моментом, массой и моментом инерции, линейным ускорением и угловым ускорением.

Если вы когда-нибудь крутили велосипедное колесо или толкали карусель, вы знаете, что для изменения угловой скорости необходима сила, как показано на рис. 1. На самом деле ваша интуиция надежно предсказывает многие из задействованных факторов . Например, мы знаем, что дверь открывается медленно, если мы прислоняем ее слишком близко к петлям. Кроме того, мы знаем, что чем массивнее дверь, тем медленнее она открывается. Первый пример подразумевает, что чем дальше приложена сила от оси вращения, тем больше угловое ускорение; другое следствие состоит в том, что угловое ускорение обратно пропорционально массе. Эти отношения должны казаться очень похожими на знакомые отношения между силой, массой и ускорением, воплощенные во втором законе движения Ньютона. На самом деле существуют точные вращательные аналоги как силы, так и массы.

Рисунок 1. Для вращения велосипедного колеса требуется сила. Чем больше сила, тем больше угловое ускорение. Чем массивнее колесо, тем меньше угловое ускорение. Если надавить на спицу ближе к оси, угловое ускорение будет меньше.

Чтобы установить точное соотношение между силой, массой, радиусом и угловым ускорением, рассмотрим, что произойдет, если мы приложим силу [латекс]{F}[/латекс] к точечной массе [латекс]{м}[/латекс], которая находится на расстоянии [латекс]{r}[/латекс] от точки вращения, как показано на рисунке 2. Поскольку сила перпендикулярна [латекс]{r},[/латекс] ускорение [латекс]{а= \frac{F}{m}}[/latex] получается в направлении [latex]{F}.[/latex] Мы можем изменить это уравнение так, что [latex]{F=ma}[/latex] и затем ищите способы связать это выражение с выражениями для вращательных величин. Заметим, что [latex]{a=r\omega},[/latex] и подставим это выражение в [latex]{F=ma},[/latex], получив 92}[/latex] называется

вращательной инерцией или моментом инерции точки массы [латекс]{m}[/латекс] на расстоянии [латекс]{r}[/латекс] от центра вращения .

Рис. 2. Объект поддерживается горизонтальным столом без трения и прикреплен к точке поворота шнуром, создающим центростремительную силу. Сила F приложена к объекту перпендикулярно радиусу r , заставляя его ускоряться относительно точки вращения. Сила направлена ​​перпендикулярно р .

ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ: ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Динамика вращательного движения полностью аналогична линейной или поступательной динамике. Динамика занимается силой и массой и их влиянием на движение. Для вращательного движения мы найдем прямые аналоги силы и массы, которые ведут себя именно так, как мы и ожидали, исходя из нашего предыдущего опыта.

Прежде чем мы сможем рассмотреть вращение чего-либо, кроме точечной массы, подобной той, что изображена на рис. 2, мы должны распространить идею инерции вращения на все типы объектов. Чтобы расширить наше понятие инерции вращения, мы определяем 92},[/latex], где [latex]{M}[/latex] — его общая масса, а [latex]{R}[/latex] — его радиус.

2}[/latex] ), как и следовало ожидать. из его определения.

Общее соотношение между крутящим моментом, моментом инерции и угловым ускорением составляет

.

[латекс] {\ текст {нетто} \ тау = I \ альфа} [/ латекс]

или

[латекс] {\ альфа \: =} [/латекс] [латекс] {\ гидроразрыва {\ текст {сеть} \ тау} {I}}, [/латекс]

, где net [латекс] {\ тау} [/латекс] — это общий крутящий момент от всех сил относительно выбранной оси. Для простоты мы будем рассматривать только крутящие моменты, создаваемые силами в плоскости вращения. Такие крутящие моменты бывают положительными или отрицательными и складываются как обычные числа. Соотношение в [latex]{\ tau = I \ alpha}, \: {\ alpha = \ frac {\ text {net} \ tau} {I}} [/latex] является вращательным аналогом второго закона Ньютона и представляет собой весьма общеприменимо. Это уравнение действительно справедливо для

любой крутящий момент, примененный к любому объекту относительно любой оси .

Как и следовало ожидать, чем больше крутящий момент, тем больше угловое ускорение. Например, чем сильнее ребенок толкает карусель, тем быстрее она разгоняется. Кроме того, чем массивнее карусель, тем медленнее она разгоняется при том же крутящем моменте. Основное соотношение между моментом инерции и угловым ускорением заключается в том, что чем больше момент инерции, тем меньше угловое ускорение. Но есть дополнительный нюанс. Момент инерции зависит не только от массы тела, но и от его

распределение массы относительно оси, вокруг которой он вращается. Например, будет намного легче разогнать карусель, полную детей, если они будут стоять близко к ее оси, чем если все они будут стоять на внешнем краю. Масса одинакова в обоих случаях; но момент инерции намного больше, когда дети находятся на краю.

ЭКСПЕРИМЕНТ ДЛЯ ДОМА

Вырежьте круг радиусом около 10 см из плотного картона. Рядом с краем круга напишите числа от 1 до 12, как часы на циферблате. Расположите круг так, чтобы он мог свободно вращаться вокруг горизонтальной оси, проходящей через его центр, как колесо.

(Вы можете свободно прибить круг к стене.) Держите круг неподвижно и, расположив цифру 12 вверху, прикрепите кусок синей замазки (клейкий материал, используемый для крепления постеров к стенам) к цифре 3. Какого размера глыба должна быть, чтобы просто вращать круг? Опишите, как можно изменить момент инерции окружности. Как это изменение повлияет на количество синей замазки, необходимое под номером 3, чтобы просто повернуть круг? Измените момент инерции круга, а затем попробуйте повернуть круг, используя разное количество синей замазки. Повторите этот процесс несколько раз.

СТРАТЕГИЯ РЕШЕНИЯ ЗАДАЧ ДЛЯ ДИНАМИКИ ВРАЩЕНИЯ

1. Изучите ситуацию, чтобы определить, что крутящий момент и масса участвуют во вращении . Нарисуйте тщательный набросок ситуации.
2. Определить интересующую систему .
3. Нарисуйте свободную диаграмму тела . То есть нарисуйте и обозначьте все внешние силы, действующие на интересующую вас систему.
4. Применить [латекс] {\ текст {сеть} \ тау = I \ альфа}, \: {\ альфа = \ гидроразрыва {\ текст {сетка} \ тау {I}}, [/латекс] вращательный эквивалент второго закона Ньютона для решения задачи . Необходимо соблюдать осторожность, чтобы использовать правильный момент инерции и учитывать крутящий момент вокруг точки вращения.
5. Как всегда, проверьте решение, чтобы убедиться, что оно разумно .

ВЫПОЛНЕНИЕ СОЕДИНЕНИЙ

В статике чистый крутящий момент равен нулю, а угловое ускорение отсутствует. При вращательном движении чистый крутящий момент является причиной углового ускорения, точно так же, как во втором законе движения Ньютона для вращения.

Рисунок 3. Некоторые инерции вращения.

Пример 1. Расчет влияния распределения массы на карусель

Рассмотрим отца, толкающего игровую карусель на рис. 4. Он прикладывает силу 250 Н к краю карусели весом 50,0 кг. круговой, который имеет радиус 1,50 м. Вычислите угловое ускорение, создаваемое (а), когда на карусели никого нет, и (б), когда ребенок массой 18,0 кг сидит на расстоянии 1,25 м от центра. Считайте саму карусель однородным диском с пренебрежимо малым тормозящим трением.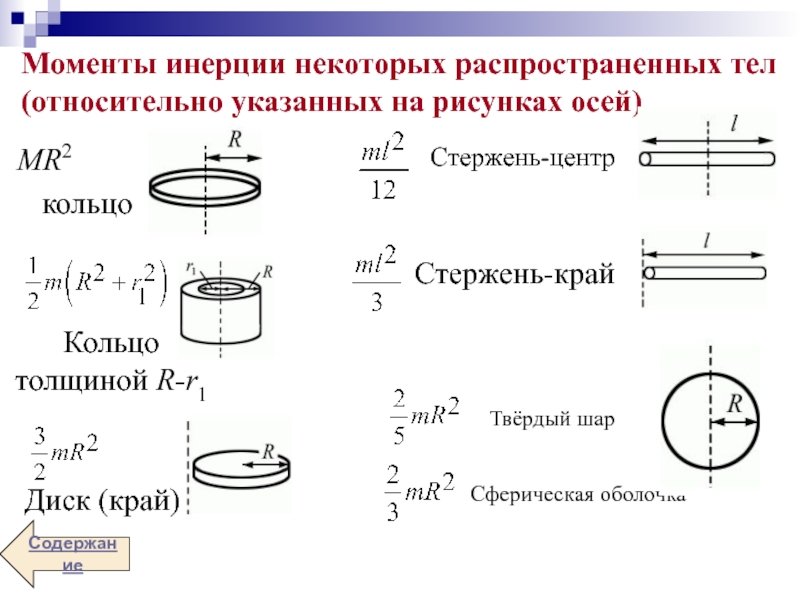

Рис. 4. Отец толкает игровую карусель за ее край и перпендикулярно ее радиусу для достижения максимального крутящего момента.

Стратегия

Угловое ускорение определяется непосредственно выражением :=}[/latex] [latex]{\frac{\tau}{I}}.[/latex]

Чтобы найти [латекс]{\alpha},[/latex], мы должны сначала вычислить крутящий момент [ латекс]{\тау}[/латекс] (одинаковый в обоих случаях) и момент инерции [латекс]{I}[/латекс] (больше во втором случае). Чтобы найти крутящий момент, заметим, что приложенная сила перпендикулярна радиусу, а трением можно пренебречь, так что 92}}.[/latex]

Решение для (b)

Мы ожидаем, что угловое ускорение системы будет меньше в этой части, потому что момент инерции больше, когда ребенок находится на карусели -круглый. Чтобы найти общий момент инерции [latex]{I},[/latex], мы сначала находим момент инерции ребенка [latex]{I_{\textbf{c}}}[/latex], считая ребенка эквивалентным к точечной массе на расстоянии 1,25 м от оси.

2}.[/латекс] 92}}.[/latex]

Обсуждение

Угловое ускорение меньше, когда ребенок находится на карусели, чем когда карусель пуста, как и ожидалось. Найденные угловые ускорения довольно велики, отчасти из-за того, что трение считалось пренебрежимо малым. Если бы, например, отец продолжал толкать перпендикулярно в течение 2,00 с, он придал бы карусели угловую скорость 13,3 рад/с, когда она пуста, и только 8,89 рад/с, когда на ней находится ребенок. В пересчете на обороты в секунду эти угловые скорости составляют 2,12 об/с и 1,41 об/с соответственно. В первом случае отец будет бежать со скоростью около 50 км/ч. Летние Олимпийские игры, вот и он! Подтверждение этих цифр оставлено читателю в качестве упражнения.

• Чем дальше приложена сила от оси вращения, тем больше угловое ускорение; угловое ускорение обратно пропорционально массе.
• Если мы приложим силу [латекс]{F}[/латекс] к точечной массе [латекс]{м}[/латекс], которая находится на расстоянии [латекс]{r}[/латекс] от точки вращения и поскольку сила перпендикулярна [латексу]{r},[/латекс] ускорение [латекс]{а = F/m}[/латекс] получается в направлении [латекса]{F}. [/латекс] Мы можем изменить это уравнение так, что

  [латекс]{F = ма},[/латекс]

  , а затем искать способы связать это выражение с выражениями для вращательных величин. Заметим, что [latex]{a = r\alpha},[/latex] и подставим это выражение в [latex]{F=ma},[/latex], что даст

  [латекс]{F=г-н\альфа}[/латекс]

• Крутящий момент — это вращающая способность силы. В этом случае, поскольку [латекс]{F}[/латекс] перпендикулярен [латексу]{r},[/латекс] крутящий момент будет просто [латекс]{\тау=rF}.[/латекс] Если мы умножим оба части уравнения выше на [латекс]{r},[/латекс] мы получаем крутящий момент в левой части. То есть, 92}.[/латекс]

• Общая взаимосвязь между крутящим моментом, моментом инерции и угловым ускорением такова:

  [латекс] {\ тау = I \ альфа} [/ латекс]

  или

  [латекс] {\ альфа =} [/ латекс] [латекс] {\ гидроразрыва {\ текст {сеть} \ тау} {I}} [/ латекс]

крутящий момент

поворотная эффективность силы

инерция вращения

сопротивление изменению вращения. Чем больше инерция вращения у объекта, тем труднее его вращать 92}[/latex] и, поскольку любой объект может быть построен из набора точечных масс, это соотношение является основой для всех других моментов инерции

 

Нахождение момента инерции колеса Vex с помощью теоремы о параллельных осях

Новая игра Vex «ничего, кроме сетки» может включать в себя вращающиеся стрелковые колеса. Мы знаем, что если бы вся масса колеса располагалась на его ободе, то момент инерции относительно оси его вращения (I_rim) был бы равен

92 * m   , где m — масса колеса, а r — радиус колеса. Но мы знаем, что колеса на самом деле имеют массу, которая неравномерно распределена по радиусу, поэтому момент инерции I_wheel будет меньше, чем I_rim.

Простой эксперимент для определения I_wheel, если мы знаем его массу.

Мы можем определить I_wheel экспериментально, используя теорему о параллельных осях и динамику маятника.

Теорема о параллельной оси гласит, что любой объект, который вращается вокруг оси, параллельной и на расстоянии d от оси, проходящей через центр тяжести объекта, добавит величину =  m*d^2 к моменту инерции относительно его центроид.