Чем больше будет масса бусинки, тем труднее будет сдвинуть ее, это логично. Но почему момент инерции материальной точки растет по мере удаления от оси вращения?
Представьте себя лилипутом, который по какой-то неведомой причине решил сообщить бусинке из примера наверху угловую скорость \omega. Не щадя себя, вы разогнались от нуля до некоторой скорости v, после чего, достигнув своей цели, остановились, позволив шарику двигаться дальше.
Теперь увеличим длину практически невесомого стержня в два раза и проделаем тот же самый мысленный эксперимент.
Даже если предположить, что вы не упадете замертво где-то на середине дистанции и сможете бежать с таким же ускорением, как и в первом случае, вы все равно почувствуете разницу. Чем дальше шарик будет находиться от оси вращения, тем труднее будет изменить его угловую скорость, соответственно, тем больше будет его момент инерции.
Кстати, благодаря формуле, представленной наверху, сразу становится понятно, для чего нужно соблюдение всех этих странных теоретических требований.
Вы можете сказать: «Для чего нам вообще нужен момент инерции материальной точки? Все равно, безразмерных тел в природе не существует».
Вы правы. Материальная точка – это математическая абстракция. И все-таки есть случаи, когда эта модель работает с хорошей степенью точности. Например, когда вы изучаете движение Луны вокруг Земли, вы запросто можете представить Луну в виде материальной точки и найти ее момент инерции при помощи приведенной выше формулы.
Но, конечно, вращаться могут не только материальные точки, но и другие тела. Например, можно представить, что мы имеем дело не с невесомой палочкой, а с железным стержнем массой m. 2
2
Теперь больше массы будет находиться ближе к оси вращения, отсюда и уменьшение момента инерции.
Если вас когда-нибудь спросят, чему равен момент инерции такого-то тела, знайте, что это хитрый вопрос. Значение момента инерции, помимо всего прочего, зависит от расположения оси вращения.
Момент инерции твердого тела относительно постоянной оси вращения. Определение.
Момент инерции материальной точки относительно оси вращения определяется как величина, равная произведению массы материальной точки на квадрат расстояния от этой точки до оси вращения: .
Момент инерции твердого тела
относительно оси вращения – мера
инертности твердого тела во вращательном
движении (аналог массы в поступательном
движении), определяется как величина,
равная сумме моментов инерции достаточно
малых фрагментов твердого тела. Достаточно
малым фрагментом твердого тела является
фрагмент, размеры которого малы по
сравнению с расстоянием от фрагмента
до оси вращения.
а момент инерции всего твердого тела относительно постоянной оси вращения, по формуле: .
Для вычисления интеграла необходимо свести подинтегральное выражение к одной переменной величине. Это достигается, в частности, учетом как характера распределения массы тела по его объему, так и симметрии формы тела.
Момент инерции твердого тела относительно постоянной оси вращения. Теорема о параллельных осях (теорема Штейнера).
Теорема связывает момент инерции относительно произвольной оси с моментом инерции относительно параллельной ей оси, проходящей через центр масс твердого тела: . Здесь m — масса тела, a – расстояние между осями.
Момент инерции твердого
тела относительно постоянной оси
вращения. Теорема
о взаимно перпендикулярных осях.
Момент инерции плоского тела относительно произвольной оси Z, перпендикулярной его плоскости, равен сумме моментов инерции относительно двух взаимно перпендикулярных осей
Уравнение вращательного движения твердого тела вокруг постоянной оси.
Уравнение записано в проекции на совмещенную с осью вращения координатную ось Z.
СЕМИНАР 5 МЕХАНИКА ТВЕРДОГО ТЕЛА. ЗАКОНЫ СОХРАНЕНИЯ.
Момент импульса твердого тела.
Момент импульса твердого тела относительно неподвижной оси Z, или проекция вектора момента импульса на координатную ось Z, совпадающую с осью вращения, равен произведению момента инерции тела относительно этой оси вращения на проекцию вектора угловой скорости на координатную ось
Сохранение момента импульса системы
твердых тел.
Для того чтобы момент импульса системы тел относительно некоторой оси сохранялся, необходимо чтобы суммарный момент внешних сил относительно этой оси был равен нулю.
Собственный момент импульса твердого тела относительно постоянной оси вращения.
-вычисляется относительно системы отсчета центра масс.
Кинетическая энергия твердого тела вращающегося вокруг постоянной оси.
Кинетическая энергия твердого тела в случае плоского движения.
В этом случае кинетическая энергия складывается из собственной энергии вращения вокруг оси, проходящей через центр масс и энергии поступательного движения со скоростью центра масс.
СЕМИНАР 6 ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ. Собственные колебания
Гармоническими колебаниями
материальной точки называется движение,
при котором смещение x от положения устойчивого равновесия
зависит от времени по закону
,
или
.
Здесь .
Определение амплитуды смещения и начальной фазы колебаний смещения через начальное смещение и начальную скорость.
Если используется закон движения в виде , то .
Если же закон движения имеет вид , то .
Определение частоты или периода колебаний смещения колеблющегося тела от положения устойчивого равновесия.
Сначала убеждаемся в том, что у рассматриваемого тела или системы тел имеется положение устойчивого равновесия. Для этого положения записываем условие статики. Далее используем уравнение движения или закон сохранения механической энергии. В итоге приходим к уравнению гармонического осциллятора
Затухающие колебания Уравнение затухающих колебаний
.
Здесь , .
Решение уравнения .
Амплитуда затухающих
колебаний . Коэффициент
затухания и циклическая частота
затухающих колебаний .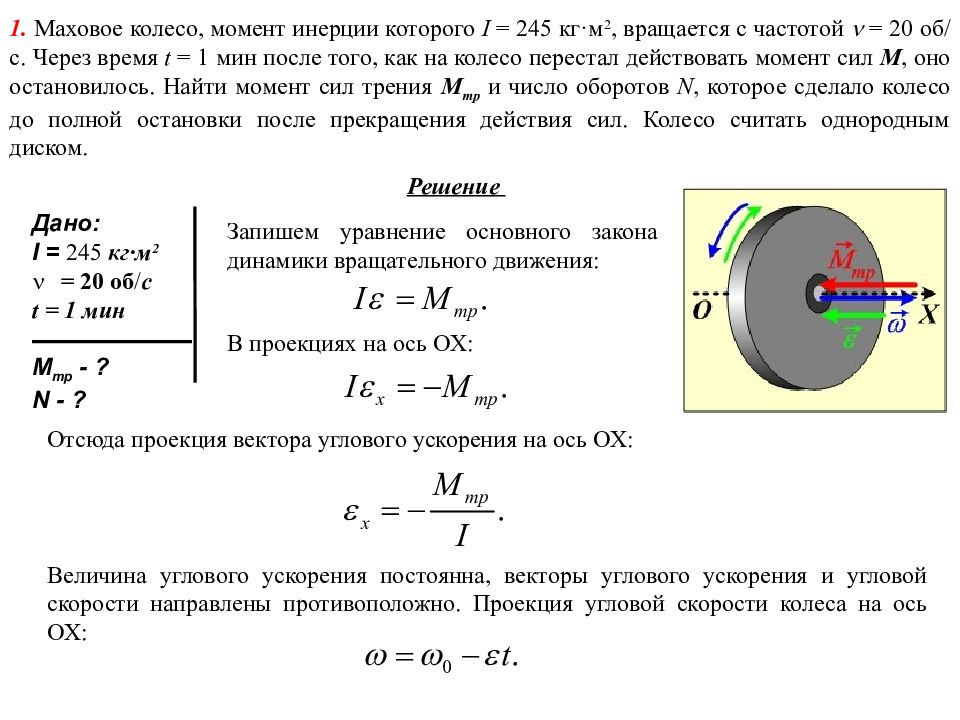 Время релаксации
,
декремент
и логарифмический
декремент
.
Число колебаний за время релаксации
.
Время релаксации
,
декремент
и логарифмический
декремент
.
Число колебаний за время релаксации
.
Добротность . Зависимость энергии затухающих колебаний от времени .
Вынужденные колебания
Уравнение вынужденных колебаний
Решение уравнения .
Амплитуда вынужденных колебаний
Тангенс разности фаз колебаний вынуждающей силы и колебаний смещения материальной точки от положения равновесия .
Частота колебаний вынуждающей силы, при которой наблюдается резонанс смещения .
Добротность, как отношение смещения при резонансе к смещению при постоянной вынуждающей силе .
Момент инерции и кинетическая энергия вращения – University Physics Volume 1
Вращение с фиксированной осью
Цели обучения
К концу этого раздела вы сможете:
- Описывать различия между вращательной и поступательной кинетической энергией
- Определить физическую концепцию момента инерции в терминах распределения массы относительно оси вращения
- Объясните, как момент инерции твердых тел влияет на их кинетическую энергию вращения
- Использование закона сохранения механической энергии для анализа систем, подвергающихся как вращению, так и поступательному перемещению
- Расчет угловой скорости вращающейся системы при наличии потерь энергии из-за неконсервативных сил
До сих пор в этой главе мы работали с кинематикой вращения: описанием движения вращающегося твердого тела с фиксированной осью вращения.
Вращательная кинетическая энергия
Любой движущийся объект обладает кинетической энергией. Мы знаем, как вычислить это для тела, совершающего поступательное движение, но как насчет твердого тела, совершающего вращательное движение? Это может показаться сложным, потому что каждая точка твердого тела имеет разную скорость. Однако мы можем использовать угловую скорость, которая одинакова для всего твердого тела, чтобы выразить кинетическую энергию вращающегося объекта. (Рисунок) показывает пример очень энергичного вращающегося тела: электрический точильный камень, приводимый в движение двигателем. Когда точильный камень выполняет свою работу, летят искры, возникают шум и вибрация. Эта система обладает значительной энергией, частично в виде тепла, света, звука и вибрации.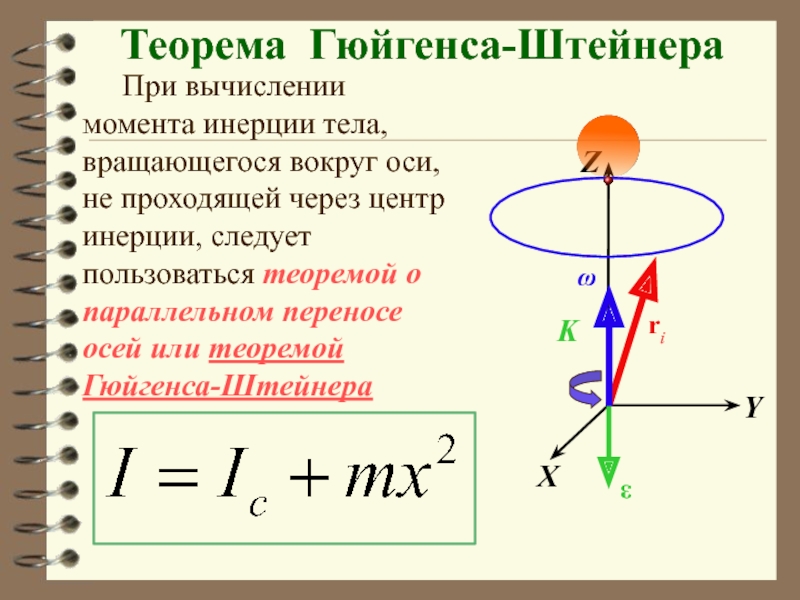 Однако большая часть этой энергии находится в форме кинетической энергии вращения. 9{2}[/latex], а скорость — это величина, разная для каждой точки тела, вращающегося вокруг оси, имеет смысл найти способ записать кинетическую энергию через переменную [latex]\omega[/ латекс], который одинаков для всех точек на твердом вращающемся теле. Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение [latex]{v}_{\text{t}}=\omega r[/latex], где 9{2}.[/latex]
Однако большая часть этой энергии находится в форме кинетической энергии вращения. 9{2}[/latex], а скорость — это величина, разная для каждой точки тела, вращающегося вокруг оси, имеет смысл найти способ записать кинетическую энергию через переменную [latex]\omega[/ латекс], который одинаков для всех точек на твердом вращающемся теле. Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение [latex]{v}_{\text{t}}=\omega r[/latex], где 9{2}.[/latex]
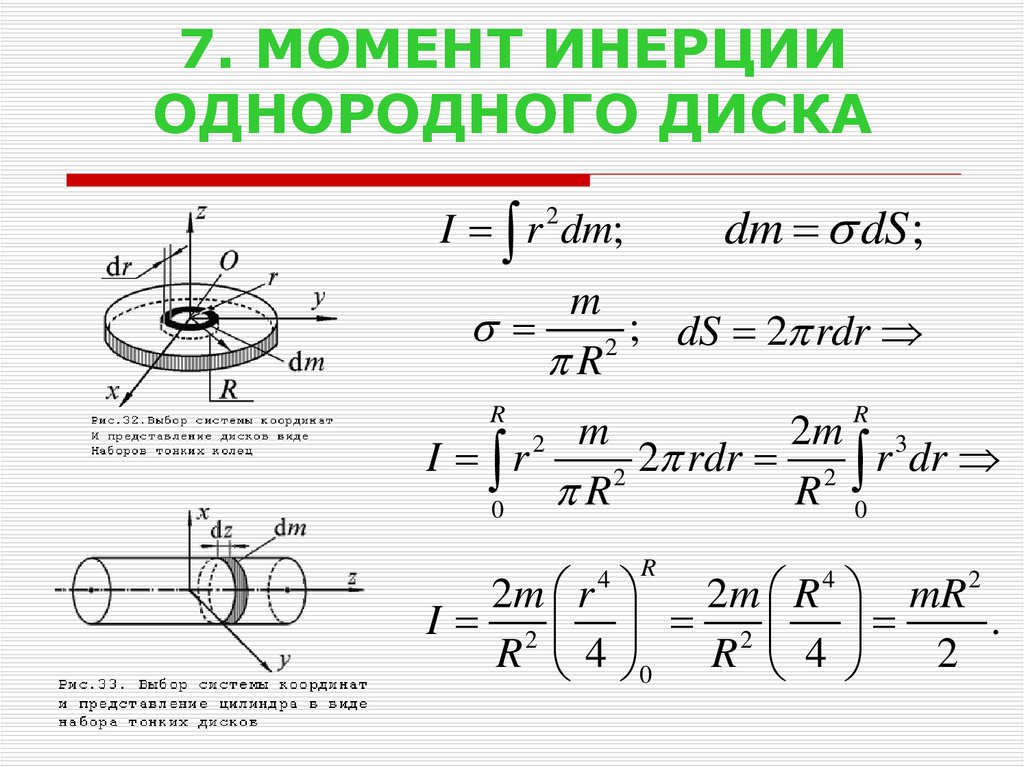
В случае твердого вращающегося тела мы можем разделить любое тело на большое количество меньших масс, каждая из которых имеет массу [latex]{m}_{j}[/latex ] и расстояние до оси вращения [латекс]{r}_{j}[/латекс], такое, чтобы общая масса тела была равна сумме отдельных масс: [латекс]М=\сумма _{ j}{m}_{j}[/латекс]. Каждая меньшая масса имеет тангенциальную скорость [латекс]{v}_{j}[/латекс], где мы временно опустили индекс t . Полная кинетическая энергия твердого вращающегося тела равна 9{2}[/latex], где r — расстояние от точечной частицы до оси вращения. В следующем разделе мы исследуем интегральную форму этого уравнения, которую можно использовать для расчета момента инерции некоторых твердых тел правильной формы.
Полная кинетическая энергия твердого вращающегося тела равна 9{2}[/latex], где r — расстояние от точечной частицы до оси вращения. В следующем разделе мы исследуем интегральную форму этого уравнения, которую можно использовать для расчета момента инерции некоторых твердых тел правильной формы.
Момент инерции есть количественная мера инерции вращения, как и в поступательном движении, а масса есть количественная мера линейной инерции, т. е. чем массивнее объект, тем больше у него инерция и тем больше его сопротивление изменению линейной скорости. Аналогично, чем больше момент инерции твердого тела или системы частиц, тем больше их сопротивление изменению угловой скорости относительно неподвижной оси вращения. Интересно посмотреть, как меняется момент инерции в зависимости от r, расстояние до оси вращения массы частицы на (рис.). Твердые тела и системы частиц с большей массой, сосредоточенные на большем расстоянии от оси вращения, обладают большими моментами инерции, чем тела и системы той же массы, но сосредоточенные вблизи оси вращения. Таким образом, мы можем видеть, что полый цилиндр имеет большую инерцию вращения, чем сплошной цилиндр той же массы при вращении вокруг оси, проходящей через центр. Подставляя (Рисунок) в (Рисунок), выражение для кинетической энергии вращающегося твердого тела принимает вид 9{2}.[/latex]
Таким образом, мы можем видеть, что полый цилиндр имеет большую инерцию вращения, чем сплошной цилиндр той же массы при вращении вокруг оси, проходящей через центр. Подставляя (Рисунок) в (Рисунок), выражение для кинетической энергии вращающегося твердого тела принимает вид 9{2}.[/latex]
Из этого уравнения видно, что кинетическая энергия вращающегося твердого тела прямо пропорциональна моменту инерции и квадрату угловой скорости. Это используется в устройствах накопления энергии маховика, которые предназначены для накопления большого количества кинетической энергии вращения. Многие автопроизводители в настоящее время испытывают в своих автомобилях накопители энергии маховика, такие как маховик или система рекуперации кинетической энергии, показанные на (рис.).
A Маховик KERS (система рекуперации кинетической энергии), используемый в автомобилях. (кредит: «cmonville»/Flickr)
Вращательные и поступательные величины для кинетической энергии и инерции приведены на (Рисунок). Столбец отношения не включен, потому что не существует константы, на которую мы могли бы умножить вращательную величину, чтобы получить поступательную величину, как это можно сделать для переменных на (рис.).
Столбец отношения не включен, потому что не существует константы, на которую мы могли бы умножить вращательную величину, чтобы получить поступательную величину, как это можно сделать для переменных на (рис.).
| Поворотный | Трансляционное |
|---|
Момент инерции системы частиц
Шесть маленьких шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы и длиной 0,5 м. Масса каждой шайбы 20 г. Стержень вращается вокруг оси, расположенной на расстоянии 25 см, как показано на (рис.). а) Чему равен момент инерции системы? б) Если убрать две ближние к оси шайбы, каков будет момент инерции оставшихся четырех шайб? в) Если система с шестью шайбами вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
Стержень вращается вокруг оси, расположенной на расстоянии 25 см, как показано на (рис.). а) Чему равен момент инерции системы? б) Если убрать две ближние к оси шайбы, каков будет момент инерции оставшихся четырех шайб? в) Если система с шестью шайбами вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
Шесть шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы и вращаются вокруг вертикальной оси.
Стратегия
- Мы используем определение момента инерции для системы частиц и выполняем суммирование для оценки этой величины. Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования.
- Делаем аналогичный расчет.
- Подставим результат (а) в выражение для кинетической энергии вращения. 9{2}=1,73\phantom{\rule{0.2em}{0ex}}\text{J}[/latex].
Значение
Мы можем видеть индивидуальные вклады в момент инерции. Массы вблизи оси вращения вносят очень небольшой вклад. Когда мы их убрали, это очень мало повлияло на момент инерции.
Когда мы их убрали, это очень мало повлияло на момент инерции.
В следующем разделе мы обобщим уравнение суммирования для точечных частиц и разработаем метод расчета моментов инерции твердых тел. Однако на данный момент (Рисунок) дает значения инерции вращения для обычных форм объектов вокруг указанных осей.
Значения инерции вращения для обычных форм объектов.
Применение вращательной кинетической энергии
Теперь давайте применим идеи вращательной кинетической энергии и таблицу моментов инерции, чтобы получить представление об энергии, связанной с несколькими вращающимися объектами. Следующие примеры также помогут вам освоиться с этими уравнениями. Во-первых, давайте рассмотрим общую стратегию решения проблем с вращательной энергией.
Стратегия решения проблем: энергия вращения
- Определите, какая энергия или работа связана с вращением.
- Определите интересующую систему. Эскиз обычно помогает.
- Проанализируйте ситуацию, чтобы определить виды работы и энергии.

- Если нет потерь энергии из-за трения и других неконсервативных сил, механическая энергия сохраняется, то есть [латекс] {K} _ {\ text {i}} + {U} _ {\ text {i}} ={K}_{\text{f}}+{U}_{\text{f}}[/латекс].
- Если присутствуют неконсервативные силы, механическая энергия не сохраняется, и другие формы энергии, такие как тепло и свет, могут входить в систему или выходить из нее. Определите, каковы они, и рассчитайте их по мере необходимости.
- Удалите термины везде, где это возможно, чтобы упростить алгебру.
- Оцените численное решение, чтобы увидеть, имеет ли оно смысл в физической ситуации, представленной в формулировке задачи.
Расчет энергии вертолета
Типичный небольшой спасательный вертолет имеет четыре лопасти: каждая имеет длину 4,00 м и массу 50,0 кг ((Рисунок)). Лопасти можно представить как тонкие стержни, которые вращаются вокруг одного конца оси, перпендикулярной их длине. Вертолет имеет полную загруженную массу 1000 кг. а) Рассчитайте кинетическую энергию вращения лопастей, когда они вращаются со скоростью 300 об/мин. (b) Рассчитайте поступательную кинетическую энергию вертолета, когда он летит со скоростью 20,0 м/с, и сравните ее с энергией вращения лопастей.
а) Рассчитайте кинетическую энергию вращения лопастей, когда они вращаются со скоростью 300 об/мин. (b) Рассчитайте поступательную кинетическую энергию вертолета, когда он летит со скоростью 20,0 м/с, и сравните ее с энергией вращения лопастей.
(а) Эскиз четырехлопастного вертолета. b) спасательная операция на воде с участием вертолета Оклендской спасательной вертолетной службы Westpac. (кредит b: «111 Emergency»/Flickr)
Стратегия
Вращательная и поступательная кинетическая энергия может быть рассчитана по их определениям. Формулировка задачи дает все необходимые константы для вычисления выражений для вращательной и поступательной кинетических энергий.
Раствор
- 9{2}.[/латекс]
- Мы используем закон сохранения механической энергии. Поскольку бумеранг запускается под углом, нам нужно записать полную энергию системы в терминах ее линейной кинетической энергии, используя скорость в направлениях x и y . Полная энергия, когда бумеранг покидает руку, равна 9{2}\right)}=18,97\phantom{\rule{0.2em}{0ex}}\text{m}.[/latex]
Мы должны преобразовать угловую скорость в радианы в секунду и рассчитать момент инерции, прежде чем мы сможем найти K . Угловая скорость [латекс]\омега[/латекс] равна
[латекс]\omega =\frac{300\phantom{\rule{0.2em}{0ex}}\text{rev}}{1. {2}[/латекс].
9{2}=450.0\phantom{\rule{0.2em}{0ex}}\text{J}.[/latex]
{2}[/латекс].
9{2}=450.0\phantom{\rule{0.2em}{0ex}}\text{J}.[/latex]
Таким образом, полная энергия бумеранга равна
[латекс] {K} _ {\ text {Всего}} = {K} _ {\ text {R}} + {K} _ {\ text {T}} = 80,93 + 450,0 = 530,93 \ фантом {\ правило {0.2em}{0ex}}\text{J}.[/latex]
Значение
В части (b) решение демонстрирует, как сохранение энергии является альтернативным методом решения проблемы, которая обычно решается с использованием кинематики. При отсутствии сопротивления воздуха кинетическая энергия вращения не учитывалась в решении для максимальной высоты.
Проверьте свое понимание Момент инерции винта атомной подводной лодки составляет [латекс]800,0\phantom{\rule{0. {2 }[/латекс]. Если погружной гребной винт имеет скорость вращения 4,0 об/с при выключенном двигателе, какова будет скорость вращения гребного винта через 5,0 с, когда сопротивление воды уберет из системы 50 000 Дж? 9{2}[/latex] момент инерции увеличивается как квадрат расстояния до фиксированной оси вращения. Момент инерции является вращательным аналогом массы в линейном движении.
{2 }[/латекс]. Если погружной гребной винт имеет скорость вращения 4,0 об/с при выключенном двигателе, какова будет скорость вращения гребного винта через 5,0 с, когда сопротивление воды уберет из системы 50 000 Дж? 9{2}[/latex] момент инерции увеличивается как квадрат расстояния до фиксированной оси вращения. Момент инерции является вращательным аналогом массы в линейном движении.
Концептуальные вопросы
Что, если бы другая планета размером с Землю была выведена на орбиту вокруг Солнца вместе с Землей. Момент инерции системы увеличится, уменьшится или останется прежним?
Твердый шар вращается вокруг оси, проходящей через его центр, с постоянной скоростью вращения.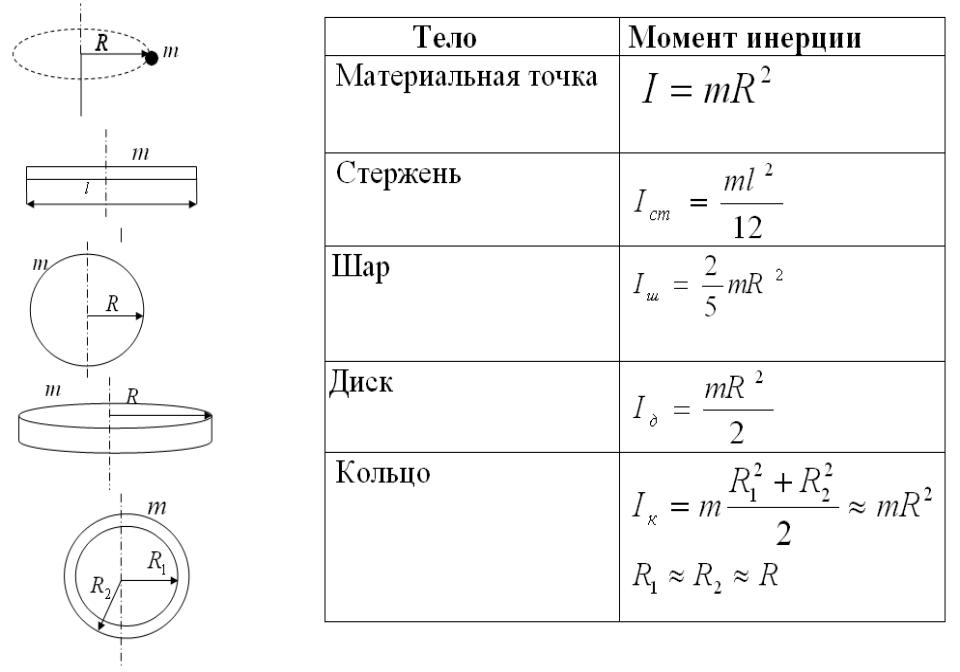 Другая полая сфера той же массы и радиуса вращается вокруг своей оси, проходящей через центр, с той же скоростью вращения. Какой шар имеет большую кинетическую энергию вращения?
Другая полая сфера той же массы и радиуса вращается вокруг своей оси, проходящей через центр, с той же скоростью вращения. Какой шар имеет большую кинетическую энергию вращения?
Полая сфера, так как масса распределена дальше от оси вращения.
Задачи
Система точечных частиц показана на следующем рисунке. Каждая частица имеет массу 0,3 кг и все они лежат в одной плоскости. а) Чему равен момент инерции системы относительно данной оси? б) Если система вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
(a) Рассчитайте кинетическую энергию вращения Земли вокруг своей оси. б) Какова кинетическая энергия вращения Земли на ее орбите вокруг Солнца? 9{33}\phantom{\rule{0.2em}{0ex}}\text{J}[/latex]
Рассчитайте кинетическую энергию вращения колеса мотоцикла массой 12 кг, если его угловая скорость равна 120 рад/с, а внутренний радиус составляет 0,280 м, а внешний радиус 0,330 м.
Бейсбольный питчер бросает мяч движением, при котором происходит вращение предплечья вокруг локтевого сустава, а также другие движения. {2}[/latex], какова вращательная кинетическая энергия предплечья? 9{2}[/латекс] и массой 200 кг. Сопротивлением воздуха пренебречь. а) С какой поступательной скоростью гребной винт ударяется о землю? б) Какова скорость вращения пропеллера в момент удара?
{2}[/latex], какова вращательная кинетическая энергия предплечья? 9{2}[/латекс] и массой 200 кг. Сопротивлением воздуха пренебречь. а) С какой поступательной скоростью гребной винт ударяется о землю? б) Какова скорость вращения пропеллера в момент удара?
а. [латекс] {v} _ {\ text {f}} = 86,5 \ phantom {\ rule {0.2em} {0ex}} \ text {m} \ text{/} \ text {s} [/latex];
б. Скорость вращения винта остается прежней и составляет 20 об/с.
Если в предыдущей задаче присутствует сопротивление воздуха и оно снижает кинетическую энергию вращения пропеллера при ударе на 30 %, какова скорость вращения пропеллера при ударе? 9{42}\phantom{\rule{0.2em}{0ex}}\text{J}[/latex]
Электрическая шлифовальная машина, состоящая из вращающегося диска массой 0,7 кг и радиусом 10 см, вращается со скоростью 15 об/сек. При нанесении на грубую деревянную стену скорость вращения уменьшается на 20%. а) Чему равна конечная кинетическая энергия вращения вращающегося диска? б) Насколько уменьшилась его кинетическая энергия вращения?
Система состоит из диска массой 2,0 кг и радиусом 50 см, на котором закреплен кольцевой цилиндр массой 1,0 кг с внутренним радиусом 20 см и внешним радиусом 30 см (см. ниже). Система вращается вокруг оси, проходящей через центр диска и кольцевой цилиндр со скоростью 10 об/с. а) Чему равен момент инерции системы? б) Какова его кинетическая энергия вращения? 9{2}[/латекс];
ниже). Система вращается вокруг оси, проходящей через центр диска и кольцевой цилиндр со скоростью 10 об/с. а) Чему равен момент инерции системы? б) Какова его кинетическая энергия вращения? 9{2}[/латекс];
б. [латекс] K = 621,8 \ фантом {\ правило {0.2em} {0ex}} \ текст {J} [/латекс]
Глоссарий
- момент инерции
- вращающаяся масса твердых тел, которая относится к тому, насколько легко или сложно будет изменить угловую скорость вращающегося твердого тела
- вращательная кинетическая энергия
- кинетическая энергия за счет вращения объекта; это часть его полной кинетической энергии
10.4 Момент инерции и кинетическая энергия вращения – Университетская физика Том 1
10 Вращение с фиксированной осью
Цели обучения
К концу этого раздела вы сможете:
- Описывать различия между вращательной и поступательной кинетической энергией
- Определить физическую концепцию момента инерции в терминах распределения массы относительно оси вращения
- Объясните, как момент инерции твердых тел влияет на их кинетическую энергию вращения
- Использование закона сохранения механической энергии для анализа систем, подвергающихся как вращению, так и поступательному перемещению
- Расчет угловой скорости вращающейся системы при наличии потерь энергии из-за неконсервативных сил
До сих пор в этой главе мы работали с кинематикой вращения: описанием движения вращающегося твердого тела с фиксированной осью вращения. В этом разделе мы определяем две новые величины, полезные для анализа свойств вращающихся объектов: момент инерции и кинетическую энергию вращения. Определив эти свойства, мы получим два важных инструмента, необходимых для анализа динамики вращения.
В этом разделе мы определяем две новые величины, полезные для анализа свойств вращающихся объектов: момент инерции и кинетическую энергию вращения. Определив эти свойства, мы получим два важных инструмента, необходимых для анализа динамики вращения.
Вращательная кинетическая энергия
Любой движущийся объект обладает кинетической энергией. Мы знаем, как вычислить это для тела, совершающего поступательное движение, но как насчет твердого тела, совершающего вращательное движение? Это может показаться сложным, потому что каждая точка твердого тела имеет разную скорость. Однако мы можем использовать угловую скорость, которая одинакова для всего твердого тела, чтобы выразить кинетическую энергию вращающегося объекта. На рисунке показан пример очень энергичного вращающегося тела: электрический точильный камень, приводимый в движение двигателем. Когда точильный камень выполняет свою работу, летят искры, возникают шум и вибрация. Эта система обладает значительной энергией, частично в виде тепла, света, звука и вибрации. Однако большая часть этой энергии находится в форме 9{2}[/latex], а скорость — это величина, разная для каждой точки тела, вращающегося вокруг оси, имеет смысл найти способ записать кинетическую энергию через переменную [latex]\omega[/ латекс], который одинаков для всех точек на твердом вращающемся теле. Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение [latex]{v}_{\text{t}}=\omega r[/latex], где 9{2}.[/latex]
Однако большая часть этой энергии находится в форме 9{2}[/latex], а скорость — это величина, разная для каждой точки тела, вращающегося вокруг оси, имеет смысл найти способ записать кинетическую энергию через переменную [latex]\omega[/ латекс], который одинаков для всех точек на твердом вращающемся теле. Для одиночной частицы, вращающейся вокруг фиксированной оси, это легко вычислить. Мы можем связать угловую скорость с величиной поступательной скорости, используя соотношение [latex]{v}_{\text{t}}=\omega r[/latex], где 9{2}.[/latex]
В случае твердого вращающегося тела мы можем разделить любое тело на большое количество меньших масс, каждая из которых имеет массу [latex]{m}_{j}[/latex ] и расстояние до оси вращения [латекс]{r}_{j}[/латекс], такое, чтобы общая масса тела была равна сумме отдельных масс: [латекс]М=\сумма _{ j}{m}_{j}[/латекс]. Каждая меньшая масса имеет тангенциальную скорость [латекс]{v}_{j}[/латекс], где мы временно опустили индекс t . Полная кинетическая энергия твердого вращающегося тела равна 9{2}[/latex], где r — расстояние от точечной частицы до оси вращения. В следующем разделе мы исследуем интегральную форму этого уравнения, которую можно использовать для расчета момента инерции некоторых твердых тел правильной формы.
В следующем разделе мы исследуем интегральную форму этого уравнения, которую можно использовать для расчета момента инерции некоторых твердых тел правильной формы.
Момент инерции есть количественная мера инерции вращения, как и в поступательном движении, а масса есть количественная мера линейной инерции, т. е. чем массивнее объект, тем больше у него инерция и тем больше его сопротивление изменению линейной скорости. Аналогично, чем больше момент инерции твердого тела или системы частиц, тем больше их сопротивление изменению угловой скорости относительно неподвижной оси вращения. Интересно посмотреть, как меняется момент инерции в зависимости от r, расстояние до оси вращения массы частицы на рис. Твердые тела и системы частиц с большей массой, сосредоточенные на большем расстоянии от оси вращения, обладают большими моментами инерции, чем тела и системы той же массы, но сосредоточенные вблизи оси вращения. Таким образом, мы можем видеть, что полый цилиндр имеет большую инерцию вращения, чем сплошной цилиндр той же массы при вращении вокруг оси, проходящей через центр. Подставляя рисунок в рисунок, выражение для кинетической энергии вращающегося твердого тела принимает вид 9{2}.[/latex]
Подставляя рисунок в рисунок, выражение для кинетической энергии вращающегося твердого тела принимает вид 9{2}.[/latex]
Из этого уравнения видно, что кинетическая энергия вращающегося твердого тела прямо пропорциональна моменту инерции и квадрату угловой скорости. Это используется в накопителях энергии маховика , которые предназначены для накопления большого количества вращательной кинетической энергии. Многие автопроизводители в настоящее время испытывают в своих автомобилях накопители энергии маховика, такие как маховик или система рекуперации кинетической энергии, показанные на рисунке.
Рисунок 10.18 Маховик KERS (система рекуперации кинетической энергии), используемый в автомобилях. (кредит: «cmonville»/Flickr) Вращательные и поступательные величины для кинетической энергии и инерции представлены на рисунке. Столбец отношений не включен, потому что не существует константы, на которую мы могли бы умножить вращательную величину, чтобы получить поступательную величину, как это можно сделать для переменных на рисунке.
Пример
Момент инерции системы частиц
На стержне ничтожной массы и длины 0,5 м на расстоянии 10 см друг от друга расположены шесть маленьких шайб. Масса каждой шайбы 20 г. Стержень вращается вокруг оси, расположенной на расстоянии 25 см, как показано на рис. а) Чему равен момент инерции системы? б) Если убрать две ближние к оси шайбы, каков будет момент инерции оставшихся четырех шайб? в) Если система с шестью шайбами вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
Рисунок 10. 19 Шесть шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы, вращающемся вокруг вертикальной оси.
19 Шесть шайб расположены на расстоянии 10 см друг от друга на стержне незначительной массы, вращающемся вокруг вертикальной оси.Стратегия
- Мы используем определение момента инерции для системы частиц и выполняем суммирование для оценки этой величины. Все массы одинаковы, поэтому мы можем поставить это количество перед символом суммирования.
- Делаем аналогичный расчет.
- Подставим результат (а) в выражение для кинетической энергии вращения. 9{2}=1,73\,\text{J}[/латекс].
Значение
Мы можем видеть индивидуальные вклады в момент инерции. Массы вблизи оси вращения вносят очень небольшой вклад. Когда мы их убрали, это очень мало повлияло на момент инерции.
В следующем разделе мы обобщим уравнение суммирования для точечных частиц и разработаем метод расчета моментов инерции твердых тел. Однако пока на рисунке приведены значения инерции вращения для обычных форм объектов вокруг заданных осей.
Рисунок 10. 20 Значения инерции вращения для обычных форм объектов
20 Значения инерции вращения для обычных форм объектовПрименение вращательной кинетической энергии
Теперь давайте применим идеи вращательной кинетической энергии и таблицу моментов инерции, чтобы получить представление об энергии, связанной с несколькими вращающимися объектами. Следующие примеры также помогут вам освоиться с этими уравнениями. Во-первых, давайте рассмотрим общую стратегию решения проблем с вращательной энергией.
Стратегия решения проблем: энергия вращения
- Определите, какая энергия или работа связана с вращением.
- Определите интересующую систему. Эскиз обычно помогает.
- Проанализируйте ситуацию, чтобы определить виды работы и энергии.
- Если нет потерь энергии из-за трения и других неконсервативных сил, механическая энергия сохраняется, то есть [латекс] {K} _ {\ text {i}} + {U} _ {\ text {i}} ={K}_{\text{f}}+{U}_{\text{f}}[/латекс].
- Если присутствуют неконсервативные силы, механическая энергия не сохраняется, и другие формы энергии, такие как тепло и свет, могут входить в систему или выходить из нее.
 Определите, каковы они, и рассчитайте их по мере необходимости.
Определите, каковы они, и рассчитайте их по мере необходимости. - Удалите термины везде, где это возможно, чтобы упростить алгебру.
- Оцените численное решение, чтобы увидеть, имеет ли оно смысл в физической ситуации, представленной в формулировке задачи.
Пример
Расчет энергии вертолета
Типичный небольшой спасательный вертолет имеет четыре лопасти: каждая имеет длину 4,00 м и массу 50,0 кг (рисунок). Лопасти можно представить как тонкие стержни, которые вращаются вокруг одного конца оси, перпендикулярной их длине. Вертолет имеет полную загруженную массу 1000 кг. а) Рассчитайте кинетическую энергию вращения лопастей, когда они вращаются со скоростью 300 об/мин. (b) Рассчитайте поступательную кинетическую энергию вертолета, когда он летит со скоростью 20,0 м/с, и сравните ее с энергией вращения лопастей.
Рисунок 10.21 (a) Эскиз четырехлопастного вертолета. b) спасательная операция на воде с участием вертолета Оклендской спасательной вертолетной службы Westpac. (кредит b: «111 Emergency»/Flickr)
(кредит b: «111 Emergency»/Flickr)Стратегия
Кинетическая энергия вращения и поступательного движения может быть рассчитана по их определениям. Формулировка задачи дает все необходимые константы для вычисления выражений для вращательной и поступательной кинетических энергий.
Раствор
9{2}.[/латекс]Мы должны преобразовать угловую скорость в радианы в секунду и рассчитать момент инерции, прежде чем мы сможем найти K . Угловая скорость [латекс]\омега[/латекс] равна
[латекс]\omega =\frac{300\,\text{rev}}{1.00\,\text{min}}\,\frac{2\pi \,\text{rad}}{\text{1 rev}}\,\frac{1.00\,\text{min}}{60.0\,\text{s}}=\,31.4\,\frac{\text{rad}}{\text{s}}. [/латекс]
Момент инерции одной лопасти равен моменту инерции тонкого стержня, вращающегося вокруг своего конца, указанному на рис. Всего 9{2}=450,0\,\text{J}.[/latex]
Таким образом, полная энергия бумеранга равна
[латекс] {K} _ {\ text {Всего}} = {K} _ {\ text {R}} + {K} _ {\ text {T}} = 80,93 + 450,0 = 530,93 \, \ text { J}. {2}[/латекс]. Если погружной гребной винт имеет скорость вращения 4,0 об/с при выключенном двигателе, какова будет скорость вращения гребного винта через 5,0 с, когда сопротивление воды уберет из системы 50 000 Дж? 9{2}[/latex] момент инерции увеличивается как квадрат расстояния до фиксированной оси вращения. Момент инерции является вращательным аналогом массы в линейном движении.
{2}[/латекс]. Если погружной гребной винт имеет скорость вращения 4,0 об/с при выключенном двигателе, какова будет скорость вращения гребного винта через 5,0 с, когда сопротивление воды уберет из системы 50 000 Дж? 9{2}[/latex] момент инерции увеличивается как квадрат расстояния до фиксированной оси вращения. Момент инерции является вращательным аналогом массы в линейном движении.
Концептуальные вопросы
Что, если бы другая планета размером с Землю была выведена на орбиту вокруг Солнца вместе с Землей. Момент инерции системы увеличится, уменьшится или останется прежним?
Твердый шар вращается вокруг оси, проходящей через его центр, с постоянной скоростью вращения. Другая полая сфера той же массы и радиуса вращается вокруг своей оси, проходящей через центр, с той же скоростью вращения. Какой шар имеет большую кинетическую энергию вращения?
Другая полая сфера той же массы и радиуса вращается вокруг своей оси, проходящей через центр, с той же скоростью вращения. Какой шар имеет большую кинетическую энергию вращения?
Полая сфера, так как масса распределена дальше от оси вращения.
Задачи
Система точечных частиц показана на следующем рисунке. Каждая частица имеет массу 0,3 кг и все они лежат в одной плоскости. а) Чему равен момент инерции системы относительно данной оси? б) Если система вращается со скоростью 5 об/с, какова ее кинетическая энергия вращения?
(a) Рассчитайте кинетическую энергию вращения Земли вокруг своей оси. б) Какова кинетическая энергия вращения Земли на ее орбите вокруг Солнца? 9{33}\,\text{J}[/латекс]
Рассчитайте кинетическую энергию вращения колеса мотоцикла массой 12 кг, если его угловая скорость равна 120 рад/с, внутренний радиус равен 0,280 м, а внешний радиус равен 0,330 м.
Бейсбольный питчер бросает мяч движением, при котором происходит вращение предплечья вокруг локтевого сустава, а также другие движения.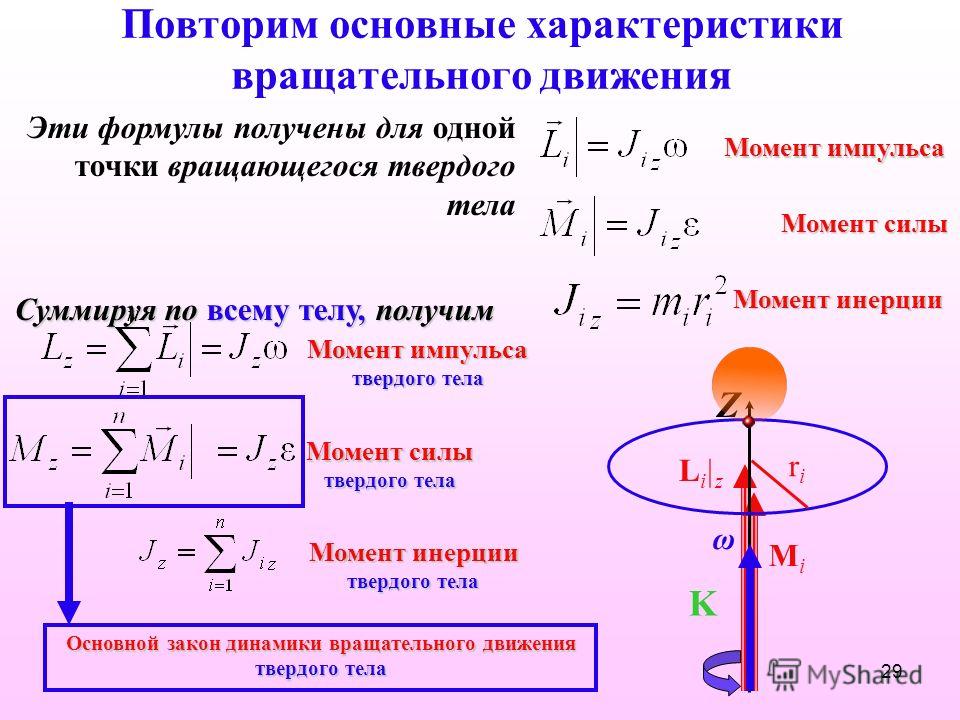 {2}[/latex], какова кинетическая энергия вращения предплечья? 9{2}[/латекс] и массой 200 кг. Сопротивлением воздуха пренебречь. а) С какой поступательной скоростью гребной винт ударяется о землю? б) Какова скорость вращения пропеллера в момент удара?
{2}[/latex], какова кинетическая энергия вращения предплечья? 9{2}[/латекс] и массой 200 кг. Сопротивлением воздуха пренебречь. а) С какой поступательной скоростью гребной винт ударяется о землю? б) Какова скорость вращения пропеллера в момент удара?
а. [латекс] {v}_{\text{f}}=86,5\,\text{m}\text{/}\text{s}[/latex];
б. Скорость вращения винта остается прежней и составляет 20 об/с.
Если в предыдущей задаче присутствует сопротивление воздуха и оно снижает кинетическую энергию вращения пропеллера при ударе на 30 %, какова скорость вращения пропеллера при ударе? 9{42}\,\text{J}[/латекс]
Электрический шлифовальный станок, состоящий из вращающегося диска массой 0,7 кг и радиусом 10 см, вращается со скоростью 15 об/сек. При нанесении на грубую деревянную стену скорость вращения уменьшается на 20%. а) Чему равна конечная кинетическая энергия вращения вращающегося диска? б) Насколько уменьшилась его кинетическая энергия вращения?
Система состоит из диска массой 2,0 кг и радиусом 50 см, на котором закреплен кольцевой цилиндр массой 1,0 кг с внутренним радиусом 20 см и внешним радиусом 30 см (см.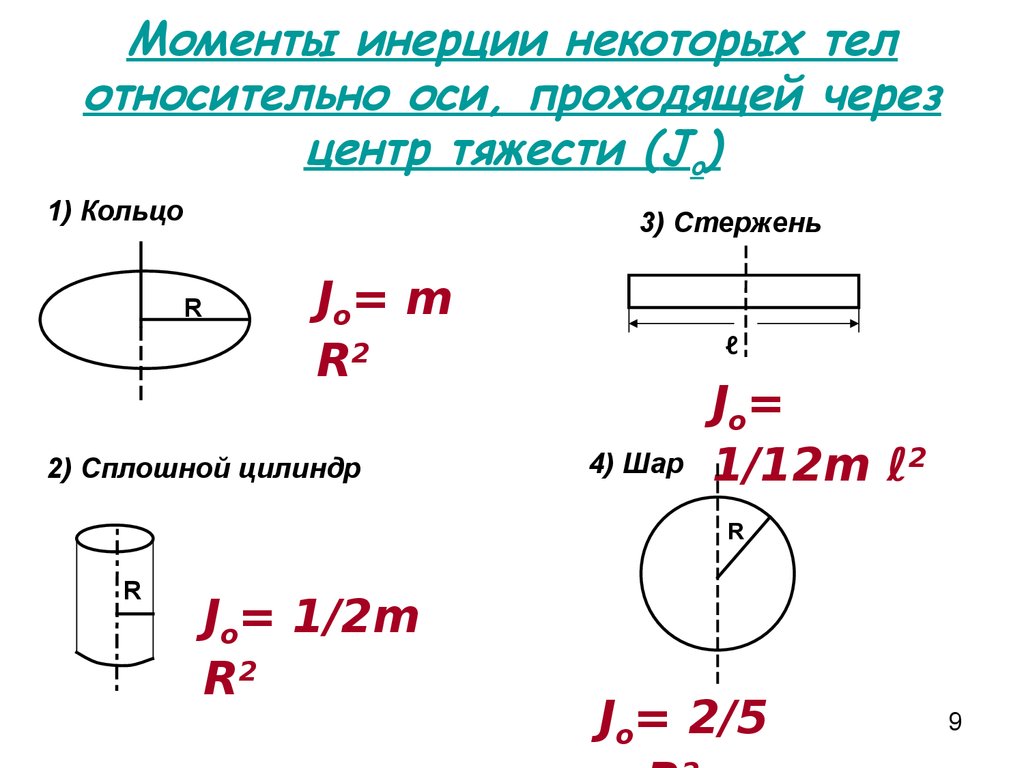



 Определите, каковы они, и рассчитайте их по мере необходимости.
Определите, каковы они, и рассчитайте их по мере необходимости.