Момент инерции абсолютно твердого тела. Урок №14
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
Физика. 10 класс. Урок №14.
«Недостаточно только получить знания, надо
найти им применение. Недостаточно только
желать, надо делать.»
Гёте
© Фокина Лидия Петровна
Знаешь ли ты?
Почему вместо обычных колес на
велосипедах гонщиков устанавливают
сплошные диски?
Если ты затрудняешься ответить на данный вопрос
сейчас, то я уверенн, что ты на него сможешь ответить
в конце этого урока.
© Фокина Лидия Петровна
Физика. 10 класс. Урок №14.
Тема урока:
Момент инерции
абсолютно твердого тела
Цели обучения:
10.2.2.5 – использовать теорему Штейнера для
расчета момента инерции материальных тел
© Фокина Лидия Петровна
Давайте вспомним!
1. Что такое инерция?
Инерция – это физическое явление. Оно
состоит в том, что любое тело, на которое не
действуют другие тела (или действие других
тел скомпенсировано), сохраняет состояние
покоя или движется равномерно и
прямолинейно
2. Какое тело в физике называют абсолютно
твердым телом?
Абсолютно твердое тело – это тело,
расстояние между частями которого не
меняется при действии на него любых сил.
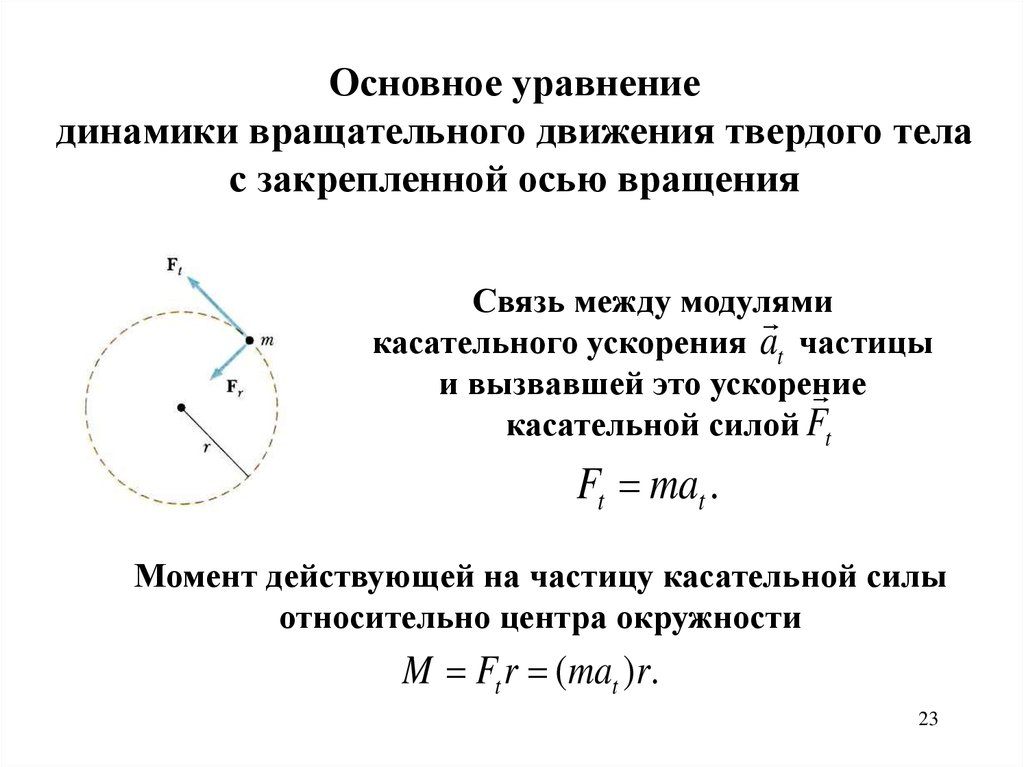
Рассмотрим вращение материальной точки
массой m вокруг неподвижного центра О.
Докажем, что инерциальные свойства данной
точки зависят не только от массы, но и от
радиуса вращения.
Запишем второй закон
Ньютона для точки массой m,
движущейся по окружности
под действием силы ,
тангенциальное ускорение
будет создавать касательная
к траектории составляющая
© Фокина Лидия Петровна
Тангенциальное ускорение связано с угловым
ускорением формулой
Учитывая это получим:
Умножим обе части данного уравнения на радиус
окружности, по которой двигалась
рассматриваемая точка, получим:
, где
M — момент силы
© Фокина Лидия Петровна
Величину, равную произведению массы на
квадрат радиуса окружности, по которой
движется тело, называют моментом
инерции.

Момент инерцииобозначают
буквой I.
Единица измерения момента
инерции [I] = 1 кг м2
-второй закон Ньютона для
вращающегося тела
© Фокина Лидия Петровна
Мы нашли момент инерции материальной точки,
вращающейся вокруг неподвижного центра.
А как найти момент инерции абсолютно твердого тела?
Момент инерции твердого тела равен сумме
которых состоит это тело:
Инертные свойства вращающихся тел зависят
не только от массы, но и от ее распределения
по объему тела и радиуса вращения.
© Фокина Лидия Петровна
стр 49-50 Таблица 6. Моменты инерции тел
© Фокина Лидия Петровна
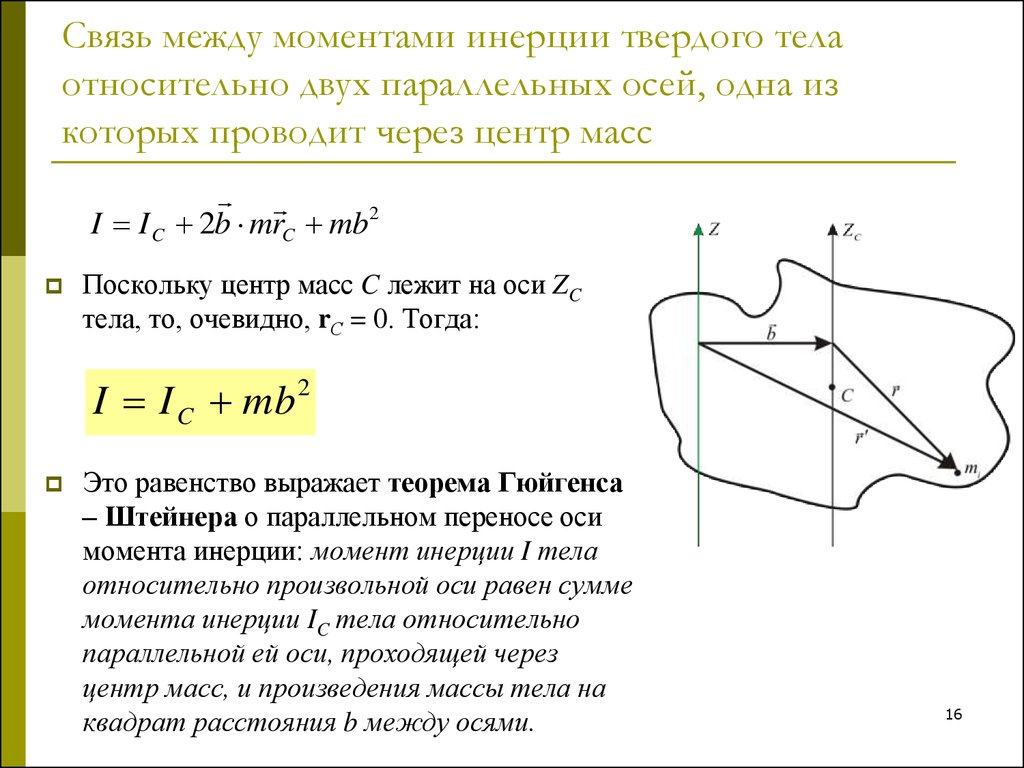
Теорема Штейнера
Если для тела известен момент инерции I0
относительно оси, проходящей через центр
масс, то момент инерции относительно любой
оси, параллельной центральной, можно найти
по формуле, полученной швейцарским ученымматематиком Штейнером:
d – расстояние от центра масс до оси вращения
© Фокина Лидия Петровна
Задача №1
Определите момент инерции I тонкого однородного стержня
стержню и проходящей через: 1) его конец; 2) его середину; 3)
точку отстоящую от конца стержня на 1/3 его длины
Дано: CИ
Решение:
(из таблицы)
l= 30 см 0,3 м
m = 100 г 0,1 кг
I-?
1) расстояние от центра масс до
конца стержня
© Фокина Лидия Петровна
2) ось вращения проходит через центр масс
3) Расстояние от центра масс до оси, отстоящей
от конца стержня на 1/3 его длины
Ответ:
© Фокина Лидия Петровна
Выполни самостоятельно!
1.
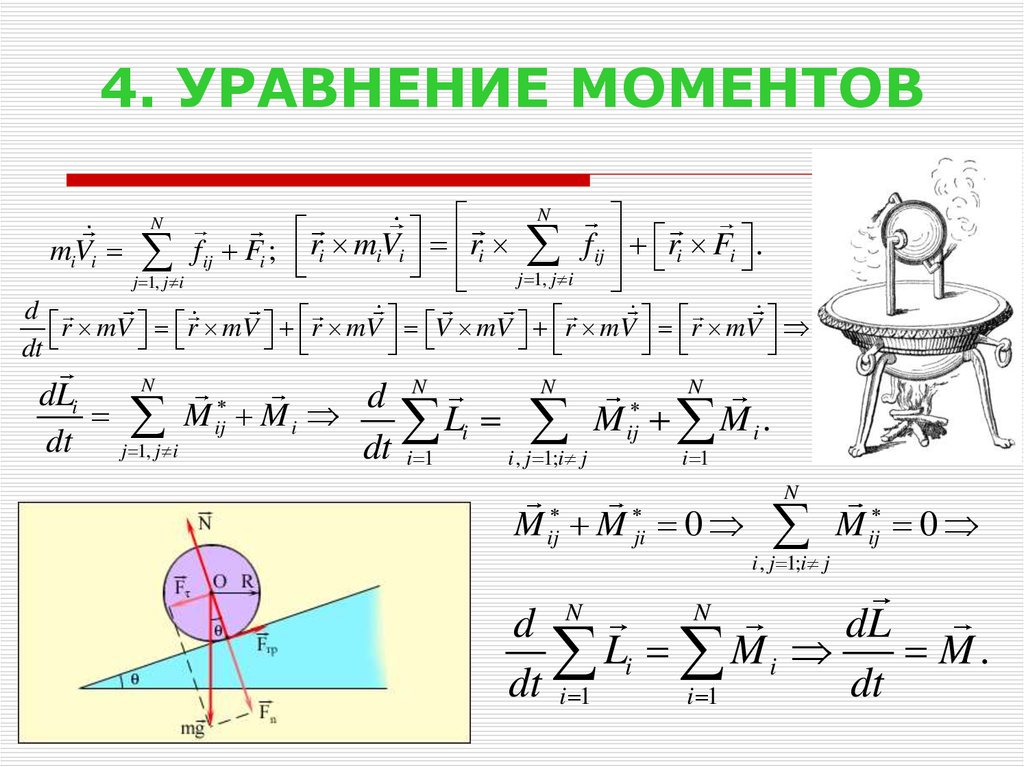
Определите момент инерции стержня длиной l,
увеличился момент инерции в сравнении с моментом
инерции стержня, вращающегося вокруг центра масс?
2.
Определите момент инерции материальной точки, масса
которой 50 г, относительно оси, отстоящей от точки на
расстоянии 20 см.
3.
Найти момент инерции обруча массой и
радиусом относительно оси, проходящей через его край
перпендикулярно обручу.
§9 стр 48-51
© Фокина Лидия Петровна
Итоги урока
Момент инерции – скалярная физическая величина, мера
инертности во вращательном движении вокруг оси,
подобно тому, как масса тела является мерой его
инертности в поступательном движении.
© Фокина Лидия Петровна
вращающейся по окружности радиуса R,
можно рассчитать по формуле …
I=mR2
Момент инерции тела измеряется в …
кг м2
Момент инерции тела относительно
любой оси, параллельной центральной,
можно вычислить применяя …
теорему
Штейнера
Формула, полученная Штейнером …
I=I0+ md2
© Фокина Лидия Петровна
English Русский Правила
3.
 МЕХАНИКА ТВЕРДОГО ТЕЛА | Политех в Сети
МЕХАНИКА ТВЕРДОГО ТЕЛА | Политех в СетиОсновные формулы
Мерой инертности твердого тела при вращательном движении является момент инерции:
I = Σ Mi∙ Ri2,
Где Mi – элементарная масса I – го кусочка тела, Ri – расстояние этого кусочка от оси вращения.
Моменты инерции некоторых твердых тел относительно оси, проходящей через их центры масс:
Полый цилиндр I = M ( R12 + R22).
Тонкий обруч I = MR2.
Сплошной цилиндр I = mR2.
Шар I = mR2.
Тонкий стержень I =
Ml2.
Если ось вращения не проходит через центр масс, для расчета момента инерции используют теорему Штейнера:
I = I0 + Ma2,
Где I – момент инерции тела относительно данной оси, I0 – момент инерции этого тела относительно оси, параллельной данной, и проходящей через центр масс, M – масса тела, А – расстояние между осями.
Основное уравнение динамики вращательного движения твердого тела: I e = M,
Где I – момент инерции твердого тела, относительно оси вращения, e – его угловое ускорение, М – суммарный момент сил, действующий на тело относительно данной оси.
Момент силы F равен: M = F L,
Где L – расстояние от линии, вдоль которой действует сила, до оси вращения.
Момент импульса твердого тела относительно неподвижной оси: L = I ω,
Где I – момент инерции твердого тела относительно данной оси, ω – угловая скорость его вращения.
Момент импульса материальной точки относительно неподвижной оси: L = M υ R,
Где M – масса частицы, υ – ее скорость, R – расстояние от линии, вдоль которой движется частица, до данной оси.
В замкнутой системе частиц полный момент импульса не меняется: ΣLi = const.
Кинетическая энергия вращающегося тела:
EK =
,
Где I – момент инерции тела, ω – его угловая скорость.
Кинетическая энергия катящегося тела:
EK =
+ ,
Где M – масса тела, υ0 – скорость поступательного движения центра масс, I0 – момент инерции тела относительно оси, проходящей через центр масс, ω – угловая скорость вращения тела.
Примеры решения задач
Задача 13
Прямой круглый однородный конус имеет массу M и радиус основания R. Найти момент инерции конуса относительно его оси.
Решение
Разобьём конус на цилиндрические слои Ось толщиной Dr. Масса такого слоя
Dm = rpR2Dr,
Где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя
DI = Dm.R2.
Момент инерции всего конуса складывается из моментов инерции всех слоёв:
I =
= ρπ R 4 Dr = ρR5.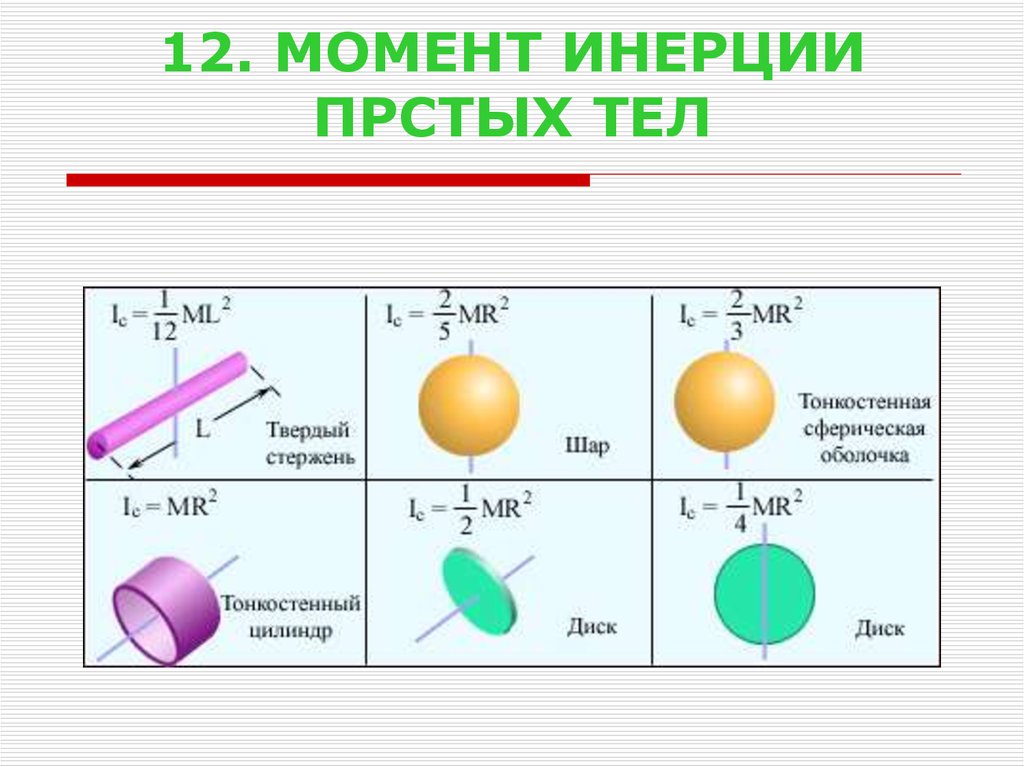
Остаётся выразить его через массу всего цилиндра:
M =
==R3,
Отсюда ρ = ,
I = = mR2.
Задача 14
Маховое колесо, имеющее момент инерции 245 кг∙м2, вращается с частотой 20 об/с. Через минуту после того, как на колесо перестал действовать вращающий момент, оно остановилось. Найти: 1) момент сил трения; 2) число оборотов, которое сделало колесо до полной остановки после прекращения действия сил.
Решение
При торможении угловое ускорение отрицательно. Найдём его модуль из кинематического соотношения для угловой скорости.
ω 0 = 2 π ν0, ω = 0,
0 = 2 π ν0 — ε T,
Отсюда ε =
.
Это ускорение обусловлено действием момента сил трения
MТр = I ε =
.
Полный угол поворота при равнозамедленном движении находится из соотношения:
φ = ω0 T—
,
φ =2π N, ω 0 = 2 π ν0, ε =
.
Перепишем соотношения для угла в виде:
2π N = 2 π ν0 T —
= 2 π ν0 T — = .
Для нахождения числа оборотов получим:
N =
.
Подставив числовые значения, найдём:
MТр = = 506 Нм,
N =
= 600 об.
Задача 15
На барабан радиусом R = 20 см, момент инерции которого равен I = 0,1 кг∙м2, намотан шнур, к которому привязан груз массой M = 0,5 кг. До начала вращения высота груза над полом равна H1 = 1 м. Найти: 1) через какое время груз опустился до пола; 2) кинетическую энергию груза в момент удара о пол; 3) натяжение нити. Трением пренебречь.
Решение
На груз действует сила тяжести Mg и сила натяжения шнура Т. Уравнение поступательного движения груза Ma = Mg – T.
Барабан вращается вокруг неподвижной оси. Его уравнение движения M = I ε,
Где М – момент силы натяжения шнура, М = TR, I – момент инерции барабана, ε =
– его угловое ускорение.
TR = I .
Выражаем отсюда силу натяжения шнура:
T = I (10)
И подставляем ее в уравнение движения груза:
Mg = A(M + ) = Am(1 + ).
Получаем ускорение груза:
A =
. (11)
Время движения груза можно найти из уравнения:
H1 =
,
T =
= .
В момент удара о пол груз имел скорость:
υ = At = .
Следовательно, его кинетическая энергия:
EK =
=.
Подставив выражение для ускорения (11) в формулу (10), получим: T = = .
Подставив числовые значения, определим искомые величины:
T =
= 1,1 c,
EK =
= 0,82 Дж,
T =
= 4,1 Н.
Задача 16
Шар массой M = 1 кг, катящийся без скольжения, ударяется о стенку и откатывается от нее. Скорость шара до удара о стенку υ = 10 см/с, после удара 8 см/с. Найти количество тепла Q, выделившееся при ударе.
Решение
Кинетическая энергия катящегося тела равна:
EK =
+ . (12)
Момент инерции шара I = ,
Угловая скорость вращения w =
.
Подставляем эти величины в формулу (12):
EK =
+ = M υ 2.
Количество тепла, выделившегося при ударе, равно разнице его кинетических энергий до и после удара:
Q = EK1 – EK2 = M υ12 — M υ22 = M(υ12 — υ22).
Подставив числовые значения, получим:
а =
∙1(100∙10-4 – 64.10-4) = 10-4 = 2,25∙10-3 Дж = 2,52 МДж.
Задача 17
Найти кинетическую энергию велосипеда, едущего со скоростью υ = 9 км/ч. Масса велосипедиста вместе с велосипедом M = 78 кг, причем на колеса приходится масса M1 = 3 кг. Колеса считать тонкими обручами.
Решение
Кинетическая энергия велосипеда складывается из кинетической энергии поступательного движения и кинетической энергии вращательного движения колес.
EK =
+ .
Момент инерции колес, представляющих собой тонкие обручи, равен I = , а угловая скорость вращения w = .
Подставляем эти значения в выражение для кинетической энергии: EK =
+ = .
Скорость надо перевести в м/с: υ = 2,5 м/с.
Подстановка числовых значений дает: EK =253 Дж.
Задача 18
Однородный стержень длиной 85см подвешен на горизонтальной оси, проходящей через верхний конец стержня. Какую наименьшую скорость надо сообщить нижнему концу стержня, чтобы он сделал полный оборот вокруг оси?
Решение
Чтобы стержень смог сделать полный оборот вокруг оси, он должен подняться до вертикального положения В.
Если отсчитывать потенциальную энергию стержня от начального положения А, то в положении В центр масс его поднят на
Высоту С2-С1=L – длина стержня. Стержень приобретает потенциальную энергию ЕN = Mgℓ за счет кинетической энергии,
В которую ему сообщили в положении А.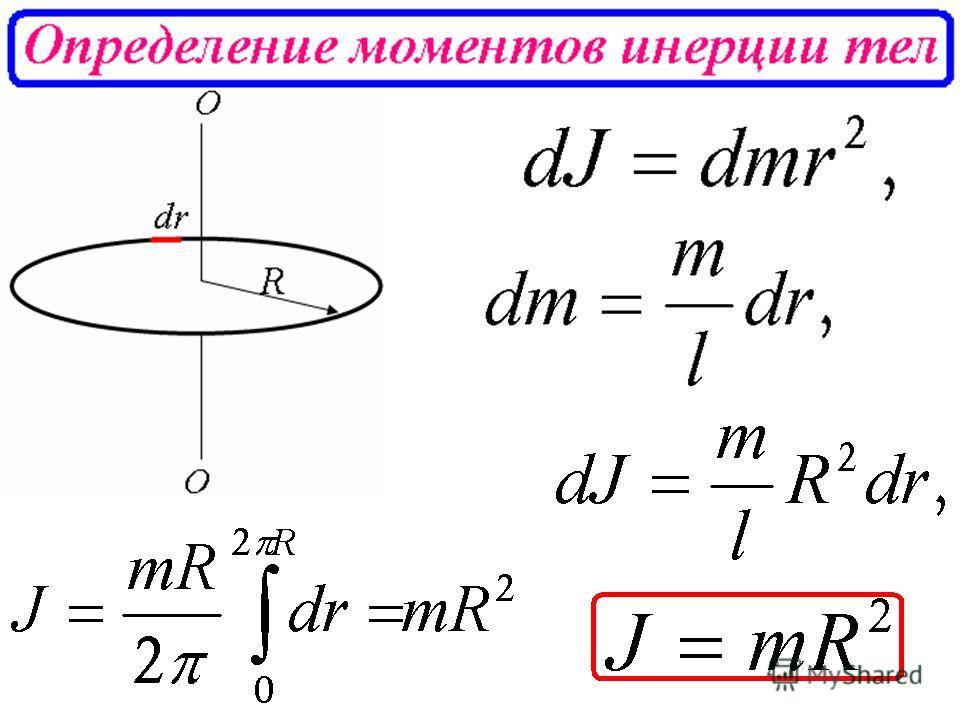 Если
Если
υ – наименьшая скорость нижнего конца, при которой он сможет сделать полный оборот, то
угловая скорость стержня w =
.
Момент инерции стержня относительно оси, проходящей через его конец, определятся по теореме Штейнера:
I = M L2 = M
= M L2,
Где Ml2–момент инерции стержня относительно перпендикулярной к нему оси, проходящей через центр масс,
– расстояние от центра масс до требуемой оси.
Кинетическая энергия вращательного движения:
EK =
=.= .
По закону сохранения энергии, кинетическая энергия стержня в положении А равна его потенциальной энергии в положении В:
= Mgl ,
Отсюда υ = .
Подставляем числовые значения: υ =
»7 м/с.
Задача 19
Человек массой M1 = 60 кг находится на неподвижной платформе массой M = 100 кг. Какое число оборотов в минуту будет делать платформа, если человек будет двигаться по окружности радиуса 5 м вокруг оси вращения? Скорость движения человека относительно платформы равна 4 км/ч. Радиус платформы 10 м. Считать платформу однородным диском, а человека – точечной массой.
Решение
Первоначально платформа с человеком покоилась,
Момент импульса этой системы был равен нулю. Когда человек начнет двигаться по платформе, платформа будет вращаться в противоположном направлении. Если расстояние от человека до оси вращения платформы R, в месте нахождения человека U = w R. Таким образом, если человек движется относительно платформы со скоростью
υ, то относительно земли он будет двигаться со скоростью υ – w R, его момент импульса относительно оси платформы L1 = M1(υ – wR)R.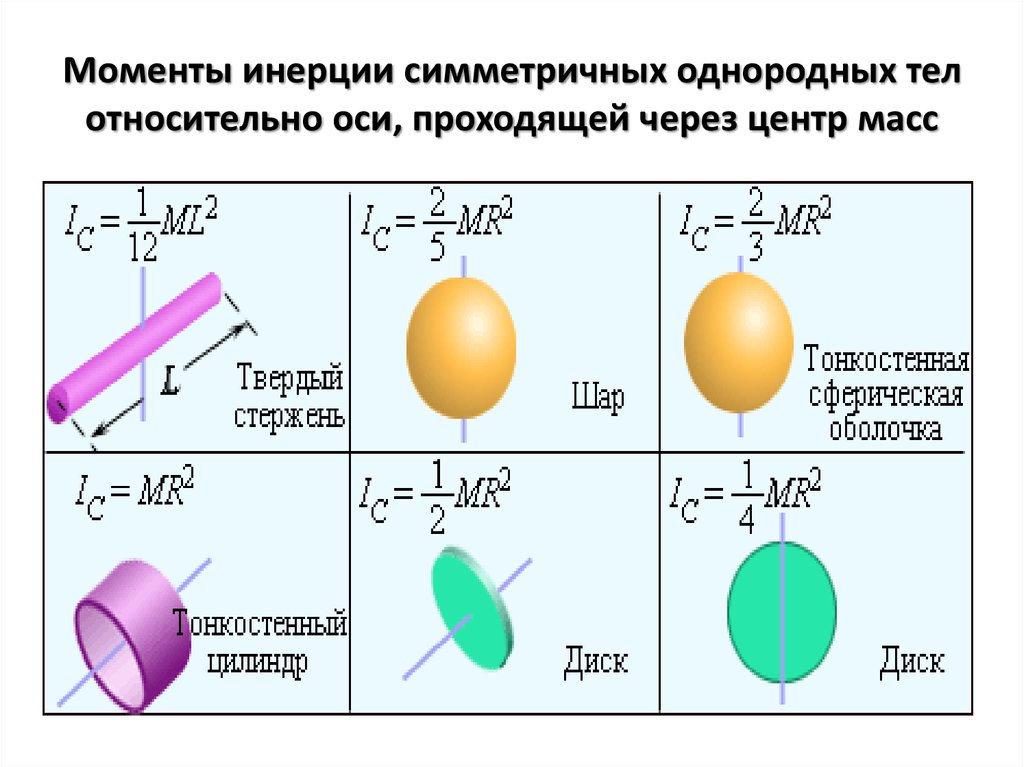 Момент импульса платформы относительно ее оси:
Момент импульса платформы относительно ее оси:
L = – IW,
где I – момент инерции платформы.
Поскольку платформа представляет собой однородный диск, то ее момент инерции относительно оси, проходящей через центр:
I = MR2.
Запишем закон сохранения момента импульса для данной системы:
O = L1 + L = M1(υ – w R) R – MR2w,
Отсюда можно определить угловую скорость вращения платформы:
W =
.
Число оборотов платформы в минуту определится из соотношения:
N = 60 = .
Подстановка числового значений дает:
N = = 0,49 об/мин.
Кинетическая энергия вращающегося твердого тела и момент инерции
Мы можем получить общее представление о вращении твердых тел и сравнить его с реальными ситуациями, или мы можем рассматривать некоторые реальные тела как почти твердые, чтобы получить наши результаты.
Это означает, что мы сначала находим кинетическую энергию вращающегося твердого тела и сравниваем ее с кинетической энергией частицы в прямолинейном движении, где мы можем найти меру массы вращающегося тела, называемую моментом инерции.
Кинетическая энергия вращающегося твердого тела
Рассмотрим твердое тело, которое вращается вокруг оси Y, как показано на рисунке 1. Тело состоит из большого количества частиц с массами $m_1$, $m_2$, $m_3$ и так далее. Масса $m_1$ находится на расстоянии $r_1$, а масса $m_2$ — на расстоянии $r_2$ от оси вращения и так далее. При вращении тела каждая частица тела движется по своей окружности определенного радиуса с центром на оси.
Угловая скорость $\omega$ всех частиц одинакова, но модуль линейной скорости (линейной скорости) не одинаков для всех частиц. Это связано с тем, что частице, находящейся на большем расстоянии от оси вращения тела, необходимо двигаться по окружности большего радиуса, но время, за которое все частицы совершают один оборот, одинаково, то есть угловая скорость для всех частиц постоянна. 92}$.
Это связано с тем, что частице, находящейся на большем расстоянии от оси вращения тела, необходимо двигаться по окружности большего радиуса, но время, за которое все частицы совершают один оборот, одинаково, то есть угловая скорость для всех частиц постоянна. 92}$.
На словах можно определить момент инерции тела, вращающегося вокруг оси, как произведение его массы на квадрат расстояния от оси вращения.
Если тело является не только точечной массой, но и твердым телом с равномерным распределением массы, вы не можете просто взять тело как одну точечную массу, вместо этого вы должны определить конкретный элемент тела и использовать интегрирование, чтобы найти момент инерции всего тела.
Момент инерции равномерного распределения масс
На самом деле нельзя точно сказать, какой момент инерции имеет то или иное тело. Это означает, что вы можете сделать как можно больше осей, вокруг которых может вращаться твердое тело. Поэтому момент инерции одного и того же тела различен для разных осей вращения.
Здесь мы обсуждаем момент инерции некоторых однородных распределений масс. Момент инерции не является постоянным для нетвердых тел даже при одной и той же оси вращения, а это связано с тем, что расстояние частиц нетвердого тела от оси вращения неодинаково.
Момент инерции стержня
Рассмотрим стержень длины $L$, перпендикулярный оси вращения через точку $O$, как показано на рис. 2. Теперь рассмотрим бесконечно малый элемент стержня массы $dm$ и толщины $dx$ на расстоянии $x $ от оси вращения.
Рис. 2 Стержень вращается вокруг оси, перпендикулярной стержню.Здесь также видно, что момент инерции различен для разных осей вращения.
Момент инерции цилиндра
Здесь находим момент инерции цилиндра. Также можно найти момент инерции диска (по сути диск — это цилиндр). Позже мы воспользуемся моментом инерции диска, чтобы найти момент инерции твердого шара.
Также можно найти момент инерции диска (по сути диск — это цилиндр). Позже мы воспользуемся моментом инерции диска, чтобы найти момент инерции твердого шара.
Сначала рассмотрим цилиндр высотой $h$, внутренний радиус которого равен $R_1$, а внешний радиус равен $R_2$, как показано на рисунке 3. Цилиндр вращается вокруг оси, проходящей через центры поперечных сечений цилиндра.
И рассмотрим бесконечно малый элемент объема цилиндра массы $dm$ и толщины $dr$. Внутренний радиус элемента равен $r$, а внешний радиус равен $r + dr$. Объем элемента цилиндра равен $dV = 2\pi r{\kern 1pt} dr{\kern 1pt} h$, а масса элемента равна $dm = \rho dV = 2\rho \pi r{ \kern 1pt} dr{\kern 1pt} h$. Здесь $\rho$ — плотность цилиндра. Значит момент инерции элемента равен 92$. Это то же самое, что и момент инерции тела массы $M$ относительно оси на расстоянии $R$ от оси вращения. Этот результат такой же, как момент инерции тонкого круглого кольца относительно оси, проходящей через его центр и перпендикулярной его плоскости.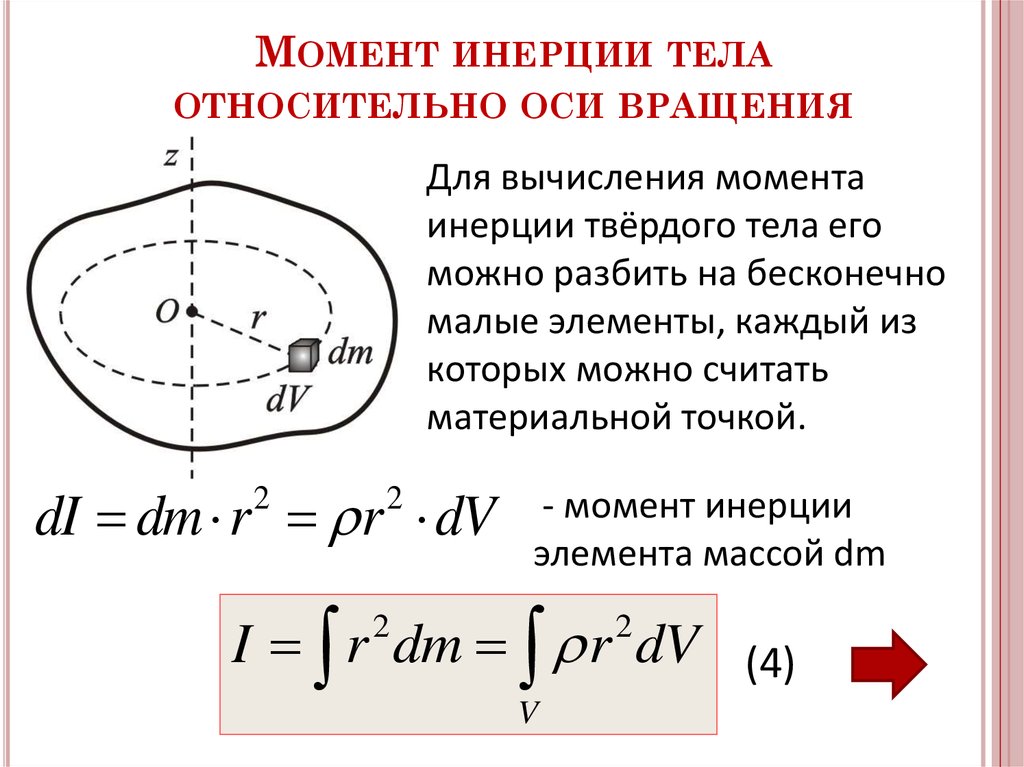
Момент инерции сферической оболочки
Рассмотрим сферическую оболочку, которая вращается вокруг оси x с центром в начале нашей системы координат, как показано на рисунке 4. Радиус сферической оболочки равен $R$. Для нахождения момента инерции сферической оболочки рассмотрим бесконечно малый элемент площади сферической оболочки массы $dm$, радиуса $r$ и толщины $dx$ на расстоянии $x$ от центра. 92} \конец{выравнивание*}\]
Момент инерции твердого шара
Теперь найдем момент инерции твердого шара радиуса $R$ относительно оси x вдоль его одного диаметра, как показано на рисунке 5. Центр шара является началом нашей системы координат. Вместо того, чтобы рассматривать сферическую оболочку как бесконечно малый элемент сферы, возьмем бесконечно малый диск радиуса $r$ и толщины $dx$ на расстоянии $x$ от центра сферы. Сначала найдем момент инерции элемента диска массой $dm$. 92}\]
Выполните интеграцию, и результат будет таким же, как вы видите здесь.
Была ли эта статья полезной?
Однородный круглый обруч радиусом R и массой m. Ось n проходит через центр обруча и ортогональна плоскости, содержащей обруч [5 баллов] В S0, [5 баллов] М;
Вопрос
Пошаговый ответ
Рассчитайте момент инерции следующих твердых тел относительно заданной неподвижной оси n. В каждом случае твердое тело имеет однородную массовую плотность: Круглый равномерный обруч…
Рассчитайте момент инерции следующих твердых тел относительно заданной неподвижной оси n. В каждом случае твердое тело имеет однородную массовую плотность:
Однородный круглый обруч радиуса R и массы m. Ось n проходит через центр обруча и ортогональна плоскости, содержащей обруч [5 баллов]
(6) Та же установка, что и деталь (а), но с заменой обруча однородным диском. 5 знаков] однородный стержень длины и массы In_ с двумя точечными массами М, прикрепленными к его концам: ось / взята через t0, проходящую через середине стержня и быть ортогональны стержню. добавка, [otal [красный пункт Inaen Подсказка: In S0, [5 баллов]
М;
добавка, [otal [красный пункт Inaen Подсказка: In S0, [5 баллов]
М;
Видеоответ:
Решено проверенным экспертом
Лучшее совпадение Вопрос:
Рассчитайте момент инерции следующих твердых тел относительно заданной неподвижной оси n. В каждом случае твердое тело имеет однородную массовую плотность: Однородный круглый обруч радиуса R и массы m. Ось n проходит через центр обруча и ортогональна плоскости, содержащей обруч [5 баллов] (6) Та же установка, что и деталь (а), но с заменой обруча однородным диском. 5 знаков] однородный стержень длины и массы In_ с двумя точечными массами М, прикрепленными к его концам: ось / взята через t0, проходящую через середине стержня и быть ортогональны стержню. добавка, [otal [красный пункт Inaen Подсказка: In S0, [5 баллов] М;
Рекомендованные видео
Стенограмма
Вопрос про момент инерции. В вопросе несколько частей. В первой части вопроса мы должны найти момент инерции кольца относительно его центральной оси, то есть момент инерции кольца.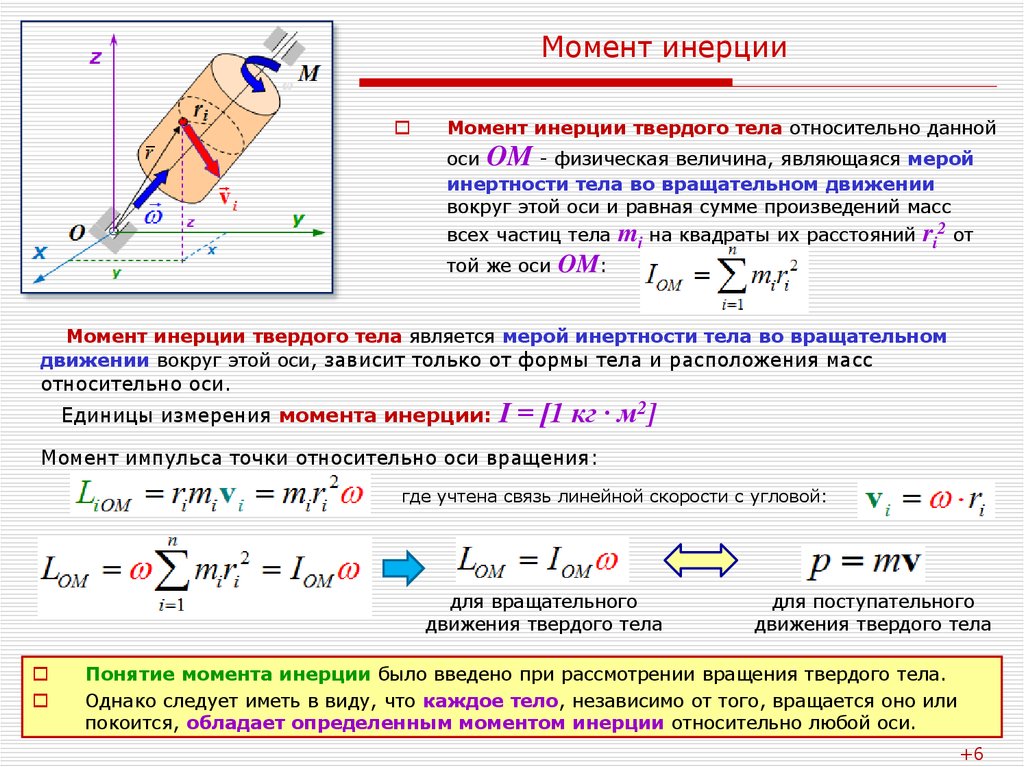 Итак, чтобы найти это, диаграмма будет выглядеть так: на диаграмме d m — наименьшая масса кольца на расстоянии r, поэтому его момент инерции будет равен di, что является дифференциальным моментом инерции для дифференциальной массы будет d m умножить на квадрат расстояния, и расстояния равны, а r остается одинаковым для всех тусклых масс, поэтому, чтобы получить полный момент инерции, интегрируйте это уравнение, так что оно станет d m r квадратным интегрированием. С обеих сторон. Теперь это станет полным моментом инерции и квадратом r из интегрирования и интегрирования d m. Теперь нашим окончательным ответом будет i, равное m r в квадрате, потому что интегрирование d m равно m. Это наш первый ответ в части b вопроса: существует тонкое кольцо толщиной d r на расстоянии r от центра, поэтому в части b мы дали это тонкое кольцо, как показано на рисунке 10 кольцо радиуса r в Предыдущее кольцо радиуса прописной r, есть тонкое кольцо радиуса. Небольшое r, поэтому масса на единицу длины будет одинаковой.
Итак, чтобы найти это, диаграмма будет выглядеть так: на диаграмме d m — наименьшая масса кольца на расстоянии r, поэтому его момент инерции будет равен di, что является дифференциальным моментом инерции для дифференциальной массы будет d m умножить на квадрат расстояния, и расстояния равны, а r остается одинаковым для всех тусклых масс, поэтому, чтобы получить полный момент инерции, интегрируйте это уравнение, так что оно станет d m r квадратным интегрированием. С обеих сторон. Теперь это станет полным моментом инерции и квадратом r из интегрирования и интегрирования d m. Теперь нашим окончательным ответом будет i, равное m r в квадрате, потому что интегрирование d m равно m. Это наш первый ответ в части b вопроса: существует тонкое кольцо толщиной d r на расстоянии r от центра, поэтому в части b мы дали это тонкое кольцо, как показано на рисунке 10 кольцо радиуса r в Предыдущее кольцо радиуса прописной r, есть тонкое кольцо радиуса. Небольшое r, поэтому масса на единицу длины будет одинаковой. Масса на единицу площади. То есть массовая плотность для кольца будет одинаковой. Предположим, что сигма — это массовая плотность, поэтому это будет массовое предложение, деленное на pi r квадрат. Теперь из этого уравнения мы можем упростить. Мы можем получить d m равным 2 pi r d r, умноженным на сигму, поэтому оно будет равно m после m, деленного на pi r в квадрате, умноженного на 2, pi r d r. Теперь, интегрируя, мы получим интегрирование di, равное интегрированию, d, m r квадрат: это новое уравнение. Теперь интеграция будет от 0 до капитала. I, который является полным моментом инерции здесь. D м составляет 2 м. Делится на r в квадрате. Интеграция от 0 до прописной, r и r d. R, умноженный на r квадрат, остается, как теперь из этого уравнения. После интегрирования мы получим полный момент инерции для данного кольца, i равный m r квадрату на 2. Это наш второй ответ сейчас, в части c, есть 1 стержень, для которого сначала мы должны найти момент инерция без стрелкового человека и еще один с стрелочным манипулятором.
Масса на единицу площади. То есть массовая плотность для кольца будет одинаковой. Предположим, что сигма — это массовая плотность, поэтому это будет массовое предложение, деленное на pi r квадрат. Теперь из этого уравнения мы можем упростить. Мы можем получить d m равным 2 pi r d r, умноженным на сигму, поэтому оно будет равно m после m, деленного на pi r в квадрате, умноженного на 2, pi r d r. Теперь, интегрируя, мы получим интегрирование di, равное интегрированию, d, m r квадрат: это новое уравнение. Теперь интеграция будет от 0 до капитала. I, который является полным моментом инерции здесь. D м составляет 2 м. Делится на r в квадрате. Интеграция от 0 до прописной, r и r d. R, умноженный на r квадрат, остается, как теперь из этого уравнения. После интегрирования мы получим полный момент инерции для данного кольца, i равный m r квадрату на 2. Это наш второй ответ сейчас, в части c, есть 1 стержень, для которого сначала мы должны найти момент инерция без стрелкового человека и еще один с стрелочным манипулятором.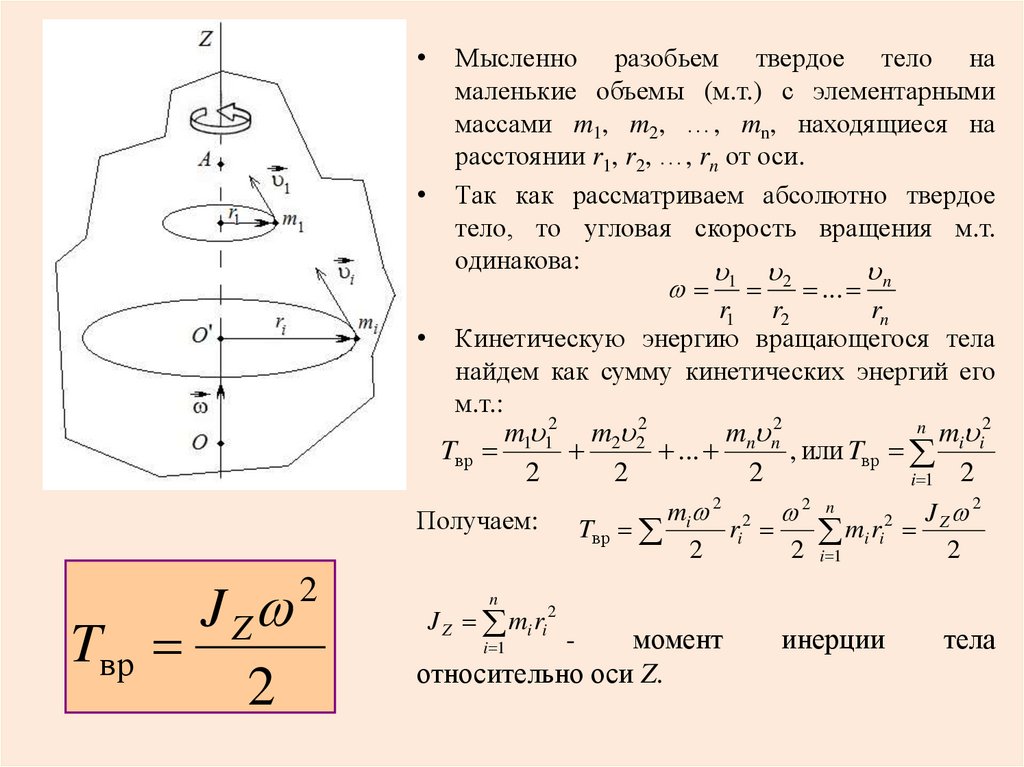 Итак, прежде всего, найдем момент инерции родаина на собственной оси. Итак, схема будет такой. Имеется 1 стержень и эта точка является его центром. Рассмотрим центральную ось так: возьмем наименьшую массу d m или наименьшую длину стержня dx на расстоянии x x. I, наименьшая длина, общая длина стержня капитальна. L теперь длина половинки будет плюс l на 2 и длина половинки вдоль отрицательной оси x. Это минус l на 2. Теперь из этого уравнения d m будет равно m на l, умноженное на de x теперь di. Мы знаем, что d, i равно d m s. Масса этого маленького элемента стержня и di – его момент инерции, поэтому он будет равен d m. Массу умножить на квадрат расстояния, так что di — момент инерции наименьшей части, и найти общий момент инерции. Применим интегрирование от 0. К i d i, и оно будет равно значению d m — m l. Теперь, интегрирование, минус l на 2 до плюс l на 2 d x x квадрат теперь после упрощения этого уравнения, мы получим m на m разделить на 3. L и оставшаяся часть будет l, куб, деленный на 8 минус минус l куб, деленный на 8 Пи.
Итак, прежде всего, найдем момент инерции родаина на собственной оси. Итак, схема будет такой. Имеется 1 стержень и эта точка является его центром. Рассмотрим центральную ось так: возьмем наименьшую массу d m или наименьшую длину стержня dx на расстоянии x x. I, наименьшая длина, общая длина стержня капитальна. L теперь длина половинки будет плюс l на 2 и длина половинки вдоль отрицательной оси x. Это минус l на 2. Теперь из этого уравнения d m будет равно m на l, умноженное на de x теперь di. Мы знаем, что d, i равно d m s. Масса этого маленького элемента стержня и di – его момент инерции, поэтому он будет равен d m. Массу умножить на квадрат расстояния, так что di — момент инерции наименьшей части, и найти общий момент инерции. Применим интегрирование от 0. К i d i, и оно будет равно значению d m — m l. Теперь, интегрирование, минус l на 2 до плюс l на 2 d x x квадрат теперь после упрощения этого уравнения, мы получим m на m разделить на 3. L и оставшаяся часть будет l, куб, деленный на 8 минус минус l куб, деленный на 8 Пи.