23. Вычисление момента инерции тонкого однородного стержня относительно перпендикулярной оси.

Пусть тонкий стержень имеет длину l и массу m. Разделим его на малые элементы длины dx (рис.27), масса которых . Если выбранный элемент находится на расстоянии x от оси, то его момент инерции , т.е.

Интегрируя последнее соотношение в пределах от 0 до l/2 и удваивая полученное выражение (для учета левой половины стержня), получим

(п.1)

Это выражение может быть получено и другим способом, с помощью метода подобия. Будем считать, что рассматриваемый стержень состоит из двух половин (рис.28). Каждая из них имеет массу m/2 и длину l/2 .

Выражение для момента инерции стержня должно включать его массу и длину, так как это единственные параметры, определяющие его инерционные свойства при вращении. Пусть (п. 2)

где k— неизвестный коэффициент.

Для каждой из половин стержня при вращении вокруг оси AA^` можно найти момент инерции, используя (п.2) (п.3)

Полный момент инерции стержня

(п.4)

Но этот же момент инерции, согласно (п.2) равен kml². Приравнивая (п.4) и (п.2) имеем

(п.5)

или и, следовательно,

(п.6)

т.е. , что совпадает с (п.1)

24. Вычисление момента инерции бесконечно круглого кольца относительно оси, перпендикулярной плоскости кольца.

Для расчета моментов инерции тонкого кольца/диска массы

m и радиуса R выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рис. 32). Определим момент инерции тонкого однородного кольца/диска относительно оси z , перпендикулярной к плоскости диска. Рассмотрим бесконечно тонкое кольцо с внутренним радиусом r и наружным r+dr. Площадь такого кольца ds=2r $\pi$ dr, а его масса , где S= $\pi$ R² — площадь всего кольца/диска. Момент инерции тонкого кольца найдется по формуле dJ=dmr². Момент инерции всего диска определяется интегралом

(п.18)

Для определения J_x воспользуемся симметрией диска (J_x=J_y) и утверждением (п.10), полученным при расчете момента инерции прямоугольной пластины. При этом из (п.10) получаем

J_z=2J_x (п.19)

Откуда

(п. 20)

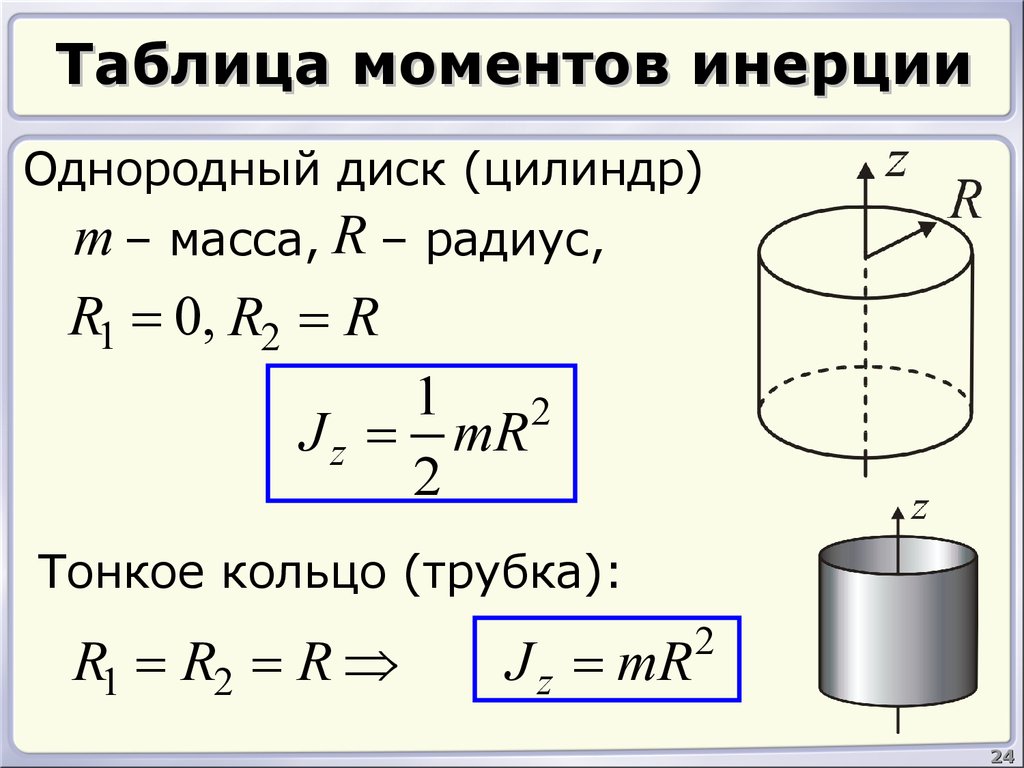
25. Вычисление момента инерции однородного сплошного цилиндра (диска) относительно продольной геометрической оси.

Выберем оси системы координат, совпадающие с главными центральными осями так, как показано на рис.33. Определим момент инерции цилиндра относительно оси z. Цилиндр представляет собой набор тонких дисков с массами dm и моментами инерции . Момент инерции цилиндра равен сумме моментов инерций dJ_z тонких дисков

(п.21)

где — радиус цилиндра, — его масса.

Пусть теперь ось вращения проходит через центр масс цилиндра перпендикулярно его продольной оси (рис.33) и совпадает с осью координат x. Представим цилиндр как совокупность тонких дисков толщиной

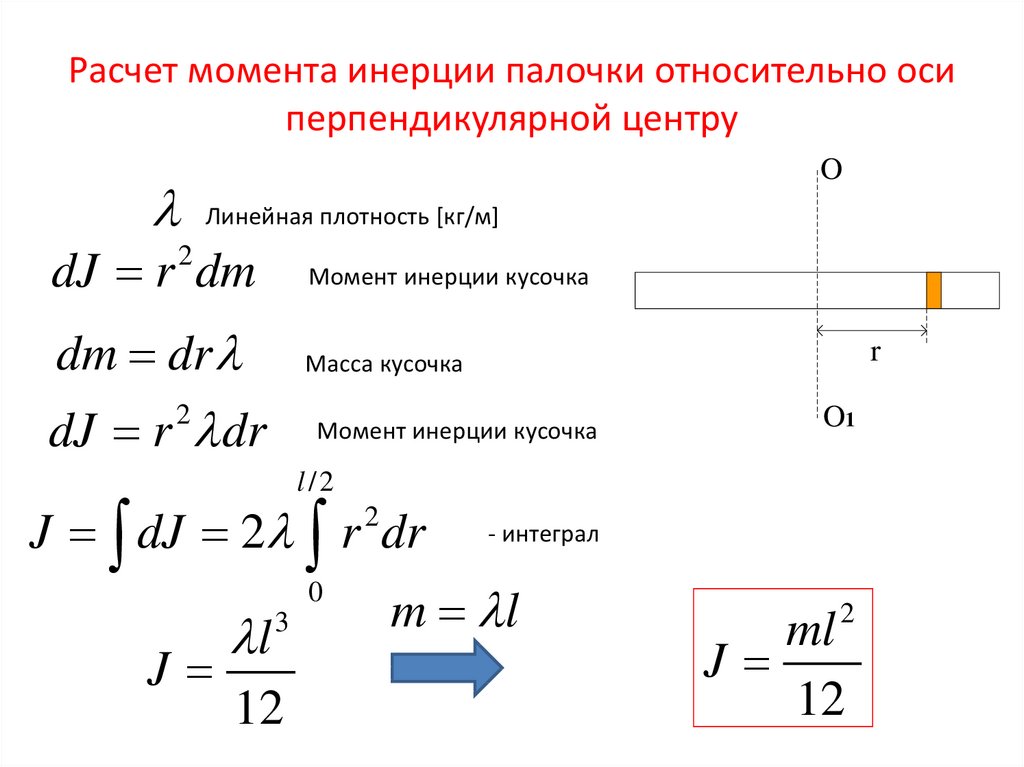dz, массой ( l — длина цилиндра). Момент инерции тонкого диска относительно оси Ox dJ^`_x в соответствии с (п. 20) и теоремой Гюйгенса-Штейнера равен

(п.22)

где z — расстояние от диска до центра цилиндра.

Момент инерции всего цилиндра найдем после интегрирования по z (по всей длине цилиндра)

(п.23)

Откуда получаем

(п.24)

Момент инерции стержня однородного и тонкого. Использование теоремы Штейнера. Пример задачи

В физике для описания инерционных качеств поступательного или линейного движения пользуются понятием массы тела. Если же движение рассматривается вокруг некоторой оси вращения, то используют несколько иную физическую характеристику — момент инерции. В данной статье рассмотрим, что это за величина и как можно рассчитать момент инерции тонкого стержня.

Вращение и момент инерции

Инерции момент проще всего ввести для материальной точки.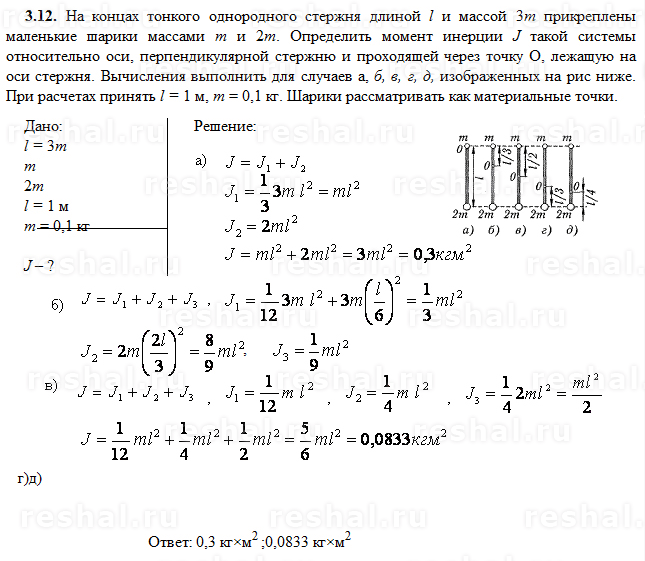 Когда она, обладая массой M, вращается вокруг оси, описывая окружность радиусом R, то момент инерции для нее определяется по формуле:

I = M*R².

Любое реальное тело, какой бы сложной геометрической формой оно не обладало, можно представить как совокупность материальных точек. Это означает, что для всего тела или системы твердых тел величину I можно вычислить, если проинтегрировать по элементарным массам dm выражение выше. Общая формула для определения момента инерции имеет вид:

I = ∫_m(r²*dm).

Через объем и плотность это равенство записывается в таком виде:

I = ∫_V(ρ*r²*dV).

Его часто применяют для вычисления значений I конкретных геометрических объектов.

Физический смысл инерции момента I заключается в том, что он определяет, насколько «сложно» данной силе, создающей некоторый крутящий момент, раскрутить или остановить вращающуюся систему. Иными словами, I характеризует инерционные свойства изучаемой системы.

Вопрос на засыпку – это веселая игра или неловкая ситуация?

Зыбучий, ненадежный, неустойчивый песок – плохая опора, и об этом знает каждый из нас. Более того,…

Самым известным примером использования момента инерции является маховик двигателя внутреннего сгорания в автомобилях. Благодаря большому значению величины I, маховик обеспечивает плавность движения автомобиля, сглаживая любые резкие воздействия на коленчатый вал. Пример иного характера, где также важно знать момент инерции, — это закон сохранения момента импульса. Применяется он для поворота вокруг оси искусственных спутников в космическом пространстве Земли.

Тонкий стержень и оси вращения

Далее будет рассмотрен момент инерции стержня относительно осей (разных). Вычисления будут проводиться для тонкого стержня, который обладает однородным распределением массы, то есть его плотность во всех точках является постоянной величиной.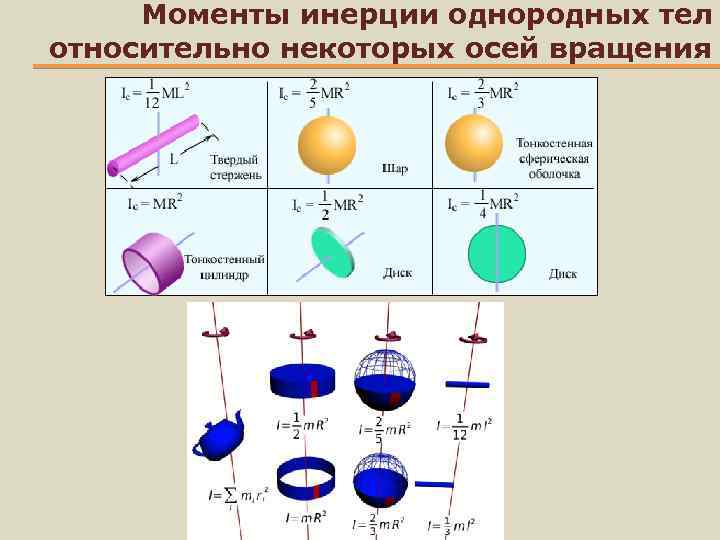 Под тонким понимают такой стержень, у которого ширина (толщина) намного меньше, чем его длина L. Для обозначения его массы будем использовать букву M.

Из приведенных выше формул следует, что величина I зависит от относительного положения тела и оси вращения. Для стержня можно выделить три основных оси. Одна из них проходит через длину всего стержня. Поскольку его толщина стремится к нулю, то момент инерции для такого положения тела также будет стремиться к этому значению.

Две другие оси перпендикулярны длине рассматриваемого тела. Одна из них проходит через центр масс, назовем ее O₁, вторая — через конец стержня, обозначим ее O₂. Относительно них и вычислим величину I.

Момент инерции относительно O1

В первую очередь выпишем общую формулу. Имеем:

Вопрос на засыпку – это веселая игра или неловкая ситуация?

Зыбучий, ненадежный, неустойчивый песок – плохая опора, и об этом знает каждый из нас. Более того,…

I = ∫_V(ρ*r²*dV).

Обозначим площадь сечения стержня буквой S. Очевидно, что она стремится к нулю, поскольку стержень тонкий. Но это обозначение удобно ввести для выполнения дальнейших расчетов.

Теперь мысленно разобьем стержень на бесконечное количество мелких кусочков, каждый из которых будет иметь сечение S и толщину dl. Заменяя r на l в формуле выше, получаем:

I = ∫_L(ρ*S*l²*dl).

Остается только подставить правильные пределы интегрирования и записать конечную формулу. Поскольку ось O₁ проходит через середину стержня, то пределы интегрирования будут следующими:

I = ∫_-L/2^L/2(ρ*S*l²*dl).

Результатом вычисления этого интеграла является следующая формула:

I = M*L²/12.

Таким образом, момент инерции тонкого стержня определяется его массой и длиной.

Инерции момент относительно O2

Теперь рассмотрим ситуацию, когда ось вращения будет проходить через любой из концов стержня и будет ему перпендикулярна. Соответствующую формулу можно получить из записанного выше интеграла, если правильно подставить пределы интегрирования. Однако мы пойдем несколько иным путем и определим инерции момент с помощью теоремы Штейнера.

Она говорит о том, что если две оси являются параллельными друг другу и одна из них (ось O) проходит через центр масс тела, то момент инерции относительно второй оси может быть вычислен с помощью такого равенства:

I = I₀ + M*h².

Здесь I₀ — момент инерции стержня относительно оси O, h — дистанция между осями.

Эту формулу можно с успехом применить для нашего случая. Поскольку I₀ мы рассчитали в предыдущем пункте статьи относительно оси O₁, и расстояние между O₁ и O₂ составляет L/2, то с использованием теоремы Штейнера получаем следующий результат:

I = I₀ + M*h² = M*L²/12 + M*L²/4 = M*L²/3.

Таким образом, для стержня величина I относительно оси O₂ в 4 раза больше, чем относительно оси O₁. Это означает, что для придания одинакового углового ускорения стержню в случае вращения вокруг оси O₂ следует приложить в 4 раза больший крутящий момент, чем в случае оси O₁.

Пример задачи

Дан тонкий стержень длиною 0,5 м и массой 5 кг. На расстоянии 2/5 от его конца расположена ось вращения, перпендикулярная стержню. Чему равен момент инерции системы?

Для решения задачи воспользуемся теоремой Штейнера. Расстояние между осями O₁ и заданной в задаче равно:

h = 0,25 — 0,2 = 0,05 м.

Тогда получаем момент инерции стержня (однородного):

I = I₀ + M*h² = 0,5²/12 + 0,05² = 0,117 кг*м².

В СИ момент инерции стержня измеряется в указанных единицах.

11.6: Расчет моментов инерции

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

18253

• OpenStax
• OpenStax

Цели обучения

• Расчет момента инерции твердых тел однородной формы
• Применить теорему о параллельных осях, чтобы найти момент инерции относительно любой оси, параллельной уже известной
• Расчет момента инерции для составных объектов

В предыдущем подразделе мы определили момент инерции, но не показали, как его вычислить. В этом подразделе мы покажем, как рассчитать момент инерции для нескольких стандартных типов объектов, а также как использовать известные моменты инерции, чтобы найти момент инерции для смещенной оси или для составного объекта. Этот раздел очень полезен для того, чтобы увидеть, как применять общее уравнение к сложным объектам (навык, который имеет решающее значение для более продвинутых курсов физики и инженерии). 92 \]

для всех точечных масс, составляющих объект. Поскольку \(r\) — это расстояние до оси вращения от каждой части массы, из которой состоит объект, момент инерции любого объекта зависит от выбранной оси. Чтобы убедиться в этом, давайте возьмем простой пример двух масс на конце безмассового (пренебрежимо малой массы) стержня (рис. \(\PageIndex{1}\)) и рассчитаем момент инерции относительно двух разных осей. В этом случае суммирование по массам простое, потому что две массы на конце штанги можно аппроксимировать как точечные массы, и поэтому сумма состоит только из двух членов.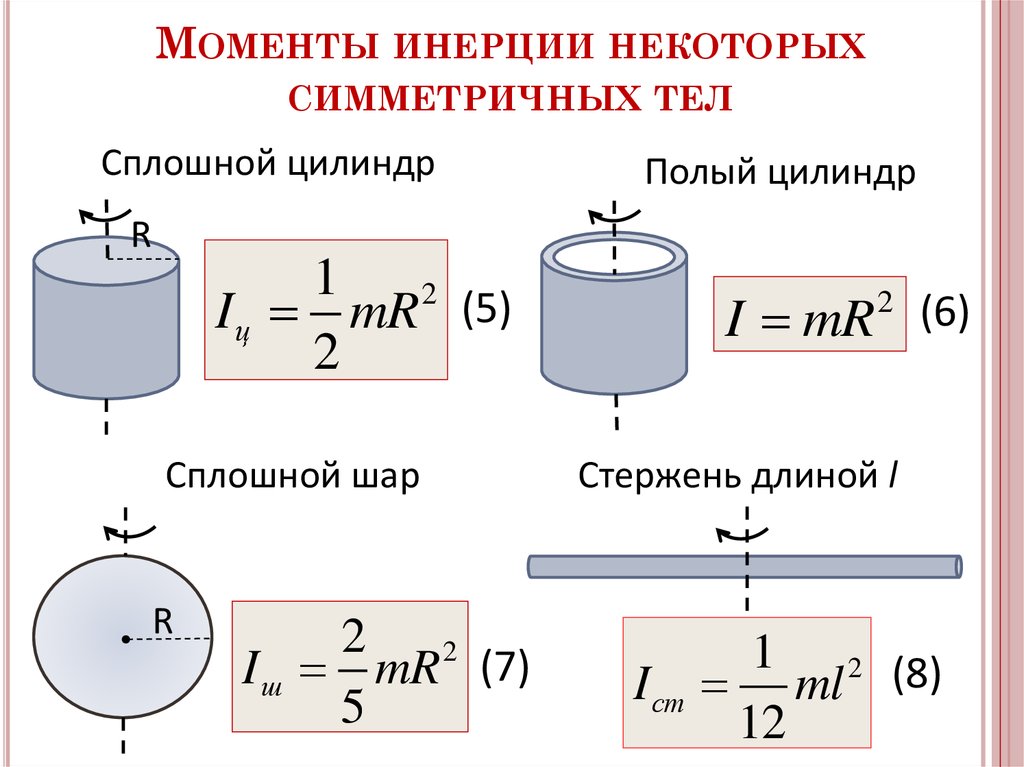

9{2} \ldotp\]

Из этого результата можно сделать вывод, что вращать штангу вокруг конца в два раза труднее, чем вокруг ее центра.

Рисунок \(\PageIndex{1}\): (a) Штанга с осью вращения, проходящей через ее центр; (b) штанга с осью вращения через один конец.

В этом примере у нас было две точечные массы, и их сумму было просто вычислить. Однако, чтобы иметь дело с объектами, которые не являются точечными, нам нужно тщательно продумать каждый член уравнения. Уравнение просит нас просуммировать по каждой «части массы» на определенном расстоянии от оси вращения. Но что именно означает каждый «кусок массы»? Напомним, что в нашем выводе этого уравнения каждая часть массы имела одинаковую величину скорости, что означает, что вся часть должна была иметь единственное расстояние r до оси вращения. Однако это невозможно, если мы не возьмем бесконечно малый кусок массы dm, как показано на рисунке \(\PageIndex{2}\). 9{2} dm \ldotp \label{10.19}\]

Фактически это та форма, которая нам нужна для обобщения уравнения для сложных форм.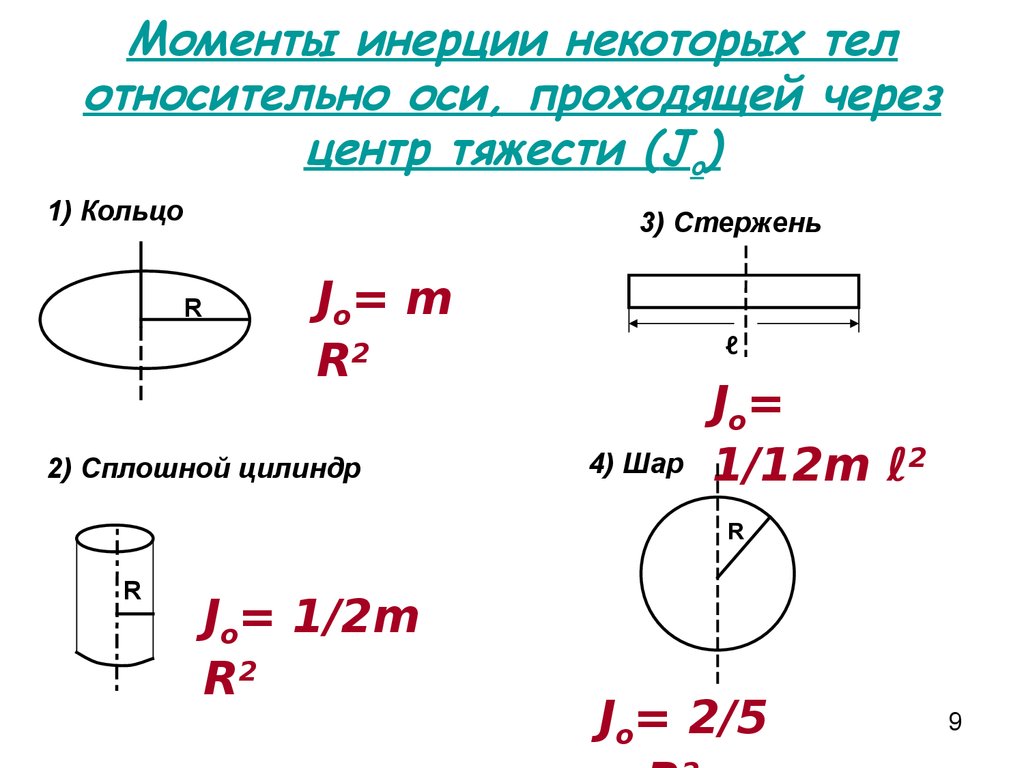 Лучше всего детально проработать конкретные примеры, чтобы понять, как рассчитать момент инерции для конкретных форм. Это основное внимание в остальной части этого раздела.

Однородный тонкий стержень с осью, проходящей через центр

Рассмотрим однородный (по плотности и форме) тонкий стержень массы M и длины L, как показано на рисунке \(\PageIndex{3}\). Нам нужен тонкий стержень, так что мы можем предположить, что площадь поперечного сечения стержня мала, и стержень можно рассматривать как цепочку масс вдоль одномерной прямой линии. В этом примере ось вращения перпендикулярна стержню и для простоты проходит через его середину. Наша задача — вычислить момент инерции относительно этой оси. Ориентируем оси так, чтобы ось z была осью вращения, а ось x проходила по длине стержня, как показано на рисунке. Это удобный выбор, потому что тогда мы можем интегрировать по оси x.

Рисунок \(\PageIndex{3}\): Расчет момента инерции I для однородного тонкого стержня относительно оси, проходящей через центр стержня.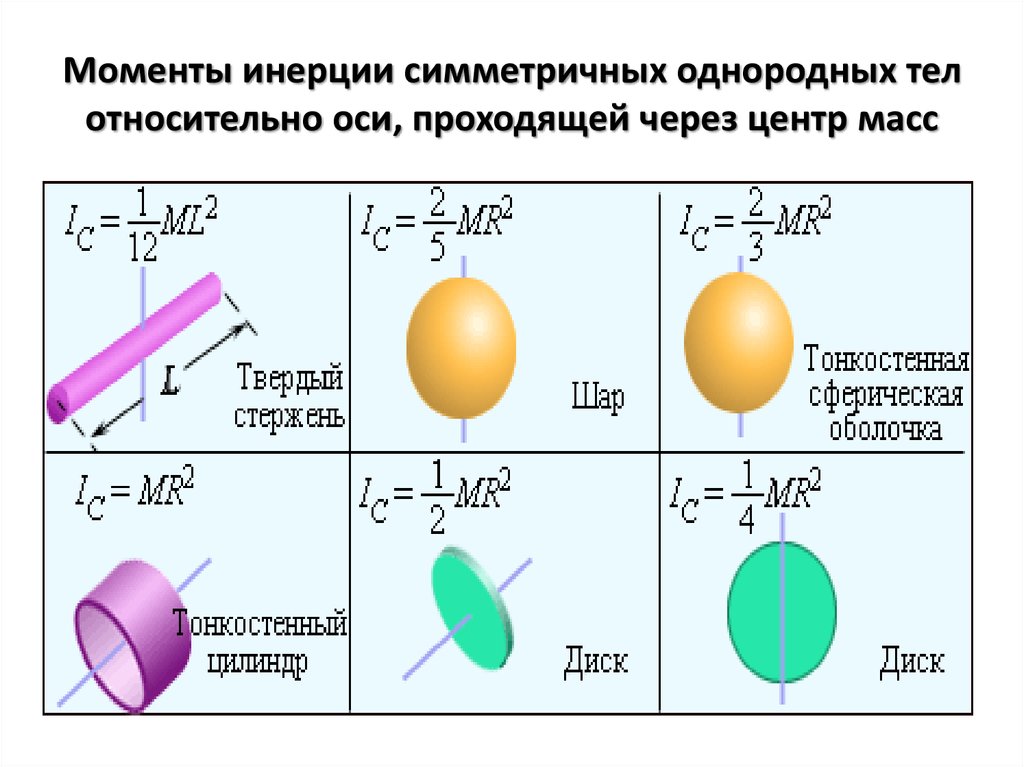

Мы определяем dm как небольшой элемент массы, из которого состоит стержень. Интеграл момента инерции представляет собой интеграл по распределению масс. Однако мы умеем интегрировать по пространству, а не по массе. Поэтому нам нужно найти способ связать массу с пространственными переменными. Мы делаем это, используя линейную плотность массы \(\лямбда\) объекта, которая является массой на единицу длины. Поскольку массовая плотность этого объекта однородна, мы можем написать

\[\lambda = \frac{m}{l}\; или же\; m = \lambda l \ldotp\]

Если мы возьмем дифференциал каждой части этого уравнения, мы найдем

\[dm = d(\lambda l) = \lambda (dl)\]

, так как \( \лямбда\) постоянна. Мы решили сориентировать стержень вдоль оси x для удобства — именно здесь этот выбор становится очень полезным. Заметим, что кусок стержня dl полностью лежит вдоль оси x и имеет длину dx; на самом деле в этой ситуации dl = dx. Поэтому мы можем записать dm = \(\lambda\)(dx), что дает нам переменную интегрирования, с которой мы знаем, как работать. Расстояние каждого куска массы dm от оси задается переменной x, как показано на рисунке. Складываем все вместе, получаем 9{2} \ldotp \end{split}\]

Далее мы вычисляем момент инерции для того же однородного тонкого стержня, но с другим выбором оси, чтобы можно было сравнить результаты. Мы ожидаем, что момент инерции будет меньше относительно оси, проходящей через центр масс, чем ось конечной точки, как это было в примере со штангой в начале этого раздела. Это происходит потому, что больше массы распределено дальше от оси вращения.

Однородный тонкий стержень с осью на конце

Теперь рассмотрим тот же однородный тонкий стержень массой \(M\) и длиной \(L\), но на этот раз мы перенесем ось вращения на конец стержня. Мы хотим найти момент инерции относительно этой новой оси (рисунок \(\PageIndex{4}\)).

Рисунок \(\PageIndex{4}\): Расчет момента инерции \(I\) однородного тонкого стержня относительно оси, проходящей через конец стержня.

Величина \(dm\) снова определяется как малый элемент массы, из которого состоит стержень. {2} \lambda dx \ldotp\] 9{2} \ldotp \label{ThinRod} \end{align} \]

Обратите внимание, что инерция вращения стержня относительно его конечной точки больше, чем инерция вращения вокруг его центра (в соответствии с примером со штангой) в четыре раза .

Теорема о параллельной оси

Сходство между процессом нахождения момента инерции стержня относительно оси, проходящей через его середину, и относительно оси, проходящей через его конец, поразительно и предполагает, что может существовать более простой метод определения момент инерции стержня относительно любой оси, параллельной оси, проходящей через центр масс. Такая ось называется 9{2} \ldotp\]

Этот результат согласуется с нашим более длинным расчетом (уравнение \ref{ThinRod}). Уравнение \ref{10.20} — полезное уравнение, которое мы применяем в некоторых примерах и задачах.

Exrecise \(\PageIndex{1}\)

Чему равен момент инерции цилиндра радиуса \(R\) и массы \(m\) относительно оси, проходящей через точку на поверхности, как показано ниже ?

Ответить

\[I_{параллельная ось} = I_{центр\; из\; масса} + md^{2} = mR^{2} + mR^{2} = 2mR^{2} \nonumber \]

Однородный тонкий диск вокруг оси, проходящей через центр ось через его центр (рис.

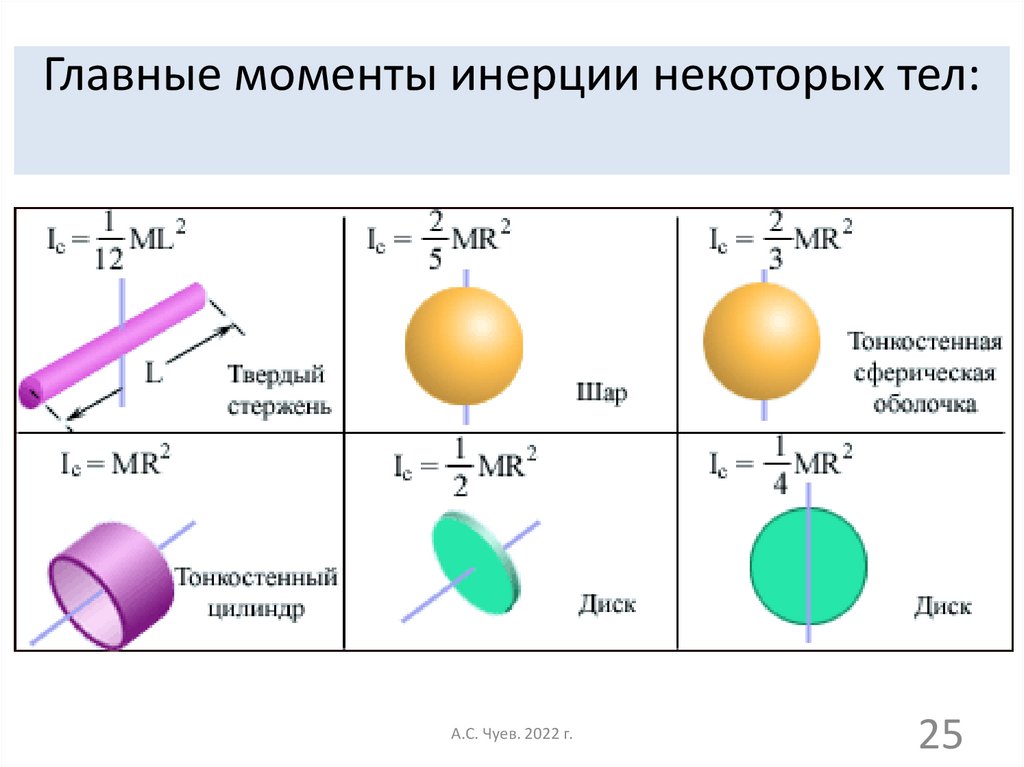\(\PageIndex{5}\)).

Рисунок \(\PageIndex{5}\): Расчет момента инерции тонкого диска относительно оси, проходящей через его центр.

Поскольку диск тонкий, мы можем считать, что масса полностью распределена в плоскости xy. Мы снова начинаем с отношения для поверхностная массовая плотность , которая представляет собой массу на единицу площади поверхности. Поскольку она однородна, поверхностная массовая плотность \(\sigma\) постоянна:

\[\sigma = \frac{m}{A}\] или \[\sigma A = m\], поэтому \[dm = \sigma (dA)\]

Теперь используем упрощение площади. Площадь можно представить как состоящую из ряда тонких колец, где каждое кольцо представляет собой приращение массы dm радиуса \(r\), равноудаленное от оси, как показано в части (b) рисунка. Таким образом, бесконечно малая площадь каждого кольца \(dA\) определяется как длина каждого кольца (\(2 \pi r\)) умноженная на бесконечно малую ширину каждого кольца \(dr\): 9{2} \ldotp \end{split}\]

Обратите внимание, что это соответствует значению, указанному на рис. 10.5.4.

Расчет момента инерции для составных объектов

Теперь рассмотрим составной объект, подобный показанному на рисунке \(\PageIndex{6}\), на котором изображен тонкий диск на конце тонкого стержня. Это не может быть легко интегрировано, чтобы найти момент инерции, потому что это объект неоднородной формы. Однако, если мы вернемся к первоначальному определению момента инерции как суммы, мы можем сделать вывод, что момент инерции составного объекта может быть найден из суммы каждой части объекта:

\[I_{total} = \sum_{i} I_{i} \ldotp \label{10.21}\]

Важно отметить, что моменты инерции объектов в уравнении \(\PageIndex{6 }\) вокруг общей оси . В случае этого объекта это будет стержень длиной L, вращающийся вокруг своего конца, и тонкий диск радиуса \(R\), вращающийся вокруг оси, смещенной от центра на расстояние \(L + R\) , где \(R\) — радиус диска. Определим массу стержня как m _r , а массу диска как \(m_d\). 9{2} \ldotp\]

Применение расчета момента инерции для решения задач

Теперь давайте рассмотрим некоторые практические применения расчета момента инерции.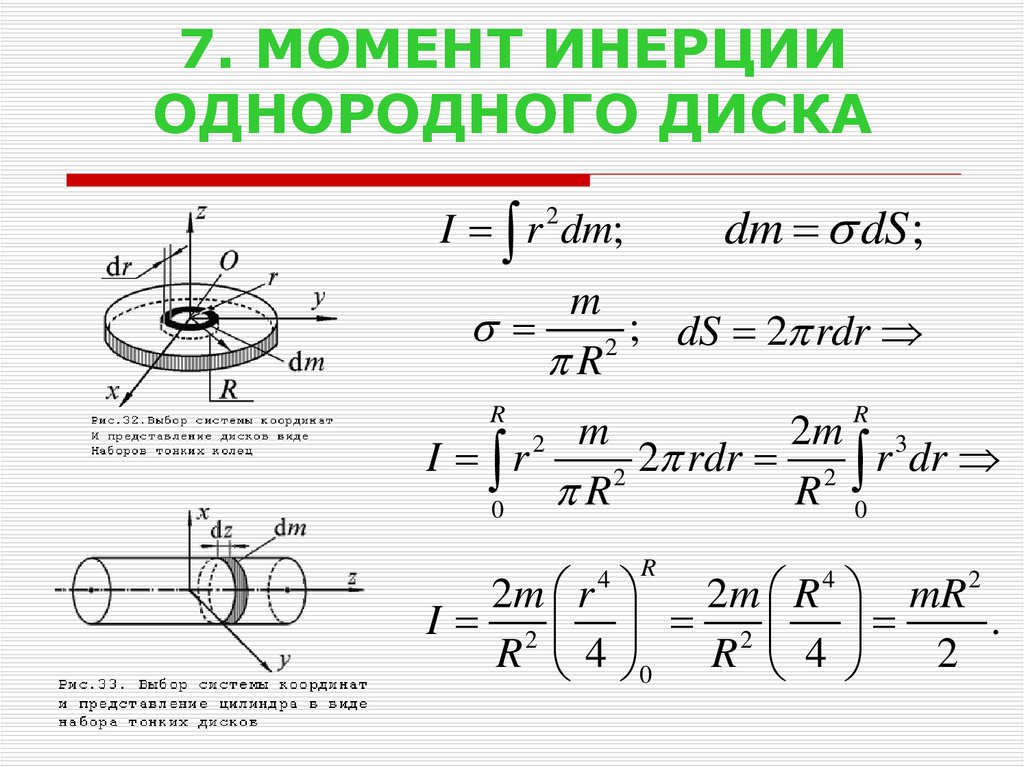

Пример \(\PageIndex{1}\): Человек на карусели

Ребенок массой 25 кг стоит на расстоянии \(r = 1,0\, м\) от оси вращающейся карусели. обход (Рисунок \(\PageIndex{7}\)). Карусель можно представить как однородный сплошной диск массой 500 кг и радиусом 2,0 м. Найдите момент инерции этой системы.

Рисунок \(\PageIndex{7}\): Расчет момента инерции ребенка на карусели.

Стратегия

Эта задача включает расчет момента инерции. Нам даны масса и расстояние до оси вращения ребенка, а также масса и радиус карусели. Поскольку масса и размер ребенка намного меньше карусели, мы можем аппроксимировать ребенка как точечную массу. Используемые обозначения: m _c = 25 кг, r 9{2} \ldotp \nonumber \]

Значимость

Значение должно быть близко к моменту инерции самой карусели, потому что она имеет гораздо большую массу, распределенную от оси, чем ребенок .

Пример \(\PageIndex{2}\): Стержень и твердая сфера

Найдите момент инерции комбинации стержня и сплошной сферы относительно двух осей, как показано ниже.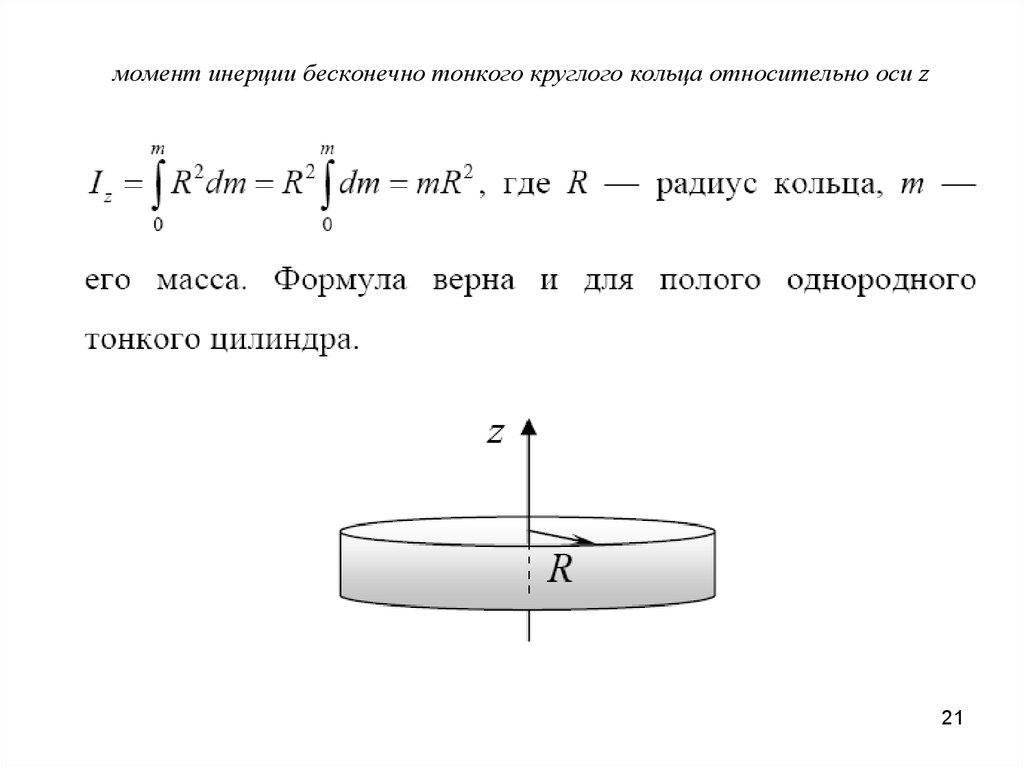 Стержень имеет длину 0,5 м и массу 2,0 кг. Радиус шара 20 см, масса 1 кг.

Стратегия

Поскольку в обоих случаях у нас есть составной объект, мы можем использовать теорему о параллельных осях, чтобы найти момент инерции относительно каждой оси. В (а) центр масс сферы расположен на расстоянии \(L + R\) от оси вращения. В (б) центр масс сферы расположен на расстоянии \(R\) от оси вращения. В обоих случаях момент инерции стержня направлен вокруг оси на одном конце. Обратитесь к Таблице 10.4 для моментов инерции для отдельных объектов. 9{2} \ldotp \end{split}\]

Значение

Использование теоремы о параллельных осях упрощает вычисление момента инерции составных объектов. Мы видим, что момент инерции больше в (а), чем в (б). Это связано с тем, что ось вращения ближе к центру масс системы в (б). Простая аналогия — стержень. Момент инерции относительно одного конца равен \(\frac{1}{3}\)mL ² , а момент инерции через центр масс по его длине равен \(\frac{1}{12}\ )мл ² .

Пример \(\PageIndex{3}\): угловая скорость маятника

Маятник в форме стержня (рисунок \(\PageIndex{8}\)) выходит из состояния покоя под углом 30° . Имеет длину 30 см и массу 300 г. Какова его угловая скорость в нижней точке?

Рисунок \(\PageIndex{8}\): Маятник в виде стержня выпущен из состояния покоя под углом 30°.

Стратегия

Используйте сохранение энергии для решения проблемы. В момент выпуска маятник обладает гравитационной потенциальной энергией, которая определяется по высоте центра масс над его нижней точкой при качании. В нижней части качелей вся гравитационная потенциальная энергия преобразуется во вращательную кинетическую энергию. 9{2}) \left(\dfrac{3}{0,3\; m}\right) (1 — \cos 30)} = 3,6\; рад/с \ldotp \nonumber\]

Значение

Обратите внимание, что угловая скорость маятника не зависит от его массы.

---

1. Наверх

• Была ли эта статья полезной?

1. Тип артикула

   Раздел или Страница

   Автор

   ОпенСтакс

   Лицензия

   СС BY

   Показать оглавление

   нет

   Включено

   да

2. Теги

   1. линейная массовая плотность
   2. параллельная ось
   3. теорема о параллельных осях
   4. источник-физ-4031
   5. поверхностная массовая плотность

Если ${{I}_{1}}$ — момент инерции тонкого стержня относительно оси, перпендикулярной его длине и проходящей через его центр масс, и ${{I}_{2}}$ — момент инерции (относительно центральной оси) кольца, образованного изгибом стержня, тогда $\text{A}\text{.

{2}}:3$$\text{C}\text{. }{{I}_{1}}:{{I}_{2}}=\pi :4$$\text{D}\text{. {{I}_{1}}:{{I}_{2}}=3:5$ 9{2}}$

Полный пошаговый ответ:
Давайте сначала получим выражение для обоих моментов инерции, а затем разделим их, чтобы найти соотношение.
Пусть масса стержня M и длина стержня L.
Для момента инерции (${{I}_{1}}$) стержня относительно оси, перпендикулярной его длине и проходящей через его центра масс рассмотрим небольшой элемент массой dm. Пусть длина этой массы dm равна dx и пусть она находится на расстоянии x от центра масс стержня. Предположим, что масса стержня распределена равномерно и, следовательно, центром масс будет центр (середина) стержня. 9{2}}:3$

Итак, правильный ответ — «Вариант Б».

Примечание: Обратите внимание, что это не упоминается в вопросе, но все же мы предположили, что стержень имеет однородную плотность массы. Если масса имеет неоднородную плотность, то ответ будет другим. Это означает, что $\dfrac{dm}{dx}$ не является постоянной величиной.