Момент инерции тела относительно оси. Радиус инерции
Момент инерции тела относительно оси. Радиус инерции.
Положение центра масс характеризует распределение масс системы не полностью. Например (рис.32), если расстояния h от оси Oz каждого из одинаковых шаров А и В увеличить на одну и ту же величину, то положение центра масс системы не изменится, а распределение масс станет другим, и это скажется на движении системы (вращение вокруг оси Oz при прочих равных условиях будет происходить медленнее).
Рис.32
Поэтому в механике вводится еще одна характеристика распределения масс — момент инерции. Моментом инерциитела (системы) относительно данной оси Oz (или осевым моментом инерции) называется скалярная величина, равная сумме произведений масс всех точек тела (системы) на квадраты их расстояний от этой оси
Из определения следует, что момент инерции тела (или системы) относительно любой оси является величиной положительной и не равной нулю.
Заметим также, что момент инерции тела – это геометрическая характеристика тела, не зависящая от его движения.
Осевой момент инерции играет при вращательном движении тела такую же роль, какую масса при поступательном, т.е. что осевой момент инерции является мерой инертности тела при вращательном движении.
Согласно формуле момент инерции тела равен сумме моментов инерции всех его частей относительно той же оси. Для одной материальной точки, находящейся на расстоянии h от оси, .
Часто в ходе расчетов пользуются понятием радиуса инерции. Радиусом инерции тела относительно оси Оz называется линейная величина , определяемая равенством
,
где М — масса тела. Из определения следует, что радиус инерции геометрически равен расстоянию от оси Оz той точки, в которой надо сосредоточить массу всего тела, чтобы момент инерции одной этой точки был равен моменту инерции всего тела.
В случае сплошного тела, разбивая его на элементарные части, найдем, что в пределе сумма, стоящая в равенстве , обратится в интеграл.
В результате, учитывая, что , где — плотность, а V-объем, получим
или
Интеграл здесь распространяется на весь объем V тела, а плотность и расстояние h зависят от координат точек тела.
Моменты инерции некоторых однородных тел:
1.Тонкий однородный стержень длины l и массы М. Вычислим его момент инерции относительно оси Аz, перпендикулярной к стержню и проходящей через его конец А (рис. 33).
Рис.33
Направим вдоль АВ координатную ось Ах. Тогда для любого элементарного отрезка длины dx величина h=x, а масса , где — масса единицы длины стержня. В результате
Заменяя здесь его значением, найдем окончательно:
2. Тонкое круглое однородное кольцо радиуса R и массы М. Найдем его момент инерции относительно оси Cz, перпендикулярной плоскости кольца и проходящей через его центр (рис.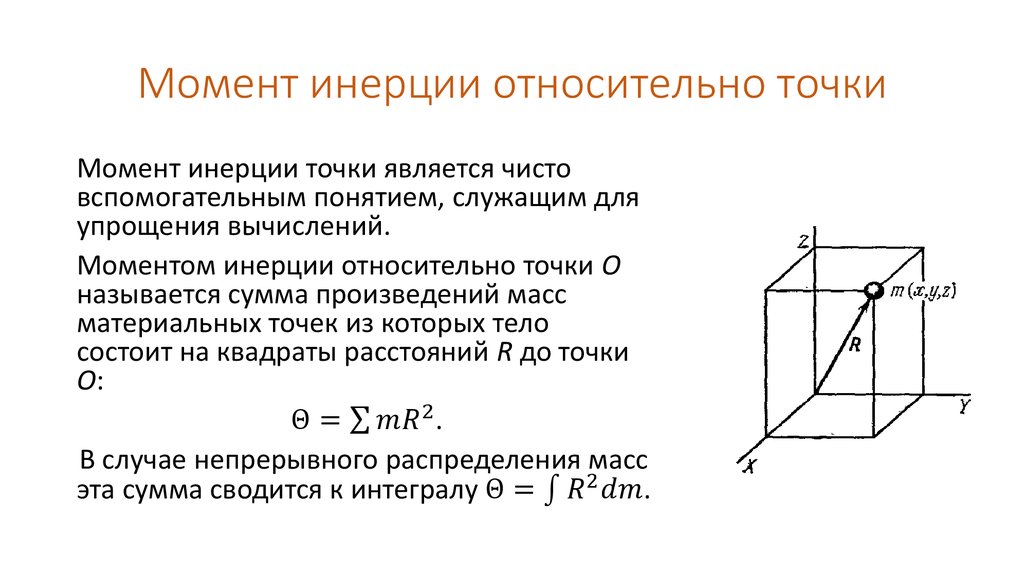
34,а).Так как все точки кольца находятся от оси Cz на расстоянии hk=R, то
Следовательно, для кольца
Очевидно, такой же результат получится для момента инерции тонкой цилиндрической оболочки массы М и радиуса R относительно ее оси.
3. Круглая однородная пластина или цилиндр радиуса R и массы М. Вычислим момент инерции круглой пластины относительно оси Сz, перпендикулярной к пластине и проходящей через ее центр (см. рис.34,а). Для этого выделим элементарное кольцо радиуса r и ширины dr (рис.34,б).
Рис.34
Площадь этого кольца равна , а масса , где — масса единицы площади пластины. Тогда для выделенного элементарного кольца будет
а для всей пластины . Заменяя здесь его значением, найдем окончательно
Такая же формула получится, очевидно, и для момента инерции однородного круглого цилиндра массы М и радиуса R относительно его оси Оz (риc.
34,в).
Обратите внимание на лекцию «Методы разрушения нефтяных эмульсий».
4. Прямоугольная пластина, конус, шар. Опуская выкладки, приведем формулы, определяющие моменты инерции следующих тел:
а) сплошная прямоугольная пластина массы М со сторонами АВ = а и BD = b (ось х направлена вдоль стороны AB, ось у — вдоль BD):
б) прямой сплошной круглый конус массы М с радиусом основания R (ось z направлена вдоль оси конуса):
г) сплошной шар массы М и радиуса R (ось z направлена вдоль диаметра):
5.4: Момент инерции — Физика LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 17392
- Тимон Идема
- Делфтский технологический университет через TU Delft Open
Предположим, у нас есть масса m на конце безмассовой палки длиной \(r\), вращающаяся вокруг другого конца палки.
Если мы хотим увеличить скорость вращения, нам нужно применить тангенциальное ускорение на
\[\boldsymbol{a}_{\mathrm{t}}=r \boldsymbol{\alpha} \nonumber\]
, для чего по второму закону Ньютона нужна сила
\[\boldsymbol{F}=m \boldsymbol{a}_{\mathrm{t}}=\operatorname{mr} \boldsymbol{\alpha}. \номер\]
Эта сила, в свою очередь, создает крутящий момент величиной 92\). По аналогии с массой, представляющей инерцию тела, подвергающегося линейному ускорению, мы идентифицируем эту величину как инерцию тела, подвергающегося вращательному ускорению, которую мы назовем моментом инерции и обозначим через \(I\):
\[\boldsymbol{\tau}=I \boldsymbol{\alpha} \label{крутящий момент}\]
Уравнение \ref{момент} является вращательным аналогом второго закона Ньютона. Расширяя наш предыдущий пример, мы можем найти момент инерции произвольного набора частиц с массами \(m_\alpha\) и расстояниями до оси вращения \(r_\alpha\) (где \(\alpha\) работает по всем частицам), и запишем: 92\) соответственно.
| Объект | Ось вращения | Момент инерции | 9{2} \label{result}\]
|---|
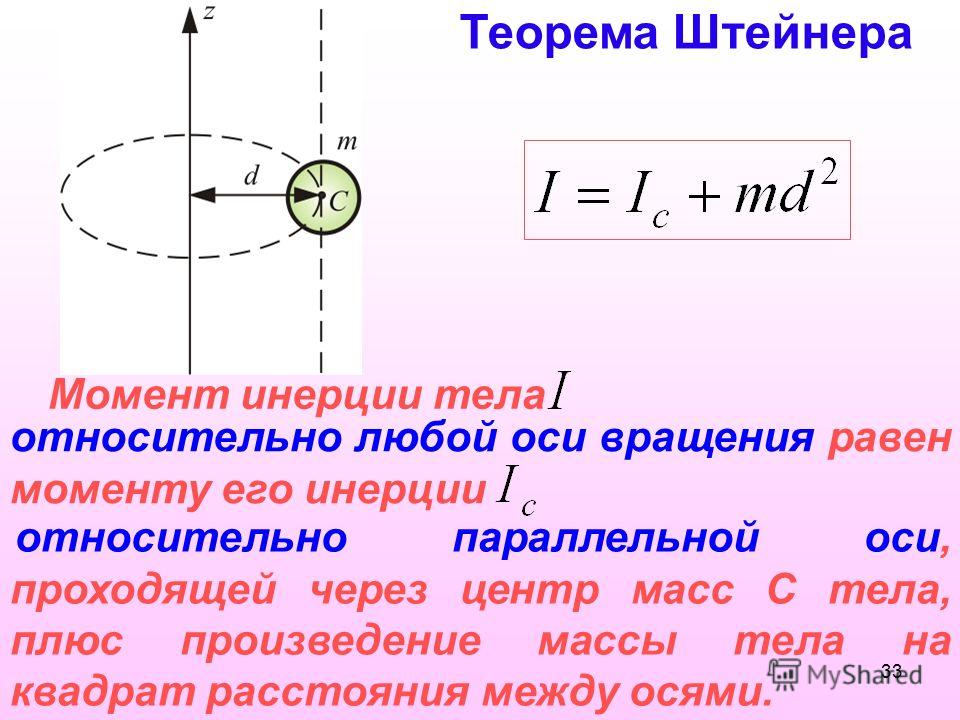
Последний интеграл в последней строке \ref{proof} равен положению центра масс, которое мы выбрали в начале координат, поэтому последний член равен нулю, и мы получаем \ref{result}. Обратите внимание, что первые две строки таблицы 5.1 (моменты инерции стержня) удовлетворяют теореме об перпендикулярных осях.
4: Moment of Inertia распространяется под лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Тимоном Идема (TU Delft Open) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.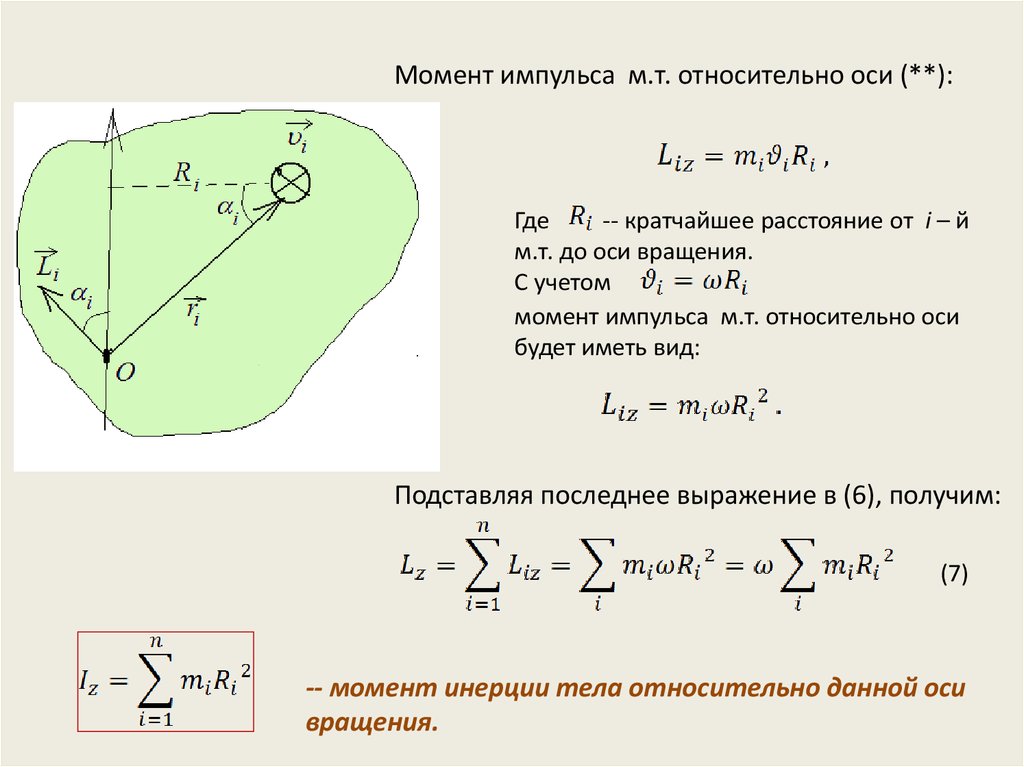
open.tudelft.nl/textbooks/catalog/book/14
I — момент инерции, измеренный в килограммах на квадратный метр (кг·м 2 ), m — масса, измеренная в килограммах (кг), и r — расстояние по перпендикуляру к оси вращения, измеренное в метрах (м).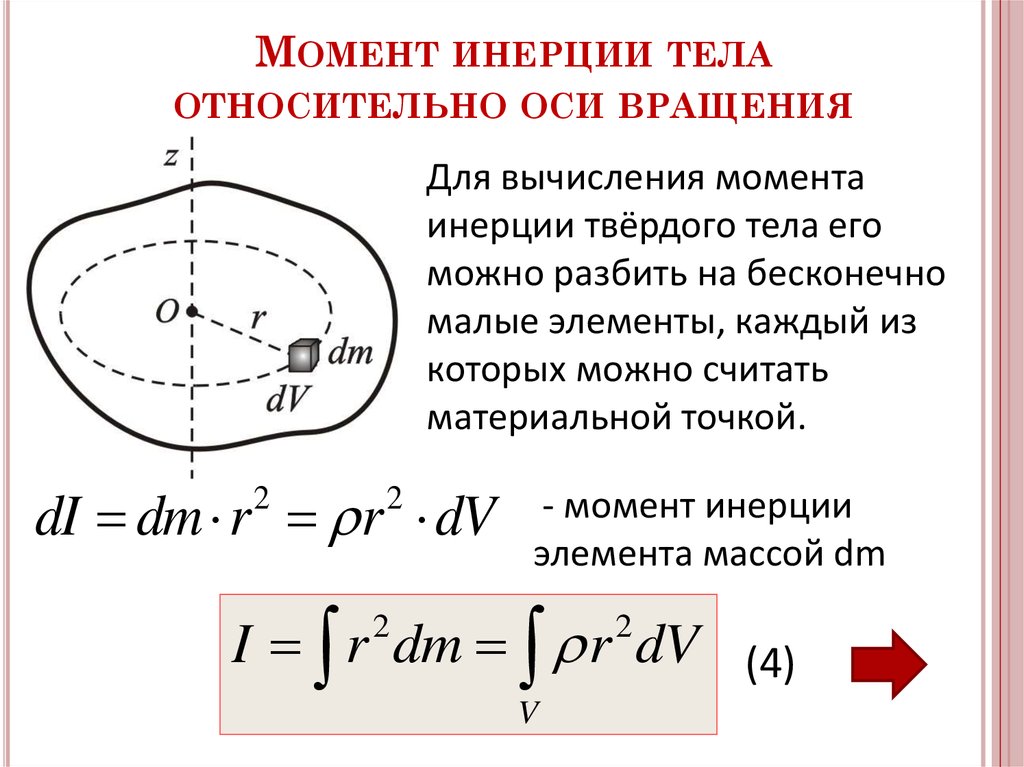
Однако поступательное ускорение при вращательном движении равно произведению углового ускорения α на радиус r.
Когда спортсмен отводит руки назад, расстояние между отягощением и осью вращения уменьшается, а вместе с ним и момент инерции.
org/Thing» data-name=»flashcards-dot»> Викторина «Последний момент инерции»
