Инертность масса плотность момент инерции атт

Автор Сфера закона На чтение 7 мин Просмотров 5 Опубликовано 21 августа 2022

Содержание

1. Момент инерции МТ и АТТ. Теорема Штейнера. Расчет момента инерции тонкого стержня
2. Момент инерции МТ и АТТ. Теорема Штейнера. Расчет момента инерции тонкого стержня
3. Момент силы. Момент инерции и момент импульса АТТ

Момент инерции МТ и АТТ. Теорема Штейнера. Расчет момента инерции тонкого стержня

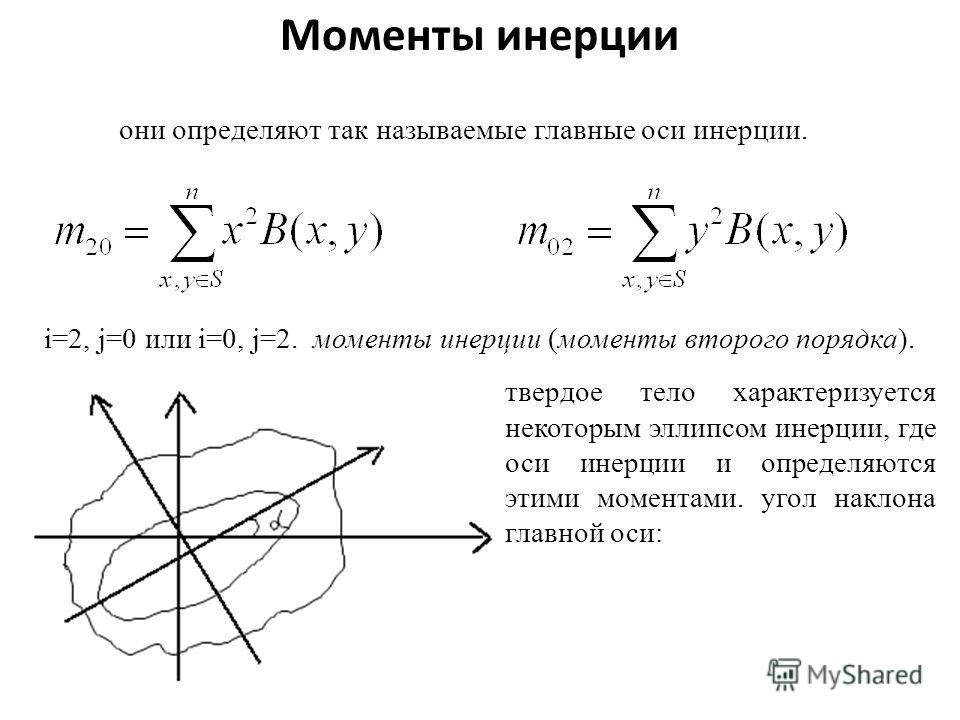
момент инерции АТТ отн. оси вращ. Z.

: момент инерции МТ отн.оси.

Физ.смысл: момент инерции тела явл. Мерой инертности тела при его вращательном движении, причём момент инертности любой оси характеризует его независимо от того, покоится тело или движется.

1. Теорема Штейнера:

2. Правило сложения : момент инерции системы отн.некоторой оси=сумме моментов инерций частей этой системы отн. этой же оси.

Расчёт момента инерции системы тонкого стержня:

Момент инерции тонкого стержня отн.оси АА’, проходящей через середину. Длина-l, масса-m.

1. Разделим на малые элементы длины dx с массой на расстояние x от оси. Момент инерции элемента:

2. Интегрируем в пределах от 0 до и удваиваем:

Вопрос 25 Работа при вращательном движении. Кинетическая энергия вращения МТ, системы МТ, АТТ вокруг оси. Полная кинетическая энергия АТТ. Закон изменения кинетической энергии при вращательном движении.

Работа , совершаемая всеми приложенными к телу силами, идет

на изменение его кинетической энергии: δA = dК . Подставим в последнее выражение уравнение (4.9.3 см. ниже) и продифференцируем , учитывая, что , получим : Тогда элементарная работа , совершаемая силами, приложенными к телу : и полная работа при повороте тела на угол φ за время t :

Линейная скорость элементарной массы m_i равна υ_i = ωR_i , где R_i − расстояние от элементарной массы до оси вращения. Кинетическая энергия этой элементарной массы получается выражением
. Кинетическая энергия тела складывается из кинетических энергий его частей, т.е. . Так как величина есть момент инерции тела относительно оси вращения, то кинетическая энергия тела , вращающегося вокруг неподвижной оси (4.9.3).

Кинетическая энергия тела при плоском движении слагается из энергии поступательного движения со скоростью , равной скорости центра масс , и энергии вращения вокруг оси, проходящей через центр масс тела , т. е.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.004 сек.)

Источник

Момент инерции МТ и АТТ. Теорема Штейнера. Расчет момента инерции тонкого стержня

момент инерции АТТ отн. оси вращ. Z.

: момент инерции МТ отн.оси.

Физ.смысл: момент инерции тела явл. Мерой инертности тела при его вращательном движении, причём момент инертности любой оси характеризует его независимо от того, покоится тело или движется.

1. Теорема Штейнера:

2. Правило сложения : момент инерции системы отн.некоторой оси=сумме моментов инерций частей этой системы отн.этой же оси.

Расчёт момента инерции системы тонкого стержня:

Момент инерции тонкого стержня отн.оси АА’, проходящей через середину. Длина-l, масса-m.

1. Разделим на малые элементы длины dx с массой на расстояние x от оси. Момент инерции элемента:

2. Интегрируем в пределах от 0 до и удваиваем:

Вопрос 25 Работа при вращательном движении. Кинетическая энергия вращения МТ, системы МТ, АТТ вокруг оси. Полная кинетическая энергия АТТ. Закон изменения кинетической энергии при вращательном движении.

Работа , совершаемая всеми приложенными к телу силами, идет

на изменение его кинетической энергии: δA = dК . Подставим в последнее выражение уравнение (4.9.3 см. ниже) и продифференцируем , учитывая, что , получим : Тогда элементарная работа , совершаемая силами, приложенными к телу : и полная работа при повороте тела на угол φ за время t :
Линейная скорость элементарной массы m_i равна υ_i = ωR_i , где R_i − расстояние от элементарной массы до оси вращения.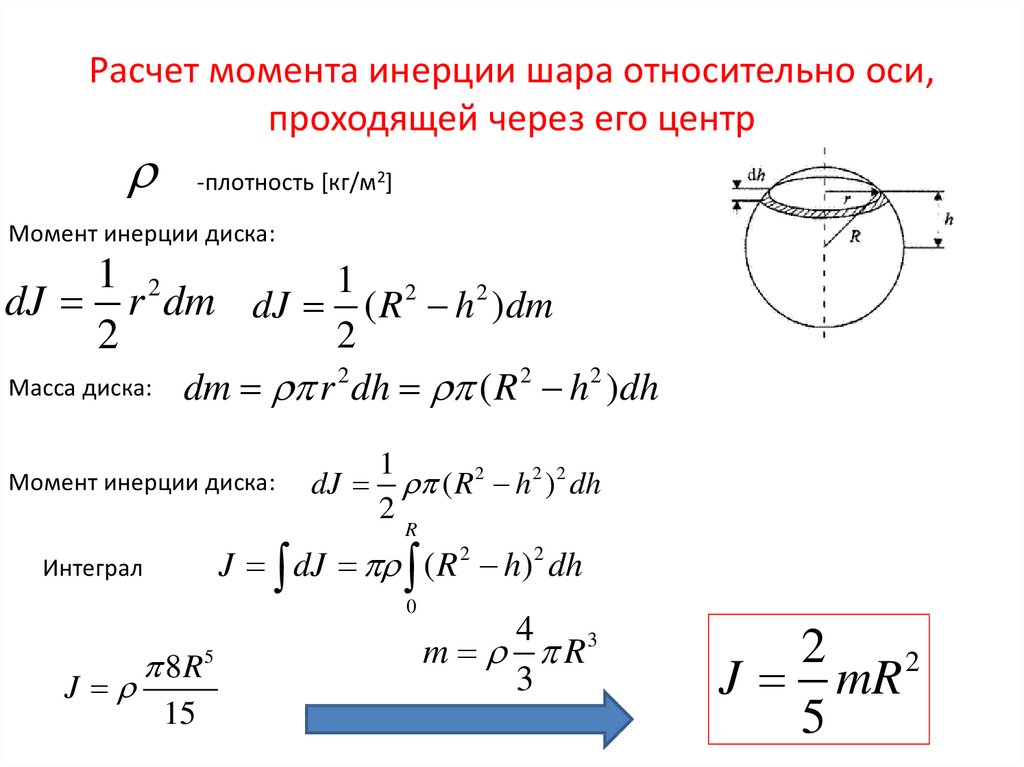

Кинетическая энергия этой элементарной массы получается выражением
. Кинетическая энергия тела складывается из кинетических энергий его частей, т.е. . Так как величина есть момент инерции тела относительно оси вращения, то кинетическая энергия тела , вращающегося вокруг неподвижной оси (4.9.3).

Кинетическая энергия тела при плоском движении слагается из энергии поступательного движения со скоростью , равной скорости центра масс , и энергии вращения вокруг оси, проходящей через центр масс тела , т. е.

Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Студалл.Орг (0.003 сек.)

Источник

Момент силы. Момент инерции и момент импульса АТТ

Момент силы — величина, характеризующая вращательный эффект силы. При вращении АТТ вокруг неподвижной оси Oz проекция момента силы относительно любой точки О, лежащей на этой оси, который определяется векторным произведением радиуса-вектора проведенного из точки О в точку приложения силы, на вектор силы :

, (32)

совпадает с моментом силы М_zотносительно этой оси.

Если угловая скорость направлена по оси Ozи проекция момента силы на ось вращения положительна, то такой момент силы называют вращающим, иначе – тормозящим.

Момент инерции – величина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении.

Моментом инерции тела относительно неподвижной оси Оz называется скалярная величина

(33)

где m_i — масса i-й частицы тела;

r_i — расстояние от i-й частицы тела до оси вращения Оz;

N — число частиц, из которых состоит тело.

Индекс «z» у момента инерции обозначает, что момент инерции определяется относительно оси Оz.

В случае непрерывного распределения массы тела сумма, стоящая в формуле (33), заменяется интегралом:

(34)

Определение интеграла (34) в общем случае представляет собой сложную задачу. Однако ситуация упрощается, когда нужно вычислить моменты инерции однородных симметричных тел относительно осей, проходящих через центры масс тел и являющихся осями симметрии.

Центр инерции (центр масс) АТТ (системы частиц) – это такая точка, координаты которой определяются из соотношений:

; (35) ; (36) . (37)

Скорость центра инерции (центра масс)АТТ (системы частиц)можно рассчитать по формуле:

. (38)

Результаты вычисления моментов инерции ряда тел правильной геометрической формы относительно оси

Оz, проведенной через центр масс твердого тела, приведены в табл. 1.

Моменты инерции некоторых тел правильной геометрической

формы относительно оси, проходящей через их центр масс

Обруч (полый цилиндр)	Диск (сплошной цилиндр)	Шар	Стержень

Если ось Оz не проходит через центр масс, то момент инерции определяется по теореме Гюйгенса-Штейнера:

(39)

где — момент инерции относительно оси вращения Оz;

— момент инерции относительно оси симметрии, параллельной оси

Оz и проходящей через центр масс;

d – расстояние между осями;

Момент импульса (момент количества движения, кинетический момент) твердого тела — характеристика вращательного движения.

Момент импульса абсолютно твердого тела относительно неподвижного центра О равен геометрической сумме моментов импульсов всех точек тела относительно того же центра:

(40)

Если абсолютно твердое тело вращается вокруг неподвижной оси Оz, то

(41)

где — проекция момента импульса на ось Оz;

— момент инерции твердого тела относительно оси

Оz.

41.(1) В плоскости yОz на частицу, координаты которой y = 4,1 м , z = 2,8 м, действует cила 6,3 Н, направленная под прямым углом к радиус-вектору частицы (рис. 2). Чему равен момент этой силы относительно точки О?

42.(1) По окружности радиусом 5,5 м (центр окружности – точка О) в плоскости yОz со скоростью 0,98 м/с движется частица массой 12 кг (рис.3.). Чему равен момент импульса этой частицы относительно точки О?

43.(2) Определить момент инерции тонкого кольца радиусом 20 см и массой 100 г относительно оси, перпендикулярной плоскости кольца и проходящей через любую точку на кольце.

44.(2) Найти момент импульса Земли относительно собственной оси вращения.

45.(2) Механическая система состоит из двух частиц, массы которых равны соответственно 0,12 г и 0,24 г. Первая частица находится в точке с координатами (3; 5; 0), вторая – в точке (6; 2; 0) (координаты даны в сантиметрах). Вычислить: 1) координаты центра масс; 2) скорость центра масс, если частицы начнут движение вдоль оси х навстречу друг другу каждая со скоростью 11 см/с относительно этой оси. Показать на чертеже положение центра масс и вектор скорости центра масс.

Источник

Момент инерции диска. Явление инерции

Многие люди замечали: когда они едут в автобусе, и он увеличивает свою скорость, их тела прижимаются к креслу. И наоборот, при остановке транспортного средства пассажиров будто выбрасывает из посадочных мест. Все это происходит из-за инерции. Рассмотрим это явление, а также объясним, что такое момент инерции диска.

Что представляет собой инерция?

Под инерцией в физике понимают способность всех тел, обладающий массой, сохранять покоящееся состояние либо двигаться с одинаковой скоростью в одном и том же направлении. Если необходимо изменить механическое состояние тела, то приходится прикладывать некоторую внешнюю силу к нему.

В данном определении следует обратить внимание на два момента:

• Во-первых, это вопрос состояния покоя. В общем случае такого состояния не существует в природе. Все в ней находится в постоянном движении. Тем не менее, когда мы едем в автобусе, то нам кажется, что водитель не двигается со своего места. В таком случае идет речь об относительности движения, то есть относительно пассажиров водитель находится в покое. Отличие между состояниями покоя и равномерного движения заключается лишь в системе отсчета. В примере выше пассажир в состоянии покоя относительно автобуса, в котором едет, но движется относительно остановки, которую проезжает.
• Во-вторых, инерция тела пропорциональна его массе. Наблюдаемые нами объекты в жизни все имеют ту или иную массу, поэтому все они характеризуются некоторой инертностью.

Таким образом, инерция характеризует степень трудности изменения состояния движения (покоя) тела.

Инерция. Галилей и Ньютон

Когда изучают вопрос инерции в физике, то как правило, связывают ее с первым ньютоновским законом. Этот закон гласит:

Любое тело, на которое не действуют внешние силы, сохраняет свое состояние покоя либо равномерного и прямолинейного движения.

Считается, что этот закон сформулировал Исаак Ньютон, и произошло это в середине XVII века. Отмеченный закон справедлив всегда и во всех процессах, описываемых классической механикой. Но когда ему приписывают фамилию английского ученого, следует сделать некоторую оговорку…

В 1632 году, то есть за несколько десятков лет до постулирования закона инерции Ньютоном, итальянский ученый Галилео Галилей в одной из своих работ, в которой он сравнивал системы мира Птолемея и Коперника, по сути сформулировал 1-й закон «Ньютона»!

Галилей говорит, что если тело движется по гладкой горизонтальной поверхности, и силами трения и сопротивления воздуха можно пренебречь, то это движение будет сохраняться вечно.

Вращательное движение

Приведенные выше примеры рассматривают явление инерции с точки зрения прямолинейного перемещения тела в пространстве. Однако существует еще один тип движения, который распространен в природе и Вселенной — это вращение вокруг точки или оси.

Масса тела характеризует его инерционные свойства поступательного движения. Для описания же аналогичного свойства, которое проявляет себя при вращении, вводят понятие момента инерции. Но перед тем как рассматривать эту характеристику, следует познакомиться с самим вращением.

Круговое перемещение тела вокруг оси или точки описывается двумя важными формулами. Ниже они приводятся:

1) L = I*ω;

2) dL/dt = I*α = M.

В первой формуле L — это момент импульса, I — момент инерции, ω — угловая скорость. Во втором выражении α — это ускорение угловое, которое равно производной по времени от угловой скорости ω, M — момент силы системы. Он рассчитывается как произведение результирующей внешней силы на плечо, к которому она приложена.

Первая формула описывает вращательное движение, вторая — его изменение во времени. Как видно, в обеих этих формулах присутствует момент инерции I.

Момент инерции

Сначала приведем его математическую формулировку, а затем объясним физический смысл.

Итак, момент инерции I рассчитывается следующим образом:

I = ∑_i(m_i*r_i²).

Если перевести это выражение с математического на русский язык, то оно означает следующее: все тело, которое имеет некоторую ось вращения O, разбивается на мелкие «объемчики» массой m_i, находящиеся на расстоянии r_i от оси O. Момент инерции рассчитывается путем возведения в квадрат этого расстояния, его умножения на соответствующую массу m_i и сложения всех полученных слагаемых.

Если разбить все тело на бесконечно малые «объемчики», тогда сумма выше будет стремиться к следующему интегралу по объему тела:

I = ∫_V(ρ *r²dV), где ρ — плотность вещества тела.

Из приведенного математического определения следует, что момент инерции I зависит от трех важных параметров:

• от значения массы тела;
• от распределения массы в теле;
• от положения оси вращения.

Физический смысл момента инерции заключается в том, что он характеризует, насколько «тяжело» привести в движение вращения данную систему или изменить ее скорость вращения.

Момент инерции диска однородного

Полученные в предыдущем пункте знания применимы для расчета момента инерции однородного цилиндра, который в случае h<r принято называть диском (h — высота цилиндра).

Для решения поставленной задачи достаточно рассчитать интеграл по объему этого тела. Выпишем исходную формулу:

I = ∫_V(ρ *r²dV).

Если ось вращения проходит перпендикулярно плоскости диска через его центр, тогда можно представить этот диск в виде нарезанных мелких колечек, толщина каждого из них является очень малой величиной dr. В этом случае объем такого колечка можно рассчитать так:

dV = 2*pi*r*h*dr.

Это равенство позволяет интеграл по объему заменить на интегрирование по радиусу диска. Имеем:

I = ∫_r(ρ *r²*2*pi*r*h*dr) = 2*pi*h*ρ*∫_r(r³*dr).

Вычисляя первообразную подынтегрального выражения, а также учитывая, что интегрирование проводится по радиусу, который изменяется от 0 до r, получаем:

I = 2*pi*h*ρ*r⁴/4 = pi*h*ρ*r⁴/2.

Поскольку масса рассматриваемого диска (цилиндра) равна:

m = ρ*V и V = pi*r²*h,

то получаем конечное равенство:

I = m*r²/2.

Эта формула момента инерции диска справедлива для абсолютно любого цилиндрического однородного тела произвольной толщины (высоты), ось вращения которого проходит через его центр.

Разные виды цилиндров и положения осей вращения

Аналогичное интегрирование можно провести для разных тел цилиндрической формы и совершенно любого положения осей их вращения и получить момент инерции для каждого случая. Ниже приводится список часто встречающихся ситуаций:

Из всех этих формул следует, что при одинаковой массе m наибольшим моментом инерции I обладает кольцо.

Где используют инерционные свойства вращающегося диска: маховик

Наиболее ярким примером применения момента инерции диска является маховик в автомобиле, который жестко соединен с коленвалом. Благодаря наличию такого массивного атрибута обеспечивается плавность движения автомобиля, то есть маховик сглаживает любые моменты сил импульсивного характера, которые действуют на коленвал. Более того, этот тяжелый металлический диск способен запасать огромную энергию, обеспечивая тем самым инерционное движение транспортного средства даже при заглушенном двигателе.

В настоящее время инженеры некоторых автомобильных компаний работают над проектом использования маховика в качестве накопителя энергии торможения транспортного средства с целью ее последующего использования при ускорении авто.

Другие понятия об инерции

Хотелось бы завершить статью несколькими словами о других «инерциях», отличных от рассмотренного явления.

В той же физике существует понятие о температурной инерции, которая характеризует, насколько «трудно» нагреть или охладить данное тело. Температурная инерция прямо пропорциональна теплоемкости.

В более широком философском смысле инерция описывает сложность изменения какого-либо состояния. Так, инертным людям сложно начинать делать что-то новое из-за лени, привычки к рутинному образу жизни и удобству. Кажется, лучше оставить вещи такими, какие они есть, поскольку так жить гораздо проще…

момент инерции

момент инерции

Астрофизика (Индекс)

О

Момент инерции

(характеристика распределения массы внутри планеты)

---

Момент инерции астрономического тела фактор (сокращенно от полярный момент и коэффициент инерции , вид интереса о планетах и ​​звездах) мера, характеризующая распределение массы внутри тела, использования при разработке динамики вращения тел, полезно для таких объектов, как звезды, планеты и луны. Он не зависит от массы и радиуса объекта, и является скаляром в диапазоне от 0 до 1. Пример (полярный) момент инерции коэффициент значения:

sphere of uniform density	0.4
sphere with higher density away from the axis	>0.4
sphere with higher density nearer the axis	<0.4
Sun	0.070
Меркурий	0,346
Венера	0,337
Earth	0.3307
Moon	0.3929
Mars	0.3644
Jupiter	0.2756
Saturn	0.22
Uranus	0.23
Neptune	0,23

Меньшее число указывает на большую массу по направлению к оси, это случай тела с плотным «ядром», и большая общая масса тела и меньшая жесткость способствовать этому. Число представляет интерес с точки зрения истории вращения объекта, такие как шкала времени, необходимая для того, чтобы приливные силы произвели приливная блокировка. Сферический объект полярный момент с коэффициентом инерции :

C/MR²
 

• С — полярный момент инерции.
• М — масса объекта.
• R — радиус объекта.

полярный момент инерции объекта ( момент инерции вокруг оси вращения) есть скаляр, характеризующий подразумеваемое сопротивление объекта вокруг его оси вращения (аналогично тому, как масса характеризует линейное ускорение от заданной силы). такой момент инерции объекта относительно оси является мерой отношения между крутящим моментом на объекте относительно к этой оси и угловое ускорение, создаваемое этим крутящим моментом:

С = L/ω
или же
С = τ/α
 

Для характеризуемой оси:

• С — момент инерции.
• L — угловой момент.
• ω — угловая скорость.
• τ — крутящий момент.
• α — угловое ускорение.

Если полярный (или какая-то другая конкретная ось) не указана или не предполагается, одного скаляра недостаточно, чтобы охарактеризовать объект сопротивление крутящему моменту по любой оси. Для большей общности, 3×3 матрица (в частности, 3×3 тензор ) может характеризовать все моменты инерции объектов или коэффициенты момента инерции которые проходят по всем осям через его центр масс.

---

( физика,мера ) Дальнейшее чтение:
https://en.wikipedia.org/wiki/Moment_of_inertia_factor
https://en.wikipedia.org/wiki/Moment_of_inertia
https://geo.libretexts.org/Courses/University_of_California_Davis/UCD_GEL_56_-_Introduction_to_Geophysics/Geophysics_is_everywhere_in_geology…/03%3A_Planetary_Geophysics/3.02%3A_Layered_Structure_of_a_Planet

---

Индекс

Массово-инерционные характеристики основных сегментов тела человека

• ID корпуса: 229746655

 @inproceedings{Zatsiorsky1983TheMA,
  title={Массовые и инерционные характеристики основных сегментов человеческого тела},
  автор={Владимир Михайлович Зациорский},
  год = {1983}
} 

• В. Зациорский
• Опубликовано в 1983 г.
• Информатика

Влияние фильтрации нижних частот на моменты в суставах из обратной динамики: последствия для предотвращения травм.

• Э. Кристианслунд, Т. Кроссхауг, А. Дж. ван ден Богерт

• Инжиниринг

  Journal of biomechanics

• 2012

ESTIMATING BODY SEGMENT INERTIAL PARAMETERS OF THE HUMAN BODY USING A MICROSOFT KINECT

• Pawel Kudzia

• Materials Science

• 2015

Thesis (Master, Mechanical and Materials Engineering ) — Queen’s University, 2015-10-27 15:28:47.274

Нелинейное управление с упреждением и обратной связью неопределенной модели скелетно-мышечной руки с задержкой по времени для использования в функциональной электрической стимуляции

• П. Куман

• Инженерное дело

• 2014

Траектория движения человека во время перехода из положения сидя в положение стоя: новый подход к моделированию, основанный на декомпозиции движения и многофазной функции стоимости F.

Bahrami, M. Parnianpour

Биология

Экспериментальные исследования мозга

2013

Вычислительная модель для описания задачи «сидеть-встать» (STS), а не только для прогнозирования общих особенностей STS с достаточной точностью , но также показал потенциальную гибкость, позволяющую различать стратегии движения от одного субъекта к другому.

Расчет параметров инерции сегментов тела на основе одного быстрого сканирования с помощью Microsoft Kinect потенциал для недорогой системы, которая может обеспечить быстрые и точные предметные оценки BSIP и показывает сопоставимые и во многих случаях более точные объемные оценки, чем обычно используемая геометрическая модель BSIP.

Новый надежный метод реконструкции движения, основанный на оптимизации с избыточными ограничениями и естественными координатами.

• S. Ausejo-Muñoz, J.T. Celigueta-Lizarza, A. Suescun-Cruces

• Engineering

• 2011

анимация и инженерия. Элементы, участвующие в анализе движения человека…

Компьютерный алгоритм оптимального планирования движения подвешивания одной рукой

• C. Chiu

• Инженерное дело

• 2009

Основная цель этого исследования заключалась в разработке набора алгоритмов, которые могут вычислять оптимальную траекторию (ОТ) для трехмерного движения человека в подвешенном состоянии одной рукой. To achieve this goal, the study first…

Modélisation biomécanique du mouvement : vers un outil d’évaluation pour l’instrumentation en orthopédie

• J. Lepoutre

• Philosophy

• 2007

L’objectif de ce труд является новым подходом к оценке дисфункций тела человека, проводящего локомотивы по патологиям, по параметрам…

Инерционные свойства туловища мужчин, определенные с помощью магнитно-резонансной томографии

Сегментарные параметры туловища самцов, оцененные in vivo с использованием магнитно-резонансной томографии и объемных оценок, показали, что они близко соответствуют значениям МРТ, за исключением грудной клетки, что указывает на то, что объемные метод может быть эффективным для получения сегментарных параметров для больших сегментов туловища.