«Определение моментов инерции тел методом крутильных колебаний», Физико-математические науки
- Выдержка
- Другие работы
- Помощь в написании
Определение моментов инерции тел методом крутильных колебаний (реферат, курсовая, диплом, контрольная)
Московский государственный университет путей сообщения РФ (МИИТ)
Кафедра «Физика-2»
ОТЧЁТ ПО ЛАБОРАТОРНОЙ РАБОТЕ
ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТЕЛ МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
1. Цель работы
Определение моментов инерции тел правильной геометрической формы
2. Принципиальная схема установки
рис 1 — Устройство прибора для измерения крутильных колебаний Для измерения момента инерции в данной лабораторной работе используются крутильные колебания изображенного на рисунке устройства, состоящего из диска 1 и лежащих на нем одного или нескольких тел 2.
В работе используется эталонное тело (ЭТ) с известным моментом инерции. Диск расположен на станине 3, имеющей винты 4 для корректировки горизонтального положения плоскости диска. Пружина 5 служит для возвращения диска в положение равновесия и создания колебательного движения относительно вертикальной оси (рис.1).
3. Основные теоретические положения к данной работе
Инертные свойства тела при вращении определяются не только массой тела, но и расположением отдельных частей тела по отношению к оси вращения. Для характеристики этих свойств вводится понятие момента инерции.
Абсолютно твердое тело можно рассматривать как систему из материальных точек с неизменными расстояниями между ними.
Момент инерции Iiматериальной точки относительно некоторой оси вращения определяется как произведение ее массы mi; на квадрат расстояния ri, до оси вращения
Момент инерции твердого тела равен сумме моментов инерции отдельных его частей — материальных точек
.
Если абсолютно твердое тело имеет форму тела вращения относительно оси, проходящей через его центр инерции, то выражение для момента инерции принимает более простой вид:
I kmR2, (1)
где m и R — масса и радиус тела соответственно;
k — коэффициент, зависящий от формы тела.
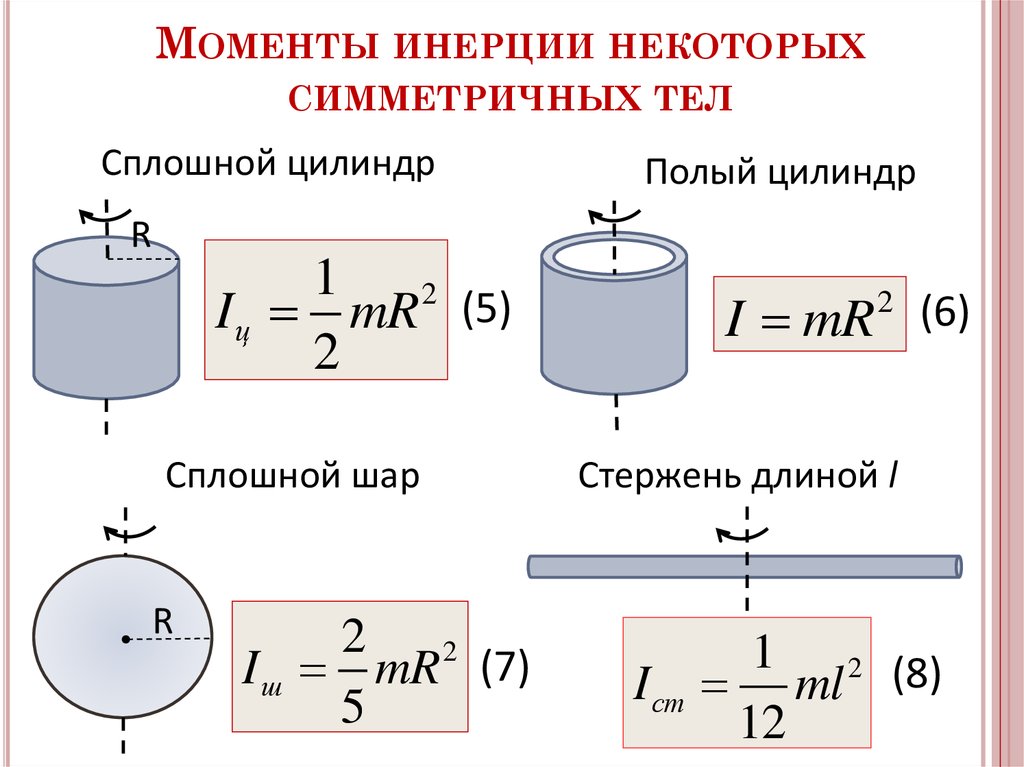
Для обруча и тонкостенного цилиндра k 1, для сплошного цилиндра и диска k =½, для шара k = 2/5.
Если ось вращения не проходит через центр инерции тела, то для вычисления его момента инерции пользуются теоремой Штейнера:
Момент инерции I относительно произвольной оси равен сумме момента инерции Iо относительно оси, проходящей через центр масс тела параллельно данной, и произведения массы тела на квадрат расстояния, а между осями
(2)
Момент инерции системы тел относительно некоторой оси равен сумме моментов инерции относительно этой оси всех тел, входящих в систему:
I I1 I2 I3 … IN.
(3)
Момент инерции тела как характеристика его инертных свойств входит в уравнения динамики вращательного движения. При вращении твердого тела относительно неподвижной оси основное уравнение динамики вращательного движения можно записать в виде:
M I, (4)
где М — проекция результирующего момента всех внешних сил на ось вращения; — угловое ускорение.
Так как угловое ускорение может быть записано как вторая производная по времени от угла поворота:
то уравнение (4) можно представить в виде
.
При отклонении диска на некоторый угол (в пределах упругой деформации пружины) со стороны пружины на диск действует возвращающая сила, проекция момента которой пропорциональна углу отклонения:
М b, (6)
где b — упругая постоянная пружины.
Если пренебречь влиянием силы трения, то уравнение движения диска на основании формул (5) и (6) примет вид
где I — момент инерции диска с лежащими на нем грузами.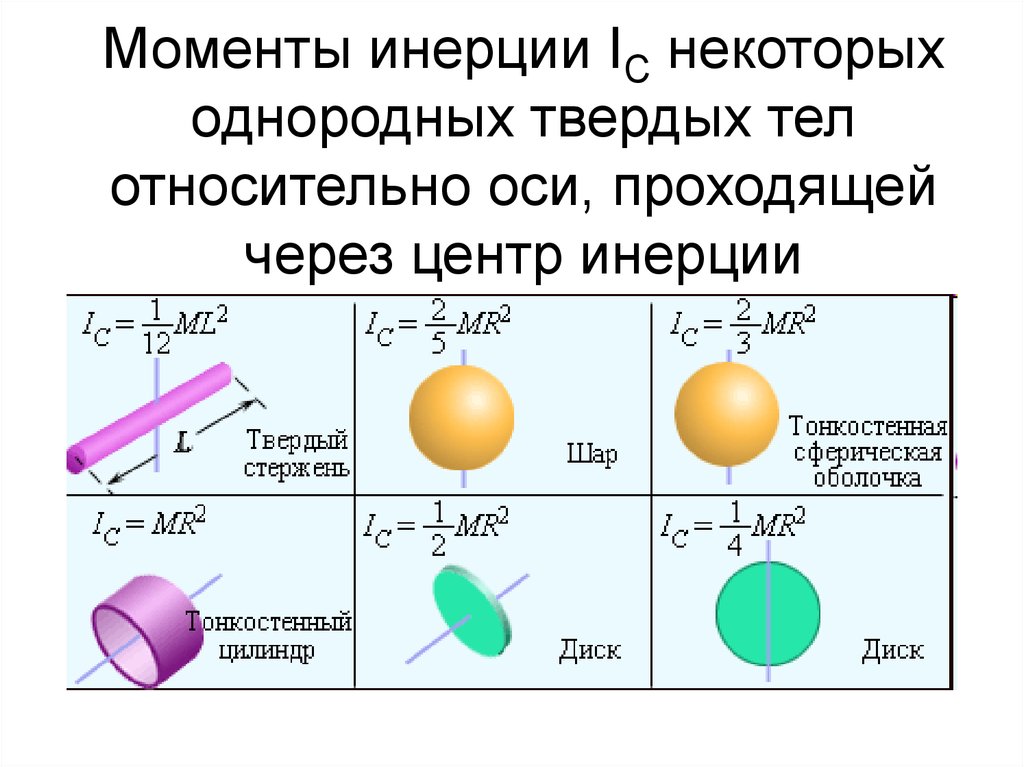
Решение этого уравнения имеет вид
то есть угол отклонения диска от положения равновесия изменяется по гармоническому закону и вся система совершает гармонические колебания с амплитудой 0 и круговой частотой. Величину (t ) называют фазой колебания, — начальной фазой, определяющей угол отклонения при t 0 [18, «https://bakalavr-info.ru»].
Найдя первую и вторую производные угла по времени t и подставив их в уравнение (7), получим
I 2 0cos (t ) b 0cos (t ),
откуда найдем
а затем формулу для периода колебаний T:
Если колеблется только диск, то его период колебаний
(8)
где Iд — момент инерции диска без грузов.
Если на диске лежит эталонное тело, то период колебаний системы TЭТ, в этом случае можно записать аналогично:
. (9)
Используя выражения (8) и (9), получим:
.
Если диск колеблется вместе с телом, момент инерции которого Ix требуется определить, то период его колебаний
откуда
Ix .
Используя полученные выражения для b и Iд, получим окончательную формулу для определения момента инерции исследуемого тела:
4. Таблицы и графики Графики выполняются на миллиметровой бумаге или в компьютерном виде с использованием программ построения графиков. Необходимо соблюдать правила построения графиков.
Таблица 1 — измерения полных колебаний с эталонным телом
№ опыта | Число колебаний, n | Колебания диска без грузов | Колебания диска с эталонным телом | |||
t, c | T0, c | t, c | TЭТ, c | |||
4,4 4,8 5,8 | 1,1 0,96 0,96 | 5,3 5,8 7,7 | 1,32 1,16 1,28 | |||
Средняя величина | __________ | ________ | 1,01 | _______ | 1,25 | |
Таблица 2 — измерения полных колебаний с исследуемым телом
Номер тела | Число колебаний n | t, c | Tх, c | Ix, кгм2 | |
5,7 | 1,42 | 2,28 | |||
6,8 | 1,36 | 2,06 | |||
1,33 | 1,86 | ||||
4,2 | 1,05 | 0,21 | |||
5,3 | 1,06 | 0,25 | |||
6,5 | 1,16 | 0,81 | |||
Таблица 3 — измерения полных колебаний с эталонным и с исследуемым телом с учетом форм тел
Номер тела | Форма тела | Масса тела m, кг | Радиус тела R, м | Ix, кгм2 по формуле (1) | Ixср, кгм2 из табл. | |
Цилиндр Цилиндр | 1,258 0,5 | 4,0= 4,0 | 0,028 0,45 | 2,05 0,42 | ||
2Таблица 4 — измерения полных колебаний с эталонным и с исследуемым телом
№ опыта | n | t, c | T, c | Момент инерции двух тел по формуле (10) Ix кгм2 | |
5,5 6,5 8,2 | 1,38 1,3 1,36 | 2,20 1,68 2,07 | |||
Среднее значение | _____ | ________ | 1,35 | 0,002 | |
Момент инерции двух тел: IxIx1срIx2ср | 2,48 | ||||
Таблица 5 — измерения полных колебаний с эталонным телом, находящимся на некотором расстоянии от центра диска
№ опыта | n | t, c | T, c | Момент инерции по формуле (10), Ix кгм2 | |
5,4 6,8 8,3 | 1,35 1,36 1,38 | 0,0213 0,002 0,0024 | |||
Среднее значение | ____ | ___ | 1,36 | 0,002 | |
Момент инерции по формуле (2): I = … | 5,625 | ||||
5.
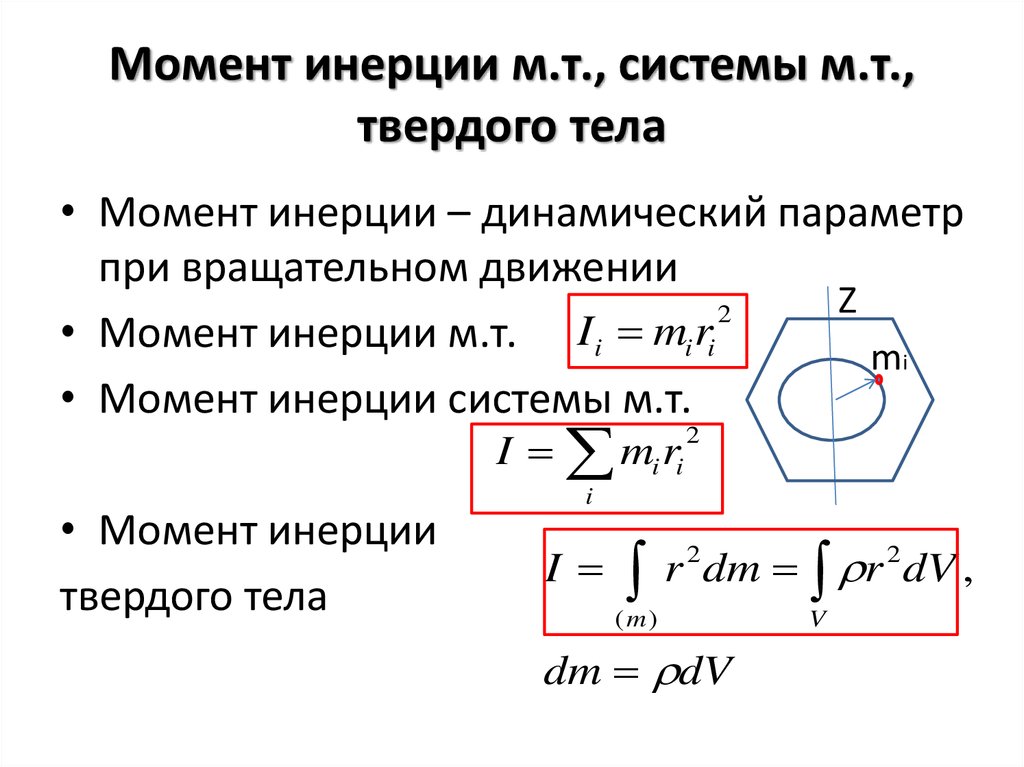Расчёт погрешностей измерений
T .
T .
Tх1 .
Tх2 .
6. Окончательные результаты:
инерция тело ось колебание
2,6 100,05
0,42 100,07
Показать весь текстЗаполнить форму текущей работой
Определение момента инерции системы тел — Мегаобучалка
Цель работы : экспериментальное определение момента инерции системы тел и сравнение полученного результата с теоретически рассчитанным значением для этой же системы тел.
Краткая теория
При описании вращения твердых тел различной формы пользуются понятием – момент инерции ( J ). Моментом инерции системы (тела) относительно данной оси называется скалярная физическая величина, равная сумме произведений масс n материальных точек системы на квадрат расстояния до рассматриваемой оси.
J = , (3.1) где mi – масса i – ой частицы твердого тела,
ri — радиус-вектор вращения i – ой частицы относительно оси вращения.
В случае непрерывного распределения масс эта сумма сводится к интегралу:
Расчет моментов инерции для некоторых тел правильной геометрической формы дает следующие табличные выражения:
1. Сплошной цилиндр, диск: J =
2. Шар : J =
3. Полый, тонкостенный цилиндр: J = mr 2
Момент инерции ( J ) системы твердых тел – величина аддитивная, равная сумме моментов инерции отдельных тел
( J 1 ; J 2 ; …. ; Jn ) этой системы :
J=J1+J2
(3.2)Воспользовавшись формулой ( 2.2 ) , момент инерции для системы тел можно записать в виде :
J системы = J диска + J вала + J прилива , (3.3)
J шкива в виду малости вклада не учитывается.
Теоретически момент инерции можно рассчитать , если тела имеют правильную геометрическую форму, именно так можно поступить в нашем случае :
J системы = . (3.4)
( ε ) , с которым тело вращается вокруг неподвижной оси, прямо пропорционально вращательному моменту сил, действующих на тело, и обратно пропорционально моменту инерции тела:
ε = , (3.
5)
где ε — угловое ускорение,
J — момент инерции.
M — момент сил, действующей на систему тел.
При постоянном моменте сил ( М = const ) тело вращается равнопеременно ( = const ) . Измерив величину углового ускорения , можно определить момент инерции системы тел.
J = . (3.6)
Экспериментальная установка ( рис.3.1 ) состоит из массивного металлического диска А , который крепится на валу В при помощи прилива С. На деревянный шкив К наматывается нить, с закрепленным на ней сменным грузом массой m гр .
Рис.3.1 Общий вид установки
По третьему закону Ньютона, реакция нити N по модулю равна силе F, действующей на нить со стороны груза ( рис.3.2 ). Под действием груза создается момент силы относительно оси вращения:
M = F , (3.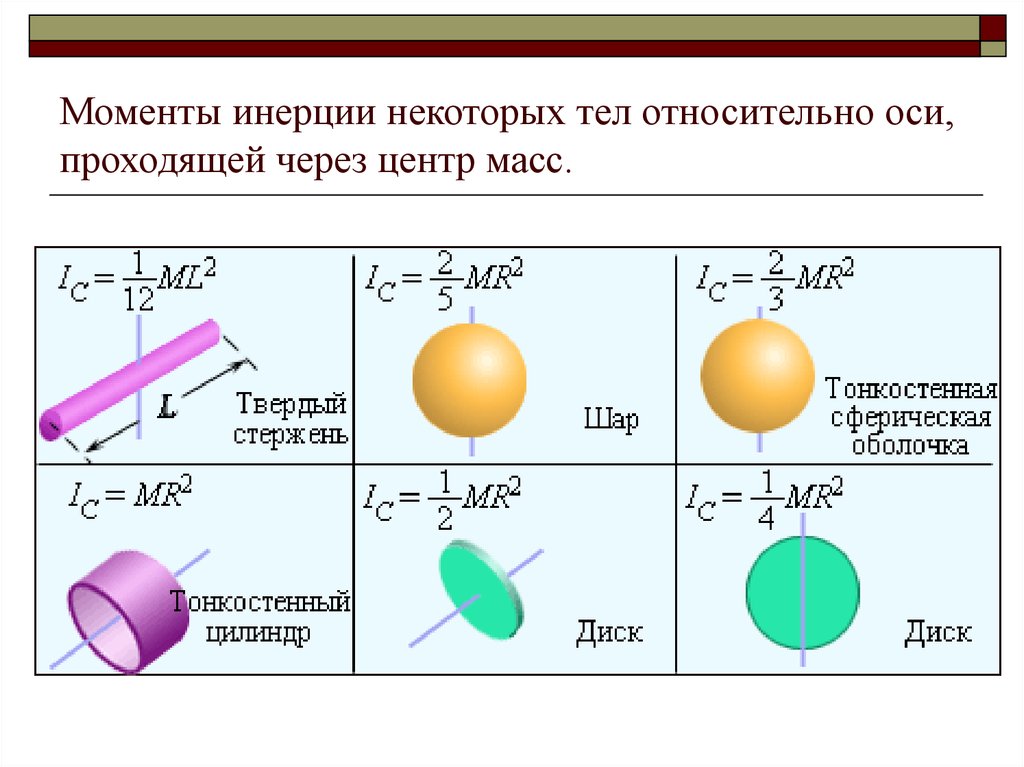
7)
где F – модуль силы , приложенной посредством нити к шкиву,
D — диаметр деревянного шкива.
Для нахождения величины силы F
На груз действуют две силы: сила
тяжести ( ) и сила реакции нити ( ).
Согласно второму закону динамики для
поступательного движения,
спроецировав вектора на ось х , можно
записать для данного случая равенство:
m гр a = m гр g – N , (3.8)
Рис.3.2 где а – линейное ускорение движения
Схема приложения груза,
сил g – ускорение свободного падения
( g = 9,81 м/с2 )
Отсюда выразим силу реакции нити :
N=m гр (g – a) .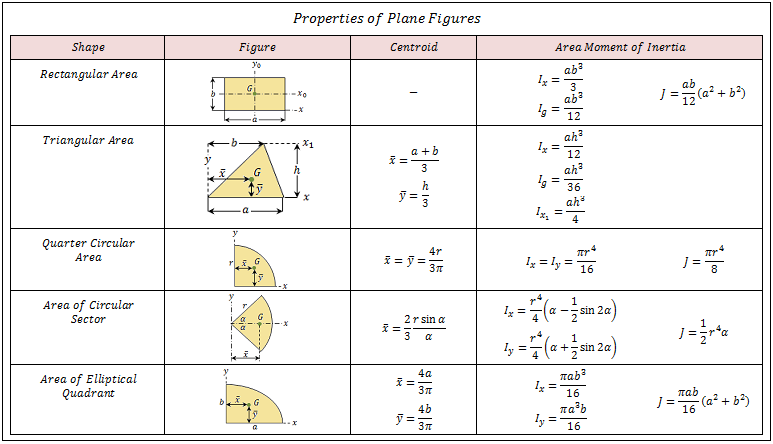
(3.9)
Перепишем выражение ( 3.7 ) для момента силы, подставив вместо F выражение для N :
M=m гр (g – a) . (3.10)
Подставив выражение для М ( 3.10 ) в формулу ( 3.6 ) получим выражение для момента инерции :
J= m гр (g – a) . (3.11)
Угловое ускорение вращающейся системы , связано с линейным ускорением движения груза вниз , соотношением :
. (3.12)
Линейное ускорение груза , опускающегося с высоты h можно рассчитать из соотношения :
. (3.13)
Подставив в формулу ( 3.11 ) для расчета момента инерции соотношение ( 3.12 ) и соотношение ( 3.13 ) получим искомую расчетную формулу для экспериментального определения момента инерции системы тел в окончательном виде :
.
(3.14)
Проведя расчеты и сравнив полученные значения момента инерции системы тел экспериментально и теоретически мы сможем написать вывод о проделанной работе.
Выполнение работы
Приборы и материалы: лабораторная установка ( рис.3.1 ) , секундомер, штангенциркуль, линейка, набор грузов
( 1, 2, 3 кг ) .
Порядок выполнения работы :
1. Теоретически рассчитывают момент инерции системы тел. Для этого параметры диска, прилива и вала заносим в таблицу № 3.1 . По этим данным рассчитывают моменты инерции отдельных тел , их величины суммируют по формуле
( 3.3 ) и заносят в таблицу № 3.1.
Таблица № 3.1
Данные для теоретического расчета момента инерции системы тел
тело | масса ( кг ) | диаметр ( м ) | момент инерции ( кг м2 ) | |
| отдельных тел | системы тел | |||
| Диск | 11,00 0,01 | 0,243 0,001 | ||
| Прилив | 0,40 0,01 | |||
| Вал | 0,90 0,01 | |||
2.
Экспериментальное определение момента инерции этой же системы тел
Измеряют штангенциркулем диаметр деревянного шкива
(Таблица № 3.2).
Прикрепляют конец нити к первому грузу m 1. Вращая диск наматывают нить на деревянный шкив, поднимая груз на высоту
№ 3.2 заносят три значения времени падения груза m 1 = 1 кг. Из трех значений рассчитывают среднее время , заносят его в таблицу. Опыт повторяют с грузами m 2 = 2 кг и m 3 = 3 кг, полученные данные заносят в таблицу № 3.2. Используя средние значения времени падения грузов, по формуле ( 3.14 ) рассчитывают три раза (соответственно трем значениям времени падения груза) момент инерции системы тел . Затем находят среднее значение момента инерции .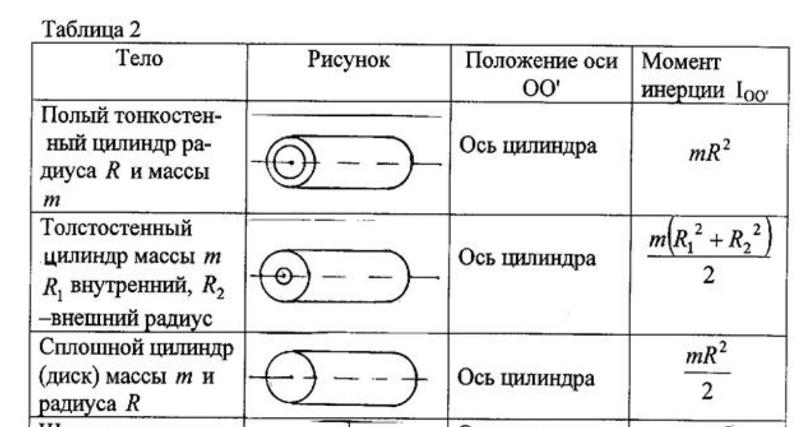
Таблица № 3.2
Данные для экспериментального определения момента инерции системы тел
| масса груза | Время падения груза t ( сек ) | < t > ( сек ) | J (кг м2) | Δ J (кг м2) | ||
| m1 = 1 кг | ||||||
| m2 = 2 кг | ||||||
| m3 = 3 кг | ||||||
Диаметр деревянного шкива D = ( м ) | < J >= | <Δ J>= | ||||
Вычисление погрешностей и окончательный результат
Находят абсолютные погрешности ΔJ1 , ΔJ2 , ΔJ3 моментов инерции , вычисленных для трех случаев , по ним определяют среднюю абсолютную погрешность <ΔJ> .
Относительная погрешность определения момента инерции :
% . (3.15)
Окончательный результат :
. (3.16)
Проводят сравнение значений момента инерции системы тел определенных экспериментально и рассчитанных теоретически.
Записывают выводы.
Момент инерции
Момент инерции, часто известный как вращательная инерция, является важным термином в физике. На самом деле это mr2 вокруг центральной точки вращения, поэтому единицей измерения является кгм2. Обозначается знаком I. Это описывается как сопротивление, которое тело оказывает своей скорости вращения или угловому ускорению вдоль оси, применяя вращающую силу, также известную как крутящий момент. Поскольку момент инерции зависит от формы и размера тела, в следующих разделах он рассчитывается независимо. Выводы имеют решающее значение для численных задач, основанных на этой теме.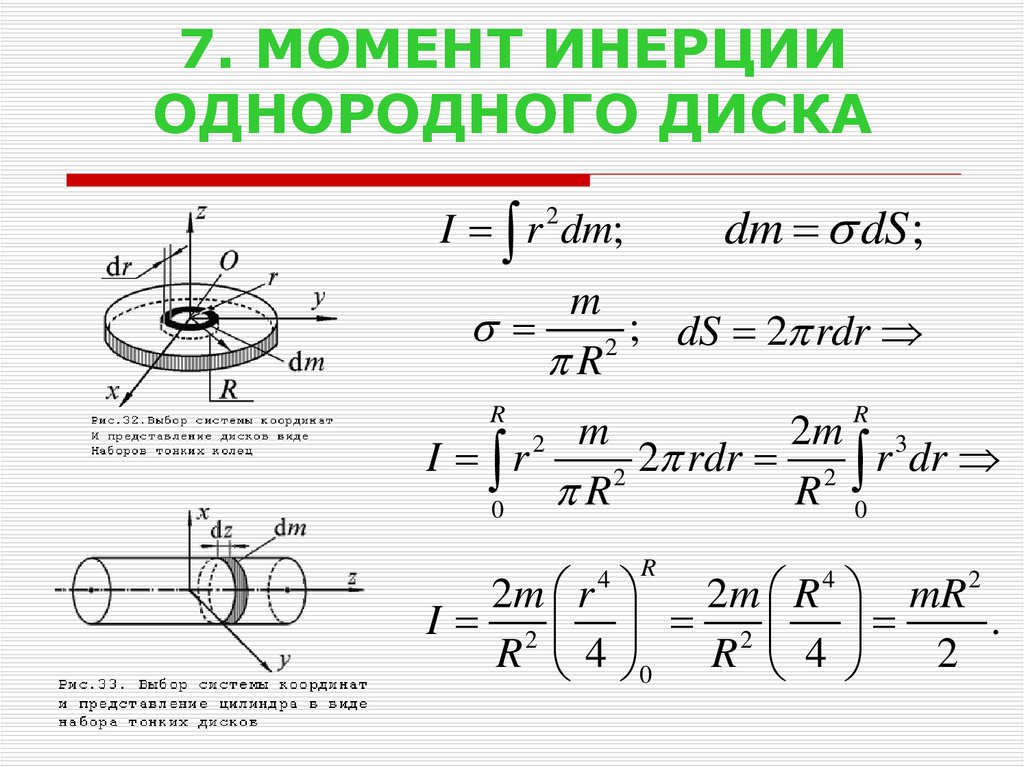
Момент инерции
Определение
Момент инерции твердого тела, также известный как момент инерции массы, угловая масса, второй момент массы или, точнее, инерция вращения, представляет собой величину, определяющую требуемый крутящий момент. для желаемого углового ускорения вокруг оси вращения, аналогично тому, как масса определяет силу, необходимую для желаемого ускорения. Он определяется распределением массы тела и выбранной осью, причем более высокие моменты требуют большего крутящего момента для изменения скорости вращения тела.
Момент инерции объекта — это расчетное измерение твердого тела, вращающегося вокруг фиксированной оси. Ось может быть внутренней или внешней, и она может быть фиксированной или нефиксированной. Однако момент инерции (I) всегда указывается относительно этой оси.
На момент инерции влияет распределение массы вокруг оси вращения. MOI изменяется в зависимости от выбранного положения оси. То есть один и тот же предмет может иметь разные значения моментов инерции в зависимости от положения и направления оси вращения.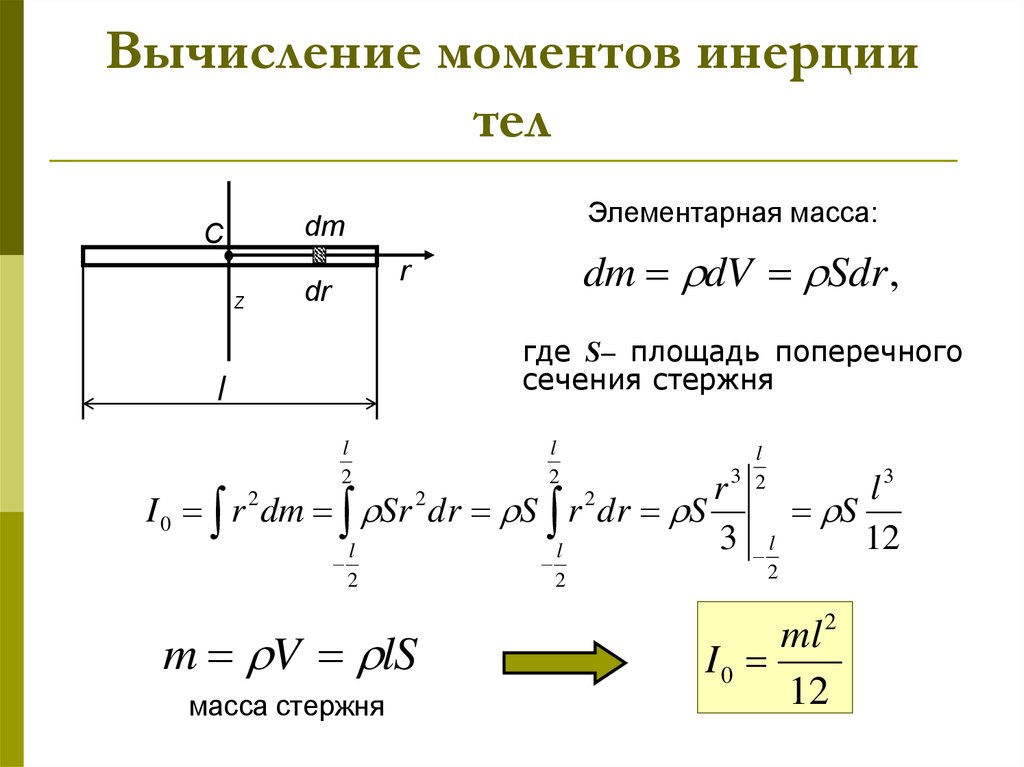
Момент инерции
Обычно момент инерции записывается как I = m r2.
Где m = сумма произведений массы
r = расстояние от оси вращения.
Интегральная форма: I = ∫ r2 dm
Момент инерции играет очень важную роль, как и масса в прямолинейном движении.
Это также измерение сопротивления тела, подобное изменению вращательного движения.
Момент инерции постоянен для заданной жесткой рамы, а также для оси вращения.
Момент инерции, I =∑ mi ri2… (1)
Кинетическая энергия, K =½ I ω2……………. (2)
Примеры момента инерции
Момент инерции молекулы водорода имел историческое значение. Подсчитать просто: ядра (протоны) содержат 99,95% массы, поэтому традиционное изображение двух точечных масс, разделенных заданным расстоянием, дает I=12ma2. Проблема в девятнадцатом веке заключалась в том, что равнораспределение энергии, которое давало хорошее объяснение удельной теплоемкости практически всех газов, не работало для водорода — по-видимому, при низких температурах эти двухатомные молекулы не вращались, а постоянно сталкиваются друг с другом.
Вывод заключался в том, что момент инерции был настолько мал, что требовалось много энергии, чтобы зажечь начальное состояние квантованного углового момента, L=. Этого не произошло с более тяжелыми двухатомными газами, поскольку их энергия была выше. Для молекул с большими моментами инерции состояние с наименьшим угловым моментом E=L2/2I=ℏ2/2I ниже.
Момент инерции для различных объектов
На момент инерции влияет ось вращения. Все, что мы обнаружили до сих пор, — это момент инерции этих предметов, когда ось проходит через их центр масс. Когда вы выберете две уникальные оси, вы увидите, что предмет по-разному сопротивляется изменению вращения.
Момент инерции сферы
Момент инерции сферы обычно представляется как;
I = (⅖)MR2
R и M обозначают радиус и массу сферы соответственно. Кроме того, момент инерции сферы относительно своей оси на поверхности представляется как;
I = (7/5) MR2
Вывод
Рассчитайте момент инерции однородного твердого шара относительно любой оси, проходящей через его центр.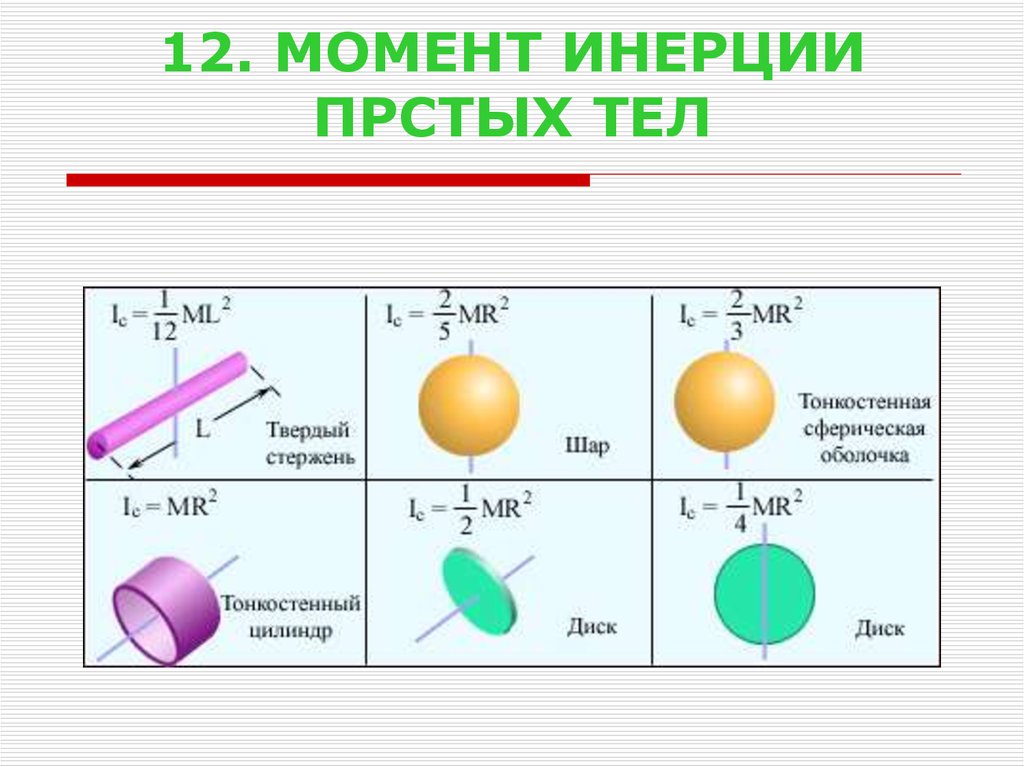
I = 1/2MR2
Теперь,
DI = 1/2R2 DM
для поиска DM
DM = ρdv
для DV
DV = πR2 DX
после положения стоимости DV в DM
dm=ρπr2 dx
Теперь подставим значение dm в dI
dI=1/2ρπr4 dx
Теперь мы должны ввести x в уравнение. Выше обратите внимание, как x, r и R образуют треугольник. По теореме Пифагора.
r2=R2–x2
или,
dI=1/2ρπ(R2–x2)dx2
Следовательно,
I=1/2ρπR∫−R(R2–x2)dx2 После интегрирования
I=1/2ρπ(16/15)R5
Теперь необходимо определить плотность шара:
ρ=MV
ρ=M/(4/3πR3)
После подстановки значения 2/5 MR2
Заключение
Поскольку момент инерции зависит от формы и размера тела.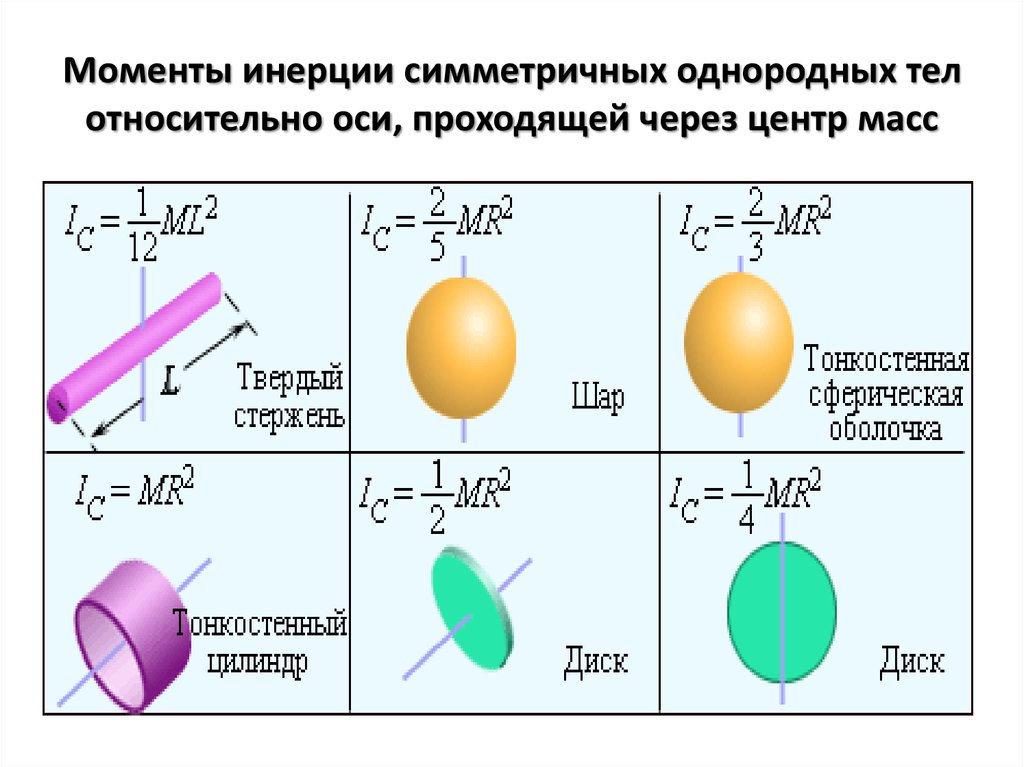
Момент инерции твердого тела, также известный как его массовый момент инерции, угловая масса, второй момент массы или, точнее, вращательная инерция, представляет собой величину, которая определяет крутящий момент, необходимый для желаемого углового ускорения вокруг оси вращения, аналогично тому, как масса определяет силу, необходимую для желаемого ускорения. На момент инерции влияет распределение массы вокруг оси вращения. То есть один и тот же объект может иметь разные значения моментов инерции в зависимости от положения и направления оси вращения. Формула выражается как I = m r2, где m = сумма произведений массы, r = расстояние от оси вращения.
Пусть I(1) и I(2) — моменты инерции двух тел одинаковой геометрической формы, первое из которых изготовлено из алюминия, а второе — из железа.
AAKASH СЕРИЯ-СИСТЕМА ЧАСТИЦ И ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ-Упражнение-I
20 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Pro и dekho sari видео bina kisi ad ki rukaavat!
Войдите в систему, если она уже приобретена
Обновлено: 27 июня 2022 г.
0003
A
I1 B I1 = I2 C I1> I2 D RELATIOAN между I1 и I2 В зависимости от фактических соревнований . is A Ответ Пошаговое решение, разработанное экспертами, чтобы помочь вам сомневаться в чистоте и получить отличные оценки на экзаменах. Видео по теме Пусть I_(1) и I_(2) — моменты инерции однородной квадратной пластины относительно осей, показанных на рисунке. Тогда отношение I_(1):I_(2) равно 10964175 Пусть IA и IB — моменты инерции тела относительно двух осей A и B соответственно. Ось A проходит через центр масс тела, а B нет 11301246 Пусть IA и IB — моменты инерции тела относительно двух осей A и B соответственно. Ось A проходит через центр масс тела, а B нет 11301258 Text Solution Пусть I1 и I2 — моменты инерции однородной квадратной пластины относительно осей APC и OPO соответственно, как показано на рисунке. 12229745 एक जैसी ज्यामितीय आकृत्तियों वाली दो वस्तुओं के जड़त्व आघूर्ण i1 तथा i2 हैं।।।।।।। हैं हैं हैं हैं पहली वस्तु ऐलुमिनियम की तथा दूसरी लोहे की बनी ही ही इनमें सही कथन बताएँ। 110487363 घूर्णी गति क Как दो पिंडों के कोणीय संवेग समान है।।।। यदि उनके जड़त्व आघूर्ण i1 व i2 हों तथा i1> i2 हो किस पिंड की घू घू000 गतिज ऊर्जा अधिक होगी? 234020619 Утверждение — 1: Пусть I_(1) и I_(2) будут моментами инерции двух тел одинаковой геометрической формы, первое из которых изготовлено из алюминия, а второе из железа, тогда I_(1) lt I_(2 ). Поскольку Утверждение — 2: Момент инерции не зависит от формы 327884471 Если I_(1) , I_(2) и I_(3) — моменты инерции диска относительно его геометрической оси, диаметра и касательной в его плоскости, то 479322731 Пусть IA и IB — моменты инерции тела относительно двух осей A и B соответственно. Ось А проходит через центр масс тела, а В нет. 642595244 Если I_(1)I_(2) и I_(3) моменты инерции диска относительно его геометрической оси, диаметра и касательной в его плоскости, то 642674552 Пусть IA и IB — моменты инерции тела относительно двух осей A и B соответственно. Ось А проходит через центр масс тела, а В нет. 642674587 Если I1,I2 и I – моменты инерции диска относительно его геометрической оси, диаметра и касательной в его плоскости, то 642708415 Текст Решение Пусть IA и IB – моменты инерции тела вокруг двух осей А и В соответственно. Ось А проходит через центр масс тела, а В — нет.0003 642708450 Text Solution Моменты инерции двух вращающихся тел A и B равны I_(A) и I_(B) (I_(A) gt I_(B) ). Если их угловые моменты равны, то 642733016 Текст Решение Если I1I2, и I3 — моменты инерции диска относительно его геометрической оси, диаметра и касательной в его плоскости, то 642845539 Пусть и IB — моменты инерции тела относительно двух осей A и B соответственно.
.P — центр квадрата. Отношение моментов инерции I1I2 равно —
.
Тогда
