|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
Стр 1 из 4Следующая ⇒ МЕХАНИКА ЛАБОРАТОРНАЯ РАБОТА № 5 МОМЕНТ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ. ТЕОРЕМА ШТЕЙНЕРА
САНКТ-ПЕТЕРБУРГ 2012 г. РАБОТА 5. МОМЕНТ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ. ТЕОРЕМА ШТЕЙНЕРА
Цель работы – измерить моменты инерции различных тел. Проверить теорему Штейнера.
Теоретические основы лабораторной работы Момент инерции тела является мерой инертности тела при вращательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения. Момент инерции сплошного твёрдого тела определяется по формуле , где — расстояние от элемента объема с массой dm до оси вращения, r — плотность вещества.
Рис. 5.1. Общий вид экспериментальной установки
Таким образом, момент инерции тел различной формы можно найти как результат интегрирования по соответствующему объёму тела. Частные случаи. 1. Момент инерции материальной точки массой m , находящейся на расстоянии R от оси вращения (5.1) 2. Момент инерции сплошного цилиндра относительно оси, перпендикулярной к плоскости основания цилиндра и проходящей через его центр масс (ось цилиндра) (5.2) здесь R, m — радиус и масса цилиндра. Так как момент инерции не зависит от высоты цилиндра, эта же формула справедлива для момента инерции однородного диска относительно оси перпендикулярной к плоскости диска. 3. Момент инерции полого цилиндра с внутренним радиусом R (5.3) 4. Момент инерции шара массой m и радиуса R относительно оси проходящей через его центр масс (5. 5. Момент инерции тонкого стержня массой m и длиной l относительно оси проходящей через его середину перпендикулярно стержню. (5.5) Эти формулы справедливы для момента инерции относительно оси симметрии. Момент инерции относительно произвольной оси параллельной оси симметрии можно найти с помощью теоремы Штейнера. Момент инерции относительно произвольной оси О (5.6) Например, с помощью теоремы Штейнера, зная момент инерции стержня относительно оси перпендикулярной к стержню и проходящей через его центр масс, можно получить формулу для вычисления момента инерции стержня относительно оси проходящей через его конец. (5.7) В общем случае расчет момента инерции представляет собой достаточно сложную задачу. В данной работе для экспериментального измерения моментов инерции различных тел используется метод крутильных колебаний. Исследуемые тела насаживаются на ось спиральной пружины. В результате деформации пружины при её закручивании на угол j возникнет упругая сила. Эта сила создает крутящий момент (момент силы) . Модуль момента пропорционален углу закручивания пружины M=Dj (5.8) В этой формуле коэффициентом пропорциональности D является модуль кручения пружины. С другой стороны из определения момента силы следует, что это вектор, модуль которого определяется по формуле М=Fl (5.9) Крутящий момент стремится вернуть пружину в исходное (равновесное) состояние. В результате возникают крутильные колебания. В соответствии с теорией период крутильных колебаний определяется по формуле (5.10) Отсюда момент инерции тела (5.11) Таким образом, измеряя период крутильных колебаний и зная модуль кручения D пружины, можно вычислить момент инерции тела, насаженного на ось пружины. Методика лабораторной работы позволяет измерять моменты инерции стержня без грузов, стержня с грузами, сплошного цилиндра, полого цилиндра, диска и шара.
Порядок выполнения работы I. Определение модуля кручения пружины. 1. Возьмите стержень с грузами и насадите его на ось пружины. Грузы сдвиньте к центру. 2. Поверните стержень на 90о (p/2 радиан).
3. 4. Проделайте эти измерения для углов j, равных 180о, 270о, 360о. 5. Полученные данные занесите в таблицу 5.1. МЕХАНИКА ЛАБОРАТОРНАЯ РАБОТА № 6 Г. МЕХАНИКА ЛАБОРАТОРНАЯ РАБОТА № 7 Г. Описание установки
Общий вид установки представлен на рис.7.2. В основании 1 закреплена колонка с электронным секундомером 2, к которой прикреплен неподвижно верхний кронштейн 9 и подвижный нижний кронштейн 7. На верхнем кронштейне находится электромагнит 10 и фотоэлектрический датчик 11, а на нижнем кронштейне – фотоэлектронный датчик 3. Маятник представляет собой диск 5, закрепленный на оси 6, подвешенной на двух нитях 4 (бифилярный подвес). Маятник удерживается в верхнем положении электромагнитом 10. Фотоэлектрические датчики 3 и 11 соединены с электронным секундомером 2. Верхний электронный датчик фиксирует момент начала движения маятника, а нижний — окончания движения (опускания) маятника. Порядок выполнения работы
8. Повторить пп.1-7 еще десять раз.
МЕХАНИКА ЛАБОРАТОРНАЯ РАБОТА № 5 МОМЕНТ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ. ТЕОРЕМА ШТЕЙНЕРА
САНКТ-ПЕТЕРБУРГ 2012 г. 1234Следующая ⇒ Читайте также: Организация работы процедурного кабинета Статус республик в составе РФ Понятие финансов, их функции и особенности Сущность демографической политии |
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 894; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Момент инерции различных тел. Теорема Штейнера
Лабораторная работа 15
МОМЕНТ ИНЕРЦИИ РАЗЛИЧНЫХ ТЕЛ. ТЕОРЕМА ШТЕЙНЕРА.Экспериментальная установка
Общие сведения
Момент инерции тела является мерой инертности тела при вращательном движении, подобно тому, как масса тела является мерой инертности тела при поступательном движении. Момент инерции тела зависит от размеров и формы тел и от распределения массы тела относительно оси вращения. Для вычисления момента инерции твердого тела относительно некоторой оси ОО разобьем мысленно тело на большое число весьма малых элементов — материальных точек (рис.1). Тогда момент инерции такой отдельной элементарной массы
где —
расстояние от элемента объема до оси вращения, r — плотность вещества.
Момент инерции всего тела
,
Таким образом, момент инерции различных тел можно найти с помощью интегрирования.
Рассмотрим результаты расчета для некоторых частных случаев.
1. Момент инерции материальной точки массой m , находящейся на расстоянии R от оси вращения
(1)
2. Момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр. Радиус диска R, его масса m.
(2)
.Эта же формула справедлива для момента инерции сплошного цилиндра относительно оси совпадающей с осью цилиндра..
3. Момент инерции полого цилиндра с внутренним радиусом R1 и внешним радиусом R2 относительно оси , совпадающей с осью цилиндра.
(3)
4.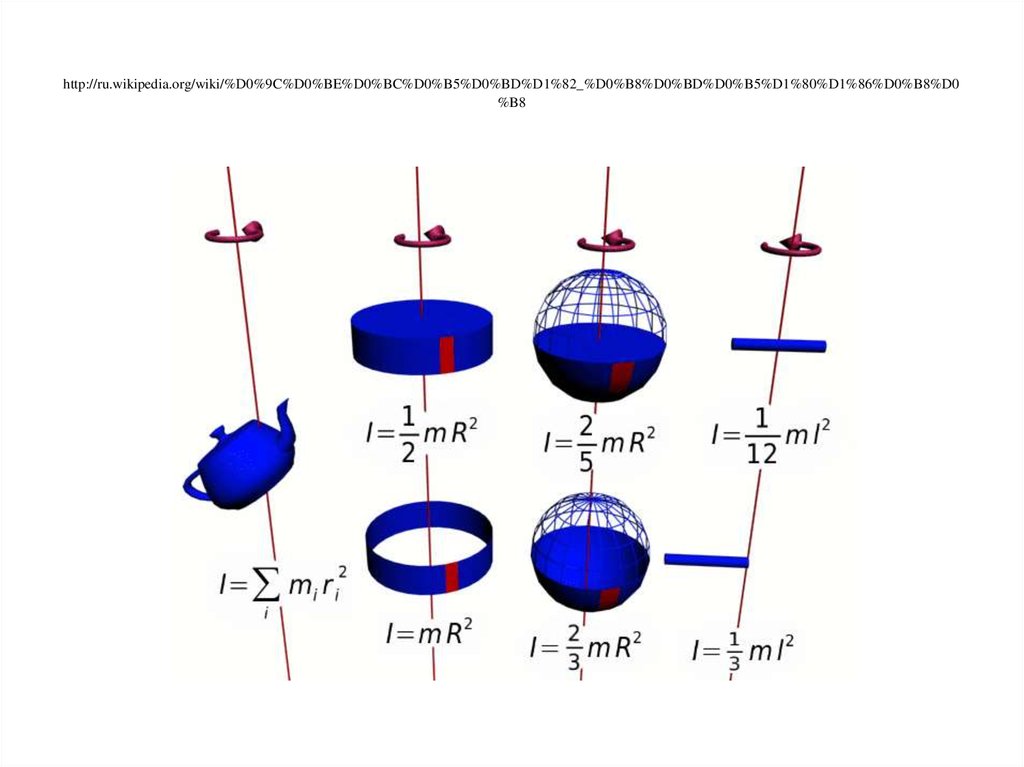 Момент инерции шара радиуса R относительно оси
проходящей через его центр.
Момент инерции шара радиуса R относительно оси
проходящей через его центр.
(4)
5. Момент инерции тонкого стержня относительно оси перпендикулярной к стержню и проходящей через его середину. Длина стержня l,
(5)
Эти формулы для моментов инерции относительно оси симметрии.
Момент инерции относительно произвольной оси можно найти с помощью теоремы Штейнера:
Момент инерции относительно произвольной оси О1О1 равен сумме момента инерции I0, относительно оси OO, параллельной данной и проходящей через центр инерции тела и произведения массы тела на квадрат расстояния d между осями.
Получим с помощью
этой теоремы формулу момента инерции стержня относительно оси перпендикулярной
к стержню и проходящей через его конец.
(6)
В общем случае расчет момента инерции представляет собой достаточно сложную задачу, и часто он определяется экспериментально с помощью основного уравнения динамики вращательного движения, методом крутильных колебаний и др.
В данной работе для экспериментального измерения моментов инерции различных тел используется метод крутильных колебаний.
Исследуемые тела насаживаются на ось спиральной пружины. Если зкрутить пружину на угол j, то в результате деформации пружины возникнет упругая сила. Она создает крутящий момент (момент силы) М
M=Dj (7)
Здесь D – модуль кручения пружины.
Этот крутящий момент стремится вернуть пружину в исходное (равновесное) состояние. В результате возникают крутильные колебания.
Из теории крутильных колебаний следует формула для периода колебаний
(8)
где J — момент инерции.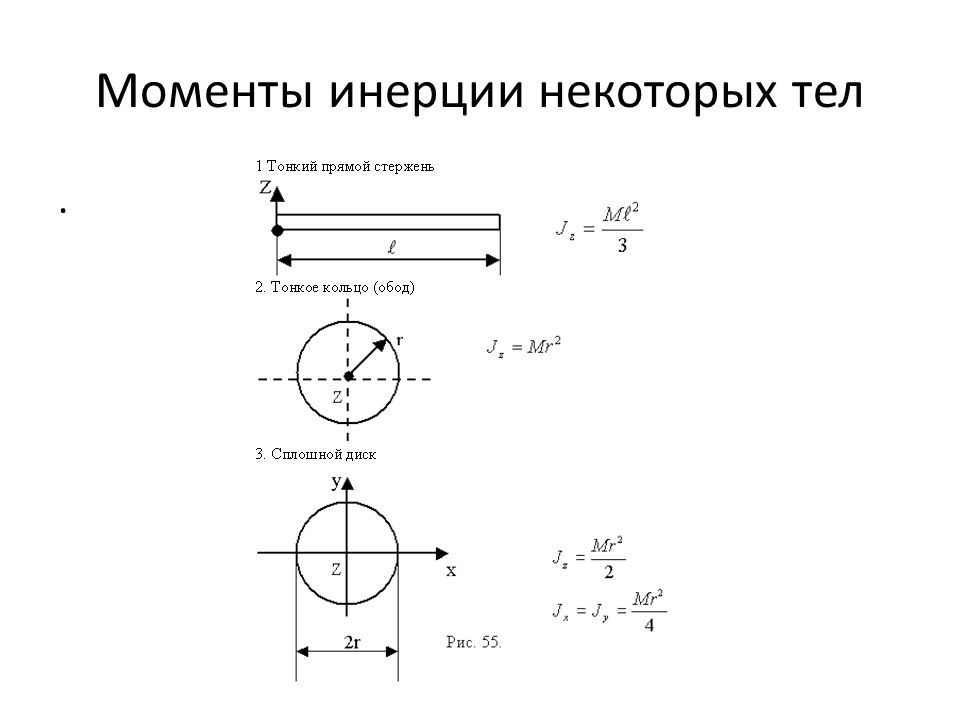
Отсюда
(9)
Таким образом, измеряя период крутильных колебаний и зная модуль кручения D пружины, можно вычислить момент инерции тела, насаженного на ось пружины.
Порядок выполнения работы.
Для определения модуля кручения D пружины возьмите стержень с грузами и насадите его на ось пружины. Грузы сдвиньте к центру.
Поверните стержень на 90о (p/2 радиан). Прикрепите к стержню (у края грузов) динамометр и измерьте силу F. Необходимую для удержания стержня в этом положении (динамометр держите перпендикулярно стержню).
Вычислите момент силы М
М=Fl
Здесь l – плечо силы, то есть расстояние от оси вращения до места приложения силы (до места прикрепления динамометра).
Момент инерции массы
Момент инерции масс:
Момент инерции массы является одной из мер распределения
масса объекта относительно данной оси. Момент инерции масс обозначается через I и дается для одной частицы массой m как
Момент инерции масс обозначается через I и дается для одной частицы массой m как
Io = r2m
, где O-O — ось, вокруг которой оценивается момент инерции массы, а r — перпендикулярное расстояние между массой и ось О-О. Как видно из приведенного уравнения, момент инерции массы имеет единицы массы, умноженной на длину в квадрате, . Массовый момент инерции должен не путать с моментом инерции площади, который имеет единицы длины в степени четыре. Массовые моменты инерции естественным образом появляются в уравнениях движения и обеспечивают информация о насколько сложно (сколько инерции) вращать частицу вокруг заданной оси.
Момент инерции массы твердого тела: При расчете
массовый момент инерции для твердого тела, тело рассматривается как сумма частиц,
каждая имеет массу дм . Интегрирование используется для суммирования момента инерции
каждый дм, чтобы получить момент инерции массы тела. Уравнение для массового момента
инерция твердого тела равна
Уравнение для массового момента
инерция твердого тела равна
Интеграция по массу можно заменить интегрированием по объему, площади или длине. На целых три пространственного тела с помощью плотности можно связать элемент массы с элементом объем. В этом случае плотность имеет единицы массы на длину в кубе, и соотношение указано как
и уравнение для момент инерции становится равным
Интеграл фактически тройной интеграл. Если используемая система координат прямоугольная, то dV=dxdydz . Если в качестве координат используются цилиндрические координаты, то
Для двухмерного тела в виде пластины или оболочки можно использовать плотность на единицу площади (единицы массы на квадрат длины), чтобы изменить интегрирование с использованием соотношения
, где A — площадь поверхности, а dA — дифференциальный элемент
область.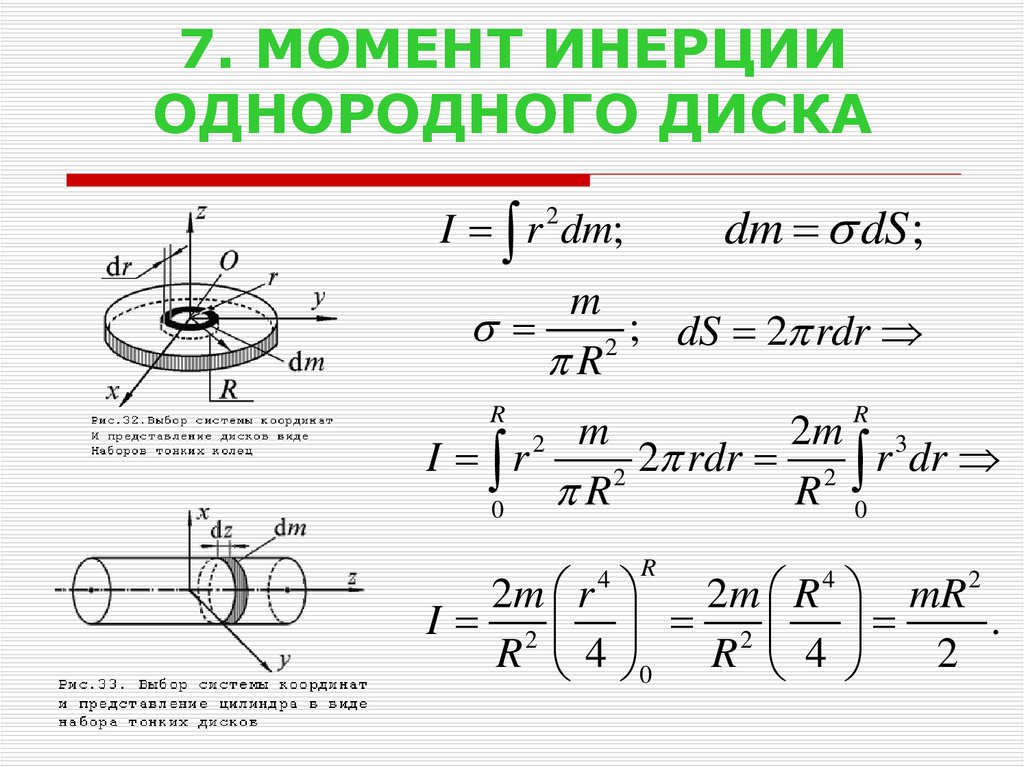 Например, для прямоугольных координат dA=dxdy и для полярных координат
. После этой замены получается уравнение для расчета момента инерции массы как
Например, для прямоугольных координат dA=dxdy и для полярных координат
. После этой замены получается уравнение для расчета момента инерции массы как
Если тело представляет собой стержень , подобный объекту , то один можно использовать отношение
чтобы получить
где l — координата по длине стержня и плотность в единицах массы на единицу длины.
Радиус вращения:
Когда-то вместо момента инерции масс стоит радиус гирация к предусмотрена. Момент инерции массы можно рассчитать по формуле к . используя отношение
где м — это полная масса тела. Радиус вращения можно интерпретировать как
расстояние от оси, на котором можно было бы положить одну частицу массой м равной
массы твердого тела, и эта частица имеет такой же массовый момент инерции, как
оригинальное тело.
Теорема о параллельных осях:
Можно рассчитать момент инерции вокруг любой оси от момента инерции вокруг параллельной оси, проходящей через центр масс. Уравнение для расчета этого называется теоремой о параллельных осях и задается как
, где d — расстояние между исходной осью а ось, проходящая через центр масс, м — полная масса тела, и – момент инерции вокруг оси, проходящей через центр масс.
Композитные корпуса:
Если тело состоит из нескольких тел, для расчета момент инерции относительно данной оси можно просто вычислить момент инерции каждую часть вокруг заданной оси, а затем сложите их, чтобы получить момент инерции массы общее тело.
Как рассчитать момент инерции?
Момент инерции, называемый угловой массой или инерцией вращения относительно оси вращения, представляет собой величину, определяющую величину крутящего момента, необходимого для достижения желаемого углового ускорения, или характеристику тела, препятствующую угловому ускорению.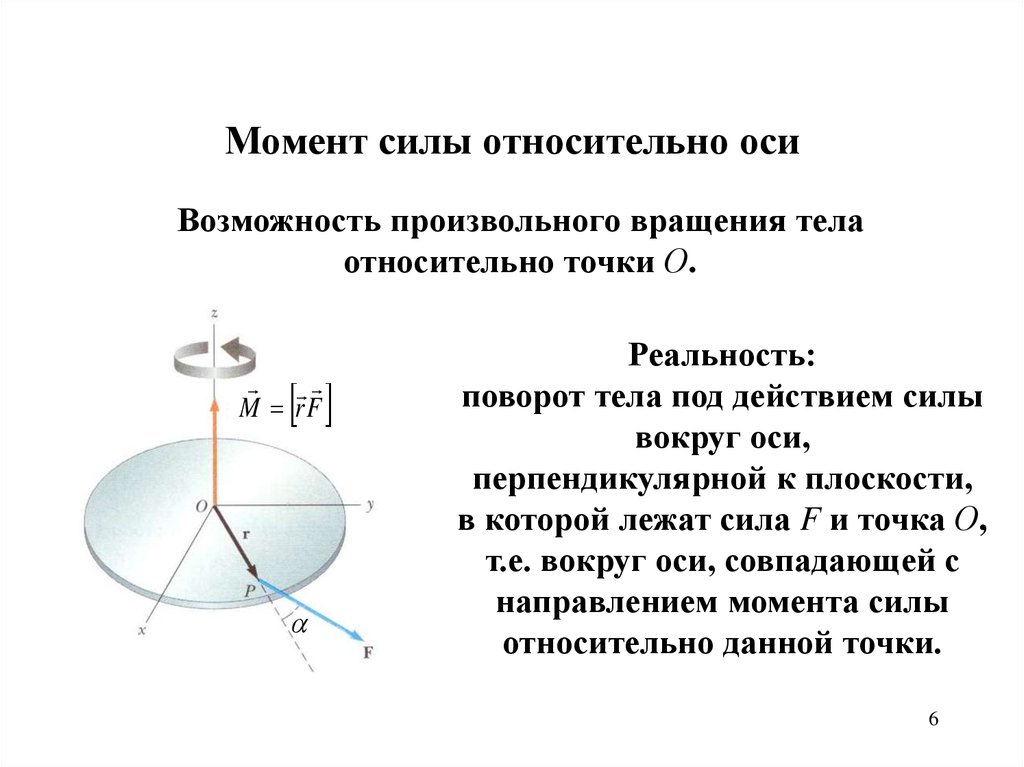 Момент инерции рассчитывается как произведение массы каждой частицы на квадрат ее расстояния от оси вращения.
Момент инерции рассчитывается как произведение массы каждой частицы на квадрат ее расстояния от оси вращения.
Момент инерции
Термин «момент инерции» относится к величине, которая описывает, как тело сопротивляется угловому ускорению, и рассчитывается как произведение массы каждой частицы на квадрат расстояния частицы от оси вращения. Или, другими словами, можно сказать, что это величина, определяющая, какой крутящий момент требуется для определенного углового ускорения вращающейся оси. Момент инерции часто называют вращательной инерцией или угловой массой. кг·м 2 — единица момента инерции в системе СИ.
Момент инерции системы из n частиц
Момент инерции системы точечных частиц, вращающихся вокруг неподвижной оси, равен:
где,
r i — расстояние между осью i th и
m i — масса i th частица.
Как рассчитать момент инерции?
Для расчета момента инерции любого вращающегося объекта используется несколько способов.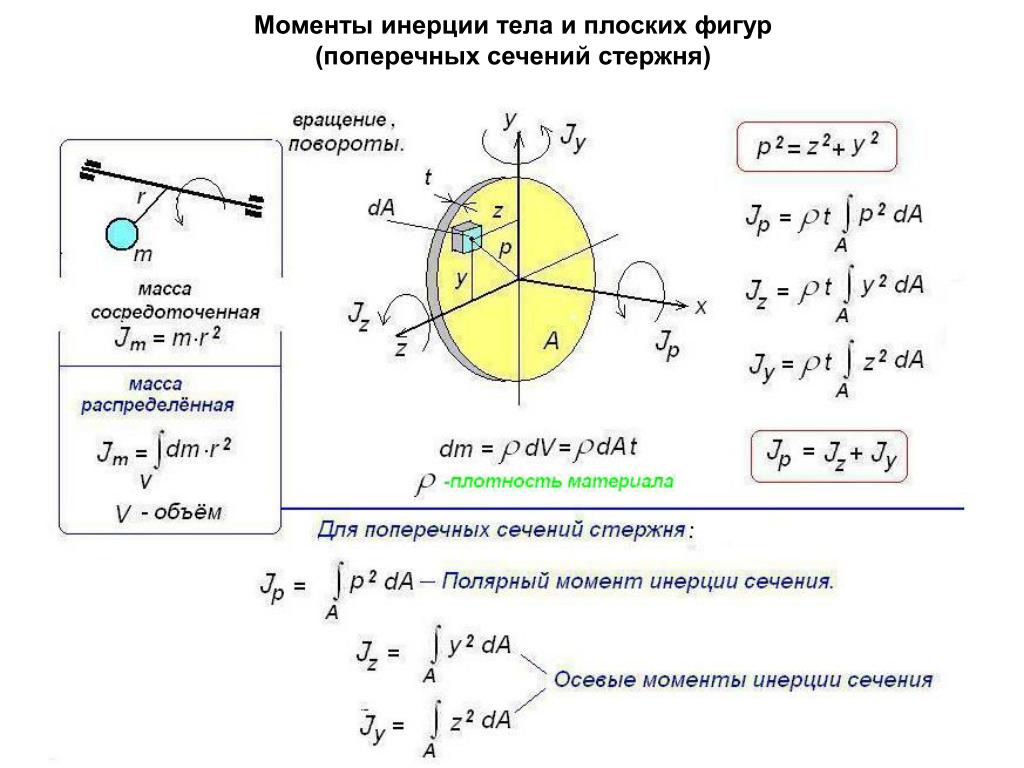
- Для однородных объектов момент инерции рассчитывается путем произведения массы объекта на квадрат расстояния от оси вращения (r 2 ).
- Для неоднородных объектов мы вычисляем момент инерции, взяв сумму произведений масс отдельных точек на каждом другом радиусе, для этого используется формула
I = ∑m i r i 2
Formulas For Calculating Moment Of Inertia
Expressions for the moment of inertia for some symmetric objects along with their axis of rotation are discussed below в этой таблице.
| Объект | Ось | Выражение момента инерции | |
|---|---|---|---|
| I = Mr 2 | |||
| Thin Ring | Diameter | I = 1/2 Mr 2 | |
| Annular Ring or Hollow Cylinder | Central | I = 1/2 M (r 2 2 + r 1 2 ) | |
| Solid Cylinder | Central | I = 1/2 Mr 2 | |
| Uniform Disc | Diameter | I = 1/4 м 2 | |
| Hollow Sphere | Central | I = 2/3 Mr 2 | |
| Solid Sphere | Central | I = 2/5 Mr 2 | |
| Uniform Symmetric Spherical Shell | Central | ||
| Uniform Plate or Rectangular Parallelepiped | Central | I = 1/12 M(a 2 + b 2 ) | |
| Thin rod | Центральный | I = 1/12 MR 2 | |
| Тонкий стержень | на конце стержня | I = 1/3 MR 2 | 9034. 10 10.10134.10134.1013.10.1013.10.1013.10.10134.10134.10134.10134.10134.10134.10134.10134.10134.10134.10134.10134.10.1013.10.10134.10134. Пример 1: Определить момент инерции твердого шара массой 22 кг и радиусом 5 м. Ответ :
2 и радиусом 10 м. Ответ :
его момент инерции. Ответ :
Пример 4: Когда однородный полый прямоугольный круговой конус имеет момент инерции 98 кг m 2 и масса 20 кг определяют радиус конуса. |


 Все правила по сольфеджио
Все правила по сольфеджио

 4)
4)

 Прикрепите к стержню (у края грузов) динамометр и измерьте величину силы F, необходимую для удержания стержня в этом положении (динамометр держите перпендикулярно стержню и оси вращения).
Прикрепите к стержню (у края грузов) динамометр и измерьте величину силы F, необходимую для удержания стержня в этом положении (динамометр держите перпендикулярно стержню и оси вращения). На диск можно насаживать сменные кольца 12, изменяя, таким образом, момент инерции системы.
На диск можно насаживать сменные кольца 12, изменяя, таким образом, момент инерции системы.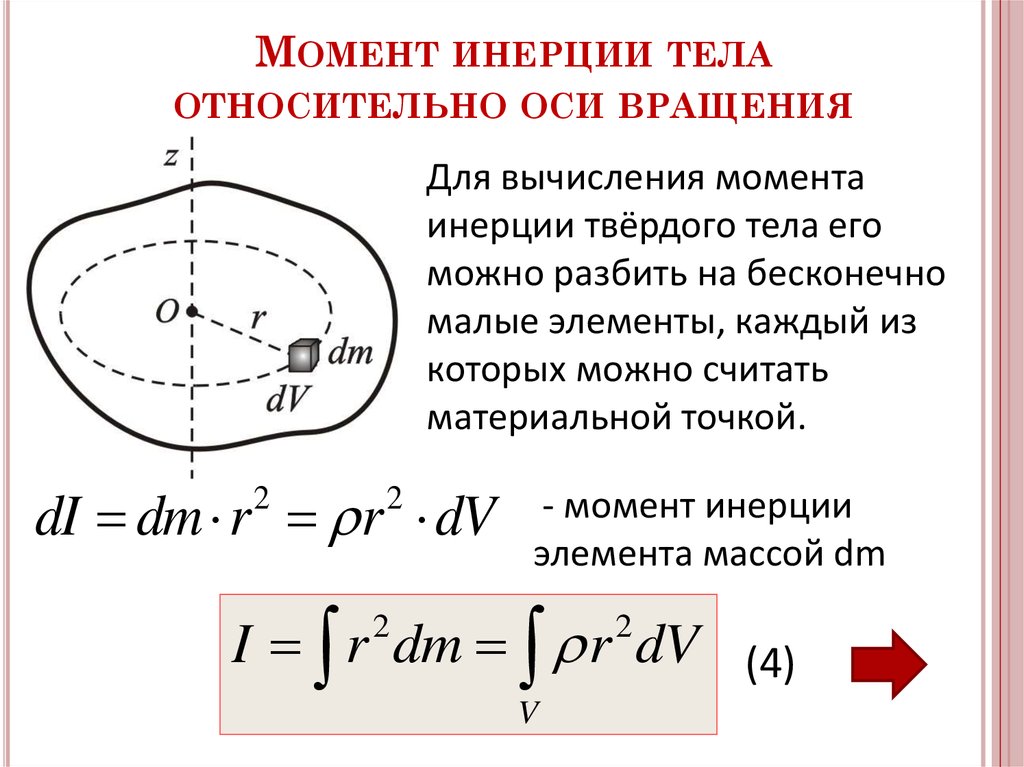
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)