Сопротивление материалов
Сопротивление материалов
ОглавлениеПРЕДИСЛОВИЕГлава 1. ОСНОВНЫЕ ПОНЯТИЯ § 2.1. РАСЧЕТНАЯ СХЕМА. НАГРУЗКИ § 3.1. ВНУТРЕННИЕ СИЛЫ. МЕТОД СЕЧЕНИЙ § 4.1. НАПРЯЖЕНИЯ § 5.1. ДЕФОРМАЦИИ И ПЕРЕМЕЩЕНИЯ § 6.1. ОСНОВНЫЕ ПРЕДПОСЫЛКИ НАУКИ О СОПРОТИВЛЕНИИ МАТЕРИАЛОВ Вопросы для самопроверки Глава 2. РАСТЯЖЕНИЕ И СЖАТИЕ § 1.  § 2.2. НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ И НАКЛОННЫХ СЕЧЕНИЯХ БРУСА § 3.2. ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ДЕФОРМАЦИИ § 4.2. ДИАГРАММЫ РАСТЯЖЕНИЯ И СЖАТИЯ § 5.2. ПЕРЕМЕЩЕНИЯ ПОПЕРЕЧНЫХ СЕЧЕНИЙ БРУСЬЕВ § 6.2. РАБОТА СИЛЫ ПРИ ЕЕ СТАТИЧЕСКОМ ДЕЙСТВИИ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ § 7.2. СОБСТВЕННЫЙ ВЕС БРУСА § 8.2. ДОПУСКАЕМЫЕ НАПРЯЖЕНИЯ. РАСЧЕТЫ НА ПРОЧНОСТЬ § 9.2. СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫЕ СИСТЕМЫ § 10.2. МЕСТНЫЕ НАПРЯЖЕНИЯ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 3. ТЕОРИЯ НАПРЯЖЕННОГО СОСТОЯНИЯ § 1.3. ВИДЫ НАПРЯЖЕННОГО СОСТОЯНИЯ § 2.3. ПЛОСКОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ § 3.3. ГЛАВНЫЕ НАПРЯЖЕНИЯ. ГЛАВНЫЕ ПЛОЩАДКИ § 4.3. ЭКСТРЕМАЛЬНЫЕ КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ § 6.3. ПОНЯТИЕ О ПРОСТРАНСТВЕННОМ НАПРЯЖЕННОМ СОСТОЯНИИ § 7.3. ОБОБЩЕННЫЙ ЗАКОН ГУКА § 8.3. ОБЪЕМНАЯ ДЕФОРМАЦИЯ § 9.3. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 4.  СДВИГ§ 1.4. ЧИСТЫЙ СДВИГ § 2.4. ДЕФОРМАЦИЯ ПРИ СДВИГЕ. ЗАКОН ГУКА ПРИ СДВИГЕ § 3.4. ОБЪЕМНАЯ ДЕФОРМАЦИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ПРИ ЧИСТОМ СДВИГЕ. ЗАВИСИМОСТЬ МЕЖДУ E, G и «мю» Расчет заклепочных соединений Расчет сварных соединений Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 5. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ СЕЧЕНИЙ § 2.5. СТАТИЧЕСКИЕ МОМЕНТЫ СЕЧЕНИЙ § 3.5. МОМЕНТЫ ИНЕРЦИИ СЕЧЕНИЙ § 4.5. ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ СЕЧЕНИЙ ПРОСТОЙ ФОРМЫ § 5.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПАРАЛЛЕЛЬНОМ ПЕРЕНОСЕ ОСЕЙ § 6.5. ИЗМЕНЕНИЕ МОМЕНТОВ ИНЕРЦИИ ПРИ ПОВОРОТЕ ОСЕЙ § 7.5. ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ. ГЛАВНЫЕ ОСИ ИНЕРЦИИ § 8.5. ИССЛЕДОВАНИЕ МОМЕНТОВ ИНЕРЦИИ ПЛОСКИХ СЕЧЕНИЙ С ПОМОЩЬЮ КРУГА МОРА Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 6.  КРУЧЕНИЕ§ 1.6. ОСНОВНЫЕ ПОНЯТИЯ. КРУТЯЩИЙ МОМЕНТ § 2.6. КРУЧЕНИЕ ПРЯМОГО БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 3.6. ГЛАВНЫЕ НАПРЯЖЕНИЯ И ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ДЕФОРМАЦИИ ПРИ КРУЧЕНИИ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ § 4.6. РАСЧЕТ БРУСА КРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ НА ПРОЧНОСТЬ И ЖЕСТКОСТЬ ПРИ КРУЧЕНИИ § 5.6. РАСЧЕТ ЦИЛИНДРИЧЕСКИХ ВИНТОВЫХ ПРУЖИН § 6.6. КРУЧЕНИЕ ПРЯМОГО БРУСА НЕКРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 7. ПРЯМОЙ ИЗГИБ § 1.7. ВНУТРЕННИЕ УСИЛИЯ § 3.7. ОПОРЫ И ОПОРНЫЕ РЕАКЦИИ § 4.7. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 5.7. ДИФФЕРЕНЦИАЛЬНЫЕ ЗАВИСИМОСТИ МЕЖДУ ИЗГИБАЮЩИМ МОМЕНТОМ, ПОПЕРЕЧНОЙ СИЛОЙ И ИНТЕНСИВНОСТЬЮ РАСПРЕДЕЛЕННОЙ НАГРУЗКИ § 6.7. ПРИМЕРЫ ПОСТРОЕНИЯ ЭПЮР ВНУТРЕННИХ УСИЛИЙ § 7.7. ПРЯМОЙ ЧИСТЫЙ ИЗГИБ § 8.7. ПРЯМОЙ ПОПЕРЕЧНЫЙ ИЗГИБ § 9.7. ГЛАВНЫЕ НАПРЯЖЕНИЯ ПРИ ПРЯМОМ ПОПЕРЕЧНОМ ИЗГИБЕ § 10.  § 11.7. РАСЧЕТЫ НА ПРОЧНОСТЬ ПРИ ИЗГИБЕ § 12.7. ПОНЯТИЕ О ЦЕНТРЕ ИЗГИБА § 13.7. ПОНЯТИЕ О РАСЧЕТЕ СОСТАВНЫХ БАЛОК § 14.7. ПОНЯТИЕ О БАЛКАХ РАЗНОРОДНОЙ УПРУГОСТИ § 15.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НЕПОСРЕДСТВЕННОГО ИНТЕГРИРОВАНИЯ § 16.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ В БАЛКАХ ПОСТОЯННОГО СЕЧЕНИЯ МЕТОДОМ НАЧАЛЬНЫХ ПАРАМЕТРОВ § 17.7. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В БАЛКАХ ГРАФО-АНАЛИТИЧЕСКИМ МЕТОДОМ § 18.7. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ БАЛОК Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 8. ТЕОРИИ ПРОЧНОСТИ § 1.8. КЛАССИЧЕСКИЕ И ЭНЕРГЕТИЧЕСКАЯ ТЕОРИИ ПРОЧНОСТИ § 3.8. ЕДИНАЯ ТЕОРИЯ ПРОЧНОСТИ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 9. СЛОЖНОЕ СОПРОТИВЛЕНИЕ § 1.9. КОСОЙ ИЗГИБ § 2.9. ВНЕЦЕНТРЕННОЕ РАСТЯЖЕНИЕ И СЖАТИЕ БРУСЬЕВ БОЛЬШОЙ ЖЕСТКОСТИ § 3.  9. ЯДРО СЕЧЕНИЯ§ 4.9. ИЗГИБ С КРУЧЕНИЕМ БРУСЬЕВ КРУГЛОГО СЕЧЕНИЯ § 5.9. ОБЩИЙ СЛУЧАЙ ДЕЙСТВИЯ СИЛ НА БРУС КРУГЛОГО СЕЧЕНИЯ § 6.9. ПОСТРОЕНИЕ ЭПЮР ВНУТРЕННИХ УСИЛИЙ ДЛЯ ПРОСТРАНСТВЕННЫХ БРУСЬЕВ С ЛОМАНОЙ ОСЬЮ Задачи для самостоятельного решения Вопросы для самопроверки Глава 10. РАСЧЕТ КРИВЫХ БРУСЬЕВ § 2.10. ЭПЮРЫ ВНУТРЕННИХ УСИЛИЙ § 3.10. НОРМАЛЬНЫЕ НАПРЯЖЕНИЯ В ПОПЕРЕЧНЫХ СЕЧЕНИЯХ БРУСА БОЛЬШОЙ КРИВИЗНЫ § 4.10. ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИЯ НЕЙТРАЛЬНОЙ ОСИ ПРИ ЧИСТОМ ИЗГИБЕ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ В УПРУГИХ СИСТЕМАХ § 1.11. РАБОТА ВНЕШНИХ СИЛ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ § 2.11. ТЕОРЕМА О ВЗАИМНОСТИ РАБОТ § 3.11. ТЕОРЕМА О ВЗАИМНОСТИ ПЕРЕМЕЩЕНИЯ 4.11. ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЯ. ИНТЕГРАЛ МОРА § 5.11. ПРАВИЛО ВЕРЕЩАГИНА Примеры расчета Вопросы для самопроверки Глава 12. РАСЧЕТ ПРОСТЕЙШИХ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СТЕРЖНЕВЫХ СИСТЕМ § 1.  12. СТАТИЧЕСКАЯ НЕОПРЕДЕЛИМОСТЬ§ 2.12. КАНОНИЧЕСКИЕ УРАВНЕНИЯ МЕТОДА СИЛ § 3.12. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ § 4.12. ИСПОЛЬЗОВАНИЕ СИММЕТРИИ § 5.12. ПОСТРОЕНИЕ ЭПЮР ПОПЕРЕЧНЫХ И ПРОДОЛЬНЫХ СИЛ § 6.12. ПРОВЕРКА ПРАВИЛЬНОСТИ ЭПЮР М, Q И N § 7.12. НЕРАЗРЕЗНЫЕ БАЛКИ ПРИМЕРЫ РАСЧЕТА Вопросы для самопроверки Глава 13. ПРОДОЛЬНЫЙ ИЗГИБ ПРЯМОГО СТЕРЖНЯ § 1.13. ПОНЯТИЕ ОБ УСТОЙЧИВОСТИ РАВНОВЕСИЯ УПРУГИХ ТЕЛ § 3.13. ПОТЕРЯ УСТОЙЧИВОСТИ ПРИ НАПРЯЖЕНИЯХ, ПРЕВЫШАЮЩИХ ПРЕДЕЛ ПРОПОРЦИОНАЛЬНОСТИ § 4.13. ПРАКТИЧЕСКИЕ РАСЧЕТЫ СТЕРЖНЕЙ НА УСТОЙЧИВОСТЬ § 5.13. ПРОДОЛЬНО-ПОПЕРЕЧНЫЙ ИЗГИБ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 14. ДИНАМИЧЕСКАЯ НАГРУЗКА § 2.14. ДИНАМИЧЕСКИЕ ЗАДАЧИ, ПРИВОДИМЫЕ К ЗАДАЧАМ СТАТИЧЕСКОГО РАСЧЕТА СИСТЕМ § 3.14. УДАР § 4.14. ЧАСТНЫЕ СЛУЧАИ УДАРНОГО ДЕЙСТВИЯ НАГРУЗКИ § 5.14. КОЛЕБАНИЯ СИСТЕМ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 15.  § 1.15. ПЕРЕМЕННЫЕ НАПРЯЖЕНИЯ. УСТАЛОСТЬ § 2.15. ПРЕДЕЛ ВЫНОСЛИВОСТИ § 3.15. ДИАГРАММЫ ПРЕДЕЛЬНЫХ АМПЛИТУД И ПРЕДЕЛЬНЫХ НАПРЯЖЕНИИ § 4.1. ОСНОВНЫЕ ФАКТОРЫ, ВЛИЯЮЩИЕ НА ВЕЛИЧИНУ ПРЕДЕЛА ВЫНОСЛИВОСТИ § 5.15. РАСЧЕТ НА ПРОЧНОСТЬ ПРИ ПЕРЕМЕННЫХ НАПРЯЖЕНИЯХ Примеры расчета Вопросы для самопроверки Глава 16. ТОНКОСТЕННЫЕ ОСЕСИММЕТРИЧНЫЕ ОБОЛОЧКИ И ТОЛСТОСТЕННЫЕ ЦИЛИНДРЫ § 1.16. РАСЧЕТ ТОНКОСТЕННЫХ ОСЕСИММЕТРИЧНЫХ ОБОЛОЧЕК § 2.16. РАСЧЕТ ТОЛСТОСТЕННЫХ ЦИЛИНДРОВ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки Глава 17. РАСЧЕТ КОНСТРУКЦИЙ ПО НЕСУЩЕЙ СПОСОБНОСТИ § 2.17. РАСТЯЖЕНИЕ И СЖАТИЕ § 4.17. ИЗГИБ БАЛОК § 5.17. МЕТОД РАСЧЕТА КОНСТРУКЦИЙ ПО РАСЧЕТНЫМ ПРЕДЕЛЬНЫМ СОСТОЯНИЯМ Примеры расчета Задачи для самостоятельного решения Вопросы для самопроверки ПРИЛОЖЕНИЯ |
Центры тяжести и моменты инерции основных простых фигур
Формулы площадей, центров тяжести, осевых и полярных моментов инерции, моментов сопротивления и других геометрических характеристик основных простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольника, круга, полукруга, четверти круга, кольцевого и тонкостенного сечений.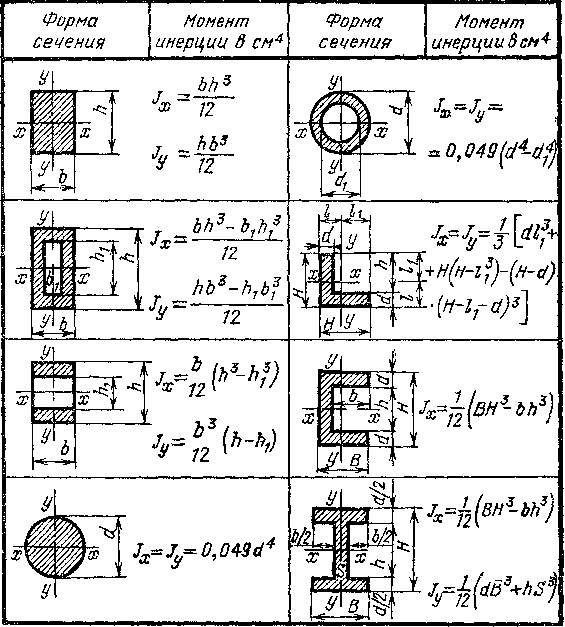
Обозначения в формулах:
C — положение центра тяжести фигуры;
A — площадь сечения;
Ix , Iy — осевые моменты инерции сечения относительно главных осей;
Ix1 , Iy1 — осевые моменты инерции относительно вспомогательных (смещённых) осей;
Iρ — полярный момент инерции сечения;
Wx , Wy — осевые моменты сопротивления;
Wρ — полярный момент сопротивления
Прямоугольник
Прямоугольник высотой h и шириной b.
Центр тяжести прямоугольника в точке пересечения его диагоналей, на расстоянии половины высоты (h/2) по вертикали и половины ширины (b/2) по горизонтали.
Площадь
Центральные осевые моменты инерции прямоугольника
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевые моменты сопротивления прямоугольного сечения
Квадрат
Квадрат — это частный случай прямоугольника, у которого высота равна ширине, т.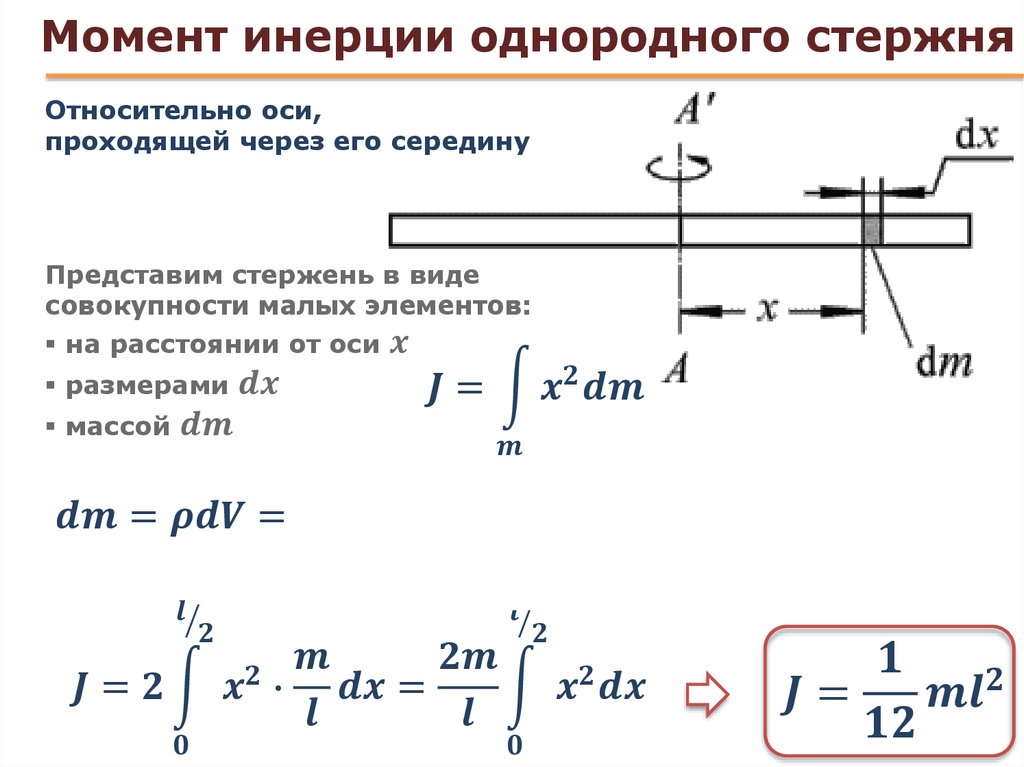
е. h=b=a.
Центр тяжести квадрата находится так же на пересечении диагоналей — на расстоянии половины стороны (a/2) по высоте и ширине.
Площадь
Центральные осевые моменты инерции квадрата
Моменты инерции относительно смещенных осей, проходящих через нижнюю левую точку
Осевой момент сопротивления квадратного сечения
Треугольник равнобедренный
Равнобедренный треугольник высотой h и шириной основания b.
Центр тяжести треугольника располагается в точке пересечения его медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от его вершин.
Площадь
Центральные осевые моменты инерции треугольника
Момент инерции относительно смещенной оси x1, проходящей через его основание
Прямоугольный треугольник
Прямоугольный треугольник высотой h и шириной основания b.
Центр тяжести прямоугольного треугольника располагается аналогично, на пересечении медиан на расстоянии 1/3 высоты от основания и 2/3 высоты от вершины.
Площадь
Центральные осевые моменты инерции прямоугольного треугольника
Моменты инерции относительно смещенных осей x1 и y1, проходящих через точку, соединяющую его катеты
Трапеция
Равнобокая трапеция высотой H и шириной оснований: малого a и большого b.
Площадь трапеции
Центр тяжести на линии, соединяющей середины оснований трапеции, на высоте, определяемой по формуле:
Круг
Круг диаметром D (d) или радиусом R (r)
Площадь круга через его диаметр и радиус
Центральные осевые и полярный моменты инерции круга
Осевые и полярный моменты сопротивления
Полукруг
Половина круга диаметром D (d) или радиусом R (r)
Площадь
Осевые моменты инерции полукруга
Четверть круга
Четверть круга диаметром D (d) или радиусом R (r)
Площадь
Центральные осевые моменты инерции четверти круга
Моменты инерции относительно смещенных осей x1 и y1
Кольцо
Кольцо с внешним диаметром D и внутренним d, (радиусами: внешним R и внутренним r)
Отношение внутреннего диаметра (радиуса) к внешнему обозначается буквой c.
Площадь
Центральные осевые и полярный моменты инерции кольца
Осевые и полярный моменты сопротивления
Тонкостенное сечение (труба)
Тонкостенный профиль (сечение трубы) средним радиусом R0 и толщиной стенки трубы t при R0>>t
Площадь
Центральные осевые и полярный моменты инерции трубного сечения
Осевые и полярный моменты сопротивления
Пример определения координат центра тяжести сложной фигуры:
Другие видео
Смотрите также:
Определение координат центра тяжести сложных фигур
Геометрические характеристики сечений
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.
НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ
На нашем сайте можно бесплатно скачать:
— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку
Сохранить или поделиться с друзьями
Помощь с решением
Поиск формул и решений задач
(Момент инерции прямоугольника)
Возможно, вы слышали о моменте инерции. Но что такое момент инерции прямоугольника? Как рассчитать момент инерции прямоугольного сечения? Если вам интересно, где получить ответы на эти вопросы, вы находитесь на правильной странице. Эта статья отвечает на все ваши вопросы, связанные с моментом инерции прямоугольника, и предоставляет читателям всю необходимую информацию.
(1) Момент инерции прямоугольника с осью, проходящей через его центр тяжестиВ конкретном случае, когда ось проходит через центр тяжести, момент инерции прямоугольника задается следующим образом:
Зарегистрируйтесь, чтобы получить бесплатный пробный тест и учебный материал обязательно)
Я согласен с условиями и политикой конфиденциальности.
I = bh 3 / 12
Ширина прямоугольника (размер, параллельный оси) обозначена буквой b, а высота обозначена буквой h (размер, перпендикулярный оси).
(2) Момент инерции прямоугольника, ось которого проходит через его основаниеМомент инерции прямоугольника выражается следующим образом, когда ось проходит через основание:
I = bh 3 / 3
Легко определяется с помощью применения теоремы о параллельных осях, поскольку центр тяжести прямоугольника расположен на расстоянии h/2 от основания.
Теорема о параллельной осиТеорема о параллельной оси может быть использована для расчета момента инерции площади любой формы, присутствующей на любой параллельной оси. Если мы узнаем момент инерции нецентроидальной оси по отношению к центроидальной оси, параллельной первой, мы можем найти его здесь. Обычно уравнение записывается как;
I = I x + Ad 2
- I x = момент инерции относительно произвольной оси
- A = площадь фигуры D
- оси x’.
I y = hb 3 / 12
Начнем с одного прямоугольного сечения ABCD, как показано на рисунке ниже. Тогда мы предположим, что одна из линий будет проходить через основание прямоугольного сечения. Мы будем использовать эту линию как линию CD. Теперь вычислим момент инерции площади для прямоугольного сечения с центром на этой линии CD.
- B считается шириной прямоугольного сечения ABCD
- D называется глубиной прямоугольного сечения ABCD
- I CD называется моментом инерции прямоугольного сечения относительно линии CD
- Следующим шагом является вычисление или выражение момента инерции прямоугольной пластины относительно линии CD. В этом случае мы будем использовать одну прямоугольную элементарную полосу толщиной dY, которая находится на расстоянии Y от линии CD.
- dA = dY. B – площадь прямоугольной элементарной полосы.
- Теперь момент инерции относительно линии CD = dA.Y 2 = B Y 2 dY
B – площадь прямоугольной элементарной полосы.После определения момента инерции прямоугольного сечения относительно линии CD перейдем к определению момента инерции всей площади прямоугольного сечения с центром на линии CD. Затем мы проинтегрируем приведенное выше уравнение от предела 0 до предела D.
Момент инерции всего прямоугольного сечения относительно линии CD обычно задается как;
I CD = O ∫ D B Y 2 DY
I CD = B O ∫ D y 2 DY
I CD = B 3 3 3 / CD = B /3 3 / CD = B [Y 3 3 3 / CD = B /3 / / / /. D
I CD = BD 3 / 3
Thus, the moment of inertia of the rectangular section about the line CD
I CD = BD 3 / 3
Вы хотите быть IITian? Что ж, вот хорошие новости.
Infinity Learn ежегодно выпускает 20 % сотрудников IIT. Присоединяйтесь к нашему специально подобранному курсу JEE , чтобы воплотить свою мечту в IIT на предстоящем экзамене JEE 2023.
Как рассчитать момент инерции?
Моменты инерции можно рассчитать путем сложения или интегрирования суммы всех «частей массы», составляющих объект, умноженной на квадрат расстояния каждой «части массы» от оси.
Чему равен момент инерции прямоугольника?
В случае, когда ось проходит через центр тяжести, момент инерции прямоугольника определяется как I = bh4 / 12.
Приложение Infinity Learn
Экзамены в нашем приложении для подготовки к экзаменам – Infinity Learn.
Связанное содержание
Момент инерции прямоугольника
Момент инерции прямоугольника вместе с его формулами относительно различных ситуаций обсуждается здесь.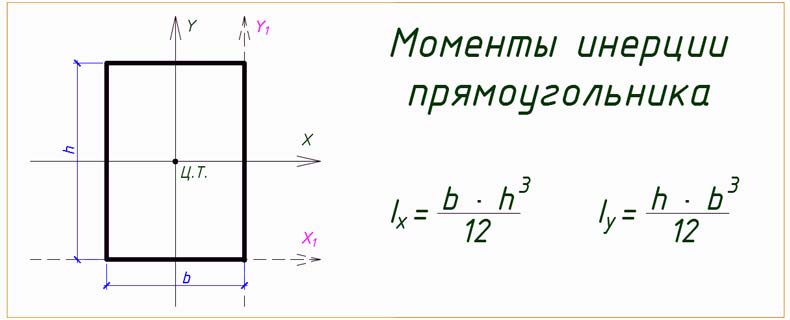
Обычно в этом уроке мы обсудим три ситуации.
1. Ось, проходящая через центр тяжести
Когда мы берем ситуацию, когда ось проходит через центр тяжести, момент инерции прямоугольника определяется как:
| I = bh 3 / 12 |
Здесь b используется для обозначения ширины прямоугольника (размер, параллельный оси), а h называется высотой (размер, перпендикулярный оси).
2. Ось, проходящая через основание
Если говорить об оси, проходящей через основание, то момент инерции прямоугольника выражается как:
| I = bh 3 / 3 |
Это можно легко определить, применив теорему о параллельных осях, поскольку мы можем считать, что центр тяжести прямоугольника расположен на расстоянии, равном h/2, от основания.
Теорема о параллельных осях
Если мы возьмем теорему о параллельной оси, ее можно использовать для определения площади момента инерции любой формы, присутствующей на любой параллельной оси.
Здесь мы можем найти нецентроидальную ось, если знаем ее момент инерции по отношению к центроидальной оси, параллельной первой. Обычно уравнение задается как;
| I = I x + Ad 2 |
I x = момент инерции произвольной оси
A = площадь формы
D = перпендикулярное расстояние между осями x и x’.
3. Центральная ось, перпендикулярная своему основанию
Когда мы возьмем центральную ось перпендикулярно его основанию, момент инерции прямоугольника можно определить, чередуя размеры b и h из первого уравнения, которое приведено выше. Мы получим следующее уравнение;
| I у = хб 3 / 12 |
Расчет момента инерции прямоугольной секции
Ниже мы научимся вычислять момент инерции прямоугольного сечения.
Возьмем одно прямоугольное сечение ABCD, как показано на рисунке ниже.
Теперь предположим, что одна из прямых будет проходить через основание прямоугольного сечения. Мы возьмем эту линию за линию CD. Теперь определим момент инерции площади прямоугольного сечения относительно этой линии CD.
B = Ширина прямоугольного сечения ABCD
D = глубина прямоугольного сечения ABCD
I CD = Момент инерции прямоугольного сечения относительно линии CD
Следующий шаг включает в себя определение значения или выражения для момента инерции прямоугольной пластины относительно линии CD. Здесь мы возьмем одну прямоугольную элементарную полосу толщиной dY, которая будет находиться на расстоянии Y от линии CD. Это видно на приведенном выше рисунке.
Площадь прямоугольной элементарной полосы определяется как dA = dY.B
Момент инерции относительно линии CD = dA.Y 2 = B Y 2 dY
После нахождения момента инерции прямоугольного сечения относительно линии CD перейдем к нахождению момента инерции всей площади прямоугольного сечения относительно линии CD.
