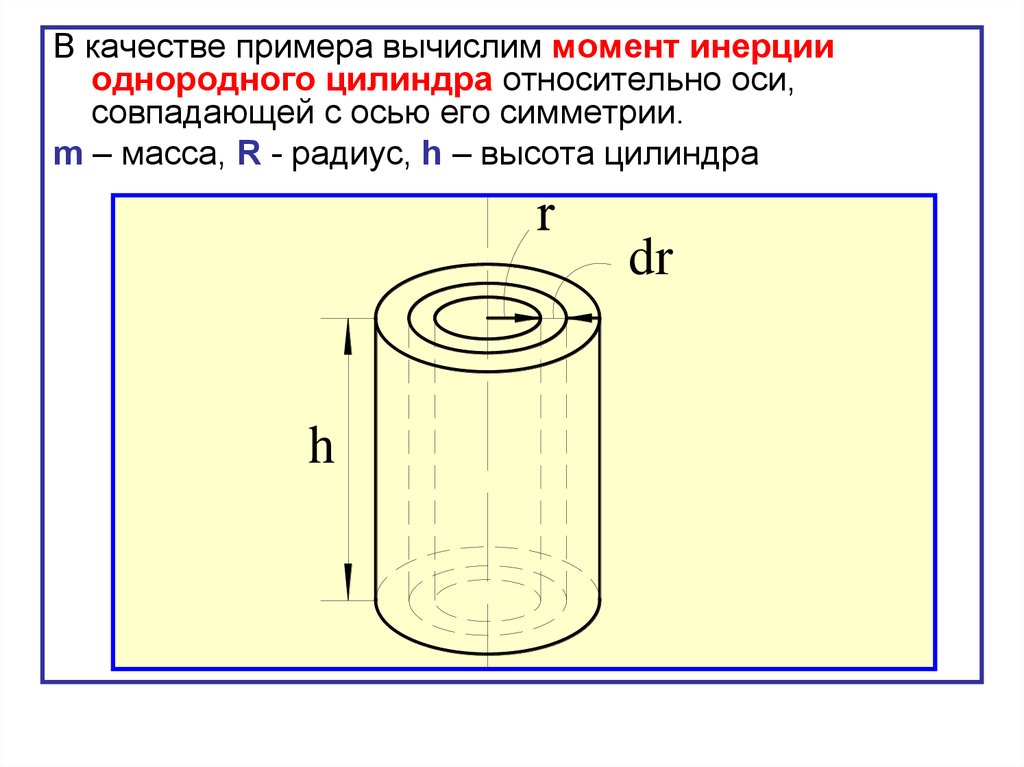
Момент инерции полого цилиндра (кольца).

Определим момент инерции полого цилиндра, вращающегося вокруг оси симметрии, используя общую формулу (13) для определения момента инерции

(13)

Через R₁ обозначим внутренний радиус кольца высотой h, а через R₂ – внешний (рис.2).Объём кольца определится через разность площадей оснований S₁ и S₂

а масса кольца

(14)

Разобьём кольцо на кольца бесконечно малой толщины dr_i.

Выделим колечко, отстоящее от оси вращения на расстоянии r_i. Объём этого колечка равен:

(15)

Подставим dV_i в формулу (13)

и проинтегрируем.

Момент инерции кольца

(16)

Перепишем формулу (16) в виде и, учитывая выражение (14) получим момент инерции кольца

(17)

рис.2

3. Описание установки.

Маятник Максвелла FPM–03 предназначен для исследования закона сохранения энергии и определения на этом основании момента инерции колец.

Общий вид маятника Максвелла FPM–03 показан на рис.3. Основание 1 оснащено регулируемыми ножками 2, которые позволяют произвести выравнивание прибора. В основании закреплена колонка 3, к которой прикреплен неподвижный верхний кронштейн 4 и подвижный нижний кронштейн 5. На верхнем кронштейне находится электромагнит 6, фотоэлектрический датчик №1–7 и вороток 8 для закрепления и регулирования длины бифилярной подвески маятника.

Нижний кронштейн вместе с прикрепленным к нему фтоэлектрическим датчиком №2 – 9 можно перемещать вдоль колонки и фиксировать в произвольно избранном положении.

Маятник 10 прибора FPM–03 – это ролик, закрепленный на оси и завешенный по бифилярному способу, на который накладываются заменные кольца 11, изменяющие таким образом момент инерции системы.

Рис.3. Общий вид маятника МаксвеллаFPM– 03.

Маятник с наложенным кольцом удерживается в верхнем положении электромагнитом. Длина маятника определяется по миллиметровой шкале на колонке прибора.

Время движения маятника фиксируется миллисекундомером. На лицевой панели миллисекундомера находятся следующие манипуляционные элементы:

/сеть/ – выключатель сети. Нажатие этой клавиши включает напряжение питания. Визуально объявляется это свечением цифровых индикаторов (высвечивающих цифру ноль) и свечением лампочек фотоэлектрических датчиков.

/сброс/ – установка ноля измерителя. Нажатие клавиши вызывает сброс схем миллисекундомера FPM– 15.

/пуск/ – управление электромагнитом. Нажатие этой клавиши обозначает освобождение электромагнита и генерирование в схеме миллисекундомера импульса разрешения на измерение.

На задней стенке миллисекундомера находятся зажим заземления.

4. Теория метода.

Метод основан на выполнении фундаментального закона сохранения энергии–механическая энергия замкнутой консервативной системы при движении системы не меняется. Когда маятник Максвелла (основные элементы: ось, ролик и кольца) находятся на высоте hс нитью, намотанной на ось, вся система обладает потенциальной энергией

(18)

Затем маятник, вращаясь, опускается и потенциальная энергия уменьшаясь переходит в кинетическую. Кинетическая энергия системы будет состоять из кинетической энергии поступательного и вращательного движения.

Кинетическая энергия поступательного движения

, где- конечная скорость системы.

При равноускоренном движении с нулевой начальной скоростью конечная скорость определится по формуле:

,

т.к. ,,.

Тогда кинетическая энергия поступательного движения будет равна:

(19)

Кинетическая энергия вращательного движения равна:

(20)

т.к.

Подставляя формулы (19) и (20) в формулу, выражающую закон сохранения энергии всей системы

.

После преобразования получим рабочую формулу для определения момента инерции

(21)

разное положение осей вращения — OneKu

Содержание статьи:

• Момент инерции: математическое определение
• Момент инерции цилиндра относительно оси, его основаниям перпендикулярной
• Момент инерции полого цилиндра
• Величина I для цилиндра, ось вращения которого проходит параллельно плоскостям его основания
• Пример решения задачи

Знание момента инерции тела позволяет воспользоваться законом сохранения момента импульса либо выражением для описания кругового движения с угловым ускорением.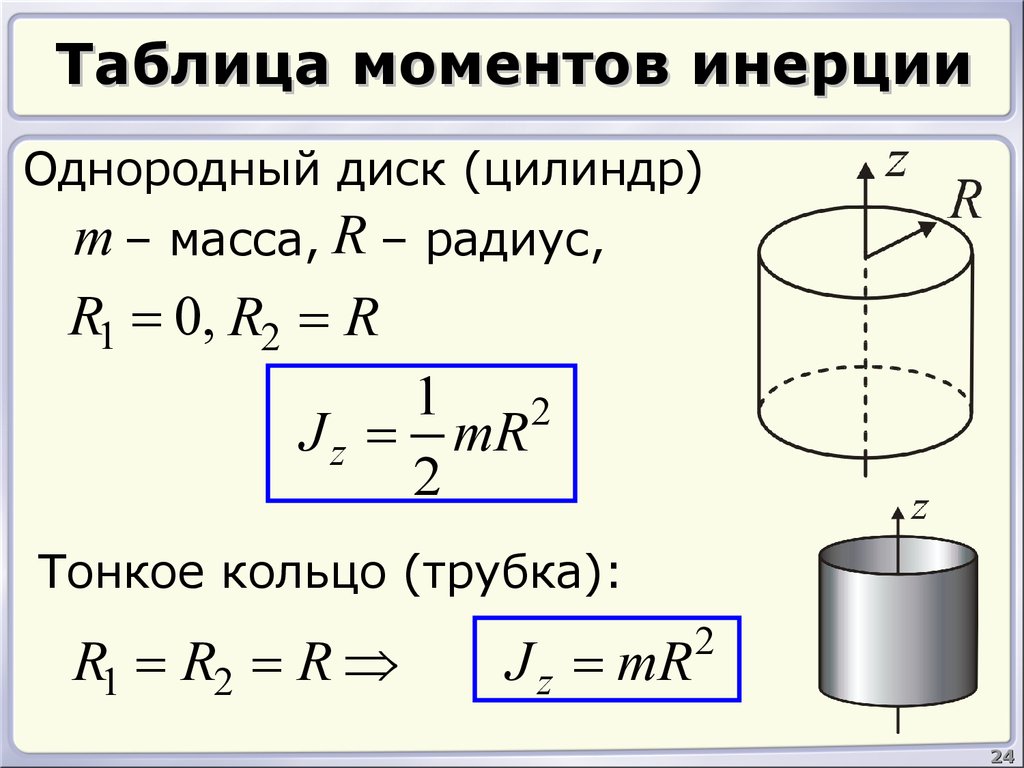 В данной статье рассмотрим, как находить для цилиндра момент инерции при различном положении осей вращения.

Момент инерции: математическое определение

Осевой момент инерции вводится в физику благодаря изучению законов вращательного движения тел. Для точки материальной с массой m, вращающейся на расстоянии r от оси, момент инерции будет равен:

Вам будет интересно:Губа — это… Значение, происхождение, синонимы

I = m*r2

В общем же случае для тела, которое имеет произвольное распределение вещества в пространстве (любую геометрическую форму), величину I можно вычислить так:

I = ∫r2dm

По сути, это выражение является обобщением предыдущего. В нем производится суммирование (интегрирование) моментов от каждой элементарной частицы dm, дистанция до оси от которой равна r.

Если говорить о физическом значении рассматриваемой величины I, то она показывает, насколько «сильно» система сопротивляется воздействию внешнего момента силы, который пытается ее раскрутить или, наоборот, остановить.

Момент инерции цилиндра относительно оси, его основаниям перпендикулярной

Из приведенной выше формулы можно понять, что величина I является характеристикой всей вращающейся системы, то есть она зависит как от формы тела и распределения в нем массы, так и от относительного положения оси.

В данном пункте рассмотрим простой случай: определить необходимо момент инерции для сплошного цилиндра, ось вращения которого перпендикулярна его основаниям и проходит через гравитационный центр фигуры.

Для решения проблемы применим интегральную формулу для I. В процессе операции интегрирования мысленно разобьем цилиндр на тонкие колечки толщиной dr. Каждое колечко будет иметь объем: dV = 2*pi*r*dr*h, здесь h — высота фигуры. Учитывая, что dm = ρ*dV, где ρ — плотность цилиндра, получаем:

I = ∫r2dm = ρ*∫r2dV = 2*pi*ρ*h*∫r3dr

Этот интеграл необходимо вычислить для пределов от 0 до R, где R — радиус фигуры. Тогда получим:

I = 2*pi*ρ*h*∫R0r3dr = 2*pi*ρ*h/4*(r4)∣R0 = pi*ρ*h*R4/2

Воспользовавшись формулой для массы цилиндра через его объем и плотность, приходим к конечному выражению:

I = m*R2/2, где m = pi*ρ*h*R2

Мы получили формулу инерции момента цилиндра однородного.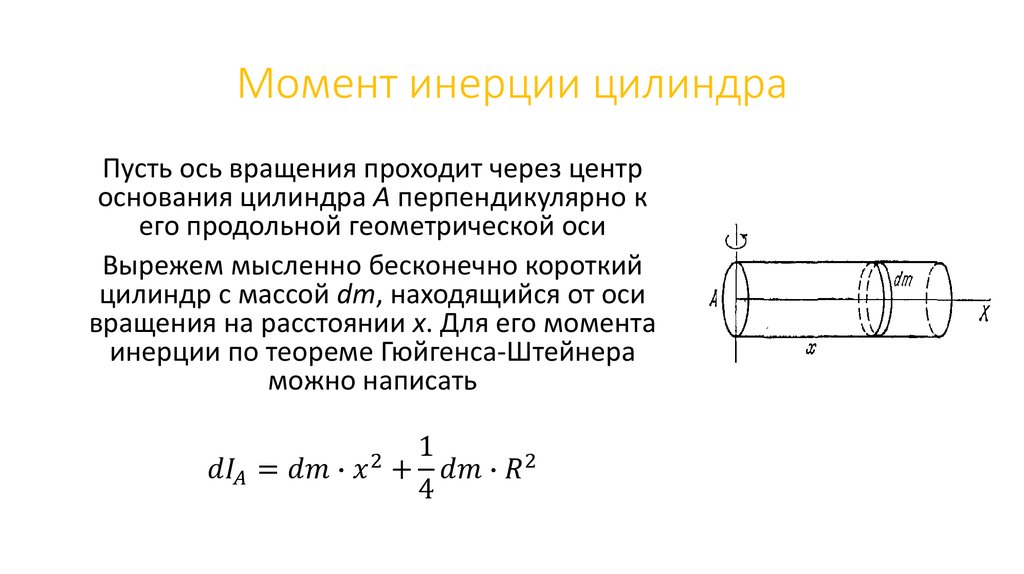 Она показывает, что величина I для этой фигуры в 2 раза меньше, чем для материальной точки аналогичной массы, которая вращается на расстоянии радиуса цилиндра от оси.

Момент инерции полого цилиндра

Теперь оставим ось на том же месте и найдем значение I для цилиндра с пустотой внутри (втулка, труба). Такую фигуру описывают двумя радиусами: внешним R1 и внутренним R2. В этом случае для интегрирования применяется абсолютно тот же подход, что и для сплошного цилиндра, только пределы теперь изменяются от R2 до R1. Имеем:

I = 2*pi*ρ*h/4*(r4)∣R1R2 = pi*ρ*h*R4/2∣R1R2 = pi*ρ*h/2*(R14-R24)

Для дальнейшего упрощения этой формулы воспользуемся разложением на множители выражения в скобках, получим:

I = pi*ρ*h*(R12-R22)*(R12+R22)/2

Часть этого выражения вместе с первыми скобками является массой полого цилиндра, поэтому получаем конечную формулу:

I = m*(R12+R22)/2

Отсюда видно, что момент инерции полого цилиндра больше этого значения для сплошного цилиндра аналогичной массы и такого же внешнего радиуса на величину m*R22/2. Этот результат не вызывает удивления, поскольку в полом цилиндре центр масс находится от оси вращения дальше, чем в сплошном.

Величина I для цилиндра, ось вращения которого проходит параллельно плоскостям его основания

В такой системе ось вращения проходит также через центр массы цилиндра, но теперь он лежит как бы на боку (на цилиндрической поверхности, см. рис. ниже).

Расчет для момента инерции цилиндра для такой ситуации является непростой задачей, поскольку требует наличия дополнительных знаний для ее решения. Тем не менее приведем необходимые математические выкладки, чтобы читатели имели более полное представление о проведении интегрирования при вычислении I.

Начинаем решать задачу. Разбиваем сплошной цилиндр на отдельные диски бесконечно малой толщины. Чтобы узнать, каким моментом инерции обладает этот диск относительно оси, которая проходит через него и параллельна его основаниям, необходимо выполнить отдельное интегрирование. Оно дает следующий результат:

Ii = R2*dm/4

Чтобы найти, величину Ii для этого диска относительно уже новой оси, которая рассматривается в задаче, необходимо воспользоваться теоремой Штейнера. Получим:

Ii = R2*dm/4 + L2*dm, здесь L — расстояние от оси до тонкого диска.

Зная, что dm = pi*R2*dL*ρ, подставляем в интегральную формулу для I и проводим интегрирование по пределам (-L0/2; +L0/2), имеем:

I = ∫mIi = ∫m(R2*dm/4 + L2*dm) = pi*R2*ρ*∫L0/2-L0/2(R2*dL/4 + L2*dL)

Решение этого интеграла приводит к конечной формуле:

I = m*(R2/4 + L02/12)

Пример решения задачи

Решим интересную задачу на нахождение осевого момента инерции цилиндра. Пусть он лежит на цилиндрической поверхности, а ось вращения расположена параллельно его основанию и проходит через конец фигуры.

Эта ситуация полностью аналогична рассмотренной в предыдущем пункте, только ось пересекает не гравитационный центр цилиндра, а конец этой фигуры. Тем не менее для решения проблемы можно воспользоваться результатом предыдущего пункта статьи. Применим вышеупомянутую теорему Штейнера, получим:

I = m*R2/4 + m*L02/12 + m*(L0/2)2 = m*R2/4 + m*L02/3

Заметим, что если R

I = m*L02/3

Этот момент инерции соответствует стержню с осью вращения на его конце.

Момент инерции — вывод для цилиндра

Введение

Привет и добро пожаловать во второй пост о выводе уравнений момента инерции для различных форм. Если вы еще не читали мой пост о вычислении момента инерции тонкого стержня, то сделайте это. Этот пост будет основан на информации, которую я объяснил в первом посте, и, по сути, это более сложный вывод, чем тонкий стержень.

Производная момента инерции – полый/сплошной цилиндр

Теперь я выведу соответствующее уравнение для момента инерции для полого цилиндра (это также охватывает момент инерции для сплошного цилиндра, так как вы можете просто установить внутренний радиус равным 0 ). Я определил полый цилиндр с внутренним радиусом R_1 , массой M , внешним радиусом R_2 и длиной L . Я также включил центральную ось (ось вращения) в виде пунктирной линии, обозначенной цифрой 9.

0004 x , который проходит прямо через центр цилиндра. Я включил это изображение ниже:

Наш общий интеграл для момента инерции остается таким же, как и в предыдущем выводе. Я включил изображение ниже, чтобы напомнить себе:

Как и раньше, мы должны преобразовать dm в термины r (и некоторые другие константы), чтобы мы могли проинтегрировать выражение. Масса одной бесконечно малой тонкости, дм , равна плотности цилиндра, ρ , умноженное на объем рассматриваемого нами кольца, дВ . Это может быть выражено в следующем выражении, приведенном ниже:

Теперь мы можем выразить дВ через дА (площадь вершины бесконечно малого кольца) и длину цилиндра, L . Это приведет к следующему выражению, показанному ниже:

Мы можем вычислить dA через dr . Площадь вершины кольца равна площади круга с бесконечно малым кольцом за вычетом площади круга без него. Это можно выразить так: 92 (я доказал это в своем посте о теореме де Муавра, посмотрите, если хотите). Отсюда мы можем просто продифференцировать выражение относительно

dr и получить следующий ответ:

Мы знаем, что dA через r и dr . Следовательно, теперь мы можем выразить dV через r и dr, как я показал ниже:

Следовательно, мы можем также выразить dm через r и 9.0004 dr , что и было нашей конечной целью. Это позволит нам заменить дм в наш предыдущий интеграл, как я показал на изображении ниже:

Плотность, ρ , является константой и, таким образом, может быть исключена из интеграла. Плотность цилиндра ρ можно выразить как M/V , где M — полная масса цилиндра, а V — общий объем. Мы также можем выразить V через R_1 и R_2 , в результате чего интеграл выглядит так:

Отсюда мы просто вычисляем интеграл с пределами R_2 и R_1 . Это приведет к следующему общему уравнению для момента инерции полого цилиндра. У меня есть изображение этого ниже:

Установив R_1 = 0 , мы можем вычислить конкретное уравнение момента инерции для сплошного цилиндра. Я включил изображение этого ниже:

Кроме того, чтобы получить момент инерции для тонкой цилиндрической оболочки (иначе называемой обручем), можно подставить R_1 = R_2 = R , так как оболочка имеет пренебрежимо малую толщину. Это приведет к следующему уравнению (обратите внимание, что R_2 — это просто R ).

Надеюсь, вам понравился этот вывод! Мне очень нравится делать их, так как я считаю, что это дает более глубокое физическое понимание концепций, а не слепое следование уравнению. Я бы очень хотел вывести много разных уравнений, поэтому, пожалуйста, прокомментируйте, какое уравнение вы хотели бы увидеть следующим! Что касается момента инерции, то скоро я получу момент инерции сферы.