Фейнмановские лекции по физике: Т.2 Пространство. Время. Движение

Фейнмановские лекции по физике: Т.2 Пространство. Время. Движение

Фейнмановские лекции по физике. Т. 2. Пространство. Время. Движение Это лекции по общей физике, которые читал физик-теоретик. Они совсем не похожи ни на один известный курс. Это может показаться странным: основные принципы классической физики, да и не только классической, но в квантовой, давно установлены, курс общей физики читается во всем мире в тысячах учебных заведений уже много лет и ему пора превратиться в стандартную последовательность известных фактов и теорий, подобно, например, элементарной геометрии в школе. Однако даже математики считают, что их науке надо учить по-другому. А уж о физике и говорить нечего: она столь интенсивно развивается, что даже лучшие педагоги все время сталкиваются с большими трудностями, когда им надо рассказывать студентам о современной пауке. Они жалуются, что им приходится ломать то, что принято называть старыми или привычными представлениями. Но откуда берутся привычные представления? Обычно они попадают в молодые головы в школе от таких же педагогов, которые потом будут говорить о недоступности идей современной науки. Поэтому прежде чем подойти к сути дела, приходится тратить много времени на то, чтобы убедить слушателей в ложности того, что было ранее внушено им как очевидная и непреложная истина. Оглавление Глава 15. СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ § 1. Принцип относительности § 2. Преобразование Лоренца § 3. Опыт Майкельсона-Морли § 4. Преобразование времени § 5. Лоренцево сокращение § 6. Одновременность § 7. Четырехвекторы § 8. Релятивистская динамика § 9. Связь массы и энергии Глава 16. РЕЛЯТИВИСТСКАЯ ЭНЕРГИЯ И РЕЛЯТИВИСТСКИЙ ИМПУЛЬС § 1. Относительность и «философы» § 2. Парадокс близнецов § 3. Преобразование скоростей § 4. Релятивистская масса § 5. Релятивистская энергия Глава 17. ПРОСТРАНСТВО-ВРЕМЯ § 1. Геометрия пространства-времени § 2. Пространственно-временные интервалы § 3. Прошедшее, настоящее, будущее § 4. Еще о четырехвекторах § 5. Алгебра четырехвекторов Глава 18. ДВУМЕРНЫЕ ВРАЩЕНИЯ § 1. Центр масс § 2. Вращение твердого тела § 3. Момент количества движения § 4. Закон сохранения момента количества движения Глава 19. ЦЕНТР МАСС; МОМЕНТ ИНЕРЦИИ § 1. Свойства центра масс § 2. Положение центра масс § 3. Вычисление момента инерции § 4. Кинетическая энергия вращения Глава 20. ВРАЩЕНИЕ В ПРОСТРАНСТВЕ § 1. Моменты сил в трехмерном пространстве § 2. Уравнения вращения в векторном виде § 3. Гироскоп § 4. Момент количества движения твердого тела Глава 21. ГАРМОНИЧЕСКИЙ ОСЦИЛЛЯТОР § 1. Линейные дифференциальные уравнения § 2. Гармонический осциллятор § 3. Гармоническое движение и движение по окружности § 4. Начальные условия § 5. Колебания под действием внешней силы Глава 22. АЛГЕБРА § 1. Сложение и умножение § 2. Обратные операции § 3. Шаг в сторону и обобщение § 4. Приближенное вычисление иррациональных чисел § 5. Комплексные числа § 6. Мнимые экспоненты Глава 23. РЕЗОНАНС § 1. Комплексные числа и гармоническое движение § 2. Вынужденные колебания с торможением § 3. Электрический резонанс § 4. Резонанс в природе Главa 24. ПЕРЕХОДНЫЕ РЕШЕНИЯ § 1. Энергия осциллятора § 2. Затухающие колебания § 3. Переходные колебания в электрических цепях Глава 25. ЛИНЕЙНЫЕ СИСТЕМЫ И ОБЗОР § 1. Линейные дифференциальные уравнения § 2. Суперпозиция решений § 3. Колебания в линейных системах § 4. Аналогии в физике § 5. Последовательные и параллельные сопротивления

18. Моменты инерции тонкого диска относительно его главных центральных осей.

     Для расчета моментов инерции тонкого диска массы m и радиуса R выберем систему координат так, чтобы ее оси совпадали с главными центральными осями (рис.32). Определим момент инерции тонкого однородного диска относительно оси z

, перпендикулярной к плоскости диска. Рассмотрим бесконечно тонкое кольцо с внутренним радиусом r и наружным r+dr. Площадь такого кольца ds=2r $\pi$ dr, а его масса , где S= $\pi$ R² — площадь всего диска. Момент инерции тонкого кольца найдется по формуле dJ=dmr². Момент инерции всего диска определяется интегралом

    (п.18)

     Для определения J_x воспользуемся симметрией диска (J_x=J_y) и утверждением (п.10), полученным при расчете момента инерции прямоугольной пластины. При этом из (п.10) получаем J_z=2J_x    (п.19)

Откуда     (п. 20)

17. Определение момента инерции тонкого стержня, относительно оси, проходящей через его середину.

     Пусть тонкий стержень имеет длину l и массу m. Разделим его на малые элементы длины dx (рис.27), масса которых . Если выбранный элемент находится на расстоянии x от оси, то его момент инерции , т.е.      Интегрируя последнее соотношение в пределах от 0 до l/2 и удваивая полученное выражение (для учета левой половины стержня), получим

    (п.1)

     Это выражение может быть получено и другим способом, с помощью метода подобия. Будем считать, что рассматриваемый стержень состоит из двух половин (рис.28). Каждая из них имеет массу

m/2 и длину l/2 .

Выражение для момента инерции стержня должно включать его массу и длину, так как это единственные параметры, определяющие его инерционные свойства при вращении. Пусть     (п.2)

где k— неизвестный коэффициент.      Для каждой из половин стержня при вращении вокруг оси AA^` можно найти момент инерции, используя (п. 2) и теорему Гюйгенса-Штейнера.     (п.3)

Полный момент инерции стержня     (п.4)

Но этот же момент инерции, согласно (п.2) равен kml

². Приравнивая (п.4) и (п.2) имеем     (п.5)

или и, следовательно,     (п.6)

т.е. , что совпадает с (п.1)

1.Основные кинематические понятия. Материальная точка. Система отсчета, система координат.

Механика – наз-ся раздел физики, изучающий закономерности взаимодействия простейших форм движения материи.

Механическое движение – взаимное перемещение тел в пространстве в зависимости от времени.

Кинематика – описывает движение тел в пространстве и времени без выяснения причин их движения.

Материальная точка – это тело размерами которого в процессе движения можно пренебречь. Возможность рассматривать тело как материальную точку зависит не от самого тела, а от характера его движения. Например, при движении Земли вокруг солнца Землю можно считать мат.

точкой, если же нас интересует суточное вращение Земли – то нельзя.

Тело отсчета – тело, относительно которого изучается движение рассм-его тела.

Система отсчёта – это тело или совокупность тел, по отношению к которым рассматривается движение других тел. С.О. состоит из тел отсчета, связанной с ним системой координат и прибором для измерения времени (часы).

Радиус-вектор – вектор(r), харак-щий изм-е положения точки за рассм-ый промежуток t.

Вектор перемещения

– вектор, харк-щий изменение положения точки за рассм-ый промежуток t.

Система координат – а) если тело движется вдоль прямой линии, то его движение определяется 1 координатой

б) при движении в нек. плоскости:2 координаты

в) при движении в пространстве: 3 координаты

3}{12}\], где

b = основание треугольника

h = высота треугольника

В этом случае b= ab=a ² и h=\[\frac{a} {\ sqrt (2)} \].

Сумма второго момента площади двух треугольников относительно их общего основания вдвое больше второго момента площади одного из треугольников.

Момент инерции квадратной пластины

Чтобы определить момент инерции квадратной пластины, нам необходимо рассмотреть следующие вещи. 92}]\] 

Применение интеграции;

Iplate = 1 / 6 M / L ²

Найдите момент инерции квадратной пластины вдоль оси

Определим МВД квадратной пластины, пересекающей ее центр и перпендикуляр. Возможно, вы не в курсе, но есть способ найти момент инерции. MOI остается неизменным, если масса, расстояние от оси и распределение массы вокруг этой оси остаются прежними».

Итак, предположим, что у нас есть молекула массы m, расположенная вокруг оси на расстоянии d. Следовательно, его MOI относительно этой оси будет md 92)}\]

Решенный пример для момента инерции квадрата

Вопрос: МВД квадратной пластинки относительно перпендикулярной оси вдоль ее центра масс составляет 20 кг-м ² . Найдите его момент инерции относительно оси, касающейся его стороны и в плоскости пластинки.

Решение:

Учитывая, что

Инерция в центре = 20 кг-м ²  

Предположим, что

Масса квадратной пластины = m

Сторона квадрата = a

Инерция относительно перпендикулярной оси в центре квадрата = Ix​ + Iy​= 2Ix​(так как стороны квадрата равны)

Ix​= 2Iz​ = 12ma2​

Край квадрата находится на расстоянии 2a​ от центра.

Используя теорему о параллельных осях, мы имеем

Iedge​ = Ix​+m2a​ ²

Iedge​ =12ma2​+m2a​ ²

IEDGE = 3MA ² = 2 × 6MA ² = 2IZ

IEDGE = 2 × 20 = 40 кг — М ²

IEDE = 40K -M ²

The MEDGE = 40K -M ²

The Edge = 40 кг -м ²

. Момент инерции является важным предметом, который рассматривается в большинстве задач физики, связанных с массой во вращательном движении. MOI обычно используется для вычисления углового момента. В следующих параграфах мы узнаем больше об этом предмете.

Что такое момент инерции?

Момент инерции определяется как величина сопротивления тела угловому ускорению, которая представляет собой сумму произведения массы каждой частицы на квадрат ее расстояния от оси вращения. Проще говоря, это число, определяющее величину крутящего момента, необходимого для определенного углового ускорения вращающейся оси. Угловая масса или инерция вращения — это другие названия момента инерции. кг м ² — это единица СИ для Момент Инерции.

Момент инерции часто выражается относительно определенной оси вращения. В основном это определяется распределением массы вокруг оси вращения. MOI изменяется в зависимости от используемой оси.

Какие факторы влияют на момент инерции?

На момент инерции влияют следующие факторы:

Плотность материала

Форма и размер тела

Ось вращения (распределение массы относительно оси)

Системы вращающихся тел дополнительно классифицируются следующим образом:

Отдельные (система частиц)

Непротиворечивые (твердое тело)

Момент инерции площади, также известный как второй момент площади или 2-й момент площади, представляет собой особенность двумерной плоской формы, показывающая, как ее точки распределяются в плоскости поперечного сечения вдоль произвольной оси.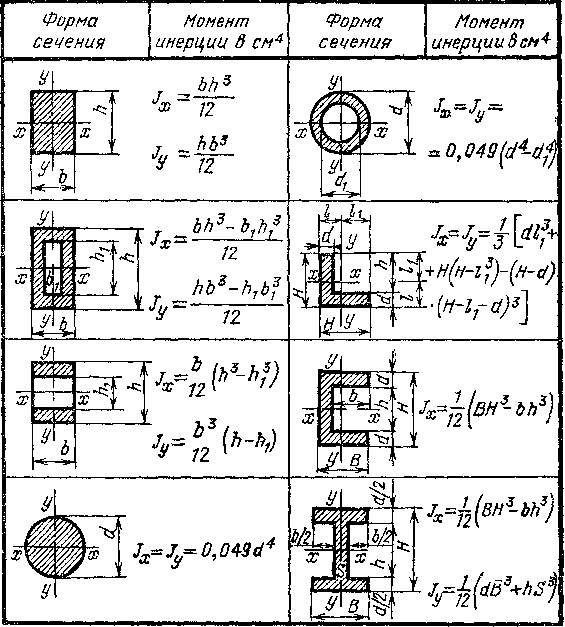 Эта характеристика по существу описывает отклонение плоской формы под действием силы.

Для оси на плоскости момент инерции площади обычно обозначается символом I. Когда ось перпендикулярна плоскости, он также обозначается как J. Единицей измерения второго момента площади является L4 (длина в степени четыре). Если мы посмотрим на международную систему единиц, единицей измерения будет метр в четвертой степени, или м4. Это могут быть дюймы в четвертой степени, in4, если мы используем имперскую систему единиц.

Эта тема часто встречается в области проектирования конструкций. В этом контексте считается, что момент инерции площади является мерой жесткости балки на изгиб. Это важная характеристика, которая используется для расчета прогиба балки или для количественной оценки сопротивления балки изгибу. В этом случае мы должны рассмотреть два сценария.

Во-первых, плоский второй момент площади, где сила расположена перпендикулярно нейтральной оси, может просто характеризовать или количественно определять сопротивление балки изгибу.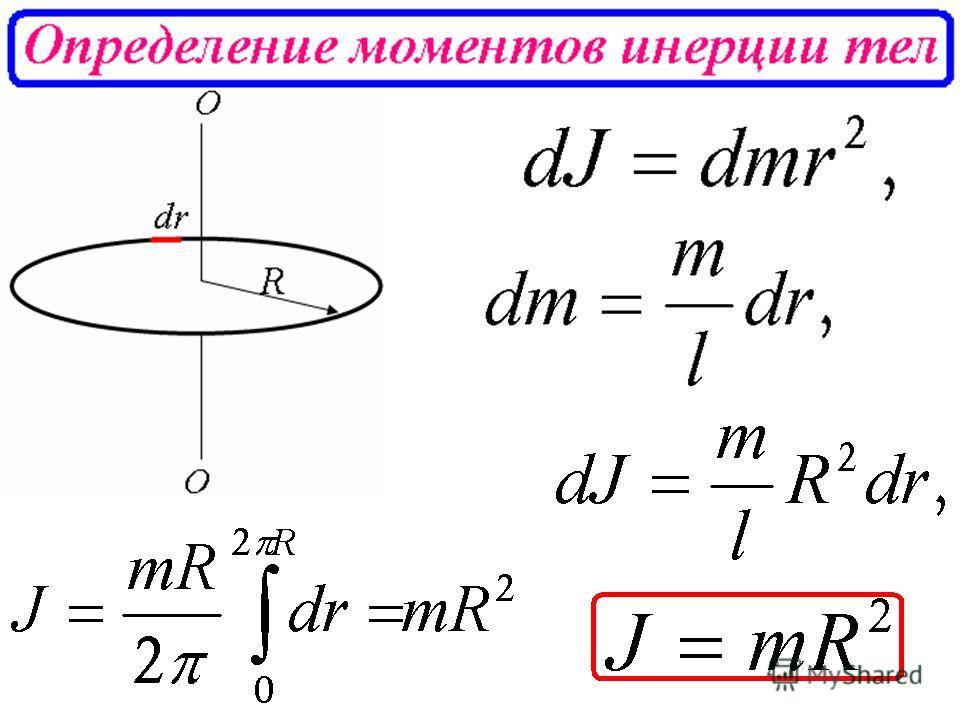

Во-вторых, когда приложенный момент параллелен поперечному сечению балки, можно использовать полярный секундный момент площади для расчета ее сопротивления. По сути, это сопротивление балки кручению.

Различные виды моментов инерции

Момент инерции классифицируется на три типа:

• МОМ Инерции в массе

• Moment of Inertia в районе

• Moment in The Inertia Polle0003

Момент инерции массы

Момент инерции массы определяется как сопротивление вращению, создаваемое телом благодаря его массе. Потолочный вентилятор, крыльчатка и маховик — все это примеры моментов инерции масс. Для минимизации энергопотребления необходимо уменьшить момент инерции массы объектов. Для таких тел инерция измеряется относительно оси вращения.

Момент инерции площади

Сопротивление, оказываемое объектом изгибу или отклонению, описывается как момент инерции площади. В этом случае инерция не зависит от массы и пропорциональна площади объекта. Луч иллюстрирует момент инерции площади.

Момент инерции на полюсах

Момент инерции на полюсах — это сопротивление, оказываемое предметом скручиванию. Полярный момент отличается от массового Момента инерции так же, как закручивание отличается от вращения. Полярный момент инерции представлен валом.

Момент инерции квадрата

Момент инерции квадрата находится по формуле.

я = а 4 / 12

Здесь a = стороны квадратного сечения. Это уравнение относится к сплошному квадрату, центр масс которого расположен вдоль оси x.

Диагональный момент инерции квадрата также можно рассчитать как;

I x = I y = a 4 / 12

 

В качестве альтернативы, если центр масс (см) перемещается на определенное расстояние (d) от оси x, мы будем использовать другое выражение для определения момента инерции того же квадрата.

я = а 4 / 3

Момент инерции квадратного производного

Момент инерции можно легко получить, используя теорему о параллельных осях, которая утверждает;

I = I _см + Ad ²

см = центр масс

Однако в этом уроке мы заменим массу (M) площадью (A). Для вывода мы также будем использовать прямоугольник в качестве эталона, чтобы найти M.O.I. вместе с интеграцией.

Если вспомнить момент инерции прямоугольника, то он определяется как;

I _X = ⅓ WH ³

Ш = ширина и В = высота

I _X = ⅓ (WH)H ²

I _X = ⅓ (A)H ²

1. Теперь, если мы посмотрим на квадрат, где его центр масс проходит через ось x, квадрат состоит из двух прямоугольников, которые равны по размеру.

 

Теперь мы можем выразить это как;

I _x = 2 [⅓ a (a / 2) ³ ]

I _x = [⅔ a ( a ³ / 8) ]

I _х = (1/12)а ⁴

I _Xcm = a ⁴ / 12

2.