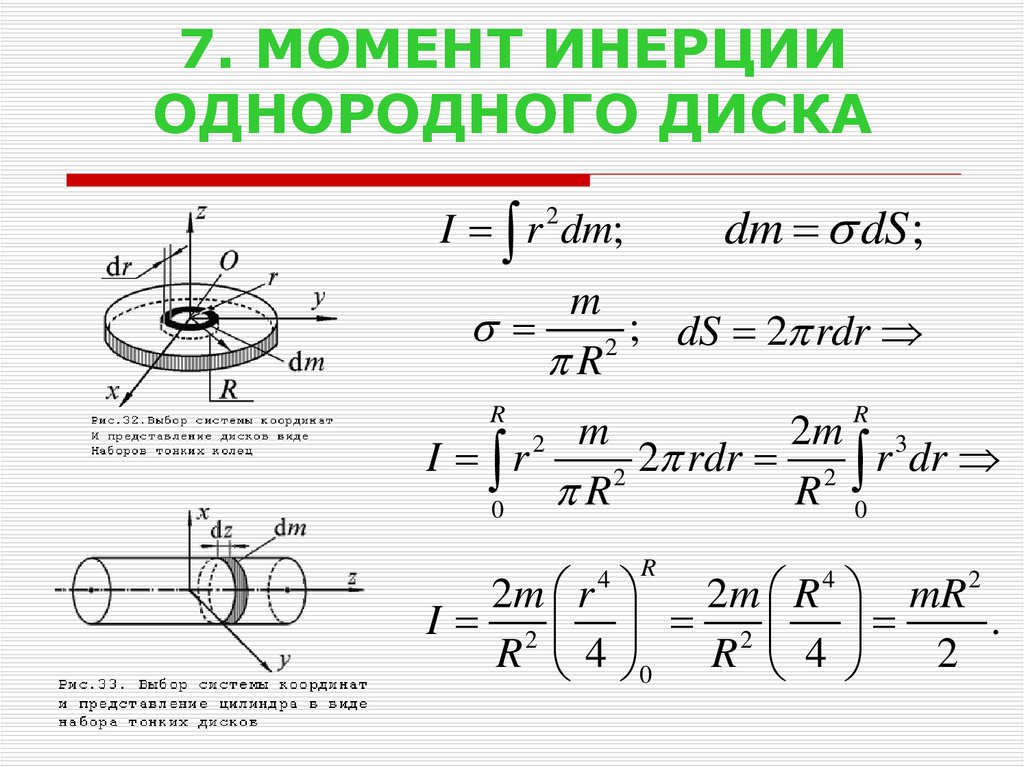
Определение момента инерции тела и положения центра масс

+7 (495) 781 39 39

Главная/Испытательное оборудование/SPACE ELECTRONICS/Определение момента инерции и положения центра масс

Space Electronics KSR — самые точные инструменты в мире для определения момента инерции (МИ) и положения центра масс (ЦМ).
Данная линейка инструментов настоятельно рекомендуется для определения масс-инерционных характеристик ракет, спутников и баллистических объектов.
Оборудование может быть использовано для полезной нагрузки массой от 100 грамм до 10 тонн и тяжелее.

Концепция измерения
Сферический подшипник поддерживает поворотный стол и выступает в роли шарнира для измерения дисбаланса, возникающего от смещения центра масс испытуемого объекта относительно оси подшипника.

Определение момента инерции тела происходит при помощи торсиона, зажатого снизу и прикрепленного сверху к газовому подшипнику, образуя, таким образом, перевернутый крутильный маятник.

Ключевые особенности
Наилучшая достигаемая точность — измерение ЦМ с точностью до 25 микрон и МИ с точностью до 0.1% Один инструмент может измерять полезную нагрузку, вес которой составляет всего 4% от максимального веса, на который рассчитан инструмент.

Полная автоматизация процесса — выберите определение момента инерции или центра масс на экране компьютера и процесс измерения запуститься автоматически.
Использование газовых подшипников значит полную совместимость с чистыми комнатами. Нет риска загрязнения, нет высокого давления, нет опасности взрыва.

Огромная устойчивость от опрокидывающих моментов. Инструмент не опрокидывается даже при высоком расположении ЦМ.
Полностью программная поддержка метрических и дюймовых единиц. Система координат определяется пользователем — значения ЦМ и МИ сообщаются непосредственно в системе координат полезной нагрузки.

Оборудование для калибровки согласно стандартам НИСТ входит в комплект поставки каждого инструмента.

• Дисбаланс от центра масс измеряется непосредственно;
• Изменение положения ЦМ можно наблюдать в живую;
• Автоматическое устранение ошибоквыравнивания.

Опциональная весоизмерительная платформа и манипулятор для определения координат позволяет напрямую собирать данные о весе и системе координат испытуемого объекта непосредственно на инструменте.

Общая спецификация линейки (для конкретной модели значения необходимо уточнять)
Измерения за один установ: 2 координаты центра масс и 1 значение момента инерции;
Диапазон масс нагрузок: От 100 грамм до 10 тонн;
Точность определения ЦМ: 0.1% от измеренного значения дисбаланса;
Точность определения МИ: 0.1% от измеренного значения;
Требования к электросети: 115 ВAC, 60 Hz или 220 ВAC, 50 Hz, одна фаза;
Требования к сетия сжатого воздуха: Источник чистого сухого воздуха или азота, 7 бар, 60 л/мин;
Требования к полу: Бетонный пол, 15 см. толщиной.

Цена

По запросу

Запрос стоимости (t)

Ф. И.О.*

Предприятие (работаем только с юр. лицами)*

E-mail для связи*

Телефон для связи*

Загрузка файла

не более: 5

Комментарий

 * Нажимая кнопку «Отправить» вы принимаете условия обработки информации

+7 (495) 781 39 39

107023, г. Москва, ул. Электрозаводская, д.24,
стр.3, оф. В303

Copyright © 2007 — 2021 ООО «БЛМ Синержи»

Мегагрупп.ру

Этот сайт использует cookie-файлы и другие технологии для улучшения его работы. Продолжая работу с сайтом, Вы разрешаете использование cookie-файлов. Вы всегда можете отключить файлы cookie в настройках Вашего браузера.

Хорошо

Лабораторная работа 2 определение момента инерции тел при помощи крутильного маятника

Цель работы: измерение момента инерции тела правильной геометрической формы и момента инерции тела человека.

Приборы и принадлежности: крутильный маятник, тело правильной геометрической формы (куб, параллелепипед), модель тела человека, секундомер.

Момент инерции (I) – физическая величина, являющаяся мерой инертности тела при его вращении.

Момент инерции материальной точки

, гдеm – масса точки, r – расстояние от оси вращения до рассматриваемой точки.

Момент инерции твердого тела (относительно какой-либо оси вращения) зависит от распределения масс относительно этой оси и является величиной аддитивной, т.е. равен сумме моментов инерции частей тела относительно этой оси. Вычисление момента инерции тела производится по формуле

Из этой формулы видно, что моменты инерции тел одинаковой массы, но разной конфигурации различны.

Момент инерции механической системы относительно неподвижной оси Z равен сумме моментов инерции всех его частей относительно этой оси. Для нахождения моментов инерции тела относительно произвольной оси используют

теорему Штейнера: момент инерции произвольного тела относительно выбранной оси «а» равен моменту инерцииэтого же тела относительно оси «с», проходящей через центр масс и параллельной данной, сложенной с произведением массы тела на квадрат расстояния между этими осями:

.

В некоторых разделах космической и спортивной медицины, ортопедии, бионики возникает необходимость измерения момента инерции тела человека и некоторых его частей.

При беге, например, значительная часть энергии расходуется на то, чтобы придать конечности ускорение, направленное поочередно, то вперед, то назад. Чем больше момент инерции, тем больше требуется на это энергии. У человека мускулатура конечностей расположена главным образом в области плеча и бедра, а не по всей длине руки или ноги, в этом случае момент инерции является минимальным.

Определить момент инерции тела человека сложно, поэтому мы прибегаем к модели. Зная соотношение между массой человека и массой модели, и между линейными размерами человека и модели, из теории подобия можно определить соотношениемежду моментами инерции модели и человека..

Измерив экспериментально момент инерции модели, можно рассчитать момент инерции тела человека:

. (1)

Методика эксперимента

Экспериментально определяется период колебаний Т крутильного маятника, представляющего собой рамку, в которую вставлено тело для определения его момента инерции. При повороте рамки на малый угол возникает вращающий момент, гдеk – коэффициент кручения проволоки. Предоставленный сам себе маятник, выведенный из положения равновесия, совершает гармонические колебания. Записав уравнение динамики для вращательного движения, получим уравнение этих колебаний

, (2)

где – угловое ускорение. Решением этого уравнения является функция

, (3)

где – максимальный угол поворота рамки,– собственная частота колебаний маятника. Выполняя двукратное дифференцирование этой функции и подставляяив уравнение (2), с учетом того, что, получим формулу для определения момента инерции

.

(4)

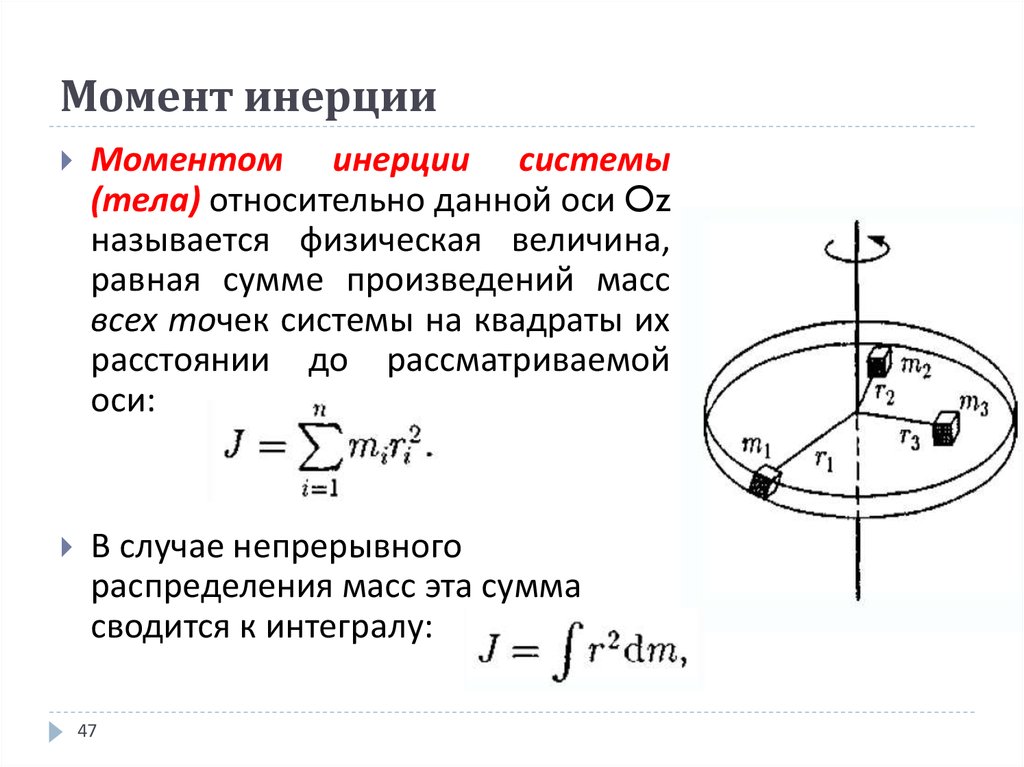
Измерив периоды колебаний рамки с исследуемым телом ирамки без тела, по формуле (4) вычисляют соответственно моменты инерциии. Тогда момент инерции тела будет равен.

Порядок выполнения работы

1. Определение момента инерции куба относительно оси Z.

1.1. Включить установку в сеть. Нажать кнопку «Сеть» на лицевой панели. Кнопка «Пуск » отжата.

1.2. Подвести флажок рамки к электромагниту. Нажать кнопку «Сброс ».

1.3. Измерить не менее трех раз время t десяти колебаний рамки с кубом. Для этого надо нажать кнопку «Пуск» и когда табло «Периоды» будет высвечивать «9» нажать на кнопку «Стоп». Записать количество колебаний

п и время . Данные занести в таблицу 1.

1.4. Отжать кнопку «Пуск», нажать кнопку «Сброс». Выключить установку.

1.5. Определить величину периода колебаний и вычислить среднее значение. Полученный результат занести в таблицу 1.

1.6. Вычислить момент инерции рамки вместе с кубом, подставляя в формулу (4) среднее.

1.7. Измерить не менее трех разных значений периодов рамки без куба. Для этого, держа левой рукой куб, правой вращать винт против часовой стрелки, пока куб не освободится из рамки. Найти среднее значение периодаповторив пункты 1.1 – 1.4. Данные занести в таблицу 2.

0. Вычислить моменты инерции и.

1. Сравнить полученное значение I с расчетным , предварительно измерив не менее трех раз длинустороны куба и найдя. Масса кубат = 1кг. Результаты занести в таблицу 2.

Таблица 1

N	, с	, с	, с

Момент инерции рамки с кубом =

Таблица 2

, с	, с	, с	, м	, м	т, кг

Момент инерции рамки без куба=

Момент инерции куба I =

домашнее задание и упражнения — Расчет момента инерции

спросил 10 лет, 1 месяц назад

Изменено 7 месяцев назад

Просмотрено 28 тысяч раз

$\begingroup$

Проблема, над которой я работаю:

Однородная, тонкая, сплошная дверь имеет высоту 2,10 м, ширину 0,835 м и массу 24,0 кг.

а) Найдите момент инерции для вращения на шарнирах.

(b) Является ли какая-либо часть данных ненужной?

Я вообще не уверен в том, что делаю. Итак, вот моя попытка, следуя схеме, данной в книге.

Из книги я знаю, что для этой задачи не обязательно знать высоту, но я не совсем уверен, почему. Что касается части (а), я действительно не знаю, как подойти к проблеме. Нужны ли мне вычислительные методы? Это один из интегралов, который я должен использовать?

• домашние задания и упражнения
• момент инерции

$\endgroup$

0

$\begingroup$

Вы правы, высота не нужна. Затем вы вычисляете момент инерции, в принципе суммируя моменты инерции элементов бесконечно малой массы. Момент инерции бесконечно малого элемента массы $\mathrm dm$ равен $\mathrm dm\cdot r^2$, где $r$ представляет собой расстояние от элемента массы до оси, относительно которой мы рассматриваем момент инерции . 2 \,\mathrm dm$. 92}{3}$. Затем вы можете заполнить числа, которые вы должны получить ответ. Обратите внимание, что я сделал это не для того, чтобы сделать за вас домашнее задание, а хотел показать общие мысли, лежащие в основе расчета момента инерции.

$\endgroup$

6

$\begingroup$

Это инициатива, я имею в виду, что очевидно, что для формы однородной двери масса каждого среза одинакова, вам не нужно вычислять $x\times h$, но вы можете сказать $m=\rho V = \rho A L$, где $ \rho$ — плотность, а $A=w h$ — площадь, умноженная на высоту. Таким образом, для приведенного выше значения $\lambda = m / L = \rho A = \rho w h $, но $w \times h$ является постоянным.

$\endgroup$

$\begingroup$

В этом случае распределение массы относительно оси вращения в основном такое же, как у тонкого стержня, длина которого равна ширине двери.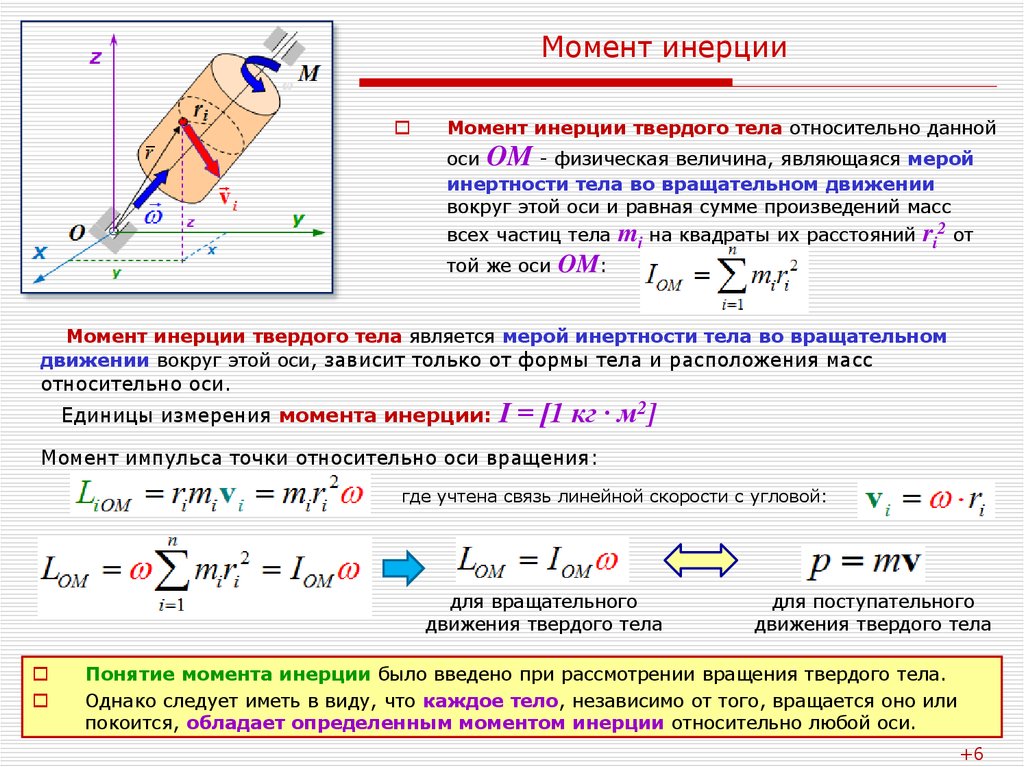

$\endgroup$

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Как рассчитать момент инерции

••• mipan/iStock/Getty Images

Обновлено 24 апреля 2017 г. что во многом определяет его устойчивость к изменениям в движении — или инерцию. Однако для вещей, которые вращаются или вращаются, картина становится более сложной; вместо массы физики говорят о моменте инерции объекта. Форма объекта сильно влияет на момент инерции, как и расположение центра вращения. Хотя расчет момента инерции может быть очень сложным, такие формы, как сферы, стержни и диски, значительно упрощают математику. 92” или путем умножения цифры на саму себя. Например, по полу катится цилиндр весом 5000 грамм. Его радиус равен 5 см. Пять в квадрате равно 25.

Умножьте предыдущий результат на массу. В этом примере 25 умножить на 5 000 — это 125 000.

Разделить на два; это дает момент инерции. Продолжая пример, 125 000/2 равняется 62 500. Единицы в граммах, умноженных на сантиметры в квадрате.

Катящаяся твердая сфера

Измерьте радиус сферы от центра до края в сантиметрах; введите эту цифру в калькулятор.