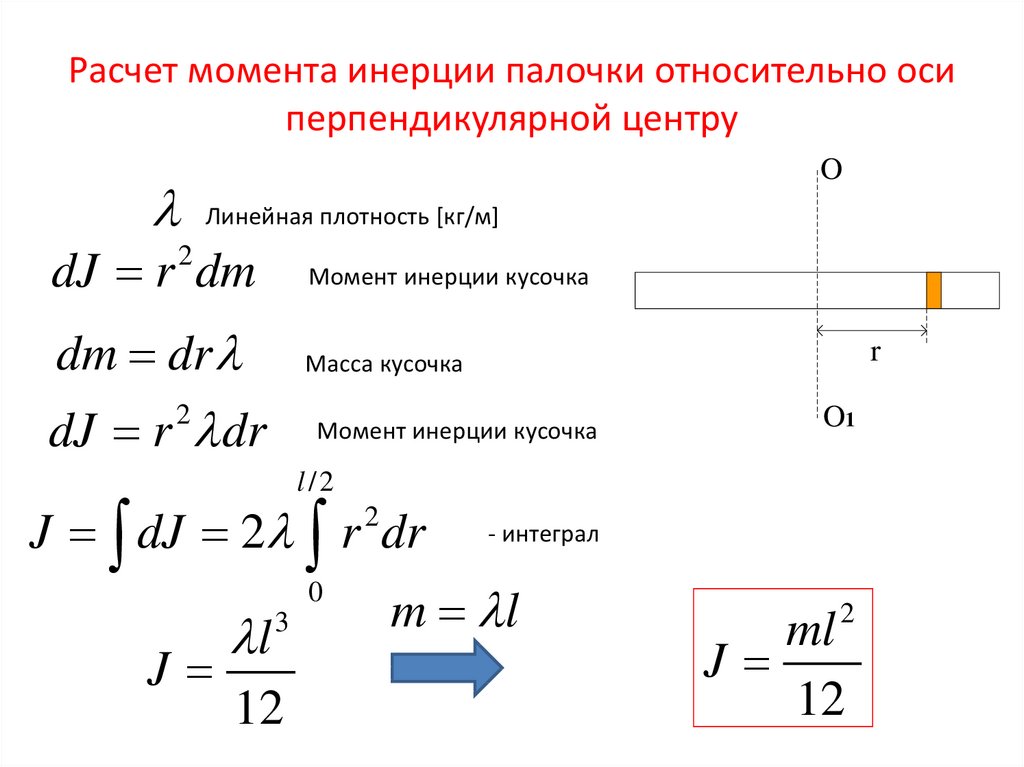
14. Момент инерции
Моментом инерции системы (тела) относительно данной оси называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси: В случае непрерывного распределения масс эта сумма сводится к интегралу где интегрирование производится по всему объему тела. При этом величина r в есть функция положения точки с координатами х, у, z. В качестве примера будем искать момент инерции однородного сплошного цилиндра высотой h и радиусом R относительно его геометрической оси (рис. 1).
Рис.1
Разобьем
цилиндр на отдельные полые концентрические
цилиндры бесконечно малой толщины dr с
внутренним радиусом r и внешним r+dr.
Момент инерции отдельного полого
цилиндра dJ=r2dm
(так как dr<<r, то считаем, что расстояние
всех точек цилиндра от оси равно r), где
dm — масса всего элементарного цилиндра;
его объем 2πrhdr. Если ρ-плотность материала,
то dm=2πrhρdr и dJ=2πhρr
Тогда момент инерции сплошного
цилиндра
но
так как πR2h — объем цилиндра, то его масса
m=πR2hρ, а момент инерции
Если
мы знаем момент инерции тела относительно
оси, проходящей через его центр масс,
то мы можем найти и момент инерции
относительно любой другой параллельной
этой оси, который можно найти с
помощью теоремы
Гюйгенса-Штейнера: момент
инерции тела J относительно произвольной
оси равен моменту его инерции
Jc относительно
параллельной оси, проходящей через
центр масс С тела, сложенному с
произведением массы m тела на квадрат
расстояния а между осями:
Приведем
значения моментов инерции (табл. 1) для
некоторых тел (тела считаются однородными,
m — масса тела).
Материал из Википедии — свободной энциклопедии
Иллюстрация теоремы для момента площади.
У этого термина существуют и другие значения, см. Теорема Штейнера (значения).
Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнераи голландского математика, физика и астронома Христиана Гюйгенса): момент инерции тела J относительно произвольной оси равен сумме момента инерции этого тела JC относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела
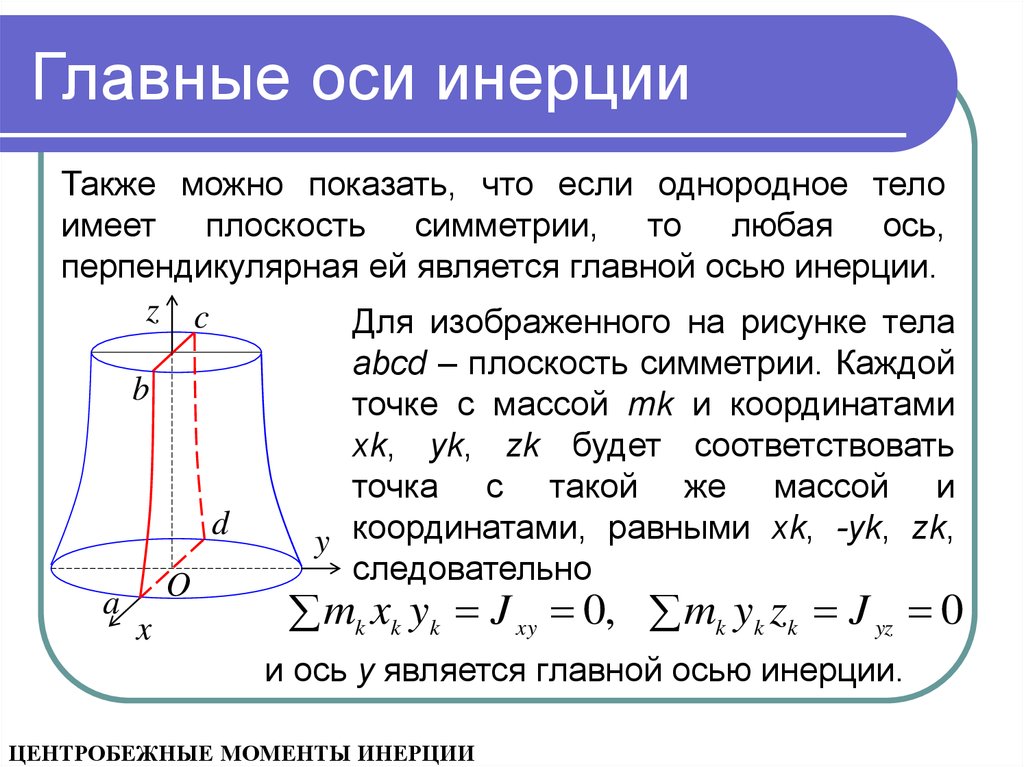
Момент инерции, по определению: Радиус-вектор можно расписать как разность двух векторов: ,где — радиус-вектор расстояния между старой и новой осью вращения. Тогда выражение для момента инерции примет вид:
Вынося за сумму , получим:
Поскольку старая ось проходит через центр масс, то суммарный импульс тела будет равен нулю:
Тогда:
Откуда и следует искомая формула:
,
где JC — известный момент инерции относительно оси, проходящей через центр масс тела.
Помогите решить / разобраться (Ф)
Сообщения без ответов | Активные темы | Избранное
| |||
24/11/14 |
| ||
| |||
| ||||
23/07/08 |
| |||
| ||||
| Munin |
| |||
30/01/06 |
| |||
| ||||
| DimaM |
| |||
28/12/12 |
| |||
| ||||
| Fass |
| ||
24/11/14 |
| ||
| |||
| DimaM |
| |||
28/12/12 |
| |||
| ||||
| realeugene |
| ||
27/08/16 |
| ||
| |||
| Fass |
| ||
24/11/14 |
| ||
| |||
| DimaM |
| |||
28/12/12 |
| |||
| ||||
09.2016, 13:02 | Fass |
| ||
24/11/14 |
| ||
| |||
09.2016, 14:54 | Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 10 ] |
Модераторы: photon, whiterussian, profrotter, Jnrty, Aer, Парджеттер, Eule_A, Супермодераторы
Кто сейчас на конференции |
Сейчас этот форум просматривают: нет зарегистрированных пользователей |
| Вы не можете начинать темы Вы не можете отвечать на сообщения Вы не можете редактировать свои сообщения Вы не можете удалять свои сообщения Вы не можете добавлять вложения |
| Найти: |
классическая механика — Момент инерции сплошного цилиндра
спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 22к раз
$\begingroup$
Я хочу вычислить момент инерции сплошного цилиндра радиуса $r$, длины $l$ и массы $M$ относительно оси, проходящей через центр цилиндра.
92$. Это неправильно, там должен быть множитель $\frac{1}{2}$. Но я не понимаю, почему. Некоторые решения, которые я видел в Интернете, рассматривают концентрические диски, но я не понимаю, почему этот метод не работает.
- классическая механика
- момент инерции
$\endgroup$
4
$\begingroup$
Рассчитанная вами сумма $dm$ неверна. Радиус будет разным. Который вы приняли за константу. Итак, 9{h}dz$$
Ваш ответ неверен, потому что вы угрожали r, как если бы это была константа, я полагаю.
$\endgroup$
1
$\begingroup$
Я думаю, что вам трудно осмыслить свой $dm$, и это нормально, потому что поначалу это непросто. Считайте $dm$ крошечной частицей материи в вашем цилиндре.
Бит, заключенный между радиусом $r$ и $r+dr$, $z$ и $z+dz$ и $\theta$ и $\theta+d\theta$, где все $dx$ являются бесконечно малым приращением. 92$ конечный результат (опять же ориентируясь только на радиальную часть результата)
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
