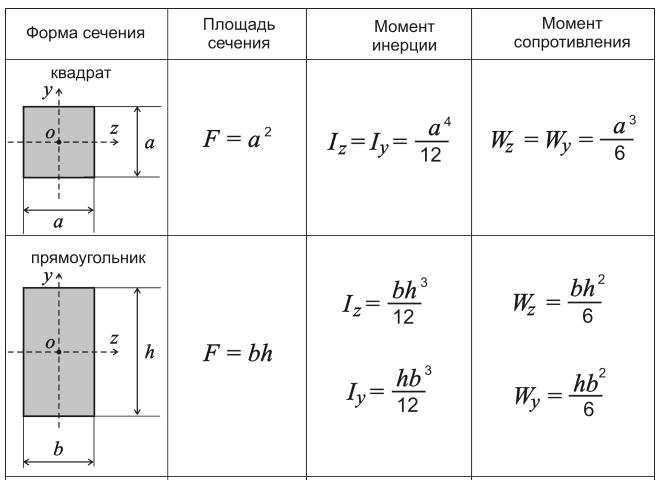
статический момент площади — MIDAS IT
Геометрические свойства сечений являются показателями конструктивных характеристик и несущей способности сечений. Они нужны для расчета прочности, устойчивости, изгибных и сдвиговых напряжений, прогибов — важных факторов в процессе общего проектирования конструкций мостов. Характеризуются формой и размерами сечений независимо от свойств материала.
В этой статье мы рассмотрим, как можно вычислить эти свойства сечений самостоятельно «в ручном режиме». В конце статьи вы можете скачать два калькулятора свойств двутаврового и коробчатого сечений в формате Excel для самостоятельного использования. А если вы хотите полностью избежать утомительной работы и сэкономить время, избежать повторяющихся задач и рутины — используйте программный комплекс midas Civil. В нем свойства сечений вычисляются автоматически.
Рисунок 1. Свойства коробчатого сечения, которые вычисляются в midas Civil
Давайте рассмотрим среди свойств сечения соотношение между центром тяжести сечения, статическим моментом площади сечения и моментом инерции, применяемым в формулах изгибных и сдвиговых напряжений, и то, как эти величины можно вычислить.
Статический момент площади сечения и центр тяжести
Статический момент площади используется для расчета центра тяжести сечений и касательного напряжения балочных элементов.
-
Формулу можно получить следующим образом:
Линейная область, удовлетворяющая закону Гука, подтверждается при помощи диаграммы отношения между напряжением и деформацией. Отношение между напряжением и деформацией материала с линейным упругим поведением может быть выражено наряду с соотношением между деформацией и кривизной.
Применив указанное выражение к сечению, в котором действует только изгиб без осевых усилий, как показано на изображении ниже, можно получить выражение, которым вычисляют статический момент площади сечения. Таким образом, сумма нормальных напряжений равна нулю, поскольку действует только изгиб без осевых усилий.
Напряжение «σ1», которое действует на элемент, расположенный на расстоянии «y» от нейтральной оси, и бесконечно малую площадь «dA» в пределах сечения, можно вычислить через выражение, приведенное выше.
Из приведенного расчета можно понять, что в случае использования линейно-упругих материалов нейтральная ось становится центром тяжести поперечного сечения; при этом статический момент площади сечения по отношению к центру тяжести сечения равен 0.
Рисунок 2. Выведение формулы статического момента площади сечения
С помощью показанного на Рисунке 2 выражения можно вычислить статический момент площади сечения и расположение центра тяжести поперечного сечения для тех случаев, когда ось «x» выступает в качестве их базисной оси.
Примеры вычисления статического момента площади
Пример 1
-
Вычислив статический момент площади сечения относительно оси «x’», которая расположена на расстоянии «e» от координатной оси «x».
 Из полученных результатов можно понять, что по мере увеличения расстояния от координатной оси статический момент площади сечения увеличивается на величину «e».
Из полученных результатов можно понять, что по мере увеличения расстояния от координатной оси статический момент площади сечения увеличивается на величину «e». - Расстояние «y’» — расстояние от оси «x’» до соответствующего элемента, можно учитывать отдельно как «y» и «e».
Пример 2
- В этом примере ось «x» задается в качестве базисной оси, и статический момент площади сечения можно вычислить путем вычленения из «y» величин «y0», которая представляет собой расстояние от оси «x» до центра тяжести поперечного сечения, и «y»», которая является расстоянием от центра тяжести поперечного сечения до произвольной области.
- Поскольку статический момент площади сечения от центра тяжести поперечного сечения равен «0», величина «y»» становится «0».
-
Таким образом, статический момент площади сечения вычисляется путем умножения общей площади поперечного сечения на значение расстояния от оси «x» до центра тяжести поперечного сечения.

- Следует отметить, что статический момент площади сечения можно вычислить путем умножения общей площади поперечного сечения на расстояние от координатной оси до центра тяжести поперечного сечения.
Пример 3
- Статический момент площади сечения можно рассчитать путем сложения произведения площади каждого сечения и расстояния от оси «x» до центра тяжести поперечного сечения.
- Когда известно место расположения центра тяжести поперечного сечения, и когда эти три сечения объединены, статический момент площади сечения можно вычислить как произведение общей площади поперечного сечения и «y0», как показано на примере.
- Из полученного результата можно вывести обобщенное выражение, которое позволит найти центр тяжести поперечного сечения через статический момент площади сечения.
Обобщенную формулу центра тяжести поперечного сечения можно сопоставить с результатами непосредственного расчета центра тяжести поперечного сечения через условия равновесия.
Рисунок 3: Формула центра тяжести поперечного сечения и применение уравнений равновесия
Формула центра тяжести поперечного сечения, полученная через условия равновесия, представляет собой ту же формулу, которая была получена через статический момент площади сечения.
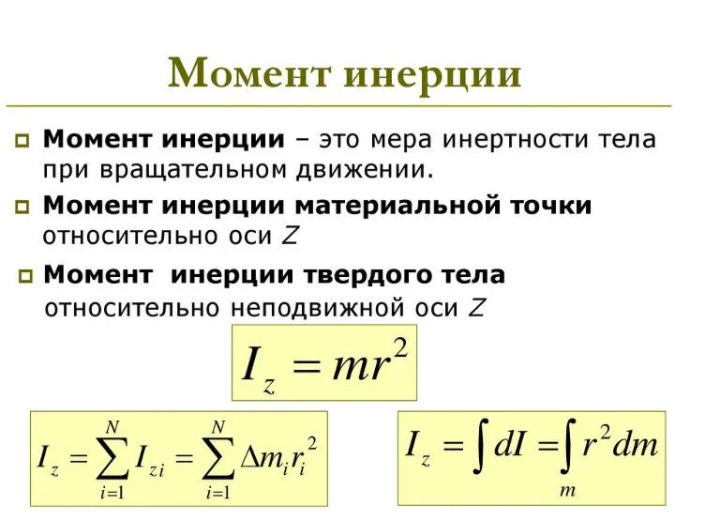
Момент инерции площади поперечного сечения
Момент инерции используется в качестве критерия для определения изгибной жесткости сечения и расчета прогибов, изгибных напряжений и касательных напряжений конструкций. Формулу расчета момента инерции можно получить как соотношение между моментом и кривизной, а также в результате вычисления этого соотношения.
Как показано на Рисунке 4, сумма моментов, создаваемых нормальными напряжениями, которые воздействуют на сечение, равна моменту «M». Эту формулу можно преобразовать в уравнение для напряжения, которое воздействует на сечение, разделенное на n-бесконечно малых элементов. При этом обобщенная формула выглядит так:
При этом обобщенная формула выглядит так:
Рисунок 4. Выведение формулы момента инерции
В случае, если полученную выше формулу заменить формулой расчета напряжений линейно-упругого материала, она будет выражена следующим образом: выражение суммы произведения квадрата «y» и площади поперечного сечения называется моментом инерции и обозначается как «I». Поскольку момент инерции является произведением длины в квадрате и площади поперечного сечения, единица выражена как длина в четвертой степени.
Приведенная выше формула суммируется для кривизны и момента следующим образом: кривизна «κ» пропорциональна моменту и обратно пропорциональна изгибной жесткости «EI». Изгибная жесткость «EI» применяется в качестве стандарта для измерения уровня, на котором элемент конструкции может противостоять изгибу. Благодаря этой формуле можно понять, что модуль упругости и форма, представляющие собой внутренние физические свойства элементов конструкции, являются важными факторами, которые определяют прочность конструкций.
Когда используется материал с большим модулем упругости или поперечное сечение с большим моментом инерции площади, изгибная жесткость увеличивается. С увеличением изгибной жесткости повышается способность конструкции противостоять изгибу, при этом уменьшается ее прогиб, так как угол прогиба или отклонения и момент инерции площади сечения обратно пропорциональны.
Формулу расчета момента инерции площади сечения, полученную указанным способом, можно обобщить на Рисунке 5. Момент инерции площади произвольного сечения при оси «x» в качестве координатной оси рассчитывается следующим образом: расстояние от координатной оси «x» до центра тяжести площади сечения составляет «r», а расстояние от центра тяжести площади сечения до n-бесконечно малых элементов можно подразделить на «yn».
Рисунок 5. Теорема о параллельном переносе осей для момента инерции
Поскольку статический момент площади сечения «QG», вычисляемый как интегральное произведение «yn» и бесконечно малой площади «dA», равен 0, то момент инерции относительно оси «x» можно вычислить как сумму момента инерции «I» и произведение «r Кроме того, площадь поперечного сечения «A» и «r2» всегда являются положительными величинами. Поэтому, когда координатная ось принимается как центр тяжести поперечного сечения, моментом инерции становится наименьшее значение.
Кроме того, площадь поперечного сечения «A» и «r2» всегда являются положительными величинами. Поэтому, когда координатная ось принимается как центр тяжести поперечного сечения, моментом инерции становится наименьшее значение.
Момент инерции обозначен как «I», когда координатной осью является центр тяжести поперечного сечения, и как «Ix», когда координатной осью является ось «x». Из приведенного выше процесса выведения видно, что значение момента инерции варьируется в зависимости от координатной оси. Перемещение координатной оси от центра тяжести поперечного сечения к оси «x» с целью получения обобщенного выражения момента инерции площади сечения сообразно с координатной осью называется теоремой о параллельном переносе осей.
По прямоугольному сечению на Рисунке 6 можно проверить, как момент инерции площади сечения варьируется сообразно с координатной осью.
Рисунок 6. Пример изменения момента инерции в зависимости от местоположения координатной оси
Можно наблюдать, насколько отличается момент инерции прямоугольного сечения, когда координатная ось расположена в центре тяжести поперечного сечения и когда координатная ось расположена по оси x.
Калькуляторы свойств коробчатого сечения и двутаврового сечения в Excel
В разделе «Поддержка – Пособия – Калькуляторы» вы можете скачать шаблоны калькуляторов свойств двутаврового и коробчатого сечения в формате Excel. Просто вводите требуемые размеры сечений и получайте результаты для центра тяжести поперечного сечения, момента инерции площади поперечного сечения и момента инерции двутавровых сечений.
Скачайте демо-версию midas Civil
Начните пользоваться уже сегодня! После скачивания демо-версии
вам будут доступны обучающие материалы по началу работы.
Сортамент горячекатаных равнополочных уголков по ГОСТ 8509-93
Сортамент горячекатаных равнополочных уголков по ГОСТ 8509-93Главная страница | Общие данные | Перечень расчетов | Форум
Вернуться к списку сортаментов
Условные обозначения:
b - ширина полки;
t - толщина полки;
R - радиус внутреннего закругления;
r - радиус закругления полки;
I - момент инерции;
W - момент сопротивления;
i - радиус инерции;
x0 - расстояние от центра тяжести до наружной грани полки;
Jxy - центробежный момент инерции
|
Сортамент горячекатаных равнополочных уголков по ГОСТ 8509-93
Геометрические характеристики вычислены по программе КМБП (http://hdru. com/russian/kmbp_2/rec_2_02.htm)
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 2.
com/russian/kmbp_2/rec_2_02.htm)
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 2. 0 │ 20│ 3.0│ 3.5│ 1.2│ 1.13 │ 0.40│ 0.28│ 0.59│ 0.63│ 0.75│ 0.17│ 0.20│ 0.39│ -0.23│ 0.60 │ 0.89 ║
║ │ 20│ 4.0│ 3.5│ 1.2│ 1.46 │ 0.50│ 0.37│ 0.58│ 0.78│ 0.73│ 0.22│ 0.24│ 0.38│ -0.28│ 0.64 │ 1.15 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 2.5 │ 25│ 3.0│ 3.5│ 1.2│ 1.43 │ 0.81│ 0.46│ 0.75│ 1.29│ 0.95│ 0.34│ 0.33│ 0.49│ -0.47│ 0.73 │ 1.12 ║
║ │ 25│ 4.0│ 3.5│ 1.2│ 1.86 │ 1.03│ 0.59│ 0.74│ 1.62│ 0.93│ 0.44│ 0.40│ 0.48│ -0.59│ 0.76 │ 1.46 ║
║ │ 25│ 5.0│ 3.5│ 1.2│ 2.27 │ 1.22│ 0.72│ 0.73│ 1.91│ 0.92│ 0.53│ 0.47│ 0.48│ -0.69│ 0.80 │ 1.78 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 2.8 │ 28│ 3.0│ 4.0│ 1.3│ 1.62 │ 1.17│ 0.58│ 0.85│ 1.
0 │ 20│ 3.0│ 3.5│ 1.2│ 1.13 │ 0.40│ 0.28│ 0.59│ 0.63│ 0.75│ 0.17│ 0.20│ 0.39│ -0.23│ 0.60 │ 0.89 ║
║ │ 20│ 4.0│ 3.5│ 1.2│ 1.46 │ 0.50│ 0.37│ 0.58│ 0.78│ 0.73│ 0.22│ 0.24│ 0.38│ -0.28│ 0.64 │ 1.15 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 2.5 │ 25│ 3.0│ 3.5│ 1.2│ 1.43 │ 0.81│ 0.46│ 0.75│ 1.29│ 0.95│ 0.34│ 0.33│ 0.49│ -0.47│ 0.73 │ 1.12 ║
║ │ 25│ 4.0│ 3.5│ 1.2│ 1.86 │ 1.03│ 0.59│ 0.74│ 1.62│ 0.93│ 0.44│ 0.40│ 0.48│ -0.59│ 0.76 │ 1.46 ║
║ │ 25│ 5.0│ 3.5│ 1.2│ 2.27 │ 1.22│ 0.72│ 0.73│ 1.91│ 0.92│ 0.53│ 0.47│ 0.48│ -0.69│ 0.80 │ 1.78 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 2.8 │ 28│ 3.0│ 4.0│ 1.3│ 1.62 │ 1.17│ 0.58│ 0.85│ 1. 84│ 1.07│ 0.48│ 0.43│ 0.55│ -0.68│ 0.80 │ 1.27 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 3.0 │ 30│ 3.0│ 4.0│ 1.3│ 1.74 │ 1.45│ 0.67│ 0.91│ 2.29│ 1.15│ 0.60│ 0.50│ 0.59│ -0.85│ 0.85 │ 1.36 ║
║ │ 30│ 4.0│ 4.0│ 1.3│ 2.27 │ 1.84│ 0.87│ 0.90│ 2.92│ 1.13│ 0.77│ 0.61│ 0.58│ -1.07│ 0.89 │ 1.78 ║
║ │ 30│ 5.0│ 4.0│ 1.3│ 2.78 │ 2.21│ 1.06│ 0.89│ 3.47│ 1.12│ 0.94│ 0.72│ 0.58│ -1.27│ 0.93 │ 2.18 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 3.2 │ 32│ 3.0│ 4.5│ 1.5│ 1.86 │ 1.77│ 0.77│ 0.97│ 2.80│ 1.23│ 0.74│ 0.58│ 0.63│ -1.03│ 0.89 │ 1.46 ║
║ │ 32│ 4.0│ 4.5│ 1.5│ 2.43 │ 2.26│ 1.00│ 0.96│ 3.58│ 1.21│ 0.94│ 0.71│ 0.62│ -1.32│ 0.94 │ 1.91 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 3.
84│ 1.07│ 0.48│ 0.43│ 0.55│ -0.68│ 0.80 │ 1.27 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 3.0 │ 30│ 3.0│ 4.0│ 1.3│ 1.74 │ 1.45│ 0.67│ 0.91│ 2.29│ 1.15│ 0.60│ 0.50│ 0.59│ -0.85│ 0.85 │ 1.36 ║
║ │ 30│ 4.0│ 4.0│ 1.3│ 2.27 │ 1.84│ 0.87│ 0.90│ 2.92│ 1.13│ 0.77│ 0.61│ 0.58│ -1.07│ 0.89 │ 1.78 ║
║ │ 30│ 5.0│ 4.0│ 1.3│ 2.78 │ 2.21│ 1.06│ 0.89│ 3.47│ 1.12│ 0.94│ 0.72│ 0.58│ -1.27│ 0.93 │ 2.18 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 3.2 │ 32│ 3.0│ 4.5│ 1.5│ 1.86 │ 1.77│ 0.77│ 0.97│ 2.80│ 1.23│ 0.74│ 0.58│ 0.63│ -1.03│ 0.89 │ 1.46 ║
║ │ 32│ 4.0│ 4.5│ 1.5│ 2.43 │ 2.26│ 1.00│ 0.96│ 3.58│ 1.21│ 0.94│ 0.71│ 0.62│ -1.32│ 0.94 │ 1.91 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 3. 5 │ 35│ 3.0│ 4.5│ 1.5│ 2.04 │ 2.35│ 0.93│ 1.07│ 3.72│ 1.35│ 0.97│ 0.71│ 0.69│ -1.37│ 0.97 │ 1.60 ║
║ │ 35│ 4.0│ 4.5│ 1.5│ 2.67 │ 3.01│ 1.21│ 1.06│ 4.76│ 1.33│ 1.25│ 0.87│ 0.68│ -1.76│ 1.01 │ 2.10 ║
║ │ 35│ 5.0│ 4.5│ 1.5│ 3.28 │ 3.61│ 1.48│ 1.05│ 5.71│ 1.32│ 1.52│ 1.02│ 0.68│ -2.10│ 1.05 │ 2.58 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 4.0 │ 40│ 3.0│ 5.0│ 1.7│ 2.35 │ 3.55│ 1.22│ 1.23│ 5.63│ 1.55│ 1.47│ 0.96│ 0.79│ -2.08│ 1.09 │ 1.85 ║
║ │ 40│ 4.0│ 5.0│ 1.7│ 3.08 │ 4.58│ 1.60│ 1.22│ 7.26│ 1.53│ 1.90│ 1.18│ 0.78│ -2.68│ 1.13 │ 2.42 ║
║ │ 40│ 5.0│ 5.0│ 1.7│ 3.79 │ 5.53│ 1.96│ 1.21│ 8.75│ 1.52│ 2.30│ 1.39│ 0.78│ -3.23│ 1.17 │ 2.98 ║
║ │ 40│ 6.0│ 5.0│ 1.7│ 4.48 │ 6.41│ 2.30│ 1.20│ 10.
5 │ 35│ 3.0│ 4.5│ 1.5│ 2.04 │ 2.35│ 0.93│ 1.07│ 3.72│ 1.35│ 0.97│ 0.71│ 0.69│ -1.37│ 0.97 │ 1.60 ║
║ │ 35│ 4.0│ 4.5│ 1.5│ 2.67 │ 3.01│ 1.21│ 1.06│ 4.76│ 1.33│ 1.25│ 0.87│ 0.68│ -1.76│ 1.01 │ 2.10 ║
║ │ 35│ 5.0│ 4.5│ 1.5│ 3.28 │ 3.61│ 1.48│ 1.05│ 5.71│ 1.32│ 1.52│ 1.02│ 0.68│ -2.10│ 1.05 │ 2.58 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 4.0 │ 40│ 3.0│ 5.0│ 1.7│ 2.35 │ 3.55│ 1.22│ 1.23│ 5.63│ 1.55│ 1.47│ 0.96│ 0.79│ -2.08│ 1.09 │ 1.85 ║
║ │ 40│ 4.0│ 5.0│ 1.7│ 3.08 │ 4.58│ 1.60│ 1.22│ 7.26│ 1.53│ 1.90│ 1.18│ 0.78│ -2.68│ 1.13 │ 2.42 ║
║ │ 40│ 5.0│ 5.0│ 1.7│ 3.79 │ 5.53│ 1.96│ 1.21│ 8.75│ 1.52│ 2.30│ 1.39│ 0.78│ -3.23│ 1.17 │ 2.98 ║
║ │ 40│ 6.0│ 5.0│ 1.7│ 4.48 │ 6.41│ 2.30│ 1.20│ 10. 13│ 1.50│ 2.70│ 1.58│ 0.78│ -3.71│ 1.21 │ 3.52 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Сотамент горячекатаных равнополочных уголков по ГОСТ 8509-93
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 4.
13│ 1.50│ 2.70│ 1.58│ 0.78│ -3.71│ 1.21 │ 3.52 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Сотамент горячекатаных равнополочных уголков по ГОСТ 8509-93
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 4. 5 │ 45│ 3.0│ 5.0│ 1.7│ 2.65 │ 5.13│ 1.56│ 1.39│ 8.13│ 1.75│ 2.12│ 1.24│ 0.89│ -3.00│ 1.21 │ 2.08 ║
║ │ 45│ 4.0│ 5.0│ 1.7│ 3.48 │ 6.63│ 2.04│ 1.38│ 10.52│ 1.74│ 2.74│ 1.54│ 0.89│ -3.89│ 1.26 │ 2.73 ║
║ │ 45│ 5.0│ 5.0│ 1.7│ 4.29 │ 8.03│ 2.51│ 1.37│ 12.74│ 1.72│ 3.33│ 1.81│ 0.88│ -4.71│ 1.30 │ 3.37 ║
║ │ 45│ 6.0│ 5.0│ 1.7│ 5.08 │ 9.35│ 2.95│ 1.36│ 14.80│ 1.71│ 3.90│ 2.07│ 0.88│ -5.45│ 1.33 │ 3.99 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 5.0 │ 50│ 3.0│ 5.5│ 1.8│ 2.96 │ 7.11│ 1.94│ 1.55│ 11.27│ 1.95│ 2.95│ 1.56│ 1.00│ -4.16│ 1.33 │ 2.32 ║
║ │ 50│ 4.0│ 5.5│ 1.8│ 3.89 │ 9.21│ 2.54│ 1.54│ 14.63│ 1.94│ 3.80│ 1.95│ 0.99│ -5.41│ 1.38 │ 3.05 ║
║ │ 50│ 5.0│ 5.5│ 1.8│ 4.80 │ 11.20│ 3.13│ 1.53│ 17.
5 │ 45│ 3.0│ 5.0│ 1.7│ 2.65 │ 5.13│ 1.56│ 1.39│ 8.13│ 1.75│ 2.12│ 1.24│ 0.89│ -3.00│ 1.21 │ 2.08 ║
║ │ 45│ 4.0│ 5.0│ 1.7│ 3.48 │ 6.63│ 2.04│ 1.38│ 10.52│ 1.74│ 2.74│ 1.54│ 0.89│ -3.89│ 1.26 │ 2.73 ║
║ │ 45│ 5.0│ 5.0│ 1.7│ 4.29 │ 8.03│ 2.51│ 1.37│ 12.74│ 1.72│ 3.33│ 1.81│ 0.88│ -4.71│ 1.30 │ 3.37 ║
║ │ 45│ 6.0│ 5.0│ 1.7│ 5.08 │ 9.35│ 2.95│ 1.36│ 14.80│ 1.71│ 3.90│ 2.07│ 0.88│ -5.45│ 1.33 │ 3.99 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 5.0 │ 50│ 3.0│ 5.5│ 1.8│ 2.96 │ 7.11│ 1.94│ 1.55│ 11.27│ 1.95│ 2.95│ 1.56│ 1.00│ -4.16│ 1.33 │ 2.32 ║
║ │ 50│ 4.0│ 5.5│ 1.8│ 3.89 │ 9.21│ 2.54│ 1.54│ 14.63│ 1.94│ 3.80│ 1.95│ 0.99│ -5.41│ 1.38 │ 3.05 ║
║ │ 50│ 5.0│ 5.5│ 1.8│ 4.80 │ 11.20│ 3.13│ 1.53│ 17. 77│ 1.92│ 4.63│ 2.31│ 0.98│ -6.57│ 1.42 │ 3.77 ║
║ │ 50│ 6.0│ 5.5│ 1.8│ 5.69 │ 13.07│ 3.69│ 1.52│ 20.72│ 1.91│ 5.43│ 2.63│ 0.98│ -7.64│ 1.46 │ 4.47 ║
║ │ 50│ 7.0│ 5.5│ 1.8│ 6.56 │ 14.84│ 4.24│ 1.50│ 23.47│ 1.89│ 6.21│ 2.93│ 0.97│ -8.63│ 1.50 │ 5.15 ║
║ │ 50│ 8.0│ 5.5│ 1.8│ 7.41 │ 16.51│ 4.76│ 1.49│ 26.03│ 1.87│ 6.98│ 3.22│ 0.97│ -9.53│ 1.53 │ 5.82 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 5.6 │ 56│ 4.0│ 6.0│ 2.0│ 4.38 │ 13.10│ 3.21│ 1.73│ 20.79│ 2.18│ 5.41│ 2.51│ 1.11│ -7.69│ 1.53 │ 3.44 ║
║ │ 56│ 5.0│ 6.0│ 2.0│ 5.41 │ 15.97│ 3.96│ 1.72│ 25.36│ 2.17│ 6.59│ 2.97│ 1.10│ -9.38│ 1.57 │ 4.25 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 6.
77│ 1.92│ 4.63│ 2.31│ 0.98│ -6.57│ 1.42 │ 3.77 ║
║ │ 50│ 6.0│ 5.5│ 1.8│ 5.69 │ 13.07│ 3.69│ 1.52│ 20.72│ 1.91│ 5.43│ 2.63│ 0.98│ -7.64│ 1.46 │ 4.47 ║
║ │ 50│ 7.0│ 5.5│ 1.8│ 6.56 │ 14.84│ 4.24│ 1.50│ 23.47│ 1.89│ 6.21│ 2.93│ 0.97│ -8.63│ 1.50 │ 5.15 ║
║ │ 50│ 8.0│ 5.5│ 1.8│ 7.41 │ 16.51│ 4.76│ 1.49│ 26.03│ 1.87│ 6.98│ 3.22│ 0.97│ -9.53│ 1.53 │ 5.82 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 5.6 │ 56│ 4.0│ 6.0│ 2.0│ 4.38 │ 13.10│ 3.21│ 1.73│ 20.79│ 2.18│ 5.41│ 2.51│ 1.11│ -7.69│ 1.53 │ 3.44 ║
║ │ 56│ 5.0│ 6.0│ 2.0│ 5.41 │ 15.97│ 3.96│ 1.72│ 25.36│ 2.17│ 6.59│ 2.97│ 1.10│ -9.38│ 1.57 │ 4.25 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 6. 0 │ 60│ 4.0│ 7.0│ 2.3│ 4.72 │ 16.21│ 3.70│ 1.85│ 25.69│ 2.33│ 6.72│ 2.94│ 1.19│ -9.49│ 1.62 │ 3.71 ║
║ │ 60│ 5.0│ 7.0│ 2.3│ 5.83 │ 19.79│ 4.56│ 1.84│ 31.40│ 2.32│ 8.18│ 3.48│ 1.18│ -11.61│ 1.66 │ 4.58 ║
║ │ 60│ 6.0│ 7.0│ 2.3│ 6.92 │ 23.21│ 5.40│ 1.83│ 36.81│ 2.31│ 9.60│ 3.99│ 1.18│ -13.61│ 1.70 │ 5.43 ║
║ │ 60│ 8.0│ 7.0│ 2.3│ 9.04 │ 29.55│ 7.00│ 1.81│ 46.77│ 2.27│ 12.34│ 4.90│ 1.17│ -17.21│ 1.78 │ 7.10 ║
║ │ 60│ 10.0│ 7.0│ 2.3│ 11.08 │ 35.32│ 8.52│ 1.79│ 55.64│ 2.24│ 15.00│ 5.72│ 1.16│ -20.32│ 1.85 │ 8.70 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 6.3 │ 63│ 4.0│ 7.0│ 2.3│ 4.96 │ 18.86│ 4.09│ 1.95│ 29.90│ 2.46│ 7.81│ 3.27│ 1.26│ -11.05│ 1.69 │ 3.90 ║
║ │ 63│ 5.0│ 7.0│ 2.3│ 6.13 │ 23.06│ 5.05│ 1.94│ 36.
0 │ 60│ 4.0│ 7.0│ 2.3│ 4.72 │ 16.21│ 3.70│ 1.85│ 25.69│ 2.33│ 6.72│ 2.94│ 1.19│ -9.49│ 1.62 │ 3.71 ║
║ │ 60│ 5.0│ 7.0│ 2.3│ 5.83 │ 19.79│ 4.56│ 1.84│ 31.40│ 2.32│ 8.18│ 3.48│ 1.18│ -11.61│ 1.66 │ 4.58 ║
║ │ 60│ 6.0│ 7.0│ 2.3│ 6.92 │ 23.21│ 5.40│ 1.83│ 36.81│ 2.31│ 9.60│ 3.99│ 1.18│ -13.61│ 1.70 │ 5.43 ║
║ │ 60│ 8.0│ 7.0│ 2.3│ 9.04 │ 29.55│ 7.00│ 1.81│ 46.77│ 2.27│ 12.34│ 4.90│ 1.17│ -17.21│ 1.78 │ 7.10 ║
║ │ 60│ 10.0│ 7.0│ 2.3│ 11.08 │ 35.32│ 8.52│ 1.79│ 55.64│ 2.24│ 15.00│ 5.72│ 1.16│ -20.32│ 1.85 │ 8.70 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 6.3 │ 63│ 4.0│ 7.0│ 2.3│ 4.96 │ 18.86│ 4.09│ 1.95│ 29.90│ 2.46│ 7.81│ 3.27│ 1.26│ -11.05│ 1.69 │ 3.90 ║
║ │ 63│ 5.0│ 7.0│ 2.3│ 6.13 │ 23.06│ 5.05│ 1.94│ 36. 59│ 2.44│ 9.52│ 3.88│ 1.25│ -13.54│ 1.74 │ 4.81 ║
║ │ 63│ 6.0│ 7.0│ 2.3│ 7.28 │ 27.06│ 5.98│ 1.93│ 42.94│ 2.43│ 11.18│ 4.45│ 1.24│ -15.88│ 1.78 │ 5.72 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 7.0 │ 70│ 4.5│ 8.0│ 2.7│ 6.20 │ 29.04│ 5.67│ 2.16│ 46.03│ 2.72│ 12.04│ 4.53│ 1.39│ -17.00│ 1.88 │ 4.87 ║
║ │ 70│ 5.0│ 8.0│ 2.7│ 6.86 │ 31.94│ 6.27│ 2.16│ 50.67│ 2.72│ 13.22│ 4.91│ 1.39│ -18.73│ 1.90 │ 5.38 ║
║ │ 70│ 6.0│ 8.0│ 2.7│ 8.15 │ 37.58│ 7.43│ 2.15│ 59.64│ 2.71│ 15.52│ 5.65│ 1.38│ -22.06│ 1.95 │ 6.40 ║
║ │ 70│ 7.0│ 8.0│ 2.7│ 9.42 │ 42.98│ 8.57│ 2.14│ 68.19│ 2.69│ 17.77│ 6.33│ 1.37│ -25.21│ 1.99 │ 7.39 ║
║ │ 70│ 8.0│ 8.0│ 2.7│ 10.67 │ 48.16│ 9.68│ 2.13│ 76.35│ 2.67│ 19.97│ 6.97│ 1.37│ -28.19│ 2.02 │ 8.37 ║
║ │ 70│ 10.
59│ 2.44│ 9.52│ 3.88│ 1.25│ -13.54│ 1.74 │ 4.81 ║
║ │ 63│ 6.0│ 7.0│ 2.3│ 7.28 │ 27.06│ 5.98│ 1.93│ 42.94│ 2.43│ 11.18│ 4.45│ 1.24│ -15.88│ 1.78 │ 5.72 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 7.0 │ 70│ 4.5│ 8.0│ 2.7│ 6.20 │ 29.04│ 5.67│ 2.16│ 46.03│ 2.72│ 12.04│ 4.53│ 1.39│ -17.00│ 1.88 │ 4.87 ║
║ │ 70│ 5.0│ 8.0│ 2.7│ 6.86 │ 31.94│ 6.27│ 2.16│ 50.67│ 2.72│ 13.22│ 4.91│ 1.39│ -18.73│ 1.90 │ 5.38 ║
║ │ 70│ 6.0│ 8.0│ 2.7│ 8.15 │ 37.58│ 7.43│ 2.15│ 59.64│ 2.71│ 15.52│ 5.65│ 1.38│ -22.06│ 1.95 │ 6.40 ║
║ │ 70│ 7.0│ 8.0│ 2.7│ 9.42 │ 42.98│ 8.57│ 2.14│ 68.19│ 2.69│ 17.77│ 6.33│ 1.37│ -25.21│ 1.99 │ 7.39 ║
║ │ 70│ 8.0│ 8.0│ 2.7│ 10.67 │ 48.16│ 9.68│ 2.13│ 76.35│ 2.67│ 19.97│ 6.97│ 1.37│ -28.19│ 2.02 │ 8.37 ║
║ │ 70│ 10. 0│ 8.0│ 2.7│ 13.11 │ 57.90│ 11.82│ 2.10│ 91.52│ 2.64│ 24.27│ 8.17│ 1.36│ -33.63│ 2.10 │ 10.29 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 7.5 │ 75│ 5.0│ 9.0│ 3.0│ 7.38 │ 39.53│ 7.21│ 2.31│ 62.65│ 2.91│ 16.41│ 5.75│ 1.49│ -23.12│ 2.02 │ 5.80 ║
║ │ 75│ 6.0│ 9.0│ 3.0│ 8.78 │ 46.57│ 8.57│ 2.30│ 73.87│ 2.90│ 19.28│ 6.61│ 1.48│ -27.30│ 2.06 │ 6.89 ║
║ │ 75│ 7.0│ 9.0│ 3.0│ 10.15 │ 53.34│ 9.89│ 2.29│ 84.61│ 2.89│ 22.07│ 7.41│ 1.48│ -31.27│ 2.10 │ 7.96 ║
║ │ 75│ 8.0│ 9.0│ 3.0│ 11.50 │ 59.84│ 11.18│ 2.28│ 94.89│ 2.87│ 24.80│ 8.17│ 1.47│ -35.04│ 2.15 │ 9.02 ║
║ │ 75│ 9.0│ 9.0│ 3.0│ 12.83 │ 66.10│ 12.43│ 2.27│ 104.72│ 2.86│ 27.48│ 8.89│ 1.46│ -38.62│ 2.19 │ 10.07 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 8.
0│ 8.0│ 2.7│ 13.11 │ 57.90│ 11.82│ 2.10│ 91.52│ 2.64│ 24.27│ 8.17│ 1.36│ -33.63│ 2.10 │ 10.29 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 7.5 │ 75│ 5.0│ 9.0│ 3.0│ 7.38 │ 39.53│ 7.21│ 2.31│ 62.65│ 2.91│ 16.41│ 5.75│ 1.49│ -23.12│ 2.02 │ 5.80 ║
║ │ 75│ 6.0│ 9.0│ 3.0│ 8.78 │ 46.57│ 8.57│ 2.30│ 73.87│ 2.90│ 19.28│ 6.61│ 1.48│ -27.30│ 2.06 │ 6.89 ║
║ │ 75│ 7.0│ 9.0│ 3.0│ 10.15 │ 53.34│ 9.89│ 2.29│ 84.61│ 2.89│ 22.07│ 7.41│ 1.48│ -31.27│ 2.10 │ 7.96 ║
║ │ 75│ 8.0│ 9.0│ 3.0│ 11.50 │ 59.84│ 11.18│ 2.28│ 94.89│ 2.87│ 24.80│ 8.17│ 1.47│ -35.04│ 2.15 │ 9.02 ║
║ │ 75│ 9.0│ 9.0│ 3.0│ 12.83 │ 66.10│ 12.43│ 2.27│ 104.72│ 2.86│ 27.48│ 8.89│ 1.46│ -38.62│ 2.19 │ 10.07 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 8. 0 │ 80│ 5.5│ 9.0│ 3.0│ 8.63 │ 52.68│ 9.03│ 2.47│ 83.56│ 3.11│ 21.80│ 7.12│ 1.59│ -30.88│ 2.17 │ 6.78 ║
║ │ 80│ 6.0│ 9.0│ 3.0│ 9.38 │ 56.97│ 9.80│ 2.46│ 90.40│ 3.10│ 23.54│ 7.61│ 1.58│ -33.43│ 2.19 │ 7.36 ║
║ │ 80│ 7.0│ 9.0│ 3.0│ 10.85 │ 65.31│ 11.32│ 2.45│ 103.66│ 3.09│ 26.97│ 8.55│ 1.58│ -38.34│ 2.23 │ 8.51 ║
║ │ 80│ 8.0│ 9.0│ 3.0│ 12.30 │ 73.36│ 12.80│ 2.44│ 116.39│ 3.08│ 30.32│ 9.45│ 1.57│ -43.03│ 2.27 │ 9.65 ║
║ │ 80│ 10.0│ 9.0│ 3.0│ 15.14 │ 88.58│ 15.67│ 2.42│ 140.31│ 3.04│ 36.85│ 11.10│ 1.56│ -51.73│ 2.35 │ 11.88 ║
║ │ 80│ 12.0│ 9.0│ 3.0│ 17.90 │ 102.74│ 18.42│ 2.40│ 162.27│ 3.01│ 43.21│ 12.61│ 1.55│ -59.53│ 2.42 │ 14.05 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Сотамент горячекатаных равнополочных уголков по ГОСТ 8509-93
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 9.
0 │ 80│ 5.5│ 9.0│ 3.0│ 8.63 │ 52.68│ 9.03│ 2.47│ 83.56│ 3.11│ 21.80│ 7.12│ 1.59│ -30.88│ 2.17 │ 6.78 ║
║ │ 80│ 6.0│ 9.0│ 3.0│ 9.38 │ 56.97│ 9.80│ 2.46│ 90.40│ 3.10│ 23.54│ 7.61│ 1.58│ -33.43│ 2.19 │ 7.36 ║
║ │ 80│ 7.0│ 9.0│ 3.0│ 10.85 │ 65.31│ 11.32│ 2.45│ 103.66│ 3.09│ 26.97│ 8.55│ 1.58│ -38.34│ 2.23 │ 8.51 ║
║ │ 80│ 8.0│ 9.0│ 3.0│ 12.30 │ 73.36│ 12.80│ 2.44│ 116.39│ 3.08│ 30.32│ 9.45│ 1.57│ -43.03│ 2.27 │ 9.65 ║
║ │ 80│ 10.0│ 9.0│ 3.0│ 15.14 │ 88.58│ 15.67│ 2.42│ 140.31│ 3.04│ 36.85│ 11.10│ 1.56│ -51.73│ 2.35 │ 11.88 ║
║ │ 80│ 12.0│ 9.0│ 3.0│ 17.90 │ 102.74│ 18.42│ 2.40│ 162.27│ 3.01│ 43.21│ 12.61│ 1.55│ -59.53│ 2.42 │ 14.05 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Сотамент горячекатаных равнополочных уголков по ГОСТ 8509-93
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 9. 0 │ 90│ 6.0│ 10.0│ 3.3│ 10.61 │ 82.10│ 12.49│ 2.78│ 130.22│ 3.50│ 33.97│ 9.89│ 1.79│ -48.12│ 2.43 │ 8.33 ║
║ │ 90│ 7.0│ 10.0│ 3.3│ 12.28 │ 94.30│ 14.45│ 2.77│ 149.67│ 3.49│ 38.94│ 11.14│ 1.78│ -55.36│ 2.47 │ 9.64 ║
║ │ 90│ 8.0│ 10.0│ 3.3│ 13.93 │ 106.11│ 16.36│ 2.76│ 168.42│ 3.48│ 43.80│ 12.32│ 1.77│ -62.31│ 2.51 │ 10.93 ║
║ │ 90│ 9.0│ 10.0│ 3.3│ 15.56 │ 117.54│ 18.24│ 2.75│ 186.51│ 3.46│ 48.58│ 13.45│ 1.77│ -68.97│ 2.56 │ 12.21 ║
║ │ 90│ 10.0│ 10.0│ 3.3│ 17.17 │ 128.60│ 20.07│ 2.74│ 203.93│ 3.45│ 53.27│ 14.52│ 1.76│ -75.33│ 2.59 │ 13.48 ║
║ │ 90│ 12.0│ 10.0│ 3.3│ 20.33 │ 149.67│ 23.65│ 2.71│ 236.88│ 3.41│ 62.46│ 16.54│ 1.75│ -87.21│ 2.67 │ 15.96 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 10.0 │ 100│ 6.5│ 12.0│ 4.0│ 12.82 │ 122.10│ 16.69│ 3.09│ 193.
0 │ 90│ 6.0│ 10.0│ 3.3│ 10.61 │ 82.10│ 12.49│ 2.78│ 130.22│ 3.50│ 33.97│ 9.89│ 1.79│ -48.12│ 2.43 │ 8.33 ║
║ │ 90│ 7.0│ 10.0│ 3.3│ 12.28 │ 94.30│ 14.45│ 2.77│ 149.67│ 3.49│ 38.94│ 11.14│ 1.78│ -55.36│ 2.47 │ 9.64 ║
║ │ 90│ 8.0│ 10.0│ 3.3│ 13.93 │ 106.11│ 16.36│ 2.76│ 168.42│ 3.48│ 43.80│ 12.32│ 1.77│ -62.31│ 2.51 │ 10.93 ║
║ │ 90│ 9.0│ 10.0│ 3.3│ 15.56 │ 117.54│ 18.24│ 2.75│ 186.51│ 3.46│ 48.58│ 13.45│ 1.77│ -68.97│ 2.56 │ 12.21 ║
║ │ 90│ 10.0│ 10.0│ 3.3│ 17.17 │ 128.60│ 20.07│ 2.74│ 203.93│ 3.45│ 53.27│ 14.52│ 1.76│ -75.33│ 2.59 │ 13.48 ║
║ │ 90│ 12.0│ 10.0│ 3.3│ 20.33 │ 149.67│ 23.65│ 2.71│ 236.88│ 3.41│ 62.46│ 16.54│ 1.75│ -87.21│ 2.67 │ 15.96 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 10.0 │ 100│ 6.5│ 12.0│ 4.0│ 12.82 │ 122.10│ 16.69│ 3.09│ 193. 46│ 3.89│ 50.73│ 13.37│ 1.99│ -71.37│ 2.68 │ 10.06 ║
║ │ 100│ 7.0│ 12.0│ 4.0│ 13.75 │ 130.59│ 17.90│ 3.08│ 207.01│ 3.88│ 54.16│ 14.15│ 1.99│ -76.42│ 2.71 │ 10.79 ║
║ │ 100│ 8.0│ 12.0│ 4.0│ 15.60 │ 147.19│ 20.30│ 3.07│ 233.46│ 3.87│ 60.92│ 15.66│ 1.98│ -86.27│ 2.75 │ 12.25 ║
║ │ 100│ 10.0│ 12.0│ 4.0│ 19.24 │ 178.95│ 24.97│ 3.05│ 283.83│ 3.84│ 74.08│ 18.49│ 1.96│ -104.87│ 2.83 │ 15.10 ║
║ │ 100│ 12.0│ 12.0│ 4.0│ 22.80 │ 208.90│ 29.47│ 3.03│ 330.95│ 3.81│ 86.84│ 21.08│ 1.95│ -122.06│ 2.91 │ 17.90 ║
║ │ 100│ 14.0│ 12.0│ 4.0│ 26.28 │ 237.15│ 33.83│ 3.00│ 374.98│ 3.78│ 99.32│ 23.49│ 1.94│ -137.83│ 2.99 │ 20.63 ║
║ │ 100│ 15.0│ 12.0│ 4.0│ 27.99 │ 250.68│ 35.95│ 2.99│ 395.87│ 3.76│ 105.48│ 24.64│ 1.94│ -145.20│ 3.03 │ 21.97 ║
║ │ 100│ 16.0│ 12.0│ 4.0│ 29.68 │ 263.82│ 38.04│ 2.98│ 416.04│ 3.74│ 111.61│ 25.76│ 1.94│ -152.22│ 3.06 │ 23.30 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 11.
46│ 3.89│ 50.73│ 13.37│ 1.99│ -71.37│ 2.68 │ 10.06 ║
║ │ 100│ 7.0│ 12.0│ 4.0│ 13.75 │ 130.59│ 17.90│ 3.08│ 207.01│ 3.88│ 54.16│ 14.15│ 1.99│ -76.42│ 2.71 │ 10.79 ║
║ │ 100│ 8.0│ 12.0│ 4.0│ 15.60 │ 147.19│ 20.30│ 3.07│ 233.46│ 3.87│ 60.92│ 15.66│ 1.98│ -86.27│ 2.75 │ 12.25 ║
║ │ 100│ 10.0│ 12.0│ 4.0│ 19.24 │ 178.95│ 24.97│ 3.05│ 283.83│ 3.84│ 74.08│ 18.49│ 1.96│ -104.87│ 2.83 │ 15.10 ║
║ │ 100│ 12.0│ 12.0│ 4.0│ 22.80 │ 208.90│ 29.47│ 3.03│ 330.95│ 3.81│ 86.84│ 21.08│ 1.95│ -122.06│ 2.91 │ 17.90 ║
║ │ 100│ 14.0│ 12.0│ 4.0│ 26.28 │ 237.15│ 33.83│ 3.00│ 374.98│ 3.78│ 99.32│ 23.49│ 1.94│ -137.83│ 2.99 │ 20.63 ║
║ │ 100│ 15.0│ 12.0│ 4.0│ 27.99 │ 250.68│ 35.95│ 2.99│ 395.87│ 3.76│ 105.48│ 24.64│ 1.94│ -145.20│ 3.03 │ 21.97 ║
║ │ 100│ 16.0│ 12.0│ 4.0│ 29.68 │ 263.82│ 38.04│ 2.98│ 416.04│ 3.74│ 111.61│ 25.76│ 1.94│ -152.22│ 3.06 │ 23.30 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 11. 0 │ 110│ 7.0│ 12.0│ 4.0│ 15.15 │ 175.61│ 21.83│ 3.40│ 278.54│ 4.29│ 72.68│ 17.39│ 2.19│ -102.93│ 2.96 │ 11.89 ║
║ │ 110│ 8.0│ 12.0│ 4.0│ 17.20 │ 198.17│ 24.77│ 3.39│ 314.51│ 4.28│ 81.83│ 19.29│ 2.18│ -116.34│ 3.00 │ 13.50 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 12.0 │ 120│ 8.0│ 12.0│ 4.0│ 18.80 │ 259.75│ 29.68│ 3.72│ 412.45│ 4.68│ 107.04│ 23.30│ 2.39│ -152.71│ 3.25 │ 14.76 ║
║ │ 120│ 10.0│ 12.0│ 4.0│ 23.24 │ 317.16│ 36.59│ 3.69│ 503.79│ 4.66│ 130.54│ 27.70│ 2.37│ -186.62│ 3.33 │ 18.24 ║
║ │ 120│ 12.0│ 12.0│ 4.0│ 27.60 │ 371.80│ 43.30│ 3.67│ 590.28│ 4.63│ 153.33│ 31.77│ 2.36│ -218.48│ 3.41 │ 21.67 ║
║ │ 120│ 15.0│ 12.0│ 4.0│ 33.99 │ 448.90│ 52.98│ 3.63│ 711.32│ 4.58│ 186.48│ 37.38│ 2.34│ -262.42│ 3.53 │ 26.68 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 12.
0 │ 110│ 7.0│ 12.0│ 4.0│ 15.15 │ 175.61│ 21.83│ 3.40│ 278.54│ 4.29│ 72.68│ 17.39│ 2.19│ -102.93│ 2.96 │ 11.89 ║
║ │ 110│ 8.0│ 12.0│ 4.0│ 17.20 │ 198.17│ 24.77│ 3.39│ 314.51│ 4.28│ 81.83│ 19.29│ 2.18│ -116.34│ 3.00 │ 13.50 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 12.0 │ 120│ 8.0│ 12.0│ 4.0│ 18.80 │ 259.75│ 29.68│ 3.72│ 412.45│ 4.68│ 107.04│ 23.30│ 2.39│ -152.71│ 3.25 │ 14.76 ║
║ │ 120│ 10.0│ 12.0│ 4.0│ 23.24 │ 317.16│ 36.59│ 3.69│ 503.79│ 4.66│ 130.54│ 27.70│ 2.37│ -186.62│ 3.33 │ 18.24 ║
║ │ 120│ 12.0│ 12.0│ 4.0│ 27.60 │ 371.80│ 43.30│ 3.67│ 590.28│ 4.63│ 153.33│ 31.77│ 2.36│ -218.48│ 3.41 │ 21.67 ║
║ │ 120│ 15.0│ 12.0│ 4.0│ 33.99 │ 448.90│ 52.98│ 3.63│ 711.32│ 4.58│ 186.48│ 37.38│ 2.34│ -262.42│ 3.53 │ 26.68 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 12. 5 │ 125│ 8.0│ 14.0│ 4.6│ 19.69 │ 294.36│ 32.20│ 3.87│ 466.76│ 4.87│ 121.96│ 25.68│ 2.49│ -172.40│ 3.36 │ 15.46 ║
║ │ 125│ 9.0│ 14.0│ 4.6│ 22.02 │ 327.48│ 36.00│ 3.86│ 519.57│ 4.86│ 135.38│ 28.14│ 2.48│ -192.10│ 3.40 │ 17.29 ║
║ │ 125│ 10.0│ 14.0│ 4.6│ 24.33 │ 359.82│ 39.74│ 3.85│ 571.04│ 4.84│ 148.59│ 30.50│ 2.47│ -211.22│ 3.44 │ 19.10 ║
║ │ 125│ 12.0│ 14.0│ 4.6│ 28.89 │ 422.23│ 47.06│ 3.82│ 670.02│ 4.82│ 174.43│ 34.97│ 2.46│ -247.80│ 3.53 │ 22.68 ║
║ │ 125│ 14.0│ 14.0│ 4.6│ 33.37 │ 481.76│ 54.17│ 3.80│ 763.90│ 4.79│ 199.62│ 39.14│ 2.45│ -282.14│ 3.61 │ 26.20 ║
║ │ 125│ 16.0│ 14.0│ 4.6│ 37.77 │ 538.56│ 61.09│ 3.78│ 852.84│ 4.75│ 224.29│ 43.06│ 2.44│ -314.27│ 3.68 │ 29.65 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 14.0 │ 140│ 9.0│ 14.0│ 4.6│ 24.72 │ 465.72│ 45.55│ 4.34│ 739.
5 │ 125│ 8.0│ 14.0│ 4.6│ 19.69 │ 294.36│ 32.20│ 3.87│ 466.76│ 4.87│ 121.96│ 25.68│ 2.49│ -172.40│ 3.36 │ 15.46 ║
║ │ 125│ 9.0│ 14.0│ 4.6│ 22.02 │ 327.48│ 36.00│ 3.86│ 519.57│ 4.86│ 135.38│ 28.14│ 2.48│ -192.10│ 3.40 │ 17.29 ║
║ │ 125│ 10.0│ 14.0│ 4.6│ 24.33 │ 359.82│ 39.74│ 3.85│ 571.04│ 4.84│ 148.59│ 30.50│ 2.47│ -211.22│ 3.44 │ 19.10 ║
║ │ 125│ 12.0│ 14.0│ 4.6│ 28.89 │ 422.23│ 47.06│ 3.82│ 670.02│ 4.82│ 174.43│ 34.97│ 2.46│ -247.80│ 3.53 │ 22.68 ║
║ │ 125│ 14.0│ 14.0│ 4.6│ 33.37 │ 481.76│ 54.17│ 3.80│ 763.90│ 4.79│ 199.62│ 39.14│ 2.45│ -282.14│ 3.61 │ 26.20 ║
║ │ 125│ 16.0│ 14.0│ 4.6│ 37.77 │ 538.56│ 61.09│ 3.78│ 852.84│ 4.75│ 224.29│ 43.06│ 2.44│ -314.27│ 3.68 │ 29.65 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 14.0 │ 140│ 9.0│ 14.0│ 4.6│ 24.72 │ 465.72│ 45.55│ 4.34│ 739. 42│ 5.47│ 192.03│ 35.96│ 2.79│ -273.70│ 3.78 │ 19.41 ║
║ │ 140│ 10.0│ 14.0│ 4.6│ 27.33 │ 512.29│ 50.32│ 4.33│ 813.62│ 5.46│ 210.96│ 39.06│ 2.78│ -301.33│ 3.82 │ 21.45 ║
║ │ 140│ 12.0│ 14.0│ 4.6│ 32.49 │ 602.49│ 59.66│ 4.31│ 956.98│ 5.43│ 248.01│ 44.94│ 2.76│ -354.48│ 3.90 │ 25.50 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 15.0 │ 150│ 10.0│ 14.0│ 4.6│ 29.33 │ 634.76│ 58.07│ 4.65│ 1008.60│ 5.86│ 260.97│ 45.35│ 2.98│ -373.80│ 4.07 │ 23.02 ║
║ │ 150│ 12.0│ 14.0│ 4.6│ 34.89 │ 747.48│ 68.90│ 4.63│ 1187.90│ 5.83│ 307.09│ 52.30│ 2.97│ -440.39│ 4.15 │ 27.39 ║
║ │ 150│ 15.0│ 14.0│ 4.6│ 43.08 │ 908.38│ 84.66│ 4.59│ 1442.60│ 5.79│ 374.17│ 61.96│ 2.95│ -534.21│ 4.27 │ 33.82 ║
║ │ 150│ 18.0│ 14.0│ 4.6│ 51.09 │ 1060.10│ 99.86│ 4.55│ 1680.90│ 5.74│ 439.24│ 70.83│ 2.93│ -620.84│ 4.38 │ 40.11 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 16.
42│ 5.47│ 192.03│ 35.96│ 2.79│ -273.70│ 3.78 │ 19.41 ║
║ │ 140│ 10.0│ 14.0│ 4.6│ 27.33 │ 512.29│ 50.32│ 4.33│ 813.62│ 5.46│ 210.96│ 39.06│ 2.78│ -301.33│ 3.82 │ 21.45 ║
║ │ 140│ 12.0│ 14.0│ 4.6│ 32.49 │ 602.49│ 59.66│ 4.31│ 956.98│ 5.43│ 248.01│ 44.94│ 2.76│ -354.48│ 3.90 │ 25.50 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 15.0 │ 150│ 10.0│ 14.0│ 4.6│ 29.33 │ 634.76│ 58.07│ 4.65│ 1008.60│ 5.86│ 260.97│ 45.35│ 2.98│ -373.80│ 4.07 │ 23.02 ║
║ │ 150│ 12.0│ 14.0│ 4.6│ 34.89 │ 747.48│ 68.90│ 4.63│ 1187.90│ 5.83│ 307.09│ 52.30│ 2.97│ -440.39│ 4.15 │ 27.39 ║
║ │ 150│ 15.0│ 14.0│ 4.6│ 43.08 │ 908.38│ 84.66│ 4.59│ 1442.60│ 5.79│ 374.17│ 61.96│ 2.95│ -534.21│ 4.27 │ 33.82 ║
║ │ 150│ 18.0│ 14.0│ 4.6│ 51.09 │ 1060.10│ 99.86│ 4.55│ 1680.90│ 5.74│ 439.24│ 70.83│ 2.93│ -620.84│ 4.38 │ 40.11 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 16. 0 │ 160│ 10.0│ 16.0│ 5.3│ 31.43 │ 774.24│ 66.19│ 4.96│ 1229.10│ 6.25│ 319.38│ 52.48│ 3.19│ -454.86│ 4.30 │ 24.67 ║
║ │ 160│ 11.0│ 16.0│ 5.3│ 34.42 │ 844.21│ 72.44│ 4.95│ 1340.70│ 6.24│ 347.77│ 56.58│ 3.18│ -496.45│ 4.35 │ 27.02 ║
║ │ 160│ 12.0│ 16.0│ 5.3│ 37.39 │ 912.89│ 78.62│ 4.94│ 1450.00│ 6.23│ 375.78│ 60.55│ 3.17│ -537.11│ 4.39 │ 29.35 ║
║ │ 160│ 14.0│ 16.0│ 5.3│ 43.27 │ 1046.50│ 90.77│ 4.92│ 1662.10│ 6.20│ 430.81│ 68.14│ 3.15│ -615.66│ 4.47 │ 33.97 ║
║ │ 160│ 16.0│ 16.0│ 5.3│ 49.07 │ 1175.20│ 102.64│ 4.89│ 1865.70│ 6.17│ 484.64│ 75.32│ 3.14│ -690.54│ 4.55 │ 38.52 ║
║ │ 160│ 18.0│ 16.0│ 5.3│ 54.79 │ 1299.20│ 114.24│ 4.87│ 2061.00│ 6.13│ 537.46│ 82.13│ 3.13│ -761.79│ 4.63 │ 43.01 ║
║ │ 160│ 20.0│ 16.0│ 5.3│ 60.43 │ 1418.80│ 125.60│ 4.85│ 2248.30│ 6.10│ 589.43│ 88.61│ 3.12│ -829.41│ 4.70 │ 47.44 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Сотамент горячекатаных равнополочных уголков по ГОСТ 8509-93
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 18.
0 │ 160│ 10.0│ 16.0│ 5.3│ 31.43 │ 774.24│ 66.19│ 4.96│ 1229.10│ 6.25│ 319.38│ 52.48│ 3.19│ -454.86│ 4.30 │ 24.67 ║
║ │ 160│ 11.0│ 16.0│ 5.3│ 34.42 │ 844.21│ 72.44│ 4.95│ 1340.70│ 6.24│ 347.77│ 56.58│ 3.18│ -496.45│ 4.35 │ 27.02 ║
║ │ 160│ 12.0│ 16.0│ 5.3│ 37.39 │ 912.89│ 78.62│ 4.94│ 1450.00│ 6.23│ 375.78│ 60.55│ 3.17│ -537.11│ 4.39 │ 29.35 ║
║ │ 160│ 14.0│ 16.0│ 5.3│ 43.27 │ 1046.50│ 90.77│ 4.92│ 1662.10│ 6.20│ 430.81│ 68.14│ 3.15│ -615.66│ 4.47 │ 33.97 ║
║ │ 160│ 16.0│ 16.0│ 5.3│ 49.07 │ 1175.20│ 102.64│ 4.89│ 1865.70│ 6.17│ 484.64│ 75.32│ 3.14│ -690.54│ 4.55 │ 38.52 ║
║ │ 160│ 18.0│ 16.0│ 5.3│ 54.79 │ 1299.20│ 114.24│ 4.87│ 2061.00│ 6.13│ 537.46│ 82.13│ 3.13│ -761.79│ 4.63 │ 43.01 ║
║ │ 160│ 20.0│ 16.0│ 5.3│ 60.43 │ 1418.80│ 125.60│ 4.85│ 2248.30│ 6.10│ 589.43│ 88.61│ 3.12│ -829.41│ 4.70 │ 47.44 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Сотамент горячекатаных равнополочных уголков по ГОСТ 8509-93
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 18. 0 │ 180│ 11.0│ 16.0│ 5.3│ 38.82 │ 1216.40│ 92.47│ 5.60│ 1933.10│ 7.06│ 499.78│ 72.94│ 3.59│ -716.66│ 4.84 │ 30.47 ║
║ │ 180│ 12.0│ 16.0│ 5.3│ 42.19 │ 1316.60│ 100.41│ 5.59│ 2092.80│ 7.04│ 540.45│ 78.19│ 3.58│ -776.16│ 4.89 │ 33.12 ║
║ │ 180│ 15.0│ 16.0│ 5.3│ 52.18 │ 1607.40│ 123.74│ 5.55│ 2555.00│ 7.00│ 659.73│ 93.11│ 3.56│ -947.63│ 5.01 │ 40.96 ║
║ │ 180│ 18.0│ 16.0│ 5.3│ 61.99 │ 1884.10│ 146.36│ 5.51│ 2992.70│ 6.95│ 775.44│ 106.94│ 3.54│-1108.60│ 5.13 │ 48.66 ║
║ │ 180│ 20.0│ 16.0│ 5.3│ 68.43 │ 2061.10│ 161.07│ 5.49│ 3271.30│ 6.91│ 850.92│ 115.62│ 3.53│-1210.20│ 5.20 │ 53.72 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 20.0 │ 200│ 12.0│ 18.0│ 6.0│ 47.10 │ 1822.80│ 124.61│ 6.22│ 2896.20│ 7.84│ 749.40│ 98.64│ 3.99│-1073.40│ 5.37 │ 36.97 ║
║ │ 200│ 13.0│ 18.0│ 6.0│ 50.85 │ 1960.80│ 134.44│ 6.21│ 3116.
0 │ 180│ 11.0│ 16.0│ 5.3│ 38.82 │ 1216.40│ 92.47│ 5.60│ 1933.10│ 7.06│ 499.78│ 72.94│ 3.59│ -716.66│ 4.84 │ 30.47 ║
║ │ 180│ 12.0│ 16.0│ 5.3│ 42.19 │ 1316.60│ 100.41│ 5.59│ 2092.80│ 7.04│ 540.45│ 78.19│ 3.58│ -776.16│ 4.89 │ 33.12 ║
║ │ 180│ 15.0│ 16.0│ 5.3│ 52.18 │ 1607.40│ 123.74│ 5.55│ 2555.00│ 7.00│ 659.73│ 93.11│ 3.56│ -947.63│ 5.01 │ 40.96 ║
║ │ 180│ 18.0│ 16.0│ 5.3│ 61.99 │ 1884.10│ 146.36│ 5.51│ 2992.70│ 6.95│ 775.44│ 106.94│ 3.54│-1108.60│ 5.13 │ 48.66 ║
║ │ 180│ 20.0│ 16.0│ 5.3│ 68.43 │ 2061.10│ 161.07│ 5.49│ 3271.30│ 6.91│ 850.92│ 115.62│ 3.53│-1210.20│ 5.20 │ 53.72 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 20.0 │ 200│ 12.0│ 18.0│ 6.0│ 47.10 │ 1822.80│ 124.61│ 6.22│ 2896.20│ 7.84│ 749.40│ 98.64│ 3.99│-1073.40│ 5.37 │ 36.97 ║
║ │ 200│ 13.0│ 18.0│ 6.0│ 50.85 │ 1960.80│ 134.44│ 6.21│ 3116. 20│ 7.83│ 805.35│ 105.16│ 3.98│-1155.40│ 5.42 │ 39.92 ║
║ │ 200│ 14.0│ 18.0│ 6.0│ 54.58 │ 2096.70│ 144.17│ 6.20│ 3332.70│ 7.81│ 860.71│ 111.53│ 3.97│-1236.00│ 5.46 │ 42.85 ║
║ │ 200│ 16.0│ 18.0│ 6.0│ 61.98 │ 2362.60│ 163.37│ 6.17│ 3755.40│ 7.78│ 969.74│ 123.80│ 3.96│-1392.80│ 5.54 │ 48.65 ║
║ │ 200│ 18.0│ 18.0│ 6.0│ 69.30 │ 2620.60│ 182.22│ 6.15│ 4164.50│ 7.75│ 1076.70│ 135.52│ 3.94│-1543.90│ 5.62 │ 54.40 ║
║ │ 200│ 20.0│ 18.0│ 6.0│ 76.54 │ 2871.20│ 200.73│ 6.13│ 4560.40│ 7.72│ 1181.90│ 146.72│ 3.93│-1689.30│ 5.70 │ 60.08 ║
║ │ 200│ 24.0│ 18.0│ 6.0│ 90.78 │ 3350.70│ 236.77│ 6.08│ 5313.60│ 7.65│ 1387.70│ 167.78│ 3.91│-1962.90│ 5.85 │ 71.26 ║
║ │ 200│ 25.0│ 18.0│ 6.0│ 94.29 │ 3466.20│ 245.59│ 6.06│ 5494.00│ 7.63│ 1438.40│ 172.80│ 3.91│-2027.80│ 5.89 │ 74.02 ║
║ │ 200│ 30.0│ 18.0│ 6.0│ 111.54 │ 4019.60│ 288.57│ 6.00│ 6351.00│ 7.55│ 1688.20│ 196.64│ 3.89│-2331.40│ 6.07 │ 87.56 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 22.
20│ 7.83│ 805.35│ 105.16│ 3.98│-1155.40│ 5.42 │ 39.92 ║
║ │ 200│ 14.0│ 18.0│ 6.0│ 54.58 │ 2096.70│ 144.17│ 6.20│ 3332.70│ 7.81│ 860.71│ 111.53│ 3.97│-1236.00│ 5.46 │ 42.85 ║
║ │ 200│ 16.0│ 18.0│ 6.0│ 61.98 │ 2362.60│ 163.37│ 6.17│ 3755.40│ 7.78│ 969.74│ 123.80│ 3.96│-1392.80│ 5.54 │ 48.65 ║
║ │ 200│ 18.0│ 18.0│ 6.0│ 69.30 │ 2620.60│ 182.22│ 6.15│ 4164.50│ 7.75│ 1076.70│ 135.52│ 3.94│-1543.90│ 5.62 │ 54.40 ║
║ │ 200│ 20.0│ 18.0│ 6.0│ 76.54 │ 2871.20│ 200.73│ 6.13│ 4560.40│ 7.72│ 1181.90│ 146.72│ 3.93│-1689.30│ 5.70 │ 60.08 ║
║ │ 200│ 24.0│ 18.0│ 6.0│ 90.78 │ 3350.70│ 236.77│ 6.08│ 5313.60│ 7.65│ 1387.70│ 167.78│ 3.91│-1962.90│ 5.85 │ 71.26 ║
║ │ 200│ 25.0│ 18.0│ 6.0│ 94.29 │ 3466.20│ 245.59│ 6.06│ 5494.00│ 7.63│ 1438.40│ 172.80│ 3.91│-2027.80│ 5.89 │ 74.02 ║
║ │ 200│ 30.0│ 18.0│ 6.0│ 111.54 │ 4019.60│ 288.57│ 6.00│ 6351.00│ 7.55│ 1688.20│ 196.64│ 3.89│-2331.40│ 6.07 │ 87.56 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 22. 0 │ 220│ 14.0│ 21.0│ 7.0│ 60.38 │ 2814.40│ 175.18│ 6.83│ 4470.20│ 8.61│ 1158.60│ 138.03│ 4.38│-1655.80│ 5.93 │ 47.40 ║
║ │ 220│ 16.0│ 21.0│ 7.0│ 68.58 │ 3175.40│ 198.71│ 6.80│ 5045.40│ 8.58│ 1305.50│ 153.35│ 4.36│-1869.90│ 6.02 │ 53.83 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 25.0 │ 250│ 16.0│ 24.0│ 8.0│ 78.40 │ 4717.10│ 258.43│ 7.76│ 7492.10│ 9.78│ 1942.10│ 203.53│ 4.98│-2775.00│ 6.75 │ 61.55 ║
║ │ 250│ 18.0│ 24.0│ 8.0│ 87.72 │ 5247.20│ 288.82│ 7.73│ 8336.70│ 9.75│ 2157.80│ 223.32│ 4.96│-3089.50│ 6.83 │ 68.86 ║
║ │ 250│ 20.0│ 24.0│ 8.0│ 96.96 │ 5764.90│ 318.76│ 7.71│ 9159.70│ 9.72│ 2370.00│ 242.35│ 4.94│-3394.90│ 6.92 │ 76.11 ║
║ │ 250│ 22.0│ 24.0│ 8.0│ 106.12 │ 6270.30│ 348.26│ 7.69│ 9961.60│ 9.69│ 2579.00│ 260.69│ 4.93│-3691.30│ 7.00 │ 83.31 ║
║ │ 250│ 25.0│ 24.0│ 8.0│ 119.71 │ 7006.40│ 391.72│ 7.65│11126.
0 │ 220│ 14.0│ 21.0│ 7.0│ 60.38 │ 2814.40│ 175.18│ 6.83│ 4470.20│ 8.61│ 1158.60│ 138.03│ 4.38│-1655.80│ 5.93 │ 47.40 ║
║ │ 220│ 16.0│ 21.0│ 7.0│ 68.58 │ 3175.40│ 198.71│ 6.80│ 5045.40│ 8.58│ 1305.50│ 153.35│ 4.36│-1869.90│ 6.02 │ 53.83 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 25.0 │ 250│ 16.0│ 24.0│ 8.0│ 78.40 │ 4717.10│ 258.43│ 7.76│ 7492.10│ 9.78│ 1942.10│ 203.53│ 4.98│-2775.00│ 6.75 │ 61.55 ║
║ │ 250│ 18.0│ 24.0│ 8.0│ 87.72 │ 5247.20│ 288.82│ 7.73│ 8336.70│ 9.75│ 2157.80│ 223.32│ 4.96│-3089.50│ 6.83 │ 68.86 ║
║ │ 250│ 20.0│ 24.0│ 8.0│ 96.96 │ 5764.90│ 318.76│ 7.71│ 9159.70│ 9.72│ 2370.00│ 242.35│ 4.94│-3394.90│ 6.92 │ 76.11 ║
║ │ 250│ 22.0│ 24.0│ 8.0│ 106.12 │ 6270.30│ 348.26│ 7.69│ 9961.60│ 9.69│ 2579.00│ 260.69│ 4.93│-3691.30│ 7.00 │ 83.31 ║
║ │ 250│ 25.0│ 24.0│ 8.0│ 119.71 │ 7006.40│ 391.72│ 7.65│11126. 00│ 9.64│ 2887.30│ 287.00│ 4.91│-4119.10│ 7.11 │ 93.97 ║
║ │ 250│ 28.0│ 24.0│ 8.0│ 133.12 │ 7716.90│ 434.25│ 7.61│12244.00│ 9.59│ 3189.90│ 312.01│ 4.90│-4527.00│ 7.23 │ 104.50 ║
║ │ 250│ 30.0│ 24.0│ 8.0│ 141.96 │ 8176.80│ 462.11│ 7.59│12965.00│ 9.56│ 3389.00│ 328.03│ 4.89│-4787.80│ 7.30 │ 111.44 ║
║ │ 250│ 35.0│ 24.0│ 8.0│ 163.71 │ 9281.00│ 530.11│ 7.53│14683.00│ 9.47│ 3879.30│ 366.13│ 4.87│-5401.70│ 7.49 │ 128.51 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
00│ 9.64│ 2887.30│ 287.00│ 4.91│-4119.10│ 7.11 │ 93.97 ║
║ │ 250│ 28.0│ 24.0│ 8.0│ 133.12 │ 7716.90│ 434.25│ 7.61│12244.00│ 9.59│ 3189.90│ 312.01│ 4.90│-4527.00│ 7.23 │ 104.50 ║
║ │ 250│ 30.0│ 24.0│ 8.0│ 141.96 │ 8176.80│ 462.11│ 7.59│12965.00│ 9.56│ 3389.00│ 328.03│ 4.89│-4787.80│ 7.30 │ 111.44 ║
║ │ 250│ 35.0│ 24.0│ 8.0│ 163.71 │ 9281.00│ 530.11│ 7.53│14683.00│ 9.47│ 3879.30│ 366.13│ 4.87│-5401.70│ 7.49 │ 128.51 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Момент инерции – определение, формула, примеры, единицы измерения, уравнения
Содержание
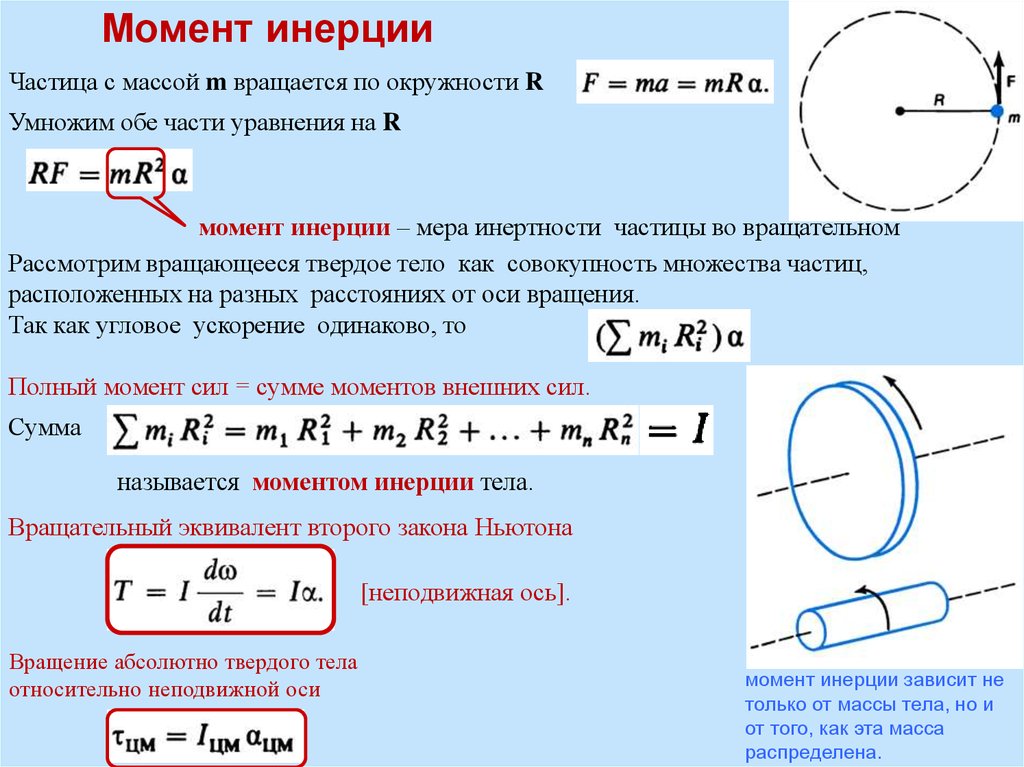
Момент инерции Определение Момент инерции твердого тела, также известный как массовый момент инерции, угловая масса, секунда Момент массы или, точнее, инерция вращения — это величина, которая определяет крутящий момент, необходимый для желаемого углового ускорения относительно оси вращения, точно так же, как масса определяет силу, необходимую для желаемого ускорения.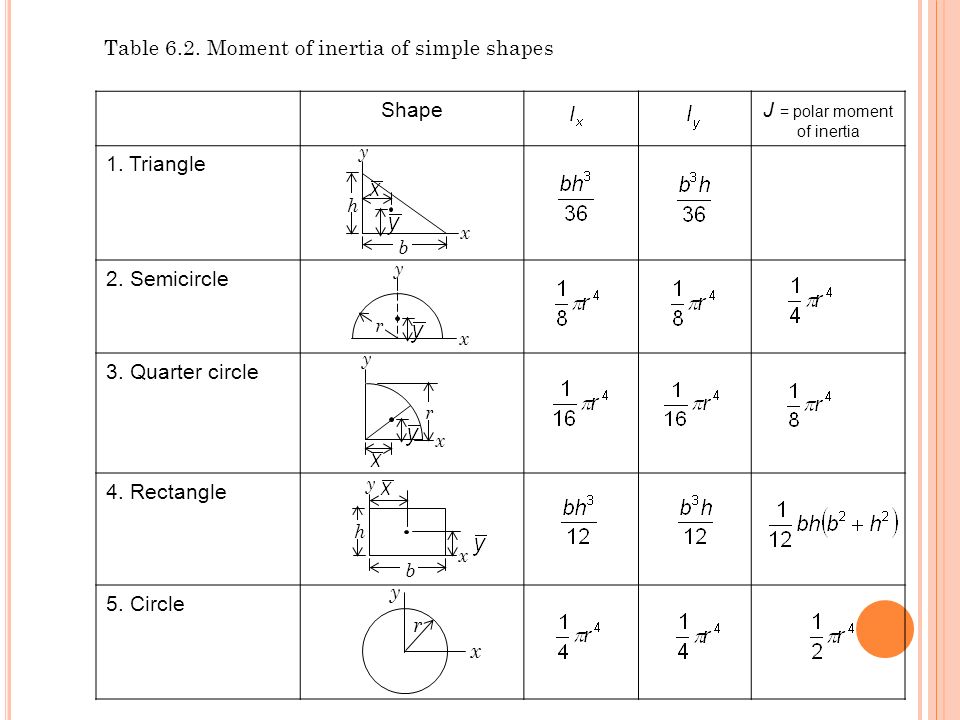 Он зависит от распределения массы тела и выбранной оси, при этом более высокие моменты требуют большего крутящего момента, чтобы повлиять на скорость вращения. Это расширенное свойство, момент инерции для точечной массы — это просто произведение массы на квадрат перпендикулярного расстояния до оси вращения. Момент инерции жесткой составной системы равен сумме моментов инерции составляющих ее подсистем (отнесенных относительно одной оси). Второй момент массы по отношению к расстоянию от оси является самым простым определением.
Он зависит от распределения массы тела и выбранной оси, при этом более высокие моменты требуют большего крутящего момента, чтобы повлиять на скорость вращения. Это расширенное свойство, момент инерции для точечной массы — это просто произведение массы на квадрат перпендикулярного расстояния до оси вращения. Момент инерции жесткой составной системы равен сумме моментов инерции составляющих ее подсистем (отнесенных относительно одной оси). Второй момент массы по отношению к расстоянию от оси является самым простым определением.
Крутящий момент должен быть приложен к телу, которое может свободно вращаться вокруг оси, чтобы изменить его угловой момент. Момент инерции тела пропорционален величине крутящего момента, необходимого для создания любого заданного углового ускорения (скорости изменения угловой скорости).
Единица измерения момента инерции Моменты инерции измеряются в килограммах на квадратный метр (кгм2) в единицах СИ и в фунтах-футах-секундах в квадрате (lbffts2) в имперских единицах и единицах США.
Формула момента инерции
Произведение массы сечения и квадрата расстояния между базовой осью и центром тяжести сечения является моментом инерции.
Подтягивая руки, вращающиеся фигуристы могут минимизировать свой момент инерции, позволяя им вращаться быстрее благодаря сохранению углового момента.
Момент инерции демонстрируется в этом видео эксперимента с вращающимся стулом. Когда вращающийся профессор тянет руки, его момент инерции падает, а его угловая скорость увеличивается для сохранения углового момента.
Отношение чистого углового момента системы L к ее угловой скорости ω вокруг большой оси также известно как момент инерции
Если угловой момент системы остается постоянным, угловая скорость должна увеличиваться по мере уменьшения момента инерции. Чтобы быстрее вращаться, фигуристы вытягивают вытянутые руки, а ныряльщики сгибают тело во время прыжка.
В общем случае эффективный радиус k может быть определен для объекта массой м , который зависит от конкретной оси вращения и имеет такое значение, что его момент инерции вокруг оси равен
Радиус вращение вокруг оси известно как k .
На момент инерции твердого тела влияет множество факторов. Момент инерции определяется положением оси вращения движения, расстоянием между различными точечными массами от этой оси вращения и плотностью материала или предмета, который нужно вращать вдоль фиксированной оси. Чем больше вклад массовых точек в момент инерции системы, тем они шире друг от друга. У вас будет больше инерции, если у вас будет больше массовых точек.
На момент инерции тела влияют следующие факторы:
i) Масса тела.
ii) Размер и форма тела.
iii) Распределение массы вокруг оси вращения
iv) Положение и ориентация оси вращения относительно корпуса.
Момент инерции Примеры Момент инерции Пример 1: Простой маятник
инерция простого маятника. Было обнаружено, что это произведение массы частицы m и квадрата ее расстояния r от оси вращения базового маятника, то есть
| I = m r 2 |
Момент инерции Пример 2: МАХОВИК автомобиля
Маховик представляет собой большую массу, расположенную на коленчатом валу двигателя. Момент инерции маховика чрезвычайно велик, что способствует накоплению энергии.
Момент инерции маховика чрезвычайно велик, что способствует накоплению энергии.
В отличие от сплошного вала, полый вал передает большую мощность (оба имеют одинаковую массу). По сравнению со сплошным валом полый вал имеет более высокий момент инерции.
Момент инерции Пример 4: СудостроениеВ судостроении момент инерции оказывает значительное влияние. Корабль может утонуть, если он качается, но он никогда не утонет, если его кинет.
Момент инерции на хиндиएक कठो शा की जड़ता का क्षण जिसे जड़त जड़ता का द्रव्यम क क कोणीय कोणीय कोणीय कोणीय कोणीय कोणीय कोणीय ूप ूप ूप ूप ूप ूप ूपfroूप य ूप ूपvenन य दvenन य दvenन य दvro ूप क दvenन य दvenन य दvenन य दvenन य दvenन य द दvenन य द दvenन य द दvenन य द दvenन य द दvenन य द द दvenन ूप द द द द chy कठो द द द द द द द द द द जिसे जिसे जिसे जिसे जिसे द द द द जिसे जिसे जिसे जिसे जिसे जिसे की कठो जिसे, मात्रा है जो घू घूर्णी अक्ष के बारे में वांछित कोणीय तшить , वैसे ही द्रव्यमान वांछित त्वरण के आवश आवश्यक बल नि नि000 यह श выполнительный के के पैम पैम000 यह एक विस्तारित संपत्ति है, एक द द्रव्यमान के जड़त जड़ता का क्षण, घूर्णन अक्ष के दू के व वर्ग क द्enन समय। दू दू के व व क द Вивра अक। दू दू दू दू दू दू दू दू दू दू दू दू दू दू दू दू।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।।। एक कठोर समग्र प्रणाली की जड़त क000 किसी अक्ष से दूरी के संबंध में दшить
टोक़ एक श शा को आपू आपूर्ति की ज च च जो अपने कोणीय गति को संशोधित क क के लिए अक अक के च ओ घूमने लिए स स के अक अक के च च ओ के लिए स ने है।। के च च के श выполнительный
जड़ता का क्षण: इकाई
जड़ता क्षणों को एसआई इकाइयों में किलोग्राम मीटाइयों वर्ग (кгм2) और श औ выполнительный
जड़ता का क्षण: सूत्र
खंड द द्रव्यमान का गुणनफल औरать संद्ष औान क औ औ संद000
.
. जब कत|
किसी निक|
Уравнения момента инерции на хинди
| I = L / ω |
यदि किसी निक| तेजी से के लिए फिग, फिगर स्केटर्स अपनी फैली हुई भुज भुज को हैं हैं, जबकि गोत गोत गोत गोत गोत लग के दौ दौ अपने श श टक की स में घुम हैं हैं। श को की स में घुम हैं हैं।।।। हैं हैं।।।।।।।।।।।।।।।।।।।।।।। हैं हैं
सामान्य तौर पर, एक प्रभावी त्रिज्या k को द्रव्यमान m की एक वस्तु के लिए परिभाषित किया जा सकता है जो रोटेशन के एक विशेष अक्ष पर निर्भर है और इसका एक मूल्य है जैसे कि अक्ष के चारों ओर जड़ता का क्षण बराबर होता है
अक्ष के चारों ओरिकरिक्रमण की त्रिज्या k के रूप में जानी जाती है।।।।।
जड़ता का क्षण: कारक
एक कठोर शरीा जड़ता का क्षण गति के 000 धु धु धु की स्थिति ोटेशन उस अक अक अक से विभिन्न बिंदु द दtra द बीच दू दू दू औ औ निश निश अक्चित अक स य य य य य य्चित अक वस्चित अक्चित अकáить य वस वस्चित chytra स chytrou सिस्टम की जड़ता के क्षण में बड़े पैमाने पर योगदान जितना बड़ा होगा, वे उतने ही वшить व होंगे होंगे।।।।।।।।। यदि आपके पास द दшить
निम्नलिखित कारक शा की जड़ता के क्षण प प похоже
ii) शरीर का आकार और आकार।
iii) रोटेशन की धु выполнительный
Связанный пост:
- Магнитный поток — определение, плотность, формула, единица СИ
- Полная форма RRB NTPC для железных дорог
- Реакция электролиза Кольбе – определение, механизм
- Полная форма PCS — провинциальная государственная служба
- Законы движения Ньютона — первое, второе, третье, приложения
Момент инерции: часто задаваемые вопросы
Что такое момент инерции?
Момент инерции объекта — это расчетная мера твердого тела, вращающегося вокруг фиксированной оси: он измеряет, насколько сложно изменить скорость вращения объекта.
Как рассчитать момент инерции?
Суммирование или интегрирование каждой «части массы», составляющей объект, умноженное на квадрат расстояния каждой «части массы» до оси, дает моменты инерции.
В чем разница между инерцией и моментом инерции?
Сопротивление угловому ускорению известно как момент инерции (т.е. распределение массы). Инерция — это атрибут линейной массы, который описывает, насколько хорошо объект сопротивляется изменению движения, вызванному силой, или насколько он массивен.
Каков момент инерции диска?
Размерность моментов инерции масс измеряется в (длина массы3). Важно не перепутать второй момент площади с моментом, который используется в расчетах луча. Массовый момент инерции, также известный как вращательная инерция или угловая масса, является термином, используемым для описания вращательной инерции.
Как объяснить инерцию очень простыми словами?
Склонность тела сопротивляться изменению движения или покоя называется инерцией.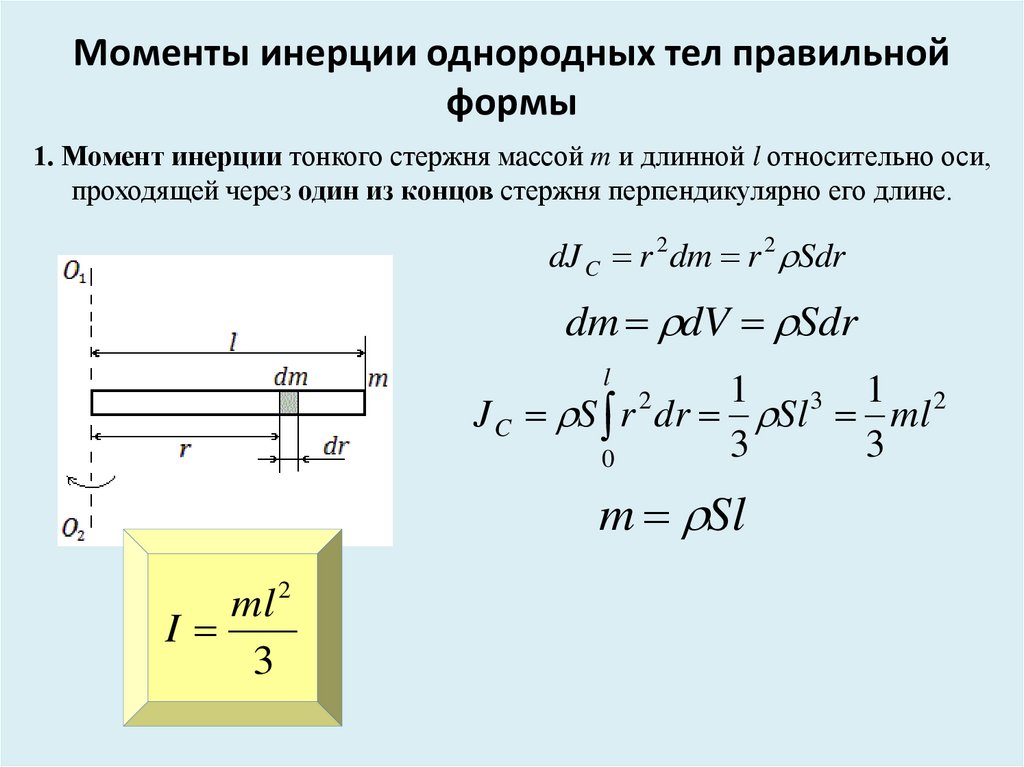 Когда вы полностью останавливаетесь в транспортном средстве, вы, как правило, дергаетесь вперед. Когда автомобиль начнет двигаться, вы точно так же дернетесь назад.
Когда вы полностью останавливаетесь в транспортном средстве, вы, как правило, дергаетесь вперед. Когда автомобиль начнет двигаться, вы точно так же дернетесь назад.
Делиться заботой!
15
акции
Моменты площади
Первый и второй момент площади
Момент в физике
В физике момент (или крутящий момент) равен силы, умноженной на расстояние :
Но есть и другие Моменты, читайте дальше!
Первый момент Зоны
Первый момент площади равен площадь, умноженная на расстояние (до некоторой опорной линии):
Первый момент площади = A x d
Для этого простого случая мы можем умножить всю площадь на расстояние (от ее середины до опорной линии).
Пример:
Площадь 20 мм x 10 мм = 200 мм 2
Первый момент площади (относительно нижней линии) = 200 мм 2 x 25 мм = 9000 мм 3
03 (Обратите внимание, что единицей измерения является мм 3 , а не объем!)Одним из его замечательных применений является нахождение центроида, который представляет собой среднее положение всех точек объекта:
Плоская фигура, вырезанная из куска картона, будет идеально балансировать по центру тяжести.
Чтобы найти расстояние до центра тяжести от любой оси, мы делим первый момент площади на общую площадь:
Расстояние до центра тяжести = Первый момент площади Общая площадь
Когда мы делаем это как для оси x, так и для оси y, мы получаем центр тяжести.
Мы можем оценить , где центроид использует квадраты:
Второй момент площади
Для второго момента площади мы умножаем площадь на расстояние в квадрате :
(нужно бесконечно много крошечных квадратов)
Но будьте осторожны! Нам нужно умножить каждую крошечную часть площади на квадрат расстояния, потому что площадь, находящаяся дальше, имеет больший эффект (из-за возведения в квадрат расстояния).
Называется «Вторым» моментом, потому что мы возводим в квадрат расстояние «x 2 »
Его также называют моментом инерции площади .
Мы можем оценить второй момент, используя квадраты, но это очень неточно:
Мы можем использовать ось x или y в качестве опорной линии, или мы можем использовать центроид для опорной линии . Вы можете попробовать этот вариант выше.
Вы можете попробовать этот вариант выше.
Обозначение : Символ представляет собой букву «I», за которой следует маленькая буква «x» или «y» для базовой оси.
I x относительно оси x (и мы используем y расстояния, умноженные на площадь)
I y относительно оси y (и мы используем x расстояния, площадь) )
Буква I относится к Инерция в «момент инерции площади».
По возможности используйте точную формулу, например:
I x = шв 3 3
я у = б 3 ч 3
I x = шв 3 12
I у = б 3 ч 12
I x = шв 3 12
I Y = B 3 H+B 2 HA+BHA 2 12
I x = πr 4 9304303030430303030303030303049 4 = .


 Из полученных результатов можно понять, что по мере увеличения расстояния от координатной оси статический момент площади сечения увеличивается на величину «e».
Из полученных результатов можно понять, что по мере увеличения расстояния от координатной оси статический момент площади сечения увеличивается на величину «e».
 com/russian/kmbp_2/rec_2_02.htm)
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 2.
com/russian/kmbp_2/rec_2_02.htm)
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 2. 0 │ 20│ 3.0│ 3.5│ 1.2│ 1.13 │ 0.40│ 0.28│ 0.59│ 0.63│ 0.75│ 0.17│ 0.20│ 0.39│ -0.23│ 0.60 │ 0.89 ║
║ │ 20│ 4.0│ 3.5│ 1.2│ 1.46 │ 0.50│ 0.37│ 0.58│ 0.78│ 0.73│ 0.22│ 0.24│ 0.38│ -0.28│ 0.64 │ 1.15 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 2.5 │ 25│ 3.0│ 3.5│ 1.2│ 1.43 │ 0.81│ 0.46│ 0.75│ 1.29│ 0.95│ 0.34│ 0.33│ 0.49│ -0.47│ 0.73 │ 1.12 ║
║ │ 25│ 4.0│ 3.5│ 1.2│ 1.86 │ 1.03│ 0.59│ 0.74│ 1.62│ 0.93│ 0.44│ 0.40│ 0.48│ -0.59│ 0.76 │ 1.46 ║
║ │ 25│ 5.0│ 3.5│ 1.2│ 2.27 │ 1.22│ 0.72│ 0.73│ 1.91│ 0.92│ 0.53│ 0.47│ 0.48│ -0.69│ 0.80 │ 1.78 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 2.8 │ 28│ 3.0│ 4.0│ 1.3│ 1.62 │ 1.17│ 0.58│ 0.85│ 1.
0 │ 20│ 3.0│ 3.5│ 1.2│ 1.13 │ 0.40│ 0.28│ 0.59│ 0.63│ 0.75│ 0.17│ 0.20│ 0.39│ -0.23│ 0.60 │ 0.89 ║
║ │ 20│ 4.0│ 3.5│ 1.2│ 1.46 │ 0.50│ 0.37│ 0.58│ 0.78│ 0.73│ 0.22│ 0.24│ 0.38│ -0.28│ 0.64 │ 1.15 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 2.5 │ 25│ 3.0│ 3.5│ 1.2│ 1.43 │ 0.81│ 0.46│ 0.75│ 1.29│ 0.95│ 0.34│ 0.33│ 0.49│ -0.47│ 0.73 │ 1.12 ║
║ │ 25│ 4.0│ 3.5│ 1.2│ 1.86 │ 1.03│ 0.59│ 0.74│ 1.62│ 0.93│ 0.44│ 0.40│ 0.48│ -0.59│ 0.76 │ 1.46 ║
║ │ 25│ 5.0│ 3.5│ 1.2│ 2.27 │ 1.22│ 0.72│ 0.73│ 1.91│ 0.92│ 0.53│ 0.47│ 0.48│ -0.69│ 0.80 │ 1.78 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 2.8 │ 28│ 3.0│ 4.0│ 1.3│ 1.62 │ 1.17│ 0.58│ 0.85│ 1.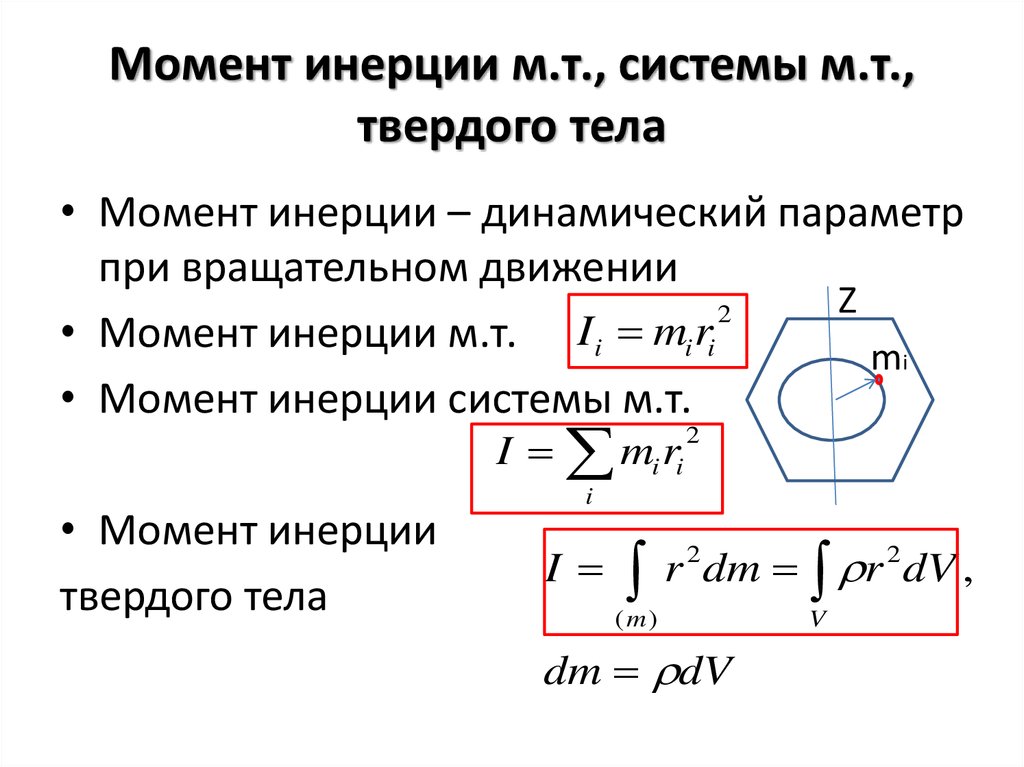 84│ 1.07│ 0.48│ 0.43│ 0.55│ -0.68│ 0.80 │ 1.27 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 3.0 │ 30│ 3.0│ 4.0│ 1.3│ 1.74 │ 1.45│ 0.67│ 0.91│ 2.29│ 1.15│ 0.60│ 0.50│ 0.59│ -0.85│ 0.85 │ 1.36 ║
║ │ 30│ 4.0│ 4.0│ 1.3│ 2.27 │ 1.84│ 0.87│ 0.90│ 2.92│ 1.13│ 0.77│ 0.61│ 0.58│ -1.07│ 0.89 │ 1.78 ║
║ │ 30│ 5.0│ 4.0│ 1.3│ 2.78 │ 2.21│ 1.06│ 0.89│ 3.47│ 1.12│ 0.94│ 0.72│ 0.58│ -1.27│ 0.93 │ 2.18 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 3.2 │ 32│ 3.0│ 4.5│ 1.5│ 1.86 │ 1.77│ 0.77│ 0.97│ 2.80│ 1.23│ 0.74│ 0.58│ 0.63│ -1.03│ 0.89 │ 1.46 ║
║ │ 32│ 4.0│ 4.5│ 1.5│ 2.43 │ 2.26│ 1.00│ 0.96│ 3.58│ 1.21│ 0.94│ 0.71│ 0.62│ -1.32│ 0.94 │ 1.91 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 3.
84│ 1.07│ 0.48│ 0.43│ 0.55│ -0.68│ 0.80 │ 1.27 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 3.0 │ 30│ 3.0│ 4.0│ 1.3│ 1.74 │ 1.45│ 0.67│ 0.91│ 2.29│ 1.15│ 0.60│ 0.50│ 0.59│ -0.85│ 0.85 │ 1.36 ║
║ │ 30│ 4.0│ 4.0│ 1.3│ 2.27 │ 1.84│ 0.87│ 0.90│ 2.92│ 1.13│ 0.77│ 0.61│ 0.58│ -1.07│ 0.89 │ 1.78 ║
║ │ 30│ 5.0│ 4.0│ 1.3│ 2.78 │ 2.21│ 1.06│ 0.89│ 3.47│ 1.12│ 0.94│ 0.72│ 0.58│ -1.27│ 0.93 │ 2.18 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 3.2 │ 32│ 3.0│ 4.5│ 1.5│ 1.86 │ 1.77│ 0.77│ 0.97│ 2.80│ 1.23│ 0.74│ 0.58│ 0.63│ -1.03│ 0.89 │ 1.46 ║
║ │ 32│ 4.0│ 4.5│ 1.5│ 2.43 │ 2.26│ 1.00│ 0.96│ 3.58│ 1.21│ 0.94│ 0.71│ 0.62│ -1.32│ 0.94 │ 1.91 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 3.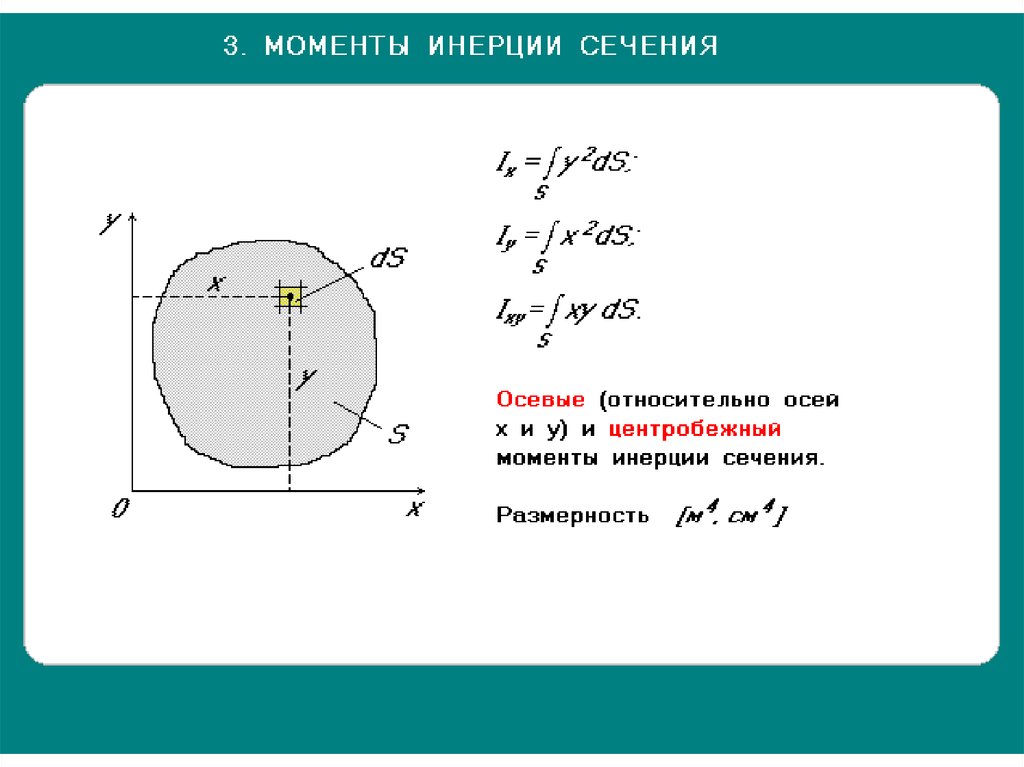 5 │ 35│ 3.0│ 4.5│ 1.5│ 2.04 │ 2.35│ 0.93│ 1.07│ 3.72│ 1.35│ 0.97│ 0.71│ 0.69│ -1.37│ 0.97 │ 1.60 ║
║ │ 35│ 4.0│ 4.5│ 1.5│ 2.67 │ 3.01│ 1.21│ 1.06│ 4.76│ 1.33│ 1.25│ 0.87│ 0.68│ -1.76│ 1.01 │ 2.10 ║
║ │ 35│ 5.0│ 4.5│ 1.5│ 3.28 │ 3.61│ 1.48│ 1.05│ 5.71│ 1.32│ 1.52│ 1.02│ 0.68│ -2.10│ 1.05 │ 2.58 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 4.0 │ 40│ 3.0│ 5.0│ 1.7│ 2.35 │ 3.55│ 1.22│ 1.23│ 5.63│ 1.55│ 1.47│ 0.96│ 0.79│ -2.08│ 1.09 │ 1.85 ║
║ │ 40│ 4.0│ 5.0│ 1.7│ 3.08 │ 4.58│ 1.60│ 1.22│ 7.26│ 1.53│ 1.90│ 1.18│ 0.78│ -2.68│ 1.13 │ 2.42 ║
║ │ 40│ 5.0│ 5.0│ 1.7│ 3.79 │ 5.53│ 1.96│ 1.21│ 8.75│ 1.52│ 2.30│ 1.39│ 0.78│ -3.23│ 1.17 │ 2.98 ║
║ │ 40│ 6.0│ 5.0│ 1.7│ 4.48 │ 6.41│ 2.30│ 1.20│ 10.
5 │ 35│ 3.0│ 4.5│ 1.5│ 2.04 │ 2.35│ 0.93│ 1.07│ 3.72│ 1.35│ 0.97│ 0.71│ 0.69│ -1.37│ 0.97 │ 1.60 ║
║ │ 35│ 4.0│ 4.5│ 1.5│ 2.67 │ 3.01│ 1.21│ 1.06│ 4.76│ 1.33│ 1.25│ 0.87│ 0.68│ -1.76│ 1.01 │ 2.10 ║
║ │ 35│ 5.0│ 4.5│ 1.5│ 3.28 │ 3.61│ 1.48│ 1.05│ 5.71│ 1.32│ 1.52│ 1.02│ 0.68│ -2.10│ 1.05 │ 2.58 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 4.0 │ 40│ 3.0│ 5.0│ 1.7│ 2.35 │ 3.55│ 1.22│ 1.23│ 5.63│ 1.55│ 1.47│ 0.96│ 0.79│ -2.08│ 1.09 │ 1.85 ║
║ │ 40│ 4.0│ 5.0│ 1.7│ 3.08 │ 4.58│ 1.60│ 1.22│ 7.26│ 1.53│ 1.90│ 1.18│ 0.78│ -2.68│ 1.13 │ 2.42 ║
║ │ 40│ 5.0│ 5.0│ 1.7│ 3.79 │ 5.53│ 1.96│ 1.21│ 8.75│ 1.52│ 2.30│ 1.39│ 0.78│ -3.23│ 1.17 │ 2.98 ║
║ │ 40│ 6.0│ 5.0│ 1.7│ 4.48 │ 6.41│ 2.30│ 1.20│ 10. 13│ 1.50│ 2.70│ 1.58│ 0.78│ -3.71│ 1.21 │ 3.52 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Сотамент горячекатаных равнополочных уголков по ГОСТ 8509-93
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 4.
13│ 1.50│ 2.70│ 1.58│ 0.78│ -3.71│ 1.21 │ 3.52 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Сотамент горячекатаных равнополочных уголков по ГОСТ 8509-93
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 4. 5 │ 45│ 3.0│ 5.0│ 1.7│ 2.65 │ 5.13│ 1.56│ 1.39│ 8.13│ 1.75│ 2.12│ 1.24│ 0.89│ -3.00│ 1.21 │ 2.08 ║
║ │ 45│ 4.0│ 5.0│ 1.7│ 3.48 │ 6.63│ 2.04│ 1.38│ 10.52│ 1.74│ 2.74│ 1.54│ 0.89│ -3.89│ 1.26 │ 2.73 ║
║ │ 45│ 5.0│ 5.0│ 1.7│ 4.29 │ 8.03│ 2.51│ 1.37│ 12.74│ 1.72│ 3.33│ 1.81│ 0.88│ -4.71│ 1.30 │ 3.37 ║
║ │ 45│ 6.0│ 5.0│ 1.7│ 5.08 │ 9.35│ 2.95│ 1.36│ 14.80│ 1.71│ 3.90│ 2.07│ 0.88│ -5.45│ 1.33 │ 3.99 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 5.0 │ 50│ 3.0│ 5.5│ 1.8│ 2.96 │ 7.11│ 1.94│ 1.55│ 11.27│ 1.95│ 2.95│ 1.56│ 1.00│ -4.16│ 1.33 │ 2.32 ║
║ │ 50│ 4.0│ 5.5│ 1.8│ 3.89 │ 9.21│ 2.54│ 1.54│ 14.63│ 1.94│ 3.80│ 1.95│ 0.99│ -5.41│ 1.38 │ 3.05 ║
║ │ 50│ 5.0│ 5.5│ 1.8│ 4.80 │ 11.20│ 3.13│ 1.53│ 17.
5 │ 45│ 3.0│ 5.0│ 1.7│ 2.65 │ 5.13│ 1.56│ 1.39│ 8.13│ 1.75│ 2.12│ 1.24│ 0.89│ -3.00│ 1.21 │ 2.08 ║
║ │ 45│ 4.0│ 5.0│ 1.7│ 3.48 │ 6.63│ 2.04│ 1.38│ 10.52│ 1.74│ 2.74│ 1.54│ 0.89│ -3.89│ 1.26 │ 2.73 ║
║ │ 45│ 5.0│ 5.0│ 1.7│ 4.29 │ 8.03│ 2.51│ 1.37│ 12.74│ 1.72│ 3.33│ 1.81│ 0.88│ -4.71│ 1.30 │ 3.37 ║
║ │ 45│ 6.0│ 5.0│ 1.7│ 5.08 │ 9.35│ 2.95│ 1.36│ 14.80│ 1.71│ 3.90│ 2.07│ 0.88│ -5.45│ 1.33 │ 3.99 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 5.0 │ 50│ 3.0│ 5.5│ 1.8│ 2.96 │ 7.11│ 1.94│ 1.55│ 11.27│ 1.95│ 2.95│ 1.56│ 1.00│ -4.16│ 1.33 │ 2.32 ║
║ │ 50│ 4.0│ 5.5│ 1.8│ 3.89 │ 9.21│ 2.54│ 1.54│ 14.63│ 1.94│ 3.80│ 1.95│ 0.99│ -5.41│ 1.38 │ 3.05 ║
║ │ 50│ 5.0│ 5.5│ 1.8│ 4.80 │ 11.20│ 3.13│ 1.53│ 17. 77│ 1.92│ 4.63│ 2.31│ 0.98│ -6.57│ 1.42 │ 3.77 ║
║ │ 50│ 6.0│ 5.5│ 1.8│ 5.69 │ 13.07│ 3.69│ 1.52│ 20.72│ 1.91│ 5.43│ 2.63│ 0.98│ -7.64│ 1.46 │ 4.47 ║
║ │ 50│ 7.0│ 5.5│ 1.8│ 6.56 │ 14.84│ 4.24│ 1.50│ 23.47│ 1.89│ 6.21│ 2.93│ 0.97│ -8.63│ 1.50 │ 5.15 ║
║ │ 50│ 8.0│ 5.5│ 1.8│ 7.41 │ 16.51│ 4.76│ 1.49│ 26.03│ 1.87│ 6.98│ 3.22│ 0.97│ -9.53│ 1.53 │ 5.82 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 5.6 │ 56│ 4.0│ 6.0│ 2.0│ 4.38 │ 13.10│ 3.21│ 1.73│ 20.79│ 2.18│ 5.41│ 2.51│ 1.11│ -7.69│ 1.53 │ 3.44 ║
║ │ 56│ 5.0│ 6.0│ 2.0│ 5.41 │ 15.97│ 3.96│ 1.72│ 25.36│ 2.17│ 6.59│ 2.97│ 1.10│ -9.38│ 1.57 │ 4.25 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 6.
77│ 1.92│ 4.63│ 2.31│ 0.98│ -6.57│ 1.42 │ 3.77 ║
║ │ 50│ 6.0│ 5.5│ 1.8│ 5.69 │ 13.07│ 3.69│ 1.52│ 20.72│ 1.91│ 5.43│ 2.63│ 0.98│ -7.64│ 1.46 │ 4.47 ║
║ │ 50│ 7.0│ 5.5│ 1.8│ 6.56 │ 14.84│ 4.24│ 1.50│ 23.47│ 1.89│ 6.21│ 2.93│ 0.97│ -8.63│ 1.50 │ 5.15 ║
║ │ 50│ 8.0│ 5.5│ 1.8│ 7.41 │ 16.51│ 4.76│ 1.49│ 26.03│ 1.87│ 6.98│ 3.22│ 0.97│ -9.53│ 1.53 │ 5.82 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 5.6 │ 56│ 4.0│ 6.0│ 2.0│ 4.38 │ 13.10│ 3.21│ 1.73│ 20.79│ 2.18│ 5.41│ 2.51│ 1.11│ -7.69│ 1.53 │ 3.44 ║
║ │ 56│ 5.0│ 6.0│ 2.0│ 5.41 │ 15.97│ 3.96│ 1.72│ 25.36│ 2.17│ 6.59│ 2.97│ 1.10│ -9.38│ 1.57 │ 4.25 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 6. 0 │ 60│ 4.0│ 7.0│ 2.3│ 4.72 │ 16.21│ 3.70│ 1.85│ 25.69│ 2.33│ 6.72│ 2.94│ 1.19│ -9.49│ 1.62 │ 3.71 ║
║ │ 60│ 5.0│ 7.0│ 2.3│ 5.83 │ 19.79│ 4.56│ 1.84│ 31.40│ 2.32│ 8.18│ 3.48│ 1.18│ -11.61│ 1.66 │ 4.58 ║
║ │ 60│ 6.0│ 7.0│ 2.3│ 6.92 │ 23.21│ 5.40│ 1.83│ 36.81│ 2.31│ 9.60│ 3.99│ 1.18│ -13.61│ 1.70 │ 5.43 ║
║ │ 60│ 8.0│ 7.0│ 2.3│ 9.04 │ 29.55│ 7.00│ 1.81│ 46.77│ 2.27│ 12.34│ 4.90│ 1.17│ -17.21│ 1.78 │ 7.10 ║
║ │ 60│ 10.0│ 7.0│ 2.3│ 11.08 │ 35.32│ 8.52│ 1.79│ 55.64│ 2.24│ 15.00│ 5.72│ 1.16│ -20.32│ 1.85 │ 8.70 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 6.3 │ 63│ 4.0│ 7.0│ 2.3│ 4.96 │ 18.86│ 4.09│ 1.95│ 29.90│ 2.46│ 7.81│ 3.27│ 1.26│ -11.05│ 1.69 │ 3.90 ║
║ │ 63│ 5.0│ 7.0│ 2.3│ 6.13 │ 23.06│ 5.05│ 1.94│ 36.
0 │ 60│ 4.0│ 7.0│ 2.3│ 4.72 │ 16.21│ 3.70│ 1.85│ 25.69│ 2.33│ 6.72│ 2.94│ 1.19│ -9.49│ 1.62 │ 3.71 ║
║ │ 60│ 5.0│ 7.0│ 2.3│ 5.83 │ 19.79│ 4.56│ 1.84│ 31.40│ 2.32│ 8.18│ 3.48│ 1.18│ -11.61│ 1.66 │ 4.58 ║
║ │ 60│ 6.0│ 7.0│ 2.3│ 6.92 │ 23.21│ 5.40│ 1.83│ 36.81│ 2.31│ 9.60│ 3.99│ 1.18│ -13.61│ 1.70 │ 5.43 ║
║ │ 60│ 8.0│ 7.0│ 2.3│ 9.04 │ 29.55│ 7.00│ 1.81│ 46.77│ 2.27│ 12.34│ 4.90│ 1.17│ -17.21│ 1.78 │ 7.10 ║
║ │ 60│ 10.0│ 7.0│ 2.3│ 11.08 │ 35.32│ 8.52│ 1.79│ 55.64│ 2.24│ 15.00│ 5.72│ 1.16│ -20.32│ 1.85 │ 8.70 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 6.3 │ 63│ 4.0│ 7.0│ 2.3│ 4.96 │ 18.86│ 4.09│ 1.95│ 29.90│ 2.46│ 7.81│ 3.27│ 1.26│ -11.05│ 1.69 │ 3.90 ║
║ │ 63│ 5.0│ 7.0│ 2.3│ 6.13 │ 23.06│ 5.05│ 1.94│ 36.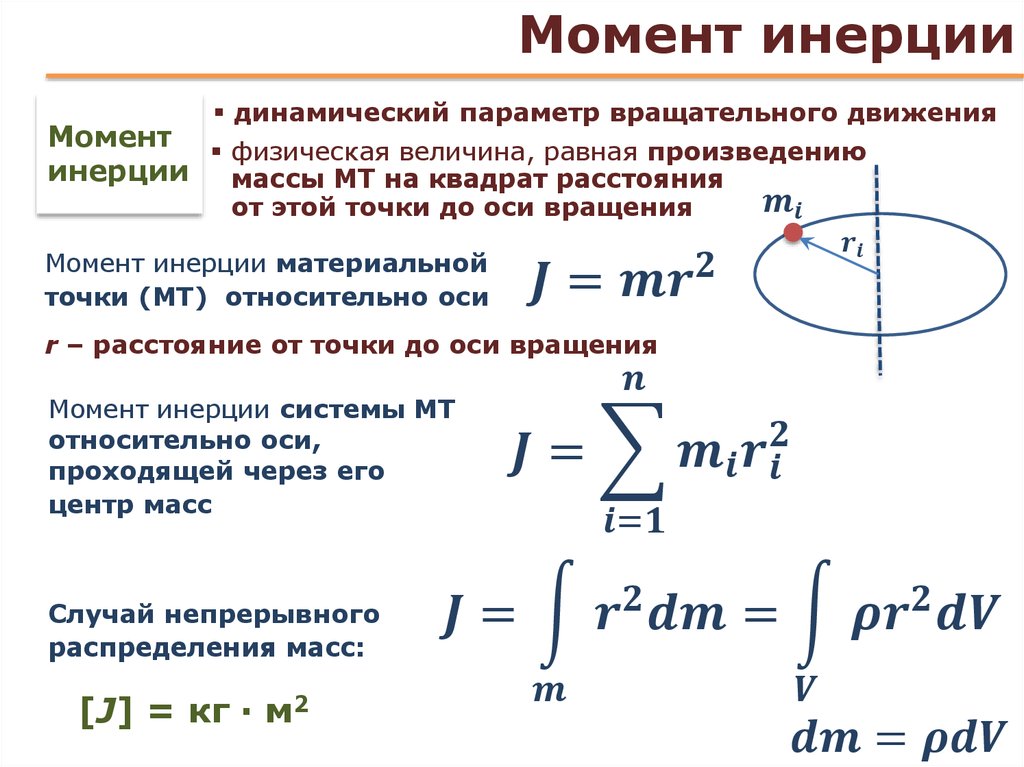 59│ 2.44│ 9.52│ 3.88│ 1.25│ -13.54│ 1.74 │ 4.81 ║
║ │ 63│ 6.0│ 7.0│ 2.3│ 7.28 │ 27.06│ 5.98│ 1.93│ 42.94│ 2.43│ 11.18│ 4.45│ 1.24│ -15.88│ 1.78 │ 5.72 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 7.0 │ 70│ 4.5│ 8.0│ 2.7│ 6.20 │ 29.04│ 5.67│ 2.16│ 46.03│ 2.72│ 12.04│ 4.53│ 1.39│ -17.00│ 1.88 │ 4.87 ║
║ │ 70│ 5.0│ 8.0│ 2.7│ 6.86 │ 31.94│ 6.27│ 2.16│ 50.67│ 2.72│ 13.22│ 4.91│ 1.39│ -18.73│ 1.90 │ 5.38 ║
║ │ 70│ 6.0│ 8.0│ 2.7│ 8.15 │ 37.58│ 7.43│ 2.15│ 59.64│ 2.71│ 15.52│ 5.65│ 1.38│ -22.06│ 1.95 │ 6.40 ║
║ │ 70│ 7.0│ 8.0│ 2.7│ 9.42 │ 42.98│ 8.57│ 2.14│ 68.19│ 2.69│ 17.77│ 6.33│ 1.37│ -25.21│ 1.99 │ 7.39 ║
║ │ 70│ 8.0│ 8.0│ 2.7│ 10.67 │ 48.16│ 9.68│ 2.13│ 76.35│ 2.67│ 19.97│ 6.97│ 1.37│ -28.19│ 2.02 │ 8.37 ║
║ │ 70│ 10.
59│ 2.44│ 9.52│ 3.88│ 1.25│ -13.54│ 1.74 │ 4.81 ║
║ │ 63│ 6.0│ 7.0│ 2.3│ 7.28 │ 27.06│ 5.98│ 1.93│ 42.94│ 2.43│ 11.18│ 4.45│ 1.24│ -15.88│ 1.78 │ 5.72 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 7.0 │ 70│ 4.5│ 8.0│ 2.7│ 6.20 │ 29.04│ 5.67│ 2.16│ 46.03│ 2.72│ 12.04│ 4.53│ 1.39│ -17.00│ 1.88 │ 4.87 ║
║ │ 70│ 5.0│ 8.0│ 2.7│ 6.86 │ 31.94│ 6.27│ 2.16│ 50.67│ 2.72│ 13.22│ 4.91│ 1.39│ -18.73│ 1.90 │ 5.38 ║
║ │ 70│ 6.0│ 8.0│ 2.7│ 8.15 │ 37.58│ 7.43│ 2.15│ 59.64│ 2.71│ 15.52│ 5.65│ 1.38│ -22.06│ 1.95 │ 6.40 ║
║ │ 70│ 7.0│ 8.0│ 2.7│ 9.42 │ 42.98│ 8.57│ 2.14│ 68.19│ 2.69│ 17.77│ 6.33│ 1.37│ -25.21│ 1.99 │ 7.39 ║
║ │ 70│ 8.0│ 8.0│ 2.7│ 10.67 │ 48.16│ 9.68│ 2.13│ 76.35│ 2.67│ 19.97│ 6.97│ 1.37│ -28.19│ 2.02 │ 8.37 ║
║ │ 70│ 10.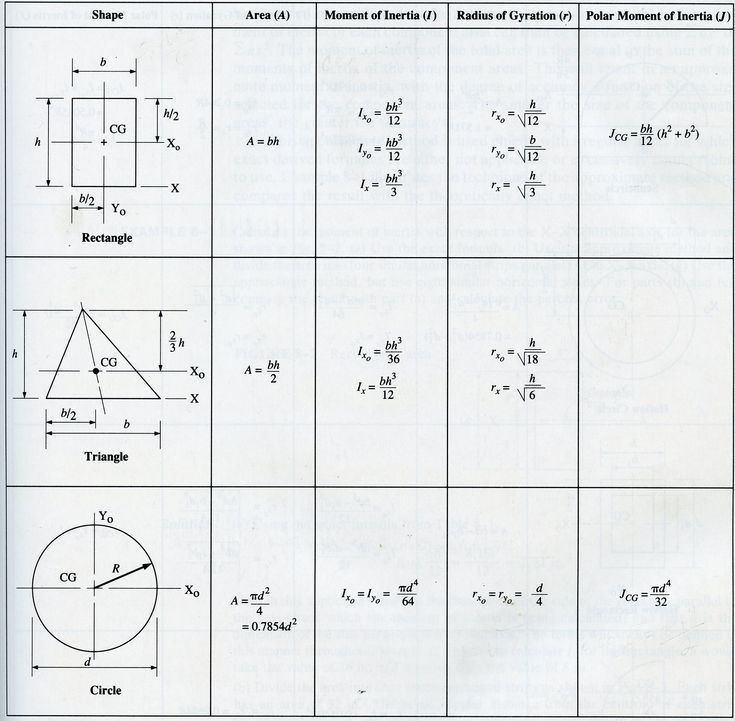 0│ 8.0│ 2.7│ 13.11 │ 57.90│ 11.82│ 2.10│ 91.52│ 2.64│ 24.27│ 8.17│ 1.36│ -33.63│ 2.10 │ 10.29 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 7.5 │ 75│ 5.0│ 9.0│ 3.0│ 7.38 │ 39.53│ 7.21│ 2.31│ 62.65│ 2.91│ 16.41│ 5.75│ 1.49│ -23.12│ 2.02 │ 5.80 ║
║ │ 75│ 6.0│ 9.0│ 3.0│ 8.78 │ 46.57│ 8.57│ 2.30│ 73.87│ 2.90│ 19.28│ 6.61│ 1.48│ -27.30│ 2.06 │ 6.89 ║
║ │ 75│ 7.0│ 9.0│ 3.0│ 10.15 │ 53.34│ 9.89│ 2.29│ 84.61│ 2.89│ 22.07│ 7.41│ 1.48│ -31.27│ 2.10 │ 7.96 ║
║ │ 75│ 8.0│ 9.0│ 3.0│ 11.50 │ 59.84│ 11.18│ 2.28│ 94.89│ 2.87│ 24.80│ 8.17│ 1.47│ -35.04│ 2.15 │ 9.02 ║
║ │ 75│ 9.0│ 9.0│ 3.0│ 12.83 │ 66.10│ 12.43│ 2.27│ 104.72│ 2.86│ 27.48│ 8.89│ 1.46│ -38.62│ 2.19 │ 10.07 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 8.
0│ 8.0│ 2.7│ 13.11 │ 57.90│ 11.82│ 2.10│ 91.52│ 2.64│ 24.27│ 8.17│ 1.36│ -33.63│ 2.10 │ 10.29 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 7.5 │ 75│ 5.0│ 9.0│ 3.0│ 7.38 │ 39.53│ 7.21│ 2.31│ 62.65│ 2.91│ 16.41│ 5.75│ 1.49│ -23.12│ 2.02 │ 5.80 ║
║ │ 75│ 6.0│ 9.0│ 3.0│ 8.78 │ 46.57│ 8.57│ 2.30│ 73.87│ 2.90│ 19.28│ 6.61│ 1.48│ -27.30│ 2.06 │ 6.89 ║
║ │ 75│ 7.0│ 9.0│ 3.0│ 10.15 │ 53.34│ 9.89│ 2.29│ 84.61│ 2.89│ 22.07│ 7.41│ 1.48│ -31.27│ 2.10 │ 7.96 ║
║ │ 75│ 8.0│ 9.0│ 3.0│ 11.50 │ 59.84│ 11.18│ 2.28│ 94.89│ 2.87│ 24.80│ 8.17│ 1.47│ -35.04│ 2.15 │ 9.02 ║
║ │ 75│ 9.0│ 9.0│ 3.0│ 12.83 │ 66.10│ 12.43│ 2.27│ 104.72│ 2.86│ 27.48│ 8.89│ 1.46│ -38.62│ 2.19 │ 10.07 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 8. 0 │ 80│ 5.5│ 9.0│ 3.0│ 8.63 │ 52.68│ 9.03│ 2.47│ 83.56│ 3.11│ 21.80│ 7.12│ 1.59│ -30.88│ 2.17 │ 6.78 ║
║ │ 80│ 6.0│ 9.0│ 3.0│ 9.38 │ 56.97│ 9.80│ 2.46│ 90.40│ 3.10│ 23.54│ 7.61│ 1.58│ -33.43│ 2.19 │ 7.36 ║
║ │ 80│ 7.0│ 9.0│ 3.0│ 10.85 │ 65.31│ 11.32│ 2.45│ 103.66│ 3.09│ 26.97│ 8.55│ 1.58│ -38.34│ 2.23 │ 8.51 ║
║ │ 80│ 8.0│ 9.0│ 3.0│ 12.30 │ 73.36│ 12.80│ 2.44│ 116.39│ 3.08│ 30.32│ 9.45│ 1.57│ -43.03│ 2.27 │ 9.65 ║
║ │ 80│ 10.0│ 9.0│ 3.0│ 15.14 │ 88.58│ 15.67│ 2.42│ 140.31│ 3.04│ 36.85│ 11.10│ 1.56│ -51.73│ 2.35 │ 11.88 ║
║ │ 80│ 12.0│ 9.0│ 3.0│ 17.90 │ 102.74│ 18.42│ 2.40│ 162.27│ 3.01│ 43.21│ 12.61│ 1.55│ -59.53│ 2.42 │ 14.05 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Сотамент горячекатаных равнополочных уголков по ГОСТ 8509-93
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 9.
0 │ 80│ 5.5│ 9.0│ 3.0│ 8.63 │ 52.68│ 9.03│ 2.47│ 83.56│ 3.11│ 21.80│ 7.12│ 1.59│ -30.88│ 2.17 │ 6.78 ║
║ │ 80│ 6.0│ 9.0│ 3.0│ 9.38 │ 56.97│ 9.80│ 2.46│ 90.40│ 3.10│ 23.54│ 7.61│ 1.58│ -33.43│ 2.19 │ 7.36 ║
║ │ 80│ 7.0│ 9.0│ 3.0│ 10.85 │ 65.31│ 11.32│ 2.45│ 103.66│ 3.09│ 26.97│ 8.55│ 1.58│ -38.34│ 2.23 │ 8.51 ║
║ │ 80│ 8.0│ 9.0│ 3.0│ 12.30 │ 73.36│ 12.80│ 2.44│ 116.39│ 3.08│ 30.32│ 9.45│ 1.57│ -43.03│ 2.27 │ 9.65 ║
║ │ 80│ 10.0│ 9.0│ 3.0│ 15.14 │ 88.58│ 15.67│ 2.42│ 140.31│ 3.04│ 36.85│ 11.10│ 1.56│ -51.73│ 2.35 │ 11.88 ║
║ │ 80│ 12.0│ 9.0│ 3.0│ 17.90 │ 102.74│ 18.42│ 2.40│ 162.27│ 3.01│ 43.21│ 12.61│ 1.55│ -59.53│ 2.42 │ 14.05 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Сотамент горячекатаных равнополочных уголков по ГОСТ 8509-93
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 9.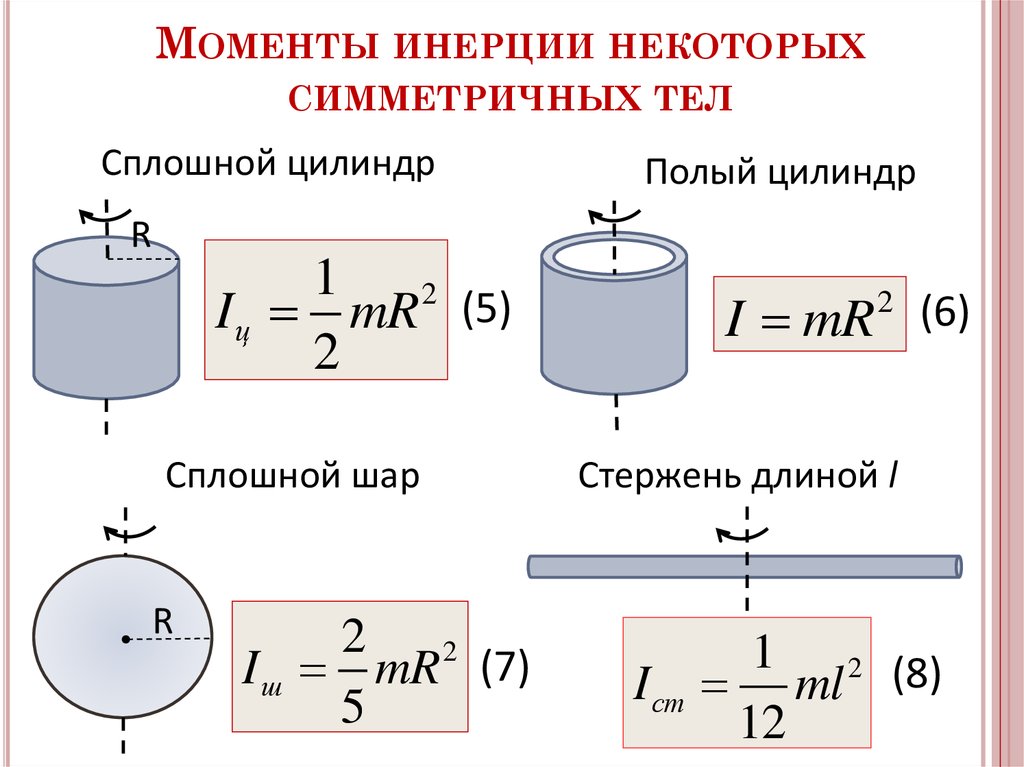 0 │ 90│ 6.0│ 10.0│ 3.3│ 10.61 │ 82.10│ 12.49│ 2.78│ 130.22│ 3.50│ 33.97│ 9.89│ 1.79│ -48.12│ 2.43 │ 8.33 ║
║ │ 90│ 7.0│ 10.0│ 3.3│ 12.28 │ 94.30│ 14.45│ 2.77│ 149.67│ 3.49│ 38.94│ 11.14│ 1.78│ -55.36│ 2.47 │ 9.64 ║
║ │ 90│ 8.0│ 10.0│ 3.3│ 13.93 │ 106.11│ 16.36│ 2.76│ 168.42│ 3.48│ 43.80│ 12.32│ 1.77│ -62.31│ 2.51 │ 10.93 ║
║ │ 90│ 9.0│ 10.0│ 3.3│ 15.56 │ 117.54│ 18.24│ 2.75│ 186.51│ 3.46│ 48.58│ 13.45│ 1.77│ -68.97│ 2.56 │ 12.21 ║
║ │ 90│ 10.0│ 10.0│ 3.3│ 17.17 │ 128.60│ 20.07│ 2.74│ 203.93│ 3.45│ 53.27│ 14.52│ 1.76│ -75.33│ 2.59 │ 13.48 ║
║ │ 90│ 12.0│ 10.0│ 3.3│ 20.33 │ 149.67│ 23.65│ 2.71│ 236.88│ 3.41│ 62.46│ 16.54│ 1.75│ -87.21│ 2.67 │ 15.96 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 10.0 │ 100│ 6.5│ 12.0│ 4.0│ 12.82 │ 122.10│ 16.69│ 3.09│ 193.
0 │ 90│ 6.0│ 10.0│ 3.3│ 10.61 │ 82.10│ 12.49│ 2.78│ 130.22│ 3.50│ 33.97│ 9.89│ 1.79│ -48.12│ 2.43 │ 8.33 ║
║ │ 90│ 7.0│ 10.0│ 3.3│ 12.28 │ 94.30│ 14.45│ 2.77│ 149.67│ 3.49│ 38.94│ 11.14│ 1.78│ -55.36│ 2.47 │ 9.64 ║
║ │ 90│ 8.0│ 10.0│ 3.3│ 13.93 │ 106.11│ 16.36│ 2.76│ 168.42│ 3.48│ 43.80│ 12.32│ 1.77│ -62.31│ 2.51 │ 10.93 ║
║ │ 90│ 9.0│ 10.0│ 3.3│ 15.56 │ 117.54│ 18.24│ 2.75│ 186.51│ 3.46│ 48.58│ 13.45│ 1.77│ -68.97│ 2.56 │ 12.21 ║
║ │ 90│ 10.0│ 10.0│ 3.3│ 17.17 │ 128.60│ 20.07│ 2.74│ 203.93│ 3.45│ 53.27│ 14.52│ 1.76│ -75.33│ 2.59 │ 13.48 ║
║ │ 90│ 12.0│ 10.0│ 3.3│ 20.33 │ 149.67│ 23.65│ 2.71│ 236.88│ 3.41│ 62.46│ 16.54│ 1.75│ -87.21│ 2.67 │ 15.96 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 10.0 │ 100│ 6.5│ 12.0│ 4.0│ 12.82 │ 122.10│ 16.69│ 3.09│ 193.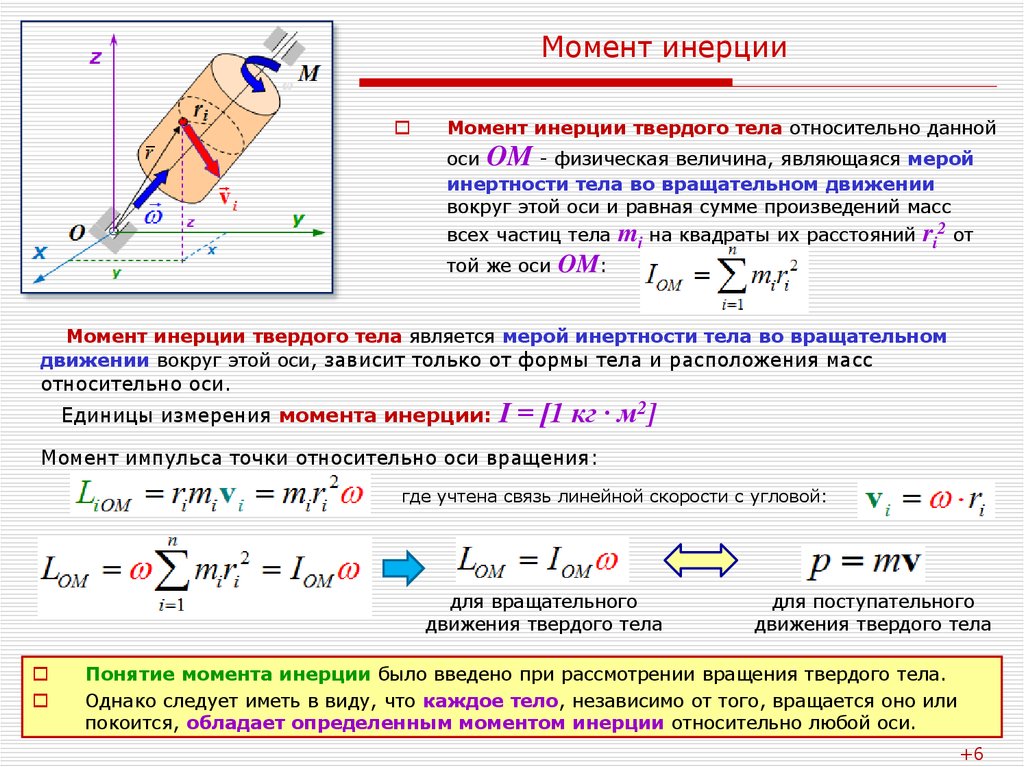 46│ 3.89│ 50.73│ 13.37│ 1.99│ -71.37│ 2.68 │ 10.06 ║
║ │ 100│ 7.0│ 12.0│ 4.0│ 13.75 │ 130.59│ 17.90│ 3.08│ 207.01│ 3.88│ 54.16│ 14.15│ 1.99│ -76.42│ 2.71 │ 10.79 ║
║ │ 100│ 8.0│ 12.0│ 4.0│ 15.60 │ 147.19│ 20.30│ 3.07│ 233.46│ 3.87│ 60.92│ 15.66│ 1.98│ -86.27│ 2.75 │ 12.25 ║
║ │ 100│ 10.0│ 12.0│ 4.0│ 19.24 │ 178.95│ 24.97│ 3.05│ 283.83│ 3.84│ 74.08│ 18.49│ 1.96│ -104.87│ 2.83 │ 15.10 ║
║ │ 100│ 12.0│ 12.0│ 4.0│ 22.80 │ 208.90│ 29.47│ 3.03│ 330.95│ 3.81│ 86.84│ 21.08│ 1.95│ -122.06│ 2.91 │ 17.90 ║
║ │ 100│ 14.0│ 12.0│ 4.0│ 26.28 │ 237.15│ 33.83│ 3.00│ 374.98│ 3.78│ 99.32│ 23.49│ 1.94│ -137.83│ 2.99 │ 20.63 ║
║ │ 100│ 15.0│ 12.0│ 4.0│ 27.99 │ 250.68│ 35.95│ 2.99│ 395.87│ 3.76│ 105.48│ 24.64│ 1.94│ -145.20│ 3.03 │ 21.97 ║
║ │ 100│ 16.0│ 12.0│ 4.0│ 29.68 │ 263.82│ 38.04│ 2.98│ 416.04│ 3.74│ 111.61│ 25.76│ 1.94│ -152.22│ 3.06 │ 23.30 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 11.
46│ 3.89│ 50.73│ 13.37│ 1.99│ -71.37│ 2.68 │ 10.06 ║
║ │ 100│ 7.0│ 12.0│ 4.0│ 13.75 │ 130.59│ 17.90│ 3.08│ 207.01│ 3.88│ 54.16│ 14.15│ 1.99│ -76.42│ 2.71 │ 10.79 ║
║ │ 100│ 8.0│ 12.0│ 4.0│ 15.60 │ 147.19│ 20.30│ 3.07│ 233.46│ 3.87│ 60.92│ 15.66│ 1.98│ -86.27│ 2.75 │ 12.25 ║
║ │ 100│ 10.0│ 12.0│ 4.0│ 19.24 │ 178.95│ 24.97│ 3.05│ 283.83│ 3.84│ 74.08│ 18.49│ 1.96│ -104.87│ 2.83 │ 15.10 ║
║ │ 100│ 12.0│ 12.0│ 4.0│ 22.80 │ 208.90│ 29.47│ 3.03│ 330.95│ 3.81│ 86.84│ 21.08│ 1.95│ -122.06│ 2.91 │ 17.90 ║
║ │ 100│ 14.0│ 12.0│ 4.0│ 26.28 │ 237.15│ 33.83│ 3.00│ 374.98│ 3.78│ 99.32│ 23.49│ 1.94│ -137.83│ 2.99 │ 20.63 ║
║ │ 100│ 15.0│ 12.0│ 4.0│ 27.99 │ 250.68│ 35.95│ 2.99│ 395.87│ 3.76│ 105.48│ 24.64│ 1.94│ -145.20│ 3.03 │ 21.97 ║
║ │ 100│ 16.0│ 12.0│ 4.0│ 29.68 │ 263.82│ 38.04│ 2.98│ 416.04│ 3.74│ 111.61│ 25.76│ 1.94│ -152.22│ 3.06 │ 23.30 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 11. 0 │ 110│ 7.0│ 12.0│ 4.0│ 15.15 │ 175.61│ 21.83│ 3.40│ 278.54│ 4.29│ 72.68│ 17.39│ 2.19│ -102.93│ 2.96 │ 11.89 ║
║ │ 110│ 8.0│ 12.0│ 4.0│ 17.20 │ 198.17│ 24.77│ 3.39│ 314.51│ 4.28│ 81.83│ 19.29│ 2.18│ -116.34│ 3.00 │ 13.50 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 12.0 │ 120│ 8.0│ 12.0│ 4.0│ 18.80 │ 259.75│ 29.68│ 3.72│ 412.45│ 4.68│ 107.04│ 23.30│ 2.39│ -152.71│ 3.25 │ 14.76 ║
║ │ 120│ 10.0│ 12.0│ 4.0│ 23.24 │ 317.16│ 36.59│ 3.69│ 503.79│ 4.66│ 130.54│ 27.70│ 2.37│ -186.62│ 3.33 │ 18.24 ║
║ │ 120│ 12.0│ 12.0│ 4.0│ 27.60 │ 371.80│ 43.30│ 3.67│ 590.28│ 4.63│ 153.33│ 31.77│ 2.36│ -218.48│ 3.41 │ 21.67 ║
║ │ 120│ 15.0│ 12.0│ 4.0│ 33.99 │ 448.90│ 52.98│ 3.63│ 711.32│ 4.58│ 186.48│ 37.38│ 2.34│ -262.42│ 3.53 │ 26.68 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 12.
0 │ 110│ 7.0│ 12.0│ 4.0│ 15.15 │ 175.61│ 21.83│ 3.40│ 278.54│ 4.29│ 72.68│ 17.39│ 2.19│ -102.93│ 2.96 │ 11.89 ║
║ │ 110│ 8.0│ 12.0│ 4.0│ 17.20 │ 198.17│ 24.77│ 3.39│ 314.51│ 4.28│ 81.83│ 19.29│ 2.18│ -116.34│ 3.00 │ 13.50 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 12.0 │ 120│ 8.0│ 12.0│ 4.0│ 18.80 │ 259.75│ 29.68│ 3.72│ 412.45│ 4.68│ 107.04│ 23.30│ 2.39│ -152.71│ 3.25 │ 14.76 ║
║ │ 120│ 10.0│ 12.0│ 4.0│ 23.24 │ 317.16│ 36.59│ 3.69│ 503.79│ 4.66│ 130.54│ 27.70│ 2.37│ -186.62│ 3.33 │ 18.24 ║
║ │ 120│ 12.0│ 12.0│ 4.0│ 27.60 │ 371.80│ 43.30│ 3.67│ 590.28│ 4.63│ 153.33│ 31.77│ 2.36│ -218.48│ 3.41 │ 21.67 ║
║ │ 120│ 15.0│ 12.0│ 4.0│ 33.99 │ 448.90│ 52.98│ 3.63│ 711.32│ 4.58│ 186.48│ 37.38│ 2.34│ -262.42│ 3.53 │ 26.68 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 12. 5 │ 125│ 8.0│ 14.0│ 4.6│ 19.69 │ 294.36│ 32.20│ 3.87│ 466.76│ 4.87│ 121.96│ 25.68│ 2.49│ -172.40│ 3.36 │ 15.46 ║
║ │ 125│ 9.0│ 14.0│ 4.6│ 22.02 │ 327.48│ 36.00│ 3.86│ 519.57│ 4.86│ 135.38│ 28.14│ 2.48│ -192.10│ 3.40 │ 17.29 ║
║ │ 125│ 10.0│ 14.0│ 4.6│ 24.33 │ 359.82│ 39.74│ 3.85│ 571.04│ 4.84│ 148.59│ 30.50│ 2.47│ -211.22│ 3.44 │ 19.10 ║
║ │ 125│ 12.0│ 14.0│ 4.6│ 28.89 │ 422.23│ 47.06│ 3.82│ 670.02│ 4.82│ 174.43│ 34.97│ 2.46│ -247.80│ 3.53 │ 22.68 ║
║ │ 125│ 14.0│ 14.0│ 4.6│ 33.37 │ 481.76│ 54.17│ 3.80│ 763.90│ 4.79│ 199.62│ 39.14│ 2.45│ -282.14│ 3.61 │ 26.20 ║
║ │ 125│ 16.0│ 14.0│ 4.6│ 37.77 │ 538.56│ 61.09│ 3.78│ 852.84│ 4.75│ 224.29│ 43.06│ 2.44│ -314.27│ 3.68 │ 29.65 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 14.0 │ 140│ 9.0│ 14.0│ 4.6│ 24.72 │ 465.72│ 45.55│ 4.34│ 739.
5 │ 125│ 8.0│ 14.0│ 4.6│ 19.69 │ 294.36│ 32.20│ 3.87│ 466.76│ 4.87│ 121.96│ 25.68│ 2.49│ -172.40│ 3.36 │ 15.46 ║
║ │ 125│ 9.0│ 14.0│ 4.6│ 22.02 │ 327.48│ 36.00│ 3.86│ 519.57│ 4.86│ 135.38│ 28.14│ 2.48│ -192.10│ 3.40 │ 17.29 ║
║ │ 125│ 10.0│ 14.0│ 4.6│ 24.33 │ 359.82│ 39.74│ 3.85│ 571.04│ 4.84│ 148.59│ 30.50│ 2.47│ -211.22│ 3.44 │ 19.10 ║
║ │ 125│ 12.0│ 14.0│ 4.6│ 28.89 │ 422.23│ 47.06│ 3.82│ 670.02│ 4.82│ 174.43│ 34.97│ 2.46│ -247.80│ 3.53 │ 22.68 ║
║ │ 125│ 14.0│ 14.0│ 4.6│ 33.37 │ 481.76│ 54.17│ 3.80│ 763.90│ 4.79│ 199.62│ 39.14│ 2.45│ -282.14│ 3.61 │ 26.20 ║
║ │ 125│ 16.0│ 14.0│ 4.6│ 37.77 │ 538.56│ 61.09│ 3.78│ 852.84│ 4.75│ 224.29│ 43.06│ 2.44│ -314.27│ 3.68 │ 29.65 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 14.0 │ 140│ 9.0│ 14.0│ 4.6│ 24.72 │ 465.72│ 45.55│ 4.34│ 739.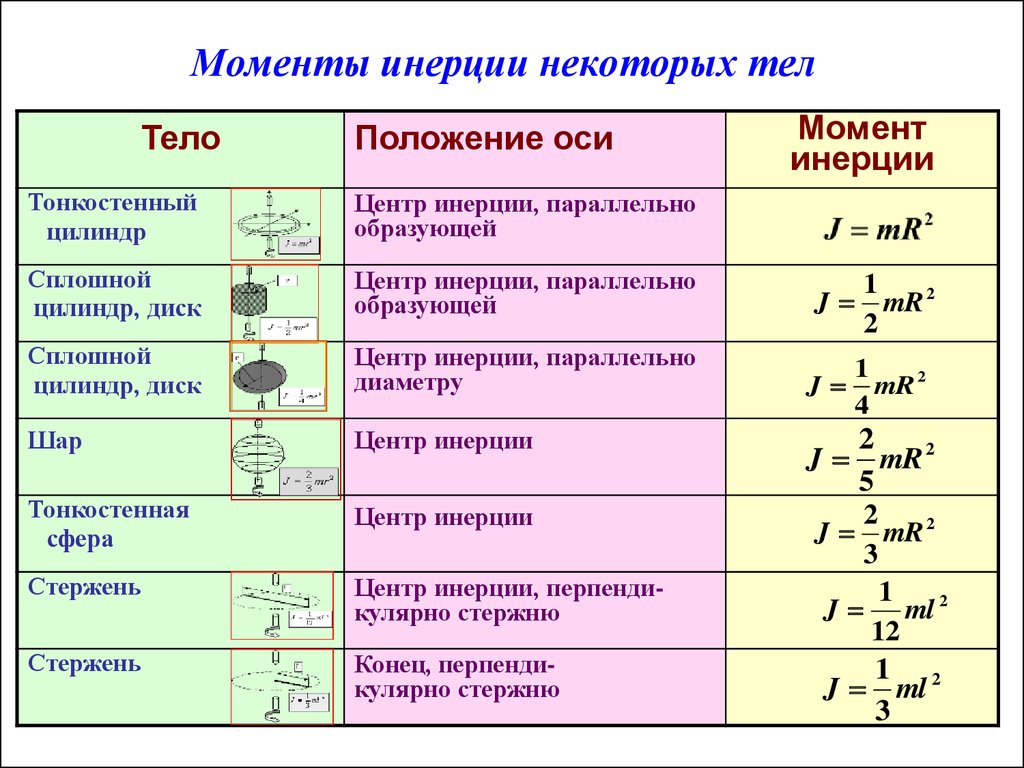 42│ 5.47│ 192.03│ 35.96│ 2.79│ -273.70│ 3.78 │ 19.41 ║
║ │ 140│ 10.0│ 14.0│ 4.6│ 27.33 │ 512.29│ 50.32│ 4.33│ 813.62│ 5.46│ 210.96│ 39.06│ 2.78│ -301.33│ 3.82 │ 21.45 ║
║ │ 140│ 12.0│ 14.0│ 4.6│ 32.49 │ 602.49│ 59.66│ 4.31│ 956.98│ 5.43│ 248.01│ 44.94│ 2.76│ -354.48│ 3.90 │ 25.50 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 15.0 │ 150│ 10.0│ 14.0│ 4.6│ 29.33 │ 634.76│ 58.07│ 4.65│ 1008.60│ 5.86│ 260.97│ 45.35│ 2.98│ -373.80│ 4.07 │ 23.02 ║
║ │ 150│ 12.0│ 14.0│ 4.6│ 34.89 │ 747.48│ 68.90│ 4.63│ 1187.90│ 5.83│ 307.09│ 52.30│ 2.97│ -440.39│ 4.15 │ 27.39 ║
║ │ 150│ 15.0│ 14.0│ 4.6│ 43.08 │ 908.38│ 84.66│ 4.59│ 1442.60│ 5.79│ 374.17│ 61.96│ 2.95│ -534.21│ 4.27 │ 33.82 ║
║ │ 150│ 18.0│ 14.0│ 4.6│ 51.09 │ 1060.10│ 99.86│ 4.55│ 1680.90│ 5.74│ 439.24│ 70.83│ 2.93│ -620.84│ 4.38 │ 40.11 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 16.
42│ 5.47│ 192.03│ 35.96│ 2.79│ -273.70│ 3.78 │ 19.41 ║
║ │ 140│ 10.0│ 14.0│ 4.6│ 27.33 │ 512.29│ 50.32│ 4.33│ 813.62│ 5.46│ 210.96│ 39.06│ 2.78│ -301.33│ 3.82 │ 21.45 ║
║ │ 140│ 12.0│ 14.0│ 4.6│ 32.49 │ 602.49│ 59.66│ 4.31│ 956.98│ 5.43│ 248.01│ 44.94│ 2.76│ -354.48│ 3.90 │ 25.50 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 15.0 │ 150│ 10.0│ 14.0│ 4.6│ 29.33 │ 634.76│ 58.07│ 4.65│ 1008.60│ 5.86│ 260.97│ 45.35│ 2.98│ -373.80│ 4.07 │ 23.02 ║
║ │ 150│ 12.0│ 14.0│ 4.6│ 34.89 │ 747.48│ 68.90│ 4.63│ 1187.90│ 5.83│ 307.09│ 52.30│ 2.97│ -440.39│ 4.15 │ 27.39 ║
║ │ 150│ 15.0│ 14.0│ 4.6│ 43.08 │ 908.38│ 84.66│ 4.59│ 1442.60│ 5.79│ 374.17│ 61.96│ 2.95│ -534.21│ 4.27 │ 33.82 ║
║ │ 150│ 18.0│ 14.0│ 4.6│ 51.09 │ 1060.10│ 99.86│ 4.55│ 1680.90│ 5.74│ 439.24│ 70.83│ 2.93│ -620.84│ 4.38 │ 40.11 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 16.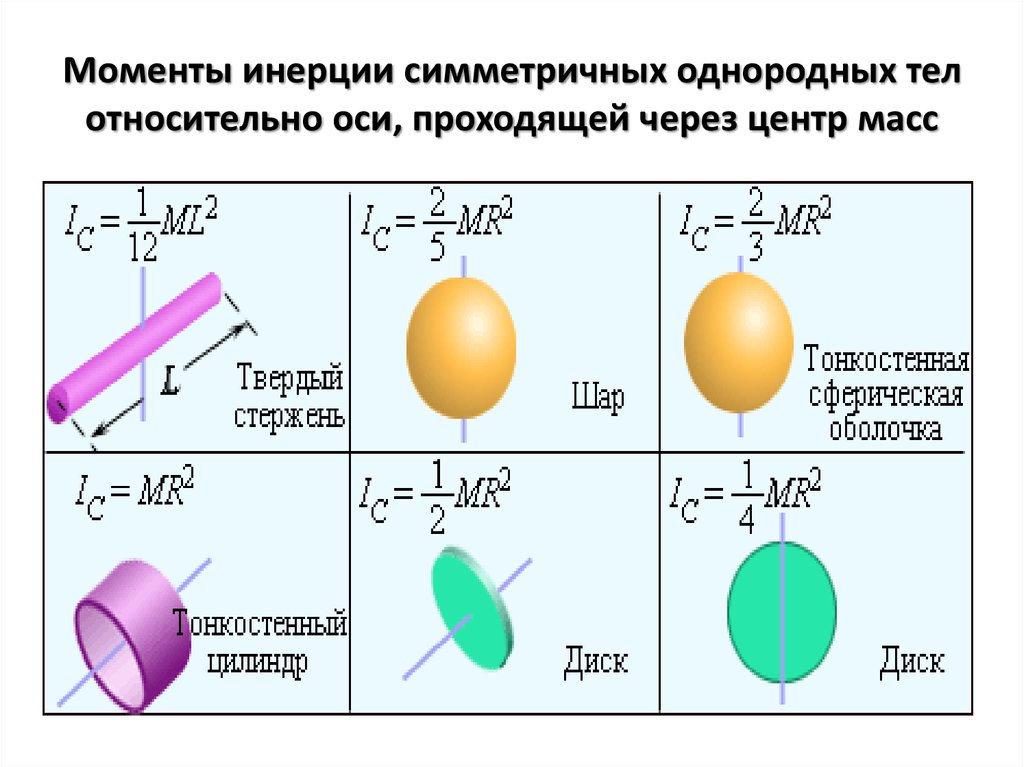 0 │ 160│ 10.0│ 16.0│ 5.3│ 31.43 │ 774.24│ 66.19│ 4.96│ 1229.10│ 6.25│ 319.38│ 52.48│ 3.19│ -454.86│ 4.30 │ 24.67 ║
║ │ 160│ 11.0│ 16.0│ 5.3│ 34.42 │ 844.21│ 72.44│ 4.95│ 1340.70│ 6.24│ 347.77│ 56.58│ 3.18│ -496.45│ 4.35 │ 27.02 ║
║ │ 160│ 12.0│ 16.0│ 5.3│ 37.39 │ 912.89│ 78.62│ 4.94│ 1450.00│ 6.23│ 375.78│ 60.55│ 3.17│ -537.11│ 4.39 │ 29.35 ║
║ │ 160│ 14.0│ 16.0│ 5.3│ 43.27 │ 1046.50│ 90.77│ 4.92│ 1662.10│ 6.20│ 430.81│ 68.14│ 3.15│ -615.66│ 4.47 │ 33.97 ║
║ │ 160│ 16.0│ 16.0│ 5.3│ 49.07 │ 1175.20│ 102.64│ 4.89│ 1865.70│ 6.17│ 484.64│ 75.32│ 3.14│ -690.54│ 4.55 │ 38.52 ║
║ │ 160│ 18.0│ 16.0│ 5.3│ 54.79 │ 1299.20│ 114.24│ 4.87│ 2061.00│ 6.13│ 537.46│ 82.13│ 3.13│ -761.79│ 4.63 │ 43.01 ║
║ │ 160│ 20.0│ 16.0│ 5.3│ 60.43 │ 1418.80│ 125.60│ 4.85│ 2248.30│ 6.10│ 589.43│ 88.61│ 3.12│ -829.41│ 4.70 │ 47.44 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Сотамент горячекатаных равнополочных уголков по ГОСТ 8509-93
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 18.
0 │ 160│ 10.0│ 16.0│ 5.3│ 31.43 │ 774.24│ 66.19│ 4.96│ 1229.10│ 6.25│ 319.38│ 52.48│ 3.19│ -454.86│ 4.30 │ 24.67 ║
║ │ 160│ 11.0│ 16.0│ 5.3│ 34.42 │ 844.21│ 72.44│ 4.95│ 1340.70│ 6.24│ 347.77│ 56.58│ 3.18│ -496.45│ 4.35 │ 27.02 ║
║ │ 160│ 12.0│ 16.0│ 5.3│ 37.39 │ 912.89│ 78.62│ 4.94│ 1450.00│ 6.23│ 375.78│ 60.55│ 3.17│ -537.11│ 4.39 │ 29.35 ║
║ │ 160│ 14.0│ 16.0│ 5.3│ 43.27 │ 1046.50│ 90.77│ 4.92│ 1662.10│ 6.20│ 430.81│ 68.14│ 3.15│ -615.66│ 4.47 │ 33.97 ║
║ │ 160│ 16.0│ 16.0│ 5.3│ 49.07 │ 1175.20│ 102.64│ 4.89│ 1865.70│ 6.17│ 484.64│ 75.32│ 3.14│ -690.54│ 4.55 │ 38.52 ║
║ │ 160│ 18.0│ 16.0│ 5.3│ 54.79 │ 1299.20│ 114.24│ 4.87│ 2061.00│ 6.13│ 537.46│ 82.13│ 3.13│ -761.79│ 4.63 │ 43.01 ║
║ │ 160│ 20.0│ 16.0│ 5.3│ 60.43 │ 1418.80│ 125.60│ 4.85│ 2248.30│ 6.10│ 589.43│ 88.61│ 3.12│ -829.41│ 4.70 │ 47.44 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
Сотамент горячекатаных равнополочных уголков по ГОСТ 8509-93
╔══════╤════╤═════╤═════╤════╤════════╤════════════════════════════════════════════════════════════════════════════╤════════╗
║Номер │ b │ t │ R │ r │Площадь │ Справочные значения для осей │ Масса ║
║уголка│ │ │ │ │попереч-├──────────────────────┬──────────────┬──────────────────────┬────────┬──────┤ 1 м ║
║ │ │ │ │ │ного │ X - X │ Xo -Xo │ Yo - Yo │ Jxy │ Zo │ уголка ║
║ │ │ │ │ │сечения ├────────┬───────┬─────┼────────┬─────┼────────┬───────┬─────┤ │ │ ║
║ │ │ │ │ │ │ Jx │ Wx │ ix │ Jxo │ixo │ Jyo │ Wyo │iyo │ │ │ ║
║ │(мм)│ (мм)│(мм) │(мм)│ (см2) │ (см4) │ (см3) │(см) │ (см4) │(см) │ (см4) │ (см3) │(см) │ (см4) │ (см) │ (кг) ║
╠══════╪════╪═════╪═════╪════╪════════╪════════╪═══════╪═════╪════════╪═════╪════════╪═══════╪═════╪════════╪══════╪════════╣
║ 18.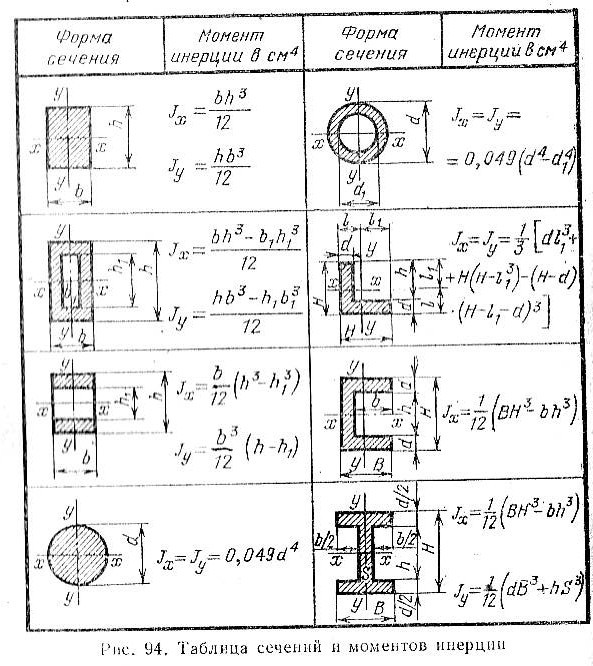 0 │ 180│ 11.0│ 16.0│ 5.3│ 38.82 │ 1216.40│ 92.47│ 5.60│ 1933.10│ 7.06│ 499.78│ 72.94│ 3.59│ -716.66│ 4.84 │ 30.47 ║
║ │ 180│ 12.0│ 16.0│ 5.3│ 42.19 │ 1316.60│ 100.41│ 5.59│ 2092.80│ 7.04│ 540.45│ 78.19│ 3.58│ -776.16│ 4.89 │ 33.12 ║
║ │ 180│ 15.0│ 16.0│ 5.3│ 52.18 │ 1607.40│ 123.74│ 5.55│ 2555.00│ 7.00│ 659.73│ 93.11│ 3.56│ -947.63│ 5.01 │ 40.96 ║
║ │ 180│ 18.0│ 16.0│ 5.3│ 61.99 │ 1884.10│ 146.36│ 5.51│ 2992.70│ 6.95│ 775.44│ 106.94│ 3.54│-1108.60│ 5.13 │ 48.66 ║
║ │ 180│ 20.0│ 16.0│ 5.3│ 68.43 │ 2061.10│ 161.07│ 5.49│ 3271.30│ 6.91│ 850.92│ 115.62│ 3.53│-1210.20│ 5.20 │ 53.72 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 20.0 │ 200│ 12.0│ 18.0│ 6.0│ 47.10 │ 1822.80│ 124.61│ 6.22│ 2896.20│ 7.84│ 749.40│ 98.64│ 3.99│-1073.40│ 5.37 │ 36.97 ║
║ │ 200│ 13.0│ 18.0│ 6.0│ 50.85 │ 1960.80│ 134.44│ 6.21│ 3116.
0 │ 180│ 11.0│ 16.0│ 5.3│ 38.82 │ 1216.40│ 92.47│ 5.60│ 1933.10│ 7.06│ 499.78│ 72.94│ 3.59│ -716.66│ 4.84 │ 30.47 ║
║ │ 180│ 12.0│ 16.0│ 5.3│ 42.19 │ 1316.60│ 100.41│ 5.59│ 2092.80│ 7.04│ 540.45│ 78.19│ 3.58│ -776.16│ 4.89 │ 33.12 ║
║ │ 180│ 15.0│ 16.0│ 5.3│ 52.18 │ 1607.40│ 123.74│ 5.55│ 2555.00│ 7.00│ 659.73│ 93.11│ 3.56│ -947.63│ 5.01 │ 40.96 ║
║ │ 180│ 18.0│ 16.0│ 5.3│ 61.99 │ 1884.10│ 146.36│ 5.51│ 2992.70│ 6.95│ 775.44│ 106.94│ 3.54│-1108.60│ 5.13 │ 48.66 ║
║ │ 180│ 20.0│ 16.0│ 5.3│ 68.43 │ 2061.10│ 161.07│ 5.49│ 3271.30│ 6.91│ 850.92│ 115.62│ 3.53│-1210.20│ 5.20 │ 53.72 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 20.0 │ 200│ 12.0│ 18.0│ 6.0│ 47.10 │ 1822.80│ 124.61│ 6.22│ 2896.20│ 7.84│ 749.40│ 98.64│ 3.99│-1073.40│ 5.37 │ 36.97 ║
║ │ 200│ 13.0│ 18.0│ 6.0│ 50.85 │ 1960.80│ 134.44│ 6.21│ 3116.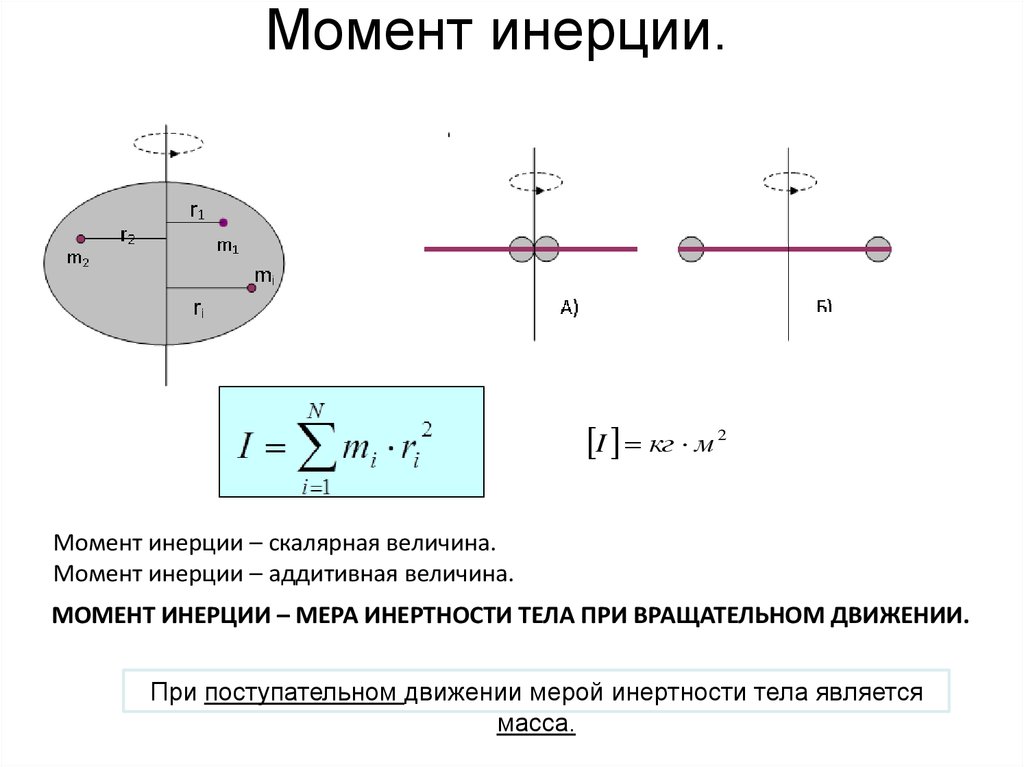 20│ 7.83│ 805.35│ 105.16│ 3.98│-1155.40│ 5.42 │ 39.92 ║
║ │ 200│ 14.0│ 18.0│ 6.0│ 54.58 │ 2096.70│ 144.17│ 6.20│ 3332.70│ 7.81│ 860.71│ 111.53│ 3.97│-1236.00│ 5.46 │ 42.85 ║
║ │ 200│ 16.0│ 18.0│ 6.0│ 61.98 │ 2362.60│ 163.37│ 6.17│ 3755.40│ 7.78│ 969.74│ 123.80│ 3.96│-1392.80│ 5.54 │ 48.65 ║
║ │ 200│ 18.0│ 18.0│ 6.0│ 69.30 │ 2620.60│ 182.22│ 6.15│ 4164.50│ 7.75│ 1076.70│ 135.52│ 3.94│-1543.90│ 5.62 │ 54.40 ║
║ │ 200│ 20.0│ 18.0│ 6.0│ 76.54 │ 2871.20│ 200.73│ 6.13│ 4560.40│ 7.72│ 1181.90│ 146.72│ 3.93│-1689.30│ 5.70 │ 60.08 ║
║ │ 200│ 24.0│ 18.0│ 6.0│ 90.78 │ 3350.70│ 236.77│ 6.08│ 5313.60│ 7.65│ 1387.70│ 167.78│ 3.91│-1962.90│ 5.85 │ 71.26 ║
║ │ 200│ 25.0│ 18.0│ 6.0│ 94.29 │ 3466.20│ 245.59│ 6.06│ 5494.00│ 7.63│ 1438.40│ 172.80│ 3.91│-2027.80│ 5.89 │ 74.02 ║
║ │ 200│ 30.0│ 18.0│ 6.0│ 111.54 │ 4019.60│ 288.57│ 6.00│ 6351.00│ 7.55│ 1688.20│ 196.64│ 3.89│-2331.40│ 6.07 │ 87.56 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 22.
20│ 7.83│ 805.35│ 105.16│ 3.98│-1155.40│ 5.42 │ 39.92 ║
║ │ 200│ 14.0│ 18.0│ 6.0│ 54.58 │ 2096.70│ 144.17│ 6.20│ 3332.70│ 7.81│ 860.71│ 111.53│ 3.97│-1236.00│ 5.46 │ 42.85 ║
║ │ 200│ 16.0│ 18.0│ 6.0│ 61.98 │ 2362.60│ 163.37│ 6.17│ 3755.40│ 7.78│ 969.74│ 123.80│ 3.96│-1392.80│ 5.54 │ 48.65 ║
║ │ 200│ 18.0│ 18.0│ 6.0│ 69.30 │ 2620.60│ 182.22│ 6.15│ 4164.50│ 7.75│ 1076.70│ 135.52│ 3.94│-1543.90│ 5.62 │ 54.40 ║
║ │ 200│ 20.0│ 18.0│ 6.0│ 76.54 │ 2871.20│ 200.73│ 6.13│ 4560.40│ 7.72│ 1181.90│ 146.72│ 3.93│-1689.30│ 5.70 │ 60.08 ║
║ │ 200│ 24.0│ 18.0│ 6.0│ 90.78 │ 3350.70│ 236.77│ 6.08│ 5313.60│ 7.65│ 1387.70│ 167.78│ 3.91│-1962.90│ 5.85 │ 71.26 ║
║ │ 200│ 25.0│ 18.0│ 6.0│ 94.29 │ 3466.20│ 245.59│ 6.06│ 5494.00│ 7.63│ 1438.40│ 172.80│ 3.91│-2027.80│ 5.89 │ 74.02 ║
║ │ 200│ 30.0│ 18.0│ 6.0│ 111.54 │ 4019.60│ 288.57│ 6.00│ 6351.00│ 7.55│ 1688.20│ 196.64│ 3.89│-2331.40│ 6.07 │ 87.56 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 22.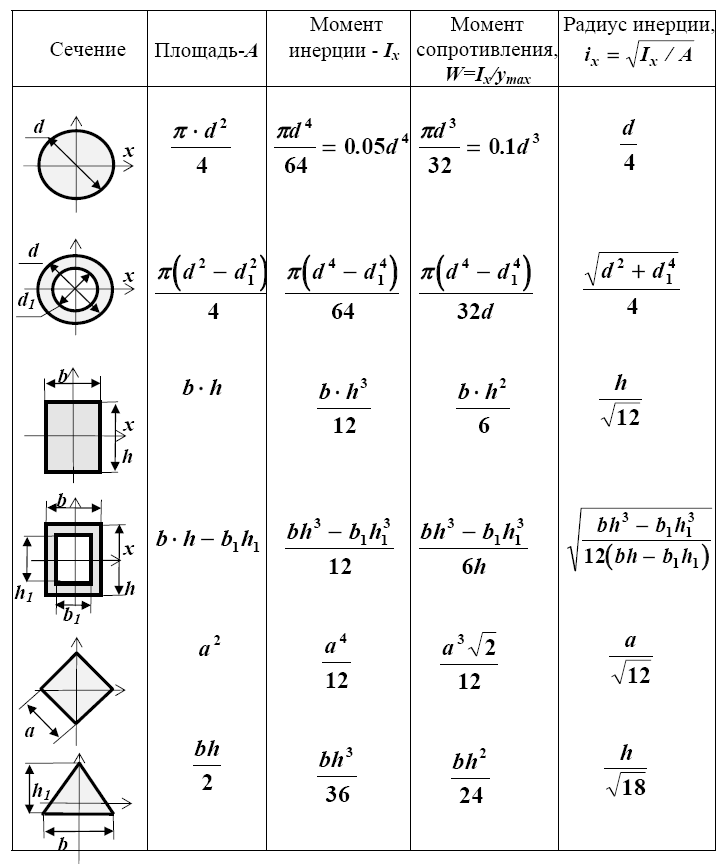 0 │ 220│ 14.0│ 21.0│ 7.0│ 60.38 │ 2814.40│ 175.18│ 6.83│ 4470.20│ 8.61│ 1158.60│ 138.03│ 4.38│-1655.80│ 5.93 │ 47.40 ║
║ │ 220│ 16.0│ 21.0│ 7.0│ 68.58 │ 3175.40│ 198.71│ 6.80│ 5045.40│ 8.58│ 1305.50│ 153.35│ 4.36│-1869.90│ 6.02 │ 53.83 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 25.0 │ 250│ 16.0│ 24.0│ 8.0│ 78.40 │ 4717.10│ 258.43│ 7.76│ 7492.10│ 9.78│ 1942.10│ 203.53│ 4.98│-2775.00│ 6.75 │ 61.55 ║
║ │ 250│ 18.0│ 24.0│ 8.0│ 87.72 │ 5247.20│ 288.82│ 7.73│ 8336.70│ 9.75│ 2157.80│ 223.32│ 4.96│-3089.50│ 6.83 │ 68.86 ║
║ │ 250│ 20.0│ 24.0│ 8.0│ 96.96 │ 5764.90│ 318.76│ 7.71│ 9159.70│ 9.72│ 2370.00│ 242.35│ 4.94│-3394.90│ 6.92 │ 76.11 ║
║ │ 250│ 22.0│ 24.0│ 8.0│ 106.12 │ 6270.30│ 348.26│ 7.69│ 9961.60│ 9.69│ 2579.00│ 260.69│ 4.93│-3691.30│ 7.00 │ 83.31 ║
║ │ 250│ 25.0│ 24.0│ 8.0│ 119.71 │ 7006.40│ 391.72│ 7.65│11126.
0 │ 220│ 14.0│ 21.0│ 7.0│ 60.38 │ 2814.40│ 175.18│ 6.83│ 4470.20│ 8.61│ 1158.60│ 138.03│ 4.38│-1655.80│ 5.93 │ 47.40 ║
║ │ 220│ 16.0│ 21.0│ 7.0│ 68.58 │ 3175.40│ 198.71│ 6.80│ 5045.40│ 8.58│ 1305.50│ 153.35│ 4.36│-1869.90│ 6.02 │ 53.83 ║
╟──────┼────┼─────┼─────┼────┼────────┼────────┼───────┼─────┼────────┼─────┼────────┼───────┼─────┼────────┼──────┼────────╢
║ 25.0 │ 250│ 16.0│ 24.0│ 8.0│ 78.40 │ 4717.10│ 258.43│ 7.76│ 7492.10│ 9.78│ 1942.10│ 203.53│ 4.98│-2775.00│ 6.75 │ 61.55 ║
║ │ 250│ 18.0│ 24.0│ 8.0│ 87.72 │ 5247.20│ 288.82│ 7.73│ 8336.70│ 9.75│ 2157.80│ 223.32│ 4.96│-3089.50│ 6.83 │ 68.86 ║
║ │ 250│ 20.0│ 24.0│ 8.0│ 96.96 │ 5764.90│ 318.76│ 7.71│ 9159.70│ 9.72│ 2370.00│ 242.35│ 4.94│-3394.90│ 6.92 │ 76.11 ║
║ │ 250│ 22.0│ 24.0│ 8.0│ 106.12 │ 6270.30│ 348.26│ 7.69│ 9961.60│ 9.69│ 2579.00│ 260.69│ 4.93│-3691.30│ 7.00 │ 83.31 ║
║ │ 250│ 25.0│ 24.0│ 8.0│ 119.71 │ 7006.40│ 391.72│ 7.65│11126. 00│ 9.64│ 2887.30│ 287.00│ 4.91│-4119.10│ 7.11 │ 93.97 ║
║ │ 250│ 28.0│ 24.0│ 8.0│ 133.12 │ 7716.90│ 434.25│ 7.61│12244.00│ 9.59│ 3189.90│ 312.01│ 4.90│-4527.00│ 7.23 │ 104.50 ║
║ │ 250│ 30.0│ 24.0│ 8.0│ 141.96 │ 8176.80│ 462.11│ 7.59│12965.00│ 9.56│ 3389.00│ 328.03│ 4.89│-4787.80│ 7.30 │ 111.44 ║
║ │ 250│ 35.0│ 24.0│ 8.0│ 163.71 │ 9281.00│ 530.11│ 7.53│14683.00│ 9.47│ 3879.30│ 366.13│ 4.87│-5401.70│ 7.49 │ 128.51 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝
00│ 9.64│ 2887.30│ 287.00│ 4.91│-4119.10│ 7.11 │ 93.97 ║
║ │ 250│ 28.0│ 24.0│ 8.0│ 133.12 │ 7716.90│ 434.25│ 7.61│12244.00│ 9.59│ 3189.90│ 312.01│ 4.90│-4527.00│ 7.23 │ 104.50 ║
║ │ 250│ 30.0│ 24.0│ 8.0│ 141.96 │ 8176.80│ 462.11│ 7.59│12965.00│ 9.56│ 3389.00│ 328.03│ 4.89│-4787.80│ 7.30 │ 111.44 ║
║ │ 250│ 35.0│ 24.0│ 8.0│ 163.71 │ 9281.00│ 530.11│ 7.53│14683.00│ 9.47│ 3879.30│ 366.13│ 4.87│-5401.70│ 7.49 │ 128.51 ║
╚══════╧════╧═════╧═════╧════╧════════╧════════╧═══════╧═════╧════════╧═════╧════════╧═══════╧═════╧════════╧══════╧════════╝