Лабораторная работа № 3 определение момента инерции маятника обербека

Цель работы: определить экспериментальным путем момент инерции маятника и исследовать экспериментальную зависимость момента инерции маятника от расстояния грузов, закрепленных на стержнях маятника.

Требуемое оборудование: Модульный учебный комплекс МУК-М1, блок секундомер электронный СЭ1, блок механический БМ1.

Описание установки.

Рис. 1

Маятник Обербека представляет собой крестовину, состоящую из четырех стержней с нанесенными на них делениями, прикрепленных к барабану с осью (рис. 1). На стержни надеваются одинаковые грузы массой , которые могут быть закреплены на расстоянииот оси вращения. На барабане имеется два шкива с различными диаметрамии. На шкив наматывается нить, к свободному концу которой прикрепляется груз массы. Под действием груза нить разматывается и приводит маятник во вращательное движение, которое предполагается равноускоренным.

Время движения грузаизмеряется электронным секундомером, включение которого производиться кнопкой «Пуск», а остановка происходит по сигналу фотодатчика. Груз опускается на расстояние, измеряемое вертикально закрепленной линейкой. Установка оснащена электромеханическим тормозным устройством, управление которым осуществляется по сигналу фотодатчика.

Краткие теоретические сведения

1) Расчет момента инерции маятника Обербека и момента сил сопротивления.

Для расчета движения механической системы маятник-груз применим уравнение динамики поступательного движения для груза, закрепленного на нити, и уравнение динамики вращательного движения для маятника.

Груз массой движется с ускорениемпод действием результирующей сил тяжестии силы натяжения нити(рис. 2). Запишем для груза второй закон Ньютона в проекции на направление движения:

. (1)

Рис.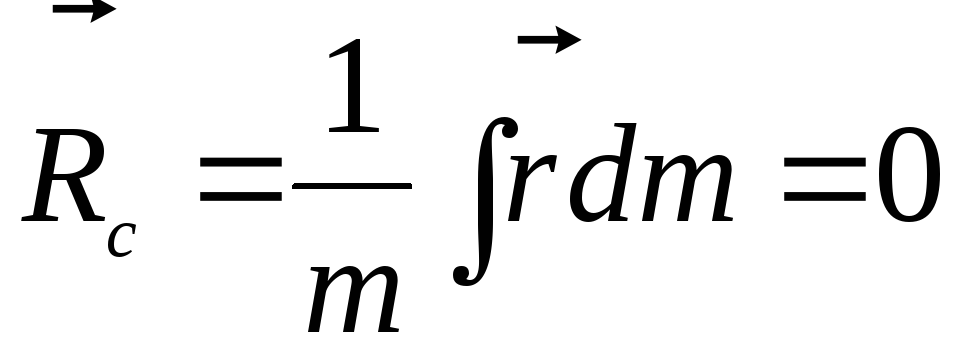 2

Сила натяжения передается нитью от груза к шкиву вращающегося маятника. Если предположить, что нить невесомая, то на шкив маятника действует сила , равная по величинеи противоположная ей по направлению (следствие третьего закона Ньютона:). Сила натяжения создает вращательный моментотносительно горизонтальной оси, направленной вдоль этой оси «от нас» и приводящей в движение маятник Обербека. Величина этого момента равна. Здесь- радиус шкива, на который намотана нить,, где- диаметр шкива. Момент силы сопротивления относительно вращениянаправлен в противоположную сторону («к нам»).

Запишем для основной закон динамики вращательного движения:

,

где — результирующий момент сил,- момент инерции маятника,- угловое ускорение. В скалярной форме это уравнение имеет вид (записаны проекции векторов моментов сил и углового ускорения на ось вращения, направление которой выбрано «от нас»)

. (2)

Используя кинематическую связь линейного и углового ускорения , а также уравнение движения груза при нулевой начальной скорости, выразимчерез измеряемые величиныи:

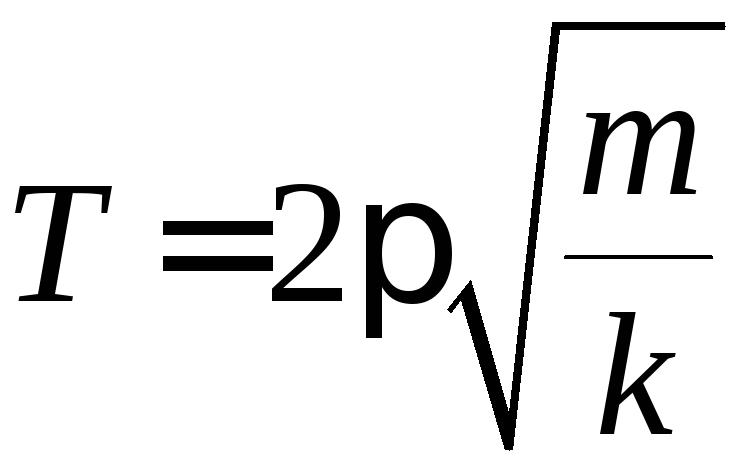. (3)

Решим систему уравнений (1) и (2), для чего умножим (1) на и сложим с (2):

.

Выражаем момент инерции маятника Обербека:

. (4)

Все величины, кроме , входящие в это уравнение, известны. Поставим задачу экспериментального определения.

Пусть — момент инерции маятника Обербека без грузов. Из (4) следует, что

.

В условиях эксперимента , что позволяет считать зависимостьлинейной. Эту зависимость можно использовать для экспериментальной оценки величины. Действительно, если полученную экспериментально зависимостьэкстраполировать до пересечения с осью абсцисс, т.е. до точкина этой оси, для которой выполняется равенство, то это позволяет определитькак

. (6)

Для определения момента инерции маятника воспользуемся (4), где величинапредварительно определена из измеренийи формулы (6).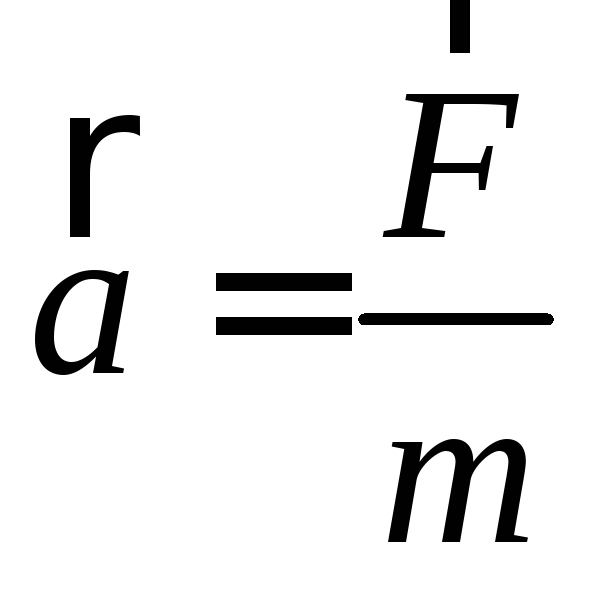

Подставив выражениеиз (3) ииз (6) в (4), получим рабочую формулу для определения момента инерции маятника

.

Для используемого в работе маятника Обербека справедливо неравенство . Учитывая это, получаем:

.

Для расчетов удобно представить момент инерции в виде:

, (7)

где .

2) Зависимость момента инерции маятника от расстояния грузов до оси вращения

Момент инерции маятника Обербека может быть представлен как сумма моментов инерции барабана со стержнями () и моментов инерции четырех грузов массой, закрепленных на расстоянияхот оси вращения (). Если размеры этих грузиков малы по сравнению с, то их можно считать материальными точками. Для материальной точки момент инерции равен. Тогда момент инерции маятника

. (8)

Эту зависимость момента инерции от расстояния грузов до оси вращения предполагается проверить, используя результаты, полученные по формуле (7).

Значение можно взять из данных эксперимента для определения момента инерции маятника Обербека без грузов, считая, что момент сил сопротивления остается постоянным.

Задание к работе

1. Получите допуск к выполнению лабораторной работы у преподавателя.

2. Приступив к работе, снимите грузы со стержней, если они там находятся.

3. Заранее выберите отметку (например, 50 см), от которой начнется движение груза .

4. Вращая маятник рукой, намотайте нить на шкив большего диаметра, следя, чтобы груз достиг выбранного положения.

5. Включите электронный секундомер.

6. Проведите первый опыт, используя в качестве груза, тянущего нить, только одну подставку массой без подгрузков. Предварительно нажатием кнопки «Режим» установите режим № 1 (светится индикатор «Реж. 1»). Затем нажмите кнопку «Пуск». При этом отключится тормозное устройство, удерживающее маятник, и одновременно включится секундомер. При включенном режиме № 1 секундомер в момент прохождения грузом нижней точки автоматически остановиться, причем одновременно сработает тормозное устройство. Внесите результаты первого опыта в таблицу измерений.

7. Проведите по одному опыту, поместив на подставку сначала один, а затем сразу два подгрузка. Результаты внесите в таблицу измерений. По формуле (3) рассчитайте величину углового ускорения для соответствующих значений.

8. Постройте зависимость по методу наименьших квадратов. Определите из графика по точке его пересечения с осью абсцисс значение, при котором. Рассчитайте по формуле (6) величину момента сил сопротивления.

9. Проведите прямые пятикратные измерения времени опускания груза для заданного расстояния .

10. Рассчитайте среднее время и определите абсолютную погрешность измеренияпри доверительной вероятности.

11. Вычислите по формуле (7) среднее значение момента инерции барабана со стержнями .

12. Определите абсолютную погрешность косвенных измерений этого момента инерции и запишите результаты в виде.

13. Закрепив грузы на стержнях маятника на равном расстоянииот оси вращения, определите это расстояние, используя деления, нанесенные на стержни.

14. Проведите однократные измерения времени опускания груза массы(выберите одно значение) для одной высоты падения при трех различных расстоянияхот оси вращения.

15. Вычислите моменты инерции маятника с грузами на стержнях по формуле (7) при различных расстояниях . При этом, как показали предварительные опыты, можно с допустимой точностью использовать в качестве величиныее значение, найденное раннее для крестовины без грузов на спицах. Сравните полученные данные со значениями момента инерции, вычисленными по формуле (8) для соответствующих значений.

    Результаты вычислений занесите в таблицу измерений.

Примечание

• Масса каждого груза, закрепляемого на спице г;

• Масса груза подставки г;

• Масса каждого подгрузка г;

• Диаметр большого шкива мм;

• Диаметр малого шкива мм;

• Диаметр цилиндра, в который ввинчиваются спицы мм;

• Расстояние между рисками на спицах мм;

• Диаметр груза на спицах мм;

• Масса спицы г;

• Масса барабана без спиц г;

• Ускорение свободного падения м/с²;

Лабораторная работа 108

Маятник Максвелла

Цель работы: Определение момента инерции маятника Максвелла.

 

Приборы и принадлежности: маятник Максвелла FРМ-03, комплект сменных колец.

 

Теоретическое введение

Момент инерции – аналог массы. Как масса является мерой инертности при поступательном движении, так и момент инерции является мерой инертности при вращательном движении. При вращении тела вокруг различных осей моменты инерции различны. Величина момента инерции относительно какой-нибудь оси определяется пространственным распределением элементарных масс тела – геометрией тела. Аналитическое вычисление величины момента инерции производится путем интегрирования выражения

 

 

где r— плотность вещества в элементе объема dV, находящегося на расстоянии r от оси вращения.

При сложной форме поверхности тела и неравномерном распределении плотности аналитический подсчет величины момента инерции может быть достаточно сложной задачей.

Экспериментальное же определение момента инерции осуществить легко. В настоящей работе измеряется момент инерции металлических колец с помощью маятника Максвелла.

Маятник Максвелла – небольшой ролик, насаженный туго на ось, опускается под действием силы тяжести на двух нитях, предварительно намотанных на ось диска (рис.1).

 Нити во время движения вниз разматываются до полной длины, раскрутившийся диск продолжает вращательное движение и наматывает нити на ось, вследствие чего он поднимается вверх, замедляя при этом свое вращение. Дойдя до верхней точки, диск опять будет опускаться вниз и т.д. Диск будет совершать колебания вверх и вниз, поэтому такое устройство называется маятником.

Уравнение движения маятника Максвелла можно записать, используя основной закон динамики поступательного и вращательного движений. Уравнения движения маятника Максвелла без учета сил трения имеют вид:

Для поступательного движения, исходя из II законы Ньютона

 

 

А для вращательного движения

 

 

Связь между тангенциальным ускорением () поступательного движения и угловым ускорением () вращательного движения имеет вид:

 

 

где m — масса маятника, J - момент инерции маятника,
T — натяжение одной нити, r -радиус оси маятника вместе с намотанной на нее нитью подвески.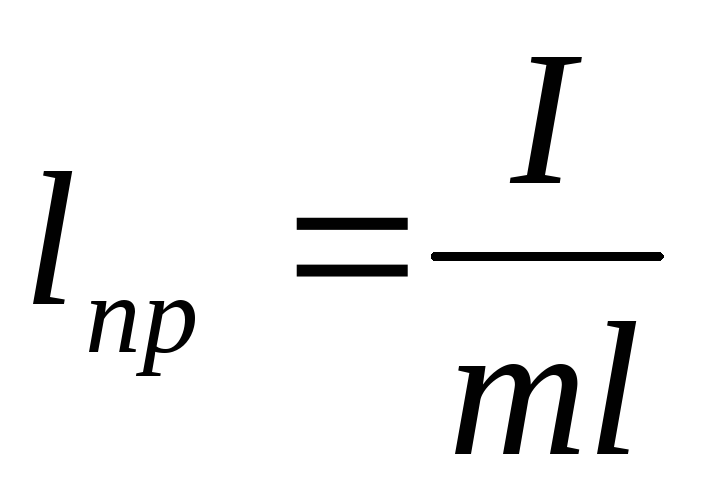

Ускорение a может быть найдено через измеренное время движения t и проходимое маятником расстояние h из известного уравнения

 

 

Из уравнений (1) – (4) может быть получена расчетная формула для момента инерции маятника Максвелла:

 

 

где D – внешний диаметр оси маятника вместе с намотанной на нее нитью подвески определяется по формуле

 

 

где D₀– диаметр оси маятника в м; D_n– диаметр нити подвески в м; h – длина маятника, равная высоте, на которую он поднимается в м; m – масса маятника вместе с кольцом в кг.

 

 

где m₀ – масса оси маятника в кг; m_р – масса ролика в кг; m_к – масса кольца, аксиально положенного на ролик в кг.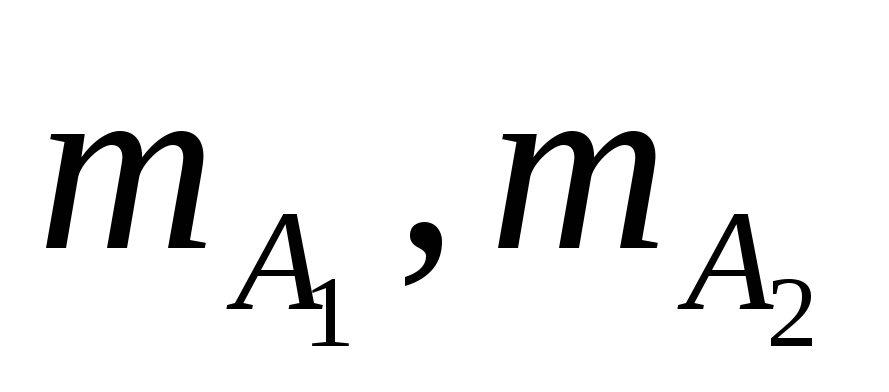

 

 

Описание рабочей установки и метода измерений

 

Параметры маятника:

• максимальная длина маятника h = 410 мм;

• количество сменных колец 3;

• размеры маятника: диаметр оси маятника D₀ = 10 мм;

внешний диаметр ролика D_р= 86 мм;

внешний диаметр колец D_к= 105 мм;

диаметр нити подвески D_n= 0,5 мм.

Общий вид маятника FРМ показан на рис. 2.

Основание 1 оснащено регулируемыми ножками 2, которые позволяют произвести выравнивание прибора. В основании закреплена колонка 3, к которой прикреплен неподвижный верхний кронштейн 4 и подвижный нижний 5. На верхнем кронштейне находится электромагнит 6, фотоэлектрический датчик №1-7 и вороток 8 для закрепления и регулирования длины бифилярной подвески маятника.

Нижний кронштейн вместе с прикрепленным к нему фотоэлектрическим датчиком №2-9 можно перемещать вдоль колонки и фиксировать в произвольно избранном положении.

Маятник 10 – это ролик, закрепленный на оси и подвешенный по бифилярному способу, на который накладываются сменные кольца 11, изменяя, таким образом, момент инерции системы.

Маятник с наложенным кольцом удерживается в верхнем положении электромагнитом. Длина маятника определяется по миллиметровой шкале на колонке прибора. С целью облегчения этого измерения нижний кронштейн оснащен красным указателем, помещенным на высоте оптической оси нижнего фотоэлектрического датчика.

Ход работы

1.        Включить сетевой шнур измерителя в сеть, нажать клавишу «СЕТЬ», проверяя, все ли индикаторы измерителя высвечивают цифру ноль, и засветилась ли лампочка фотоэлектрического датчика?

2.         Нижний кронштейн прибора передвинуть и зафиксировать в крайнем положении.

3.        На ролик маятника надеть кольцо, прижимая его до упора.

4.        На ось маятника намотать нить подвески и зафиксировать ее. Проверить, отвечает ли нижняя грань кольца нулю шкалы на колонке. Если нет, отвинтить верхний кронштейн и отрегулировать его высоту. Привинтить верхний кронштейн.

5.        Нажать клавишу «ПУСК» миллисекундомера FРМ-03.

6.        Открутить гайку воротка для регулирования длины бифилярной подвески. Определить длину нити таким образом, чтобы край стального кольца после опускания маятника находился на 2 мм ниже оптической оси нижнего фотоэлектрического датчика. Одновременно произвести корректировку установки маятника, чтобы его ось была параллельна основанию прибора. Закрутить гайку воротка.

7.        Отжать клавишу «ПУСК» миллисекундомера FРМ-03.

8.        Намотать на ось маятника нить подвески, обращая внимание на то, чтобы она наматывалась равномерно.

9.        Зафиксировать маятник при помощи электромагнита.

10.    Повернуть маятник в направлении его движения на угол около 5⁰.

11.    Нажать клавишу «СБРОС».

12.    Нажать клавишу «ПУСК».

13.    Определить значение времени падения маятника. Опыт повторить 5 раз.

14.    Определить значение среднего времени падения маятника по формуле  где n – количество выполненных замеров; t_i – значение времени, полученное в i-ом замере;
<t> — среднее значение времени падения маятника.

15.    Со шкалы на вертикальной колонке прибора определить длину маятника.

16.    Используя формулу (6) и известные значения диаметров D₀ и D_n, определить диаметр оси вместе с намотанной на неё нитью.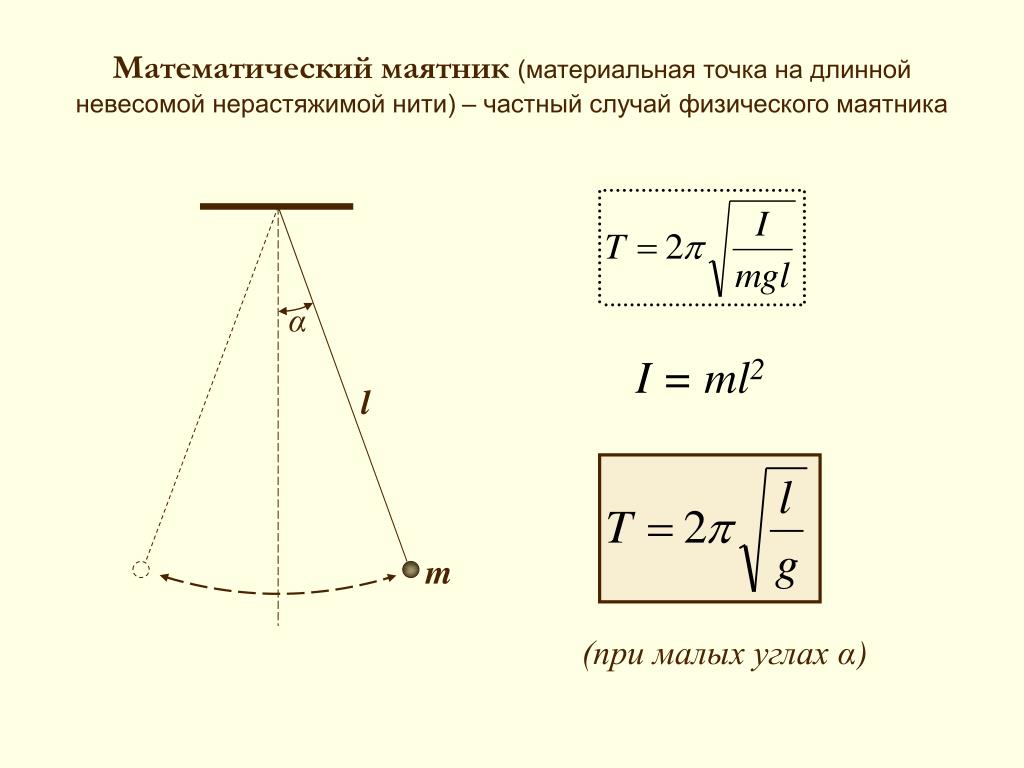

17.    По формуле (7) вычислить массу маятника вместе с аксиально наложенным кольцом. Значения масс отдельных элементов нанесены на них.

18.    По формуле (5) определить момент инерции маятника.

19.    Оценить погрешность результата измерений.

20.    Данные результатов измерений и вычислений занести в таблицу.

Таблица

№	ti	<t>	h	D	m	J	DJ	E
	с	с	м	м	кг	кг×м2	кг×м2	%

 

Вопросы для допуска к работе

1.       Какова цель работы?

2.      Дать определение момента инерции.

3.      Записать формулу момента инерции маятника Максвелла и пояснить величины, входящие в нее.

4.      Описать рабочую установку и ход работы.

Вопросы для защиты работы

1.      Записать основной закон динамики для поступательного и вращательного движения твердого тела.

2.      Вывести формулу для момента инерции маятника Максвелла.

3.      Записать закон сохранения механической энергии для маятника Максвелла.

4.      Получить дифференциальным методом формулу для расчета относительной погрешности (Е, %).

5.       Дать определение момента инерции материальной точки и твердого тела относительно неподвижной оси.

Простой маятник

Простой маятник
Следующий: Составной маятник Вверх: Колебательное движение Предыдущий: Торсионный маятник Рассмотрим груз, подвешенный на легкой нерастяжимой нити длины , такой, что масса может свободно раскачиваться из стороны в сторону в вертикальной плоскости, как показано на рис.  97. Эта установка известна как простой маятник . Пусть — угол, образуемый между струной и нисходящая вертикаль. Очевидно, что состояние равновесия простого маятника соответствует ситуация, в которой масса неподвижна и висит вертикально вниз ( т.е. , ). Угловое уравнение движения маятника просто

(523)

где – момент инерции массы, – крутящий момент, действующий на систему. Для случае, учитывая, что масса по существу является точечной частицей и находится на расстоянии от ось вращения ( т.е. , точка вращения), легко заметить, что .

Рисунок 97: Простой маятник.

На массу действуют две силы: сила тяжести, направленная вниз, и натяжение струны, . Обратите внимание, однако, что натяжение не влияет на крутящий момент, так как его линия действия явно проходит через точку опоры. Из простой тригонометрии линия действия силы тяжести проходит на расстоянии от точка опоры. Следовательно, величина гравитационного момента равна . Кроме того, гравитационный момент равен восстанавливающий момент : т.е. , если масса немного смещен от своего равновесного состояния ( т.е. , ), то явно действует гравитационная сила чтобы подтолкнуть массу обратно к этому состоянию. Таким образом, мы можем написать

(524)

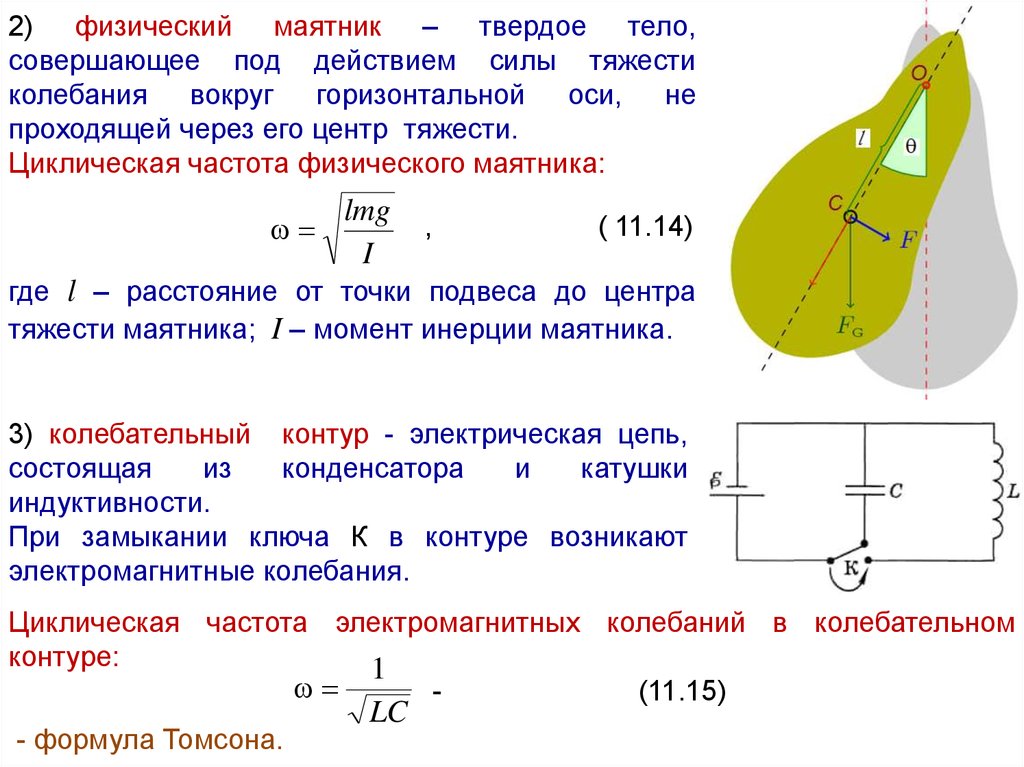
Объединяя два предыдущих уравнения, получаем следующее угловое уравнение движения маятника:

(525)

К сожалению, это , а не простое гармоническое уравнение. Действительно, приведенное выше уравнение не имеет замкнутое решение, которое может быть выражено в терминах простых функций.

Предположим, что мы ограничиваем наше внимание относительно малых отклонений от состояния равновесия. В другом Другими словами, предположим, что угол должен принимать довольно малые значения. Мы знаем, из тригонометрии, что менее чем примерно это является хорошим приближением к написать

(526)

Следовательно, в пределе малого угла , уравнение. (525) сводится к

(527)

где есть в привычной форме простого гармонического уравнения. По сравнению с нашей исходной простой гармоникой уравнение, уравнение (504), и его решение, заключаем, что угловая частота малой амплитуды колебания простого маятника задаются выражением

(528)

В этом случае частота маятника зависит только от длины маятника и местного гравитационного ускорения, и не зависит от массы маятника и амплитуды колебаний маятника (при условии, что останки хорошее приближение). Исторически, простой маятник был основой практически всех точных устройств для измерения времени до появление электронных часов. Простые маятники также можно использовать для измерения локальных изменений в . 92\theta.\]

Период физического маятника

Период физического маятника может быть получен из угловой частоты, найденной в разделе выше. Период с точки зрения угловой частоты определяется как:

\[\begin{align*}T&=\frac{1}{f}\\[8pt]&=\frac{2\pi}{\omega} \\[8pt]&=\frac{2\pi}{\sqrt{\frac{mgd}{I}}}\\[8pt]&=2\pi\sqrt{\frac{I}{mgd}} .\end{align*}\]

Физический маятник — ключевые выводы

• Физический маятник — это маятник, в котором вытянутый объект висит на точке вращения, смещенной от центра масс, относительно которого объект свободен вращать.
• Движение физического маятника определяется с помощью вращательной формы второго закона движения Ньютона; он аппроксимируется просто гармоническим для малых амплитуд колебаний.
• Период физического маятника зависит от массы, момента инерции, ускорения свободного падения и расстояния от точки вращения до центра тяжести: \(T=2\pi\sqrt{\frac{I }{mgd}}. \)
• Простой маятник — это частный случай физического маятника, который можно смоделировать как точечную массу, находящуюся на определенном расстоянии от точки вращения.

---

Каталожные номера

1. Рис. 1 — Качели из шин (https://pixabay.com/photos/outdoors-kids-playing-son-summer-1392494/) by halfpintohoney (https://pixabay.com/users /halfpintohoney-1284944/) под лицензией Pixabay (https://pixabay.com/service/license/).
2. Рис. 2. Однородный стержень в качестве маятника, StudySmarter Originals.
3. Рис. 3. Однородный стержень со смещенным шарниром, StudySmarter Originals.

Финальная викторина по физическому маятнику

Вопрос

Какое приближение нужно сделать, чтобы движение физического маятника было приблизительно просто гармоническим?

Показать ответ

Ответ

Малоугловое приближение для малых амплитуд движения.

Показать вопрос

Вопрос

От чего зависит период физического маятника , а не ?

Показать ответ

Ответ

Масса маятника.

Показать вопрос

Вопрос

Какое уравнение описывает период физического маятника?

Показать ответ

Ответ

\(T=2\pi\sqrt{\frac{I}{mgd}}\).

Показать вопрос

Вопрос

Что является примером физического маятника?

Показать ответ

Ответить

Маятник в напольных часах.

Показать вопрос

Вопрос

В чем разница между простым и физическим маятником?

Показать ответ

Ответ

Простой маятник — это тип физического маятника, который можно смоделировать как точечную массу на расстоянии от точки вращения.

Показать вопрос

Вопрос

Может ли физический маятник быть любой формы?

Показать ответ

Ответить

Показать вопрос

Вопрос

Мы можем экспериментально определить момент инерции объекта, превратив его в физический маятник и измерив период.

Показать ответ

Ответить

Показать вопрос

Вопрос

Какое из следующих уравнений мы используем, чтобы найти уравнение движения физического маятника?

Показать ответ

Ответ

\(\sum F=ma\).

Показать вопрос

Вопрос

Какое правильное уравнение для восстанавливающего крутящего момента физического маятника?

Показать ответ

Ответ

\(\tau=-mgd\sin\theta\).

Показать вопрос

Вопрос

Какова угловая частота физического маятника?

Показать ответ

Ответ

\(\omega=\sqrt{\frac{mgd}{I}}\).

Показать вопрос

Вопрос

Могут ли физические маятники одинаковой формы и веса иметь разные моменты инерции?

Показать ответ

Ответ

Показать вопрос

Вопрос

Чем отличается период простого маятника от периода физического маятника?

Показать ответ

Ответ

Период простого маятника зависит только от расстояния точки массы от точки вращения, тогда как период физического маятника зависит от массы, момента инерции и расстояния от центра тяжести.