Момент инерции твердого тела. Момент инерции математической точки, тело относительно неподвижной оси(от чего зависить) Осевой момент инерции тела

При изучении вращения твердых тел будем пользоваться понятием момента инерции.

Разобьем тело на такие малые части, что каждую из них можно считать материальной точкой. Пусть m i – масса i- й материальной точки, r i – ее расстояние до некоторой оси O .

Величина, равная произведению массы материальной точки на квадрат кратчайшего расстояния ее до данной оси, называется моментом инерции материальной точки относительно оси:

Сумма моментов инерции всех материальных точек тела называется моментом инерции тела относительно некоторой оси:

Момент инерции твердого тела зависит, как нетрудно видеть, от распределения масс относительно интересующей нас оси.

Если тело представляет собой обруч массы m , толщина которого мала по сравнению с радиусом R , то момент его инерции относительно оси, проходящей через центр и перпендикулярной к плоскости обруча, равен

Для тел более сложной формы суммирование выражения (5.

2) производится методами интегрального исчисления согласно формуле

где интегрирование производится по всему объему тела. Величина r
в этом случае есть функция положения точки с координатами x , y , z .

В качестве примера найдем момент инерции однородного диска относительно оси, перпендикулярной к плоскости диска и проходящей через его центр. Разобьем диск на кольцевые слои толщиной dr .

Все точки одного слоя будут находиться на одинаковом расстоянии от оси, равном r . Объем такого слоя равен:

,

где b – толщина диска. Поскольку диск однороден, плотность его во всех точках одинакова и

где dm –

масса кольцевого слоя.

Теперь по формуле (5.4) находим момент инерции

,

где R – радиус диска;

.

Наконец, введя массу диска m равную произведению плотности на объем диска , получим

Моменты инерции некоторых однородных твердых тел относительно оси, проходящей через центр масс тела , приведены в табл. 5.1.

Таблица 5.1

Если известен момент инерции тела относительно оси, проходящей через его центр масс, то можно найти момент инерции относительно любой другой параллельной оси. Для этого надо воспользоваться теоремой Гюйгенса – Штейнера :

момент инерции тела I относительно произвольной оси равен моменту его инерции I c относительно параллельной ей оси, проходящей через центр масс C тела, сложенному с произведением массы тела m на квадрат расстояния a между осями:

Найдем связь между моментами инерции тела относительно двух параллельных осей, одна из которых проходит через центр масс. Найдем момент инерции тела относительно оси z параллельной оси z C . Ось z C проходит через центр масс тела. Разделим мысленно тело на частицы массой m i , где i – порядковый номер. Определим положение каждой частицы относительно осей

z и z C . В соответствии с определением момента инерции , где – это кратчайшее расстояние до оси вращения (радиус окружности, которую описывает точка при своем движении вокруг оси вращения).

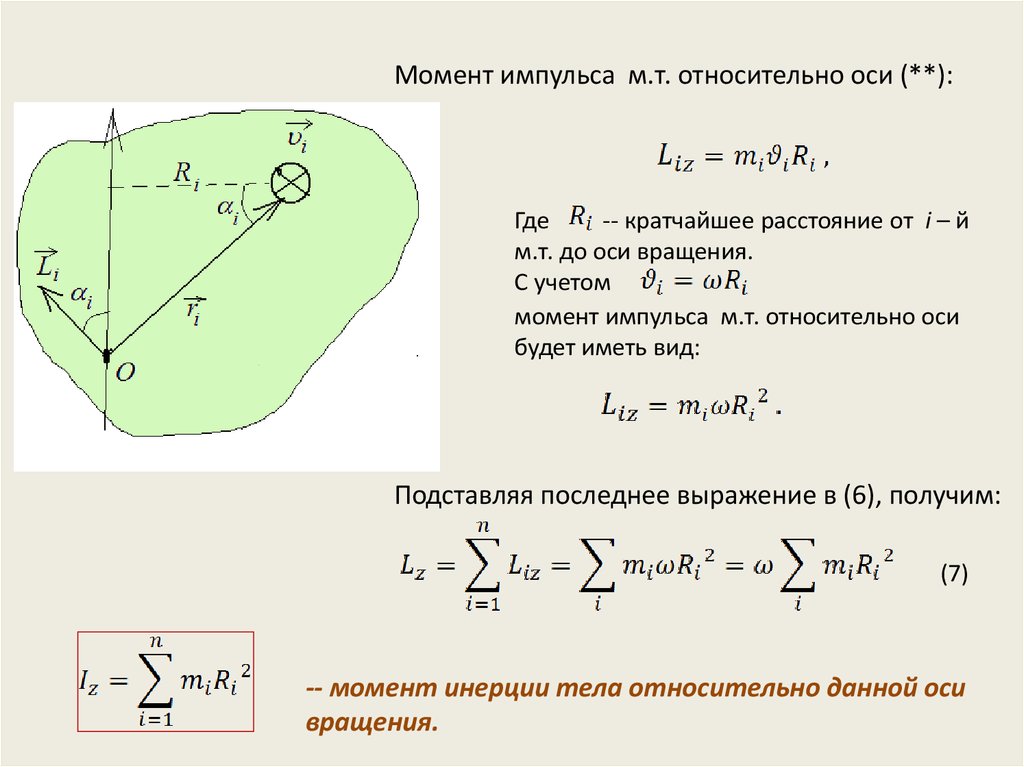
На рис. 5.3 видно, что , тогда момент инерции точки массой m i относительно оси z равен: , а для всего тела момент инерции относительно оси z равен сумме моментов инерции всех частиц тела относительно этой же оси:

(5.7)

По определению – момент инерции тела относительно оси z C , проходящей через центр масс тела; , тогда . Выражение можно преобразовать . Величина, равная определяет положение центра масс тела относительно оси

z C . Из рисунка видно, что , т.к. центр масс лежит на оси z C .

Тогда получим

(5.8)

– момент инерции I z тела относительно произвольной оси равен сумме момента инерции тела относительно параллельной ей оси z C , проходящей через центр масс, и величины ma 2 , где m – масса тела, a – расстояние между осями.

Пример. Момент инерции тонкого стержня (массы m и длины ) относительно оси, перпендикулярной стрежню и проходящей через его конец, равен.

Момент инерции

– характеристика инерциальных свойств при вращательном движении. Характеризует распределение массы относительно оси вращения.

– это точки

(это не «зе» английская, а знак такой).

Осевые моменты инерции некоторых тел:

Шар – , ось сплошного цилиндра , ось полого цилиндра — , прямой тонкий стержень — .

Теорема Штейнера – Для того, чтобы найти момент инерции относительно произвольной оси нужно сложить момент инерции этого телаотносительно оси, проходящей через центр масс тела параллельно рассматриваемой оси, и произведения массы тела на квадрат расстояния между осями.

Уравнение динамики вращательного движения твердого тела относительно неподвижной оси.

Момент силы определяет скорость изменения момента импульса.

Моментом силы F относительно неподвижной точки О называется физическая величина, определяемая векторным произведением радиуса-вектора r , проведенного из точ­ки О в точку А приложения силы, на силу F :

Здесь М — псевдовектор, его направление совпадает с направлением поступательного движения правого винта при его вращении от r к F. Модуль момента силы

где a- угол между r и F; r sina = l — кратчайшее расстояние между линией действия силы и точкой

О — плечо силы.

Моментом силы относительно неподвижной оси z называется скалярная величина M z , равная проекции на эту ось вектора М момента силы, определенного относительно произвольной точки О данной оси z. Значение момента М z не зависит от выбора положения точки О на оси z.

(18.3)

Уравнение (18.3) представляет собойуравнение динамики вращательного движения твердого тела относительно неподвижной оси.

Закон сохранения момента импульса.

В замкнутых системах моментов импульса отдельных частей с течением времени не изменяются.

(над всеми L нужен вектор «стрелка»).

В замкнутой системе момент внешних сил

Здесь мы продемонстрируем закон сохранения момента импульса с помощью скамьи Жуковского. Человек, сидящий на скамье, вращающаяся вокруг вертикальной оси, и держащий в вытянутых руках гантели (рис. 2), вращается внешним механизмом с угловой скоростью ω 1 . Если человек прижмет гантели к телу, то момент инерции системы уменьшится. Но момент внешних сил равен нулю, момент импульса системы сохраняется и угловая скорость вращения ω 2 увеличивается. Аналогичным образом, гимнаст во время прыжка через голову поджимает к туловищу руки и ноги, с целью уменьшить свой момент инерции и тем самым увеличить угловую скорость вращения.

Похожая информация:

1. Cатический момент сечения относительно оси, проходящей через центр тяжести сечения будет
2. В зависимости от места крепления ремней безопасности и положения тела рабочего в момент нагрузки, различные предохранительные пояса имеют различные преимущества.

Пусть имеется твердое тело. Выберем некоторую прямую ОО (рис.6.1), которую будем называть осью (прямая OO может быть и вне тела). Разобьем тело на элементарные участки (материальные точки) массами
, находящиеся от оси на расстоянии
соответственно.

Моментом инерции материальной точки относительно оси (OO) называется произведение массы материальной точки на квадрат ее расстояния до этой оси:

. (6.1)

Моментом инерции (МИ) тела относительно оси (OO) называется сумма произведений масс элементарных участков тела на квадрат их расстояния до оси:

. (6.2)

Как видно момент инерции тела есть величина аддитивная – момент инерции всего тела относительно некоторой оси равен сумме моментов инерции отдельных его частей относительно той же оси.

В данном случае

.

Измеряется момент инерции в кгм 2 . Так как

, (6.3)

где  – плотность вещества,

– объемi — го участка, то

,

или, переходя к бесконечно малым элементам,

. (6.4)

Формулу (6.4) удобно использовать для вычисления МИ однородных тел правильной формы относительно оси симметрии, проходящей через центр масс тела. Например, для МИ цилиндра относительно оси, проходящей через центр масс параллельно образующей, эта формула дает

,

где т — масса; R — радиус цилиндра.

Большую помощь при вычислении МИ тел относительно некоторых осей оказывает теорема Штейнера: МИ тела I относительно любой оси равен сумме МИ этого тела

I c относительно оси, проходящей через центр масс тела и параллельной данной, и произведения массы тела на квадрат расстояния d между указанными осями:

. (6.5)

Момент силы относительно оси

Пусть на тело действует сила F . Примем для простоты, что сила F лежит в плоскости, перпендикулярной некоторой прямой ОО (рис.6.2,а ), которую назовем осью (например, это ось вращения тела). На рис. 6.2,а А — точка приложения силы F ,
— точка пересечения оси с плоскостью, в которой лежит сила;r — радиус-вектор, определяющий положение точки А относительно точки О «; O «B = b — плечо силы. Плечом силы относительно оси называется наименьшее расстояние от оси до прямой, на которой лежит вектор силы F (длина перпендикуляра, проведенного из точки к этой прямой).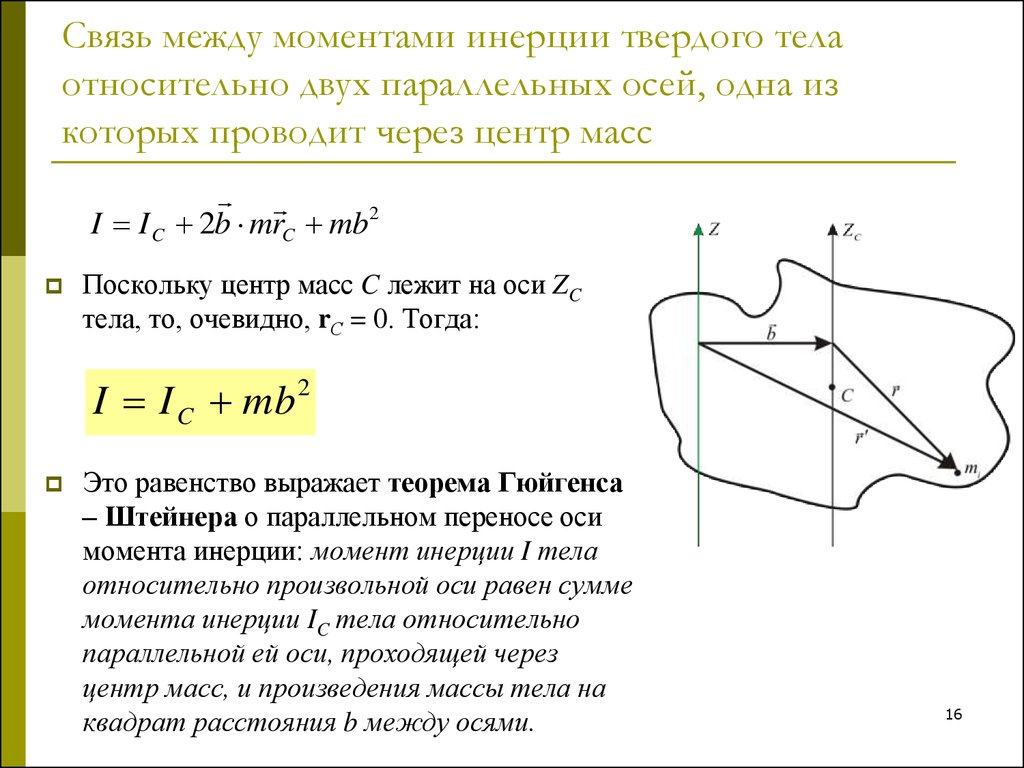

Моментом силы относительно оси называется векторная величина, определяемая равенством

. (6.6)

Модуль этого вектора . Иногда, поэтому говорят, что момент силы относительно оси – это произведение силы на ее плечо.

Если сила F направлена произвольно, то ее можно разложить на две составляющие; и(рис.6.2,б ), т.е.
+, где- составляющая, направленная параллельно оси ОО, алежит в плоскости, перпендикулярной оси. В этом случае под моментом силыF относительно оси OO понимают вектор

. (6.7)

В соответствии с выражениями (6.6) и (6.7) вектор М направлен вдоль оси (см. рис.6.2, а ,б ).

Момент импульса тела относительно оси вращения

Пусть тело вращается вокруг некоторой оси ОО с угловой скоростью
. Разобьем это тело мысленно на элементарные участки с массами
, которые находятся от оси соответственно на расстояниях
и вращаются по окружностям, имея линейные скорости
Известно, что величина равная
— есть импульсi -участка. Моментом импульса i -участка (материальной точки) относительно оси вращения называется вектор (точнее псевдовектор)

, (6.8)

где r i – радиус-вектор, определяющий положение i — участка относительно оси.

Моментом импульса всего тела относительно оси вращения называют вектор

(6.9)

модуль которого
.

В соответствии с выражениями (6.8) и (6.9) векторы
инаправлены по оси вращения (рис.6.3). Легко показать, что момент импульса тела L относительно оси вращения и момент инерции I этого тела относительно той же оси связаны соотношением

. (6.10)

1.10. УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

Твердое тело как система материальных точек. Движение центра инерции твердого тела. Кинетическая энергия вращающе гося тела. Понятие момента инерции относительно неподвижной оси. Теорема Штейнера. Моменты инерции некоторых простейших тел. Уравнение динамики вращательного движения относительно неподвижной оси.

Движение твердого тела в общем случае определяется двумя векторными уравнениями. Одно из них — уравнение движения центра масс (4.11), другое-уравнение моментов в С -системе (6.24):

(10 . 1 )

Зная законы действующих внешних сил, точки их приложения и начальные условия, можно с помощью этих уравнений найти как скорость, так и положение каждой точки твердого тела в любой момент времени, т. е. полностью решить задачу о движении тела. Однако, несмотря на кажущуюся простоту уравнений (10.1), решение их в общем случае представляет собой весьма трудную задачу. Это прежде всего обусловлено тем обстоятельством, что связь между собственным моментом импульса и скоростями отдельных точек твердого тела в С -системе оказывается сложной, за исключением немногих частных случаев. Мы не будем рассматривать эту задачу в общем виде (она решается в курсе теоретической механики) и ограничимся в дальнейшем только отдельными частными случаями.

Если перенести силы вдоль направления их действия, то ясно, что не изменятся ни их результирующая , ни их суммарный момент . При этом уравнения (10.1) тоже не изменятся, а следовательно не изменится и движение твердого тела. Поэтому точки приложения внешних сил можно переносить вдоль направления действия сил — удобный прием решения задач, которым постоянно пользуются.

Рассмотрим теперь понятие равнодействующей силы. В тех случаях, когда суммарный момент всех внешних сил оказывается перпендикулярным результирующей силе, т. е. , все внешние силы могут быть сведены к одной силе , действующей вдоль определенной прямой. В самом деле, если относительно некоторой точки О суммарный момент , то всегда можно найти такой вектор (рис. 10.1), что при заданных и

При этом выбор неоднозначен: прибавление к нему любого вектора ,

параллельного , не изменит последнего равенства. А это означает, что данное равенство определяет не точку «приложения» силы , а линию ее действия. Зная модули M и F соответствующих векторов, можно найти плечо l силы (рис.6.14): .

Таким образом, если , систему сил, действующих на отдельные точки твердого тела, можно заменить одной равнодействующей силой — силой, которая равна результирующей и создает момент, равный суммарному моменту всех внешних сил.

Таким случаем является действие однородного силового поля, например поля тяжести, в котором действующая на каждую частицу сила имеет вид . В этом случае суммарный момент сил тяжести относительно любой точки О равен

Стоящая в круглых скобках сумма, равна где масса тела радиус-вектор его центра масс относительно точки O . Поэтому

Это означает, что равнодействующая сил тяжести проходит через центр масс тела. Обычно говорят, что равнодействующая сил тяжести приложена к центру масс тела или к его центру тяжести. Момент этой силы относительно центра масс тела равен нулю.

Теперь перейдем к рассмотрению частных случаев движения твердого тела.

Вращение вокруг неподвижной оси.

Рассмотрим вращение твердого тела вокруг неподвижной оси. Найдем выражение для момента импульса твердого тела относительно оси 00″ (рис. 6.15). Момент импульса частицы можно записать в виде

где и — масса и расстояние от оси вращения частицы твердого тела, — его угловая скорость. Обозначив величину, стоящую в круглых скобках, через I, получим

(10 .2)

Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат кратчайшего расстояния от оси.

Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси.

Момент инерции твердого тела зависит от распределения масс относительно интересующей нас оси и является величиной аддитивной. Вычисление момента инерции тела проводится по формуле

где dm и dV — масса и объем элемента тела, находящегося на расстоянии от интересующей нас оси z, — плотность тела в данной точке.

Моменты инерции некоторых однородных твердых тел относительно оси, проходящей через центр масс тела, приведены в следующей таблице (здесь т — масса тела):

Вид твердого тела	Положение оси	Момент инерции
Тонкий стержень длины L	Перпендикулярно стержню
Сплошной цилиндр радиуса R	Совпадает с осью цилиндра
Тонкий диск радиуса R	Совпадает с диаметром диска
Шар радиуса R	Проходит через центр шара

Вычисление момента инерции твердого тела произвольной формы относительно той или иной оси представляет собой, вообще говоря, довольно кропотливую в математическом отношении задачу. Однако в некоторых случаях нахождение момента инерции значительно упрощается, если воспользоваться теоремой Штейнера : момент инерции I относительно произвольной оси z равен моменту инерции относительно оси параллельной данной и проходящей через центр масс С тела, плюс произведение массы т тела нa квадрат расстояния а между осями:

(10 . 4 )

Таким образом, если известен момент инерции то нахождение момента инерции I элементарно. Например, момент инерции тонкого стержня (массы т и длины l ) относительно оси, перпендикулярной стержню и проходящей через его конец, равен

Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением. Получим выражение для кинетической энергии вращающегося твердого тела с неподвижной осью вращения. Учитывая связь скорости частицы вращающегося твердого тела с угловой скоростью запишем

или, более коротко

где — момент инерции тела относительно оси вращения, проходящей через его центр масс, -угловая скорость тела, т — его масса, — скорость центра инерции тела в K-системе отсчета.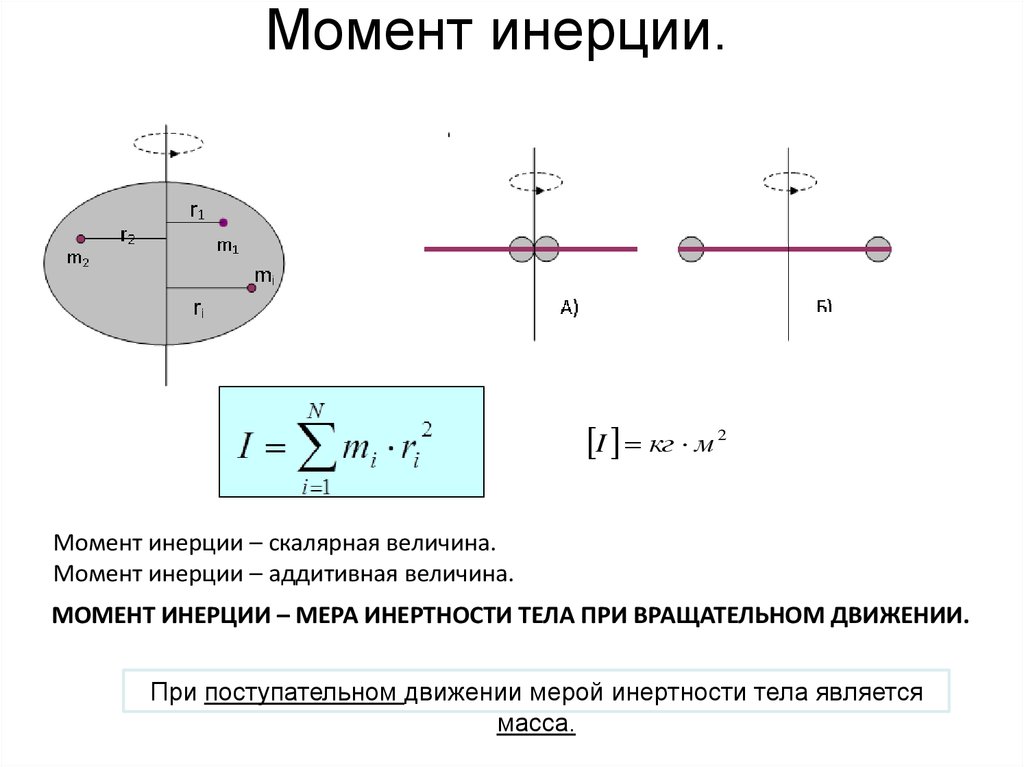 Таким образом, кинетическая энергия твердого тела при плоском движении складывается из энергии вращения в С-системе и энергии, связанной с движением центра масс .

Запишем основное уравнение динамики вращения твердого тела с неподвижной осью вращения. Это уравнение легко получить, как следствие как следствие уравнения моментов для материальной точки, если продифференцировать (10.2) по времени, тогда

(10 . 7 )

где — суммарный момент всех внешних сил относительно оси вращения, проекция углового ускорения на ось вращения. Из этого уравнения, в частности, видно, что момент инерции I определяет инерционные свойства твердого тела при вращении: при одном и том же значении момента сил тело с большим моментом инерции приобретает меньшее угловое ускорение. Моменты сил относительно оси — величины алгебраические: их знаки зависят как от выбора положительного направления оси z , совпадающей с осью вращения, так и от направления

«вращения» соответствующего момента силы.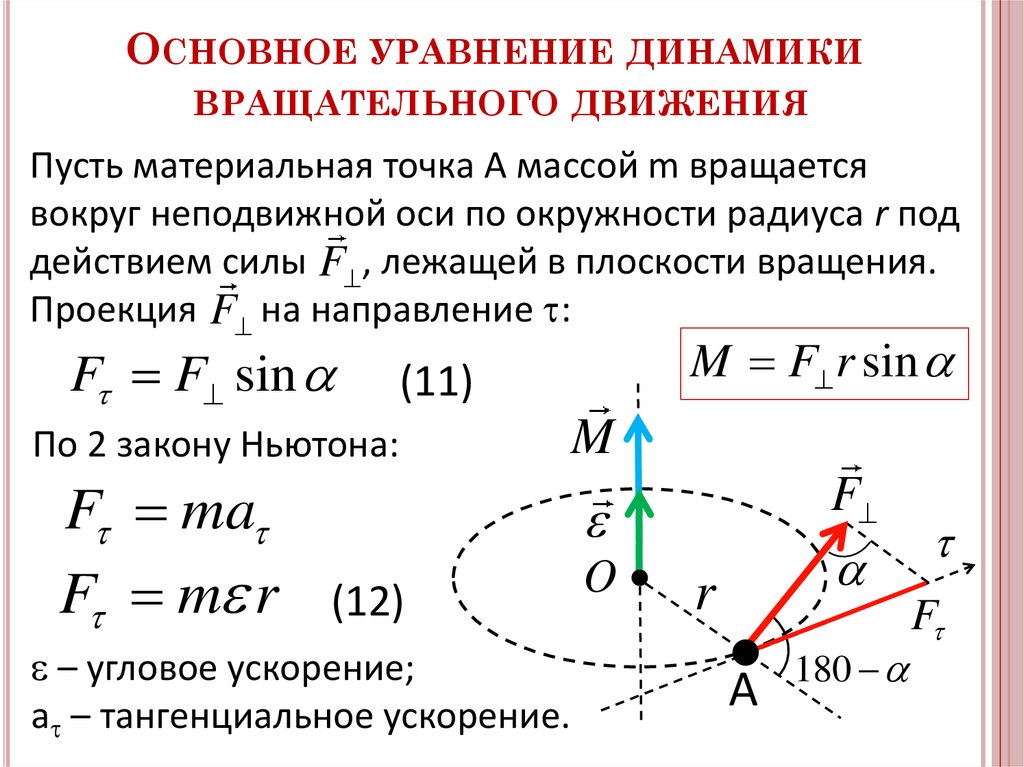 Например, выбрав положительное направление оси z , как показано на рис. 10.3, мы тем самым задаем и положительное направление отсчета угла — оба эти направления связаны правилом правого винта. Полагают, что если некоторый момент «вращает» в положительном направлении угла, то он считается положительным, и наоборот. А знак суммарного момента в свою очередь определяет знак — проекции вектора углового ускорения на ось z.

Интегрирование уравнения (10.7) с учетом начальных условий -значений угловой скорости и угла и начальный момент времени — позволяет полностью решить задачу о вращении твердого тела вокруг неподвижной оси, т. е. найти зависимость от времени угловой скорости и угла поворота.

Заметим, что уравнение (10.7) справедливо в любой системе отсчета, жестко связанной с осью вращения. Однако если система отсчета неинерциальная, то необходимо помнить, что момент сил включает в себя не только моменты сил взаимодействия с другими телами, но и моменты сил инерции.

Пусть имеется твердое тело. Выберем некоторую прямую ОО (рис.6.1), которую будем называть осью (прямая OO может быть и вне тела). Разобьем тело на элементарные участки (материальные точки) массами
, находящиеся от оси на расстоянии
соответственно.

Моментом инерции материальной точки относительно оси (OO) называется произведение массы материальной точки на квадрат ее расстояния до этой оси:

. (6.1)

Моментом инерции (МИ) тела относительно оси (OO) называется сумма произведений масс элементарных участков тела на квадрат их расстояния до оси:

. (6.2)

Как видно момент инерции тела есть величина аддитивная – момент инерции всего тела относительно некоторой оси равен сумме моментов инерции отдельных его частей относительно той же оси.

В данном случае

.

Измеряется момент инерции в кгм 2 . Так как

, (6.3)

где  – плотность вещества,
– объемi — го участка, то

,

или, переходя к бесконечно малым элементам,

. (6.4)

Формулу (6.4) удобно использовать для вычисления МИ однородных тел правильной формы относительно оси симметрии, проходящей через центр масс тела. Например, для МИ цилиндра относительно оси, проходящей через центр масс параллельно образующей, эта формула дает

,

где т — масса; R — радиус цилиндра.

Большую помощь при вычислении МИ тел относительно некоторых осей оказывает теорема Штейнера: МИ тела I относительно любой оси равен сумме МИ этого тела I c относительно оси, проходящей через центр масс тела и параллельной данной, и произведения массы тела на квадрат расстояния d между указанными осями:

. (6.5)

Момент силы относительно оси

Пусть на тело действует сила F . Примем для простоты, что сила F лежит в плоскости, перпендикулярной некоторой прямой ОО (рис.6.2,а ), которую назовем осью (например, это ось вращения тела). На рис. 6.2,а А — точка приложения силы F ,
— точка пересечения оси с плоскостью, в которой лежит сила;r — радиус-вектор, определяющий положение точки А относительно точки О «; O «B = b — плечо силы. Плечом силы относительно оси называется наименьшее расстояние от оси до прямой, на которой лежит вектор силы F (длина перпендикуляра, проведенного из точки к этой прямой).

Моментом силы относительно оси называется векторная величина, определяемая равенством

. (6.6)

Модуль этого вектора . Иногда, поэтому говорят, что момент силы относительно оси – это произведение силы на ее плечо.

Если сила F направлена произвольно, то ее можно разложить на две составляющие; и(рис.6.2,б ), т.е.
+, где- составляющая, направленная параллельно оси ОО, алежит в плоскости, перпендикулярной оси. В этом случае под моментом силыF относительно оси OO понимают вектор

. (6.7)

В соответствии с выражениями (6.6) и (6.7) вектор М направлен вдоль оси (см. рис.6.2, а ,б ).

Момент импульса тела относительно оси вращения

Пусть тело вращается вокруг некоторой оси ОО с угловой скоростью
. Разобьем это тело мысленно на элементарные участки с массами
, которые находятся от оси соответственно на расстояниях
и вращаются по окружностям, имея линейные скорости
Известно, что величина равная
— есть импульсi -участка. Моментом импульса i -участка (материальной точки) относительно оси вращения называется вектор (точнее псевдовектор)

, (6.8)

где r i – радиус-вектор, определяющий положение i — участка относительно оси.

Моментом импульса всего тела относительно оси вращения называют вектор

(6.9)

модуль которого
.

В соответствии с выражениями (6.8) и (6.9) векторы
инаправлены по оси вращения (рис.6.3). Легко показать, что момент импульса тела L относительно оси вращения и момент инерции I этого тела относительно той же оси связаны соотношением

. (6.10)

Динамика твердого тела. Основное уравнение динамики вращательного движения. Момент инерции. Вращение твердого тела вокруг неподвижной оси. Плоское движение твердого тела

Тема 12 Динамика твердого тела

1 Основное уравнение динамики вращательного движения

2 Момент инерции

3 Вращение твердого тела вокруг неподвижной оси

4 Плоское движение твердого тела

Основные понятия по теме

К основным видам движения твердого тела относятся:

— поступательное движение твердого тела;

— вращение твердого тела вокруг неподвижной оси;

— плоское движение твердого тела;

— вращение твердого тела вокруг неподвижной точки;

— свободное движение твердого тела.

Из перечисленных видов движения четыре последних типа связаны с вращательным движением. При описании этих видов движения используется уравнение моментов

,                                               (12.1)

которое принято называть основным уравнением динамики вращательного движения. Так же как и основное уравнение динамики основное уравнение динамики вращательного движения (12.1) можно записать в другом виде

,                                              (12.2)

где угловое ускорение тела.

Величина , входящая в уравнение (12.2), является аналогом массы при вращательном движении твердого тела. Ее называют момент инерции. Момент инерции материальной точки равен

,                                             (12.3)

где масса материальной точки, расстояние от материальной точки до оси вращения. Для системы материальных точек и твердого тела моменты инерции соответственно равны

;                                            (12. 4)

.                                             (12.5)

В выражении (12.5) интегрирование ведется по объему тела.

Момент инерции зависит от положения оси вращения и распределения масс относительно этой оси. Приведем выражения для моментов инерции некоторых тел относительно оси вращения,.положение которой указывается в скобках.

Сплошной цилиндр или диск радиуса R(ось симметрии)

.                                              (12.6)

Полый тонкостенный цилиндр радиуса R или обруч (ось симметрии)

.                                               (12.7)

Однородный тонкий стержень длиной l (ось перпендикулярна стержню и проходит через его середину)

 .                                              (12.8)

Шар радиуса R (ось проходит через центр шара)

.                                            (12.9)

Если известен момент инерции тела относительно оси, проходящей через его центр масс С, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера:

момент инерции тела J относительно произвольной оси Z равен сумме момента инерции тела  относительно параллельной оси, проходящей через центр масс С тела, и произведения массы m тела на квадрат расстояния а между осями.

Вращающееся тело, как и тело движущееся поступательно, обладает энергией движения.

Кинетическая энергия твердого тела вращающегося вокруг неподвижной оси Z с угловой скоростью

.                                      (12.10)

Кинетическая энергия тела совершающего плоское движение равна

,                                 (12.11)

где скорость центра масс тела, угловая скорость тела, момент инерции тела относительно собственной оси.

Вопросы для самоконтроля

1 Назовите виды движения твердого тела.

2 Что понимают под плоским движением твердого тела? Приведите примеры такого движения. Почему этот вид движения называют плоское движение?

3 Чем отличаются траектории точки твердого тела вращающегося вокруг неподвижной оси и вокруг неподвижной точки О?

4 Дайте определение момента инерции материальной точки, системы материальных точек, твердого тела. Что характеризует момент инерции? От каких факторов он зависит?

5 Объясните смысл утверждения «момент инерции это аддитивная величина».

6 Сформулируйте теорему Штейнера.

7 Что понимаю под тензором моментов инерции? Чем обусловлено необходимость введения такого понятия? Какие моменты инерции называются осевыми?, центробежными?

8 Запишите основное уравнение динамики вращательного движения в различных формах. Установите аналогию записанных выражений с уравнениями динамики поступательного движения.

9 Опишите последовательность действий при решении основной задачи динамики твердого тела.

10 Запишите выражения для энергии твердого тела вращающегося вокруг неподвижной оси, вокруг неподвижной точки. Напишите аналогичное выражение для тела, совершающего плоское движение.

Примеры решения задач

1 В схеме, показанной на рисунке 12.1, определить ускорение груза массы m. Масса М, момент инерции J, внутренний  и внешний  радиусы ступенчатого блока известны.

Решение. Силы, действующие на груз и блок, показаны на рисунке 12.1. Запишем второй закон Ньютона для груза m

.                  (1)

Для блока, который участвует в поступательном и вращательном движениях, необходимо записать второй закон Ньютона и основное уравнение динамики вращательного движения

;                                    (2)

.                                 (3)

В уравнении (3) через  обозначен момент, соответствующий силе  относительно точки О лежащей на оси блока.

В проекциях на оси системы координат XYZ система векторных уравнений () принимает вид

;                                        (4)

;                                    (5)

                                       (6)

и содержит шесть неизвестных: , , , , , .

Для решения системы уравнений () учтем, что, согласно третьему закону Ньютона . Кроме того, для точки A, участвующей в поступательном движении груза m и вращательном движении блока, и точки В, участвующей в поступательном и вращательном движениях блока, можем записать

 и .

Учитывая приведенные выше соотношения, вместо системы уравнений ()имеем

;                                        (7)

;                                 (8)

формулы, теорема Штейнера, пример решения задачи

Количественное изучение динамики и кинематики вращательного движения предполагает знание момента инерции материальной точки и твердого тела относительно оси вращения. Рассмотрим в статье, о каком параметре идет речь, а также приведем формулу для его определения.

Общие сведения о физической величине

Сначала дадим определение момента инерции материальной точки и твердого тела, а затем покажем, как его следует использовать при решении практических задач.

Под указанной физической характеристикой для точки, имеющей массу m, которая вокруг оси вращается на расстоянии r, подразумевается следующая величина:

I = m * r².

Откуда следует, что единицей измерения изучаемого параметра являются килограммы на квадратный метр (кг*м²).

Если вместо точки вокруг оси вращается тело сложной формы, которое имеет произвольное распределение массы внутри себя, то его момент инерции определяется так:

I = ∫_m(r² * dm) = ρ * ∫_V(r² * dV).

Где ρ — плотность тела. С помощью интегральной формулы можно определить величину I для абсолютно любой системы вращения.

Момент инерции имеет точно такой же смысл для вращения, как масса для поступательного движения. Например, каждый знает, что швабру для мытья полов легче всего вращать вокруг оси, проходящей через ее ручку, чем через перпендикулярную ей. Связано это с тем, что момент инерции в первом случае гораздо меньше, чем во втором.

Величина I для тел разной формы

При решении задач по физике на вращение часто необходимо знать момент инерции для тела конкретной геометрической формы, например, для цилиндра, шара или стержня. Если применить записанную выше формулу для I, то несложно получить соответствующее выражение для всех отмеченных тел. Ниже приведены формулы для некоторых из них:

стержень: I = 1 / 12 * M * L²;

цилиндр: I = 1 / 2 * M * R²;

сфера: I = 2 / 5 * M * R².

Здесь приведены I для оси вращения, которая проходит через центр массы тела. В случае цилиндра ось параллельна генератрисе фигуры. Момент инерции для других геометрических тел и вариантов расположения осей вращения можно найти в соответствующих таблицах. Заметим, что для определения I разных фигур достаточно знать всего один геометрический параметр и массу тела.

Момент инерции можно определить, если ось вращения расположена на некотором расстоянии от тела. Для этого следует знать длину этого отрезка и величину I_O тела относительно проходящей через центр его массы оси, которая должна быть параллельна рассматриваемой. Устанавливающая связь между параметром I_O и неизвестным значением I закрепляется в теореме Штейнера. Момент инерции материальной точки и твердого тела математически записывается следующим образом:

I = I_O + M * h².

Здесь M — масса тела, h — расстояние от центра массы до оси вращения, относительно которой необходимо вычислить I. Это выражение несложно получить самостоятельно, если воспользоваться интегральной формулой для I и учесть, что все точки тела находятся на расстояниях r = r₀ + h.

Теорема Штейнера значительно облегчает определение I для многих практических ситуаций. Например, если необходимо найти I для стержня длиной L и массой M относительно оси, которая проходит через его конец, то применение теоремы Штейнера позволяет записать:

I = I_O + M * (L / 2)² = 1 / 12 * M * L² + M * L² / 4 = M * L² / 3.

Можно обратится к соответствующей таблице и увидеть, что в ней приводится именно эта формула для тонкого стержня с осью вращения на его конце.

Уравнение моментов

В физике вращения существует формула, которая называется уравнением моментов. Выглядит она следующим образом:

M = I * α.

Здесь M — момент силы, α — угловое ускорение. Как видно, момент инерции материальной точки и твердого тела и момент силы линейно связаны друг с другом. Величина M определяет возможность некоторой силы F создать вращательное движение с ускорением α в системе. Для вычисления M пользуются следующим простым выражением:

M = F * d.

Где d — плечо момента, которое равно расстоянию от вектора силы F до оси вращения. Чем меньше плечо d, тем меньшей способностью создать вращение системы будет обладать сила.

Уравнение моментов по своему смыслу полностью соответствует второму закону Ньютона. При этом I играет роль инерционной массы.

Пример решения задачи

Вообразим себе систему, которая представляет собой цилиндр, закрепленный на вертикальной оси с помощью невесомого горизонтального стержня. Известно, что ось вращения и главная ось цилиндра параллельны друг другу, и расстояние между ними равно 30 см. Масса цилиндра составляет 1 кг, а его радиус равен 5 см. На фигуру действует касательная к траектории вращения сила в 10 Н, вектор которой проходит через главную ось цилиндра. Необходимо определить угловое ускорение фигуры, которое будет вызывать эта сила.

Для начала вычислим момент инерции I цилиндра. Для этого следует применить теорему Штейнера, имеем:

I = I_O + M *d² = 1 / 2 * M * R² + M * d² = 1 / 2 * 1 * 0,05² + 1 * 0,3² = 0,09125 кг*м².

Прежде чем пользоваться уравнением моментов, необходимо определить момент силы M. В данном случае имеем:

M = F * d = 10 * 0,3 = 3 Н*м.

Теперь можно определить ускорение:

α = M/I = 3/0,09125 ≈ 32,9 рад/с².

Рассчитанное угловое ускорение говорит о том, что каждую секунду скорость цилиндра будет увеличиваться на 5,2 оборота в секунду.

вращательная динамика — Угловой момент системы или индивидуально?

Спросил 1 год, 1 месяц назад

Изменено 1 год, 1 месяц назад

Просмотрено 120 раз

$\begingroup$

При решении приведенной ниже задачи она решалась с использованием закона сохранения углового момента. 2\right)\frac{8\omega}{9}$ с чем я полностью согласен.

Вот вторая задача: Имеется диск (масса $M$, радиус $R$), который может свободно вращаться вокруг своей оси. По окружности диска стоял человек. Первоначально система находится в состоянии покоя. Внезапно он побежал со скоростью $v$. Теперь нас просят найти $\omega$ диска.

Здесь, когда задача решалась, она решалась путем взятия углового момента человека отдельно по формуле $mvr_{\perp}$ и отдельно взятия углового момента диска. 92\right)\omega$ где $m$ — масса человека. Кроме того, если мы должны были вычислять угловые моменты отдельно, то почему мы не сделали то же самое в первой задаче, где мы могли вычислить угловые моменты как шаров, так и кольца?

• динамика вращения
• угловой момент
• момент инерции

$\endgroup$

2

$\begingroup$

Во второй задаче человек рассматривается как частица, не являющаяся материальной точкой, принадлежащей твердому телу диска. Вы можете свалить его инерцию с моментом инерции диска только в том случае, если он «едет вместе с диском» и действует кинематически как материальная точка диска.

Угловая скорость введена для связи скоростей, принадлежащих одному и тому же твердому телу . Если $A$ и $B$ — две материальные точки, принадлежащие одному и тому же твердому телу , то относительная скорость определяется выражением ${\bf v}_A — {\bf v}_B = {\bf \omega} \ раз ({\bf r}_A — {\bf r}_B)$, где ${\bf r}_A — {\bf r}_B$ — положение материальной точки $A$ относительно материальной точки $B$ . Эта формула не верна для человека: нельзя связать его скорость со скоростью какой-то материальной точки на диске через угловую скорость диска.

Редактировать: Вы, возможно, сможете уйти с помощью описанного вами метода, но только в начальный момент времени, когда скорость человека совпадает со скоростью материальной точки, принадлежащей краю диска. В этот расщепленный момент человек ведет себя так, как будто он принадлежит диску. 2\right)\omega$, где $m$ — масса человека.

Так что ты собираешься подключать к $\omega$? Человек и диск имеют разные угловые скорости. Если считать, что человек движется по часовой стрелке, то диск вращается против часовой стрелки. Поэтому у них нет общего $\omega$.

Но в вашем первом вопросе все тела имеют одинаковую угловую скорость.

На самом деле ваше второе уравнение верно. Это даст вам $\omega=0$, что является угловым моментом системы , как и ожидалось. Хотя вас просят найти угловую скорость диска. Поэтому вы должны рассматривать компоненты системы (человек и диск) отдельно.

$\endgroup$

0

$\begingroup$

В обеих задачах сохраняется момент импульса всей системы, где система состоит из трех и двух объектов соответственно. Объекты внутри системы могут двигаться относительно друг друга и, следовательно, не могут рассматриваться как твердое тело. 2}8$$ где $r_1, r_2$ — расстояния точечных масс от центра. 92$$ В начале у нас было $w_{\text{disk}} = w_{\text{person}} =0$, а позже у нас есть $w_{\text{person}} = \frac{v}{R}$, поэтому мы можем вычислить $w_{\text{disk}}$.

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя адрес электронной почты и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

Момент инерции | bartleby

Что такое момент инерции?

Когда твердое тело находится во вращательном движении, ему требуется крутящий момент для желаемого углового ускорения вокруг своей оси. Момент инерции есть определение этого крутящего момента, который пропорционален массе тела и квадрату расстояния от оси вращения. Масса твердого тела также определяет силу, необходимую для желаемого ускорения. Выбранная ось также отвечает за определение крутящего момента, необходимого для изменения вращения тела.

Инерция

Инерцию можно назвать сопротивлением тела изменению своего состояния. Твердое тело, первоначально находящееся в состоянии покоя, будет оказывать сопротивление, когда на него действует внешняя сила, стремящаяся изменить его состояние покоя или скорости, или тело, первоначально находящееся в движении, будет оказывать сопротивление при изменении своего состояния скорости или движения для перехода в состояние покоя. . Другими словами, первый закон движения Ньютона описывает закон инерции твердого тела.

Инерция пропорциональна массе тела, чем больше масса тела, тем больше сопротивление, которое оно оказывает при изменении своего состояния.

Инерция – это свойство, которым обладает твердое тело при прямолинейном движении (одномерное движение), криволинейном движении (двухмерное или трехмерное движение) и вращательном движении. Инерция, которой обладает тело, совершающее вращательное движение, называется инерцией вращения.

Балки и момент инерции

Балки — это элементы, которые всегда находятся под действием боковых или сдвигающих нагрузок. В таких условиях нагружения они подвергаются таким деформациям, как изгиб и прогиб. В таких условиях верхние волокна балки испытывают растяжение, а нижние — сжатие. Существует линейно изменяющееся распределение напряжения изгиба по поперечному сечению балки. Величина напряжений максимальна в верхних и нижних волокнах. Однако существует центральное сечение поперечного сечения балки, известное как нейтральная ось, где находится центр тяжести поперечного сечения. Распределение напряжения изгиба вдоль нейтральной оси равно нулю.

СС BY-SA 3.0 | Кредиты изображений: https://commons.wikimedia.org | Cdang

Распределение напряжений можно заменить системой параллельных сил. Как видно из приведенного рисунка, системы параллельных сил равны и противоположны сверху и снизу поперечного сечения балки. Это распределение силы стремится повернуть балку вокруг нейтральной оси балки. Балка благодаря своему сечению и свойствам материала пытается оказывать сопротивление этому изгибу.

Следовательно, момент инерции является мерой сопротивления изгибу под действием внешней нагрузки.

Второй момент площади или момент инерции

Площадь момента инерции или второй момент площади или квадратичный момент площади или момент инерции является свойством двумерного геометрического сечения, которое отражает то, как его точки распределяются вместе с плоское пространство двумерного сечения вокруг неподвижной оси.

Второй момент площади обозначается буквой I (момент инерции площади вдоль осей, параллельных поперечному сечению) или J (момент инерции площади вдоль оси, перпендикулярной поперечному сечению) ). Момент инерции площади, обозначаемый буквой J, также известен как полярный момент инерции.

 

Рассмотрим плоское произвольное поперечное сечение площади A. Рассмотрим бесконечно малую площадь поперечного сечения dA внутри произвольного поперечного сечения.

Первый момент малой площади элемента dA относительно осей X и Y можно записать как

dMx=ydA

и, dMy=xdA

Рассмотрим моменты первого момента площади элемента, дА; и, соответственно, приведенное выше уравнение можно записать как

dMx=yydA

и dMy=xxdA

Следовательно, чтобы вычислить для всей площади A, приведенное выше выражение следует проинтегрировать по всей площади dA

Следовательно, приведенные выше выражения записываются как , Iyy=∫x2dA            …(b)

Уравнения (a) и (b) известны как второй момент площади или момент инерции относительно оси x и y соответственно. В уравнениях оси X и Y называются осью вращения.

Радиус вращения

Радиус вращения является функцией второго момента площади и является фундаментальным свойством, учитываемым при проектировании колонн. Свойство указывает на жесткость или прочность, которую оно обеспечивает на изгиб, когда элемент используется в качестве вертикального элемента под действием сжимающих нагрузок.

Радиус инерции определяется как расстояние от оси до точки, где вся площадь может быть сосредоточена вдоль полосы, имеющей одинаковый момент инерции относительно данной оси.

Сосредоточив всю площадь A произвольного поперечного сечения на тонкой полосе той же площади, как показано на рисунке выше, момент инерции относительно оси X можно записать как

Ixx=AKx2

Член Kx называется радиусом вращения.

Во время расчета значение радиуса вращения можно рассчитать по следующему уравнению:

Kx=IxxA

Аналогичным образом можно рассчитать Ky, зная значение Iyy.

Формула переноса или теорема о параллельных осях

В практических ситуациях при проектировании элементов возникает ситуация определения момента инерции относительно различных осей. Зная момент инерции относительно центральной оси, можно оценить момент инерции относительно другой оси или нецентроидальной оси. Нецентроидальная ось должна быть параллельна центроидальной оси. Используя теорему, называемую теоремой о параллельных осях формулы переноса, можно рассчитать момент инерции относительно нецентральной оси, зная момент инерции относительно центральной оси.

Формула относится к моменту инерции любой площади по отношению к любой оси при условии, что ось параллельна центральной оси плоских пластинок.

Рассмотрим произвольную плоскость с площадью поперечного сечения A. XR и YR — центральные оси, проходящие через центр тяжести C поперечного сечения. X и Y – это две главные оси (нецентроидальные оси) или глобальные оси координат.

Рассмотрим небольшую площадь элемента dA внутри произвольной площади поперечного сечения A, момент инерции площади элемента dA относительно осей отсчета XR и YR равен 9где = Момент инерции относительно оси y

I¯yy = Момент инерции относительно центральной оси YR

I¯xx = Момент инерции относительно центральной оси XR 

Теорема о перпендикулярной оси или полярный момент инерции

Так же, как момент инерции относительно центроидальных осей дает меру сопротивления изгибу, полярный момент инерции дает меру сопротивления крутящему моменту или скручиванию вдоль перпендикулярной оси z плоского поперечного сечения.

При приложении любого внешнего крутящего момента или крутящего момента тело пытается сопротивляться этому крутящему моменту, создавая сопротивление, известное как полярный момент инерции.

Выражение для полярного момента инерции получено с использованием теоремы перпендикулярной оси.

Уравнение для полярного момента инерции относительно перпендикулярной оси z дается как0005

Izz = полярный момент инерции относительно оси z или перпендикулярной оси

Момент инерции некоторых элементарных фигур

• Момент инерции прямоугольника длиной L

Момент инерции прямоугольной плоскости профиль, имеющий длину L и высоту h относительно центральной оси x, определяется как

Ixx=Lh412

• Момент инерции треугольника с основанием b и высота h

Момент инерции треугольного поперечного сечения основания b и высоты h относительно центральной оси x

Ixx=bh436

5 5 Момент инерции окружности радиуса r

Момент инерции относительно центральной оси x окружности радиуса r определяется выражением,

Ixx=πR44

Контекст и приложения

Тема широко преподается на таких курсах, как

• Бакалавр технологий (инженерные приложения)
• Бакалавр технологий (строительная инженерия)
• Бакалавр технологий (машиностроение)
• Магистр наук (физика)
• Магистр наук (прикладная механика) или бакалавр наук
  (физика)
  • Бакалавр наук (прикладная механика)

  Практические задачи

  1. Какое из следующих названий теоремы о переносе является другим?
  1. Теорема о параллельных осях
  2. Теорема о перпендикулярных осях
  3. Оба используются в одном и том же контексте на основе положения центроидальных осей также известная как теорема о параллельных осях. Он используется для определения момента инерции нецентроидальных осей при условии, что оси параллельны центроидальным осям.

     2. Что из следующего требует применения теоремы о перпендикулярной оси?

     1. Момент инерции относительно главных осей
     2. Момент инерции относительно центральных осей
     3. Полярный момент инерции
     4. Ничего из перечисленного

     Правильный вариант- c

     известен как полярный момент инерции, и метод определения выражения для него дается теоремой о перпендикулярной оси.

     3. Какое из следующих выражений представляет полярный момент инерции Iz?

     1. Iz=∫rdA
     2.  Iz=∫r2dA
     3. Iz=r2dA
     4. Iz=rdA

     Правильный вариант- b

     Объяснение: Использование теоремы о перпендикулярности площади оси инерции dA, выражение для момента инерции относительно оси z имеет вид I=∫r2dA 

     4. Какое из следующих выражений представляет момент I инерции площади треугольника с основанием b и высотой h?

     1. I=bh436
     2. I=bh336
     3. I=bh43
     4. I=bh33

     Правильный вариант — a

     Пояснение: Момент инерции площади треугольника с основанием b и высотой h определяется выражением I=bh436

     5. Что из следующего является другой термин для второго момента площади?

     1. Момент инерции площади
     2. Центроид
     3. Момент инерции массы
     4. Ничего из перечисленного

     Правильный вариант — a

     Пояснение: Второй момент площади также известен как момент инерции площади.

     • Момент инерции массы тонкого стержня
     • Момент инерции массы вращающегося диска
     • Момент инерции площади тонкой круглой полосы
     • Тензор инерции
     • Представление slug-ft2 в размерной величине Ridgi
     Домен Жесткий домен

     Жесткий домен

     Добавьте узел Rigid Domain и выберите один или несколько геометрических объектов, чтобы сделать их твердым телом. Rigid Domain — это модель материала, имеющая только одно свойство материала: плотность массы. Его можно использовать в течение

     •	Домены в интерфейсе Solid Mechanics.

     •	Границы в интерфейсе Shell.

     •	Границы (2D) и ребра (3D) в интерфейсе Beam.

     По умолчанию добавляется узел Исходные значения (см. Исходные значения (жесткий домен)).

     Вы можете добавить функциональность к жесткому домену через следующие подузлы:

     •	Fixed Constraint (жесткая область) для полного ограничения жесткой области.

     •	Prescribed Displacement/Rotation для задания смещения отдельных степеней свободы.

     •	Applied Force (жесткая область) для приложения силы в заданной точке.

     •	Applied Moment (Rigid Domain), чтобы применить момент.

     •	Масса и момент инерции (жесткая область) для добавления дополнительной массы и момента инерции в заданной точке.

     •	Spring Foundation (Rigid Domain) для добавления поступательной или вращательной пружины или демпфера в заданной точке.

     Узел Rigid Domain доступен только для некоторых продуктов COMSOL (см. http://www.comsol.com/products/specifications/).

     В двумерных осесимметричных интерфейсах жесткая область имеет только одну степень свободы: перемещение по оси Z. В этом случае невозможно задать моментные нагрузки, момент инерции масс или вращательные пружины.

     Свойства оболочки

     Этот раздел присутствует только при использовании жесткого домена в многоуровневом интерфейсе оболочки. См. документацию по узлу Rigid Domain в главе Многоуровневая оболочка.

     Плотность

     Плотность ρ по умолчанию берется из материала. В этом случае присвоение материала домену обеспечивает массовую плотность. Для Определено пользователем введите другое значение или выражение.

     Если какой-либо материал в модели имеет массовую плотность, зависящую от температуры, и выбран параметр Из материала, в разделе Ввод модели появится список Объемная эталонная температура. По умолчанию значение Tref получается из входных данных общей модели. Вы также можете выбрать Пользовательский, чтобы ввести значение или выражение для эталонной температуры локально.

     Плотность необходима для динамического анализа или когда данные упругости задаются в терминах скорости волны. Он также используется при вычислении массовых сил для гравитационных или вращающихся нагрузок на раму, а также при вычислении массовых свойств (вычисление массовых свойств).

     См. также • Массовая плотность и объемная эталонная температура. • Использование общего входа модели • Входные данные модели по умолчанию и входные данные модели в Справочном руководстве COMSOL Multiphysics.

     Центр вращения

     Выберите центр вращения — центр массы, центр тяжести выбранных объектов или заданный пользователем. Центр вращения влияет на то, как интерпретируются смещения, а также используется по умолчанию в различных подузлах.

     •	Для Центра масс центр вращения принимается за центр масс жесткой области.

     •

     Для Центроида выбранных объектов выберите Уровень объекта — Граница, Край или Точка. Доступные варианты зависят от физического интерфейса и геометрических размеров. Центр вращения расположен в центре тяжести выбранных объектов, которые не обязательно должны быть связаны с самим жестким доменом. В качестве особого случая вы можете выбрать одну точку и, таким образом, использовать эту точку в качестве центра вращения.

     После выбора автоматически добавляется подузел по умолчанию Центр вращения: Граница, Центр вращения: Край или Центр вращения: Точка.

     •	Для определения пользователем введите глобальные координаты центра вращения, Xc, в таблицу.

     Установите флажок Смещение, чтобы добавить необязательный вектор смещения к определению центра вращения. Введите значения для вектора смещения Xoffset.

     Используемый центр вращения представляет собой сумму вектора, полученного любым из методов ввода, и вектора смещения.