Момент инерции материальной точки и твердого тела

12Следующая ⇒

 

Моментом инерции материальной точки относительно оси называется величина, равная произведению массы точки на квадрат расстояния до рассматриваемой оси:

. (8.1)

 

Единица момента инерции — килограмм-метр в квадрате (). Моментом инерции твердого тела называют сумму моментов инерции материальных точек массой , на которые можно разделить это тело, т. е.

.

 

Переходя к бесконечно малым массам dm, получаем

 

. (8.2)

На основании формулы (8.2) можно рассчитать момент инерции любого тела.

В качестве примера получим формулу момента инерции однородного сплошного цилиндра относительно его оси (рис. 8.1).

Разобьем цилиндр на кольцевые слои толщиной dr. Все точки одного слоя будут находиться на одинаковом расстоянии r от оси. Объем такого слоя

 

, (8.3)

 

где h – высота цилиндра.

Поскольку цилиндр однороден, то масса dm выделенного слоя

 

, (8.4)

 

где r — плотность тела.

Подставляя выражение (8.4) в формулу (8.2), получаем

 

. (8.5)

 

Так как — объем цилиндра, а — его масса, формулу (8.5) приводим к виду

. (8.6)

 

Эта формула применима для цилиндра любой высоты, в том числе и для диска.

Аналогично можно рассчитать моменты инерции и других однородных тел:

— для полого тонкостенного цилиндра относительно оси симметрии , где

R — радиус цилиндра;

— для прямого стержня относительно оси, перпендикулярной стержню и проходящей через его середину, , где l — длина стержня;

— для прямого стержня относительно оси, перпендикулярной стержню и проходящей через его конец, , где l — длина стержня;

— для шара относительно оси симметрии , где R — радиус шара.

При нахождении момента инерции тел относительно оси, не проходящей через центр масс тела, вычисления по формуле (8.2) значительно усложняются. Однако в подобных случаях можно воспользоваться теоремой Штейнера, которая формулируется следующим образом:

момент инерции I относительно произвольной оси равен сумме момента инерции относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния а между осями:

. (8.7)

 

Момент инерции твердого тела является мерой его инертности при вращательном движении.

 

12Следующая ⇒

Поделиться с друзьями:

---

Дата добавления: 2014-01-05; Просмотров: 45080; Нарушение авторских прав?; Мы поможем в написании вашей работы!

---

Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет

---

---

Часть 16 — Свойства тензора инерции твердого тела / Хабр

1. Что такое тензор и для чего он нужен?
2. Векторные и тензорные операции. Ранги тензоров
3. Криволинейные координаты
4. Динамика точки в тензорном изложении
5. Действия над тензорами и некоторые другие теоретические вопросы
6. Кинематика свободного твердого тела. Природа угловой скорости
7. Конечный поворот твердого тела. Свойства тензора поворота и способ его вычисления
8. О свертках тензора Леви-Чивиты
9. Вывод тензора угловой скорости через параметры конечного поворота. Применяем голову и Maxima
10. Получаем вектор угловой скорости. Работаем над недочетами
11. Ускорение точки тела при свободном движении. Угловое ускорение твердого тела
12. Параметры Родрига-Гамильтона в кинематике твердого тела
13. СКА Maxima в задачах преобразования тензорных выражений. Угловые скорость и ускорения в параметрах Родрига-Гамильтона
14. Нестандартное введение в динамику твердого тела
15. Движение несвободного твердого тела
16. Свойства тензора инерции твердого тела
17. Зарисовка о гайке Джанибекова
18. Математическое моделирование эффекта Джанибекова

Начав рассматривать динамику твердого тела мы столкнулись интересной тензорной величиной, а именно

называемой тензором инерции твердого тела. Кроме того, мы выяснили, что привычный из курса теоретической механики момент инерции твердого тела, при его вращении вокруг неподвижной оси, получается из тензора инерции с помощью простой формулы

Рассмотрим подробнее свойства тензора инерции твердого тела. И для начала изучим механические величины, вычисление которых, так же как и приведение сил инерции к данному центру, приводит к понятию тензора инерции.

Моментом количества движения материальной точки (МКД) относительно данного центра называют вектор, равный

Для твердого тела, при вращении вокруг полюса МКД элементарного объема

или в тензорной форме

Интегрируя (3) получим МКД твердого тела относительно центра

В соответствии с (4), тензор инерции есть линейный оператор, связывающий МКД твердого тела с его угловой скоростью.

Кинетическая энергия элементарного объема тела

что эквивалентно тензорному соотношению

Интегрируя последнее выражение по всему объему тела получаем выражение кинетической энергии

В выражении (5), как видно, снова фигурирует тензор инерции . При вращении тела вокруг неподвижной оси, в соответствии с выражением угловой скорости через конечный поворот тела выражение (5) трансформируется в

Формула (6) — кинетическая энергия твердого тела при вращательном движении, а , в соответствии с (2), момент инерции тела относительно оси, задаваемой ортом .

Легко показать, что тензор (1) не является симметричным. Однако, в декартовых координатах тензор инерции есть симметричный тензор, и исходя из этого факта выводятся все основные его свойства. Вместе с тем, мы не могли не заметить, что в выражениях (2) и (5) фигурирует величина вида

Полученный тензор (7) является симметричным ковариантным тензором 2-го ранга, так как нетрудно убедится в справедливости равенства .

Будем называть тензор (7) ковариантным тензором инерции. С учетом выражения (7) можно переписать выражение (2) для осевого момента инерции через контравариантные компоненты орта оси вращения

Автор не встретил в литературе только что введенного термина, но поскольку из симметричности (7) вытекают все основные свойства тензора инерции, ввод данного понятия, как будет показано ниже, вполне оправдан.

Покажем, для начала, что тензор (7), в силу своей симметричности, имеет действительные собственные значения. Пусть — произвольное собственное число, которому соответствует собственный вектор . Тогда справедливо соотношение

Допустив комплексные собственные числа и собственные векторы, умножим (9) слева на сопряженнй собственный вектор

Выполним комплексное сопряжение (10)

Здесь мы учитываем что компоненты (7) — действительные числа, а значит операция сопряжения эквивалентна транспонированию. Так как тензор (7) симметричный, , то есть, с учетом (10)

или, окончательно

Равенство (12) справедливо, если — действительное число.

Так как тензор (7) представлен матрицей в трехмерном пространстве, он имеет три действительных собственных числа , которым соответствуют действительные же собственные векторы , соответственно, можно записать тензорные соотношения

Умножим скалярно каждое из уравнений (13) на соответствующий собственный вектор

Поделив обе части уравнений (14) на квадрат модуля соответствующего собственного вектора, получим

Очевидно, что

контравариантные компоненты некоторых ортов. Значит в (15), согласно (8), в качестве собственных чисел ковариантного тензора инерции, представлены моменты инерции тела относительно осей и

Кроме того, собственные векторы и образуют ортогональную тройку векторов.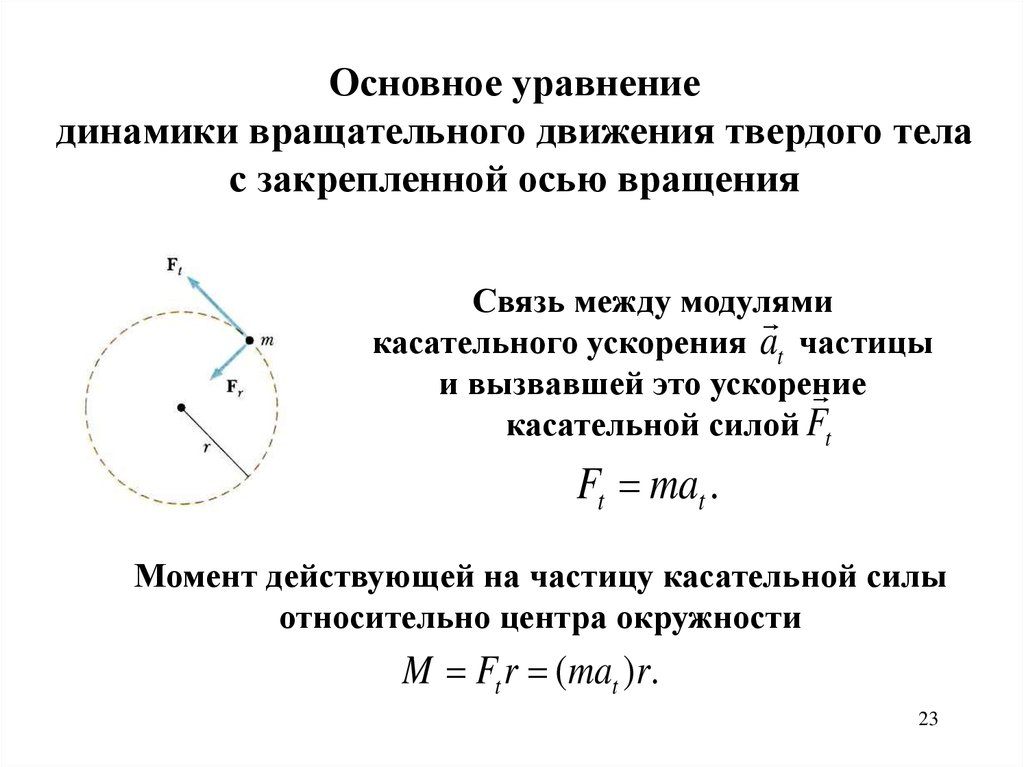 Действительно, проведем цепочку преобразований, с участием любой пары собственных векторов

Учитывая, что , получаем условие

которое, в силу того, что в общем случае , справедливо, когда скалярное произведение собственных векторов равно нулю

Это означает, что . Повторяя доказательство для любой пары собственных векторов, получим, что они действительно ортогональны друг другу.

По результатам предыдущего параграфа можно сказать, что с твердым телом связана ортогональная система координат, оси которой и направлены вдоль собственных векторов ковариантного тензора инерции. В этих осях, в соответствии с определением собственных значений, ковариантный тензор инерции приводится к диагональному виду

В диагонали стоят моменты инерции, вычисляемые по формулам (17). Эти моменты инерции называют главными моментами инерции твердого тела, а оси, направление которых задается векторами и — главными осями инерции.

Предположим, что нам известен центральный (вычисленный относительно центра масс тела) тензор инерции . Допустим, что мы хотим вычислить тензор инерции относительно точки , отстоящей от центра масс в направлении известного вектора . В этом случае радиус-вектор элементарного объема тела относительно точки можно определить как сумму

где — радиус вектор элементарного объема тела относительно центра масс

Подставим (18) в (1)

Здесь мы учитываем, что интегралы вида

задают положение центра масс тела относительно центра масс, то есть равны нулю. Окончательно получаем выражение для тензора инерции

определяющее тензор инерции относительно произвольной точки через тензор инерции относительно центра масс. Выражение (19) называют теоремой Гюйгенса-Штейнера. Приведенное доказательство этой теоремы выполнено в самой общей форме.

В декартовых координатах метрика задается единичной матрицей, то есть формально

В этом случае совпадают выражения для тензора инерции и ковариантного тензора инерции

Поэтому в декартовых координатах симметричен и тензор инерции, и для него справедливы вышеперечисленные свойства, связанные с собственными значениями и собственными векторами. В декартовых координатах тензор инерции представляется матрицей

или

где диагональные элементы называют осевыми моментами инерции, а прочие элементы — центробежными моментами инерции.

Материал данной статьи — авторская работа. В литературе господствует подход к изучению тензора инерции связанный с использованием декартовых координат. Нами же рассмотрен самый общий подход и мы убедились, что свойства тензора инерции и теорема Гюйгенса-Штейнера могут быть получены в произвольных координатах. Все приведенные в статье формулы переходят в общеизвестные из курса теоретической механики при использовании декартовой метрики.

Upd: Нашел упоминание о ковариантном тензоре инерции на каком-то богом забытом сайте. Что ж, это подтверждает идею, использованную мной в данной статье

Продолжение следует…

Примечания о моменте инерции твердых тел

Инерция — это характеристика тела, противодействующая любой силе, стремящейся сдвинуть его или, если оно движется, изменить величину или направление его скорости. Инерция твердого тела — это пассивный атрибут, который позволяет телу ничего не делать, кроме как противостоять активным агентам, таким как силы и крутящие моменты. Движущееся тело продолжает двигаться не по инерции, а потому, что нет силы, замедляющей его, изменяющей его траекторию или ускоряющей.

Момент инерции твердых тел

Момент инерции твердых тел определяет, насколько трудно повернуть требовательное тело вдоль определенной оси.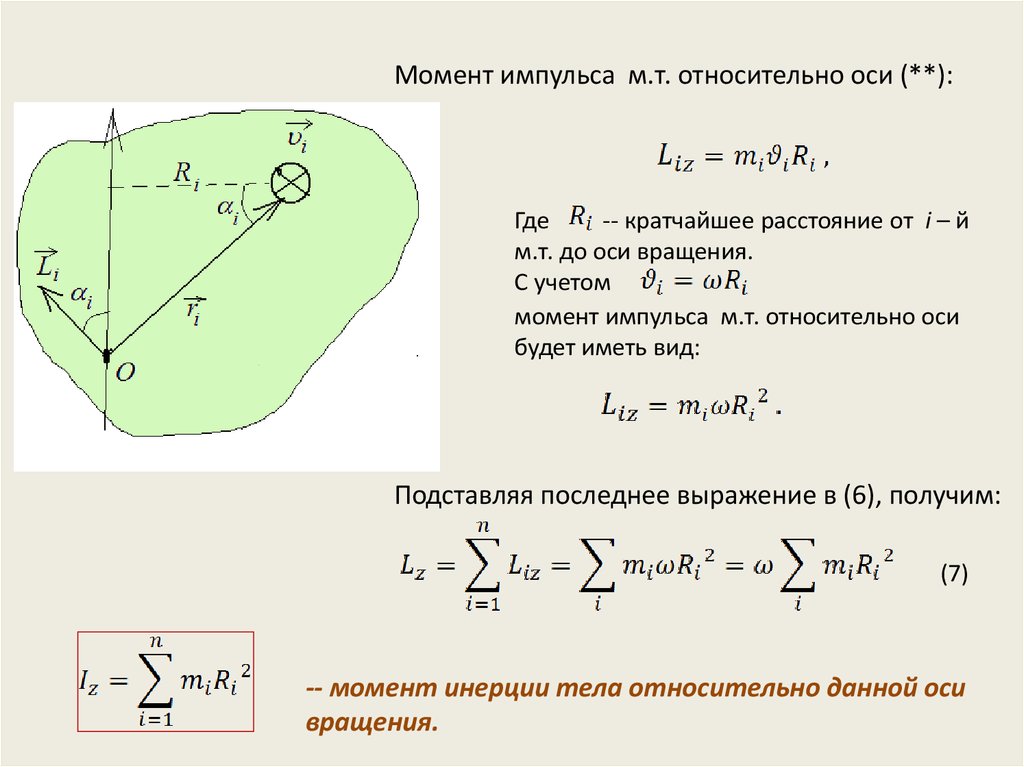 Первый закон движения Ньютона гласит, что если тело не подвергается давлению со стороны внешнего источника, известного как сила, оно должно оставаться в состоянии покоя или равномерного движения. Инерция определяется как неспособность материального тела самостоятельно изменять свое состояние покоя или равномерного движения.

Основным свойством материи является инерция. Момент инерции твердого тела — это атрибут массы, влияющий на крутящий момент, необходимый для достижения заданного углового ускорения относительно оси вращения. Это естественный атрибут вещей. Тело сопротивляется любому изменению своего состояния покоя или равномерного прямолинейного движения по инерции. Для данной силы, чем больше масса, тем больше сопротивление движению или больше инерция. При поступательном движении масса тела используется для расчета коэффициента инерции.

Точно так же при вращательном движении тело, которое может свободно вращаться вокруг определенной оси, сопротивляется любому желаемому изменению своего состояния. Величина сопротивления будет определяться массой тела и ее распределением по оси вращения. Момент инерции твердого тела относительно указанной оси является коэффициентом инерции при вращательном движении.

Значение

Значение момента инерции твердого тела следующее:

•   Чем больше концентрация массы вдали от оси, тем больше момент инерции. Момент инерции твердого тела неодинаков по отношению к разным осям вращения.
•   Имеет значение при вращательном движении. Это свойство тела сопротивляться изменению состояния при вращательном движении.
•   Он связан с вращательным движением так же, как масса связана с поступательным движением.

Единица момента инерции

Определив момент инерции твердого тела, теперь мы можем узнать его единицу измерения.

Единица момента инерции твердого тела является составной единицей измерения. В Международной системе (СИ) m измеряется в килограммах, а r измеряется в метрах, при этом I (момент инерции) имеет размерность килограмм-метр в квадрате.

Расчет момента инерции твердого тела

Зная факторы, от которых зависит момент инерции твердого тела, мы можем теперь вычислить момент инерции твердого тела.

Если объект имеет непрерывное распределение массы, момент инерции твердого тела можно вычислить путем интегрирования моментов инерции составляющих его частей. Если dm — масса любой бесконечно малой частицы тела, а r — ее перпендикулярное расстояние от оси вращения, то момент инерции твердого тела относительно оси определяется как:

I= ∫r²dm

Факторы, влияющие на момент инерции

Момент инерции твердого тела зависит от следующих факторов:

•   Индекс массы тела.
•   Размеры и форма корпуса
•   Распределение массы вокруг оси вращения
•   Положение и направление оси вращения по отношению к корпусу.

Момент инерции различных объектов:

Мы знаем, что момент инерции твердого тела зависит от различных факторов.

Следовательно, она различна для разных твердых тел. Момент инерции различных жестких объектов заключается в следующем:

• Стержень — Через центр: 1 ⁄ 12 мл²

— до конца: 1 ~ 3 мл²

• Speera

– Solder: 2: 2: 2: 2: 2: 2: 2: 2: 2: 2
• . ⁄ 5 м²

  –        Полая сфера:  2 ⁄ 3 м²

  • Обруч

  –        Диаметр обруча:  1 ⁄ 2MR²

  — Обруча о симметричной оси: MR²

  • Цилиндр

  — Сплошной цилиндр или диск, симметричная ось: 1 ~ 2 мр. Прямоугольные объекты

–        Сплошная прямоугольная коробка: 1 ⁄ 12 м (h² + w²)

–        Сплошная прямоугольная пластина: 1 ⁄ 12 м (h² + w²)

• 0 м²r : Кольцо0017 Диск :  1 ⁄ 2 м²

Вывод

Ось вращения влияет на момент инерции. После выбора двух уникальных осей предмет по-разному сопротивляется изменению вращения. Мы устанавливаем новый параметр, известный как радиус вращения, чтобы описать, как масса вращающегося твердого тела распределяется относительно оси вращения. Это связано с моментом инерции и общей массой тела. Стоит отметить, что мы можем написать I = Mk2, где k — размерность длины.

Таким образом, радиус вращения – это расстояние от оси материальной точки, масса которой равна массе всего тела, а момент инерции равен моменту инерции тела относительно оси. В результате на момент инерции влияют не только масса, форма и размеры тела, но и распределение массы внутри тела вокруг оси вращения.

Почему механика — фундаментальная наука: точка-масса и твердое тело

4 марта 2017 г. Трение, смачивание, механика и связанные с ними вопросы механики, теории

Некоторые утверждают, что механика не фундаментальная наука, а скорее прикладная дисциплина. Я принадлежу к школе механиков, которые категорически не согласны с этим утверждением. Для меня механика — это часть физики; однако она имеет ряд собственных понятий, не всегда совпадающих с аналогичными понятиями в физике. В этой серии статей я намерен привести несколько примеров фундаментальных концепций механики, которые, как правило, не столь очевидны, когда дело доходит до их логического определения.

Первая концепция точечной массы или частицы . В русской литературе (в том числе в английских переводах русских книг, таких как «Механика» Ландау и Лифшица) часто используется термин материальная точка . Что такое определение частицы (точечная масса или масса-точка)? В большинстве учебников, особенно написанных физиками, говорится, что частица в механике — это твердое тело, размером которого можно пренебречь , но нельзя игнорировать массу. Это звучит как справедливое определение.

Однако тогда вам необходимо определить, что такое твердое тело ! Недеформируемое твердое тело представляет собой систему точек, расстояние между которыми всегда остается постоянным . Один определяет понятие механической частицы, используя понятие твердого тела, в то время как твердое тело определяется, используя понятие частицы. Это звучит как старая проблема «курица или яйцо» и не кажется серьезной практической проблемой, о которой следует беспокоиться. Может быть, это даже не значительная теоретическая проблема, о которой должен волноваться математически мыслящий механик, ищущий строгих логических определений механических понятий? Однако это так!

Причина в том, что при уменьшении размера трехмерного твердого тела не все его свойства, не относящиеся к материальной точке, исчезают в пределе малых размеров. Возьмем момент инерции диска, катящегося по плоской поверхности с линейной скоростью V. Для диска радиуса R момент инерции равен J=(3/2)*M*R ² , угловая скорость V/R, а кинетическая энергия K=(J/2)*(V/R) ² . Другими словами, кинетическая энергия равна K=(3/4)M*V ² . Это не зависит от размера диска! В пределе R→0 вы по-прежнему получаете K=(3/4)M*V ² . Это не то, что вы ожидаете от точки массы, K=(1/2)M*V ² . Разве это не удивительно и нелогично?

У материальной точки всего три поступательных степени свободы, а у твердого тела шесть степеней свободы: три поступательных и три вращательных. Когда рассматривается предел очень маленького твердого тела, R → 0, нет причин, по которым вращательные степени свободы исчезают. Это приводит к некоторой двусмысленности определения точки-массы: есть ли у нее вращательные степени свободы или нет?

Более формальным образом, используя программный подход Феликса Кляйна в Эрлангене, согласно которому твердое тело характеризуется группой симметрии SO(3)xR ³ (т. е. тремя вращательными и тремя поступательными степенями свободы). Точечная масса имеет только три поступательные степени свободы, R ³ . Таким образом, определение точечной массы:

SO(3)xR ³ → R ³ .

Определение твердого тела состоит в том, что расстояния между всеми точками остаются одинаковыми. Ориентация твердого тела задается тремя точками (девять степеней свободы), к которым применяются три ограничения (парное постоянное расстояние). Каждое ограничение отнимает одну степень свободы, что приводит к подвижности твердого тела 9– 3 = 6. Следовательно, определение твердого тела дается преобразованием

R ³ xR ³ xR ³ → SO(3)xR ³ .

Неоднозначность вызвана, скорее всего, тем, что наше евклидово пространство R ³ , но обладает как трансляционной, так и вращательной SO(3)xR ³ симметриями. Если мы примем точку зрения Лейбница о том, что пространство есть лишь свойство взаимных отношений тел, мы поймем, что твердое тело имеет ту же дуальную (R ³ и SO(3)xR ³ ) природа.

Из этого примера мы находим, что строгие определения основных механических понятий, таких как точечная масса (частица, материальная точка) и твердое тело , связаны с фундаментальными понятиями движения и симметрии.