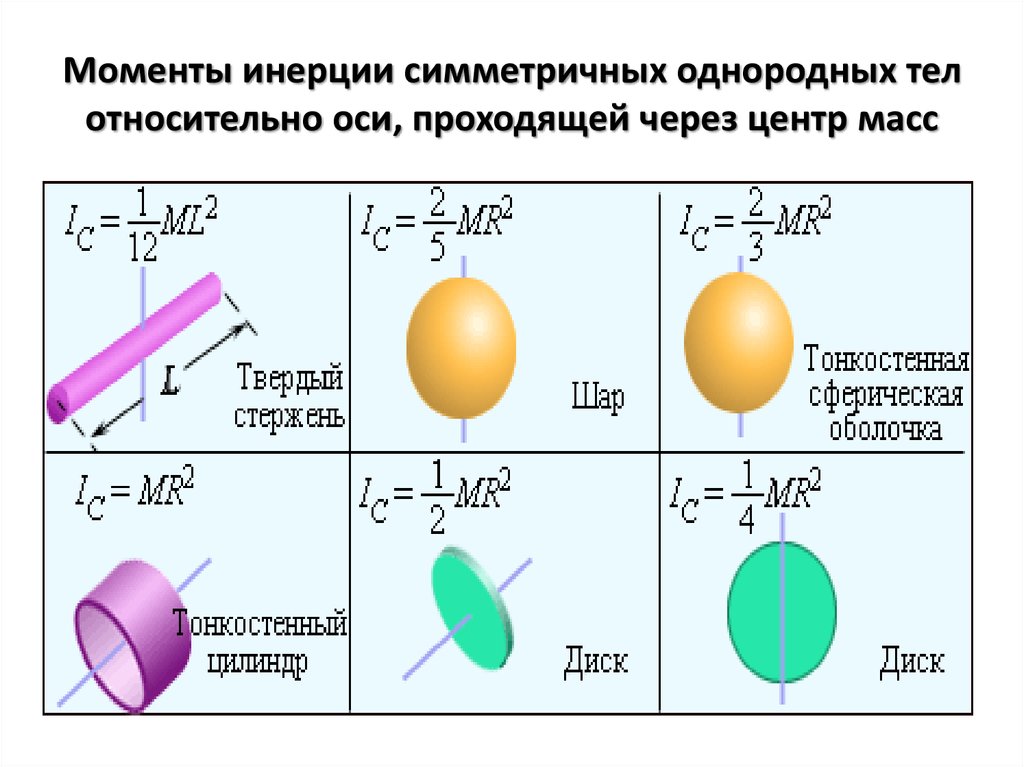
3.3 Главные оси инерции
Момент инерции твердого тела произвольной формы и распределения масс зависит от ориентации оси вращения. Допустим, что ось проходит через центр масс тела (центр инерции). Найдем такую ориентацию оси, для которой момент инерции максимален. Далее, как доказывается в теоретической механике, существует также ось перпендикулярная найденной, и проходящая через центр масс, для которой момент импульса твердого тела будет минимален. Для третьей оси, ортоганальной к первым двум, момент импульса в общем случае имеет величину промежуточную между максимальным и минимальным значениями. Введенные таким образом оси вращения называются главными осями инерции. Моменты инерции относительно этих осей не обязательно отличаются друг от друга по величине. Действительно, если однородное по плотности твердое тело обладает той или иной симметрией, то некоторые главные моменты инерции могут равняться друг другу. Так, например, однородный по плотности шар имеет три равных момента инерции относительно главных осей, каждый из которых равен: , где

Однородный куб с массой М и длиной ребра имеет также три равных момента инерции относительно главных осей инерции . Главные оси инерции перпендикулярны граням куба и проходят через центр куба..
Тонкий однородный по плотности диск имеет максимальный по величине момент инерции относительно оси, проходящей через центр диска перпендикулярно его плоскости, а также два других главных момента инерции равных друг другу.
Приведем также пример тела, когда все три момента инерции относительно главных осей инерции различны — однородный по плотности параллелепипед с отличающимися по длине ребрами.
Моментом силы относительно точки О называется вектор равный:
,
где – радиус-вектор, проведенный из точки О в точку приложения внешней силы ; – векторное произведение и .
Направление момента силы связано с направлением и правилом правого винта.
Величина момента силы определяется выражением:
,
где
– угол между направлениями векторов и
.
Размерность момента силы Нм = кг*м
Момент силы относительно оси.
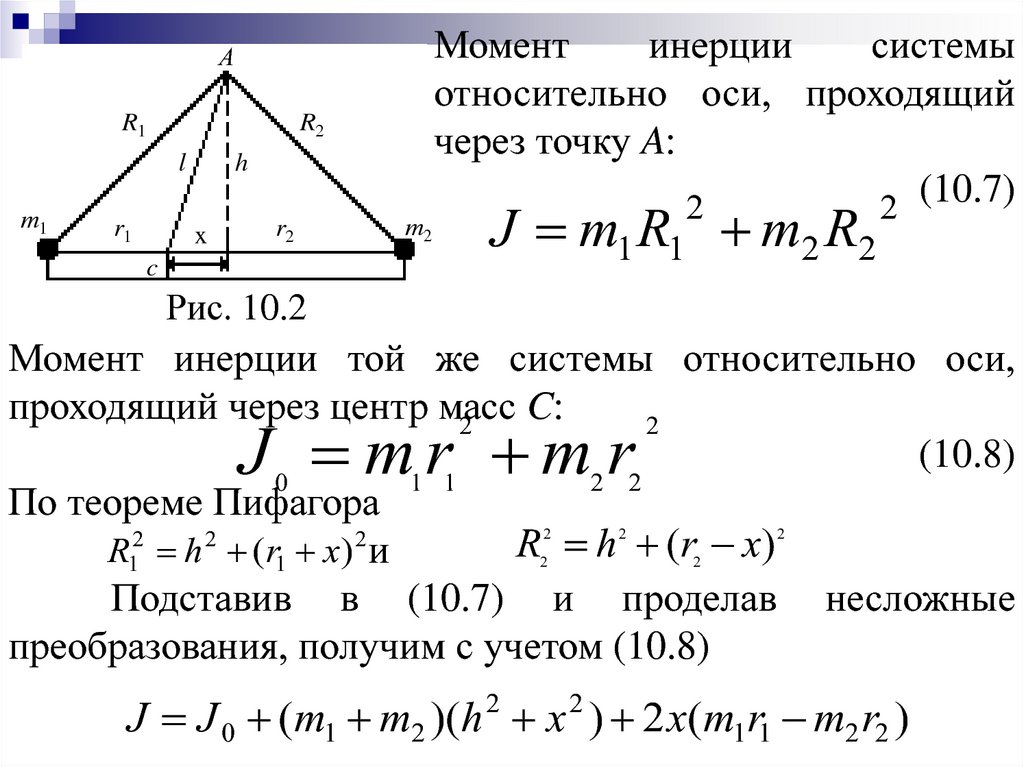
Рассмотрим теперь тело, закрепленное в двух неподвижных точках О и О1 так, что тело может вращаться только вокруг оси, проходящей через эти точки (рис.15).
Рис.15
Пусть ось вращения совпадает с осью Z системы отсчета. Допустим, что момент силы направлен произвольным образом по отношению к оси вращения. Тогда вектор можно разложить на составляющие Mx, My, Mz, каждая из которых будет стремиться повернуть тело соответственно вокруг осей
 Поэтому
вращение будет происходить только под
действием составляющей Mz.
Поэтому
вращение будет происходить только под
действием составляющей Mz.Составляющая вектора момента силы , направленная вдоль оси вращения, называется моментом силы относительно этой оси.
Строго говоря, момент силы относительно оси является скалярной величиной, так как является проекцией вектора момента силы на направление оси вращения. Однако, часто бывает удобно рассматривать его, как вектор, который направлен по оси вращения и может иметь только два направления, соответствующих вращению по или против часовой стрелки. Если момент силы вызывает вращение тела по часовой стрелке, то он считается положительным, если против – то отрицательным.
Величина момента силы относительно оси вращения равна
,
где – плечо силы (кратчайшее расстояние от оси вращения до прямой, вдоль которой действует сила).
Определим теперь момент импульса
твердого тела относительно оси вращения.
Суммируя моменты импульсов всех элементов тела, получим момент импульса твердого тела относительно фиксированной в пространстве оси вращения:
.
Постоянную величину можно вынести за знак суммы, тогда:
.
Сумма, стоящая в последнем выражении , является моментом инерции твердого тела относительно фиксированной в пространстве оси вращения, поэтому:
.
И окончательно, учитывая векторный характер угловой скорости и момента импульса, имеем:
.
Из последнего выражения ясно, что момент импульса твердого тела относительно фиксированной в пространстве оси вращения это векторная величина, модуль которой измеряется произведением момента инерции твердого тела относительно оси вращения на величину угловой скорости вращения. Направление момента импульса твердого тела относительно фиксированной в пространстве оси вращения совпадает с направлением угловой скорости
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Оценка эффективности инструментов коммуникационной политики: Внешние коммуникации — обмен информацией между организацией и её внешней средой. Теоретическая значимость работы: Описание теоретической значимости (ценности) результатов исследования должно присутствовать во введении… Интересное: Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются… Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом… Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 10 из 10
14.
14.2 .Найти момент инерции тонкого однородного стержня массы М и длины L относительно оси, перпендикулярной стержню и проходящей: 1.через один из его концов; 2.через середину стержня; 3. Через точку А, лежащую на продолжении стержня на расстоянии L от одного из его концов.
14.3 .Найти момент инерции тонкого обода радиуса 0,2 м и массы 3 кг относительно оси, перпендикулярной плоскости обода и проходящей: 1.через центр тяжести обода; 2.через конец диаметра.
14.4 .Определить момент инерции диска массы m, радиуса R относительно оси, перпендикулярной плоскости диска и проходящей через край диска.
14.5 .Определить момент инерции сплошного шара радиуса R и массы m относительно оси, проходящей: 1.через центр тяжести; 2.по касательной к шару.
14.6 .Определить момент инерции полого шара массы m относительно оси, проходящей через центр тяжести. Внешний радиус шара R, внутренний – r.
14.7 .Определить момент инерции тонкого кольца радиуса R и массы m относительно оси, проходящей через центр тяжести и лежащей в плоскости обода.
14.8 .Определить момент инерции шайбы, радиусы которой r и R, относительно оси, перпендикулярной плоскости шайбы и проходящей через ее центр масс.
14.9 .Определить момент инерции сплошного цилиндра радиуса R, массы m относительно оси цилиндра.
14.10 .Определить момент инерции полого цилиндра массы m, внутренний радиус которого r, внешний R.
14.11 .Определить момент инерции фигур, изготовленных из тонких стержней массы m, длины L относительно осей, перпендикулярных плоскости рисунка и проходящих через указанные точки (рис. 51).
а) б) в)
Рис. 51
14.12 .Определить момент инерции тонкой прямоугольной пластинки (масса m, стороны и ) относительно оси, проходящей через центр тяжести параллельно одной из сторон.
14.13 . Определить момент инерции тонкой прямоугольной пластинки (масса m, стороны и b) относительно оси, проходящей через центр тяжести перпендикулярно плоскости пластинки.
14.14 .В тонком диске массой m и радиусом R вырезают n круглых отверстий радиуса r на равных расстояниях a от центра диска. Определить момент инерции диска относительно оси, проходящей через его центр масс.
14.15 .Цилиндр массы 3 кг, диаметр которого 12 см, лежит на горизонтальной плоскости. Определить момент инерции цилиндра относительно оси, проходящей по линии контакта его боковой поверхности с плоскостью.
14.16 .Кинолента наматывается на бобину со скоростью V. Момент инерции бобины без ленты Iо, радиус rо. Определить зависимость момента инерции катушки с лентой от времени. Ширина ленты , плотность , толщина b.
14.17 .Две частицы с одинаковой массой m соединены жестким однородным стержнем длины L и массы m1.
14.18 .Поверхностная плотность тонкого диска радиуса R изменяется по закону . Найти момент инерции диска относительно оси, проходящей через центр диска перпендикулярно его плоскости.
14.19 .Прямой круглый однородный конус имеет массы m и радиус основания R. Найти момент инерции конуса относительно его оси.
14.20 .Найти момент инерции однородного куба относительно оси, проходящей через центры противолежащий граней. Масса куба m, длина ребра L.
14.21 .Вычислить момент инерции однородного круглого прямого цилиндра относительно оси, перпендикулярной к оси симметрии цилиндра и проходящей через его центр. Масса цилиндра m, радиус R, высота h. Рассмотреть предельные случаи: R << h, h << R.
14.22 .Найти момент инерции однородной пирамиды, основанием которой является квадрат со стороной , относительно оси, проходящей через вершину и центр основания.
15.ДИНАМИКА ТВЕРДОГО ТЕЛА ,ВРАЩАЮЩЕГОСЯ ВОКРУГ НЕПОДВИЖНОЙ ОСИ
15.1 . Найти ускорение грузов и натяжение нитей на машине, изображенной на рис. 52, учитывая момент инерции I блока, при условии, что нить не скользит по блоку. Определить натяжение подвеса А.
А
I, r
m2 m1
Рис. 52
15.2 . На однородный сплошной цилиндр массы М и радиуса R плотно намотана легкая нить, к концу которой прикреплен груз массы m (рис. 54). В момент времени t=0 система пришла в движение. Пренебрегая трением в оси цилиндра, найти:1. Зависимость угловой скорости от времени; 2.
М
m
Рис. 54
15.3 .Через блок радиуса 10 см, масса которого m=100 г, перекинута тонкая гибкая нерастяжимая нить, к концам которой подвешены два груза массами m1=200 г и m2=300 г (рис. 55). Определить: 1. Ускорения грузов; 2. Угловое ускорение; 3. Силы натяжения нитей.
m2
m1
Рис. 55
15.
Р
Р
Рис. 56
15.5 . На ступенчатый блок намотаны в противоположных направлениях две нити (рис 57). На конец одной нити действуют постоянной силой F, а к концу другой нити прикреплен груз массы m. Известны радиусы R1 и R2 блока и его момент инерции I относительно оси вращения. Найти угловое ускорение блока.
Рис. 57 15.6 . На горизонтальном столе лежат два тела, которые могут скользить по столу без трения. Тела связаны невесомой нерастяжимой нитью (рис. 58). Такая же нить, переброшенная через блок, связывает тело 2 с грузом массы m=0,5 кг. 1 2 М F1 М F2 М
Fm m
Рис. 58 15.7 . Однородный сплошной цилиндр массы m=1 кг висит в горизонтальном положении на двух намотанных на него невесомых нитях (рис. 59). Цилиндр опускается без толчка. А). За сколько времени t цилиндр опустится на расстояние h=50 см? б) Какое натяжение F испытывает при этом каждая из нитей?
Рис. 59
15.8 . Система, состоящая из цилиндрического катка радиуса R и гири, связанных нитью, перекинутой через блок (рис.
М
m
Рис. 60
15.9 . Из колодца с помощью ворота поднималось ведро с водой массы m. В момент, когда ведро находилось на высоте h от поверхности воды, рукоятка освободилась, и ведро стало двигаться вниз. Определить линейную скорость рукоятки в момент удара ведро о поверхность воды в колодце, если радиус рукоятки R, радиус вала ворота r, его масса m1. Трением и весом торса пренебречь.
15.
m1 m2
Рис. 61
15.11 . По наклонной плоскости, образующей угол с горизонтом, скатывается без скольжения сплошной однородный диск. Найти линейное ускорение центра диска.
15.12 . Какой путь пройдет катящийся без скольжения диск, поднимаясь вверх по наклонной плоскости с углом наклона 300,если ему сообщена начальная скорость 7 м/с, параллельная наклонной плоскости.
15.13 . Найти ускорение центра однородного шара, скатывающегося по наклонной плоскости, образующей угол с горизонтом. Чему равна сила трения шара о плоскость?
15.14 . Шар скатывается по наклонной плоскости с углом наклона 300. Какую скорость будет иметь центр шара относительно наклонной плоскости через 1,5 с, если его начальная скорость была равна нулю?
15.15 . По наклонной плоскости, составляющей с горизонтом угол 300, скатывается без скольжения сплошной цилиндр, масса которого равна 300 г. Найти величину силы трения цилиндра о плоскость.
15.16 . С одного уровня наклонной плоскости одновременно начинают скатываться сплошной цилиндр и шар одинаковых радиусов. 1)Какое тело будет иметь скорость на данном уровне? 2)Во сколько раз? 3)Во сколько раз скорость одного будет больше скорости другого в данный момент времени?
⇐ Предыдущая12345678910 Папиллярные узоры пальцев рук — маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни. Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций… |
домашних заданий и упражнений — Как рассчитать момент инерции твердого куба?
спросил
Изменено 4 года, 5 месяцев назад
Просмотрено 51к раз
$\begingroup$
Закрыто. Этот вопрос не по теме.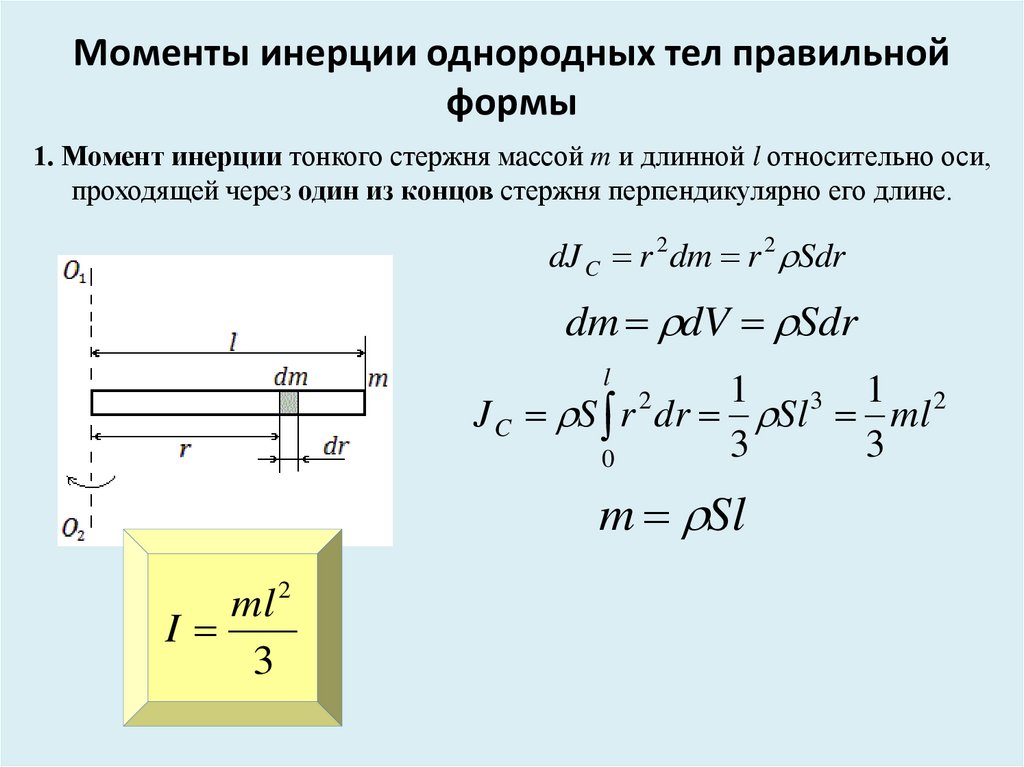 В настоящее время ответы не принимаются.
В настоящее время ответы не принимаются.
Вопросы, похожие на домашнее задание, и вопросы проверки моей работы считаются здесь не по теме, особенно когда спрашивают о конкретных вычислениях, а не об основных понятиях физики. Домашние вопросы могут быть по теме, если они полезны для более широкой аудитории. Если вы намерены изменить свой вопрос, , пожалуйста, внимательно прочитайте приведенные выше ссылки перед редактированием. Обратите внимание, что ответы с полными решениями могут быть удалены!
Закрыт 2 года назад.
Улучшить этот вопрос
Как рассчитать момент инерции однородного сплошного куба относительно оси, проходящей через его центр масс?
Я также хотел знать, не зависит ли момент инерции тела от его формы. Также недавно где-то читал, что момент инерции однородного цельного куба равен минимум вокруг оси , проходящей через его COM , потому что масса больше сконцентрирована в его центре.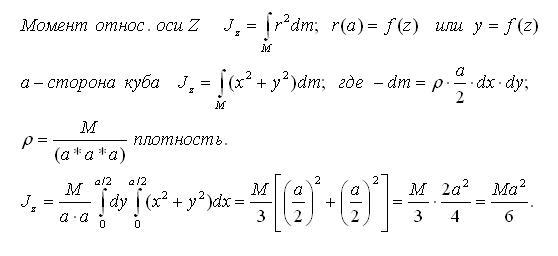 \intercal$
\intercal$
Пример:
Один оборот $\theta$ вокруг мировой оси $z$ равен
$$E = \begin{pmatrix} \cos\theta & -\sin\theta & 0 \\ \sin\theta & \cos\theta & 0 \\ 0 & 0 & 1 \end{pmatrix} $$
Если массовый момент инерции матрицы относительно главных осей $(x,y,z)$ равен
$$I_{body} = \begin{vmatrix} I_{xx} & & \\ & I_{yy} & \\ & & I_{zz} \end{vmatrix} $$
тогда момент инерции масс около мировые координаты 92 $$ где $r$ обозначает расстояние от центра масс объекта до оси вращения, а $I_{cm}$ — нормальный момент инерции объекта (например, приведенные выше).
$\endgroup$
$\begingroup$
Две теоремы, о которых стоит знать, когда дело доходит до вычислений, подобных этому:
1) Теорема о параллельных осях. Для любого объекта массы $m$ момент инерции $I_A$ относительно оси A, которая параллельна, но смещена на расстояние $x$ от оси $C$ через центр масс, определяется выражением
$$I_A = mx^2 + I_C$$ 92$ всегда будет >0 для любого ненулевого значения $x$ (смещение).
2) Теорема о перпендикулярной оси. Для пластинки (тонкого листа) момент инерции относительно оси, перпендикулярной листу, равен сумме моментов инерции относительно двух перпендикулярных осей листа.
Эта теорема удобна для вычисления момента инерции квадратной пластины массой $m$ и стороной $s$. Легко вычислить момент инерции относительно оси, лежащей в плоскости пластины и параллельной сторонам квадрата — относительно этой оси распределение массы объекта ничем не отличается от распределения стержня, для которого имеем результат 92$$
Если рассматривать куб, состоящий из пакета пластин, то момент инерции куба относительно оси, проходящей через центр масс (и через грань куба), равен выше.
Вы можете увидеть довольно полный список других моментов инерции для различных форм по этой ссылке
$\endgroup$
Очень активный вопрос . Заработайте 10 репутации (не считая бонуса ассоциации), чтобы ответить на этот вопрос. Требование к репутации помогает защитить этот вопрос от спама и отсутствия ответа.
Требование к репутации помогает защитить этот вопрос от спама и отсутствия ответа.
домашнее задание и упражнения — Момент инерции объемного куба относительно диагонали тела
спросил
Изменено 3 года, 5 месяцев назад
Просмотрено 23 тысячи раз
$\begingroup$
Как найти вышеупомянутый момент инерции?
Шаги, которые я пробовал:
1.) Тройная интеграция, которая оказалась слишком большой.
2.) Я заметил, что если мы разобьем $2\times 2\times 2$ на отдельные компоненты $1\times1\times1$, диагональ тела $2\times 2\times 2$ либо проходит через, либо параллельна к диагоналям тел кубиков $1\times 1\times 1$.
Если момент инерции $1\times 1\times 1$ относительно диагонали тела равен $I$, то момент инерции $2\times 2\times 2$ относительно диагонали тела будет равен $8I$, потому что его масса в 8 раз больше. 5$. Это означает, что момент инерции вашего куба 2x2x2 будет в 32 раза больше, чем момент инерции вашего куба 1x1x1.
5$. Это означает, что момент инерции вашего куба 2x2x2 будет в 32 раза больше, чем момент инерции вашего куба 1x1x1.
Вы получите точно такой же результат (коэффициент 32), если посчитаете, что куб 2x2x2 состоит из восьми кубов 1x1x1, и примените теорему о параллельных осях.
$\endgroup$
1
$\begingroup$
Один из больших трюков, которые вы найдете полезными, заключается в том, что матрица инерции сферы имеет ту же форму, что и матрица куба. Я опишу, что это значит.
Для сферы представьте момент инерции (MoI) относительно трех перпендикулярных осей, проходящих через центр масс. Каждый MoI будет одинаковым из-за симметрии. Теперь поверните три оси, которые вы только что использовали, и MoI по каждой оси останется прежним:
Теперь трюк говорит, что вы можете сделать то же самое для куба! Таким образом, вы можете легко рассчитать MoI относительно оси, проходящей через центр масс перпендикулярно одной из граней куба.


 ..
.. 1 .Найти момент инерции математическго маятника относительно точки подвеса.
1 .Найти момент инерции математическго маятника относительно точки подвеса.

 Найти момент инерции этой системы относительно оси, перпендикулярной стержню и проходящей через: 1.центр масс системы; 2.одну из частиц.
Найти момент инерции этой системы относительно оси, перпендикулярной стержню и проходящей через: 1.центр масс системы; 2.одну из частиц.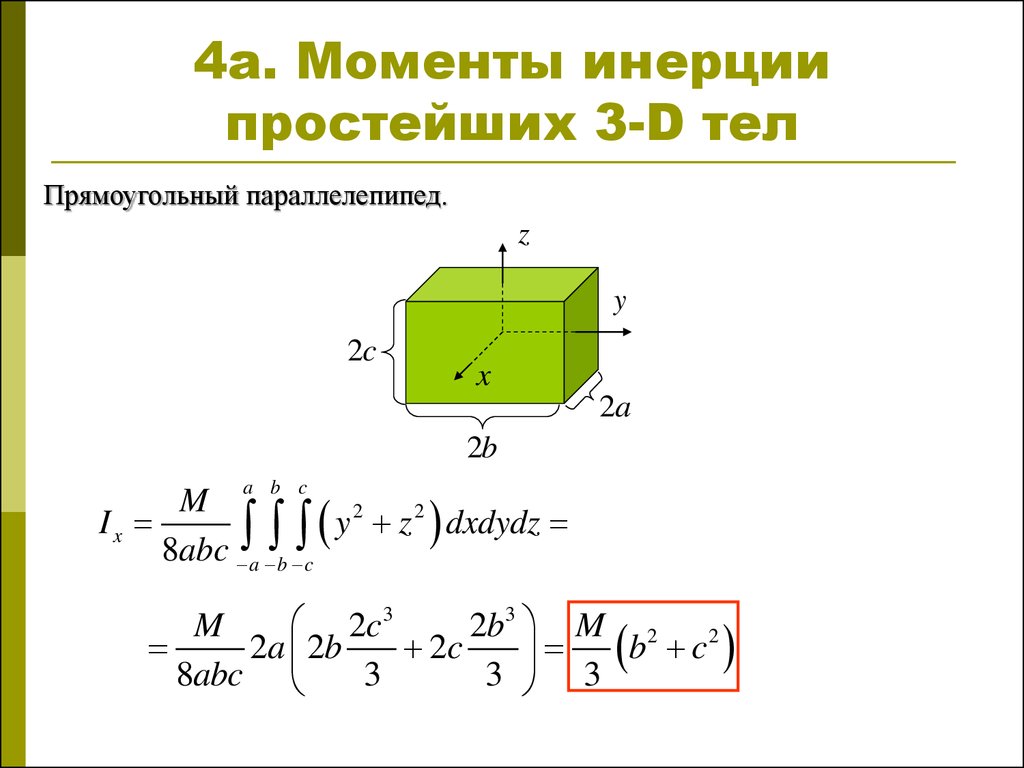 Масса пирамиды равна m.
Масса пирамиды равна m.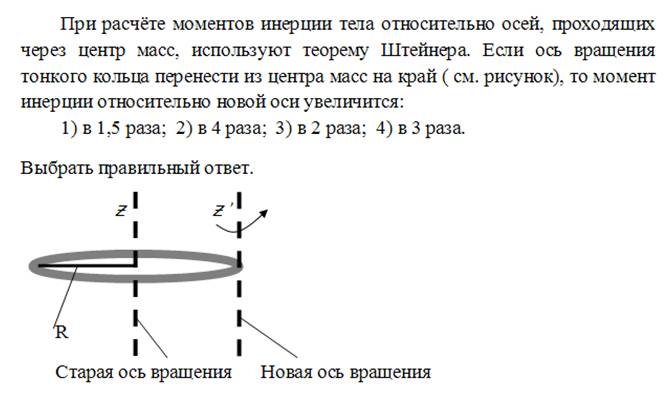 Направление векторов и ; 3. Ускорение груза; 4. Силу натяжения нити; 5. Для системы блок-груз зависимость от времени момента импульса относительно оси блока и кинетической энергии; 6. Углы поворота блока в зависимости от времени.
Направление векторов и ; 3. Ускорение груза; 4. Силу натяжения нити; 5. Для системы блок-груз зависимость от времени момента импульса относительно оси блока и кинетической энергии; 6. Углы поворота блока в зависимости от времени.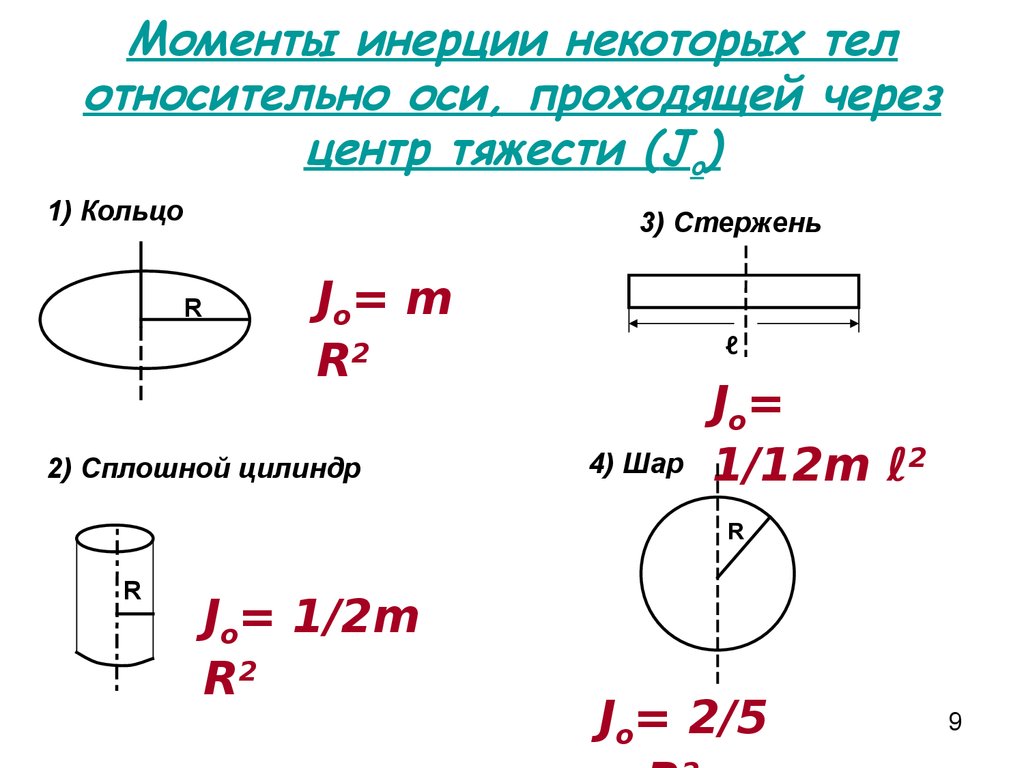 4 . Однородный цилиндр массы М и радиуса R вращается вокруг горизонтальной оси, проходящей через его центр масс, под действием грузов весом Р каждый. Найти силу натяжения нити на участках и (рис. 56).
4 . Однородный цилиндр массы М и радиуса R вращается вокруг горизонтальной оси, проходящей через его центр масс, под действием грузов весом Р каждый. Найти силу натяжения нити на участках и (рис. 56). Блок представляет собой однородный сплошной цилиндр. Масса тел и блока одинакова и равна М=1 кг. Считая, что блок вращается без трения, а нить не проскальзывает по блоку, найти ускорение тел, натяжение F12 нити, связывающей оба тела, натяжение нити F2 на участке от тела 2 до блока, натяжение нити Fm на участке от блока до груза m.
Блок представляет собой однородный сплошной цилиндр. Масса тел и блока одинакова и равна М=1 кг. Считая, что блок вращается без трения, а нить не проскальзывает по блоку, найти ускорение тел, натяжение F12 нити, связывающей оба тела, натяжение нити F2 на участке от тела 2 до блока, натяжение нити Fm на участке от блока до груза m. 60) под действием силы тяжести приходит в движение из состояния покоя. Определить ускорение a центра масс катка и силу натяжения нити. Какую скорость приобретет гиря, если она опускается с высоты h? Масса цилиндра М, масса гири m, массой блока пренебречь. Каток катится без скольжения.
60) под действием силы тяжести приходит в движение из состояния покоя. Определить ускорение a центра масс катка и силу натяжения нити. Какую скорость приобретет гиря, если она опускается с высоты h? Масса цилиндра М, масса гири m, массой блока пренебречь. Каток катится без скольжения. 10 . К концу тонкой нерастяжимой нити, намотанной на цилиндрический сплошной блок массой m1=200 г, прикреплено тело массой m2=500 г, которое находится на наклонной плоскости с углом наклона 450 (рис. 61). Нить, удерживающая тело, параллельна наклонной плоскости. Какой путь пройдет тело по наклонной плоскости за t=1 с, если коэффициент трения скольжения по наклонной плоскости равен k=0,1?
10 . К концу тонкой нерастяжимой нити, намотанной на цилиндрический сплошной блок массой m1=200 г, прикреплено тело массой m2=500 г, которое находится на наклонной плоскости с углом наклона 450 (рис. 61). Нить, удерживающая тело, параллельна наклонной плоскости. Какой путь пройдет тело по наклонной плоскости за t=1 с, если коэффициент трения скольжения по наклонной плоскости равен k=0,1?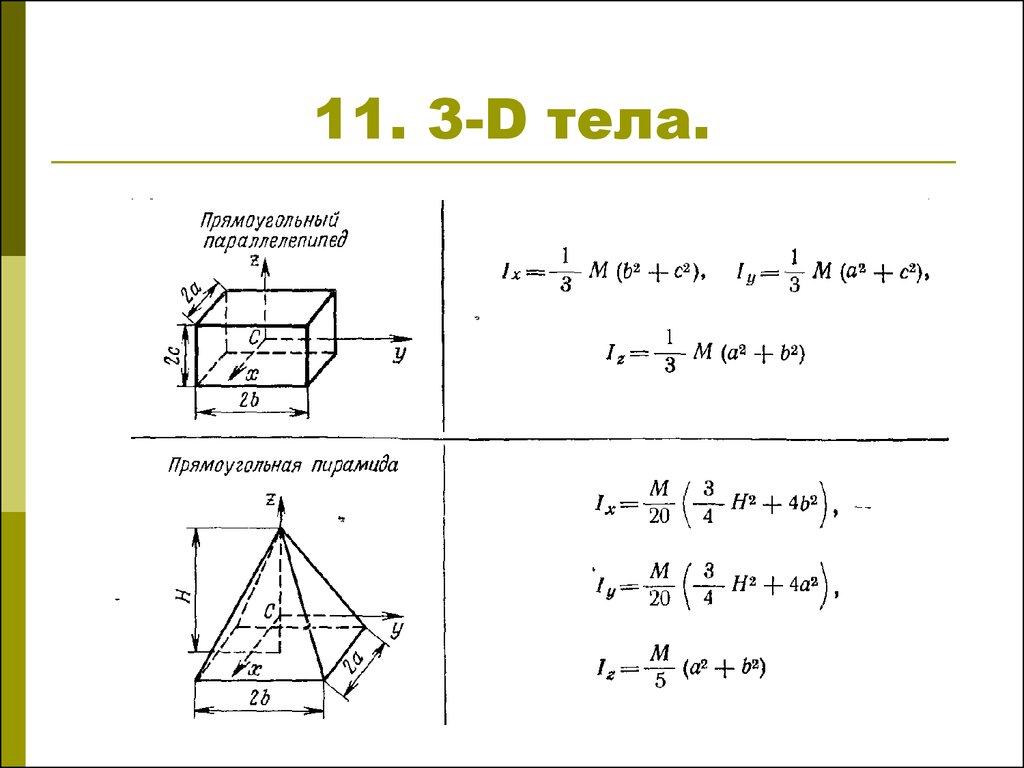
 ..
..