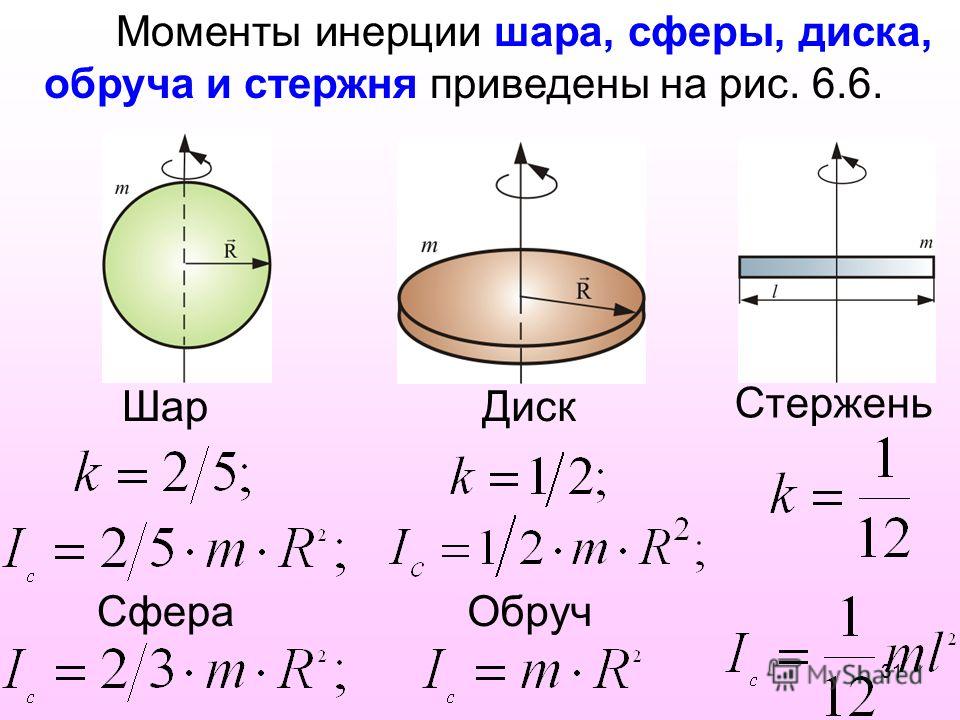
формулы для стержня и колеса
Любые перемещения тел в пространстве, траектория которых является окружностью, предполагают знание не только угловой скорости, но и момента инерции для описания этого движения. Что такое момент инерции, а также чему он равен для стержня и колеса, ответит данная статья.
Вращение и момент инерции
Физическая величина, которая называется моментом инерции, обозначается, как правило, буквой I и появляется в физике при рассмотрении момента импульса материальной точки, которая вращается вокруг оси. Момент импульса L в скалярной форме записывается следующим выражением:
L = r*m*v
Здесь r — дистанция до оси материальной точки, m — ее масса, v — линейная скорость. Используя связь последней со скоростью угловой ω, получаем выражение:
L = r2*m*ω, где ω = v/r
Отвечая на вопрос о том, что такое момент инерции, следует сказать, что это величина I = r2*m. То есть она зависит от массы вращающегося объекта, быстро растет с увеличением расстояния до оси и измеряется в кг*м2.
Общее выражение для момента инерции
Введенная в предыдущем пункте формула для величины I справедлива, если размеры объекта пренебрежимо малы по сравнению с дистанцией до оси r (вращение Земли вокруг нашей звезды). Если же линейные размеры объекта становятся сравнимыми с расстоянием r, тогда необходимо для вычисления I пользоваться более общей формулой, которая дана ниже:
I = ∫m(r2*dm)
Из нее видно, что подынтегральное выражение представляет собой момент инерции материальной точки. Сумма же всех моментов от точек с массой dm составляет полный момент инерции I для всего тела.
Эта формула является мощным инструментом для определения I тела абсолютно любой формы. Согласно формуле величина I является аддитивной, то есть позволяет разбить тело на отдельные части, вычислить их моменты инерции, а затем сложить полученные результаты для получения величины I тела.
Физический смысл величины I
Зная, что такое момент инерции, необходимо сказать несколько слов о том, как его значение отражается на поведении и характеристиках вращения реальных объектов.
Большая величина I приводит к тому, что тело очень тяжело раскрутить вокруг оси. Для этого приходится выполнить значительную работу и приложить существенные усилия. Примером тела с большим I является автомобильный маховик — тяжелый металлический диск, жестко закрепленный на коленвале двигателя. Наоборот, если величина I системы невелика, то ее можно быстро раскрутить и так же быстро и легко остановить. Примером для этого случая является алюминиевый обод велосипедного колеса.
Приведенное выше обсуждение говорит о том, что момент инерции характеризуется инерционностью процесса вращения, то есть выполняет ту же самую роль, что и масса тела при приложении к ней силы с целью придания ускорения.
Отличие массы и момента инерции заключается не только в единицах измерения, но и в том, что последний является функцией вращательной системы, а не только геометрии тела и его массы.
Момент инерции относительно оси вращения, пересекающей центр масс стержня
Рассмотрим пример использования интегральной формулы для решения реальных задач. Первым делом решим простую проблему: имеется стержень тонкий длиной l и массой m. Вращения оси проходит перпендикулярно этому стержню через центр массы объекта. Необходимо определить величину I для этой системы.
Первым делом решим простую проблему: имеется стержень тонкий длиной l и массой m. Вращения оси проходит перпендикулярно этому стержню через центр массы объекта. Необходимо определить величину I для этой системы.
Выпишем общую формулу для инерции момента стержня относительно оси, имеем:
I = ∫m(r2*dm)
Поскольку ось перпендикулярна рассматриваемому телу, и сам стержень имеет бесконечно малую толщину, то можно мысленно разрезать его на тонкие слои плоскостями, параллельными оси. В таком случае получаем, что элемент массой dm может быть представлен следующим равенством:
dm = ρ*S*dr
Здесь ρ — плотность материала, S — поперечное сечение, которое является постоянной величиной и стремится к нулю (стержень бесконечно тонкий). Подставим это выражение в общую формулу:
I = ρ*S*∫+l/2-l/2(r2*dr)
Заметим, что подставленные пределы интегрирования по r соответствуют условию задачи (ось делит стержень на две равные части). Выполняя интегрирование, получаем:
I = ρ*S*(r3/3)|+l/2-l/2 = m*l2/12, где m = ρ*S*l
Таким образом, момент инерции стержня тонкого, когда ось проходит через центр масс, в 12 раз меньше такового для материальной точки той же массы, находящейся на расстоянии l от оси.
Величина I для стержня с осью вращения на конце объекта
Рассмотрим, что такое момент инерции, в несколько иной ситуации. Имеем тот же самый объект (тонкий стержень), но теперь ось проходит через конец. Как изменится момент инерции в этом случае? Применяем тот же метод разбиения стержня и последующего интегрирования, как в предыдущем пункте, получаем:
I = ρ*S*∫l0(r2*dr)
Заметим, что изменились лишь пределы интегрирования. Решением будет следующее равенство:
I = m*l2/3
Выражение показывает, что тот же самый стержень будет обладать в 4 раза большим моментом инерции (труднее раскрутить), если ось вращения переместить с его центра на край.
Рассматривая решение этих двух задач, следует сделать важный вывод: при расчете величины I нельзя сводить всю массу объекта в его центр и выполнять расчет, как для материальной точки. Вычисление следует проводить только с использованием интегрального выражения.
Значение I для колеса со спицами
Момент инерции колеса можно определить, используя свойство аддитивности рассматриваемой величины.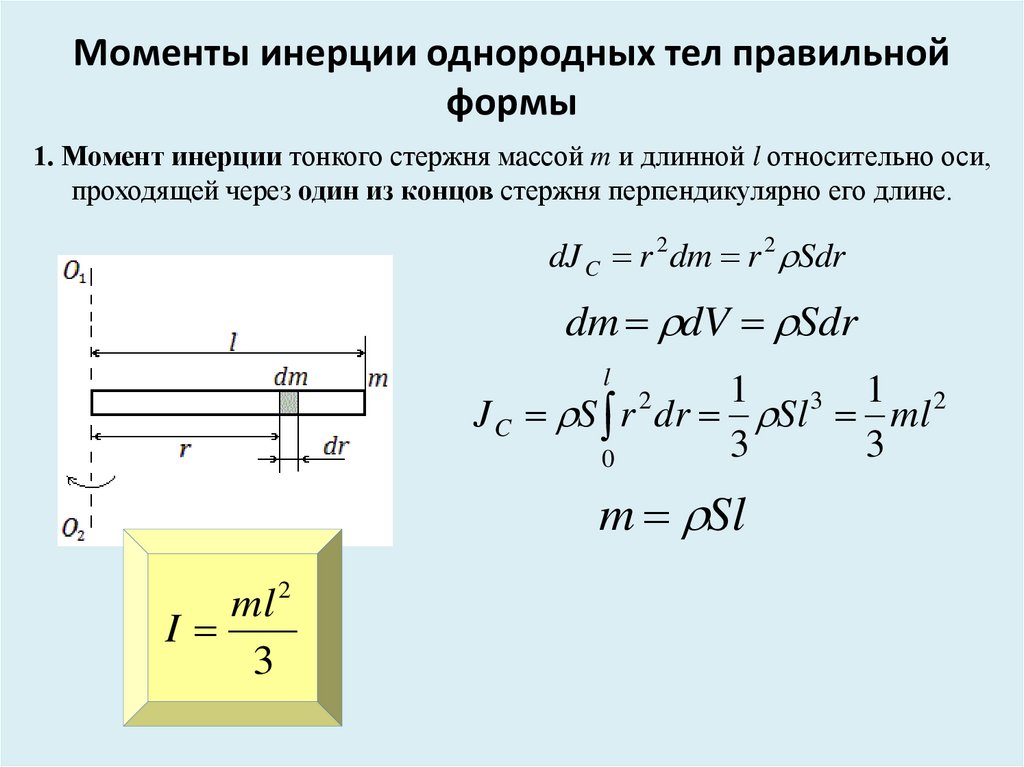 Для этого мысленно разберем колесо на отдельные части, которые представляют собой спицы и обод. Поскольку спица — это тонкий стержень, и ось ее вращения проходит через конец, то для нее справедлива формула, полученная в предыдущем пункте.
Для этого мысленно разберем колесо на отдельные части, которые представляют собой спицы и обод. Поскольку спица — это тонкий стержень, и ось ее вращения проходит через конец, то для нее справедлива формула, полученная в предыдущем пункте.
Что касается обода колеса, то его момент инерции аналогичен таковому для материальной точки, находящейся на расстоянии радиуса колеса и имеющей массу обода.
Складывая моменты инерции всех элементов, получаем:
I = n*mc*r2/3 + mo*r2
Здесь mc и mo — массы спицы и обода, соответственно, n — число спиц. Если все спицы весят намного меньше обода, тогда момент инерции колеса будет равен:
I =mo*r2, если n*mc
Знание величины I для колеса является важным при расчете скорости угловой и момента импульса вращения колес любого транспортного средства (автомобиля, велосипеда).
Определение момента инерции колеса (Лабораторная работа № 2)
Физика \ Физика
Страницы работы
4 страницы (Word-файл)
Посмотреть все страницы
Скачать файл
Содержание работы
РАБОТА №2
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ КОЛЕСА
Цель работы: определить момент инерции колеса с предельной
относительной погрешностью e, не превышающей 5%.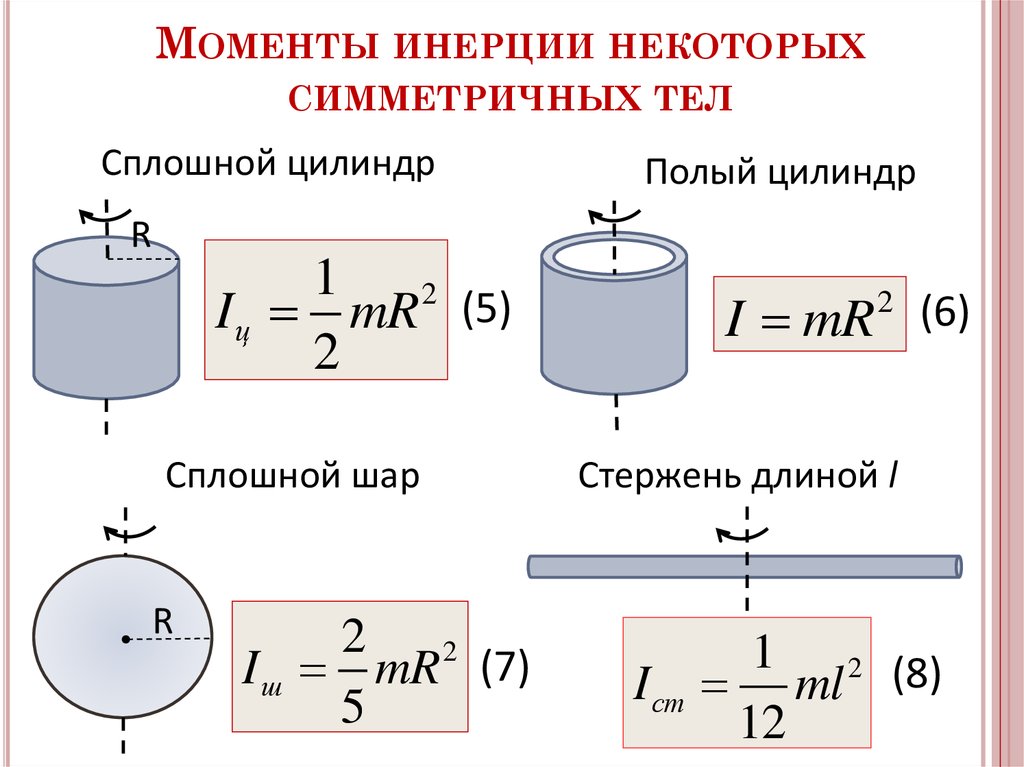
Приборы и принадлежности: колесо, платформа, набор грузов, технические весы, секундомер, штангенциркуль.
ТЕОРИЯ
Установка
состоит из колеса, на вал которого накручена нить. К нити подвешена платформа
для грузов. Накручивая нить на вал, поднимают платформу на некоторую высоту h1 (положение А на рисунке 1). Высота отсчитывается от положения
груза при полностью раскрученной нити. Если груз отпустить, он начнет двигаться
вниз под действием силы тяжести и с помощью нити приведет во вращение колесо.
Когда нить полностью раскрутится (положение В), колесо, вращаясь по инерции,
начнет поднимать груз. Дойдя до некоторой высоты h
Для определения момента инерции
колеса используем закон сохранения энергии. Так как при движении системы
колесо-груз действуют неконсервативные силы (силы трения в подшипнике и силы
сопротивления воздуха), то механическая энергия системы уменьшается.
По закону сохранения энергии приращение механической энергии равно работе неконсервативных сил:
, (1)
где Е1 и Е2 — механическая энергия системы соответственно в начальном и конечном положениях, АНК — работа неконсервативных сил при перемещении системы между этими положениями.
Применим соотношение ( l ) к перемещению системы «колесо-груз» из положения А (начальное положение) в положение В (конечное положение). Примем потенциальную энергию груза равной нулю в его нижнем положении.
Когда груз
находится на высоте h
, где (2)
m — масса груза с платформой.
Когда груз находится в нижнем положении, механическая энергия системы состоит из кинетической энергии груза и колеса:
,
(3) где v — скорость груза в нижнем положении,w — угловая скорость в этот же момент времени,
I — момент инерции колеса.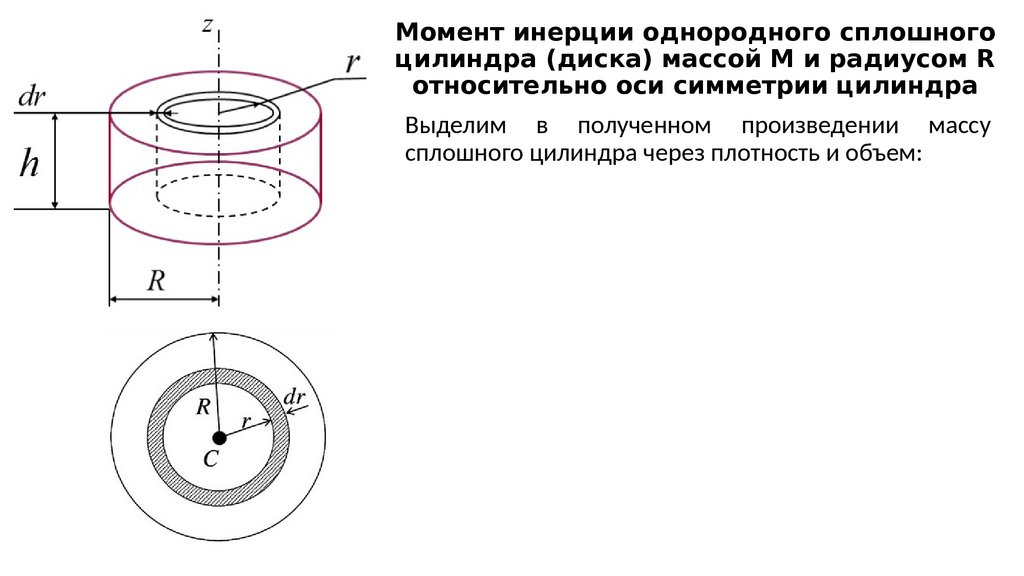
Обозначим равнодействующую всех неконсервативных сил через F. Работа этих сил при перемещении груза из верхнего в нижнее положение
. (4)
Подставив (2), (3), (4) в (I), получаем уравнение, составленное по закону сохранения энергии для рассматриваемого движения:
. (5)
Отсюда
. (6)
Определим v, w, t.
Так как груз движется равноускоренно без начальной скорости, то
, (7)
где a — ускорение груза, t — время движения груза из верхнего положения в нижнее.
Из соотношений (7) получаем
. (8)
Нить, на
которой подвешен груз, намотана на вал, поэтому точки, лежащие на поверхности
вала, имеют линейную скорость равную скорости груза.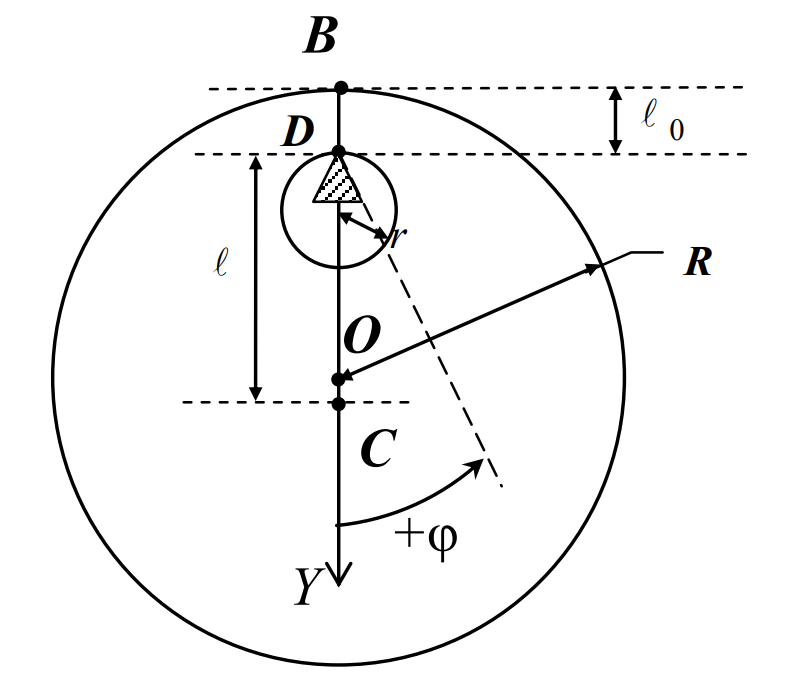 Следовательно, v=wr, где r- радиус
вала. Отсюда, используя (8), получаем
Следовательно, v=wr, где r- радиус
вала. Отсюда, используя (8), получаем
. (9)
Для определения F применим закон сохранения энергии (I) к перемещению системы «колесо-груз» из положения А в положение С. В положении С механическая энергия системы равна потенциальной энергии груза:
. (10)
При перемещении системы из А в С
. (11)
Подставим (2), (10), (11) в (1):
. (12)
Отсюда
. (13)
Подставим (8), (9), (13) в (6). После преобразования получим
. (14)
ИЗМЕРЕНИЯ
1. Измерить штангенциркулем диаметр вала и
определить радиус вала.
2. Определить на технических весах массу платформы и трех грузов.
3. Подвесить платформу с двумя грузами к нити и поднять их на высоту h1 (в таблицу записать положение А грузов, отсчитанное по вертикальной шкале). Отпустив груз, измерить секундомером время t его движения до нижнего положения, когда нить полностью раскрутится. Когда груз поднимется и остановится, зафиксировать положение колеса в этот момент и определить положение С по вертикальной шкале. Определить также нижнее положение В груза при полностью раскрученной нити. Все измерения положений А, В, С проводить одинаковом образом, например по низу платформы.
4. Измерения t и положений С провести 6 раз, накручивая вал 3 раза в одну сторону и 3 раза в другую. Это даст возможность скомпенсировать ошибку, связанную с возможной разбалансировкой колеса.
5. Определить h1 = В — А(
h1 берите одинаковым во всех измерениях), ,
h2 = B — , .
6. Измерения п.п. 2 — 5 провести также для 2-х других грузов, массу взять большe, чем в первом случае.
7. Измерения п.п. 2 — 5 провести также для 3-х других грузов.
8. Вычислить I по формуле (14) для трех различных масс грузов.
9. Рассчитать погрешности.
10.Записать окончательный результат.
Таблица.
r,м | A,м | B,м | h1,м | m,кг | t,с | C,м | h2,м | I,кг×м2 |
КОНТРОЛЬНЫЕ ВОПРОСЫ.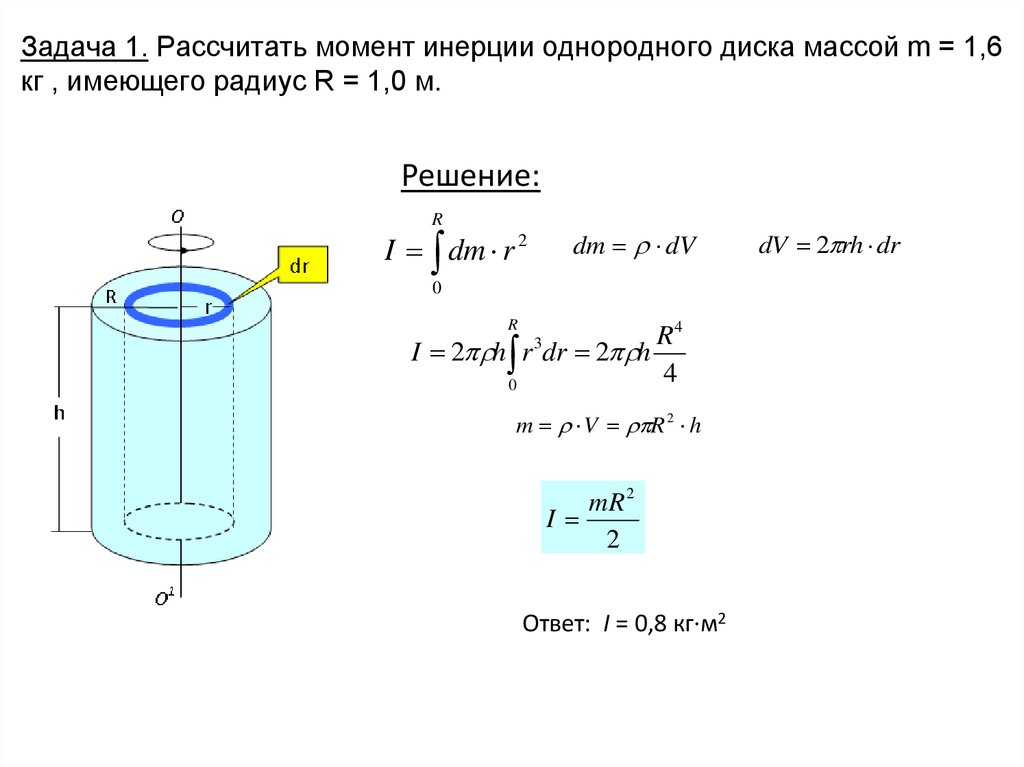
1.
a) Чему равен момент инерции материальной точки, тела?
b) Единица измерения момента инерции.
c) От чего зависит момент инерции тела?
d) Зависит ли момент инерции колеса в работе от массы груза? Обоснуйте ответ.
2. Чему равна механическая работа в случае:
a) постоянной силы (прямолинейное движение)?
b) переменной силы?
3. a) Что такое консервативные и неконсервативные силы? Какие неконсервативные силы действуют в работе?
b) Сформулируйте закон сохранения механической энергии.
4. Составьте уравнение по закону
сохранения энергии для перехода системы колесо — груз из состояния, когда груз
находится на высоте h
5. Составьте уравнение по
закону сохранения энергии для перехода системы колесо — груз из состояния,
когда груз находится на высоте h1 в состояние, когда нить полностью раскручена
и скорость системы максимальна.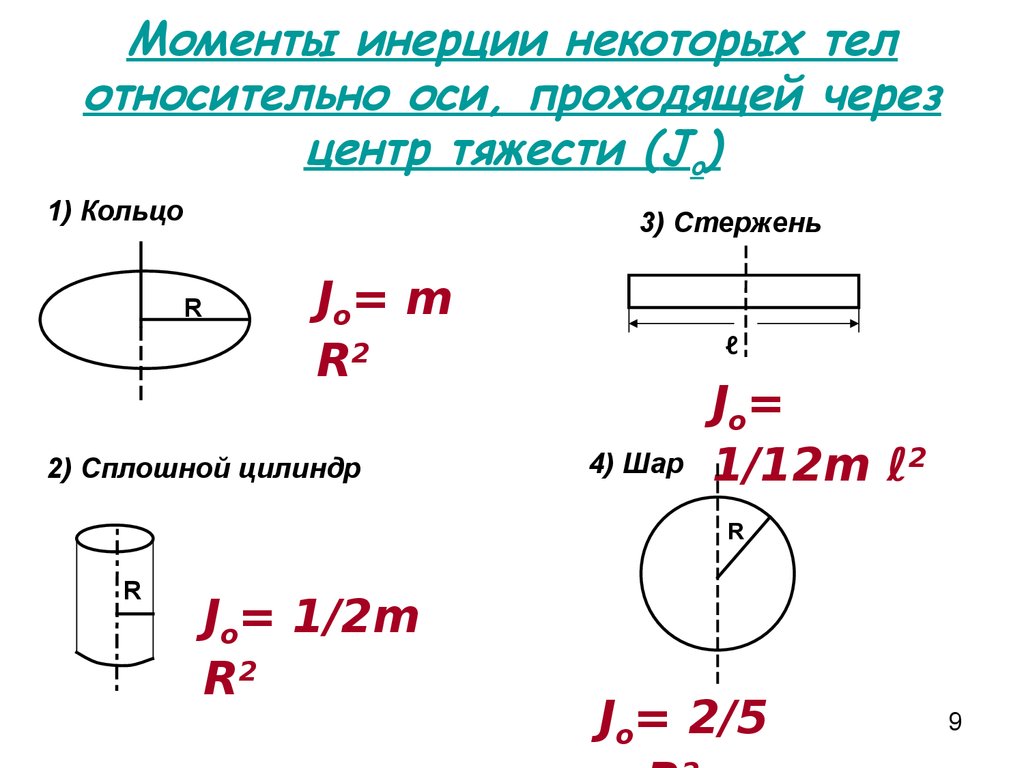
6. a) Как связаны линейная и угловая скорости ?
b) Какие точки вращающейся системы имеют линейную скорость равную скорости груза и почему?
c) Напишите основные формулы кинематики равноускоренного движения. Как они применяются в работе для вывода расчётной формулы? Почему движение груза можно считать равноускоренным?
ЛИТЕРАТУРА
1. Савельев И.В., Курс общей физики, том 1.
2. Трофимова Т.И., Курс физики.
3. Сивухин Д.В., Курс общей физики, том 1.
Похожие материалы
Информация о работе
Скачать файл
Выбери свой ВУЗ
- АлтГТУ 419
- АлтГУ 113
- АмПГУ 296
- АГТУ 267
- БИТТУ 794
- БГТУ «Военмех» 1191
- БГМУ 172
- БГТУ 603
- БГУ 155
- БГУИР 391
- БелГУТ 4908
- БГЭУ 963
- БНТУ 1070
- БТЭУ ПК 689
- БрГУ 179
- ВНТУ 120
- ВГУЭС 426
- ВлГУ 645
- ВМедА 611
- ВолгГТУ 235
- ВНУ им.
 Даля 166
Даля 166 - ВЗФЭИ 245
- ВятГСХА 101
- ВятГГУ 139
- ВятГУ 559
- ГГДСК 171
- ГомГМК 501
- ГГМУ 1966
- ГГТУ им. Сухого 4467
- ГГУ им. Скорины 1590
- ГМА им. Макарова 299
- ДГПУ 159
- ДальГАУ 279
- ДВГГУ 134
- ДВГМУ 408
- ДВГТУ 936
- ДВГУПС 305
- ДВФУ 949
- ДонГТУ 498
- ДИТМ МНТУ 109
- ИвГМА 488
- ИГХТУ 131
- ИжГТУ 145
- КемГППК 171
- КемГУ 508
- КГМТУ 270
- КировАТ 147
- КГКСЭП 407
- КГТА им.
 Дегтярева 174
Дегтярева 174 - КнАГТУ 2910
- КрасГАУ 345
- КрасГМУ 629
- КГПУ им. Астафьева 133
- КГТУ (СФУ) 567
- КГТЭИ (СФУ) 112
- КПК №2 177
- КубГТУ 138
- КубГУ 109
- КузГПА 182
- КузГТУ 789
- МГТУ им. Носова 369
- МГЭУ им. Сахарова 232
- МГЭК 249
- МГПУ 165
- МАИ 144
- МАДИ 151
- МГИУ 1179
- МГОУ 121
- МГСУ 331
- МГУ 273
- МГУКИ 101
- МГУПИ 225
- МГУПС (МИИТ) 637
- МГУТУ 122
- МТУСИ 179
- ХАИ 656
- ТПУ 455
- НИУ МЭИ 640
- НМСУ «Горный» 1701
- ХПИ 1534
- НТУУ «КПИ» 213
- НУК им.
 Макарова 543
Макарова 543 - НВ 1001
- НГАВТ 362
- НГАУ 411
- НГАСУ 817
- НГМУ 665
- НГПУ 214
- НГТУ 4610
- НГУ 1993
- НГУЭУ 499
- НИИ 201
- ОмГТУ 302
- ОмГУПС 230
- СПбПК №4 115
- ПГУПС 2489
- ПГПУ им. Короленко 296
- ПНТУ им. Кондратюка 120
- РАНХиГС 190
- РОАТ МИИТ 608
- РТА 245
- РГГМУ 117
- РГПУ им.
 Герцена 123
Герцена 123 - РГППУ 142
- РГСУ 162
- «МАТИ» — РГТУ 121
- РГУНиГ 260
- РЭУ им. Плеханова 123
- РГАТУ им. Соловьёва 219
- РязГМУ 125
- РГРТУ 666
- СамГТУ 131
- СПбГАСУ 315
- ИНЖЭКОН 328
- СПбГИПСР 136
- СПбГЛТУ им. Кирова 227
- СПбГМТУ 143
- СПбГПМУ 146
- СПбГПУ 1599
- СПбГТИ (ТУ) 293
- СПбГТУРП 236
- СПбГУ 578
- ГУАП 524
- СПбГУНиПТ 291
- СПбГУПТД 438
- СПбГУСЭ 226
- СПбГУТ 194
- СПГУТД 151
- СПбГУЭФ 145
- СПбГЭТУ «ЛЭТИ» 379
- ПИМаш 247
- НИУ ИТМО 531
- СГТУ им.
 Гагарина 114
Гагарина 114 - СахГУ 278
- СЗТУ 484
- СибАГС 249
- СибГАУ 462
- СибГИУ 1654
- СибГТУ 946
- СГУПС 1473
- СибГУТИ 2083
- СибУПК 377
- СФУ 2424
- СНАУ 567
- СумГУ 768
- ТРТУ 149
- ТОГУ 551
- ТГЭУ 325
- ТГУ (Томск) 276
- ТГПУ 181
- ТулГУ 553
- УкрГАЖТ 234
- УлГТУ 536
- УИПКПРО 123
- УрГПУ 195
- УГТУ-УПИ 758
- УГНТУ 570
- УГТУ 134
- ХГАЭП 138
- ХГАФК 110
- ХНАГХ 407
- ХНУВД 512
- ХНУ им.
 Каразина 305
Каразина 305 - ХНУРЭ 325
- ХНЭУ 495
- ЦПУ 157
- ЧитГУ 220
- ЮУрГУ 309
3.3: Колесо реакции — Инженерные тексты LibreTexts
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7637
- William L. Hallauer Jr.0010
Реактивные колеса используются для управления ориентацией космического корабля. Основным компонентом реактивного колеса является ротор, «колесо», которое обычно либо не вращается, либо вращается с постоянной, отличной от нуля, скоростью вращения. Когда двигатель увеличивает или уменьшает скорость вращения от нормального значения, на транспортное средство, к которому прикреплено реактивное колесо, действует управляющий момент.
Когда двигатель увеличивает или уменьшает скорость вращения от нормального значения, на транспортное средство, к которому прикреплено реактивное колесо, действует управляющий момент.
Блок реактивного колеса, изображенный на рисунке \(\PageIndex{1}\), представляет собой небольшое лабораторное устройство, используемое в экспериментальных исследованиях. Его основное функционирование такое же, как и у пригодного для полетов узла реактивного колеса. Вращающимися элементами являются колесо, вал и ротор двигателя. Обозначим их совокупную вращательную инерцию вокруг оси вала как \(J\), также называемую моментом инерции . Вал удерживается в подшипниках, которые смазываются, но тем не менее создают тормозной момент. Угол поворота вращающихся элементов обозначается \(\theta(t)\) и графически представлен на рисунке \(\PageIndex{1}\) двунаправленной стрелкой и Правило правой руки , указывающее полярность вращения. Скорость вращения (угловая скорость, скорость вращения) обозначается \(\dot{\theta}(t)\equiv p(t)\), этот символ обычно используется для обозначения угловой скорости в авиационных приложениях.
Скорость вращения (угловая скорость, скорость вращения) обозначается \(\dot{\theta}(t)\equiv p(t)\), этот символ обычно используется для обозначения угловой скорости в авиационных приложениях.
Мы идеализируем момент сопротивления как линейно-вязкостную форму \(c_{\theta} \times p(t)\), где \(c_{\theta}\) — постоянная вязкостного демпфирования при вращении, которую можно измерить на реальном оборудовании. Также обозначим через \(M_{m}(t)\) крутящий момент, прикладываемый к вращающимся элементам электродвигателем, причем этот крутящий момент является независимой входной величиной.
На приведенном ниже рисунке представлена диаграмма свободного тела (FBD) всех моментов (в данном случае крутящих моментов), действующих на вращающиеся элементы, при этом сопротивление подшипника показано как один крутящий момент, даже если оно фактически распределено по всем поверхностям подшипника:
Рисунок \(\PageIndex{2}\)Чтобы вывести уравнение движения, мы запишем закон Ньютона 2 и для вращения вокруг оси вала, основанный на FBD:
\[\Sigma(\text {Моменты})_{\text{об оси вала}}=(\text{инерция вращения}) \times(\text{ускорение вращения})_{\text{об оси вала} } \номер\]
\[M_{m}(t)-c_{\theta} p=J \dot{p} \quad \Rightarrow \quad J \dot{p}+c_{\theta} p=M_{m}(t )\метка{уравнение:3. 1} \]
1} \]
Преобразование уравнения \(\ref{eqn:3.1}\) в стандартную форму заказа 1 st дает
\[\dot{p}-\left(-\frac{c_{\theta}}{J}\right) p=\frac{1}{J} M_{m}(t) \Rightarrow \dot{ p} -a p = b M_ {m} (t) \ quad \ text { где } a = — \ frac {c _ {\ theta}} {J} \ text { и } b = \ frac {1} {J} \метка{уравнение:3.2} \]
Эта страница под названием 3.3: Reaction Wheel используется в соответствии с лицензией CC BY-NC 4.0. Автор, ремикс и/или куратор Уильям Л. Халлауэр-младший (Инициатива открытого образования технических библиотек Вирджинии) использует исходный контент, который был отредактировано в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Уильям Л.
 Халлауэр мл.
Халлауэр мл.
- Лицензия
- CC BY-NC
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Теги
- реактивное колесо
- источник@https://vtechworks.lib.vt.edu/handle/10919/78864
Использование видео прямого измерения для определения момента инерции вращения велосипедного колеса
Джозеф Флэки ([email protected]), Технический колледж долины Чиппева.
Резюме
Это задание дает учащимся возможность применить принципы вращательного движения к реальной ситуации, используя видео с прямыми измерениями.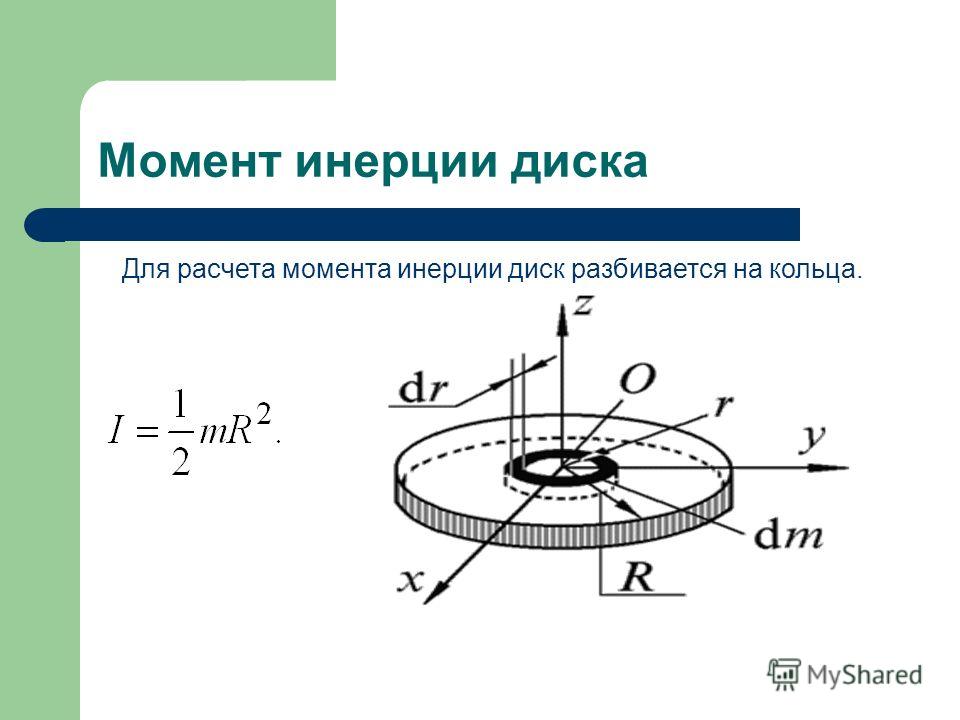 Учащиеся будут работать вместе в небольших группах, чтобы определить момент инерции велосипедного колеса, используя видео по физике прямого измерения.
Учащиеся будут работать вместе в небольших группах, чтобы определить момент инерции велосипедного колеса, используя видео по физике прямого измерения.
Развернуть для более подробной информации
Классификация видов деятельности и связь с соответствующими ресурсами
Свернуть
Темы
Классическая механикаКласс
Средняя школа (9–12), Вводный курс в колледж, Начальный уровень колледжа (13–14)Цели обучения
- Учащиеся будут применять концепции углового ускорения, крутящего момента и инерции вращения, а также второй закон Ньютона для вращения в реальной ситуации.
- Учащиеся будут применять взаимосвязь между линейным и угловым движением для вращающегося объекта.
- Учащиеся будут практиковаться в сборе данных с видео прямых измерений.
- Учащиеся также будут полагаться на свои предварительные знания по одномерному анализу силы объекта, который ускоряется.

- Учащиеся также будут развивать совместное поведение при обучении во время совместной работы.
Контекст для использования
Это задание предназначено для курса физики, основанного на алгебре, в техническом колледже. Размер класса варьируется от 20 до 24 студентов в лабораторных условиях с доступными компьютерами или ноутбуками. В зависимости от объема введения, включенного в задание, учащиеся должны потратить от 30 минут до часа на его выполнение. Для выполнения упражнения не требуется никакого дополнительного оборудования, но его можно дополнить физическим велосипедным колесом или системой шкивов. Это задание не предназначено для того, чтобы учащиеся впервые познакомились с видео с прямыми измерениями.
Перед выполнением задания учащиеся должны иметь четкое представление об ускоряющих системах, иметь опыт решения задач на соединение объектов, круговых измерений и законов движения Ньютона. Упражнение планируется использовать в 2-часовой лабораторной/лекционной обстановке.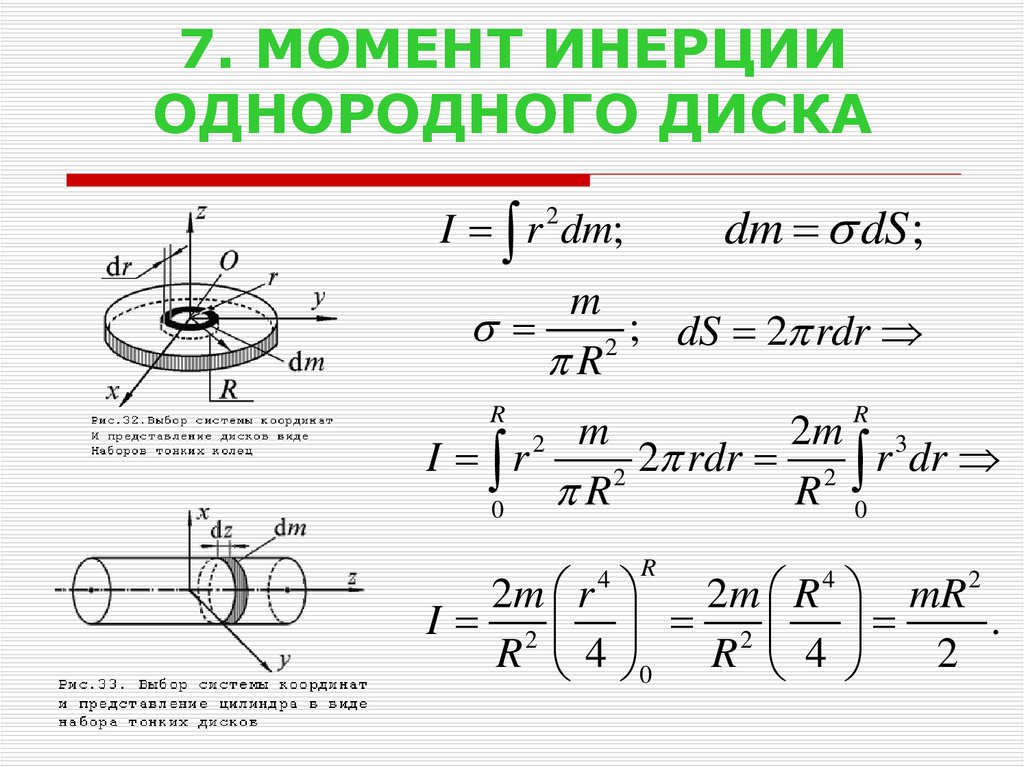 Будет представлен материал об угловом движении и моменте инерции, последует задание, а занятие завершится обсуждением наших результатов. В зависимости от уровня навыков учащихся, задание должно быть легко адаптировано к другим условиям путем включения более подробной информации/введения.
Будет представлен материал об угловом движении и моменте инерции, последует задание, а занятие завершится обсуждением наших результатов. В зависимости от уровня навыков учащихся, задание должно быть легко адаптировано к другим условиям путем включения более подробной информации/введения.
Описание и учебные материалы
Описание материала, устные инструкции для учащихся и возможные дополнительные вопросы можно найти в следующем текстовом документе:
Момент инерции для велосипедного колеса (Microsoft Word 29kB Jul13 12)
Видео, относящееся к материалу можно найти на следующем веб-сайте:
Велосипедное колесо, ускоренное падающим весом
Видео необходимо загрузить на компьютеры учащихся и открыть в QuickTime, чтобы можно было продвигать видео кадр за кадром.
Учебные заметки и советы
Это задание разделено на 3 части: представление материала, анализ видео учащимися и обсуждение. Подача материала должна содержать аналогичные проблемы, относящиеся к видео.


 Даля 166
Даля 166 Дегтярева 174
Дегтярева 174 Макарова 543
Макарова 543 Герцена 123
Герцена 123 Гагарина 114
Гагарина 114 Каразина 305
Каразина 305 Халлауэр мл.
Халлауэр мл.