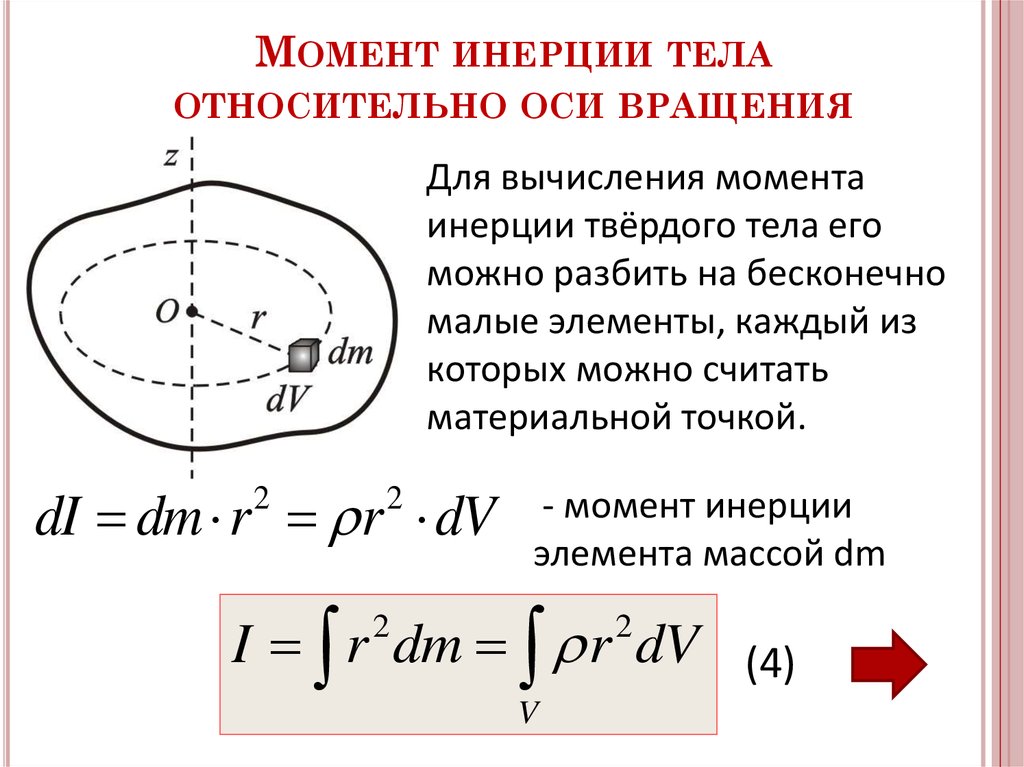
Физический смысл момента инерции

Онлайн калькуляторы

На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник

Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение

Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!

Главная Справочник Физика Физический смысл момента инерции

Определение и смысл момента инерции

Пусть материальная точка вращается по окружности вокруг неподвижной оси, которая проходит через центр траектории данной точки. Момент ее импульса (L) относительно этой оси будет равен:

   

где m – масса этой точки; v – скорость движения точки; r – радиус окружности, по которой точка движется. Если угловую скорость точки обозначить как и принять равной:

   

тогда величину момента импульса можно определить как:

   

Если представить, что вокруг рассматриваемой оси вращается несколько материальных точек с одинаковой угловой скоростью, то L будет равен:

   

В выражении (4) суммирование происходит по всем материальным точка, входящим в систему. Так как – величина постоянная, то ее можно вынести за знак суммы, тогда имеем:

   

Где – величина, равная сумме произведений масс материальных точек на расстояния в квадрате от каждой из них до оси вращения, называют моментом инерции рассматриваемой системы по отношению к оси.

Уравнение (5) отражает тот факт, что момент импульса системы при ее вращении относительно оси равен произведению момента инерции на угловую скорость. Если кроме вращения материальных точек имеется их движения по радиусам, то выражение (5) останется справедливым. Это следствие линейной зависимости момента импульса точки (L) от скорости ее движения (v). Если вектор скорости направлен по радиусу или параллельно оси вращения, то момент импульса относительно этой оси равен нулю. Вследствие чего данные виды движения не оказывают непосредственного влияния на вид связи между моментом импульса системы относительно оси вращения и угловой скоростью. Такое влияние проявляется косвенно. Момент инерции перестает быть постоянной величиной и изменяется во времени, в зависимости от конфигурации системы. Уравнение движения для такой системы имеет вид:

   

где – момент внешних сил, приложенных к телу относительно оси вращения. Уравнение (6) называют основным уравнением динамики вращательного движения тела вокруг неподвижной оси. Проведем аналогию между ним и уравнением Ньютона для поступательного движения материальной точки:

   

Роль массы в уравнении (6) играет момент инерции J, роль скорости угловая скорость, роль силы – момент силы.

Получается, что момент инерции тела относительно оси вращения выступает мерой инертности тела по отношению к вращению, так же как масса является мерой инертности в поступательном движении.

Аналогию между поступательным движением материальной точки и вращением твердого тела можно продолжить, при рассмотрении кинетической энергии твердого тела.

   

Где – кинетическая энергия твердого тела, вращающегося около неподвижной оси. Данное выражение напоминает формулу для расчета кинетической энергии при поступательном движении материальной точки.

Примеры решения задач

Понравился сайт? Расскажи друзьям!

Момент инерции тела и материальной точки. Формулы для цилиндра и стержня. Физический смысл величины

В школьном курсе физики большое внимание уделяется описанию кинематики и динамики поступательного движения тел в трехмерном пространстве. Но вращательное движение играет не менее важную роль в технике и природе. В данной статье рассмотрим, что понимают под моментом инерции тела при его вращении вокруг оси.

Динамика вращения

Прежде чем давать определение момента инерции тела, расскажем, для чего нужна эта величина и в каких уравнениях она появляется. В первую очередь, это главное уравнение динамики вращения — формула моментов. Записывается она так:

M = I*α.

Здесь M, α и I — это момент силы, ускорение угловое и инерции момент, соответственно. По сути, это уравнение можно назвать вторым ньютоновским законом для вращательного движения. Несложно догадаться, что величина I здесь играет ту же самую роль, что инерционная масса в случае поступательного движения.

Помимо приведенного уравнения, существует еще одна важная формула, которая применяется часто для решения задач на вращение тел — это закон сохранения момента импульса. Его, как правило, записывают в следующей удобной для практики форме:

I*ω = const.

Как видим, здесь инерции момент тоже является ключевой величиной, ω — это скорость угловая.

Момент инерции твердого тела

Теперь пришло время дать определение величине I. Сначала рассмотрим его для материальной точки. Ее моментом инерции называется произведение массы на квадрат расстояния до оси вращения. Если массу обозначить буквой m, а дистанцию до оси от точки буквой r, то формула для I запишется так:

I = m*r².

Как видно, I выражается в кг*м². Равенство для точки можно использовать для определения момента инерции тела относительно оси. В этом случае применяют следующее интегральное выражение:

I = ∫_m(r²*dm).

Эта формула применяется для вычисления величин I абсолютно любых систем с разными геометрическими формами. Последнее равенство также используют при решении практических задач в следующем виде:

I = ∫_V(ρ*r²*dV).

Где ρ — плотность вещества. Ниже в статье покажем, как использовать интегральное равенство для решения конкретных задач.

Величина I для цилиндра

Каждый школьник представляет себе фигуру «цилиндр». По правде говоря, они бывают самыми разными (эллиптическими, гиперболическими, наклонными). Здесь рассмотрим самый простой случай. Это круговой прямой цилиндр, который ограничен цилиндрической поверхностью и двумя одинаковыми кругами. Ось вращения фигуры проходит через ее центр масс и через центры обоих оснований. Вычислим относительно нее инерции момент тела.

Запишем исходную формулу:

I = ∫_V(ρ*r²*dV).

Чтобы ее применить, представим себе цилиндр в виде тонко нарезанных круглых одинаковых слоев. Обозначим их толщину dl, радиус фигуры равен R, а высота — L. Теперь каждый тонкий слой объемом pi*R²*dl разрежем на бесконечное множество колец, толщина каждого из которых равна dr. После выполнения всех описанных мысленных геометрических операций можно записать формулу для элементарного объема dV, то есть для объема одного кольца:

dV = 2*pi*r*dr*dl.

В результате этого представления исходное выражение для I преобразуется в формулу с двойным интегралом:

I = ∫_L∫_R(ρ*r²*2*pi*r*dr*dl) = 2*pi*ρ*L*R⁴/4 = M*R²/2.

Где буквой M обозначена масса всего цилиндра.

Таким образом, мы получили конечное выражение для инерции момента цилиндра. Как видно, он определяется только радиусом фигуры и ее массой и не зависит от длины (высоты). Последнее означает, что аналогичную формулу можно применять для определения величины I для диска любой толщины.

Величина I для стержня

Теперь применим формулу для определения момента инерции тонкого стержня. Принципиальным моментом здесь является тот факт, что его толщина должна быть намного меньше длины L. Массу стержня обозначим буквой M. Момент инерции рассчитаем для положения оси, которая проходит через центр масс тела и перпендикулярна ему.

Начнем расчет все с той же формулы, что и в случае с цилиндром:

I = ∫_V(ρ*r²*dV).

Мысленно разрежем весь стержень на тонкие слои. Обозначим площадь сечения каждого из них S, а его толщину — dl. Тогда получаем формулу для dV:

dV = S*dl.

Теперь можно вычислить инерции момент тела:

I = ∫_-L/2^+L/2(ρ*S*l²*dl).

Заметим, что каждый слой находится от оси вращения на расстоянии l, поэтому мы заменили букву r. Кроме того, обращаем внимание на пределы интегрирования, которые имеют такое значение потому, что ось проходит точно через середину стержня. В итоге получаем:

I = ∫_-L/2^+L/2(ρ*S*l²*dl) = ρ*S*l³/3|_-L/2^+L/2 = M*L²/12.

С помощью аналогичных рассуждений и вычислений можно показать, что если ось вращения проходит через какой-либо конец стержня, то его момент инерции будет в четыре раза больше, то есть:

I = M*L²/3.

Физический смысл величины

Выше мы уже сказали несколько слов о том, что означает момент инерции тела с физической точки зрения. Здесь остановимся несколько подробнее на этом вопросе.

Если внимательно посмотреть на формулу для I, то можно увидеть, что эта величина зависит не только от самой массы тела, но и от ее распределения, то есть от формы тела, а также от его положения относительно оси вращения.

Ярким примером являются обычная швабра или просто стержень. Каждый человек хоть раз в жизни раскручивал швабру вокруг оси, проходящей вдоль ее ручки или перпендикулярно ей. В первом случае легкого движения ладоней достаточно, чтобы придать угловое ускорение швабре, во втором же — приходится прилагать некоторую силу рук, чтобы раскрутить ее. Объяснить этот факт просто. В первом случае момент инерции практически равен нулю, во втором — он имеет некоторую конечную величину.

момент инерции | Определение, уравнение, единица измерения и факты

момент инерции

Просмотреть все СМИ

Похожие темы:

инерция вращения радиус вращения

См. все связанное содержание →

момент инерции , в физике, количественная мера инерции вращения тела, т. е. противодействие, которое тело проявляет при изменении скорости вращения вокруг оси при приложении крутящего момента (сила поворота). Ось может быть внутренней или внешней и может быть фиксированной или нефиксированной. Момент инерции ( I ), однако, всегда определяется по отношению к этой оси и определяется как сумма произведений, полученных путем умножения массы каждой частицы материи в данном теле на квадрат ее расстояния от оси. При расчете углового момента твердого тела момент инерции аналогичен массе в линейном импульсе. Для линейного импульса импульс

p равен массе m , умноженной на скорость v ; тогда как для углового момента угловой момент L равно моменту инерции I , умноженному на угловую скорость ω.

На рисунке показаны два стальных шарика, приваренных к стержню AB , прикрепленному к стержню OQ на C . Если пренебречь массой AB и предположить, что все частицы массой m каждого шара сосредоточены на расстоянии r от OQ , момент инерции будет равен I = 2 mr ² .

Тест «Британника»

Физика и законы природы

Какая сила замедляет движение? Каждому действию есть равное и противоположное что? В этом викторине по физике нет ничего, что E = mc было бы квадратным.

Единица момента инерции является составной единицей измерения. В Международной системе (СИ) m выражается в килограммах, а r — в метрах, причем I (момент инерции) имеет размерность килограмм-метр в квадрате. В обычной системе США м выражено в порциях (1 порция = 32,2 фунта) и r в футах, где I выражено в единицах площади улитки-фута.

Момент инерции любого тела, форма которого может быть описана математической формулой, обычно рассчитывается с помощью интегрального исчисления. Момент инерции диска на фигуре около

OQ можно было бы аппроксимировать, разрезав его на ряд тонких концентрических колец, найдя их массы, умножив массы на квадраты их расстояний от OQ и суммируя эти продукты. При использовании интегрального исчисления процесс суммирования осуществляется автоматически; ответ I = ( mR ² )/2. (См. механику; крутящий момент.)

Для тела математически не поддающейся описанию формы момент инерции можно определить экспериментальным путем.

В одной из экспериментальных методик используется связь между периодом (временем) колебаний крутильного маятника и моментом инерции подвешенной массы. Если бы диск на рисунке был подвешен на проволоке OC фиксируется на O , он будет колебаться около OC , если его скрутить и отпустить. Время одного полного колебания будет зависеть от жесткости проволоки и момента инерции диска; чем больше инерция, тем больше время.

Редакторы Британской энциклопедии Эта статья была недавно отредактирована и обновлена ​​Эриком Грегерсеном.

угловой момент — Каков физический смысл главных осей инерции?

Спросил 4 года, 7 месяцев назад

Изменено 4 года, 7 месяцев назад

Просмотрено 2к раз

$\begingroup$

Каков физический смысл главных осей инерции? Раньше я думал, что оси инерции — это в каком-то смысле единственные оси, вокруг которых может вращаться тело без «проскальзывания» углового момента на другие оси. Другими словами, я думал, что это единственные оси, вокруг которых тело может совершать движение простого вращения вокруг оси, а любая попытка повернуть тело вокруг неглавной оси приведет к сложному движению, состоящему из суперпозиции вращения вокруг более чем одной главной оси (другими словами, я думал, что главные оси аналогичны нормальным модам в вибрирующих системах, где система может вибрировать на одной частоте, только если это нормальный режим).

Однако прецессия без крутящего момента — или общее движение симметричного несферического волчка — показывает, что это не так. Симметричный несферический волчок вообще имеет вращение вокруг своей верхней оси, плюс дополнительное вращение вокруг оси, которая может составлять угол с осью волчка — и, вообще говоря, неглавное. Так что же означают главные оси инерции? Какова их физическая интерпретация (поскольку в каждой книге, которую я читал, просто говорится, что они являются собственными пространствами тензора инерции, что является утверждением, лишенным какого-либо физического смысла)?

• угловой момент
• вращательная динамика
• момент инерции
• динамика твердого тела
• угловая скорость

$\endgroup$

$\begingroup$

Одним из способов сказать это: вам не нужно применять какой-либо внешний крутящий момент, чтобы поддерживать вращение объекта вокруг главной оси.

Для поддержания постоянной угловой скорости вокруг любой оси, проходящей через центр масс, который не может быть определен как главная ось, требуется крутящий момент. 9\circ$ со стержнем. Каждой из масс потребовалась бы центростремительная сила, чтобы заставить ее двигаться по кругу. Поскольку окружности не лежат в одной плоскости, эта пара сил образует крутящий момент. Как только вы перестанете подавать этот крутящий момент, штанга переключится на вращение вокруг оси, перпендикулярной штанге (которая является главной осью).

$\endgroup$

$\begingroup$

Если объект вращается вокруг одной из своих главных осей, то направление его угловой скорости совпадает с направлением его углового момента.

Поскольку $\vec L = I \vec\omega$, $\vec \omega$, являющийся собственным вектором $I$, эквивалентен тому, что $\vec L$ параллелен $\vec\omega$.

$\endgroup$

3

$\begingroup$

Рассмотрим вращение твердого тела в отсутствие каких-либо внешних сил или моментов. Если угловой момент удовлетворяет $$ \vec{L} \propto I \vec{L}, $$ то момент количества движения $\vec{L}$ останется постоянным во времени (в системе отсчета тела). Если $\vec{L}$ — собственный вектор с наибольшим или наименьшим собственным значением, то это устойчивое равновесие. Для промежуточного собственного значения оно нестабильно.

Простейшая демонстрация этого состоит в том, чтобы повернуть книгу (или мобильный телефон, если вы будете осторожны) вокруг каждой из ее основных осей, которые, как вы предполагаете, именно такие. Книга устойчиво вращается вокруг двух осей (одной, направленной наружу от страниц книги, и другой, направленной вверх вдоль страницы), но не вокруг третьей (той, которая направлена ​​поперек страницы).

Неглавное направление вращения симметричного несферического волчка обусловлено его симметрией. Поскольку два собственных значения совпадают, больше нет шести фиксированных точек (по две на каждую ось) для эволюции $\vec{L}$. Вместо этого есть два, соответствующие вращению вокруг основной оси.