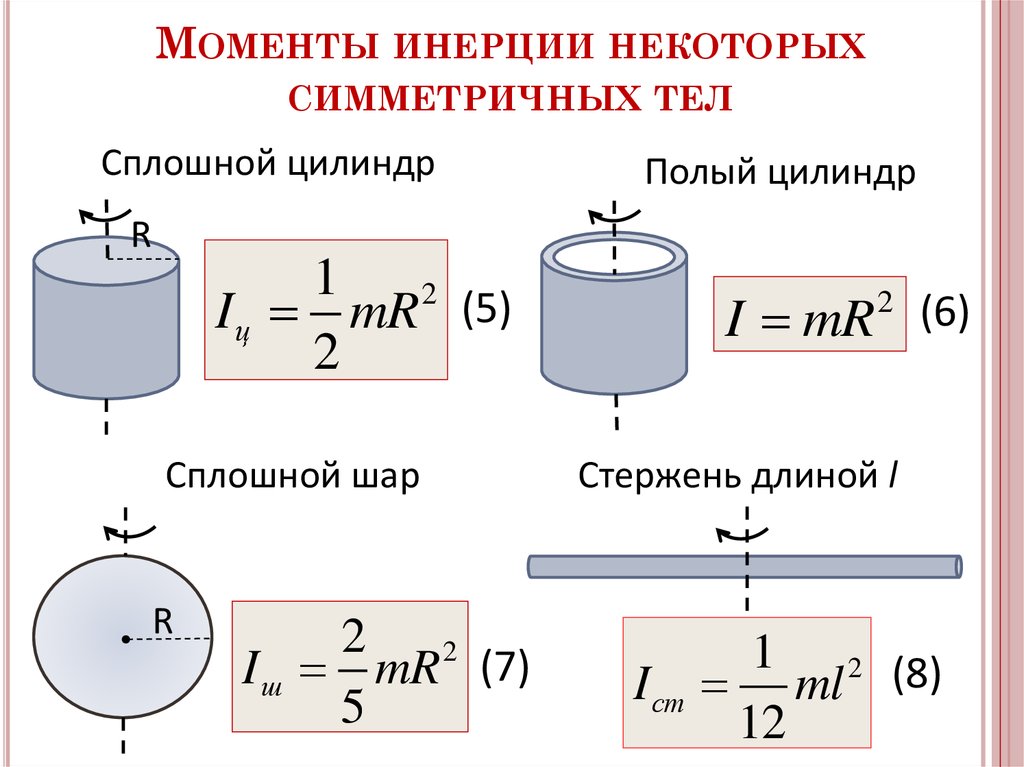
§21.Момент инерции.

Определение: Моментом инерции материальной точки относительно неподвижной оси называется скалярная физическая величина, являющаяся мерой инертности этой точки при вращательном движении и, равная произведению её массы на квадрат расстояния до оси, т.е. , а также, где- угловая скорость тела относительно данной оси.

Определение: Моментом инерции системы материальных точек относительно неподвижной оси называется скалярная физическая величина, являющаяся мерой инертности этой системы при вращательном движении и, равная алгебраической сумме произведений масс всех материальных точек системы на квадрат их расстояний до оси, т.е. .

Момент инерции определен только относительно оси.

В случае непрерывного распределения масс с плотностью сумма за­менится на интеграл по всему объему тела: (Интегрирование производится по всему объёму; пределы интегрирования устанавливаются исходя из конфигурации тела и его размеров).

Если тело однородно, то его плотность во всех точках постоянна и можно вынести из-под знака интеграла.

Найдем моменты инерции для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему, т.е. .

1. Момент инерции обручаотносительно оси, перпендикулярной к его плоскости и проходящей через его центр.

Обруч считается бесконечно тонким, т.е. толщиной обода можно пре­небречь по сравнению с радиусом R.. Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, R²можно вынести из-под знака интеграла:, где

m— полная масса обруча.

2. Момент инерции дискаотносительно оси, перпендикулярной его плоскости и проходящей через центр. Диск считается бесконечно тонким, т.е. его толщина много меньше ра­диуса R.Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей.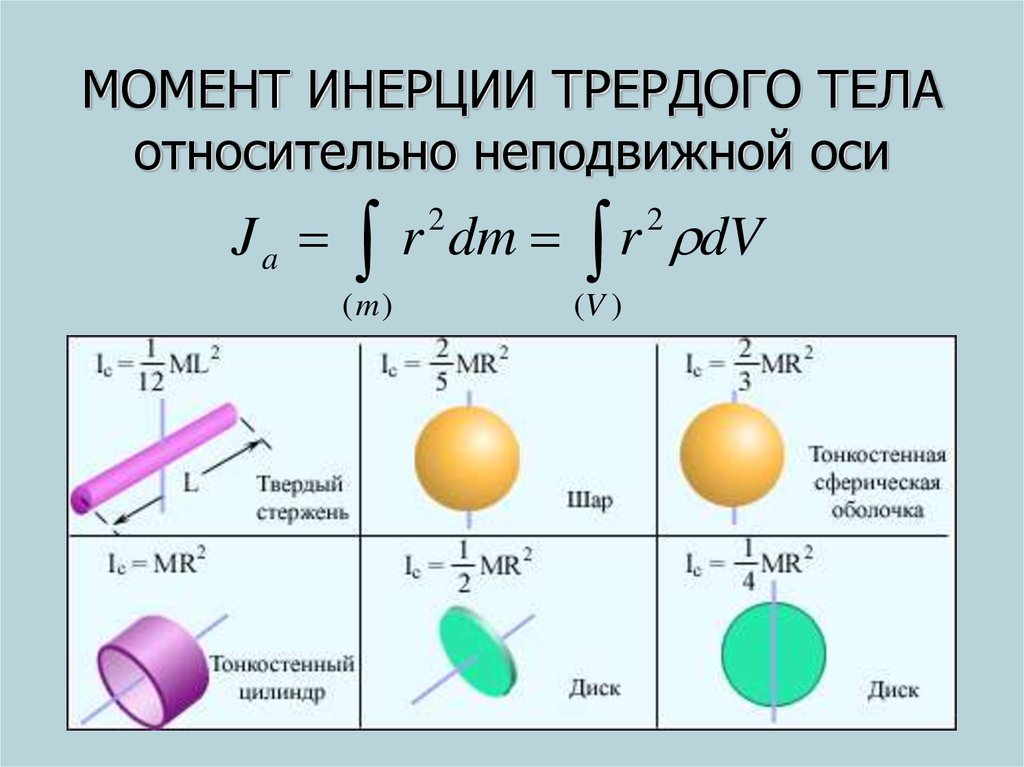 Разобьем диск на бесконечно тонкие обручи радиусомsи толщинойds (См.рис.).

Момент инерции диска относительно перпендикулярной оси, проходящей через центр.

Площадь поверхности обруча равна произведению его длины на толщину: 2  s ds.Поскольку массатдиска распределена равномерна, масса обручаdmпропорциональна площади его поверхности:

.

Момент инерции обруча мы уже знаем: . Осталось просуммировать моменты инерции всех таких обручей:.

Такой же результат получится и для момента инерции цилиндра конеч­ной длины относительно его продольной оси.

3. Момент инерции шараотносительно его диаметра. Поступим аналогичным образом: «нарежем» шар на бесконечно тон­кие диски толщинойdz.находящиеся на расстоянии

zот центра (См.рис.).

Момент инерции шара относительно диаметра.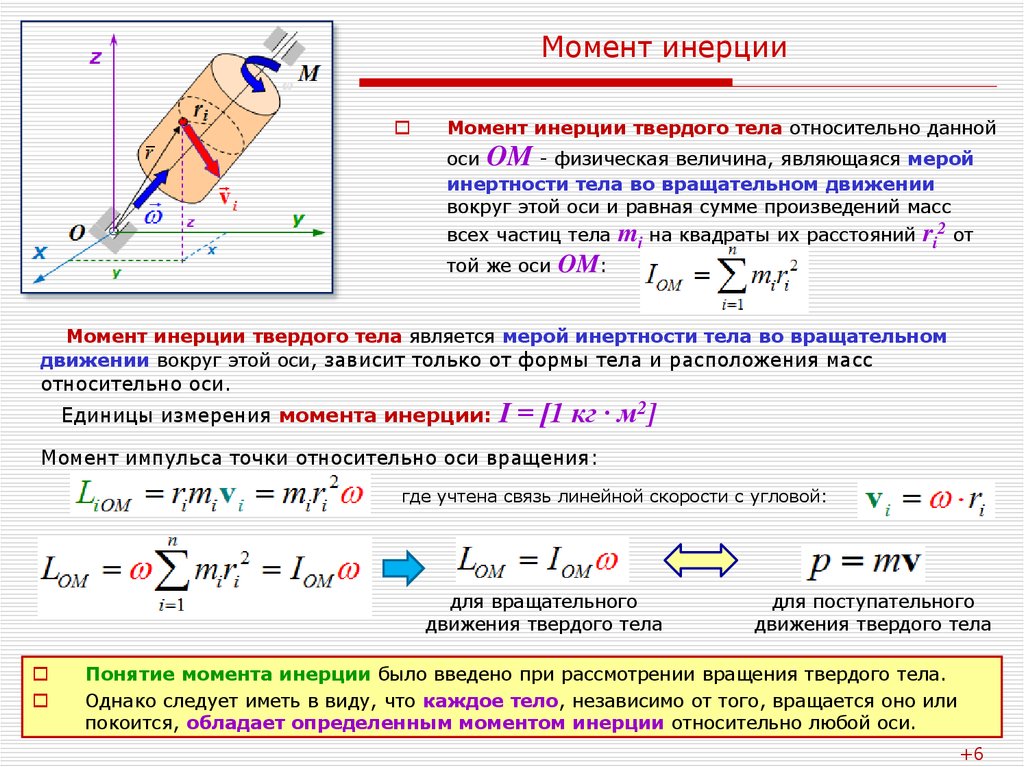

Радиус такого диска равен . Объем дискаdV_z равен произведению его площади на толщину:

. Массу дискаdmнаходим, разде­лив массу шаратна его объем, умножив на объем диска:

.

Момент инерции диска был найден выше. В применении к данному слу­чаю, он равен:

.

Момент инерции шара находится интегрированием по всем таким дискам:

4.Момент инерции тонкого стержня

относительно оси, проходящей через его середину перпендикулярно стержню.

Пусть стержень имеет длину ℓ.Направим осьxвдоль стержня. Начало координат по условию находится в центре стрежня. Возьмем эле­мент стержня длинойdx.находящийся на расстоянииxот оси враще­ния. Его масса равна

dm = (m/ℓ) dx,а момент инерцииdJ=(m/ℓ) x²  dx.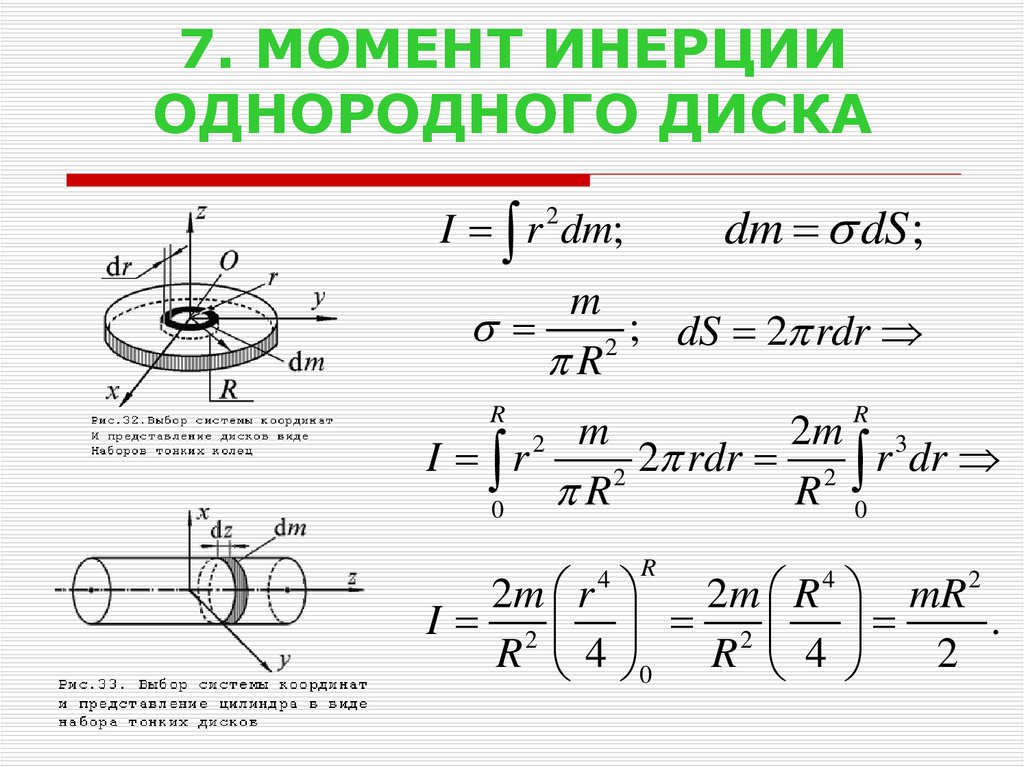 Отсюда находим момент инерции стрежня:

(*).

Момент инерции величина аддитивная, т.е. суммарный момент инерции системы тел относительно какой-либо оси, равен сумме моментов инерции каждого из тел данной системы относительно той же оси:

Физический смысл момента инерции:Инерционные свойства при поступательном движении характеризуются только массой тела, т.е. зависит только от массы. Инерционные свойства при вращательном движении характеризуются моментом инерции, т.е. зависят от его массы, расстояния до оси вращения и расположению теда по отношению к этой оси. Последнее означает, что относительно двух разных осей инерционные свойства вращательного движения одного и того же движения тела будут разными. Пример.

Момент инерции | Вращательное движение

Момент инерции – это одна из тех тем, от которых у людей иногда начинают потеть ладони и трястись коленки, поэтому сейчас нам стоит уделить ей чуть больше внимания.

Как уже было сказано в прошлом параграфе, момент инерции – это аналог массы во вращательном движении. 2}

Чем больше будет масса бусинки, тем труднее будет сдвинуть ее, это логично. Но почему момент инерции материальной точки растет по мере удаления от оси вращения?

Представьте себя лилипутом, который по какой-то неведомой причине решил сообщить бусинке из примера наверху угловую скорость \omega. Не щадя себя, вы разогнались от нуля до некоторой скорости v, после чего, достигнув своей цели, остановились, позволив шарику двигаться дальше.

Теперь увеличим длину практически невесомого стержня в два раза и проделаем тот же самый мысленный эксперимент.

Даже если предположить, что вы не упадете замертво где-то на середине дистанции и сможете бежать с таким же ускорением, как и в первом случае, вы все равно почувствуете разницу. Чем дальше шарик будет находиться от оси вращения, тем труднее будет изменить его угловую скорость, соответственно, тем больше будет его момент инерции.

Кстати, благодаря формуле, представленной наверху, сразу становится понятно, для чего нужно соблюдение всех этих странных теоретических требований. Если палочка, на которой закреплена бусинка, будет обладать большой массой, то у нее самой будет хороший момент инерции, и это усложнит расчеты. А если бусинка будет иметь большие размеры по отношению ко всей конструкции, то нам будет труднее определить, на каком расстоянии она находится от оси вращения, и это тоже усложнит нахождение момента инерции.

Вы можете сказать: «Для чего нам вообще нужен момент инерции материальной точки? Все равно, безразмерных тел в природе не существует».

Вы правы. Материальная точка – это математическая абстракция. И все-таки есть случаи, когда эта модель работает с хорошей степенью точности. Например, когда вы изучаете движение Луны вокруг Земли, вы запросто можете представить Луну в виде материальной точки и найти ее момент инерции при помощи приведенной выше формулы.

Но, конечно, вращаться могут не только материальные точки, но и другие тела. Например, можно представить, что мы имеем дело не с невесомой палочкой, а с железным стержнем массой m. 2$. Я не буду ссылаться на идеи углового момента или крутящего момента до конца, где я упомяну их определения, потому что я не хочу вести круговой спор. 9{net} \tau_i = \alpha I$

можно показать тем же способом.

Большие вопросы, связанные с этим: Почему Крутящий момент важен и почему он так сильно отличается от всего, что было изучено ранее? Кроме того, когда следует использовать крутящий момент, в отличие от законов Ньютона и кинематических уравнений?

Ответ на первый вопрос:

В большинстве вводных курсов физики инерция вводится сразу после главы о центре масс, которая следует за несколькими главами о движении твердых тел, в которых каждая частица движется с одним и тем же общим движением. Уравнения кинематики можно применять к твердым объектам из предыдущих глав, потому что каждая частица в объекте движется примерно с той же скоростью, что и любая другая частица в объекте. Когда вы дойдете до глав о центре масс, это уже не так, но из-за природы центра масс кинематические уравнения все еще могут применяться.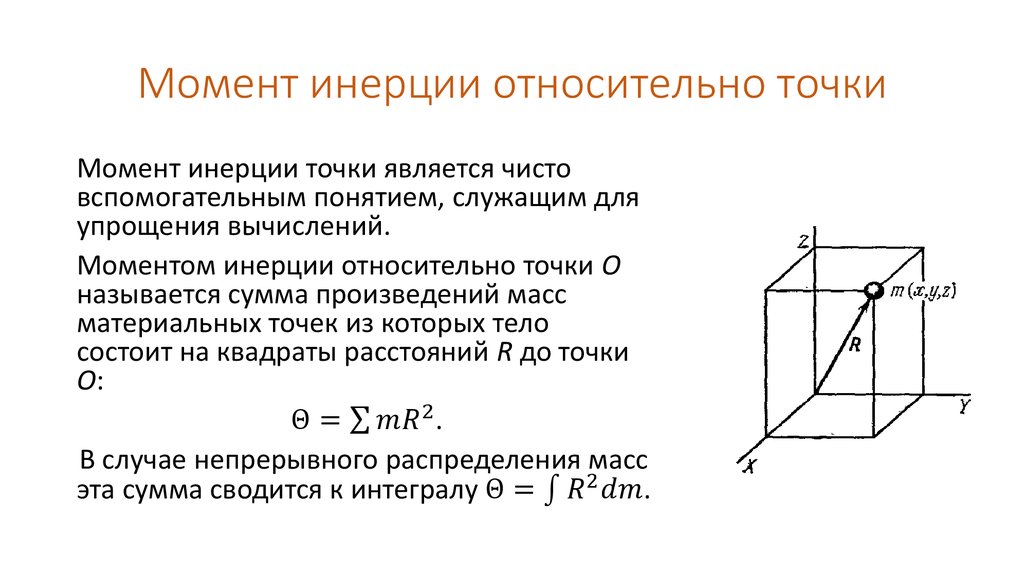 2$, заключается в том, что одна из величин $r$ исходит из того факта, что $a_T = r \alpha$, где $a_T$ — тангенциальное ускорение. . Другой исходит из того, что $s = r \theta$. Поскольку крутящий момент является производной от $W_R$ по $\theta$, а не по $s$, $r$ из $s = r \theta$ остается в уравнении. Инерция также становится вдвойне полезной для нас, потому что она также присутствует в расчете кинетической энергии вращения, и поэтому теперь это полноценное понятие со своим именем и страницей в Википедии.

Момент инерции Определение и значение

• Основные определения
• Викторина
• Примеры
• Британский
• Научный

Показывает уровень сложности слова.

Сохрани это слово!

Показывает уровень сложности слова.

---

сущ.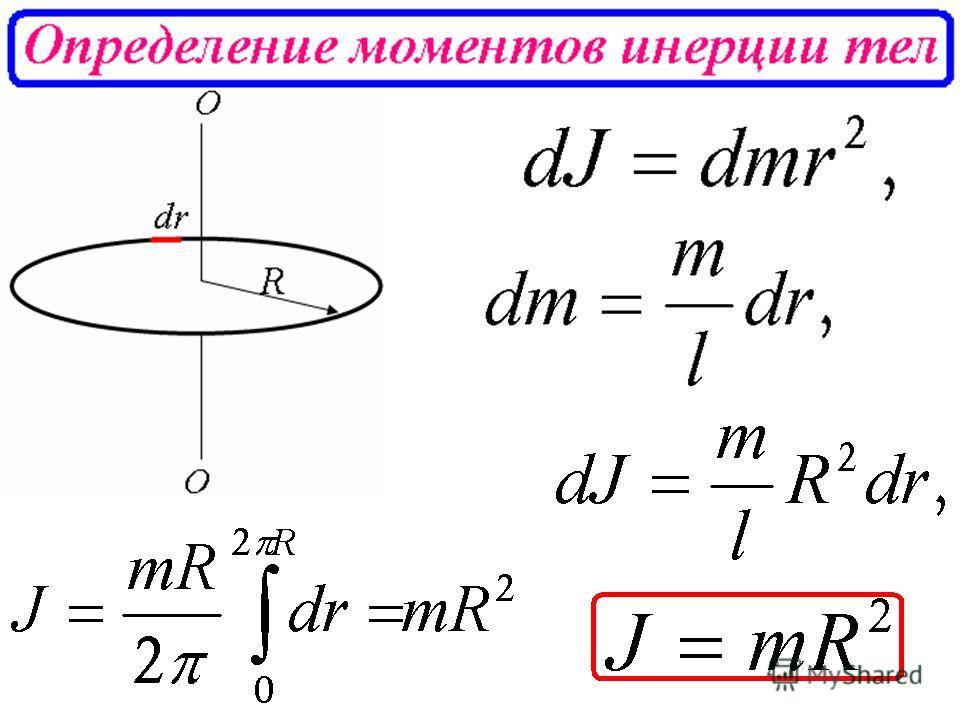 Физика.

сумма произведений массы и квадрата расстояния по перпендикуляру к оси вращения каждой частицы в теле, вращающемся вокруг оси.

ВИКТОРИНА

ТЫ ПРОШЕШЬ ИЛИ НАТЯНУСЬ НА ЭТИ ВОПРОСЫ ПО ГРАММАТИКЕ?

Плавно переходите к этим распространенным грамматическим ошибкам, которые ставят многих людей в тупик. Удачи!

Вопрос 1 из 7

Заполните пропуск: Я не могу понять, что _____ подарил мне этот подарок.

Происхождение момента инерции

Впервые записано в 1820–1830 гг. свекровь

Dictionary.com Полный текст На основе Random House Unabridged Dictionary, © Random House, Inc. 2023

Как использовать момент инерции в предложении

• В этой стране в тот момент католики практически исчезли.

  Зажигательный роман Уэльбека представляет Францию ​​с президентом-мусульманином|Пьер Ассулин|9 января 2015|DAILY BEAST

• Но Краусс сказал, что с того момента, как он и другие ученые прибыли на остров, они никогда не видели ничего неблагоприятного.

  Двойная жизнь неряшливого миллиардера: пляжные вечеринки со Стивеном Хокингом | М.Л. Nestel|8 января 2015 г.|DAILY BEAST

• Расправа над карикатуристами во французском журнале Charlie Hebdo — момент кристаллизации.

  Почему мы поддерживаем Charlie Hebdo — и вы тоже должны|Джон Авлон|8 января 2015 г.|DAILY BEAST

• На данный момент единственный шанс, который у меня есть, — это когда я иду сниматься в «Поздней ночи» с Сетом Мейерсом.

  Кофейная беседа с Фредом Армисеном: о «Портландии», встрече с Обамой и величии Тейлор Свифт | Марлоу Стерн | 7 января 2015 г. | DAILY BEAST

• А потом я встретил его до того, как начал производить впечатление о нем, когда он на мгновение был гостем на SNL.

  Кофейная беседа с Фредом Армисеном: о «Портландии», встрече с Обамой и величии Тейлор Свифт|Марлоу Стерн|7 января 2015 г.|DAILY BEAST , а тем более размышлять об этом.

  Волна|Алджернон Блэквуд

• Это очень срочные вопросы; нашим сыновьям и дочерям придется начинать заниматься ими с того момента, как они закончат колледж.

  Спасение цивилизации|H. Г. (Герберт Джордж) Уэллс

• Ее глаза на мгновение остановились с ужасным убеждением в широком и безымянном предательстве.

  The Pastor’s Fire-side Vol. 3 из 4|Джейн Портер

• Мысль, казалось, породила страшный объект, потому что в следующий момент прямо перед ним появился большой холм.

  Великан Севера|Р.М. Ballantyne

• В этот момент среди часов начался необыкновенный переполох.

  Davy and The Goblin|Charles E. Carryl

Определения момента инерции из Британского словаря

момент инерции

---

сущ. массы каждой частицы в теле и квадрата ее перпендикулярного расстояния от оси вращения Символ: I

Английский словарь Коллинза — полное и полное цифровое издание 2012 г. © William Collins Sons & Co. Ltd. 1979, 1986 © HarperCollins Publishers 1998, 2000, 2003, 2005, 2006, 2007, 2009, 2012

Научные определения момента инерции

момент инерции

[ mō′mənt ]

0 A 900 угловое сопротивление тела равное ускорению произведению массы тела на квадрат его расстояния от оси вращения.